Abstract
We consider a problem of hydrodynamic stability of the liquid displacement by gas in a porous medium in the case when a light gas is located above the liquid. The onset of instability and the evolution of the small shortwave perturbations are investigated. We show that when using the Darcy filtration law, the onset of instability may take place at an infinitely large wavenumber when the normal modes method is inapplicable. The results of numerical simulation of the nonlinear problem indicate that the anomalous growth of the amplitude of shortwave small perturbations persists, but the growth rate of amplitude decreases significantly compared to the results of linear analysis. An analysis of the stability of the gas/liquid interface is also carried out using a network model of a porous medium. It is shown that the results of surface evolution calculations obtained using the network model are in qualitative agreement with the results of the continual approach, but the continual model predicts a higher velocity of the interfacial surfaces in the capillaries. The growth rate of perturbations in the network model also increases with decreasing perturbation wavelength at a constant amplitude.
MSC:
35Q35; 35B35
1. Introduction
Stability of filtration flows with liquid/gas interfaces in rocks and soils has been studied both analytically and numerically in a large number of works. These problems are of great practical interest. Gas drainage is considered as an effective method to enhance oil recovery (see [1,2,3,4]). The efficiency of oil/water or oil/gas displacement depends on the stability of the interface between the oil-saturated region and the region containing displacement fluid (gas) [5]. An increase in the concentration of impurities and contamination of groundwater occurs when groundwater evaporates, as well as when the boundary between fresh water and solutions is unstable [6,7,8,9]. Another example where this instability plays a significant role is geothermic systems. In many cases, their existence can be explained by convective heat transfer to the surface of the Earth due to the instability of the interfaces between regions saturated with water, steam, and a steam–water mixture inside high-temperature rocks [10,11,12,13,14,15]. The problem of the stability of the water layer in the soil located above the air-saturated region was studied in [13,16] in relation to artificial underground structures. The occurrence of instability of the oil–gas interface during oil extraction from a field with a gas cap was investigated in [17].
These studies were provided by the use of the continual hydrodynamic approach. It was assumed that the filtration process is described by Darcy’s law, and there is a narrow region that separates the gas and liquid region determined by some surface equation. It was shown in the linear approximation within the use of the normal mode method that for a given amplitude of the interface perturbation there is a certain range of parameters where the rate of growth of the amplitude increases indefinitely with decreasing wavelength [13,14,15,16].
This fact casts doubt on the applicability of the Darcy equation in the context of studying the onset of instability, as well as determining geometric characteristics of the finger-like structures of a liquid or gas. In [18] the stability of oil flow in a collector with a gas cap was studied under the assumption that oil motion obeys the Brinkman law. Within the normal mode analysis, it was established that the growth rate of short wave perturbations tends to zero with increasing wavenumber.
In recent times, pore-network modeling has been used increasingly to study water imbibition and drainage in porous media. Relative permeability studies conducted using the pore-scale network models have shown that the obtained results are in qualitative agreement with the data of laboratory measurements (e.g., see [19,20,21,22,23,24,25]. In [26], a network approach to the modeling of non-Newtonian rheology was used to understand some of the more detailed features of polymer flow in porous media. This approach provided a mathematical bridge between the behavior of the non-Newtonian fluid in a single capillary and the macroscopic behavior as deduced from the pressure drop–flow rate relation across the whole network model. In [27], the network approach was presented which simulates 2-phase oil/water displacement during water imbibition. In [28], a pore-network model of the shale matrix was developed and used to simulate CO2 migration in organic-rich shale formations. The pore space is modeled as a set of pore bodies connected by pore throats. An imbibition efficiency calculation method was proposed in [29]. The acyclic pore model was improved and was used to study how the pore structure affects imbibition performance. An analytical analysis of the relationship between the pore-scale forces and the Darcy-scale pressure drops was presented in [30]. An extensive and detailed discussion of the application of network models can be found in [31,32,33].
In this work, we study the evolution of perturbations of the gas/oil contact surface with a decrease in pressure in an oil-saturated region and compare the results obtained within continual and network models of a porous media. When a liquid is displaced by a gas in a porous medium, the gas–liquid interface is linearly unstable within the continuum model using Darcy’s law (see, for example, [17]). The rate of growth of interface perturbations increases indefinitely with decreasing wavelength at a constant amplitude of the perturbation. Below, we show that linear analysis is not applicable in this case, and we will use the numerical solution. The results of the numerical solution also show that the perturbation growth rate increases without limit with decreasing wavelength. In this case, the use of the continuum model is impossible without modification, which requires studies using direct numerical simulation on the pore scale. Therefore, we use simple network models to identify the physical mechanisms that can help achieve successful modeling of the interface motion. This paper is organized as follows: Section 2 contains the formulation of the problem within the framework of the continual model using Darcy’s law. We show that the linear approximation is inapplicable for determining the growth rate of short-wave perturbations. In Section 3, we study the wavelength dependence of the growth rate of short-wave perturbations using a numerical approach in the framework of the continual model. In Section 4, a similar problem is studied within the network model of porous media. Section 5 contains a discussion of the obtained results and conclusion notes.
2. Formulation of the Problem
We consider the problem of oil extraction from the field with a gas cap. Assume that the gas cap is separated from the oil-saturated reservoir by a horizontal interface. When producing oil located under the gas zone, the pressure in the oil reservoir decreases, and the interface moves down. If the motion of the interface is unstable, gas breakdown may occur in the direction of the production well. In this case, regions saturated with immobile oil are formed. Thus, the study of the instability of filtration flows with a gas/liquid interface is an important issue when developing a field with a gas cap.
In recent years, gas gravity drainage technology has been widely used worldwide (see [1,2,3,4]). The flow diagram is shown in Figure 1 and is a simplification of the real-life example with the horizontal interlayer. Let a horizontal layer of a porous homogeneous medium be located over a high-permeability layer with constant pressure . This layer models a horizontal production well or a hydraulic fracture. For the considered problem of the evolution of interface perturbations, the pressure may be assumed to be constant, since the permeability of this layer is several orders of magnitude higher than the permeability at z > 0. The problem is solved in Cartesian coordinates with the axis z pointing upwards. In the low permeable layer at ( region) there is a liquid, and the region ( ) is filled with gas with constant pressure . Here, t is time and is the z-coordinate of the interface. The horizontal coordinate x varies in the range .
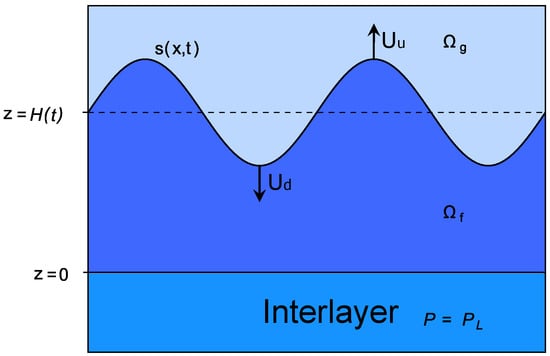
Figure 1.
The computational domain used for the Darcy scale numerical simulation. is the low-permeability liquid region, the gas region. The highly permeable layer (the interlayer) is located at .
At the gas/liquid interface, pressure jumps so that the pressure drop equals to the capillary pressure
Here, the capillary pressure is negative if the rock is wettable and positive otherwise. Similar to [17], we assume that capillary pressure depends on the vertical coordinate z.
In the region , the continuity equation is valid, and we assume that Darcy’s law is satisfied
Here, is the average pore velocity, m the ratio between the pores’ area and the total cross-sectional area, k the permeability, the viscosity of the liquid, g the gravity, and the density of the liquid. From Equation (2), it follows that the pressure inside the region satisies the Laplace equation
We neglect the evaporation of the liquid at the contact surface, so there is no mass flow through the gas/liquid interface. Therefore, the equation for the normal component of local velocity of the contact surface takes the form
Similar equations have been used in [17].
Figure 1 presents the large-scale (Darcy scale) flow through porous media. The real gas/liquid interface is located in pores. If most of the moving interface are belonged to some narrow region between gas-dominated and liquid-dominated zones, this region may be approximated by the surface [14,15] as shown in Figure 1. This surface has a radius of curvature, but this radius is not used to calculate surface tension.
We write the problem equations and boundary conditions
We introduce variable L with the dimension of length so that and define dimensionless variables
We transform the relations (5) to the form
If the contact surface is flat and perpendicular to the axis , then problem (6)–(9) has the solution independent of the coordinate
where is the coordinate of the flat gas/liquid interface.
In [16,17], the evolution of the infinitesimal harmonic perturbations of the solution (10)–(11) was studied by the normal mode method, and expression is obtained for the growth rate of the amplitude of the perturbation of the interface
where K is the wavenumber of perturbation, is its amplitude, and is given by
If , then the amplitude of perturbations increases. In the case , we obtain
In the limit we obtain
The relationship (15) predicts an arbitrarily large growth rate with increasing K for any given amplitude. This result contradicts the physical essence of the process under consideration. This problem has been repeatedly pointed out in [13,17] and others.
The relation (15) is obtained under the assumption that
Since
and
the condition (16) leads to
From inequality (17) and relation (15), we then obtain that in the limit
From expression (18), it follows that the growth rate of the amplitude is limited when condition (15) is valid. Inequality (18) is the condition for the applicability of the linear approximation. Thus, in the range of applicability of linear approximation, Darcy’s law does not lead to unphysical values of the growth rate of the perturbation and the filtration rate.
Since the linear analysis of stability is inapplicable when the amplitude of the perturbations and wave length are of the same order of magnitude, we will study the evolution of the perturbation numerically.
3. The Rate of Change of the Amplitude of the Harmonic Disturbance in the Nonlinear Case
We consider the wavelength dependence of the rate of change of the amplitude of the harmonic perturbation without using the linear approximation. We will use the system of Equation (5) assuming that the capillary pressure is constant. In this case, in all relations used, the value enters only in combination . Hence, without loss of generality, we can set . In [16], it has been shown that gravity does not affect the evolution of perturbations, so in what follows we will consider the system of equations
where . Consider the evolution of the perturbations of the main flow. The main flow is described by the equations
Here, is the coordinate of the flat gas/liquid interface.
In [34], a numerical–analytical method was proposed for evaluation of the filtration flow with gas/liquid interface under the assumption that the contact surface is infinitely thin, i.e., is a discontinuity. The Laplace Equation (3) for pressure is solved using the boundary element method. In a numerical calculation, the gas/liquid interface is a broken line composed of segments. The numerical method is described in detail in [34]. This method allows accurate and robust computation of the evolution of a multiply connected boundary of a water-saturated region in a porous media (see, e.g., [16,35,36,37]).
We set , , and and . Then, we set the coordinate of the perturbed gas/liquid interface according to the expression
The pressure on the interface is assumed constant, so the liquid velocity is directed along the normal to this surface and is equal to the normal component of this surface’s velocity. In the absence of perturbations, the flat interface would remain flat and move along the axis z with velocity . We denote by the normal velocity of the interface in the reference frame moving along axis z with velocity . For the velocity of the surface at the vertices of perturbations, we introduce notations and so that
as shown in Figure 1.
Figure 2 and Figure 3 show the normal velocity of various points of the contact surface for the wave lengths and . The results in Figure 2 were obtained for the amplitude value , so that condition (17) is satisfied. In this case, the dependency of velocity on the coordinate x can be approximately described by the linear result . The growth rates of the amplitudes upwards and downwards differ insignificantly.
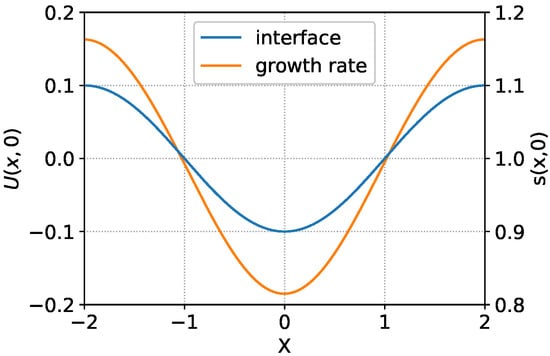
Figure 2.
The interface (blue line) and growth rate (orange line) of the perturbations. Perturbation wave length is , its amplitude is .
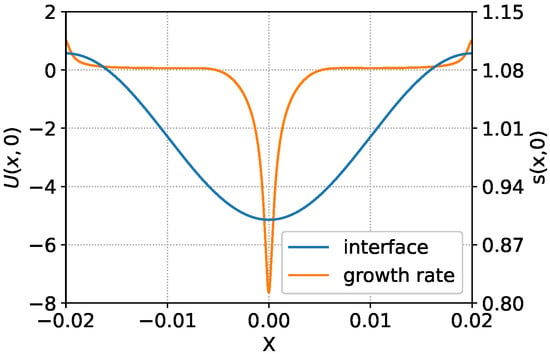
Figure 3.
The interface (blue line) and growth rate (orange line) of the perturbations. Perturbation wave length is , its amplitude is .
Figure 3 corresponds to , so condition (17) is violated. In this case, the dependency of velocity on the coordinate x differ significantly from the dependency shown in Figure 2. The growth rate of the amplitude upwards and downwards differ by more than seven times, and the velocity of the surface is close to zero outside the narrow regions in the vicinity of maximum and minimum points of the perturbation profile.
Figure 4 and Figure 5 show the dependencies of the growth rate of perturbations amplitude and on the ratio . It can be seen from Figure 4 that for the calculated values of the amplitude growth rate upwards and downwards differ insignificantly and are in good agreement with the results obtained in the linear approximation. If (see Figure 5), the growth rate is close to one. This means that the upper vertex of the perturbation profile stops, since the velocity of the interface as a whole is equal to −1. The downwards growth rate (blue line) increases linearly with , although significantly slower than linear analysis predicts (green line).
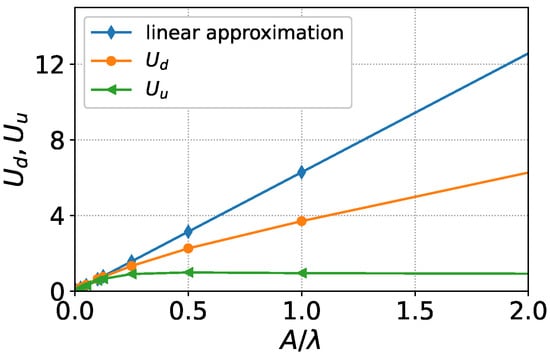
Figure 4.
Dependence of (orange line) and (green line) on the ratio . The blue line shows the linear approximation results.
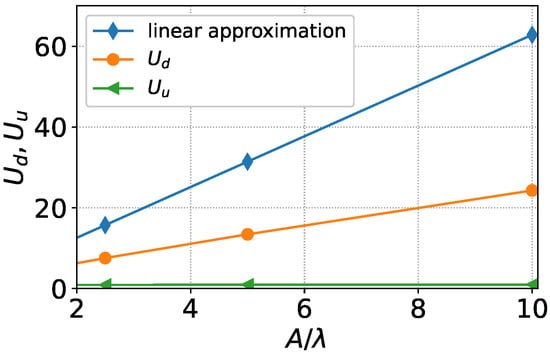
Figure 5.
Dependence of (orange line) and (green line) on the ratio . The blue line shows the linear approximation results.
From these results, it is clearly seen that the anomalous growth of short-wave perturbations is preserved in the nonlinear case.
If we introduce surface tension at the gas/liquid interface, then in the linear approximation, perturbations with a wavelength less than a certain threshold value decay, and the instability is not anomalous. In a porous medium at the pore scale, the gas / liquid interface cannot be represented as a smooth surface, since the movement occurs within individual capillaries. In this case, effective surface tension related to the curvature of the interfacial surface can only be introduced formally. Consider whether there is an unlimited increase in the growth rate of the perturbation amplitude with reduction of the wavelength, taking into account the microscopic features of the gas/liquid interface movement. To analyze the fundamental physical effects arising in this case, we will use the network model of porous media.
4. The Network Model of a Porous Medium
We represent a porous medium as a system of intersecting capillaries, as shown in Figure 6. Such a two-dimensional structure was proposed in [26] and used in [27] to calculate oil displacement by water. We assume that the gas–liquid interface in a pore throat is a simply connected surface. There is no the liquid behind the interface in a pore throat. All capillaries of the structure in each of the direction have the same length . We assign indices to each node so that its coordinate can be evaluated from relations and . Assume that the velocity of the liquid depends on the length of the capillary, the pressure on its ends and a parameter . The latter is determined via the diameter and other properties of the capillary. There is a drop of pressure on the gas–liquid interface. This pressure drop equals the capillary pressure (see Equation (1)). If capillary pressure is constant, we may add the capillary pressure to the gas pressure Pa and ignore for the sake of simplicity.
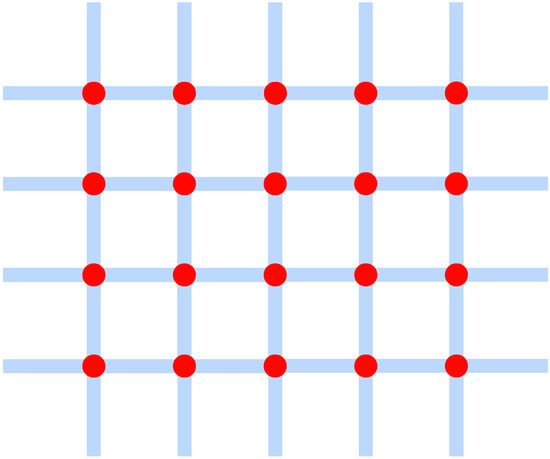
Figure 6.
The network model of a porous medium.
We introduce the variable that equals one if the node is filled with liquid, and zero if it is filled with gas. In what follows, we will assume that each node filled with gas is connected to the gas cap by capillaries (also filled with gas). In this case, the pressure in each such node is .
The velocity of the liquid in the vertical capillary connecting nodes and is given by the relation
where is the z-coordinate of the gas/liquid interface inside the capillary connecting nodes and .
Similarly, we calculate the velocity of the liquid in the horizontal capillary connecting nodes and with relations
Here, is the x-coordinate of the gas/liquid interface inside the capillary connecting nodes and .
We assume that the liquid does not accumulate inside the nodes. Hence, we obtain the conservation relation
Substituting the expressions for v and u (23), (24) into Equation (25) with we obtain
The continuous analog of Equation (26) is
Equation (27) is equivalent to Equation (3), so the latter is approximated by Equation (26).
To determine the velocity of the gas/liquid interface, we need to calculate the liquid velocities in those capillaries that are not completely filled with liquid, as shown in Figure 7.
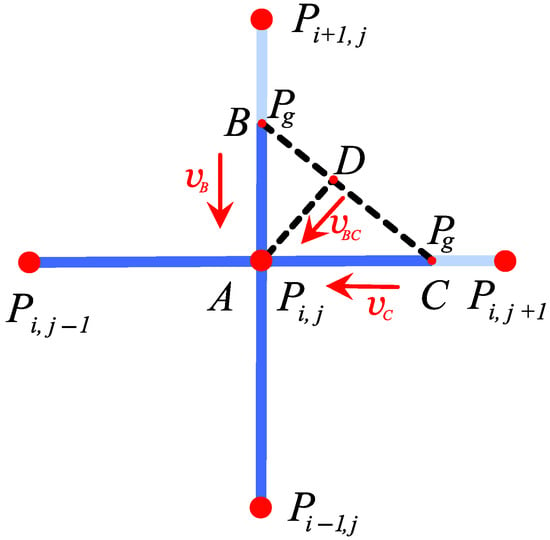
Figure 7.
Diagram of the gas/liquid interface motion in capillaries.
Inside the capillary, connecting nodes and , shown in Figure 7, liquid between points A and B have the velocity
where is the distance between points A and B. Similarly, the gas/liquid interface at the point C between nodes and has the velocity
where is the distance between points A and C.
If the stencil shown in Figure 7 is used to solve the continual model system (19) numerically, then the last equation of this system implies that the normal velocity of the interface is determined by the expression
where
The intersection point of the segment with the vertical capillary connecting nodes and moves with velocity
and the similar point on the horizontal capillary connecting nodes and moves with velocity
From these expressions, it follows that
so the network model under consideration predicts a lower interface propagation velocity than the continual model does.
The exception is when the interface is parallel to the capillaries, as shown in Figure 8. In this case, both of the models give the same value of the interface velocity
However, significant differences between the network and continual models remain. Within the network model, the velocity of the liquid in vertical capillaries is , while in horizontal capillaries the liquid is at rest. The liquid inside horizontal capillaries is not displaced by gas when the contact surface moves, as shown in Figure 8. On the other hand, the continual model assumes complete liquid displacement.
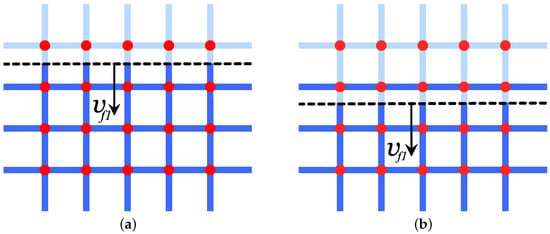
Figure 8.
The network model and gas/liquid interface at (a) and (b).
If the flat contact surface is located relative to the capillaries, as shown in Figure 9, then the liquid velocity in any capillary is
The z-component of this velocity, i.e., normal velocity of the line segment connecting the interface points, is
In this case, the liquid is displaced from all capillaries located above this line.
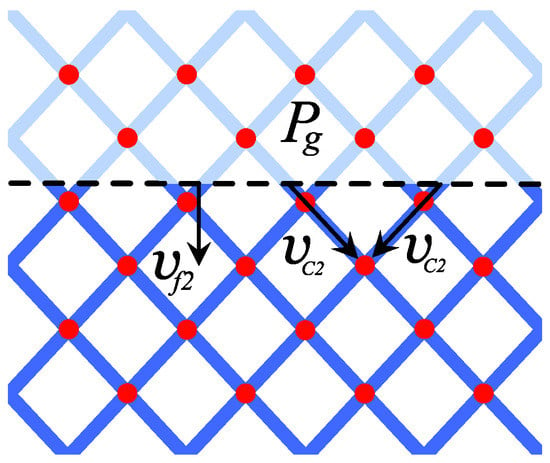
Figure 9.
The network model and gas/liquid interface.
Thus, the considered capillary model exhibits strong anisotropy. The velocity of the flat contact surface can vary by a factor of two depending on the angle between the direction of interface propagation and the capillaries. The average mass flux in the direction of the z-axis is the same in both models. In this sense, the considered network model is isotropic. In the case shown in Figure 8, the contact surface has twice the velocity as in the case shown in Figure 9; however, in the first case, only half of the liquid is displaced.
When the shape of the gas/liquid interface is not flat, the problem reduces to the numerical solution of the system of the linear algebraic Equation (26). The number of equations in the system is equal to the number of nodes with unknown pressure.
This system has a sparse band matrix with five non-zero elements in each row, three of which are on and on either side of the main diagonal. We use the library SuperLU to solve this system of linear algebraic equations (SLAE) numerically.
We consider the case , , , and . Within the linear approximation, the growth rate of the perturbation amplitude can be evaluated by the formula (14). In Figure 10, we show the results of calculating the amplitude growth rate depending on the ratio within the models mentioned above, as well as in linear approximation. The continual model predicts, as discussed above, lower velocity values.
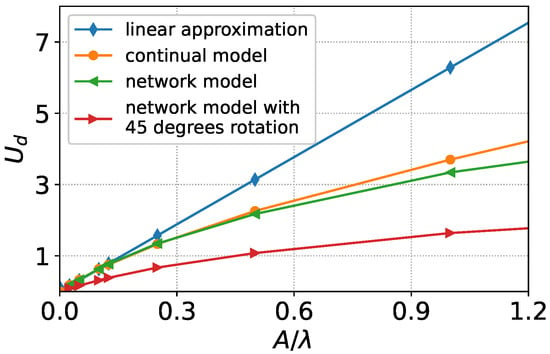
Figure 10.
Growth rate calculation results: blue line—linear approximation; orange line—continual model; green line—network model; red line—network model with 45 degrees rotation.
We show that the network model has a discrete analogue of the anomalous shortwave instability. Consider the simplified network model shown in Figure 11. The network consists of one row of nodes with vertical coordinate , and each node is connected with an interlayer by capillaries of length H. The pressure inside the interlayer is . Inside the capillaries connected to nodes from above, the height of the liquid is for the first node and for the others. The pressure at the gas/liquid interface is constant and equal to . The total number of nodes is N.
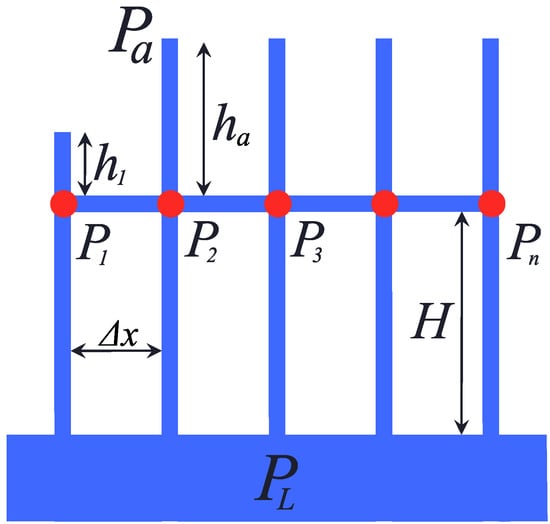
Figure 11.
Simplified network model of a porous medium with one horizontal capillar layer. The parts of the channels filled with liquid are marked with a thick line.
For the first node, we have Equation (26) in the form
For the N-th node we have
and for intermediate nodes with Equation (26) gives
In the case of from Equations (28) and (29) we obtain
If and , from (31) we obtain
where is the absolute value of the velocity of the gas/liquid interface inside the upper capillary of the first node. In the case , and , we have
From (32) and (33), it follows that the liquid velocity inside the upper capillary of node 1 increases by 1.5 times with decreasing from to 0 if the liquid height in neighboring nodes is constant and equal . The relative change of the liquid height is small compared to h.
The shortwave perturbations occurs when , , and . In this case, if , we obtain
and the value in this limiting case increases indefinetly with an increase in the number of nodes N according to the expression
Thus, the considered simplified network model with one row of nodes predicts an unbound increase in the growth rate of perturbations with decreasing wavelength.
The sophistication of the model by adding another row of nodes (see Figure 12) does not lead to a significant results change. For example, for the case shown in Figure 11 we obtain , and for the case shown in Figure 12. This estimate is made for , , , and . In the limiting case, when , , and , the result (35) stands.
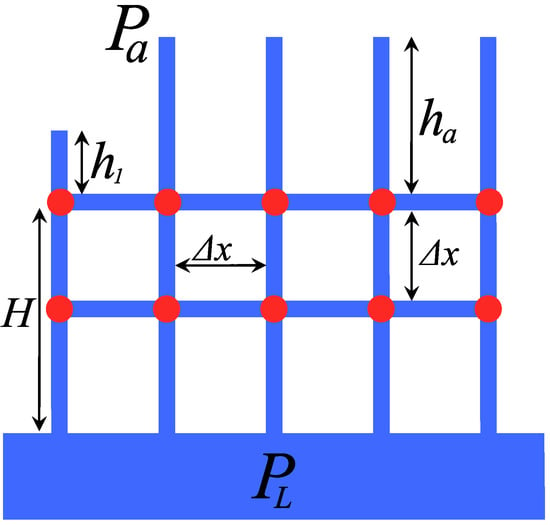
Figure 12.
Simplified network model of a porous medium with two horizontal capillary layers. The parts of the channels filled with liquid are marked with a thick line.
If the perturbation curvature radius near the perturbation vertex is comparable to the capillary length , then the height of the liquid column in neighboring vertical capillaries may vary significantly, as shown in Figure 13b. The fewer capillaries used in the network model, the greater this change. The results obtained above predict that the smaller the ratio of the heights of the liquid column in the right vertical capillary and the neighboring one, the greater the liquid velocity in the right capillary. In Figure 13a, the height of the liquid column in the right vertical capillary differs slightly from the height in the neighboring capillary. In Figure 13b, the height of the liquid column in the right capillary is several times less than in neighboring capillaries. As shown below, the calculations confirm that the interface velocities in the right capillary are significantly different for the cases shown in Figure 13a,b. We note that the positions of the perturbations differ only in the distance from the vertex to the nearest horizontal capillary filled with liquid.
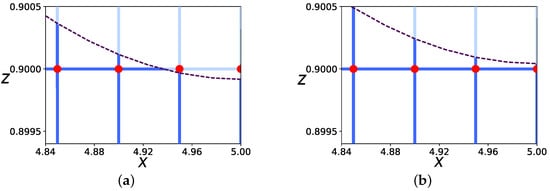
Figure 13.
Two different examples of the location of the gas/liquid interface. The vertex of interface is located below (a) and above (b) the nearest horizontal capillary.
In Figure 14, we show the dependence of the perturbation vertex growth rate on the number of capillaries per perturbation wavelength. The results are presented for two positions of the vertex of the perturbation relative to the capillaries shown in Figure 13. When the number of capillaries exceeds 300, the difference in the velocity values turns out to be less than 10%, but when the number of capillaries is 40, the velocities differ by almost a factor of two.
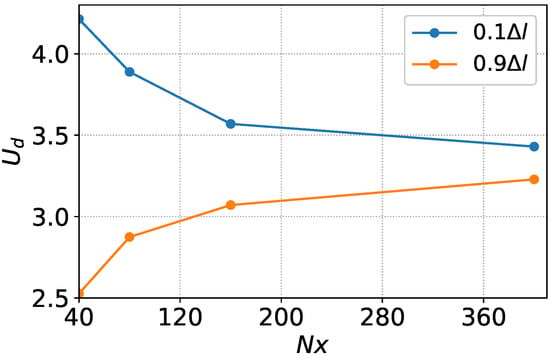
Figure 14.
Amplitude growth rate at the lower point of perturbation at , depending on the number of vertical capillaries. The upper and lower lines correspond to the cases when the size of the part of the capillary occupied by the liquid is (blue line) and (orange line), respectively (see Figure 13a,b).
5. Discussion of Results and Conclusions
An analysis of the stability of the gas/liquid interface in a porous medium under the displacement of liquid by gas has been carried out. Within the continual model using the Darcy law, it has been shown that the linear analysis of stability by the normal modes method is not applicable in the case when the wave amplitude is small compared to the characteristic dimensions of the main flow but exceeds the perturbation wavelength. The onset of the shortwave instability of solutions of the continual model has been studied within the complete model, i.e., without resorting to linearization. Such a study has been carried out using the original numerical method developed by the authors. This method allows accurate and robust computation of the evolution of perturbations of the gas/liquid interface. It has been found that the rate of amplitude growth increases with decreasing wavelength. No signs of reaching the asymptotic value have been found up to the ratio of the amplitude to the wavelength equal to 10.
The network model has also been used to study the shortwave instability as a tool for improving the understanding of the physics and micromechanics of liquid flow in a porous medium in that part of the regularities that remain outside the scope of the continual model. A model with a regular topology and a coordination number of four has been used. It has been shown that although inside the region occupied by the liquid, the equations of the network model approximate the equations of the continual model well, the movement of interfacial surfaces in capillaries is not described by the continual model. The continual model predicts a higher velocity of the interfacial surface than the network one. In this case, the network model exhibits a significant anisotropy depending on the orientation when calculating the velocity of interfacial surfaces in capillaries. In the general case, the displacement of the liquid from the capillaries occurs incompletely, and the liquid remains in a part of the capillaries even under the assumption that the instability does not onset.
The performed calculations have shown that the velocity of the interfacial surfaces in the channels also increases with a decrease in the perturbation wavelength at a constant amplitude. Thus, the considered network model, like the continual model, does not allow predicting the width of the fastest growing finger-like structures observed in the experiment and should be improved. Such improvement, which primarily takes into account the processes occurring at the intersections of capillaries and the nonuniform distribution of the coordination number, is planned to be carried out at the next stage of the study.
Author Contributions
Conceptualization, V.A.S. and G.G.T.; funding acquisition, G.G.T.; investigation, V.A.S., S.V.G. and P.I.K.; methodology, V.A.S. and G.G.T.; project administration, G.G.T.; resources, V.A.S. and G.G.T.; software, V.A.S., S.V.G. and P.I.K.; validation, Y.A.B.; supervision, V.A.S.; visualization, P.I.K.; writing—original draft, V.A.S. and G.G.T.; writing—review and editing, V.A.S., G.G.T. and Y.A.B. All authors have read and agreed to the published version of the manuscript.
Funding
The work was carried out with support from the Russian Science Foundation under the grant no. 21-11-00126.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We are grateful to four anonymous reviewers for their thorough and helpful comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rao, D.N.; Ayirala, S.C.; Kulkarni, M.M.; Sharma, A.P. Development of Gas Assisted Gravity Drainage (GAGD) Process for Improved Light Oil Recovery, SPE Improved Oil Recovery Conference, SPE-89357-MS, 2004. Available online: https://onepetro.org/SPEIOR/proceedings-pdf/04IOR/All-04IOR/SPE-89357-MS/2884931/spe-89357-ms.pdf (accessed on 17 April 2004). [CrossRef]
- Yu, H.Y.; Wang, L.; Zhou, D.; Wang, F.; Li, S.; Li, J.; Chen, X.; Cao, A.Y.; Han, H. Experimental Study on Sweep Characteristics of Gas Gravity Drainage in the Interlayer Oil Reservoir. Front. Energy Res. 2021, 9, 760315. [Google Scholar] [CrossRef]
- Lai, F.; Li, Z.; Yang, Z.; Li, H.; Guo, Z.Z. The study of components mass transfer mechanism and the rules of fluid phase alteration in the process of hydrocarbon gas drive. J. Nat. Gas Sci. Eng. 2014, 21, 411–416. [Google Scholar] [CrossRef]
- Ren, S.; Liu, Y.; Zhang, L.; Cui, G.; Gong, Z.; Wang, Y.; Han, B. Gravity Assisted Gas Injection: Assessment Model and Experimental Study. J. China Univ. Pet. (Ed. Nat. Sci.) 2018, 42, 59–66. [Google Scholar]
- Saffman, P.; Taylor, G. The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. 1958, A-245, 312–329. [Google Scholar]
- de Rooij, G. Modeling fingered flow of water in soils owing to wetting front instability: A review. J. Hydrol. 2000, 231, 277–294. [Google Scholar] [CrossRef]
- Rose, D.; Konukcul, F.; Gowing, J.; Aust, J. Effect of watertable depth on evaporation and salt accumulation from saline groundwater. Aust. J. Soil Res. 2005, 43, 565–573. [Google Scholar] [CrossRef]
- Shokri-Kuehni, S.; Raaijmakers, B.; Kurz, T.; Or, D.; Helmig, R.; Shokri, N. Water Table Depth and Soil Salinization: From Pore-Scale Processes to Field-Scale Responses. Water Resour. Res. 2020, 56, e2019WR026707. [Google Scholar] [CrossRef]
- Il’ichev, A.; Tsypkin, G.; Pritchard, D.; Richardson, C. Instability of the salinity profile during the evaporation of saline groundwater. J. Fluid Mech. 2008, 614, 87–104. [Google Scholar] [CrossRef]
- Schubert, G.; Straus, J. Gravitational stability of water over steam in vapor-dominated geothermal system. J. Geoph. Res. 1980, 85, 6505–6512. [Google Scholar] [CrossRef]
- Ramesh, P.; Torrance, K. Stability of boiling in porous media. Int. J. Heat Mass Transf. 1990, 33, 1895–1908. [Google Scholar] [CrossRef]
- Pestov, I. Stability of vapour–liquid counter flow in porous media. J. Fluid Mech. 1998, 364, 273–295. [Google Scholar] [CrossRef]
- Tsypkin, G.; Il’ichev, A. Instabilities of uniform filtration flows with phase transition. J. Exp. Theor. Phys. 2008, 107, 699–711. [Google Scholar]
- Khan, Z.; Pritchard, D. Liquid-vapour fronts in porous media: Multiplicity and stability of front positions. Int. J. Heat Mass Transf. 2013, 61, 1–17. [Google Scholar] [CrossRef]
- Khan, Z.; Pritchard, D. Anomaly of spontaneous transition to instability of liquid-vapour front in a porous medium. Int. J. Heat Mass Transf. 2015, 84, 448–455. [Google Scholar] [CrossRef]
- Shargatov, V.; Il’ichev, A.; Tsypkin, G. Dynamics and stability of moving fronts of water evaporation in a porous medium. Int. J. Heat Mass Transf. 2015, 83, 552–561. [Google Scholar] [CrossRef]
- Tsypkin, G.G. Instability of a light fluid over a heavy one under the motion of their interface in a porous medium. Fluid Dyn. 2020, 55, 213–219. [Google Scholar] [CrossRef]
- Tsypkin, G.G.; Shargatov, V.A. Linear stability of a filtration flow with gas–oil interface within the brinkman approach. Fluid Dyn. 2022, 57, 273–280. [Google Scholar] [CrossRef]
- McDougall, S.; Sorbie, K. The impact of wettability on waterflooding: Pore-scale simulation. SPE Reserv. Eng. 1995, 10, 208–213. [Google Scholar] [CrossRef]
- Blunt, M. Effects of Heterogeneity and Wetting on Relative Permeability Using Pore Level Modeling. SPE J. 1997, 2, 70–87. [Google Scholar] [CrossRef]
- Blunt, M. Pore Level Modeling of the Effects of Wettability. SPE J. 1997, 2, 494–510. [Google Scholar] [CrossRef]
- Valvatne, P.; Blunt, M. Predictive pore-scale modeling of two-phase flow in mixed wet media. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Øren, P.; Stig Bakke, S.; Arntzen, O. Extending Predictive Capabilities to Network Models. SPE J. 1998, 3, 324–336. [Google Scholar]
- Man, H.N.; Jing, X. Network modelling of wettability and pore geometry effects on electrical resistivity and capillary pressure. J. Pet. Sci. Eng. 1999, 24, 255–267. [Google Scholar] [CrossRef]
- Ryazanov, A.; Dijke, M.I.J.; Sorbie, K.S. Two-Phase Pore-Network Modelling: Existence of Oil Layers During Water Invasion. Transp. Porous Media 2009, 80, 79–99. [Google Scholar] [CrossRef]
- Sorbie, K.; Clifford, P.; Jones, E. The rheology of pseudoplastic fluids in porous media using network modeling. J. Colloid Interface Sci. 1989, 130, 508–534. [Google Scholar] [CrossRef]
- Li, J.; McDougall, R.; Sorbie, K. Dynamic pore-scale network model (PNM) of water imbibition in porous media. Adv. Water Resour. 2017, 107, 191–211. [Google Scholar] [CrossRef]
- Zhang, P.; Celia, M.; Bandilla, K.; Hu, L.; Meegoda, J.N. A Pore-Network Simulation Model of Dynamic CO2 Migration in Organic-Rich Shale Formations. Transp. Porous Media 2020, 133, 479–496. [Google Scholar] [CrossRef]
- Shen, A.; Zhang, C.; Liu, Y.; Wang, F.; Liang, S. Acyclic pore model and its applications in imbibition efficiency calculation. J. Pet. Sci. Eng. 2022, 208, 109586. [Google Scholar] [CrossRef]
- Raeini, A.Q.; Blunt, M.J.; Bijeljic, B. Direct simulations of two-phase flow on micro-CT images of porous media and upscaling of pore-scale forces. Adv. Water Resour. 2014, 74, 116–126. [Google Scholar] [CrossRef]
- Martins, A.; Laranjeira, P.; Braga, C.; Mata, T. Modeling of transport phenomena in porous media using network models. Prog. Porous Media Res. 2009, 5, 165–261. [Google Scholar]
- Hoogland, F.; Lehmann, P.; Mokso, R.; Or, D. Drainage mechanisms in porous media: From piston-like invasion to formation of corner flow networks. Water Resour. Res. 2016, 52, 8413–8436. [Google Scholar] [CrossRef]
- Wopara, O.F.; Iyuke, S. Review of studies on pore-network modeling of wettability effects on waterflood oil recovery. J. Pet. Gas Eng. 2018, 9, 11–22. [Google Scholar]
- Shargatov, V.A. Dynamics and Stability of Air Bubbles in a Porous Medium. Comput. Math. Math. Phys. 2018, 58, 1172–1187. [Google Scholar] [CrossRef]
- Tsypkin, G.G.; Shargatov, V.A. Influence of capillary pressure gradient on connectivity of flow through a porous medium. Int. J. Heat Mass Transf. 2018, 127, 1053–1063. [Google Scholar] [CrossRef]
- Shargatov, V.A.; Gorkunov, S.V.; Il’ichev, A.T. Dynamics of front-like water evaporation phase transition interfaces. Commun. Nonlinear Sci. Numer. Simul. 2019, 67, 223–236. [Google Scholar] [CrossRef]
- Shargatov, V.; Gorkunov, S.; Il’ichev, A. Stability of finite perturbations of the phase transition interface for one problem of water evaporation in a porous medium. Appl. Math. Comput. 2020, 378, 125208. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).