Investigation and Analysis of Acoustojets by Spectral Element Method
Abstract
1. Introduction
2. Mathematical Derivation of Acoustic Wave Equation
3. SEM Formulation
4. Results and Discussion
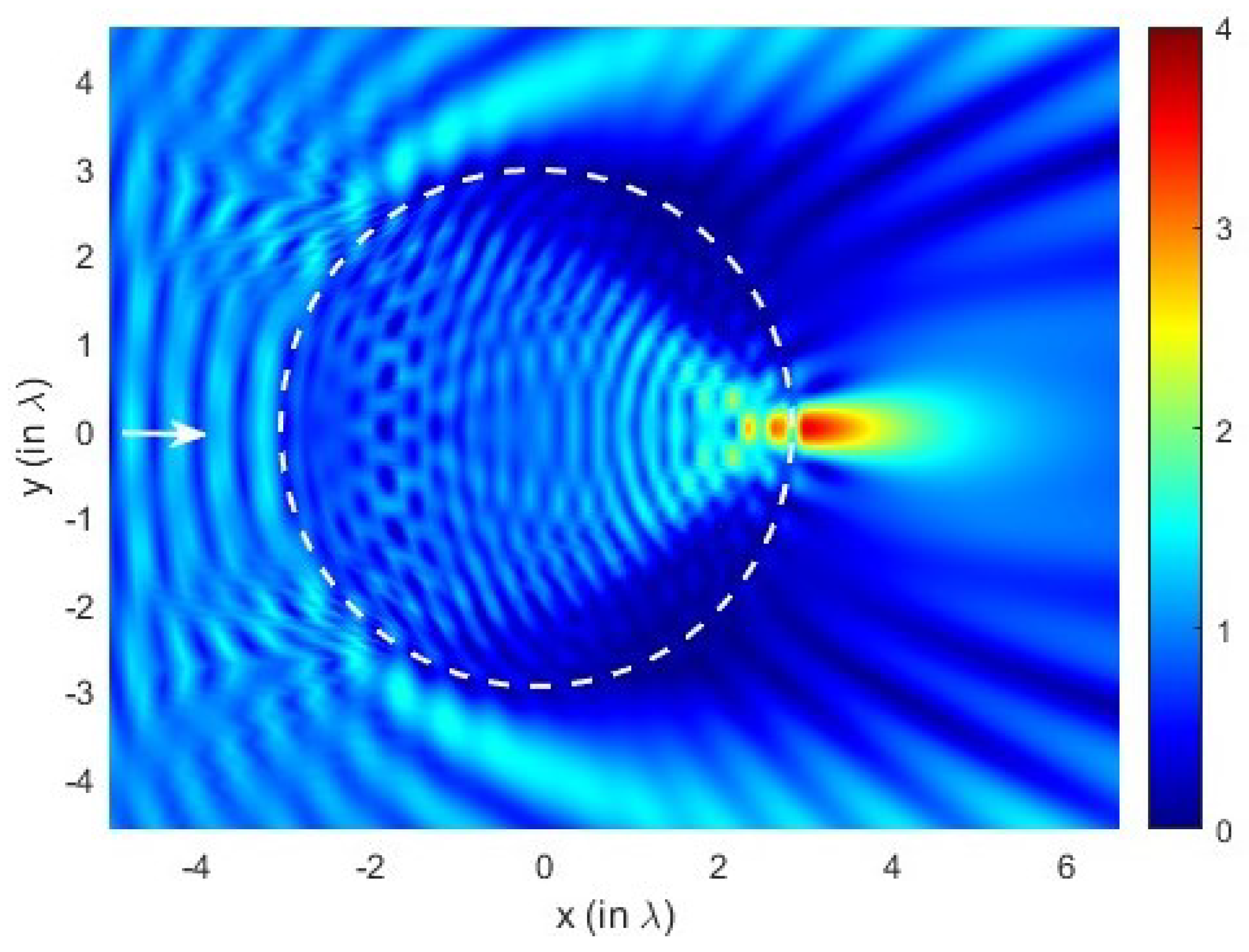

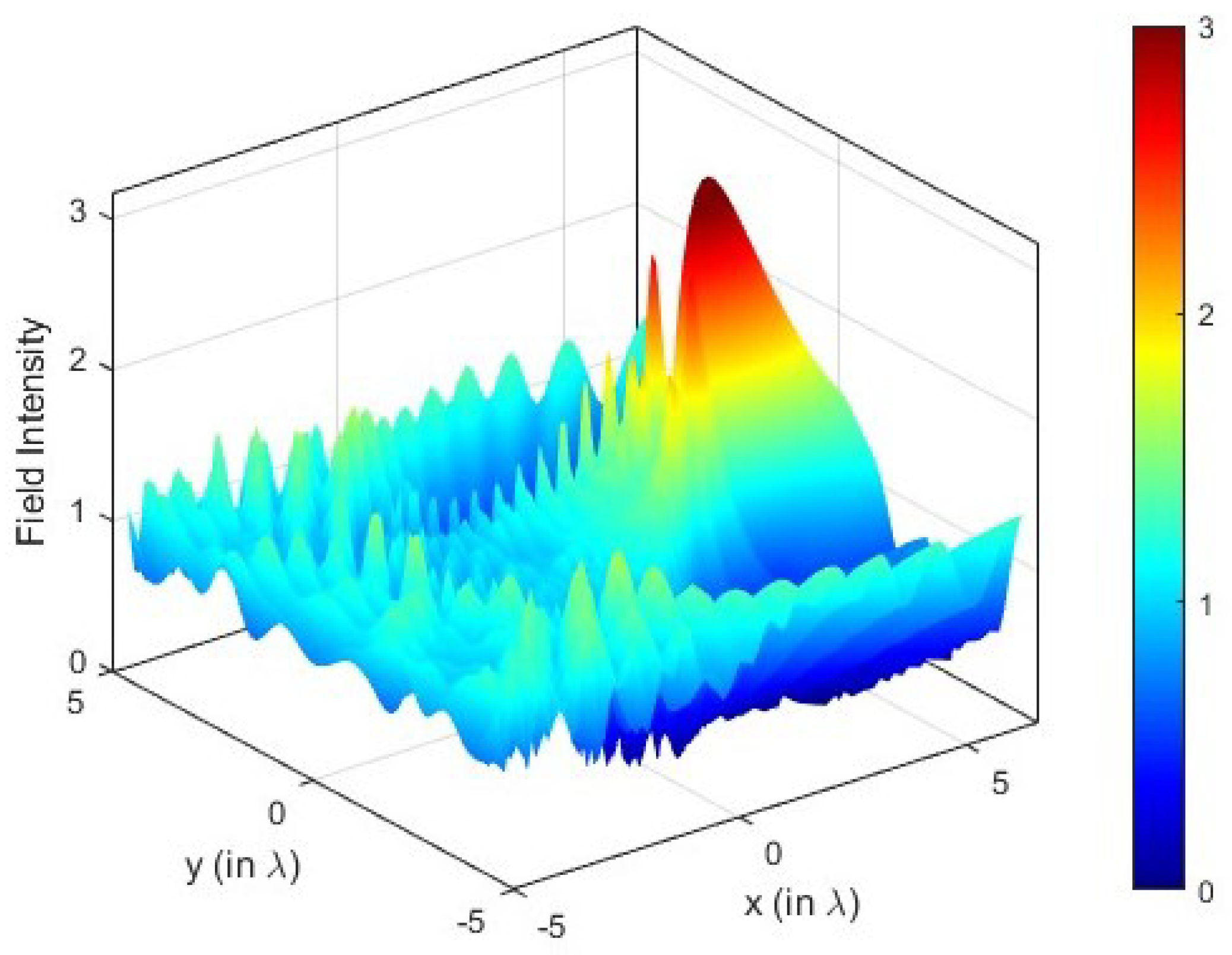
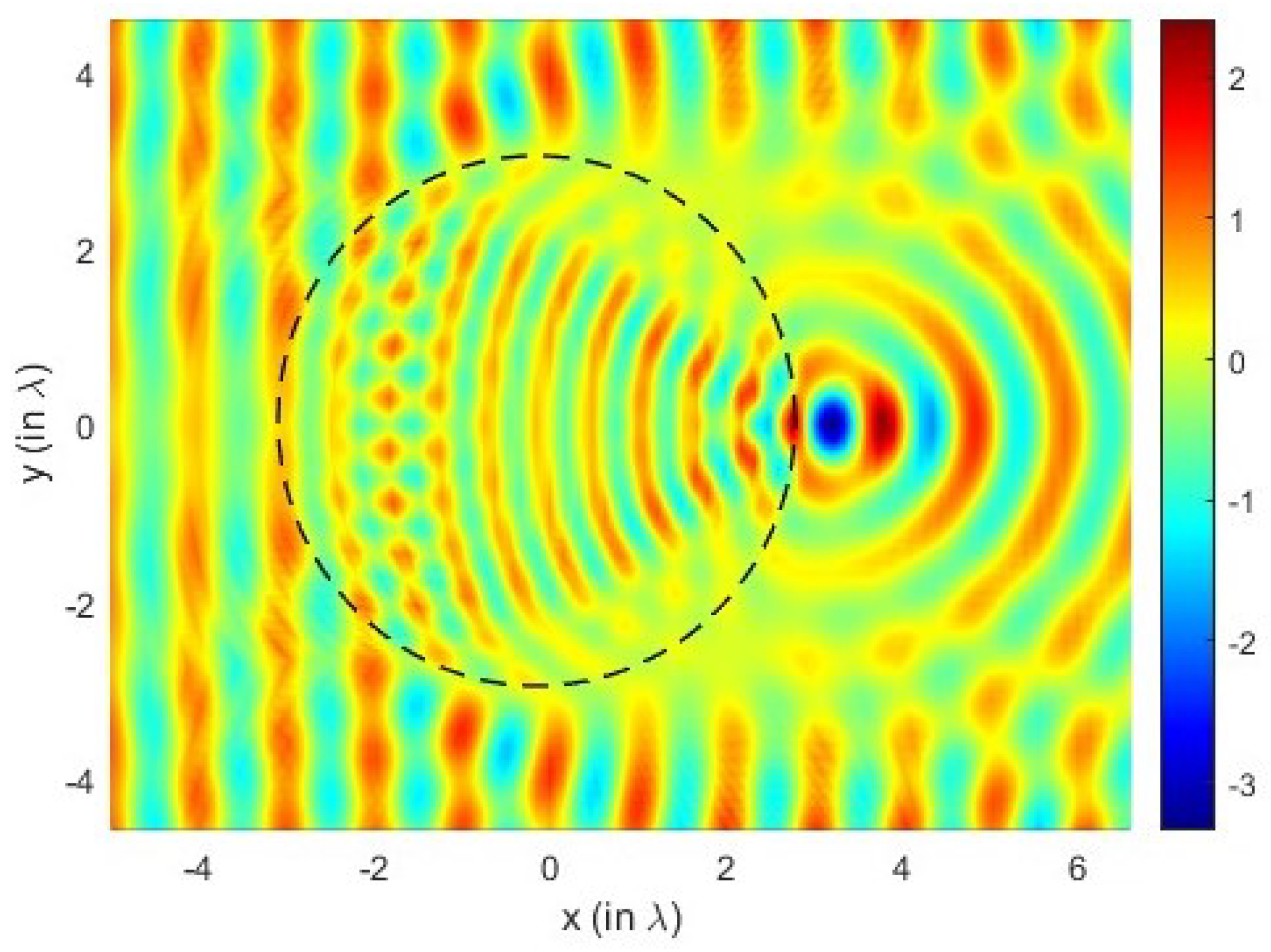
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Taflove, A.; Backman, V. Photonic nanojet enhancement of backscattering of light by nanoparticles: A potential novel visible-light ultramicroscopy technique. Opt. Express 2004, 12, 1214–1220. [Google Scholar]
- Mahariq, I.; Kuzuoğlu, M.; Tarman, I.H.; Kurt, H. Photonic nanojet analysis by spectral element method. IEEE Photonics J. 2014, 6, 6802714. [Google Scholar] [CrossRef]
- Eti, N.; Giden, I.; Hayran, Z.; Rezaei, B.; Kurt, H. Manipulation of photonic nanojet using liquid crystals for elliptical and circular core-shell variations. J. Mod. Opt. 2017, 64, 1566–1577. [Google Scholar] [CrossRef]
- Mitri, F. Ultrasonic superlensing jets and acoustic-fork sheets. Phys. Lett. A 2017, 381, 1648–1654. [Google Scholar] [CrossRef]
- Cummer, S.A.; Christensen, J.; Alù, A. Controlling sound with acoustic metamaterials. Nat. Rev. Mater. 2016, 1, 16001. [Google Scholar] [CrossRef]
- Veira Canle, D.; Kekkonen, T.; Mäkinen, J.; Puranen, T.; Nieminen, H.J.; Kuronen, A.; Franssila, S.; Kotiaho, T.; Salmi, A.; Hæggström, E. Practical realization of a sub-λ/2 acoustic jet. Sci. Rep. 2019, 9, 5189. [Google Scholar] [CrossRef]
- Zhao, L.; Horiuchi, T.; Yu, M. Broadband ultra-long acoustic jet based on double-foci Luneburg lens. JASA Express Lett. 2021, 1, 114001. [Google Scholar] [CrossRef]
- Minin, O.V.; Minin, I.V. Acoustic Hook. In The Photonic Hook: From Optics to Acoustics and Plasmonics; Springer International Publishing: Cham, Switzerland, 2021; pp. 39–53. [Google Scholar] [CrossRef]
- Castiñeira-Ibañez, S.; Tarrazó-Serrano, D.; Uris, A.; Rubio, C. Tunable acoustic hooks from Janus cylinder. Results Phys. 2021, 24, 104134. [Google Scholar] [CrossRef]
- Littlefield, A.J.; Zhu, J.; Messinger, J.F.; Goddard, L.L. Photonic Nanojets. Opt. Photonics News 2021, 32, 34–41. [Google Scholar] [CrossRef]
- Rayleigh, L. CXII. The problem of the whispering gallery. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1910, 20, 1001–1004. [Google Scholar] [CrossRef]
- Vahala, K.J. Optical microcavities. Nature 2003, 424, 839–846. [Google Scholar] [CrossRef] [PubMed]
- Matsko, A.B. Practical Applications of Microresonators in Optics and Photonics; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Mahariq, I.; Giden, I.H.; Kurt, H.; Minin, O.V.; Minin, I.V. Strong electromagnetic field localization near the surface of hemicylindrical particles. Opt. Quantum Electron. 2018, 50, 423. [Google Scholar] [CrossRef]
- Mahariq, I.; Abdeljawad, T.; Karar, A.S.; Alboon, S.A.; Kurt, H.; Maslov, A.V. Photonic nanojets and whispering gallery modes in smooth and corrugated micro-cylinders under point-source illumination. Photonics 2020, 7, 50. [Google Scholar] [CrossRef]
- Mahariq, I.; Kurt, H. Strong field enhancement of resonance modes in dielectric microcylinders. JOSA B 2016, 33, 656–662. [Google Scholar] [CrossRef]
- Mednikov, E.; Novitskii, B. Experimental study of intense acoustic streaming. Sov. Phys. Acoust. 1975, 21, 152–154. [Google Scholar]
- Lebedeva, I. Experimental study of acoustic streaming in the vicinity of orifices. Sov. Phys. Acoust. 1980, 26, 331–333. [Google Scholar]
- Thomas, D.C.; Gee, K.L.; Turley, R.S. A balloon lens: Acoustic scattering from a penetrable sphere. Am. J. Phys. 2009, 77, 197–203. [Google Scholar] [CrossRef]
- Lopes, J.; Andrade, M.; Leao-Neto, J.; Adamowski, J.; Minin, I.; Silva, G. Focusing acoustic beams with a ball-shaped lens beyond the diffraction limit. Phys. Rev. Appl. 2017, 8, 024013. [Google Scholar] [CrossRef]
- Minin, O.V.; Minin, I.V. Acoustojet: Acoustic analogue of photonic jet phenomenon based on penetrable 3D particle. Opt. Quantum Electron. 2017, 49, 54. [Google Scholar] [CrossRef]
- Patera, A.T. A spectral element method for fluid dynamics: Laminar flow in a channel expansion. J. Comput. Phys. 1984, 54, 468–488. [Google Scholar] [CrossRef]
- Maday, Y.; Patera, A.T. Spectral element methods for the incompressible Navier-Stokes equations. In State-of-the-Art Surveys on Computational Mechanics (A90-47176 21-64); American Society of Mechanical Engineers: New York, NY, USA, 1989; pp. 71–143. [Google Scholar]
- Komatitsch, D.; Tromp, J. Introduction to the spectral element method for three-dimensional seismic wave propagation. Geophys. J. Int. 1999, 139, 806–822. [Google Scholar] [CrossRef]
- Deville, M.O.; Fischer, P.F.; Fischer, P.F.; Mund, E. High-Order Methods for Incompressible Fluid Flow; Cambridge University Press: Cambridge, UK, 2002; Volume 9. [Google Scholar]
- Lee, J.H.; Xiao, T.; Liu, Q.H. A 3-D spectral-element method using mixed-order curl conforming vector basis functions for electromagnetic fields. IEEE Trans. Microw. Theory Tech. 2006, 54, 437–444. [Google Scholar]
- Lee, J.H.; Liu, Q.H. A 3-D spectral-element time-domain method for electromagnetic simulation. IEEE Trans. Microw. Theory Tech. 2007, 55, 983–991. [Google Scholar] [CrossRef]
- Lee, J.H.; Chen, J.; Liu, Q.H. A 3-D discontinuous spectral element time-domain method for Maxwell’s equations. IEEE Trans. Antennas Propag. 2009, 57, 2666–2674. [Google Scholar]
- Heikkola, E.; Mönkölä, S.; Pennanen, A.; Rossi, T. Controllability method for acoustic scattering with spectral elements. J. Comput. Appl. Math. 2007, 204, 344–355. [Google Scholar] [CrossRef][Green Version]
- Pike, E.R.; Sabatier, P.C. Scattering, Two-Volume Set: Scattering and Inverse Scattering in Pure and Applied Science; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Berenger, J.P. A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- Sacks, Z.S.; Kingsland, D.M.; Lee, R.; Lee, J.F. A perfectly matched anisotropic absorber for use as an absorbing boundary condition. IEEE Trans. Antennas Propag. 1995, 43, 1460–1463. [Google Scholar] [CrossRef]
- Werner, D.H.; Mittra, R. A new field scaling interpretation of Berenger’s PML and its comparison to other PML formulations. Microw. Opt. Technol. Lett. 1997, 16, 103–106. [Google Scholar] [CrossRef]
- Qi, Q.; Geers, T.L. Evaluation of the perfectly matched layer for computational acoustics. J. Comput. Phys. 1998, 139, 166–183. [Google Scholar] [CrossRef]
- Mahariq, I.; Kuzuoğlu, M.; Tarman, I.H. On the attenuation of the perfectly matched layer in electromagnetic scattering problems with the spectral element method. Appl. Comput. Electromagn. Soc. J. (ACES) 2014, 29, 701–710. [Google Scholar]
- Du, Y.; Zhang, J. Perfectly Matched Layers for nonlocal Helmholtz equations II: Multi-dimensional cases. J. Comput. Phys. 2022, 464, 111192. [Google Scholar] [CrossRef]
- Zhou, Q.; Xu, Z.; Liu, X. High efficiency acoustic Fresnel lens. J. Phys. D Appl. Phys. 2019, 53, 065302. [Google Scholar] [CrossRef]
- Meng, L.; Cai, F.; Li, F.; Zhou, W.; Niu, L.; Zheng, H. Acoustic tweezers. J. Phys. D Appl. Phys. 2019, 52, 273001. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahariq, I.; Giden, I.H.; Alboon, S.; Aly, W.H.F.; Youssef, A.; Kurt, H. Investigation and Analysis of Acoustojets by Spectral Element Method. Mathematics 2022, 10, 3145. https://doi.org/10.3390/math10173145
Mahariq I, Giden IH, Alboon S, Aly WHF, Youssef A, Kurt H. Investigation and Analysis of Acoustojets by Spectral Element Method. Mathematics. 2022; 10(17):3145. https://doi.org/10.3390/math10173145
Chicago/Turabian StyleMahariq, Ibrahim, Ibrahim H. Giden, Shadi Alboon, Wael Hosny Fouad Aly, Ahmed Youssef, and Hamza Kurt. 2022. "Investigation and Analysis of Acoustojets by Spectral Element Method" Mathematics 10, no. 17: 3145. https://doi.org/10.3390/math10173145
APA StyleMahariq, I., Giden, I. H., Alboon, S., Aly, W. H. F., Youssef, A., & Kurt, H. (2022). Investigation and Analysis of Acoustojets by Spectral Element Method. Mathematics, 10(17), 3145. https://doi.org/10.3390/math10173145





