Abstract
For the emergency evacuation of cruise ships in case of sudden fire, this research proposes a dynamic route optimization method based on the improved algorithm for real-time information, in order to obtain the real-time optimal evacuation route. Initially, a basic network topology diagram is established according to the internal structure of the cruise ship. Before the occurrence of the accident, the algorithm can be applied to obtain an a priori evacuation network consisting of all the optimal routes from each node to the exit. At the time of the accident, the dynamic diffusion of fire can be simulated using Fire Dynamics Simulator (FDS) based on the preliminary information of the fire, so as to estimate the impact of the fire domain on each node of the network. Then, according to the fire dynamic diffusion data, the evacuation route planning is carried out by the improved algorithm applying the breadth-first search strategy, so as to determine the optimal route from the current node to the safety exit and to reduce the possibility of casualties due to the uncertainty of the fire during the evacuation. This model allows for both people’s safety and evacuation time to dynamically avoid fire-affected nodes and helps people to reach the safe area as soon as possible. Finally, the evacuation model is established according to the open-source cruise ship structure, and the evacuation process of people under the dynamic spread of cruise ship fire is simulated. The results show that the route planning method proposed in this research works out well in evacuating mass people, which can effectively reduce the evacuation time and improve the safety of the evacuation process.
MSC:
93-10
1. Introduction
In recent years, the safe evacuation of people in public areas has received widespread attention from society. In the face of unpredictable situations such as fires, hurricanes, tsunamis, and toxic gas leaks, it is especially important to transfer people to safe areas in the shortest possible time. In addition to studying people evacuation behavior by observing historical evacuation videos, computer simulation has become a major tool for people evacuation studies. Some studies have shown [1,2,3] that, among all emergencies, accidents caused by fire have the highest frequency and cause the most serious casualties and property damage, thus the emergency evacuation in case of fire has received more and more attention from researchers. In this research, taking the sudden fire accident of a large cruise ship as an example, we focus on the evacuation of cruise ships under fire situations, combining the influence on the evacuation route caused by disturbing factors [4,5], such as the location of the exit and route topology of the cruise ship, the size and location distribution of the crowd to be evacuated, and the fire spread speed and smoke.
Fire incidents often take place suddenly because the a priori environmental information is different from the real-time environmental information in emergency situations, so the application of static route planning algorithms can be limited in practice [3,6,7]. According to some studies on sudden fire cases, it is found that crowd chaos without timely evacuation [8,9] is an important cause of high casualty rate, and in crowded buildings such as shopping centers, supermarkets, and large cruise ships, people always move irregularly, so it is necessary to search for optimal evacuation routes based on exit locations, real-time evacuation information, and evacuation numbers. Meanwhile, the local space temperature increase caused by fire, smoke, and toxic gases can also have an impact on the choice of evacuation routes. It is very dangerous to walk in passages with high temperature, smoke, and high concentration of hazardous gases [10], and the topology of the route must be adjusted in time, thus the static route planning algorithm obtained from a priori information is not applicable to this situation. To address the above issue, in order to predict the fire spread in a timely manner, Thorley, W. et al. [11] used the FDS method to simulate a cruise ship fire scenario under the failure of firefighting measures and gave firefighting strategies for different fire scenarios. However, no evacuation strategy was given accordingly. Cao, X. et al. [12] used the fuzzy comprehensive evaluation method to assess the safety of fire evacuation and obtained the necessary safe evacuation time proposed. The strategy for evacuating people in case of sudden fire in the subways was proposed, but the evacuation strategy was not updated according to the real-time fire situation changes. When the environment of some passages changes, the old route planning can no longer meet the evacuation requirements. In order to find the evacuation route in a short time, some scholars have proposed that simplifying the topology of the route can save computation time, but the requested route is not necessarily the shortest route.
Classical shortest path search algorithms include Dijkstra algorithm, algorithm, Floyd algorithm, and so on [13]. However, due to real-time changes in the evacuation environment, searching for new evacuation paths is a time-consuming process that can take too long to obtain the new evacuation paths. Thus, in order to search for new feasible evacuation paths in a short time, Lin, W.Y. et al. [14] simplified the network topology to reduce computational time. However, the incomplete route topology leads to the new path being found in a short time not being the shortest path. Literature proposed a shortest path solving algorithm for the case of sudden road interruption by using the principle of the Dijkstra algorithm to quickly solve the shortest path in the process of avoiding the interrupted section. The probability of the shortest path result is 97%. However, there is a slight error, which fails to guarantee that the evacuation path is the shortest. Zhang, R. et al. [15] designed a method to represent road sections with adjustable breakpoints and to dynamically search for shortest paths by using Floyd’s algorithm. The simulation results show that the method can effectively avoid potentially dangerous nodes, but the dynamic search of the method is a global optimization process, and the path planning time in large or dense topological graphs is relatively long. Wu, W. et al. [16,17] constructed an intelligent integrated fire rescue system, which updated the optimal route by using wireless sensors or visual cameras to detect the location of people, but real-time monitoring was hard to obtain accurate information about pedestrians and online calculations were time-consuming. Retrieval of the specific smoke sensors data indicates the presence of smoke contamination at their nodes has a time delay, and evacuees may still get injured during the fire if alternative routes are searched only after the current area has been filled with smoke.
In recent years, many scholars have applied reinforcement learning algorithms to solving the path planning problem, so as to plan evacuation paths for people through adaptive learning with the objectives of avoiding obstacles and finding exits. Yiran Xue [18] et al. constructed a simplified deep Q network (DQN) model with scene images as the input quantity, to output multiple guide signs in complex scenes. Shuo Feng [19] et al. improved the evaluation function in DQN by using correction functions to address the problem of overestimation of DQN, and the improved deep reinforcement learning networks improved the metrics in terms of loss function and convergence speed. However, in the evacuation path planning problem of large cruise ships, the adaptive learning time of reinforcement learning under complex cabin layout becomes longer, which will lead to a lag in the evacuation path decision.
With the development of intelligent algorithms, many intelligent algorithms such as ant colony algorithm, particle swarm algorithm, whale optimization algorithm, genetic algorithm, greedy algorithm, etc. [1,2,6,20,21,22,23] were used to find dynamic paths. Feng, Z. et al. [24] proposed an adaptive search radius ant colony path planning algorithm that can automatically change the search radius according to the complexity of the environment, which repeatedly searches the optimal local target point and invokes the improved ant colony algorithm to obtain the optimal path in the local area until the global target point is found. However, the planning path distance and the convergence time of the algorithm are difficult to take into account. Runze, W. et al. [25] modeled and quantified the real-time road condition information in the dynamic road network, and then used the improved dynamic ant colony algorithm to solve the optimal path that minimizes the global evacuation time and maximizes the utilization of the road network. The evacuation results show that the method can effectively reduce the average evacuation time and increase the utilization of the road network. However, although these algorithms can solve the optimal solution, the convergence speed is slowed down when dealing with dynamic evacuation problems.
The above studies provide guidance for emergency evacuation strategies for human flow in fire situations. In this paper, we refer to articles [11] and others that use the FDS method to simulate firefighting and obtain the values of fire products at each time point, refer to articles [4,5] to obtain safety indicators for evacuation of people in fire situations, and refer to articles [7,9,12]. Finally, the static evacuation paths based on a priori information is obtained by combining all the articles mentioned with algorithms. In addition, the improved algorithm is the most common method used to search for the optimal means in order to obtain the shortest evacuation route in a short period of time. During the evacuation process, owing to the expanding fire area, the uneven distribution of people on the cruise ship, the narrowness of some evacuation routes and the small number of escape exits can add to difficulties in escape. In order to guarantee the safety of people in the evacuation process, this research timely predicts the future fire trend in a short period of time based on the real-time situation of the fire, considers the changes in the accident location, danger area and obstruction route, and discerns the safety of the route by developing a safety level table of relevant influencing factors, and thus timely changes the evacuation route topology map in the cabin to optimize the evacuation route online to adapt to the real-time situation. The following study eliminates potential hazards, by predicting hazard data using FDS [11] and by including the predicted state of each node in the computational module as an early warning. In this case, the hazard data in the search algorithm are alerted before the arrival of the hazard along the exit route, facilitating the model to provide information on the safest and fastest evacuation route.
This research is structured as follows: (1) Firstly, we have constructed the overall model framework of optimal route planning based on fire prediction data. Then, we have proposed an automatic evasion route planning method in fire areas that combines both offline search and online search. (2) According to the Ship Design Principles [26] and the cruise ship passenger quota sand cabin equipment specifications, the cruise ship is modeled, and the evacuation network topology is created [27]. The fire situation is analyzed by the FDS model, which is used to predict the danger area and danger route, and to adjust the evacuation route topology diagram. (3) Based on the changes in the network topology diagram obtained from the fire situation prediction, the online optimization algorithm is used to search for the local optimal route at the corresponding moment and to quickly plan the evacuation route. (4) The results are obtained by simulation and the conclusions are drawn.
2. Automatic Avoidance Route Planning Method in Fire Areas
2.1. Model Overview
The models developed include FDS [11], and evacuation route Search Algorithm, in which the FDS fire simulation system is a simulator developed by the American Academy of Sciences for simulating fire scenarios, which has tried its best to develop and combine with the actual fire parameters correction for many years, and now it has become the most dominant tool for simulating fire.
This section proposes an automatic evasion route planning method in fire areas that combines both offline search and online search, which includes two parts: offline calculation and online search. A static algorithm is applied to search for the optimal route containing the evacuation route from each node to the exit node, so that the optimal route can be dynamically searched by comparing the online optimized real-time node information with the previous node information. The online optimization searches the local area and converges quickly, so as to obtain a new optimal route that meets the real-time requirements in a short time.
The overall model framework of optimal route planning based on fire prediction data are shown in Figure 1.
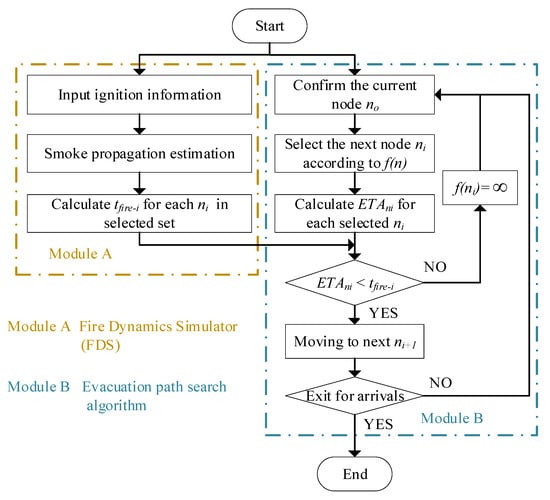
Figure 1.
Framework of the improved model.
In this model, the route search algorithm is used. Thus, the efficiency of the subsequent nodes can be used as the evaluation metric [28,29], including (1) the route distance between the current node and the subsequent nodes, and (2) the sum of the straight-line distances from the next node to each exit; the basic equations of the algorithm are as follows:
In Equation (1), is the evaluation cost of the node n, is the route distance from the node to the next node , and is the estimated cost of the shortest distance from to the target node. The value is usually calculated using the Manhattan distance or Euclidean distance, and the calculation formula is as follows:
In the formula, and are the coordinates of neighboring nodes ; and are the coordinates of the current node ; and are the coordinates of the target node i denoted as the target exit. This method evaluates the cost of multiple routes to the next node and selects the next node with the least cost to reach the exit node .
The improved algorithm requires the time that a person moves on a network edge as the weight of that evacuation network edge. The relationship between Chinese gender, age, height, weight, and speed of the person is shown after literature research [30,31].
In order to ensure that all people can avoid the fire and escape safely, this paper takes the example of a female with a height of 1.58 m and a weight of 53 kg in Table 1 as a reference, and selects a movement speed of 1 m/s. The cost replacement formula for the edges in the evacuation network is shown in Equation (4).

Table 1.
Evacuation speed of different people.
In Equation (4), represents the length of the edge , while represents the movement speed of the person: 1 m/s. By using Equation (4), the time moving from each node to the adjacent nodes can be calculated. By comparing the time to exceed the fire product at each node with the time required to evacuate personnel to that node, the danger area can be avoided, and the best node can be selected for people to evacuate to the safe area gradually.
2.2. Dynamic Optimization for Rapid Evasion of Fire Areas
This section uses the algorithm to solve the shortest path in the static road network. The algorithm is usually judged by the sum of the cost already paid and the cost to be paid, which can not only shorten the search time but also speed up the search efficiency.
When fire or other unexpected accidents do not occur, the nodes and edges in the cruise ship network topology diagram can all pass normally. In the actual evacuation process, passengers can choose to evacuate to the gathering station and then take the lifeboat to the safe sea. In this situation, the a priori evacuation network constructed offline by the algorithm can be used, which contains the shortest evacuation route and evacuation route length that is between each node in the network topology graph and the evacuation endpoint.
In the case of cruise ship fire evacuation, the shortest route solved by the conventional algorithm only considers the shortest evacuation route and does not consider the impact of fire products on people’s safety and their movement speed. The a priori evacuation network constructed offline does not take the fire location and the development of the fire situation into account. When the fire incident threatened the evacuation route planned offline, the life safety of the cruise ship passengers would be threatened if they continued to escape according to that evacuation route.
In this paper, in response to the ineffectiveness of the traditional algorithm in path planning emergency evacuation in the face of large scenarios, the cost calculation in Equation (1) is optimized. On the basis of the known path information of the network node graph, the calculation of is based on the path length, adding the influence of the path travel rate. The improved is calculated as follows:
in the calculation, l denotes the path length, denotes the flat path travel rate, and denote, respectively, the length weighting factor and speed weighting factor, taking = 0.15 and = 0.85.
as the heuristic term in the algorithm determines the degree of intelligence of the algorithm. If is too small, it will make the algorithm gradually degenerate into the Dijkstra algorithm, forming a blind search and becoming inefficient. If is too large, then it would fail to ensure that the path found is the optimal path. In the three-dimensional network diagram of this paper, the Euclidean distance cannot be used to measure the size of value because the neighboring nodes of each node are different. If we want to reach the target node, we can only gradually advance through neighboring nodes. Thus, for the node with a small Euclidean distance from the target node, it may take a longer time to reach the target node. Based on this, a priori model based on Dijkstra is used to calculate all the path lengths of each node to the target node in advance, which is used as the calculation criterion for , as shown in Equation (6). The cost calculation formula of the improved algorithm can be obtained by combining Equation (5) as shown in Equation (7):
in Equation (7), denotes the set of shortest distances from all nodes to the target node using the Dijkstra algorithm. denotes the scaling factor. We take = = 0.1 for the uniform weight. is the final cost calculation formula.
The improved algorithm can finally obtain a path that can bypass the fire product exceedance area and ensure the relatively shortest evacuation time.
In addition, the improvement of the automatic avoidance path planning algorithm consists of three parts: Firstly, the dynamic diffusion process of fire is simulated by FDS to obtain the time data of the nodes in the evacuation network affected by fire; secondly, by calculating the evacuation speed of people, the weight of each edge of the evacuation network is modified by replacing the path length with the evacuation time, and then determining whether the time of personnel arriving at each node in the evacuation network and the time of the node going to the neighboring nodes. Thirdly, the dynamic optimization of the automatic path avoidance in the fire area solves the local path planning problem, which reduces the number of nodes and paths that need to be recalculated and avoids a large number of repeated calculations.
The offline computation is based on the optimized algorithm to calculate the a priori shortest paths of all nodes. The online search is used to dynamically update and optimize the a priori evacuation paths containing the nodes in the fire region, using a breadth-first search strategy [12]. When the network topology of a cruise ship changes, the automatic fire area avoidance path planning method can find the new shortest evacuation path in a short time.
The a priori evacuation route network calculated offline by the algorithm denotes and the set of impassable nodes denotes set S. The set of neighboring nodes of the nodes in set S denotes and the number of elements in denotes . The set of starting nodes containing the a priori route through the fire region denotes and the optimized evacuation network denotes . When a fire accident occurs in the part of the route of the cruise ship which contains the nodes in the set, then the fire region automatic avoidance dynamic planning algorithm is used to optimize the a priori route through the fire area. The principle of this is shown in Algorithm 1.
| Algorithm 1: Evacuation route dynamic optimization algorithm pseudo code. |
 |
In this algorithm, denotes the impassable nodes in the fire domain; denotes the adjacent node of a node in the fire domain; denotes the starting node of an a priori route through the fire region; denotes an a priori evacuation route; denotes the number of adjacent nodes of the number of node r in the fire domain.
In the network topology diagram, the evacuation route from the start node to the evacuation end node is as follows:
in Equation (8), are the node numbers and the cost of the evacuation route are as follows:
when a fire incident occurs in a cruise ship, the nodes at the location of the fire or the nodes severely affected by the fire will be impassable. Assuming that the set of real-time impassable nodes is S, then the dynamic optimization process of automatically avoiding the fire area can be described as Equation (10), whose optimization objective is to find the shortest route between nodes to nodes, and the route must not contain nodes in the set S:
in Equation (10), the weights between the nodes are the actual costs of the evacuation routes.
Simultaneous calculation of evacuation routes of all nodes in causes redundancy in real-time computation. To save the online computation time for searching the shortest route, the dynamic optimization of the fire area auto-avoidance dynamic planning algorithm can be performed in two steps.
In the first step, Breadth-First Search is used to search for the shortest route from the nodes in to each evacuation endpoint. The principle of the Breadth-First Search algorithm is simple, and its core idea is as follows
- (1)
- start from a vertex V0 in graph G and visit V0 first;
- (2)
- visit all the vertices V1, V2, … that are adjacent to V0;
- (3)
- visit all vertices adjacent to V1, V2, … that have not been visited before;
- (4)
- follow that order, until all vertices have been visited.
Use the above breadth-first search method to visit the neighboring nodes u of the node i in . If u is in , then visit the other neighboring nodes in turn until there exists a node k not in . When the route does not contain a fire node, the a priori sparse route of the node k is used to update the sparse route from the node i to the sparse endpoint j as follows:
since the shortest route from each node to the exit in the network topology is already stored in an a priori evacuation network , the BFS can quickly obtain the shortest route information from the specified node to the exit by accessing . When the fire area auto-avoidance route planning method accesses the route information of a node, it takes a very short lookup time to obtain the relevant information from the a priori evacuation network.
In the second step, the evacuation routes of all the nodes n in are updated in a similar way, where all hazard routes containing fire nodes have been updated to . Unlike the nodes i in the network , is a feasible evacuation route that does not contain fire nodes, but it may not be the shortest one, so further optimization of the second shortest route is needed.
Assume that is the set of updated feasible evacuation routes, and there exists a certain new route that is
Visit the neighboring nodes of each node in in turn and check whether there is a shorter route using Equation (13). If the neighboring nodes z of a node s satisfy Equation (13), it means that the route distance of the node n through the node z to the end of the evacuation j is shorter than the current feasible evacuation route. According to Equation (14), the route is updated:
The dynamic optimization of the fire area automatic avoidance path planning method solves the problem of local path planning, which reduces the number of nodes and paths that need to be recalculated and avoids a lot of repeated calculation.
3. The Inner Construction of the Cruise Ship Model
In this research, the evacuation environment is a three-deck cruise ship given in the European “SAFEGUARD” project [32], and the CAD drawings of the cruise ship are imported into Analogic. The second layer of the cruise ship CAD diagram was selected as the scenario of evacuation simulation and the basis of the search route algorithm, and the cruise ship was used as the evacuation scenario. The cruise ship is constructed as shown in Figure 2a,b.
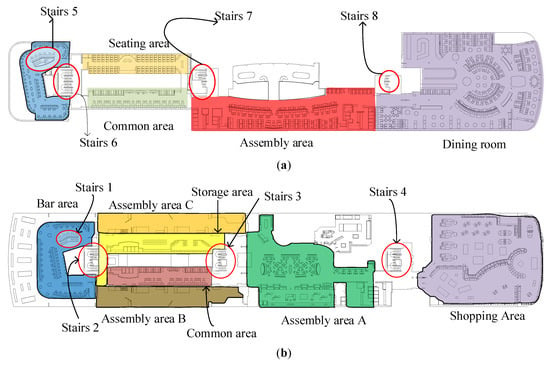
Figure 2.
The layouts of the model with Anylogic: (a) first deck layout of cruise ship; (b) second deck layout of cruise ship.
3.1. Cruise Ship Model Networking
Based on the research of domestic and foreign methods for model networking [14,33,34], the cruise ship was networked with different functional areas on the cruise ship, which was used to provide an application environment for the evacuation model. All the areas were cut according to the concave and convex shapes, and then a central node was set for all the cut areas to judge whether different areas were interconnected. Then, the central points of the interconnected areas were connected. According to the functions of different areas in the cruise ship, the second floor of the cruise ship can be divided into the bar area, stairs, the shopping area, the cabins, the storage area, the passages, and the assembly area. These areas can be connected through the corners, firstly selects the center point for these areas, then judges the connectivity between areas by the existence of corners between different areas, and finally uses the nodes of corners to connect the interconnected areas in series to generate the evacuation network. The detailed steps are shown in Figure 3.
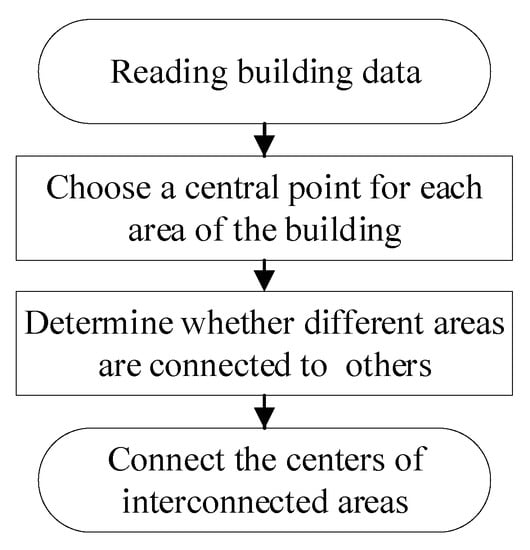
Figure 3.
Cabin model networking steps.
The location analysis of each node of the cruise ship model allows for dividing the nodes into points to be evacuated, intermediate nodes, and safety exits, in order to optimize the model and finally to network the model [7]. The second layer of the cruise ship network topology obtained through the networking step is shown in Figure 4.
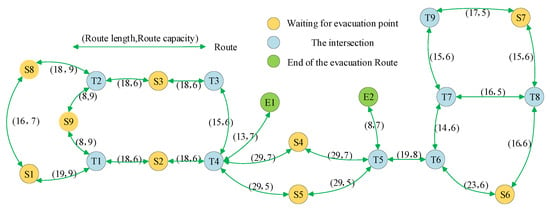
Figure 4.
Second floor network topology diagram of the cruise ship.
After generating the evacuation network using the above steps, it is also necessary to define the fire nodes and exit nodes in the evacuation network [35,36,37]. The exits for people to escape in this project are the set areas A, B, and C. In this research, only the set area C (nodes E1,E2) is chosen as the exit to verify the feasibility of the algorithm.
In Equation (15), G represents the whole sparse network, V represents the set of nodes in the sparse network, and W represents the set of corresponding weights of edges in the sparse network [7,16,35,36,37]. n in Equation (16) represents the total number of all nodes in the sparse network, while E represents the set of edges in the sparse network. The weights of neighboring nodes in the network topology diagram are shown in Table 2 below.

Table 2.
Table of weights of adjacent nodes in the network topology diagram.
When the fire did not spread and affect the pre-planned evacuation path, the cruise ship passengers could evacuate to the safe area according to the indicated path. The evacuation paths and evacuation times corresponding to different initial positions are shown in Table 3 below.

Table 3.
Static evacuation routes and evacuation time required for people at each node.
3.2. Fire Dynamics Modeling
This section completes the numerical dynamics analysis of the fire by FDS fire simulation. Based on the cruise ship data provided by the European SAFEGUARD project [32], a 3D model of the cruise ship built by PyroSim software [38,39] is shown in Figure 5. PyroSim is a software for fire simulation, suitable for FDS to conduct fire simulation. PyroSim’s graphical user interface can be used as a fire dynamic simulator, which can be used to build fire simulations and to perform accurate predictive analysis of smoke movement, temperature, and toxic gas concentration in fires.
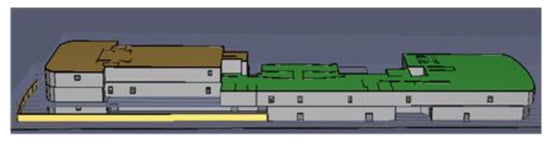
Figure 5.
The 3D model of cruise ship built by PyroSim.
This research adopts the FDS fire model to determine the safety of each node by predicting the spread of fire at each moment on the cruise ship, so as to eliminate the upcoming dangerous nodes and to ensure the safety of the evacuation plan. The FDS model performs a smoke spreading simulation based on the initial information, which includes the fire starting spot, the burning location, and the heat release rate per unit area (HRRPUA) [11]. Building materials on cruise ships is generally non-combustible, while storage areas that store luggage carried by people have a higher probability of catching fire, so the starting spot of fire is assumed to be the storage area.
Factors that affect the life safety of people in a fire include CO concentration, smoke visibility, and temperature, all of which can reduce the physiological movement ability of people. If an unsafe evacuation route is taken, people will enter the dangerous section and be harmed by the fire products, injured, or even killed. The relationship between the values of CO concentration, smoke visibility, and temperature on the degree of impact on people in a fire [10,30] is shown in Table 4, Table 5 and Table 6.

Table 4.
The effect of CO on the human body.

Table 5.
The effect of temperature on the human body.

Table 6.
The effect of the smoke visibility on the human body.
The relationship between the different ranges of CO concentration, temperature, smoke visibility, and the degree of impact on the human body in Table 4, Table 5 and Table 6 can be defined in the evacuation network diagram when all the nodes exceed the fire product standard, so as to calculate the time when all the nodes exceed the fire product standard. The paper sets the visibility as higher than 3 m, ambient temperature less than 70, and CO concentration less than 0.5 to escape people. There is no effect on the life safety of escapees. Thus, Equation (18) is obtained as follows:
PyroSim is used to build the fire model shown in Figure 6. Considering the model grid size and the computation time, the size of the model grid is set as 0.5 m × 0.5 m × 0.5 m. Based on the above definition and the locations of all nodes in the evacuation network diagram, add the CO sensors, the temperature sensors, and the smoke visibility sensors in the corresponding places in the software, all of which are at the height of 1.6 m. Using the fire source T1 fire as a reference, we assume that all fixed fire fighting equipment on the cruise ship has failed, and the cruise ship is at the normal temperature and pressure without counting the wind speed. The simulation time is 300 s.
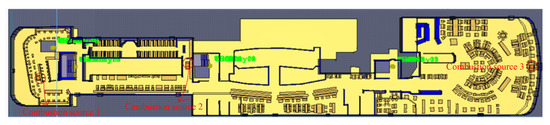
Figure 6.
Model of the fire on the second floor of the cruise ship.
After completing the initial value setting and safety state division, FDS can generate the output data of fire product changes at each node at each moment, as shown in Figure 7a–c; and can derive the distribution of fire products at 200 s from the output data as shown in Figure 8a–c.
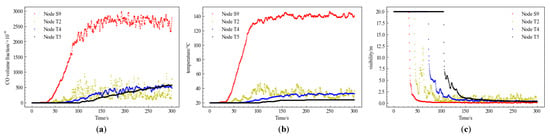
Figure 7.
(a) CO volume fraction changing with time; (b) temperature changing with time; (c) visibility changing with time.
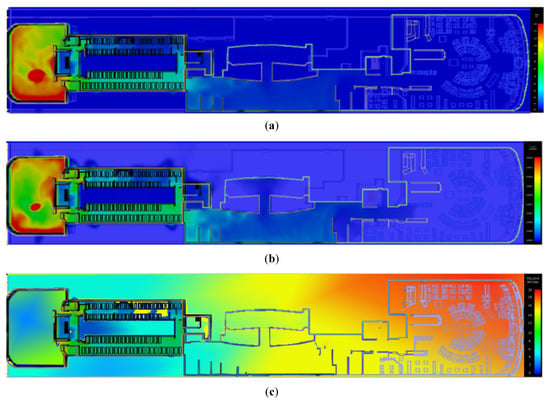
Figure 8.
(a) Temperature cloud at 200 s; (b) CO volume fraction cloud at 200 s; (c) smoke visibility cloud at 200 s.
Combining the information on the change of fire products at each node shown in Figure 8, the predicted fastest arrival time at the current node is calculated () [36,40]. The time for the safe node to become a dangerous node in the dispersal route is compared as follows:
In Equation (19), is the model calculation time and is the average speed of evacuees moving along the exit route. Comparing with , it can be concluded that, if means that the state of the node tends to become dangerous before the evacuees reach a node in the evacuation route, and vice versa, means that the state of the node is safe when evacuees reach the next node.
3.3. Evacuation Simulation
Suppose a fire incident occurs in the cruise ship network topology shown in Figure 4 and node T1 is the source point of the fire, then the set of impassable nodes . At this time, the pre-planned evacuation route containing node T1 may become dangerous. When using the fire area auto-avoidance route dynamic planning algorithm to optimize a priori evacuation routes for cruise passengers, we use to store the starting node of the a priori route containing node T1, then can be expressed as
in Equation (22), represents the neighboring nodes at the source of fire in the fire area, and all nodes in in the fire area are passing through the nodes .
Through the fire simulation with the definition of fire reach node time, all nodes of are shown in Table 7. The improved algorithm route planning can be completed in Table 7.

Table 7.
Time used for each node to change from a safe state to danger in case of sudden fire at T1.
Table 7 contains the time corresponding to the change of state of all nodes. None means that the node will not change and will be in a safe state all the time. Through the data in Table 7, we can obtain the accurate time when each node changes from a safe state to a dangerous state.
For the above fire location situation, in order to ensure the safety of cruise passengers evacuation, when the fire occurs, it is necessary to adjust the dangerous evacuation path online, and the path planning algorithm of dynamic and static combination obtains different path results. For the different fire area situations mentioned above, the statically planned evacuation path contains the fire area as well as the unsafe nodes around it, which may lead to casualties among evacuees. When the fire occurs, the shortest path obtained by constructing the topology diagram of the cruise ship network after eliminating the dangerous nodes and calculating it with the algorithm can not only guarantee the life safety of the evacuation process, but also meet the requirements of rapid evacuation.
The escape paths of people at each node in the event of a fire, and the corresponding escape times are shown in Table 8. Unlike the static network, this roadmap avoids the possibility of casualties caused by people escaping from the fire domain.

Table 8.
The dynamic evacuation route and time required for the T1 fire scenario.
The results of the dynamic optimized route using the fire area automatic avoidance route planning algorithm are shown in Figure 9 (the evacuation of people in other areas of the cabin not shown in the figure is not affected by the fire at this node), in which P1 is the a priori evacuation route after the fire area, and P2 is the route optimized by the fire area automatic avoidance route planning algorithm.
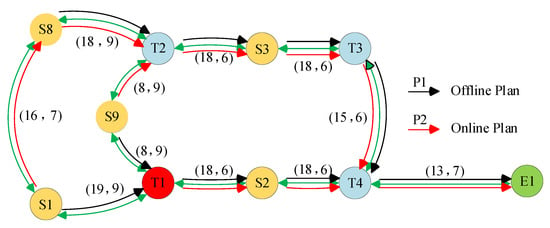
Figure 9.
The results of dynamically optimizing the route.
In order to verify the reliability of the model, node S3 and node T7 were simulated with sudden fires, and the dynamic optimized route results using the automatic fire area avoidance route planning algorithm are shown in Figure 10a,b.
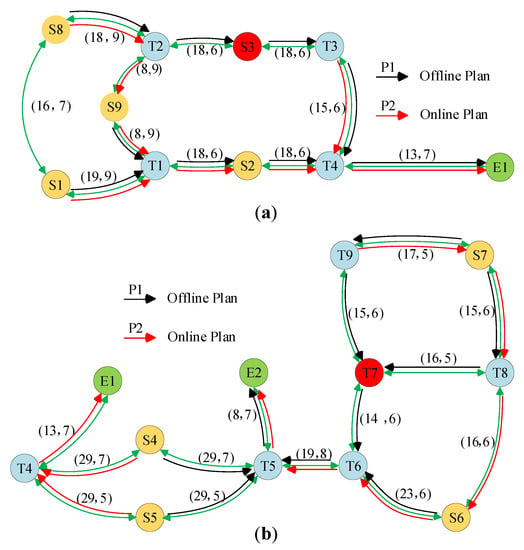
Figure 10.
The results of dynamically optimizing the route (a) node S3 was simulated with fire; (b) node T7 was simulated with sudden fire.
In terms of the calculation time of the route planning method, from the monitoring of the cruise ship’s node S3, after the fire at node T7, the fire area automatic avoidance route planning method takes only 9.4 ms to plan the global shortest evacuation route. Figure 10a,b show the new shortest escape route for people under the initial moment of fire, in which, in terms of nodes, the red node is the fire location and the green node is the evacuation exit; in terms of routes, P1 is the a priori route unaffected by fire, and P2 is the new evacuation route after local optimization.
4. Analysis of Simulation Results
4.1. The Shortest Evacuation Routes under Three Fire Conditions
The route results obtained by the combined dynamic and static route planning algorithm are different when the fire areas are different. In the topology diagram shown in Figure 4, the following three different fire location emergencies are proposed in this simulation: fire at node T1, node S3, and node T7, respectively. For different fire area situations, the evacuation routes of hazards in the static planning evacuation route results are shown in Table 9. In Table 9, the theoretical shortest evacuation route is the shortest route obtained by constructing a new cruise ship network topology diagram when a fire occurs, and then by calculating it with algorithm.

Table 9.
Hazardous a priori routes in different fire areas.
For three different fire location emergencies, the model successfully identifies the hazards in the offline initial route. Once the fire products spread to other nodes and cause harm to evacuees, such nodes are set as inaccessible nodes, and the offline initial route containing such nodes is locally optimized online to search for other normal nodes with smaller values , and so on. The evacuation route composed of these nodes is the optimal escape route in case of fire, and the model results can be obtained quickly (within 10 ms). When the evacuation route is updated, the cruise ship emergency management can instruct the passengers to follow the new evacuation route by means of radio announcements or crew commands. In particular, when simulating the situation of sudden fire at location T7, the offline initial routes of node S4 and the node S5 did not pass through the danger area, but in order to maximize the safe evacuation of people and to reduce the crowd density at escape route T5-E2, the evacuees of node S4 and node S5 can choose safety exit E1 to evacuate. The simulation results show that, although the escape time of the people in these two places increases from 37 s to 42 s, the total evacuation time decreases from 206 s to 198 s, which guarantees the safety of all people greatly and increases the evacuation success rate significantly. Although the evacuation time of people at these two locations increases from 37 s to 42 s, the overall evacuation time can be minimized and the evacuation success rate increases significantly.
4.2. Rapidity of the Dynamic Optimization Algorithm
In this section, a large network topology graph model with 1000 nodes is established, and each node generates any two paths connected at other nodes. The path weights are randomly taken as a positive integer between 1 and 100. Assuming that the safety exit nodes are node 6, node 66, and node 666, when the fire source is node 37, method2 and method3 are applied to search the shortest path from node 555 to the evacuation endpoint, respectively. In addition, the evacuation path optimization results are shown in Table 10, where method1 is the method of static search for the shortest path using algorithm, method2 and method3 are methods for searching the shortest path online respectively using the fire area auto-avoidance path planning algorithm and algorithm, based on real-time fire information.

Table 10.
Optimization results of the shortest evacuation path.
In Table 10, the lengths of evacuation paths obtained using method2 and method3 methods are significantly longer than method1, which is because node 18 is a fire node, and shortest path method1 is a hazardous path. To ensure the safety of the evacuation path, method2 and method3 circumvent the fire area by increasing the length of the evacuation path. Meanwhile, the evacuation path search results of method2 and method3 are the same, which further indicates that the automatic fire area avoidance path planning algorithm has the ability to plan to get the shortest path and can dynamically plan the safe shortest evacuation path after the fire occurs.
When the fire source nodes are different, the number of a priori evacuation routes affected by the fire are of different scales, i.e., the number of stored nodes in the set is different. In order to simulate the time performance of the fire area automatic avoidance route planning algorithm under different fire locations, this section is based on the above large network topology diagram model with 1000 nodes, among which node 1 to node 200 are set as fire nodes in turn. The relationship between the number of nodes in set and fire node locations is shown in Figure 11a. The comparison of the computation time for optimizing the path using the conventional algorithm and the sparse path dynamic optimization algorithm is shown in Figure 11b.
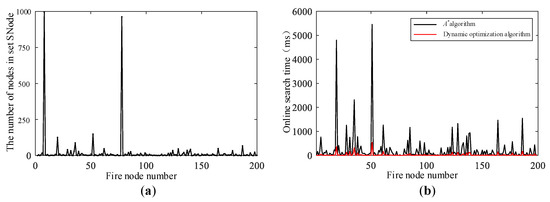
Figure 11.
(a) Number of nodes in the setwith fire nodes; (b) computation time comparison between the algorithm and evacuation route dynamic optimization algorithm for optimized routes.
The online computation time of the fire area auto-avoidance algorithm for searching for new routes is denoted by and the online computation time of algorithm for searching for new routes is denoted by . The variation in the ratio of online search time and is shown in Figure 12.
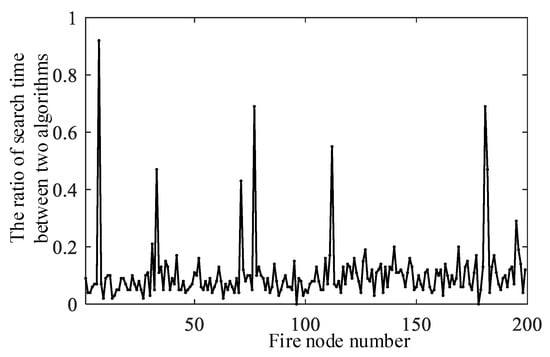
Figure 12.
Ratio r of online search time and .
From the simulation results, it can be seen that the fire area auto-avoidance route planning algorithm can quickly search for new evacuation routes for each node in in the network after the fire occurs. At the same time, when the scale of the network topology diagram model is relatively large or the structure of the network topology diagram is rather complex, the algorithm still has good timeliness and can search for the new shortest routes in a very short period of time.
4.3. Model Validation
When a fire breaks out at node T1 and the total number of evacuees is between 100 and 1000, the evacuation time required by the two evacuation strategies is shown in the following Figure 13.
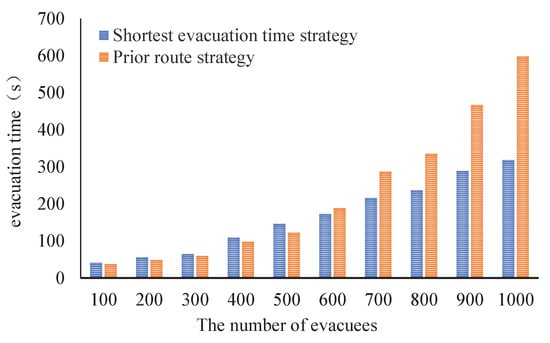
Figure 13.
Relationship between evacuees and evacuation time.
From the figure, it can be seen that the time required for the a priori route is slightly lower when the total number of people is 100 to 500. The evacuation time required for the shortest evacuation time strategy is lower than that for the a priori route when the total number of people is 600 or more, and the difference between the two gradually increases. This indicates that, although the shortest evacuation time strategy is longer than the shortest route in terms of total evacuation route length, it has little effect on the overall evacuation time when all the people are evacuated. This is because the use of a priori route not only ignores the impact of fire spread, but the simultaneous influx of people into the same section of multiple sections at a certain time will also lead to crowd congestion in the current section.
Simulating a sudden fire at node T1, the total number of people is 800 when the evacuation is carried out at time 0. A two-dimensional heat map is used to visualize the change in the number of people in each roadway during the cruise evacuation. In the map, the horizontal axis is the evacuation time t, the vertical axis is each evacuation section, and the gradient color from light to dark indicates the number of people from less to more. The heat map of the number of evacuated people in the case of sudden fire at node T1 is shown in Figure 14a,b.
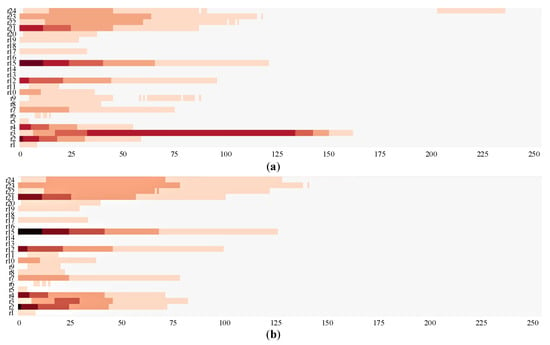
Figure 14.
Heat map of the number of people in case of sudden fire at node T1 (a) a priori route strategy; (b) shortest evacuation time strategy.
From a macro level, the optimal evacuation route dynamic planning scheme can minimize the evacuation time while ensuring the safety of passengers. At this point, it is obviously inappropriate to merely take the shortest evacuation route distance as the route evaluation criterion. As can be seen from the figure, compared with the shortest evacuation route strategy, the evacuation time shortest route planning method significantly improves the issue of the concentration of people in some sections.
In this section, evacuation channels , , , , , , and in the cruise ship network topology diagram are selected as observation objects. The shortest evacuation route strategy and the shortest evacuation time route planning method proposed in this research are applied to monitor the real-time number of people N in each of the above evacuation channels during two different emergency evacuation activities. The changes in the real-time number of people N in each road section are shown in Figure 15a,b.
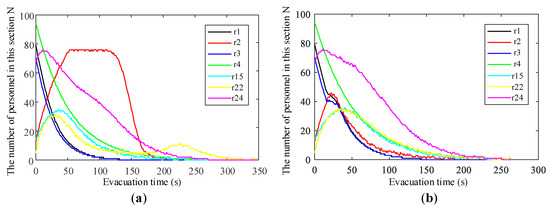
Figure 15.
(a) The variation of the number of people in each roadway section under the shortest evacuation route strategy; (b) the variation of the number of people in each roadway section under the shortest evacuation time route strategy.
Figure 15a shows the change in the number of people in the section under the shortest evacuation route strategy, in which the number of people in evacuation lane reaches the maximum number of people in the lane after about 50 s of evacuation movement of cruise passengers, resulting in obvious congestion. The congestion in evacuation lane lasted for about 70 s before it was gradually relieved. Figure 15b shows the variation of the number of people in the roadway section under the evacuation time shortest route planning method, in which each roadway section adjacent to the exit does not show significant congestion, and the evacuation movement is carried out steadily.
The route optimization results show that the automatic fire area avoidance route planning algorithm proposed in this section can effectively avoid the fire area. Moreover, the algorithm still works out well when the fire area spreads and multiple nodes are caused to be impassable.
5. Discussion and Limitations
We have conducted experiments to solve the evacuation of cruise ships in emergency situations using the proposed automatic evasive path planning algorithm. The existing algorithms based on the problem have been selected and compared with the traditional algorithms. The accuracy of the automatic evasive path planning algorithm in finding the shortest path is verified by comparing the a priori evacuation path with the dynamic evacuation path in Table 10. We have considered various performance metrics to evaluate the performance of the proposed algorithm. Figure 11 compared the computation time of our proposed algorithm with that of the conventional algorithm, and Figure 12 showed that the performance of the automatic evasive path planning algorithm is significantly higher than that of the conventional algorithm. The maximum ratio of the algorithm’s computation time values in case of fire at different locations is 0.92, and the minimum ratio is 0.02. This figure shows that the proposed method has a maximum reduction of 92.17% and a minimum reduction of 2.42% in the computation time to obtain the best path compared to other competing methods. The results show that the automatic avoidance path planning algorithm has a greater ability to obtain the best evacuation path in less computation time while guaranteeing the accuracy of the results compared to the traditional algorithm. Figure 13 showed that, compared to the traditional algorithm evacuation strategy, the automatic avoidance path planning algorithm can reduce the total evacuation time of the cruise ship, and the evacuation time is significantly reduced when the number of people increases, with a 46.76% reduction in the evacuation time for a cruise ship with 1000 passengers.
The study also shows that the existing method solves the problem of evacuee congestion and improves the resource utilization of evacuation routes, which can effectively alleviate this problem of crowding. The proposed system has been tested on a larger network topology diagram, and better results have been obtained.
Although this paper has made some improvements to the research related to the evacuation route planning method for cruise ships, it still needs further research. (1) The research of the paper is at the macro level, mainly considering the influence of objective environmental information on people’s evacuation route planning, lacking the influence of psychological and physiological factors on evacuation behavior in the evacuation process. Subsequent research can consider the influence of these factors such as panic emotion, herd mentality, etc. on people’s route planning, so as to more realistically reproduce the crowd evacuation process under unexpected accidents. (2) The evacuation of cruise ships studied in the thesis is usually carried out at sea, but when studying the influence of environmental information on the evacuation behavior of people, the influence of factors such as wind and waves on the movement speed of people is lacking. Subsequent research can revise the speed–density model of dense crowds of cruise ships by combining the experimental data of people during evacuation exercises at sea.
6. Conclusions
This paper combines FDS and improved algorithms, and proposes a combined dynamic-static fire area automatic avoidance path planning algorithm to solve the optimal path in the emergency evacuation problem to ensure the safety of people. The total evacuation process time for algorithm evaluation is used to assess the superior performance of the algorithm. Compared with the traditional algorithm, the proposed algorithm conducted simulations for a large network topology diagram containing 1000 nodes to shorten the computation time of the algorithm, which guarantees the accuracy of the shortest path, avoids the possible congestion of people during the evacuation process effectively, and improves the timeliness of the traditional evacuation path planning method, having high practical application value. The simulation results show that the method has superior timeliness and can quickly search for the shortest evacuation path to avoid the fire area.
Author Contributions
Conceptualization, K.D. and Q.Z.; methodology, K.D. and H.Z.; validation, Q.Z.; formal analysis, H.Z. and P.X.; writing—original draft preparation, K.D. and J.C.; writing—review and editing, K.D.; supervision, K.D. and H.Z.; funding acquisition, H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data in this research paper will be shared upon request to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, M.; Han, D. Multi-Grid Model for Crowd’s Evacuation in Ships Based on Cellular Automata. Pol. Marit. Res. 2015, 22, 75–81. [Google Scholar] [CrossRef][Green Version]
- Ni, B.; Li, Z.; Li, X. Agent-Based Evacuation in Passenger Ships Using a Goal-Driven Decision-Making Model. Pol. Marit. Res. 2017, 24, 56–67. [Google Scholar] [CrossRef][Green Version]
- Hu, M. Layout Characteristics of the Large Cruise Ship and Applied Research of Evacuation Modeling. Ph.D. Thesis, Wuhan University of Technology, Wuhan, China, 2018. [Google Scholar]
- Karthik, V.; Suja, S. Optimized multiple existence for pedestrian evacuation using geographic map-based route discovery. Clust. Comput. 2019, 22, 11227–11236. [Google Scholar] [CrossRef]
- Choi, M.; Chi, S. Optimal route selection model for fire evacuations based on hazard prediction data. Simul. Model. Pract. Theory 2019, 94, 321–333. [Google Scholar] [CrossRef]
- Goodwin, M.; Granmo, O.C.; Radianti, J. Escape planning in realistic fire scenarios with Ant Colony Optimisation. Appl. Intell. 2015, 42, 24–35. [Google Scholar] [CrossRef]
- Mirahadi, F.; McCabe, B.Y. EvacuSafe: A real-time model for building evacuation based on Dijkstra’s algorithm. J. Build. Eng. 2021, 34, 101687. [Google Scholar] [CrossRef]
- Mao, Y.; Fan, X.; Fan, Z.; He, W. Modeling Group Structures With Emotion in Crowd Evacuation. IEEE Access 2019, 7, 140010–140021. [Google Scholar] [CrossRef]
- Chou, J.S.; Cheng, M.Y.; Hsieh, Y.M.; Yang, I.T.; Hsu, H.T. Optimal route planning in real time for dynamic building fire rescue operations using wireless sensors and visual guidance. Autom. Constr. 2019, 99, 1–17. [Google Scholar] [CrossRef]
- Ye, C.; Liu, Y.; Sun, C.; Jiang, Y.; Wang, B. Simulation study on personnel evacuation considering impacts of fire products. China Saf. Sci. J. 2020, 30, 142–151. [Google Scholar] [CrossRef]
- Thorley, W. FDS’ competence. Br. Dent. J. 2020, 229, 400. [Google Scholar] [CrossRef]
- Cao, X.; Li, X.; Wei, X.; Li, S.; Huang, M.; Li, D. Dynamic programming of emergency evacuation route based on DijkstraACO hybrid algorithm. J. Electron. Inf. Technol. 2020, 42, 1502–1509. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Cai, Z. Research and development of path planning algorithm. Sci. J. Control. Eng. 2017, 24, 1473–1480. [Google Scholar]
- Lin, W.Y.; Lin, P.H. Intelligent generation of indoor topology (i-GIT) for human indoor pathfinding based on IFC models and 3D GIS technology. Autom. Constr. 2018, 94, 340–359. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, J.; Gu, X. Implementation of intelligent emergency evacuation path planning system. J. Jiangsu Univ. Sci. Technol. 2016, 30, 189–193. [Google Scholar]
- Wu, W.; Chen, M.; Li, J.; Liu, B.; Wang, X.; Zheng, X. Visual information based social force model for crowd evacuation. Tsinghua Sci. Technol. 2022, 27, 619–629. [Google Scholar] [CrossRef]
- Amirgaliyev, Y.; Yunussov, R.; Mamyrbayev, O. Optimization of people evacuation plans on the basis of wireless sensor networks. Open Eng. 2016, 6, 206–213. [Google Scholar]
- Xue, Y.; Wu, R.; Liu, J. Crowd evacuation guidance method based on deep reinforcement learning combined with action space. J. Harbin Inst. Technol. 2021, 53, 29–38. [Google Scholar]
- Feng, S.; Shu, H.; Xie, B. Path planning for 3D environment based on improved deep reinforcement learning. Comput. Appl. Softw. 2021, 38, 250–255. [Google Scholar]
- Zaman, M.B.; Siswantoro, N.; Zulfikar, M. Evacuation Analysis of Ship Passenger Using Agent Based Modelling Simulation. IOP Conf. Ser. Earth Environ. Sci. 2021, 698, 12017. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, H.; Xie, J.; Zhao, Q. Dynamic Evacuation Planning on Cruise Ships Based on an Improved Ant Colony System (IACS). J. Mar. Sci. Eng. 2021, 9, 220. [Google Scholar]
- Xu, D.; Huang, X.; Mango, J.; Li, X.; Li, Z. Simulating multi-exit evacuation using deep reinforcement learning. Trans. GIS 2021, 25, 1542–1564. [Google Scholar] [CrossRef]
- Yen, H.H.; Lin, C.H.; Tsao, H.W. Time-Aware and Temperature-Aware Fire Evacuation Route Algorithm in IoT-Enabled Multi-Story Multi-Exit Buildings. Sensors 2021, 21, 111. [Google Scholar] [CrossRef]
- Zhao, F.; Yang, C.; Chen, F. Adaptive search radius ant colony dynamic path planning algorithm. Comput. Eng. Appl. 2018, 54, 56–61, 87. [Google Scholar]
- Wang, R.; Wang, L.; Liu, T. Research on dynamic path planning algorithm considering real-time road condition feedback. Sci. Surv. Mapp. 2020, 45, 163–169. [Google Scholar]
- Gu, M.T. Principles of Ship Designing Introduction. Mar. Eng. Equip. Technol. 2014, 1, 102. [Google Scholar]
- Dawei, Z. Research status of passenger Ship safety evacuation and IMO Standard development analysis. China Water Transp. 2018, 18, 19–21. [Google Scholar]
- Jiang, Y.; Chen, B.; Li, X.; Ding, Z. Dynamic navigation field in the social force model for pedestrian evacuation. Appl. Math. Model. 2020, 80, 815–826. [Google Scholar] [CrossRef]
- Hu, M.; Cai, W. Evacuation simulation and layout optimization of cruise ship based on cellular automata. Int. J. Comput. Appl. 2020, 42, 36–44. [Google Scholar]
- Ronchi, E.; Gwynne, S.M.; Purser, D.A.; Colonna, P. Representation of the Impact of Smoke on Agent Walking Speeds in Evacuation Models. Fire Technol. 2013, 49, 411–431. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, F.; Liu, X. ACP-based Research on Evacuation Strategies for High-rise Building Fire. Acta Autom. Sin. 2014, 40, 185–196. [Google Scholar]
- Yang, Q.; Wang, W.; Hu, Z. Simulation and verification of passenger ship emergency evacuation under emergency. J. Dalian Marit. Univ. 2018, 44, 2732. [Google Scholar]
- Marlow, F.; Jacob, J.; Sagaut, P. A multidisciplinary model coupling Lattice-Boltzmann-based CFD and a Social Force Model for the simulation of pollutant dispersion in evacuation situations. Build. Environ. 2021, 205, 108212. [Google Scholar] [CrossRef]
- Shi, M.; Lee, E.W.M.; Ma, Y. A novel grid-based mesoscopic model for evacuation dynamics. Phys. Stat. Mech. Appl. 2018, 497, 198–210. [Google Scholar] [CrossRef]
- Wang, J.; Wei, G.; Dong, X. A dynamic fire escape route planning method with BIM. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 10253–10265. [Google Scholar] [CrossRef]
- Jiang, Z.; Wang, T.; Yan, J. Unifying Offline and Online Multi-graph Matching via Finding Shortest Routes on Supergraph. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 3648–3663. [Google Scholar] [CrossRef]
- Yao, Z.; Zhang, G.; Lu, D.; Liu, H. Data-driven crowd evacuation: A reinforcement learning method. Neurocomputing 2019, 366, 314–327. [Google Scholar] [CrossRef]
- Top, S.M.; Topraklı, A.Y. Analysis of the open or closed conditions of drum windows effect on visibility and temperature propagation with fire dynamics simulation in domed mosque design. J. Fac. Eng. Archit. Gazi Univ. 2022, 37, 1839–1853. [Google Scholar]
- Li, Z.; Li, Y.; Ge, Y.; Wang, Y. Fire Simulation and Optimal Evacuation Based on BIM Technology. Lect. Notes Inst. Comput. Sci. Soc. Inform. Telecommun. Eng. LNICST 2022, 413, 263–274. [Google Scholar]
- Li, F.; Zhang, Y.; Ma, Y.; Zhang, H. Modelling Multi-Exit Large-Venue Pedestrian Evacuation with Dual-Strategy Adaptive Particle Swarm Optimization. IEEE Access 2020, 8, 114554–114569. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).