An Adaptive Barrier Function Terminal Sliding Mode Controller for Partial Seizure Disease Based on the Pinsky–Rinzel Mathematical Model
Abstract
1. Introduction
- It analyzes the chaotic behavior of the PR model output (somatic membrane potential) using the entropy criterion.
- It designs a TSMC approach which yields finite time converges of the system to the desired value, whilst ensuring chattering free dynamics.
- An approach that relies on the barrier function, without needing any information about the boundary of perturbations, to adjust the sliding surface, decrease the error and further improve the system response.
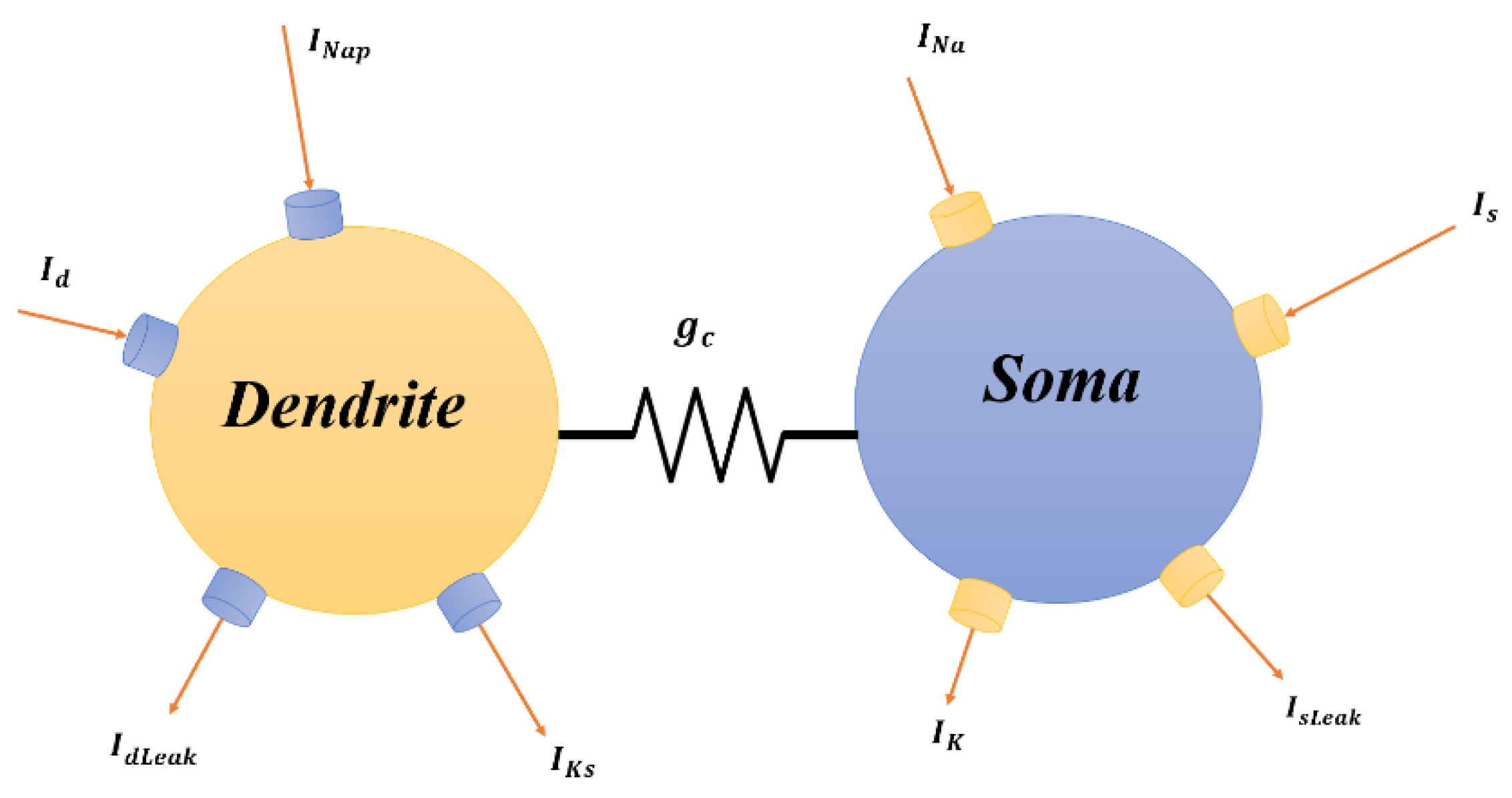
2. Two-Compartmental (PR) Model
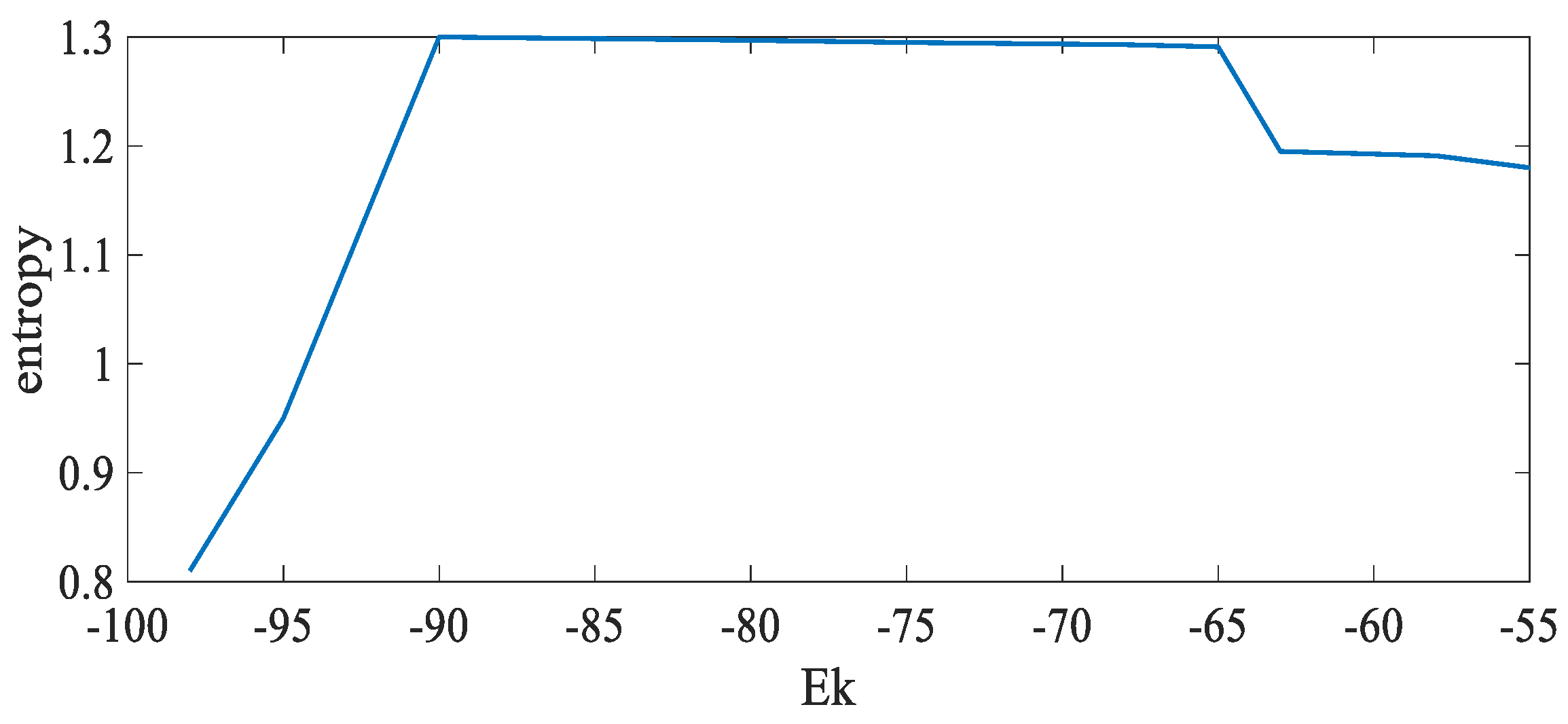
3. Analysis of Entropy
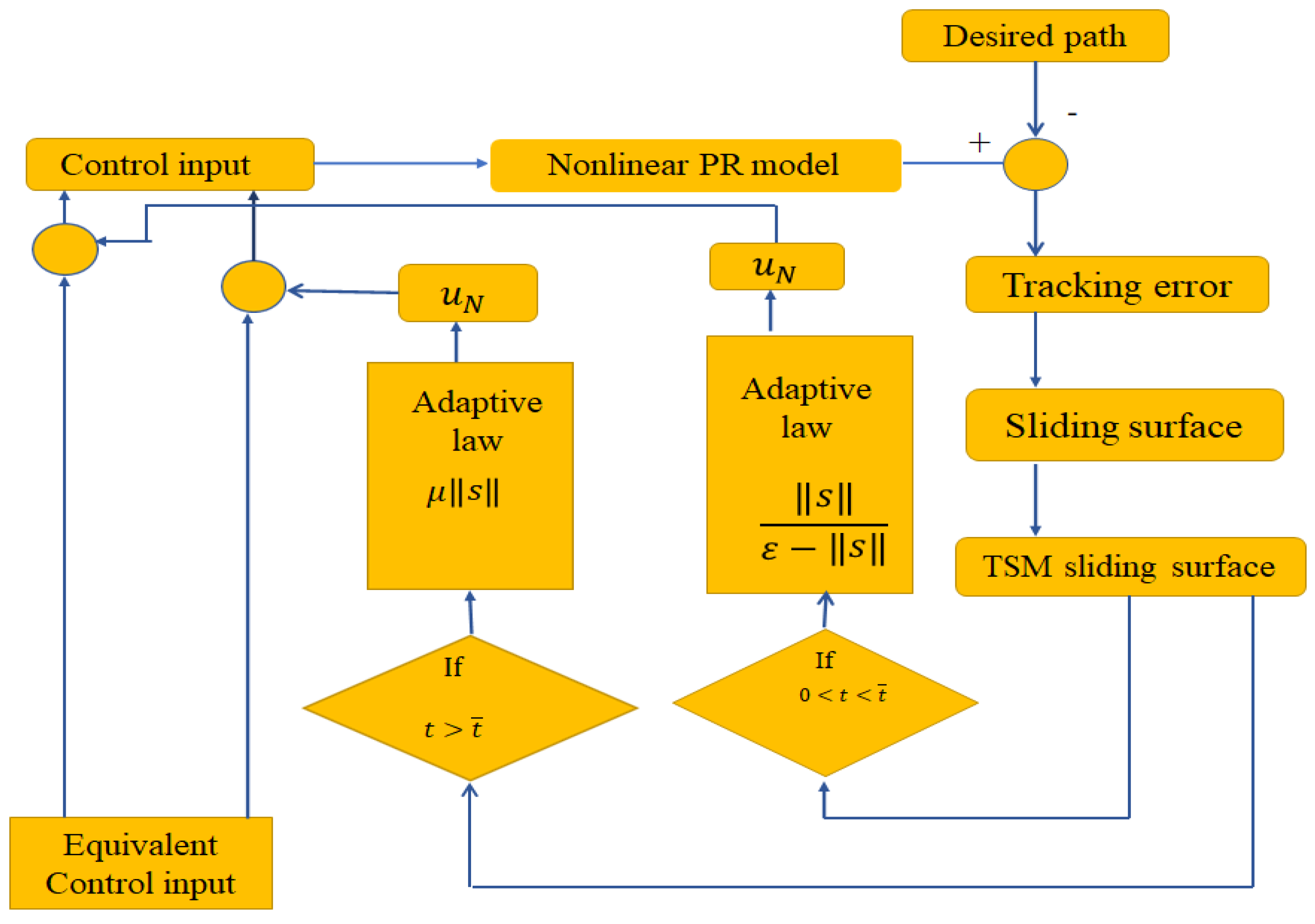
4. Adaptive Barrier Function Terminal Sliding Mode Control
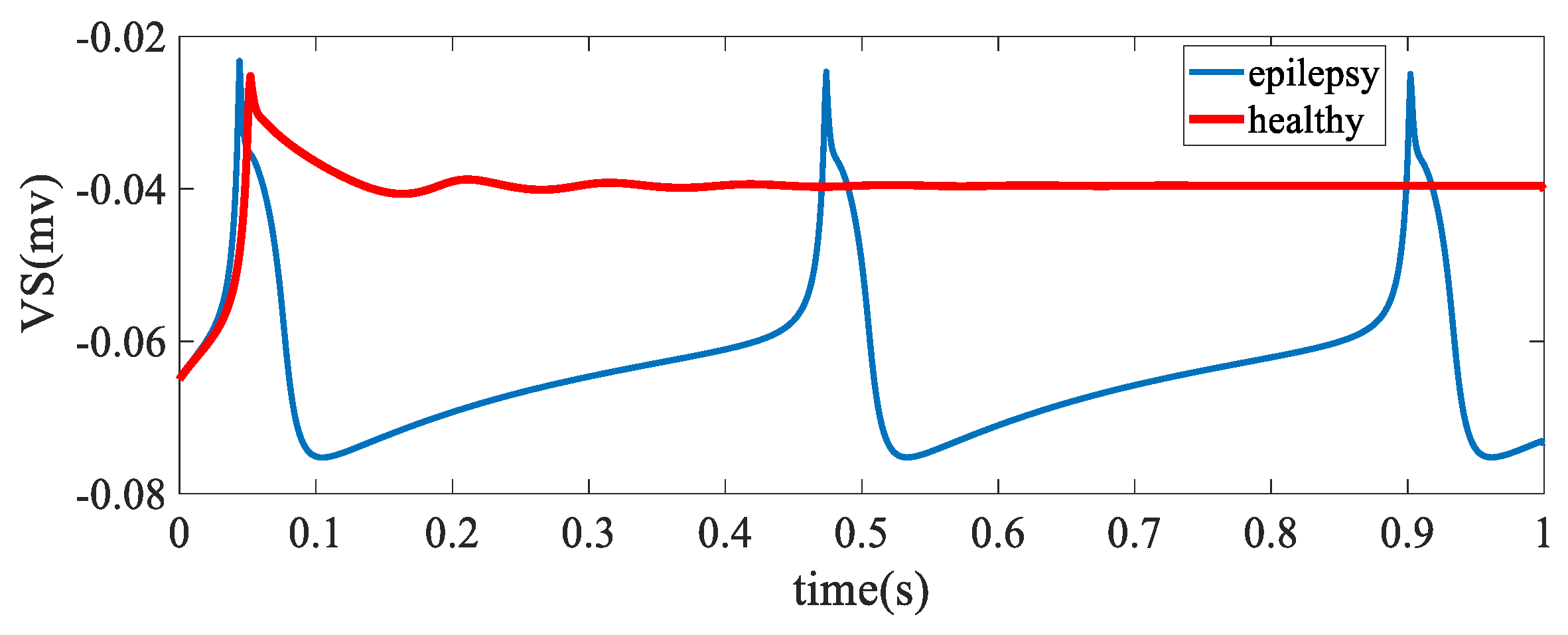
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Symbol | Quantity | Value | Unit | Symbol | Quantity | Value | Unit |
|---|---|---|---|---|---|---|---|
| Equilibrium potential | Conductance | ||||||
| Equilibrium potential | Conductance | ||||||
| Equilibrium potential | Conductance | ||||||
| Membrane capacitance | Conductance | ||||||
| Conductance | Compartment coupling | ||||||
| Conductance |
References
- Li, X.; Yang, H.; Yan, J.; Wang, X.; Yuan, Y.; Li, X. Seizure control by low-intensity ultrasound in mice with temporal lobe epilepsy. Epilepsy Res. 2019, 154, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Magiorkinis, E.; Sidiropoulou, K.; Diamantis, A. Hallmarks in the history of epilepsy: Epilepsy in antiquity. Epilepsy Behav. 2010, 17, 103–108. [Google Scholar] [CrossRef]
- Sun, M.; Wang, F.; Min, T.; Zang, T.; Wang, Y. Prediction for high risk clinical symptoms of epilepsy based on deep learning algorithm. IEEE Access 2018, 6, 77596–77605. [Google Scholar] [CrossRef]
- Ge, M.; Guo, J.; Xing, Y.; Feng, Z.; Lu, W.; Ma, X.; Geng, Y.; Zhang, X. Transient reduction in theta power caused by interictal spikes in human temporal lobe epilepsy. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju Island, Korea, 11–15 July 2017; pp. 4256–4259. [Google Scholar]
- Nakahara, S.; Adachi, M.; Ito, H.; Matsumoto, M.; Tajinda, K.; van Erp, T.G. Hippocampal pathophysiology: Commonality shared by temporal lobe epilepsy and psychiatric disorders. Neurosci. J. 2018, 2018, 4852359. [Google Scholar] [CrossRef] [PubMed]
- Al-Otaibi, F.; Baeesa, S.S.; Parrent, A.G.; Girvin, J.P.; Steven, D. Surgical techniques for the treatment of temporal lobe epilepsy. Epilepsy Res. Treat. 2012, 2012, 374848. [Google Scholar] [CrossRef]
- Blair, R.D. Temporal lobe epilepsy semiology. Epilepsy Res. Treat. 2012, 2012, 751510. [Google Scholar] [CrossRef] [PubMed]
- Duncan, J.S.; Sander, J.W.; Sisodiya, S.M.; Walker, M.C. Adult epilepsy. Lancet 2006, 367, 1087–1100. [Google Scholar] [CrossRef]
- Sisodiya, S.; Lin, W.R.; Harding, B.; Squier, M.; Thom, M. Drug resistance in epilepsy: Expression of drug resistance proteins in common causes of refractory epilepsy. Brain 2002, 125, 22–31. [Google Scholar] [CrossRef]
- Bonelli, S.B.; Thompson, P.J.; Yogarajah, M.; Powell, R.H.; Samson, R.S.; McEvoy, A.W.; Symms, M.R.; Koepp, M.J.; Duncan, J.S. Memory reorganization following anterior temporal lobe resection: A longitudinal functional MRI study. Brain 2013, 136, 1889–1900. [Google Scholar] [CrossRef] [PubMed]
- Mansouri, A.; Fallah, A.; Valiante, T.A. Determining surgical candidacy in temporal lobe epilepsy. Epilepsy Res. Treat. 2012, 2012, 706917. [Google Scholar] [CrossRef] [PubMed]
- Zangiabadi, N.; Ladino, L.D.; Sina, F.; Orozco-Hernández, J.P.; Carter, A.; Téllez-Zenteno, J.F. Deep brain stimulation and drug-resistant epilepsy: A review of the literature. Front. Neurol. 2019, 10, 601. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. Currents carried by sodium and potassium ions through the membrane of the giant axon of Loligo. J. Physiol. 1952, 116, 449. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef]
- Kriegeskorte, N.; Douglas, P.K. Cognitive computational neuroscience. Nat. Neurosci. 2018, 21, 1148–1160. [Google Scholar] [CrossRef]
- Liley, D.T.; Cadusch, P.J.; Wright, J.J. A continuum theory of electro-cortical activity. Neurocomputing 1999, 26, 795–800. [Google Scholar] [CrossRef]
- Pinsky, P.F.; Rinzel, J. Intrinsic and network rhythmogenesis in a reduced Traub model for CA3 neurons. J. Comput. Neurosci. 1994, 1, 39–60. [Google Scholar] [CrossRef]
- Suffczynski, P.; Kalitzin, S.; Da Silva, F.L. Dynamics of non-convulsive epileptic phenomena modeled by a bistable neuronal network. Neuroscience 2004, 126, 467–484. [Google Scholar] [CrossRef]
- Ullah, G.; Schiff, S.J. Tracking and control of neuronal Hodgkin-Huxley dynamics. Phys. Rev. E 2009, 79, 040901. [Google Scholar] [CrossRef]
- Chen, B.-S.; Li, C.-W. Robust observer-based tracking control of hodgkin-huxley neuron systems under environmental disturbances. Neural Comput. 2010, 22, 3143–3178. [Google Scholar] [CrossRef]
- Chen, S.; Yang, R. Control of repetitive firing in Hindmarsh-Rose model based on Krasovskii theorem. In Proceedings of the 2016 International Conference on Advanced Robotics and Mechatronics (ICARM), Macau, China, 18–20 August 2016; pp. 405–408. [Google Scholar]
- Soltan, A.; Xia, L.; Jackson, A.; Chester, G.; Degenaar, P. Fractional order PID system for suppressing epileptic activities. In Proceedings of the 2018 IEEE International Conference on Applied System Invention (ICASI), Chiba, Japan, 13–17 April 2018; pp. 338–341. [Google Scholar]
- Deng, B.; Li, G.; Wang, J.; Wei, X.; Su, F. Dynamic control of seizure states with input-output linearization method based on the Pinsky-Rinzel model. In Proceedings of the 2014 7th International Conference on Biomedical Engineering and Informatics, Fukuoka, Japan, 26–28 November 2014; pp. 425–430. [Google Scholar]
- Sinha, S.; Ditto, W.L. Controlling neuronal spikes. Phys. Rev. E 2001, 63, 056209. [Google Scholar] [CrossRef]
- Wei, W.; Wei, X.; Zuo, M.; Yu, T.; Li, Y. Seizure control in a neural mass model by an active disturbance rejection approach. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419890152. [Google Scholar] [CrossRef]
- Selvaraj, P.; Sleigh, J.W.; Freeman, W.J.; Kirsch, H.E.; Szeri, A.J. Open loop optogenetic control of simulated cortical epileptiform activity. J. Comput. Neurosci. 2014, 36, 515–525. [Google Scholar] [CrossRef][Green Version]
- Edwards, C.; Spurgeon, S. Sliding Mode Control: Theory and Applications; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Khalil, H.K. Nonlinear Systems Third Edition; Patience Hall: Hoboken, NJ, USA, 2002; Volume 115. [Google Scholar]
- Utkin, V.I. Sliding mode control design principles and applications to electric drives. IEEE Trans. Ind. Electron. 1993, 40, 23–36. [Google Scholar] [CrossRef]
- Rojsiraphisal, T.; Mobayen, S.; Asad, J.H.; Vu, M.T.; Chang, A.; Puangmalai, J. Fast terminal sliding control of underactuated robotic systems based on disturbance observer with experimental validation. Mathematics 2021, 9, 1935. [Google Scholar] [CrossRef]
- Mirzaei, A.; Ozgoli, S.; Jajarm, A.E. Chaotic analysis of the human brain cortical model and robust control of epileptic seizures using sliding mode control. Syst. Sci. Control Eng. Open Access J. 2014, 2, 216–227. [Google Scholar] [CrossRef]
- Mobayen, S. Design of LMI-based global sliding mode controller for uncertain nonlinear systems with application to Genesio’s chaotic system. Complexity 2015, 21, 94–98. [Google Scholar] [CrossRef]
- Mobayen, S. An LMI-based robust controller design using global nonlinear sliding surfaces and application to chaotic systems. Nonlinear Dyn. 2015, 79, 1075–1084. [Google Scholar] [CrossRef]
- Wu, Y.; Yu, X.; Man, Z. Terminal sliding mode control design for uncertain dynamic systems. Syst. Control Lett. 1998, 34, 281–287. [Google Scholar] [CrossRef]
- Zhihong, M.; Yu, X.H. Terminal sliding mode control of MIMO linear systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 1065–1070. [Google Scholar] [CrossRef]
- Puangmalai, J.; Tongkum, J.; Rojsiraphisal, T. Finite-time stability criteria of linear system with non-differentiable time-varying delay via new integral inequality. Math. Comput. Simul. 2020, 171, 170–186. [Google Scholar] [CrossRef]
- Qian, M.; Zhang, Z.; Zhong, G.; Bo, C. A novel nonsingular integral terminal sliding mode control scheme in epilepsy treatment. Trans. Inst. Meas. Control 2022, 44, 1194–1204. [Google Scholar] [CrossRef]
- Rezvani Ardakani, S.; Mohammad-Ali-Nezhad, S.; Ghasemi, R. Epilepsy Control in a Combination of the Cortical and Optogenetic Models using Fixed Time Integral Super Twisting Sliding Mode Controller. Iran. J. Biomed. Eng. 2019, 13, 273–289. [Google Scholar]
- Chen, J.; Shuai, Z.; Zhang, H.; Zhao, W. Path following control of autonomous four-wheel-independent-drive electric vehicles via second-order sliding mode and nonlinear disturbance observer techniques. IEEE Trans. Ind. Electron. 2020, 68, 2460–2469. [Google Scholar] [CrossRef]
- Alattas, K.A.; Mofid, O.; Alanazi, A.K.; Abo-Dief, H.M.; Bartoszewicz, A.; Bakouri, M.; Mobayen, S. Barrier Function Adaptive Nonsingular Terminal Sliding Mode Control Approach for Quad-Rotor Unmanned Aerial Vehicles. Sensors 2022, 22, 909. [Google Scholar] [CrossRef]
- Mobayen, S.; Alattas, K.A.; Assawinchaichote, W. Adaptive continuous barrier function terminal sliding mode control technique for disturbed robotic manipulator. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 4403–4412. [Google Scholar] [CrossRef]
- Obeid, H.; Fridman, L.M.; Laghrouche, S.; Harmouche, M. Barrier function-based adaptive sliding mode control. Automatica 2018, 93, 540–544. [Google Scholar] [CrossRef]
- Kepecs, A.; Wang, X.-J. Analysis of complex bursting in cortical pyramidal neuron models. Neurocomputing 2000, 32, 181–187. [Google Scholar] [CrossRef]
- Schwartzkroin, P.A. Role of the hippocampus in epilepsy. Hippocampus 1994, 4, 239–242. [Google Scholar] [CrossRef]
- Rahimian, E.; Zabihi, S.; Amiri, M.; Linares-Barranco, B. Digital implementation of the two-compartmental Pinsky–Rinzel pyramidal neuron model. IEEE Trans. Biomed. Circuits Syst. 2017, 12, 47–57. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Adeli, H.; Ghosh-Dastidar, S.; Dadmehr, N. A wavelet-chaos methodology for analysis of EEGs and EEG subbands to detect seizure and epilepsy. IEEE Trans. Biomed. Eng. 2007, 54, 205–211. [Google Scholar] [CrossRef]
- Mirzaei, A.; Ayatollahi, A.; Vavadi, H. Statistical analysis of epileptic activities based on histogram and wavelet-spectral entropy. J. Biomed. Sci. Eng. 2011, 4, 207. [Google Scholar] [CrossRef][Green Version]
- Behnamgol, V.; Vali, A.R. Terminal sliding mode control for nonlinear systems with both matched and unmatched uncertainties. Iran. J. Electr. Electron. Eng. 2015, 11, 109–117. [Google Scholar]
- Feng, Y.; Yu, X.; Man, Z. Non-singular terminal sliding mode control of rigid manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]
- Venkataraman, S.; Gulati, S. Control of nonlinear systems using terminal sliding modes. In Proceedings of the 1992 American Control Conference, Chicago, IL, USA, 24–26 June 1992. [Google Scholar]
- Alattas, K.A.; Mofid, O.; El-Sousy, F.F.; Alanazi, A.K.; Awrejcewicz, J.; Mobayen, S. Adaptive Nonsingular Terminal Sliding Mode Control for Performance Improvement of Perturbed Nonlinear Systems. Mathematics 2022, 10, 1064. [Google Scholar] [CrossRef]
- Mofid, O.; Mobayen, S.; Wong, W.-K. Adaptive terminal sliding mode control for attitude and position tracking control of quadrotor UAVs in the existence of external disturbance. IEEE Access 2020, 9, 3428–3440. [Google Scholar] [CrossRef]

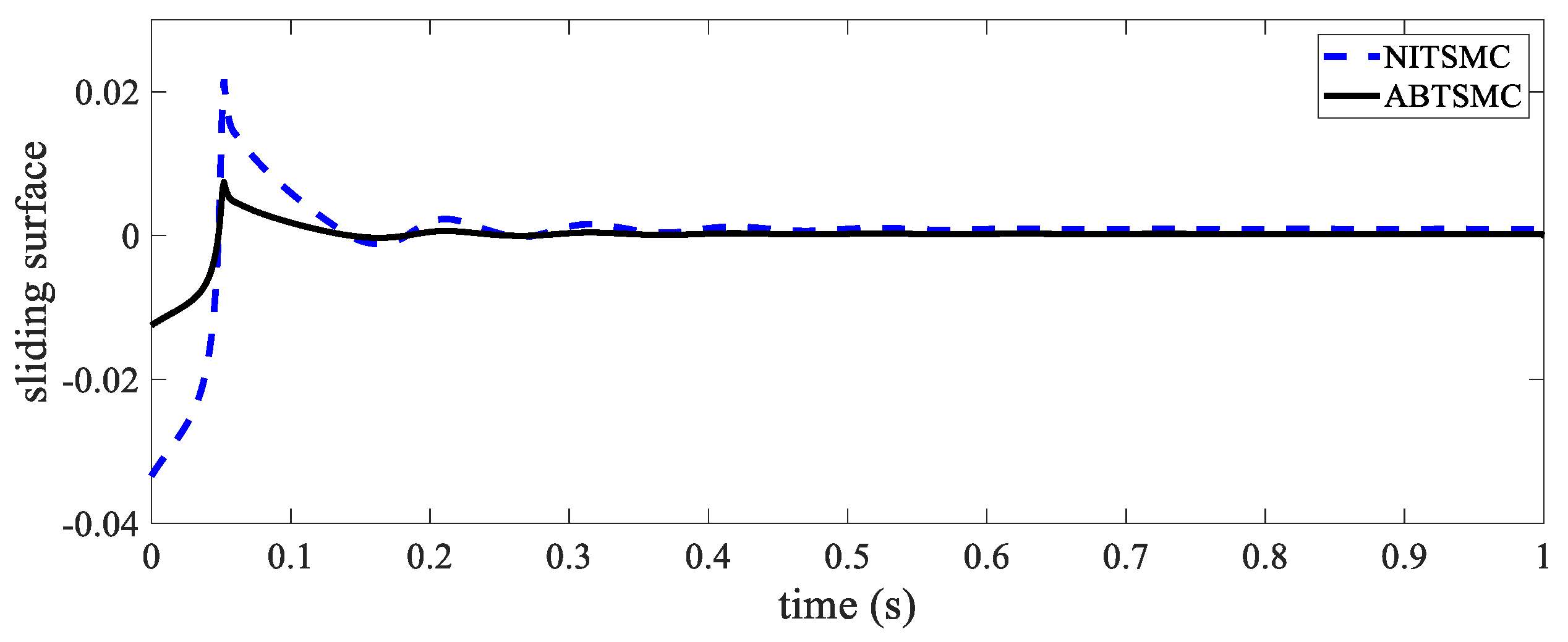
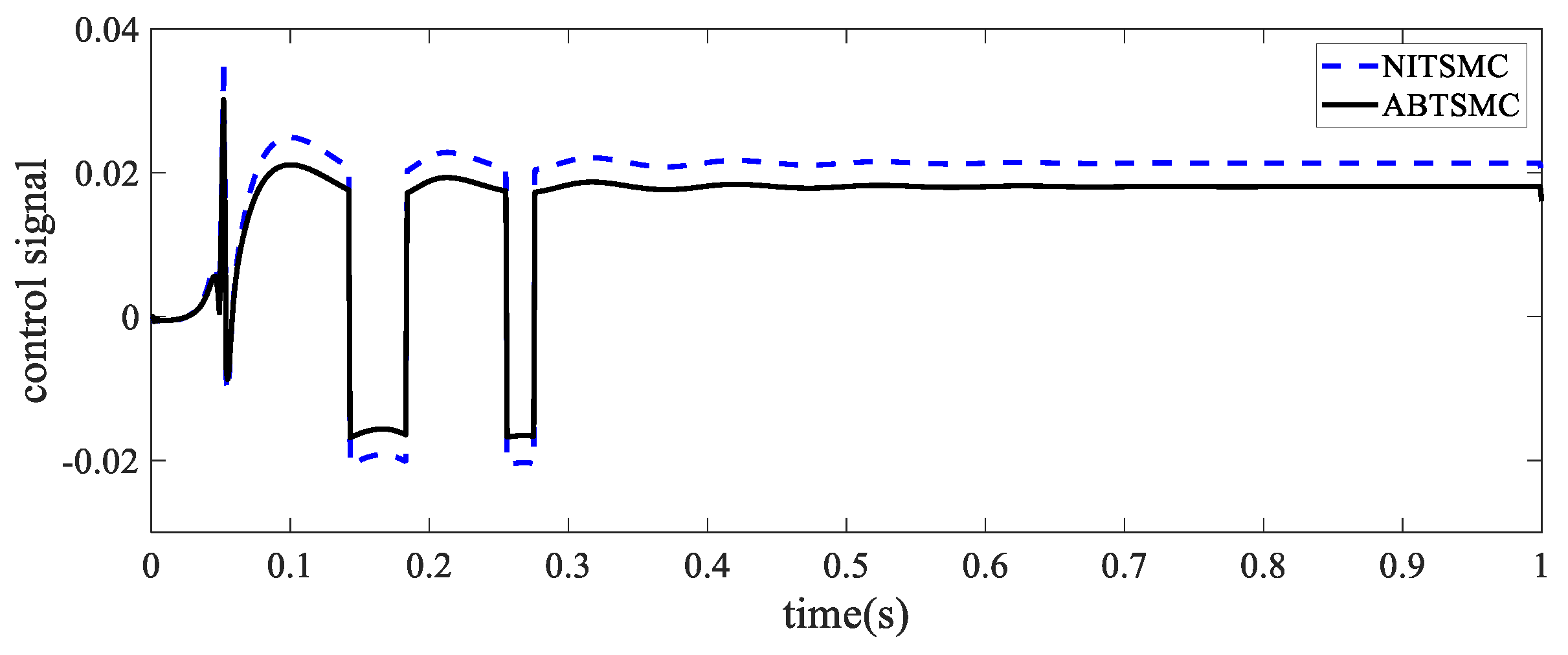

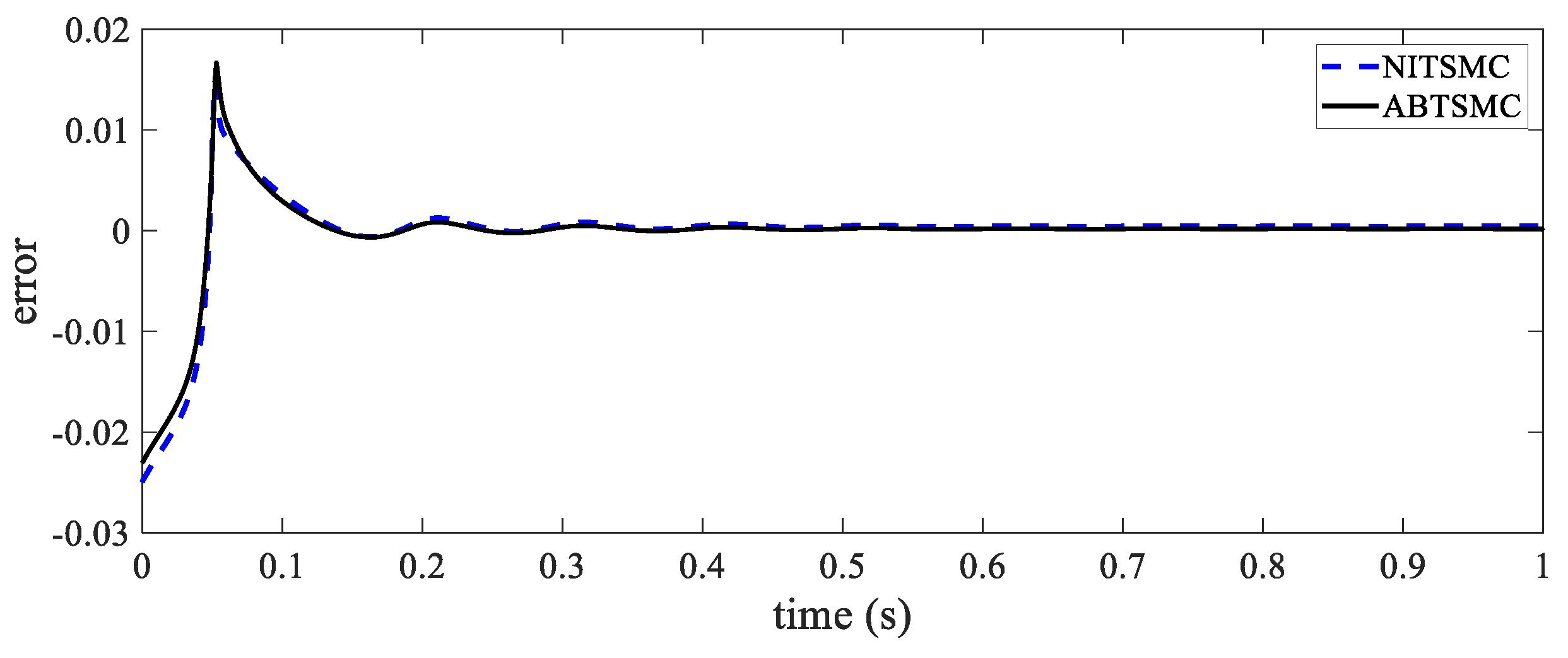
| Controller | MSE | IAE | ISV (u) | Chattering Phenomenon |
|---|---|---|---|---|
| ABTSMC | No | |||
| Method [37] | No |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mokhtare, Z.; Vu, M.T.; Mobayen, S.; Rojsiraphisal, T. An Adaptive Barrier Function Terminal Sliding Mode Controller for Partial Seizure Disease Based on the Pinsky–Rinzel Mathematical Model. Mathematics 2022, 10, 2940. https://doi.org/10.3390/math10162940
Mokhtare Z, Vu MT, Mobayen S, Rojsiraphisal T. An Adaptive Barrier Function Terminal Sliding Mode Controller for Partial Seizure Disease Based on the Pinsky–Rinzel Mathematical Model. Mathematics. 2022; 10(16):2940. https://doi.org/10.3390/math10162940
Chicago/Turabian StyleMokhtare, Zahra, Mai The Vu, Saleh Mobayen, and Thaned Rojsiraphisal. 2022. "An Adaptive Barrier Function Terminal Sliding Mode Controller for Partial Seizure Disease Based on the Pinsky–Rinzel Mathematical Model" Mathematics 10, no. 16: 2940. https://doi.org/10.3390/math10162940
APA StyleMokhtare, Z., Vu, M. T., Mobayen, S., & Rojsiraphisal, T. (2022). An Adaptive Barrier Function Terminal Sliding Mode Controller for Partial Seizure Disease Based on the Pinsky–Rinzel Mathematical Model. Mathematics, 10(16), 2940. https://doi.org/10.3390/math10162940








