Fast High-Order Algorithms for Electromagnetic Scattering Problem from Finite Array of Cavities in TE Case with High Wave Numbers
Abstract
:1. Introduction
2. The Single Cavity Scattering Problem in TE Polarization
3. Fast High-Order Schemes for the Scattering from Single Cavity
3.1. Second-Order Finite Difference Scheme
3.2. The Fast Second-Order Algorithm for the Scattering from the Single Cavity
| Algorithm 1: The procedure of the second-order fast algorithm for scattering from the single cavity (The Fast Algorithm for the Scattering Problem From the Single Cavity). |
3.3. Fourth-Order Finite Difference Scheme
3.4. The Fast Fourth-Order Algorithm for the Scattering from the Single Cavity
4. Fast High-Order Schemes for the Scattering from Finite Array of Cavities
The Fast Algorithm for the Scattering by a Finite Array of Cavities
5. Numerical Experiments
5.1. Example 1
5.2. Example 2
5.3. Example 3
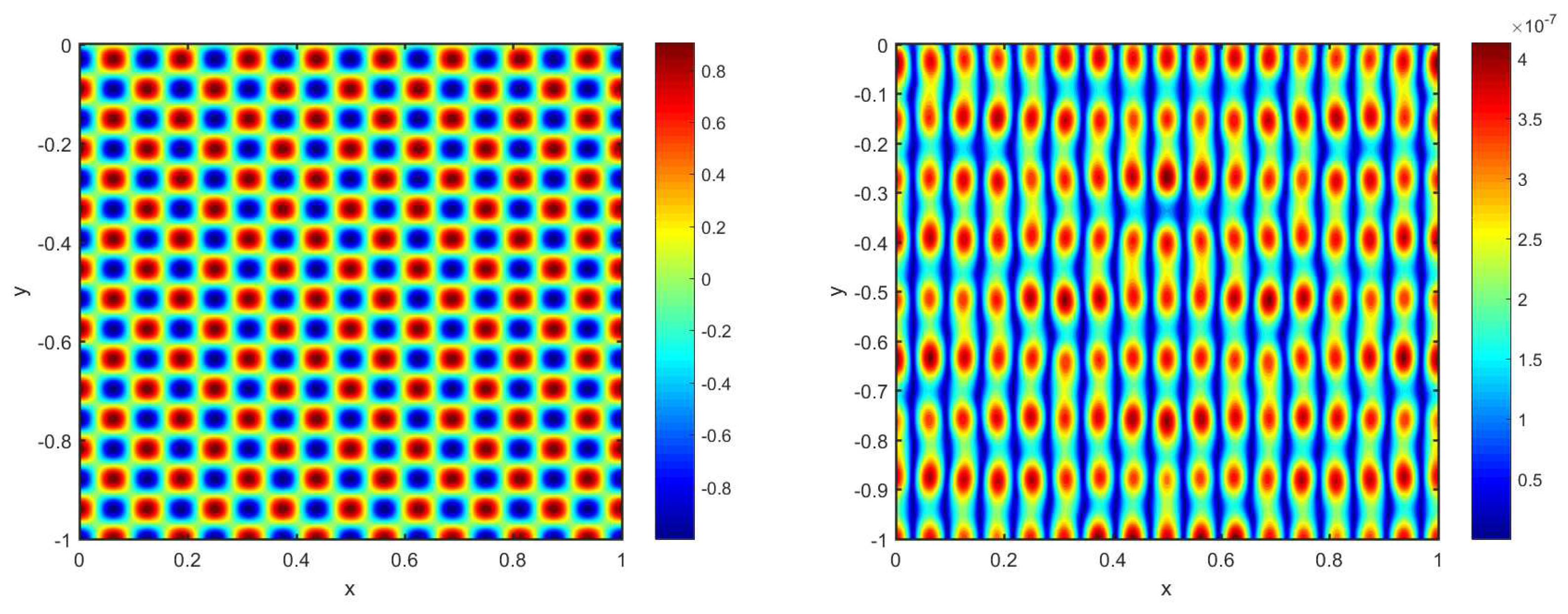
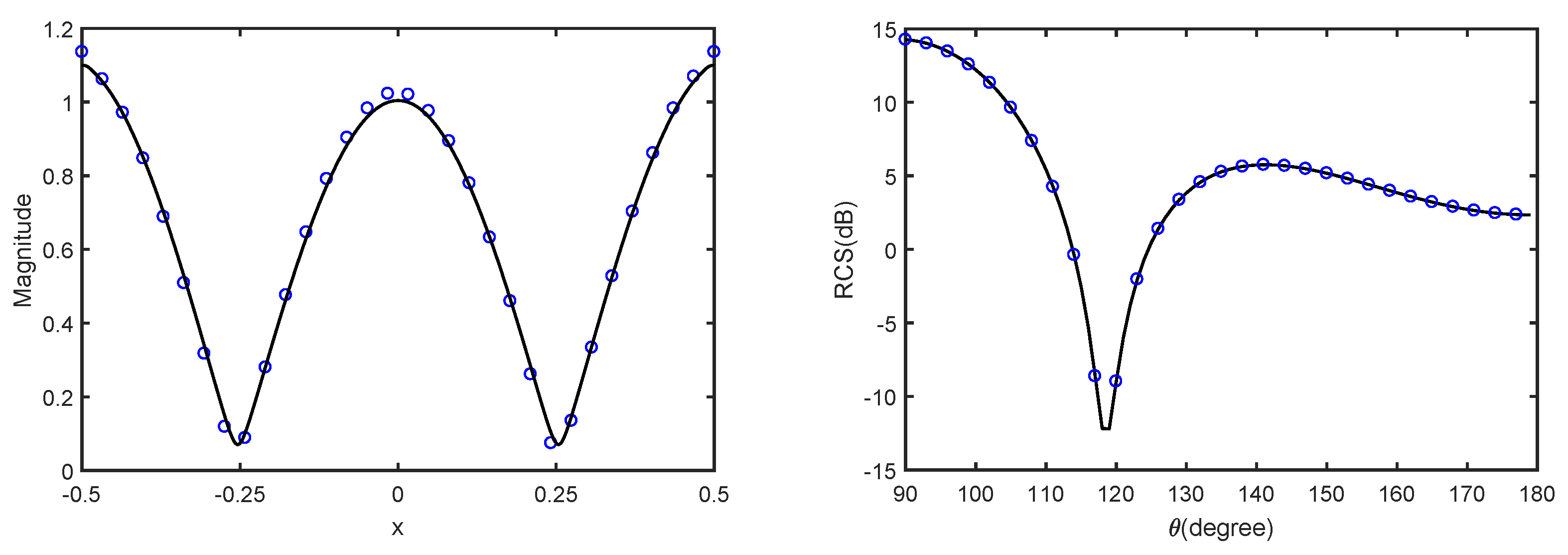
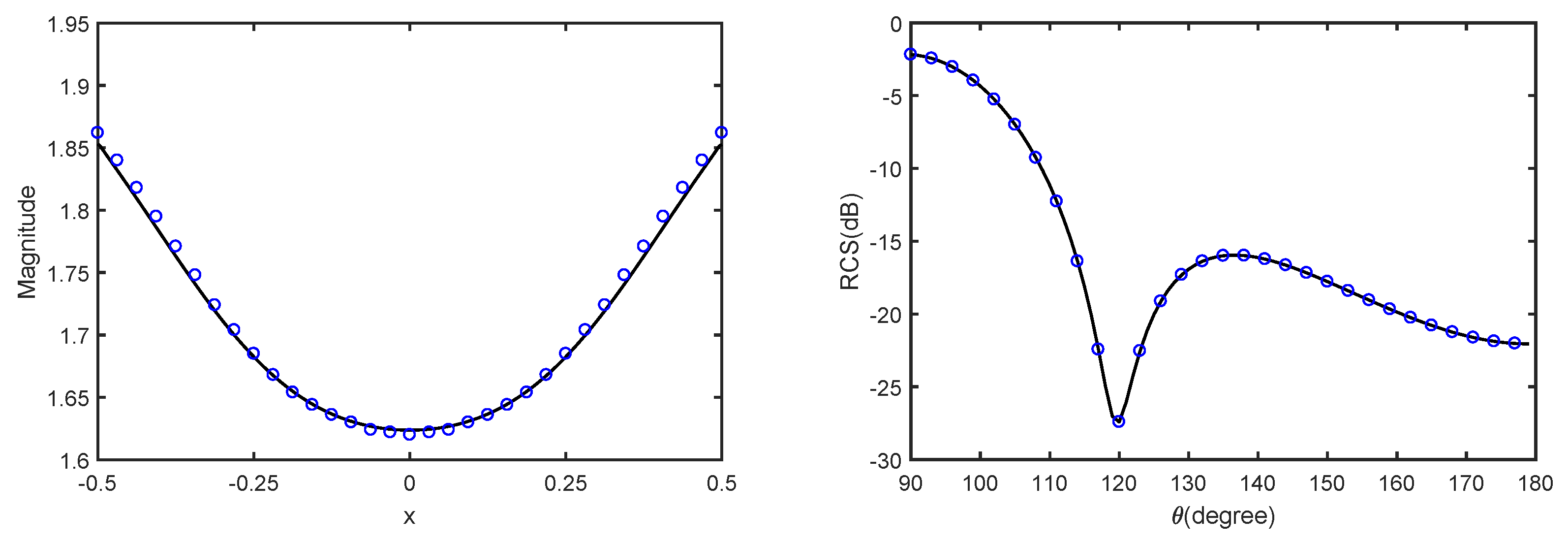
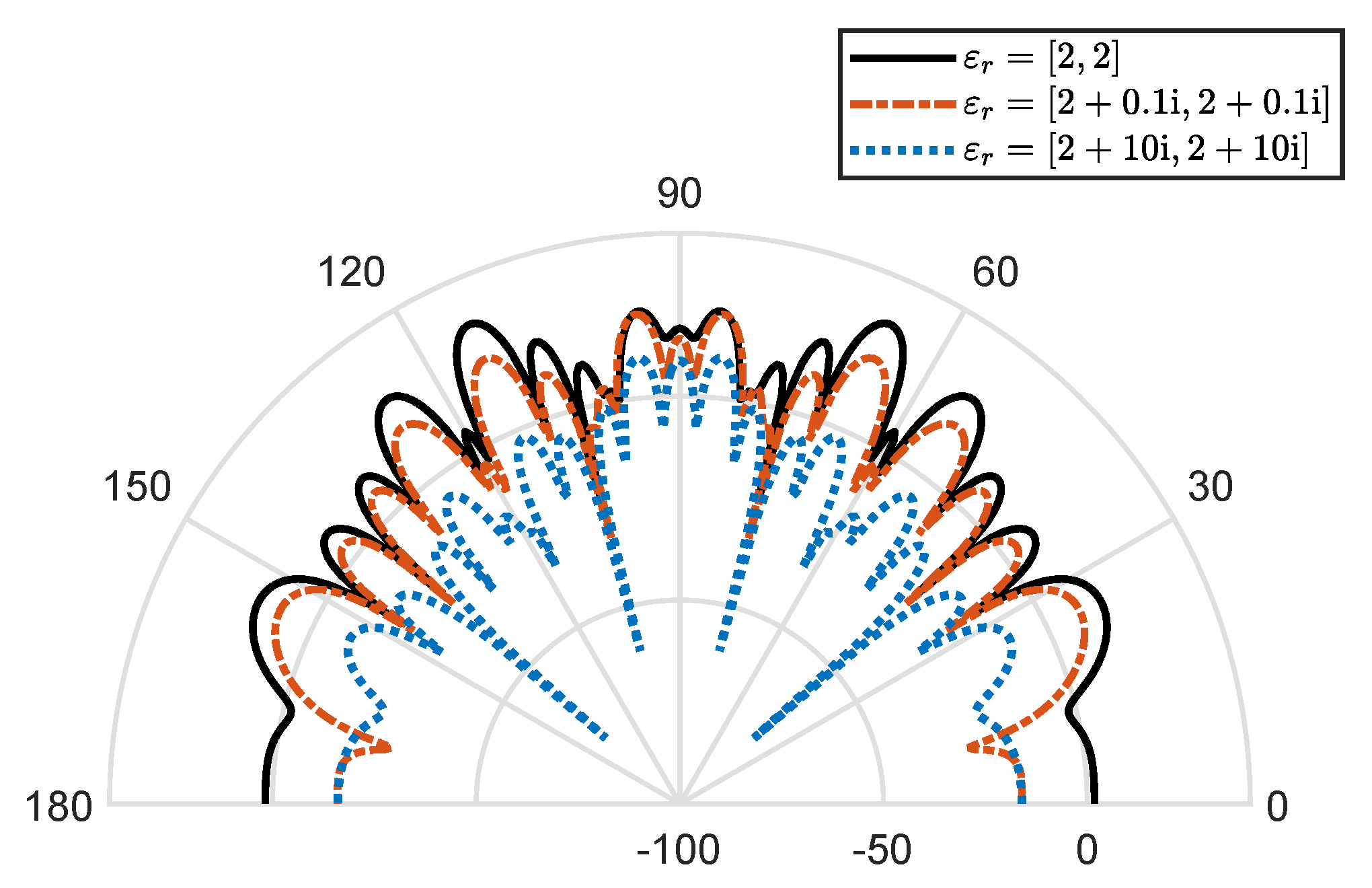
5.4. Example 4
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, C.; Gan, Y. 2D cavity modeling using method of moments and iterative solvers. J. Electromagn. Waves Appl. 2003, 17, 1739–1740. [Google Scholar] [CrossRef]
- Wood, W.; Wood, A. Development and numerical solution of integral equations for electromagnetic scattering from a trough in a ground plane. IEEE T. Antenn. Propag. 1999, 47, 1318–1322. [Google Scholar] [CrossRef]
- Jin, J. The Finite Element Method in Electromagnetics, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2002. [Google Scholar]
- Liu, J.; Jin, J. A special higher order finite-element method for scattering by deep cavities. IEEE Trans. Antennas Propag. 2000, 48, 694–703. [Google Scholar]
- Liu, J.; Jin, J. A highly effective preconditioner for solving the finite element-boundary integral matrix equation of 3-D scattering. IEEE Trans. Antennas Propag. 2002, 50, 1212–1221. [Google Scholar] [CrossRef]
- Ross, D.; Volakis, J.; Anastassiu, H. Hybrid finite element-modal analysis of jet engine inlet scattering. IEEE Trans. Antennas Propag. 1995, 43, 277–285. [Google Scholar] [CrossRef]
- Alavikia, B.; Ramahi, O. Hybrid finite-element-boundary integral algorithm to solve the problem of scattering from a finite and infinite array of cavities with stratified dielectric coating. J. Opt. Soc. Am. A 2011, 28, 1022–1031. [Google Scholar] [CrossRef] [PubMed]
- Alavikia, B.; Ramahi, O. Coupling interactions in electromagnetic scattering from finite array of cavities with stratified dielectric coating. J. Opt. Soc. Am. A 2012, 29, 1132–1140. [Google Scholar] [CrossRef] [PubMed]
- Ito, K.; Qiao, Z.; Toivanen, J. A fast preconditioned iterative algorithm for the electromagnetic scattering from a large cavity. J. Sci. Comput. 2012, 53, 435–450. [Google Scholar]
- Bao, G.; Sun, W. A fast algorithm for the electromagnetic scattering from a large cavity. SIAM J. Sci. Comput. 2005, 27, 553–574. [Google Scholar] [CrossRef]
- Ito, K.; Qiao, Z.; Toivanen, J. A domain decomposition solver for acoustic scattering by elastic objects in layered media. J. Comput. Phys. 2008, 227, 8685–8698. [Google Scholar] [CrossRef]
- Zhao, M. A fast high order iterative solver for the electromagnetic scattering by open cavities filled with the inhomogeneous media. Adv. Appl. Math. Mech. 2013, 5, 235–257. [Google Scholar] [CrossRef]
- Zhao, M.; Qiao, Z.; Tang, T. A fast high order method for electromagnetic scattering by large open cavities. J. Comput. Math. 2011, 29, 287–304. [Google Scholar] [CrossRef]
- Zhao, M.; Zhu, N. A fast preconditioned iterative method for the electromagnetic scattering by multiple cavities with high wave numbers. J. Comput. Phys. 2019, 398, 108826. [Google Scholar] [CrossRef]
- Schiavone, G.; O’Neill, K.; Paulsen, K. Scattering from groove patterns in a perfectly conducting surface. J. Opt. Soc. Am. A 1997, 14, 2212–2222. [Google Scholar] [CrossRef]
- Van, T.; Wood, A. A time-domain finite element method for helmholtz equations. J. Comput. Phys. 2002, 183, 486–507. [Google Scholar] [CrossRef]
- Li, P. A survey of open cavity scattering problems. J. Comput. Math. 2019, 36, 1–16. [Google Scholar] [CrossRef]
- Xiang, Z.; Chia, T. A hybrid BEM/WTM approach for analysis of the EM scattering from large open-ended cavities. IEEE Trans. Antennas Propag. 2001, 49, 165–173. [Google Scholar] [CrossRef]
- Li, P.; Wang, L.; Wood, A. Analysis of transient electromagnetic scattering from a three-dimensional open cavity. SIAM J. Appl. Math. 2015, 75, 1675–1699. [Google Scholar] [CrossRef]
- Jiang, X.; Li, P.; Lv, J.; Zheng, W. An adaptive finite element method for the wave scattering with transparent boundary condition. J. Sci. Comput. 2017, 72, 936–956. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, X.; Lai, J.; Li, P. A fast algorithm for the electromagnetic scattering from a large rectangular cavity in three dimensions. J. Comput. Phys. 2021, 437, 110331. [Google Scholar] [CrossRef]
- Du, K.; Sun, W.; Zhang, X. Arbitrary high-order C0 tensor product Galerkin finite element methods for the electromagnetic scattering from a large cavity. J. Comput. Phys. 2013, 242, 181–195. [Google Scholar] [CrossRef]
- Mumtaz, F.; Ashraf, M.; Dai, Y. Numerical approach to approximate the electromagnetic scattering from random PEC cylinder placed below in dielectric half-space. Optik 2020, 206, 163751. [Google Scholar] [CrossRef]
- Zhao, M.; Zhu, N.; Wang, L. Fast algorithms for the electromagnetic scattering by partly covered cavities. J. Comput. Appl. Math. 2021, 40, 7. [Google Scholar] [CrossRef]
- Ammari, H.; Bao, G.; Wood, A. A cavity problem for maxwell’s equations. Meth. Appl. Anal. 2002, 9, 249–260. [Google Scholar] [CrossRef]
- Ammari, H.; Bao, G.; Wood, A. Analysis of the electromagnetic scattering from a cavity. J. Jpn. J. Indust. Appl. Math. 2002, 19, 301–310. [Google Scholar] [CrossRef]
- Bao, G.; Zhang, W. An improved mode-matching method for large cavities. IEEE Antennas Wirel. Propag. Lett. 2005, 4, 393–396. [Google Scholar]
- Li, P.; Wood, A. A two-dimensional helmhotlz equation solution for the multiple cavity scattering problem. J. Comput. Phys. 2013, 240, 100–120. [Google Scholar] [CrossRef]
- Wu, X.; Zheng, W. An adaptive perfectly matched layer method for multiple cavity scattering problems. Commun. Comput. Phys. 2016, 19, 534–558. [Google Scholar] [CrossRef]
- Du, K. Two transparent boundary conditions for the electromagnetic scattering from two-dimensional overfilled cavities. J. Comput. Phys. 2011, 230, 5822–5835. [Google Scholar] [CrossRef]
- Uber, R. Time Domain Analysis of the Electromagnetic Scattering From Multiple Cavities Embedded in a Ground Plane. Ph.D. Thesis, Air Force Institute of Technology, Wright-Patterson AFB, OH, USA, 2016. [Google Scholar]



| h | Order | Order | CPU Time (s) | ||
|---|---|---|---|---|---|
| 1/16 | 2.0281 × | 9.7386 × | 0.0080 | ||
| 1/32 | 4.6314 × | 2.1306 | 4.4007 × | 1.1460 | 0.0982 |
| 1/64 | 1.1937 × | 1.9560 | 1.3852 × | 1.6676 | 0.0200 |
| 1/128 | 3.0142 × | 1.9856 | 3.4765 × | 1.9944 | 0.0317 |
| 1/256 | 7.5720 × | 1.9931 | 8.7693 × | 1.9871 | 0.0894 |
| h | Order | Order | CPU Time (s) | ||
|---|---|---|---|---|---|
| 1/16 | 2.9375 × | 1.6377 × | 0.0382 | ||
| 1/32 | 1.9114 × | 3.9419 | 1.1956 × | 3.7758 | 0.0561 |
| 1/64 | 1.3079 × | 3.8694 | 1.1329 × | 3.3997 | 0.0737 |
| 1/128 | 8.4704 × | 3.9486 | 8.0131 × | 3.8215 | 0.1400 |
| 1/256 | 5.3553 × | 3.9834 | 5.2272 × | 3.9382 | 0.6564 |
| h | Order | Order | CPU Time (s) | ||
|---|---|---|---|---|---|
| 1/64 | 2.1762 × | 1.4052 × | 0.0478 | ||
| 1/128 | 1.4300 × | 3.9277 | 1.2347 × | 3.5086 | 0.0908 |
| 1/256 | 9.1459 × | 3.9668 | 8.6201 × | 3.8403 | 0.5833 |
| 1/512 | 5.7521 × | 3.9910 | 5.6021 × | 3.9437 | 5.4535 |
| 1/1024 | 3.6003 × | 3.9979 | 3.5557 × | 3.9778 | 66.1697 |
| h | CPU Time of Fourth-Order Scheme (s) | CPU Time of Fast Fourth-Order Scheme (s) |
|---|---|---|
| 1/128 | 0.0211 | 0.0083 |
| 1/256 | 0.3503 | 0.0544 |
| 1/512 | 1.3928 | 0.2142 |
| 1/1024 | 8.1006 | 1.2517 |
| 1/2048 | out of memory | 10.7882 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, M.; He, J.; Zhu, N. Fast High-Order Algorithms for Electromagnetic Scattering Problem from Finite Array of Cavities in TE Case with High Wave Numbers. Mathematics 2022, 10, 2937. https://doi.org/10.3390/math10162937
Zhao M, He J, Zhu N. Fast High-Order Algorithms for Electromagnetic Scattering Problem from Finite Array of Cavities in TE Case with High Wave Numbers. Mathematics. 2022; 10(16):2937. https://doi.org/10.3390/math10162937
Chicago/Turabian StyleZhao, Meiling, Jiahui He, and Na Zhu. 2022. "Fast High-Order Algorithms for Electromagnetic Scattering Problem from Finite Array of Cavities in TE Case with High Wave Numbers" Mathematics 10, no. 16: 2937. https://doi.org/10.3390/math10162937
APA StyleZhao, M., He, J., & Zhu, N. (2022). Fast High-Order Algorithms for Electromagnetic Scattering Problem from Finite Array of Cavities in TE Case with High Wave Numbers. Mathematics, 10(16), 2937. https://doi.org/10.3390/math10162937





