A Modified Radial Point Interpolation Method (M-RPIM) for Free Vibration Analysis of Two-Dimensional Solids
Abstract
:1. Introduction
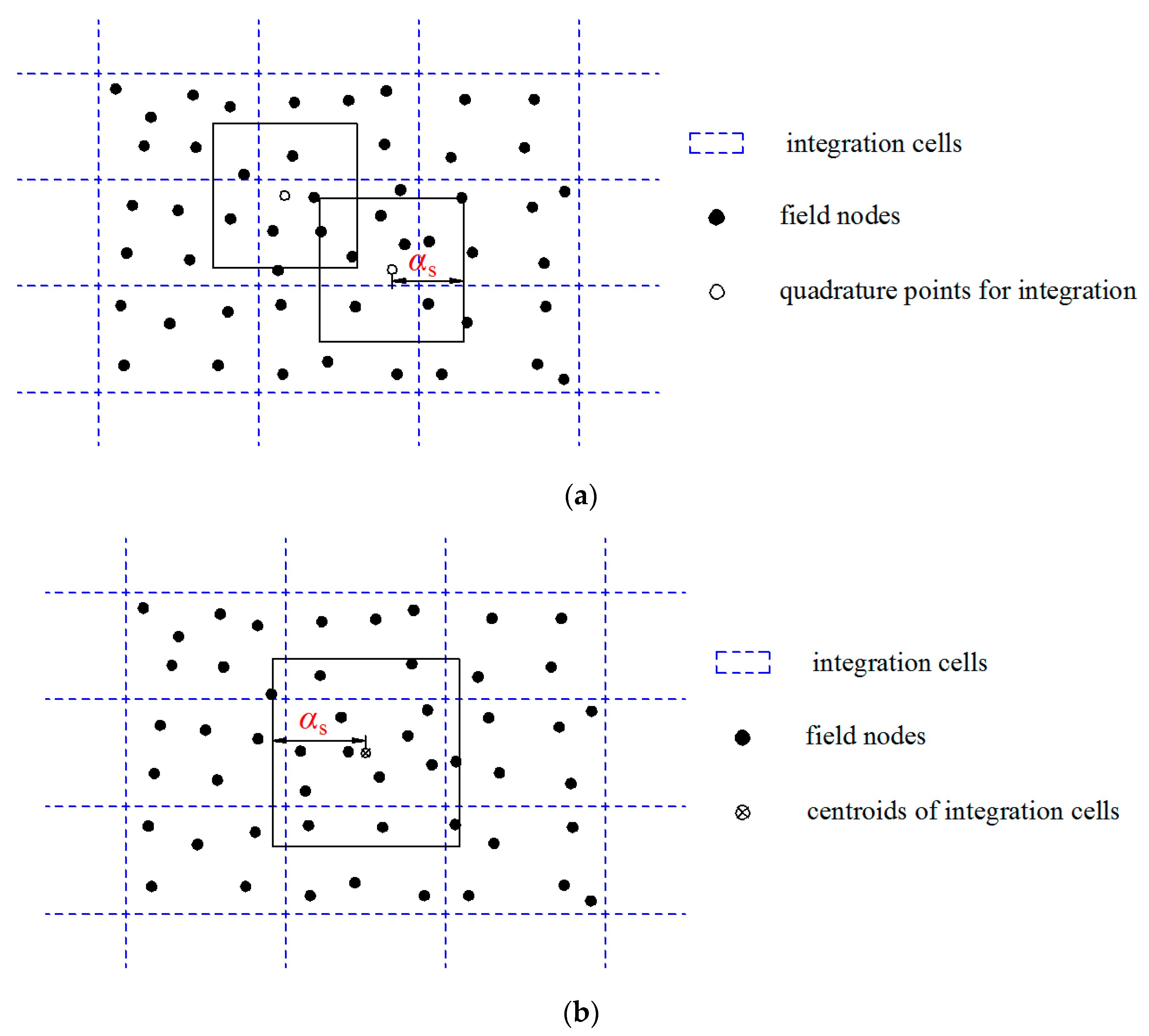
2. Formulation of the Original RPIM and the Present M-RPIM
3. Formulation of the Elastodynamics of Two-Dimensional Solids
4. Numerical Example
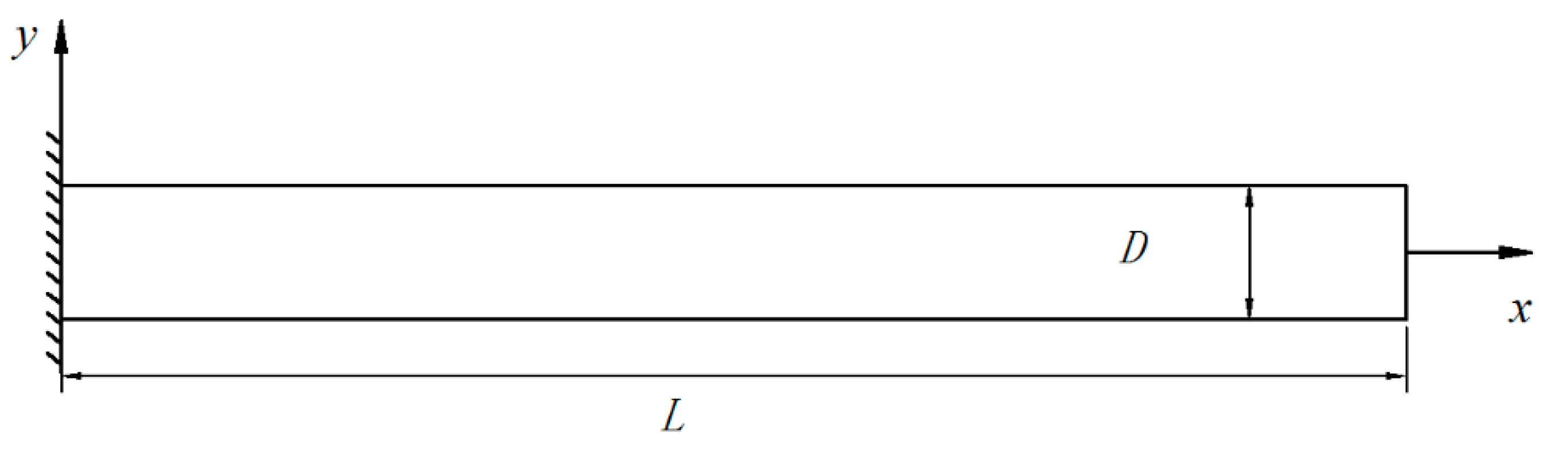
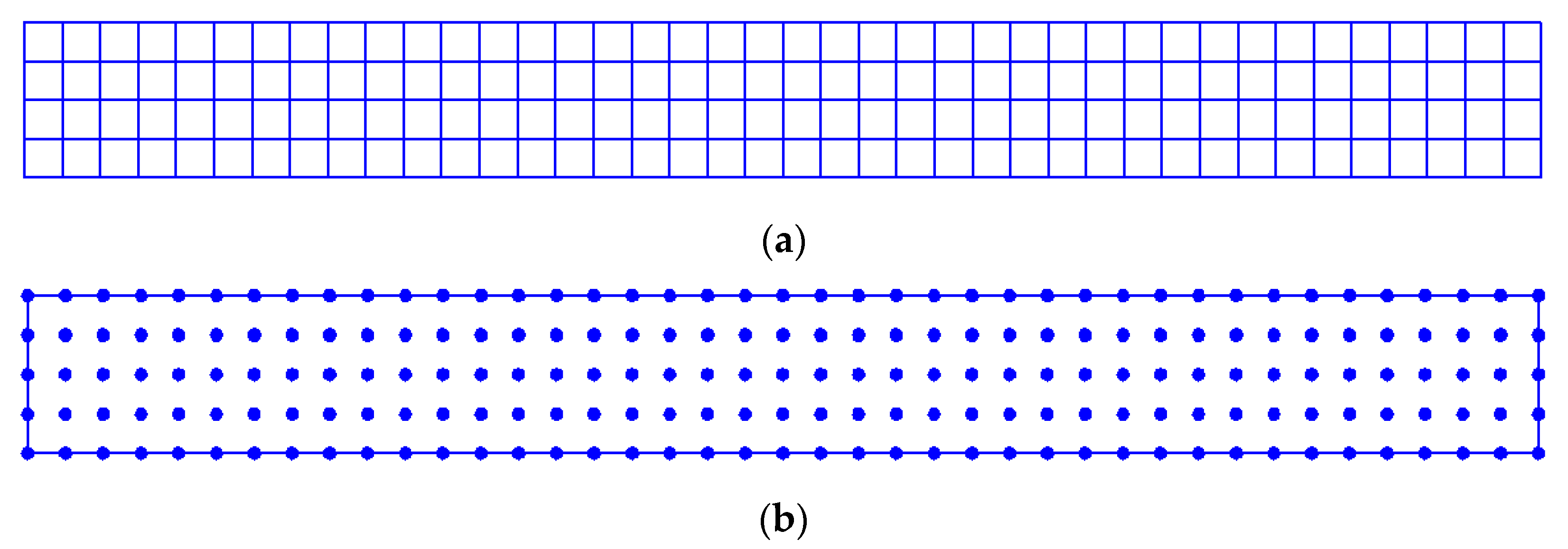
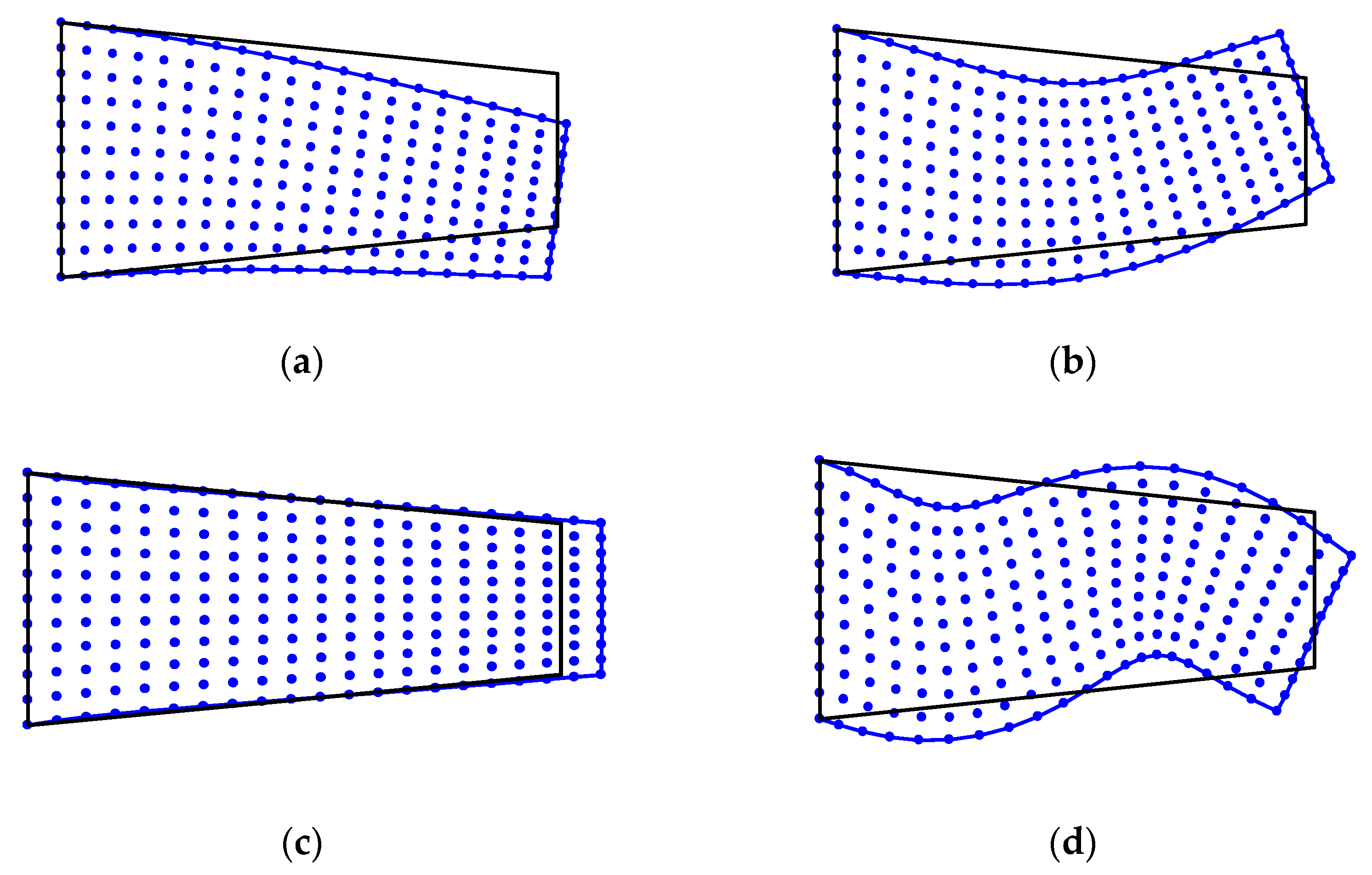
4.1. Free Vibration Analysis of the Cantilever Beam
4.1.1. Computation Accuracy Study
4.1.2. Convergence Study
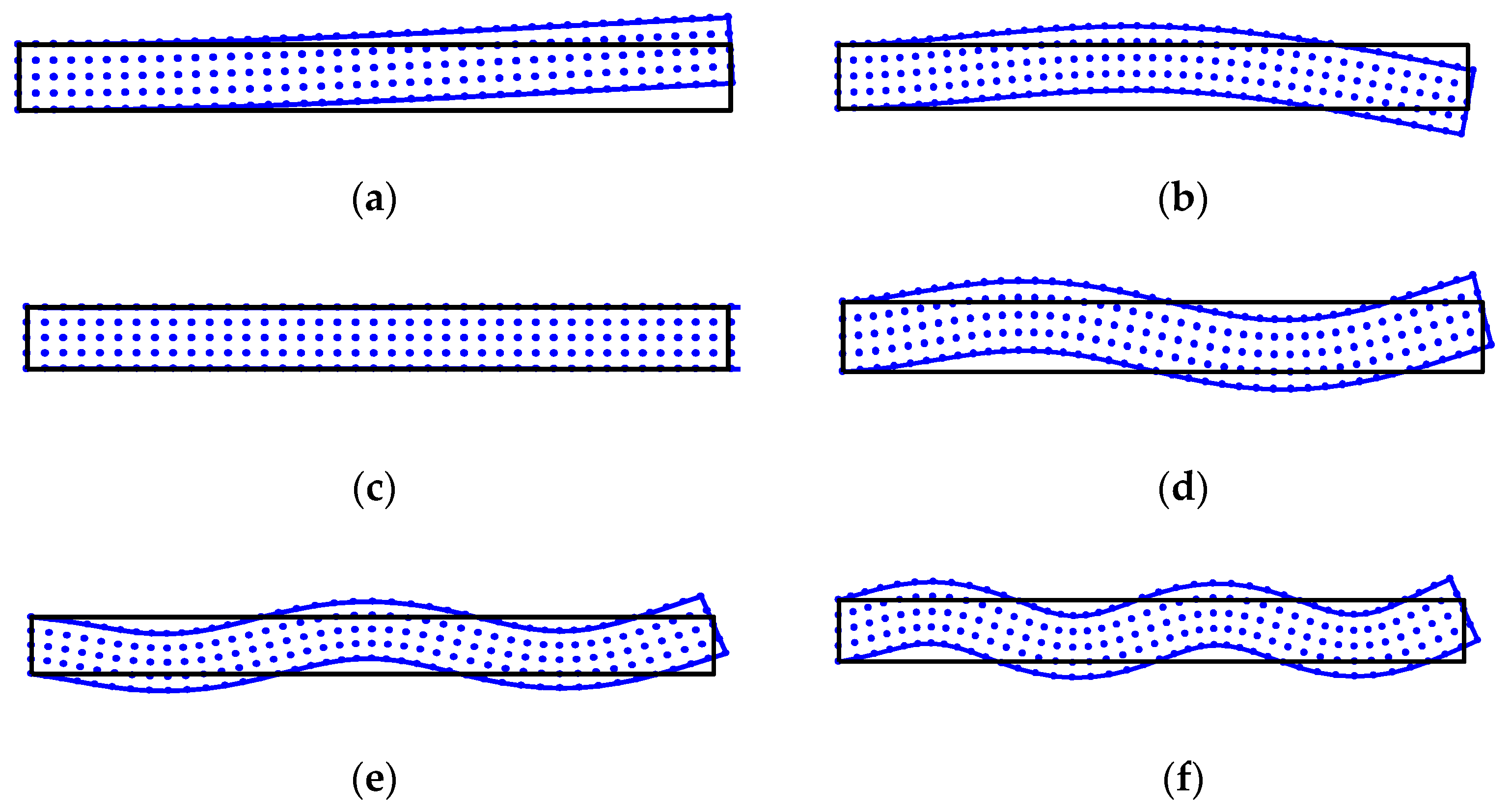
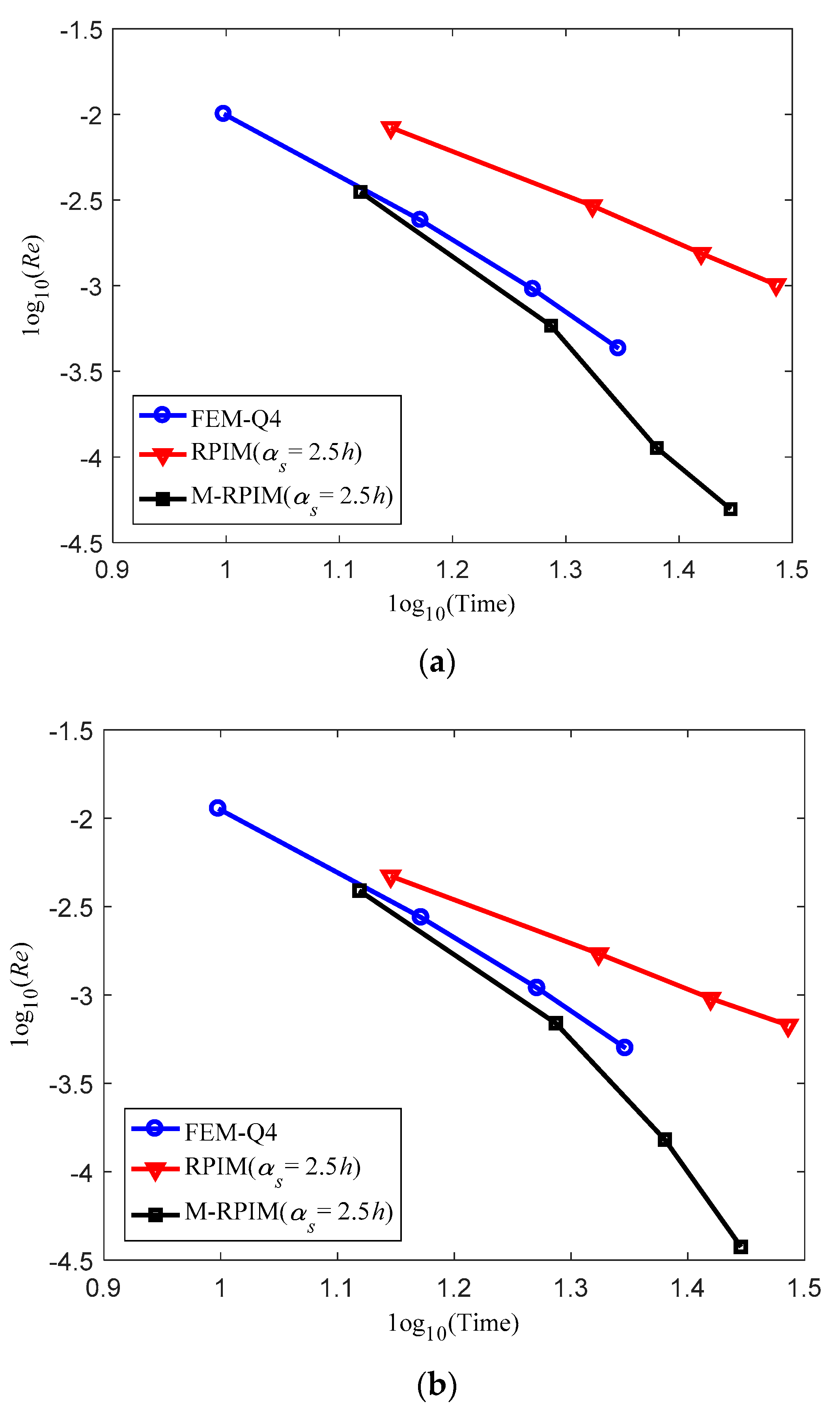
4.1.3. Computation Efficiency Study
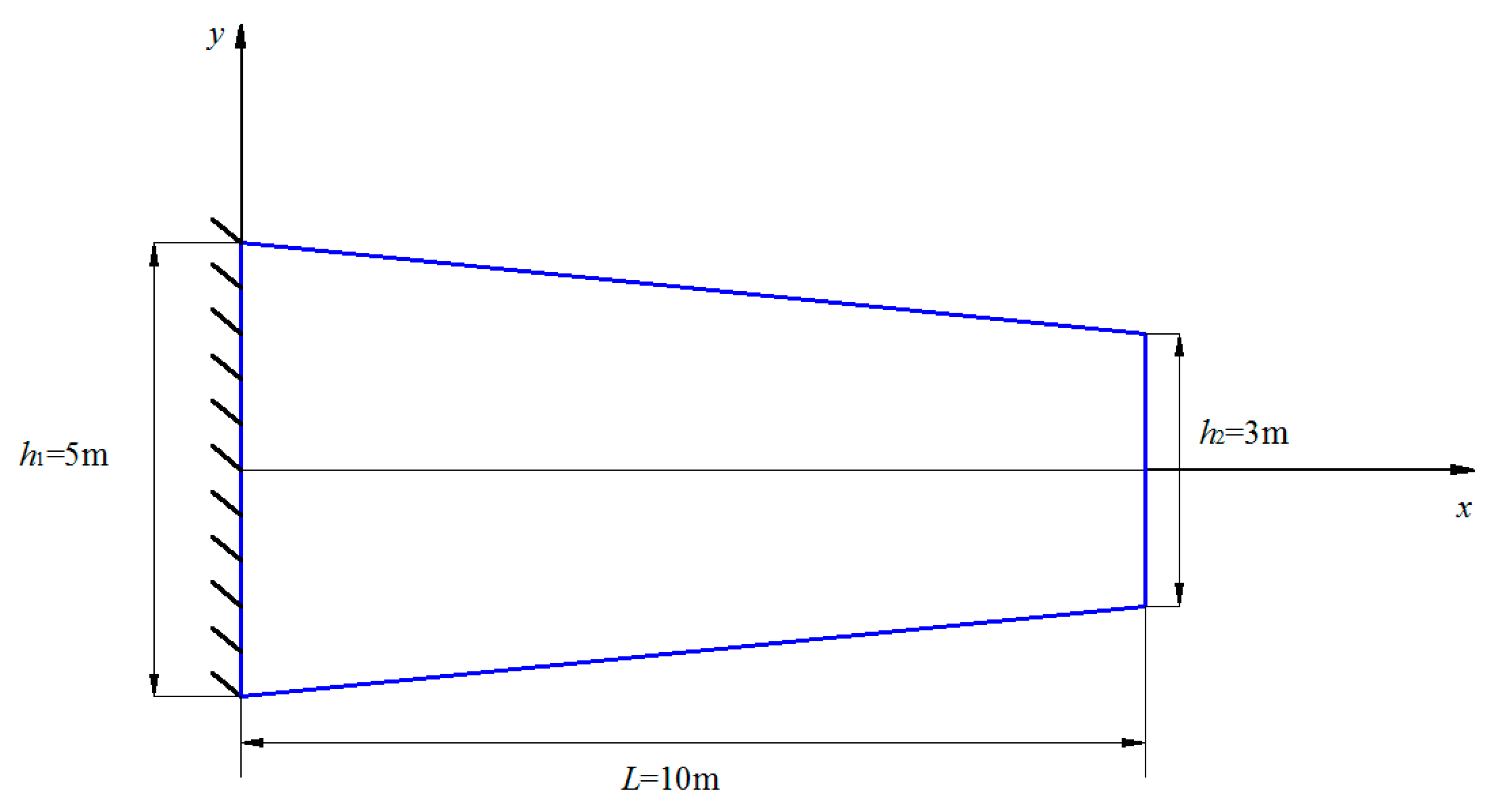
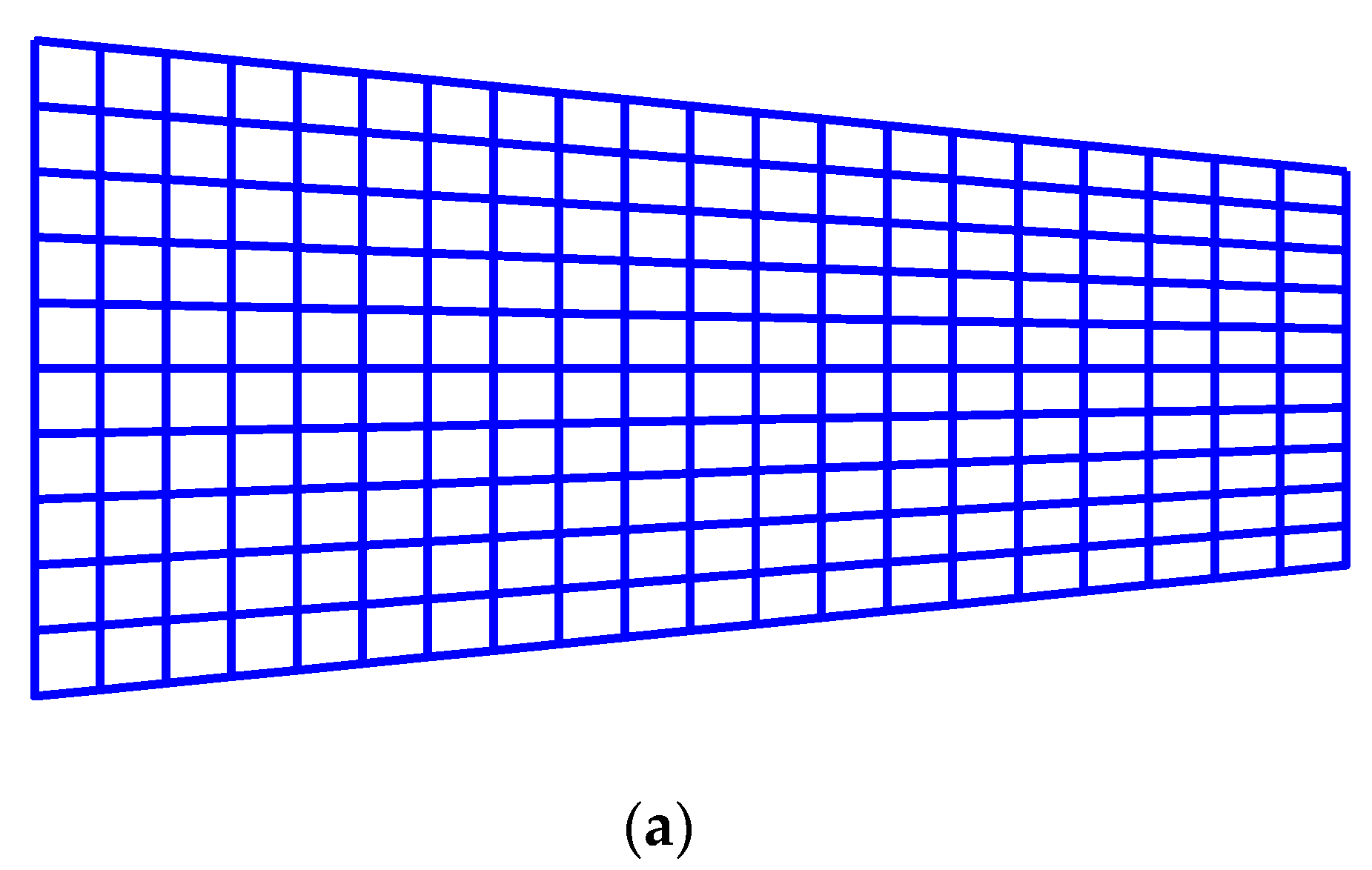
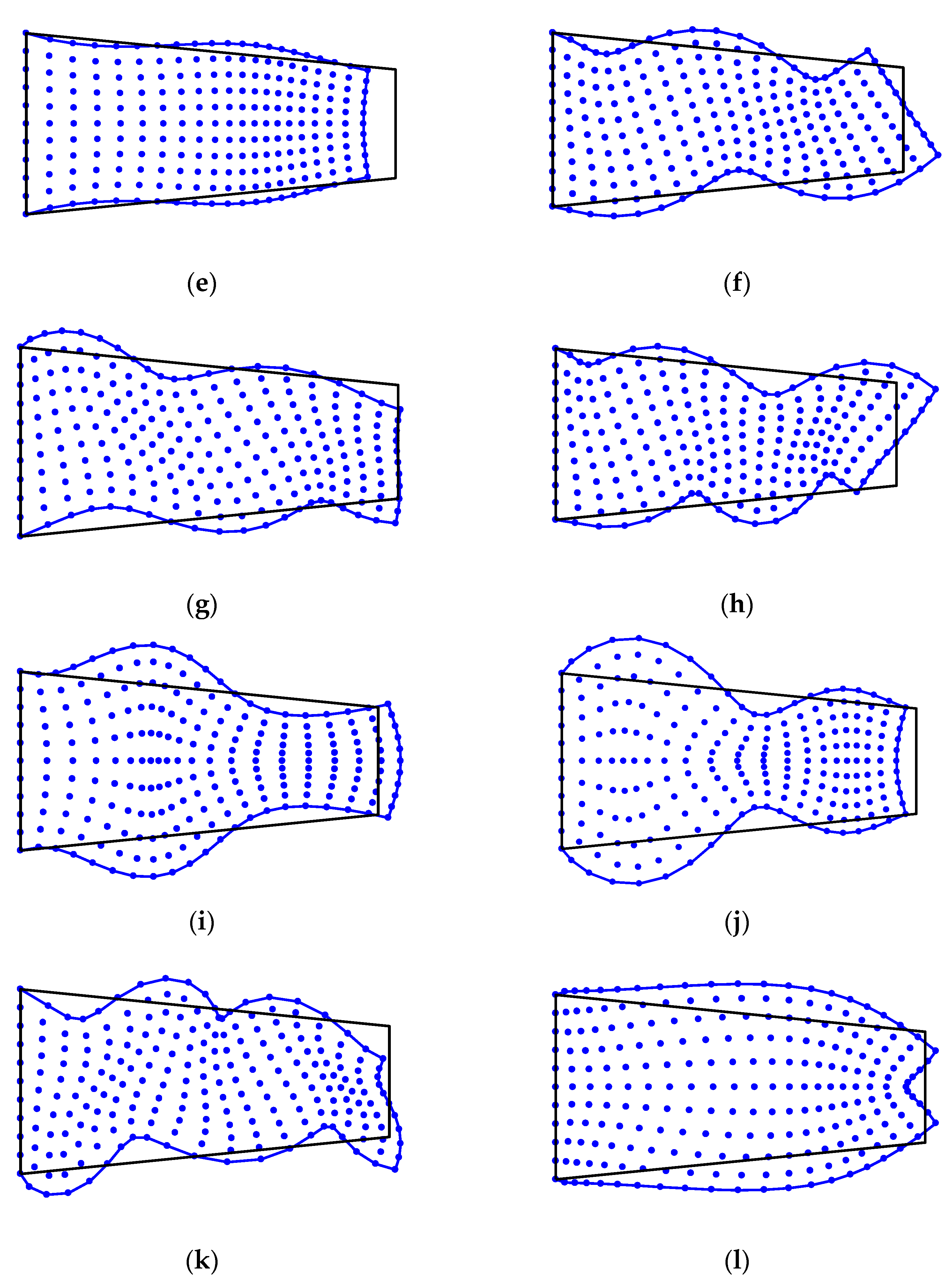
4.2. Free Vibration Analysis of the Cantilever Beam with Variable Cross-Section
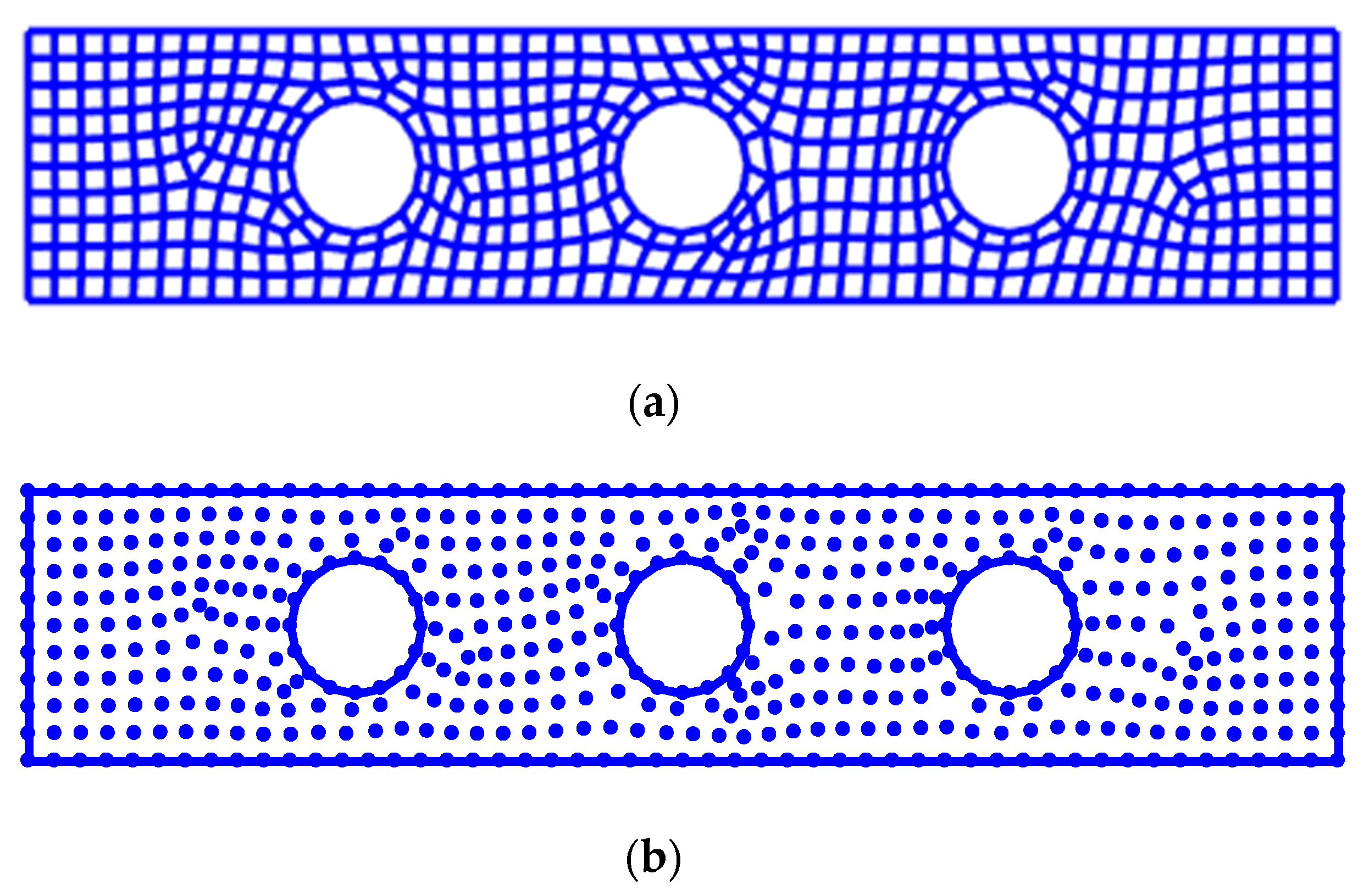
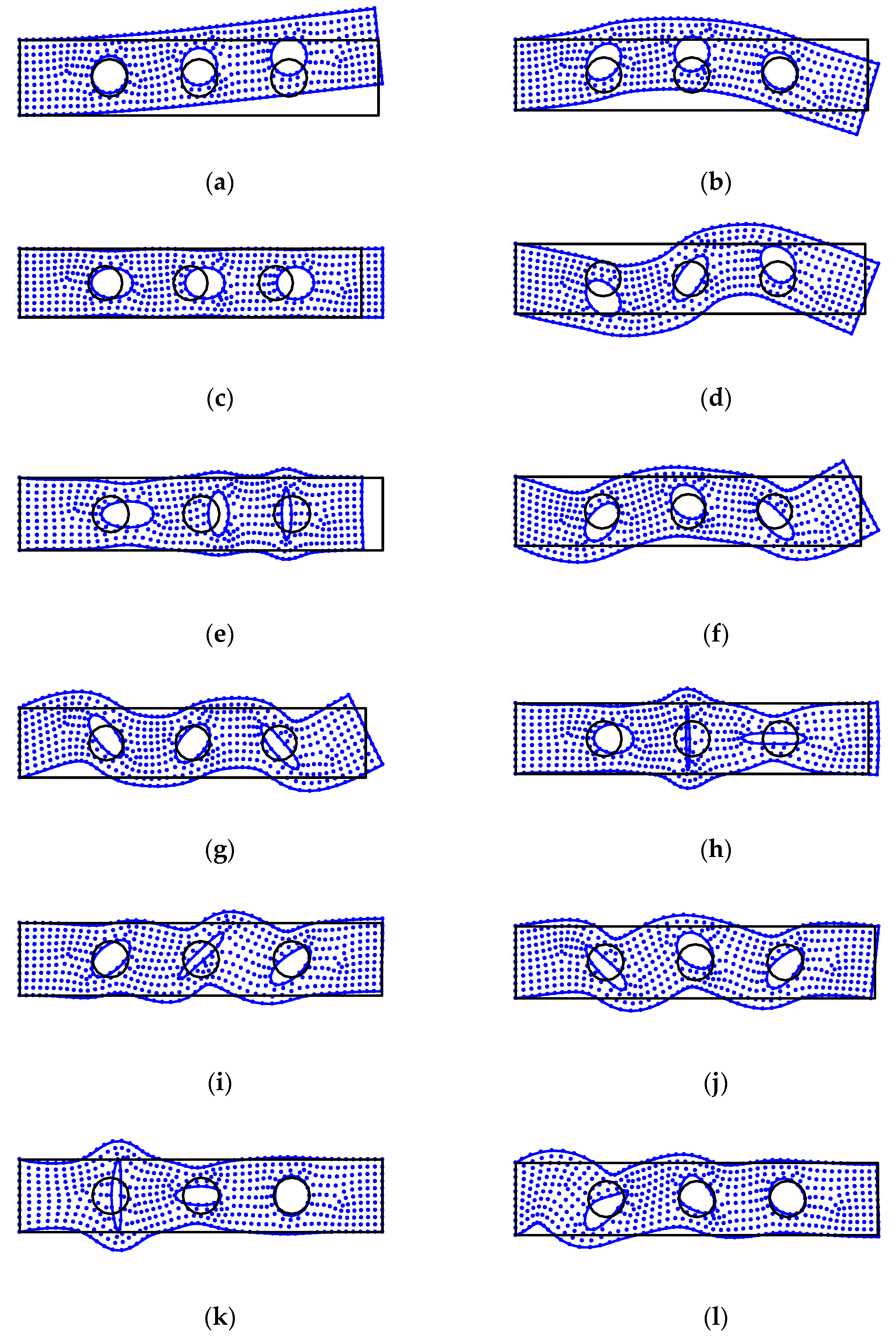
4.3. Free Vibration Analysis of the Cantilever Beam with Holes
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bathe, K.J. Finite Element Procedures, 2nd ed.; Prentice Hall: Watertown, MA, USA, 2014. [Google Scholar]
- Li, J.P.; Fu, Z.J.; Gu, Y.; Qin, Q.H. Recent advances and emerging applications of the singular boundary method for large-scale and high-frequency computational acoustics. Adv. Appl. Math. Mech. 2022, 14, 315–343. [Google Scholar] [CrossRef]
- Wu, F.; Zhou, G.; Gu, Q.Y.; Chai, Y.B. An enriched finite element method with interpolation cover functions for acoustic analysis in high frequencies. Eng. Anal. Bound. Elem. 2021, 129, 67–81. [Google Scholar] [CrossRef]
- Gu, Y.; Fan, C.M.; Fu, Z.J. Localized method of fundamental solutions for three-dimensional elasticity problems: Theory. Adv. Appl. Math. Mech. 2021, 13, 1520–1534. [Google Scholar]
- Liu, C.S.; Qiu, L.; Lin, J. Simulating thin plate bending problems by a family of two-parameter homogenization functions. Appl. Math. Model. 2020, 79, 284–299. [Google Scholar] [CrossRef]
- Li, J.P.; Zhang, L.; Qin, Q.H. A regularized method of moments for three-dimensional time-harmonic electromagnetic scattering. Appl. Math. Lett. 2021, 112, 106746. [Google Scholar] [CrossRef]
- Qiu, L.; Lin, J.; Wang, F.J.; Qin, Q.H.; Liu, C.S. A homogenization function method for inverse heat source problems in 3D functionally graded materials. Appl. Math. Model. 2021, 91, 923–933. [Google Scholar] [CrossRef]
- Gu, Y.; Lei, J. Fracture mechanics analysis of two-dimensional cracked thin structures (from micro- to nano-scales) by an efficient boundary element analysis. Results Math. 2021, 11, 100172. [Google Scholar] [CrossRef]
- Li, J.P.; Gu, Y.; Qin, Q.H.; Zhang, L. The rapid assessment for three-dimensional potential model of large-scale particle system by a modified multilevel fast multipole algorithm. Comput. Math. Appl. 2021, 89, 127–138. [Google Scholar] [CrossRef]
- Chai, Y.B.; Bathe, K.J. Transient wave propagation in inhomogeneous media with enriched overlapping triangular elements. Comput. Struct. 2020, 237, 106273. [Google Scholar] [CrossRef]
- Chai, Y.B.; Li, W.; Liu, Z.Y. Analysis of transient wave propagation dynamics using the enriched finite element method with interpolation cover functions. Appl. Math. Comput. 2022, 412, 126564. [Google Scholar] [CrossRef]
- Li, Y.C.; Dang, S.N.; Li, W.; Chai, Y.B. Free and Forced Vibration Analysis of Two-Dimensional Linear Elastic Solids Using the Finite Element Methods Enriched by Interpolation Cover Functions. Mathematics 2022, 10, 456. [Google Scholar] [CrossRef]
- Liu, M.Y.; Gao, G.J.; Zhu, H.F.; Jiang, C. A cell-based smoothed finite element method stabilized by implicit SUPG/SPGP/Fractional step method for incompressible flow. Eng. Anal. Bound. Elem. 2021, 124, 194–210. [Google Scholar] [CrossRef]
- Chai, Y.B.; Gong, Z.X.; Li, W.; Li, T.Y.; Zhang, Q.F.; Zou, Z.H.; Sun, Y.B. Application of smoothed finite element method to two dimensional exterior problems of acoustic radiation. Int. J. Comput. Methods 2018, 15, 1850029. [Google Scholar] [CrossRef]
- Liu, M.Y.; Gao, G.J.; Zhu, H.F.; Jiang, C.; Liu, G.R. A cell-based smoothed finite element method (CS-FEM) for three-dimensional incompressible laminar flows using mixed wedge-hexahedral element. Eng. Anal. Bound. Elem. 2021, 133, 269–285. [Google Scholar] [CrossRef]
- Wang, T.T.; Zhou, G.; Jiang, C.; Shi, F.C.; Tian, X.D.; Gao, G.J. A coupled cell-based smoothed finite element method and discrete phase model for incompressible laminar flow with dilute solid particles. Eng. Anal. Bound. Elem. 2022, 143, 190–206. [Google Scholar] [CrossRef]
- Li, W.; Gong, Z.X.; Chai, Y.B.; Cheng, C.; Li, T.Y.; Zhang, Q.F.; Wang, M.S. Hybrid gradient smoothing technique with discrete shear gap method for shell structures. Comput. Math. Appl. 2017, 74, 1826–1855. [Google Scholar] [CrossRef]
- Liu, G.R. Mesh Free Methods: Moving Beyond the Finite Element Method; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Cheng, S.F.; Wang, F.J.; Wu, G.Z.; Zhang, C.X. semi-analytical and boundary-type meshless method with adjoint variable formulation for acoustic design sensitivity analysis. Appl. Math. Lett. 2022, 131, 108068. [Google Scholar] [CrossRef]
- Lin, J. Simulation of 2D and 3D inverse source problems of nonlinear time-fractional wave equation by the meshless homogenization function method. Eng. Comput. 2021. [Google Scholar] [CrossRef]
- Lin, J.; Bai, J.; Reutskiy, S.; Lu, J. A novel RBF-based meshless method for solving time-fractional transport equations in 2D and 3D arbitrary domains. Eng. Comput. 2022. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, Y.H.; Reutskiy, S.; Feng, W. A novel meshless space-time backward substitution method and its application to nonhomogeneous advection-diffusion problems. Appl. Math. Comput. 2021, 398, 125964. [Google Scholar] [CrossRef]
- Wang, C.; Wang, F.J.; Gong, Y.P. Analysis of 2D heat conduction in nonlinear functionally graded materials using a local semi-analytical meshless method. AIMS Math. 2021, 6, 12599–12618. [Google Scholar] [CrossRef]
- Gu, Y.; Sun, H.G. A meshless method for solving three-dimensional time fractional diffusion equation with variable-order derivatives. Appl. Math. Model. 2020, 78, 539–549. [Google Scholar] [CrossRef]
- Li, X.; Li, S. A fast element-free Galerkin method for the fractional diffusion-wave equation. App. Math. Lett. 2021, 122, 107529. [Google Scholar] [CrossRef]
- Li, X.; Li, S. A linearized element-free Galerkin method for the complex Ginzburg–Landau equation. Comput. Math. Appl. 2021, 90, 135–147. [Google Scholar] [CrossRef]
- Atluri, S.N.; Kim, H.G.; Cho, J.Y. Critical assessment of the truly meshless local PetrovGalerkin (MLPG), and local boundary integral equation (LBIE) methods. Comput. Mech. 1999, 24, 348–372. [Google Scholar] [CrossRef]
- Liu, W.K.; Jun, S.; Zhang, Y.F. Reproducing kernel particle methods. Int. J. Numer. Methods Fluids 1995, 20, 1081–1106. [Google Scholar] [CrossRef]
- Qu, J.; Dang, S.N.; Li, Y.C.; Chai, Y.B. Analysis of the interior acoustic wave propagation problems using the modified radial point interpolation method (M-RPIM). Eng. Anal. Bound. Elem. 2022, 138, 339–368. [Google Scholar] [CrossRef]
- Gui, Q.; Zhang, Y.; Chai, Y.B.; You, X.Y.; Li, W. Dispersion error reduction for interior acoustic problems using the radial point interpolation meshless method with plane wave enrichment functions. Eng. Anal. Bound. Elem. 2022, 143, 428–441. [Google Scholar] [CrossRef]
- Qu, W.Z.; He, H. A GFDM with supplementary nodes for thin elastic plate bending analysis under dynamic loading. Appl. Math. Lett. 2022, 124, 107664. [Google Scholar] [CrossRef]
- Qu, W.Z.; Gao, H.W.; Gu, Y. Integrating Krylov deferred correction and generalized finite difference methods for dynamic simulations of wave propagation phenomena in long-time intervals. Adv. Appl. Math. Mech. 2021, 13, 1398–1417. [Google Scholar]
- Xi, Q.; Fu, Z.J.; Li, Y.; Huang, H. A hybrid GFDM–SBM solver for acoustic radiation and propagation of thin plate structure under shallow sea environment. J. Theor. Comput. Acous. 2020, 28, 2050008. [Google Scholar] [CrossRef]
- Fu, Z.J.; Xie, Z.Y.; Ji, S.Y.; Tsai, C.C.; Li, A.L. Meshless generalized finite difference method for water wave interactions with multiple-bottom-seated-cylinder-array structures. Ocean Eng. 2020, 195, 106736. [Google Scholar] [CrossRef]
- Zheng, Z.Y.; Li, X.L. Theoretical analysis of the generalized finite difference method. Comput. Math. Appl. 2022, 120, 1–14. [Google Scholar] [CrossRef]
- Wang, F.; Fan, C.M.; Zhang, C.; Lin, J. A localized space-time method of fundamental solutions for diffusion and convection-diffusion problems. Adv. Appl. Math. Mech. 2020, 12, 940–958. [Google Scholar] [CrossRef]
- Fu, Z.J.; Xi, Q.; Li, Y.; Huang, H.; Rabczuk, T. Hybrid FEM–SBM solver for structural vibration induced underwater acoustic radiation in shallow marine environment. Comput. Methods Appl. Mech. Eng. 2020, 369, 113236. [Google Scholar] [CrossRef]
- Fu, Z.J.; Chen, W.; Wen, P.H.; Zhang, C.Z. Singular boundary method for wave propagation analysis in periodic structures. J. Sound Vib. 2018, 425, 170–188. [Google Scholar] [CrossRef]
- Li, J.P.; Zhang, L. High-precision calculation of electromagnetic scattering by the Burton-Miller type regularized method of moments. Eng. Anal. Bound. Elem. 2021, 133, 177–184. [Google Scholar] [CrossRef]
- Li, J.P.; Zhang, L.; Qin, Q.H. A regularized fast multipole method of moments for rapid calculation of three-dimensional time-harmonic electromagnetic scattering from complex targets. Eng. Anal. Bound. Elem. 2022, 142, 28–38. [Google Scholar] [CrossRef]
- Zhang, Y.O.; Dang, S.N.; Li, W.; Chai, Y.B. Performance of the radial point interpolation method (RPIM) with implicit time integration scheme for transient wave propagation dynamics. Comput. Math. Appl. 2022, 114, 95–111. [Google Scholar] [CrossRef]
- You, X.Y.; Li, W.; Chai, Y.B. A truly meshfree method for solving acoustic problems using local weak form and radial basis functions. Appl. Math. Comput. 2020, 365, 124694. [Google Scholar] [CrossRef]
- Chai, Y.B.; You, X.Y.; Li, W. Dispersion Reduction for the Wave Propagation Problems Using a Coupled “FE-Meshfree” Triangular Element. Int. J. Comput. Methods 2020, 17, 1950071. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Q.; Gui, Q.; Chai, Y.B. A coupled FE-Meshfree triangular element for acoustic radiation problems. Int. J. Comput. Methods 2021, 18, 2041002. [Google Scholar] [CrossRef]
- Wang, F.; Zhao, Q.; Chen, Z.; Fan, C.M. Localized Chebyshev collocation method for solving elliptic partial differential equations in arbitrary 2D domains. Appl. Math. Comput. 2021, 397, 125903. [Google Scholar] [CrossRef]
- Xi, Q.; Fu, Z.J.; Zhang, C.Z.; Yin, D.S. An efficient localized Trefftz-based collocation scheme for heat conduction analysis in two kinds of heterogeneous materials under temperature loading. Comput. Struct. 2021, 255, 106619. [Google Scholar] [CrossRef]
- Xi, Q.; Fu, Z.J.; Wu, W.J.; Wang, H.; Wang, Y. A novel localized collocation solver based on Trefftz basis for Potential-based Inverse Electromyography. Appl. Math. Comput. 2021, 390, 125604. [Google Scholar] [CrossRef]
- Li, X.; Li, S. A finite point method for the fractional cable equation using meshless smoothed gradients. Eng. Anal. Bound. Elem. 2022, 134, 453–465. [Google Scholar] [CrossRef]
- Fu, Z.J.; Yang, L.W.; Xi, Q.; Liu, C.S. A boundary collocation method for anomalous heat conduction analysis in functionally graded materials. Comput. Math. Appl. 2021, 88, 91–109. [Google Scholar] [CrossRef]
- Tang, Z.; Fu, Z.J.; Sun, H.; Liu, X. An efficient localized collocation solver for anomalous diffusion on surfaces. Fract. Calc. Appl. Anal. 2021, 24, 865–894. [Google Scholar] [CrossRef]
- Xi, Q.; Fu, Z.J.; Rabczuk, T.; Yin, D. A localized collocation scheme with fundamental solutions for long-time anomalous heat conduction analysis in functionally graded materials. Int. J. Heat Mass Tran. 2021, 180, 121778. [Google Scholar] [CrossRef]
- Dolbow, J.; Belytschko, T. Numerical integration of the Galerkin weak form in meshfree methods. Comput. Mech. 1999, 23, 219–230. [Google Scholar] [CrossRef]
- Liu, G.R.; Gu, Y.T. Assessment and applications of point interpolation methods for computational mechanics. Int. J. Numer. Meth. Engng. 2004, 59, 1373–1397. [Google Scholar] [CrossRef]
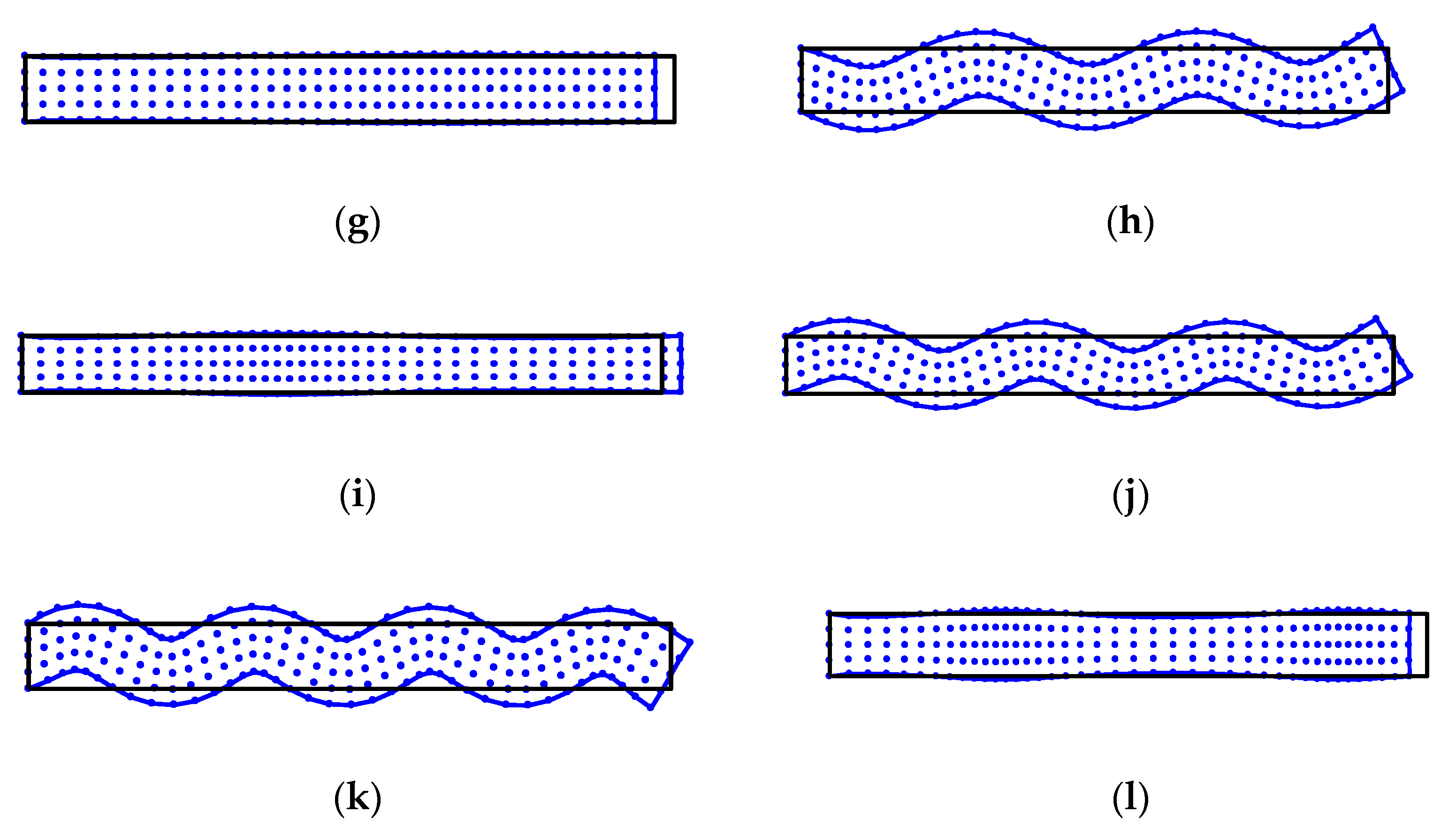



| Mode | FEM-Q4 | Error (%) | RPIM | Error (%) | M-RPIM | Error (%) | Ref. |
|---|---|---|---|---|---|---|---|
| 1 | 830.567 | 1.003 | 815.423 | 0.839 | 825.213 | 0.351 | 822.322 |
| 2 | 4989.034 | 1.132 | 4909.931 | 0.471 | 4952.383 | 0.389 | 4933.177 |
| 3 | 12,826.933 | 0.022 | 12,826.322 | 0.017 | 12,825.428 | 0.010 | 12,824.145 |
| 4 | 13,167.852 | 1.336 | 13,035.277 | 0.316 | 13,025.003 | 0.237 | 12,994.215 |
| 5 | 23,992.489 | 1.604 | 23,772.722 | 0.673 | 23,725.015 | 0.471 | 23,613.775 |
| 6 | 36,701.000 | 1.910 | 36,492.012 | 1.329 | 36,197.042 | 0.510 | 36,013.226 |
| 7 | 38,467.305 | 0.059 | 38,461.345 | 0.044 | 38,450.819 | 0.016 | 38,444.488 |
| 8 | 50,697.394 | 2.248 | 50,570.105 | 1.991 | 49,854.144 | 0.547 | 49,582.799 |
| 9 | 64,062.116 | 0.225 | 64,045.638 | 0.199 | 63,984.254 | 0.103 | 63,918.563 |
| 10 | 65,590.504 | 2.524 | 65,609.724 | 2.554 | 64,290.994 | 0.493 | 63,975.503 |
| 11 | 81,118.869 | 3.012 | 81,334.286 | 3.286 | 79,233.413 | 0.618 | 78,746.943 |
| 12 | 89,562.090 | 0.252 | 89,514.438 | 0.199 | 89,345.277 | 0.010 | 89,336.686 |
| Mode | FEM-Q4 | Error (%) | RPIM | Error (%) | M-RPIM | Error (%) | Ref. |
|---|---|---|---|---|---|---|---|
| 1 | 824.304 | 0.241 | 819.913 | 0.293 | 822.800 | 0.058 | 822.322 |
| 2 | 4946.701 | 0.274 | 4924.719 | 0.171 | 4936.588 | 0.069 | 4933.177 |
| 3 | 12,824.618 | 0.004 | 12,824.955 | 0.006 | 12,824.496 | 0.003 | 12,824.145 |
| 4 | 13,036.557 | 0.326 | 13,008.259 | 0.108 | 13,004.647 | 0.080 | 12,994.215 |
| 5 | 23,706.655 | 0.393 | 23,657.845 | 0.187 | 23,635.380 | 0.091 | 23,613.775 |
| 6 | 36,182.573 | 0.470 | 36,152.539 | 0.387 | 36,049.829 | 0.102 | 36,013.226 |
| 7 | 38,449.523 | 0.013 | 38,447.183 | 0.007 | 38,445.401 | 0.002 | 38,444.488 |
| 8 | 49,857.999 | 0.555 | 49,874.211 | 0.588 | 49,637.697 | 0.111 | 49,582.799 |
| 9 | 63,996.004 | 0.121 | 63,990.287 | 0.112 | 63,976.475 | 0.091 | 63,918.563 |
| 10 | 64,332.241 | 0.558 | 64,422.173 | 0.698 | 63,994.651 | 0.030 | 63,975.503 |
| 11 | 79,334.621 | 0.746 | 79,524.455 | 0.987 | 78,846.611 | 0.127 | 78,746.943 |
| 12 | 89,391.481 | 0.061 | 89,377.038 | 0.045 | 89,336.977 | 0.000 | 89,336.686 |
| Mode | FEM-Q4 | Error (%) | RPIM | Error (%) | M-RPIM | Error (%) | Ref. |
|---|---|---|---|---|---|---|---|
| 1 | 823.104 | 0.095 | 821.051 | 0.155 | 822.413 | 0.011 | 822.322 |
| 2 | 4938.559 | 0.109 | 4928.453 | 0.096 | 4933.920 | 0.015 | 4933.177 |
| 3 | 12,824.010 | 0.001 | 12,823.612 | 0.004 | 12,823.953 | 0.001 | 12,824.145 |
| 4 | 13,011.299 | 0.131 | 12,992.024 | 0.017 | 12,996.698 | 0.019 | 12,994.215 |
| 5 | 23,651.752 | 0.161 | 23,631.689 | 0.076 | 23,619.234 | 0.023 | 23,613.775 |
| 6 | 36,083.214 | 0.194 | 36,074.813 | 0.171 | 36,022.821 | 0.027 | 36,013.226 |
| 7 | 38,445.687 | 0.003 | 38,444.328 | 0.000 | 38,443.843 | 0.002 | 38,444.488 |
| 8 | 49,697.499 | 0.231 | 49,714.721 | 0.266 | 49,597.527 | 0.030 | 49,582.799 |
| 9 | 63,982.840 | 0.101 | 63,979.749 | 0.096 | 63,939.314 | 0.032 | 63,918.563 |
| 10 | 64,092.160 | 0.182 | 64,149.033 | 0.271 | 63,974.133 | 0.002 | 63,975.503 |
| 11 | 78,994.780 | 0.315 | 79,104.908 | 0.455 | 78,774.275 | 0.035 | 78,746.943 |
| 12 | 89,358.561 | 0.024 | 89,351.356 | 0.016 | 89,334.272 | 0.003 | 89,336.686 |
| Mode | FEM-Q4 | Error (%) | RPIM | Error (%) | M-RPIM | Error (%) | Ref. |
|---|---|---|---|---|---|---|---|
| 1 | 822.674 | 0.043 | 821.486 | 0.102 | 822.279 | 0.005 | 822.322 |
| 2 | 4935.637 | 0.050 | 4929.842 | 0.068 | 4932.985 | 0.004 | 4933.177 |
| 3 | 12,823.747 | 0.003 | 12,823.464 | 0.005 | 12,823.711 | 0.003 | 12,824.145 |
| 4 | 13,002.246 | 0.062 | 12,991.382 | 0.022 | 12,993.901 | 0.002 | 12,994.215 |
| 5 | 23,632.124 | 0.078 | 23,621.334 | 0.032 | 23,613.557 | 0.001 | 23,613.775 |
| 6 | 36,047.788 | 0.096 | 36,044.602 | 0.087 | 36,013.347 | 0.000 | 36,013.226 |
| 7 | 38,444.192 | 0.001 | 38,443.250 | 0.003 | 38,443.144 | 0.003 | 38,444.488 |
| 8 | 49,640.417 | 0.116 | 49,653.240 | 0.142 | 49,583.475 | 0.001 | 49,582.799 |
| 9 | 63,977.974 | 0.093 | 63,975.937 | 0.090 | 63,920.007 | 0.002 | 63,918.563 |
| 10 | 64,006.958 | 0.049 | 64,044.242 | 0.107 | 63,973.057 | 0.004 | 63,975.503 |
| 11 | 78,874.387 | 0.162 | 78,944.368 | 0.251 | 78,749.088 | 0.003 | 78,746.943 |
| 12 | 89,346.670 | 0.011 | 89,342.201 | 0.006 | 89,332.973 | 0.004 | 89,336.686 |
| Mode | FEM-Q4 | Error (%) | RPIM | Error (%) | M-RPIM | Error (%) | Ref. |
|---|---|---|---|---|---|---|---|
| 1 | 41.771 | 0.333 | 41.536 | 0.233 | 41.678 | 0.109 | 41.633 |
| 2 | 147.202 | 0.781 | 146.826 | 0.523 | 146.335 | 0.187 | 146.062 |
| 3 | 151.597 | 0.058 | 151.511 | 0.002 | 151.532 | 0.015 | 151.508 |
| 4 | 298.805 | 1.349 | 298.048 | 1.092 | 295.483 | 0.222 | 294.829 |
| 5 | 412.666 | 0.326 | 412.032 | 0.172 | 411.396 | 0.017 | 411.327 |
| 6 | 442.931 | 1.685 | 441.428 | 1.340 | 436.366 | 0.178 | 435.592 |
| 7 | 528.614 | 1.053 | 526.132 | 0.578 | 523.667 | 0.107 | 523.108 |
| 8 | 601.857 | 2.143 | 598.737 | 1.614 | 590.187 | 0.163 | 589.229 |
| 9 | 619.528 | 1.005 | 613.227 | 0.023 | 613.441 | 0.012 | 613.365 |
| 10 | 671.507 | 1.529 | 662.514 | 0.170 | 662.167 | 0.117 | 661.392 |
| 11 | 710.007 | 2.389 | 705.817 | 1.785 | 695.000 | 0.225 | 693.441 |
| 12 | 713.997 | 0.802 | 710.025 | 0.241 | 708.647 | 0.046 | 708.320 |
| Mode | FEM-Q4 | Error (%) | RPIM | Error (%) | M-RPIM | Error (%) | Ref. |
|---|---|---|---|---|---|---|---|
| 1 | 1626.190 | 0.617 | 1612.353 | 0.239 | 1618.711 | 0.154 | 1616.218 |
| 2 | 8272.300 | 0.174 | 8246.759 | 0.135 | 8268.312 | 0.126 | 8257.923 |
| 3 | 11,373.419 | 0.791 | 11,239.656 | 0.395 | 11,302.342 | 0.161 | 11,284.188 |
| 4 | 19,395.928 | 1.595 | 19,004.812 | 0.454 | 19,101.194 | 0.051 | 19,091.435 |
| 5 | 33,523.877 | 1.273 | 33,233.174 | 0.395 | 33,231.319 | 0.390 | 33,102.326 |
| 6 | 33,972.380 | 1.786 | 33,568.275 | 0.575 | 33,472.489 | 0.288 | 33,376.214 |
| 7 | 37,191.685 | 2.943 | 36,443.890 | 0.873 | 36,333.778 | 0.568 | 36,128.559 |
| 8 | 52,155.832 | 2.894 | 51,179.337 | 0.968 | 51,042.893 | 0.699 | 50,688.744 |
| 9 | 52,582.353 | 3.420 | 51,249.812 | 0.799 | 51,117.100 | 0.538 | 50,843.699 |
| 10 | 55,474.223 | 2.473 | 54,470.879 | 0.620 | 54,276.585 | 0.261 | 54,135.295 |
| 11 | 67,782.825 | 2.359 | 66,555.530 | 0.505 | 66,471.730 | 0.379 | 66,220.863 |
| 12 | 75,775.407 | 1.343 | 75,309.818 | 0.721 | 74,789.424 | 0.025 | 74,771.060 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, T.; Wang, P.; Zhang, G.; Chai, Y. A Modified Radial Point Interpolation Method (M-RPIM) for Free Vibration Analysis of Two-Dimensional Solids. Mathematics 2022, 10, 2889. https://doi.org/10.3390/math10162889
Sun T, Wang P, Zhang G, Chai Y. A Modified Radial Point Interpolation Method (M-RPIM) for Free Vibration Analysis of Two-Dimensional Solids. Mathematics. 2022; 10(16):2889. https://doi.org/10.3390/math10162889
Chicago/Turabian StyleSun, Tingting, Peng Wang, Guanjun Zhang, and Yingbin Chai. 2022. "A Modified Radial Point Interpolation Method (M-RPIM) for Free Vibration Analysis of Two-Dimensional Solids" Mathematics 10, no. 16: 2889. https://doi.org/10.3390/math10162889
APA StyleSun, T., Wang, P., Zhang, G., & Chai, Y. (2022). A Modified Radial Point Interpolation Method (M-RPIM) for Free Vibration Analysis of Two-Dimensional Solids. Mathematics, 10(16), 2889. https://doi.org/10.3390/math10162889





