An Extrinsic Approach Based on Physics-Informed Neural Networks for PDEs on Surfaces
Abstract
:1. Introduction
2. Methodology
2.1. Continuous Differential Operators on Surfaces and Its Extrinsic Form
2.2. Physics-Informed Neural Networks (PINNs)
2.3. The Procedure of the Extrinsic Approach Based on PINNs
| Algorithm 1 The extrinsic approach based on PINNs. |
|
3. Numerical Examples
- (1)
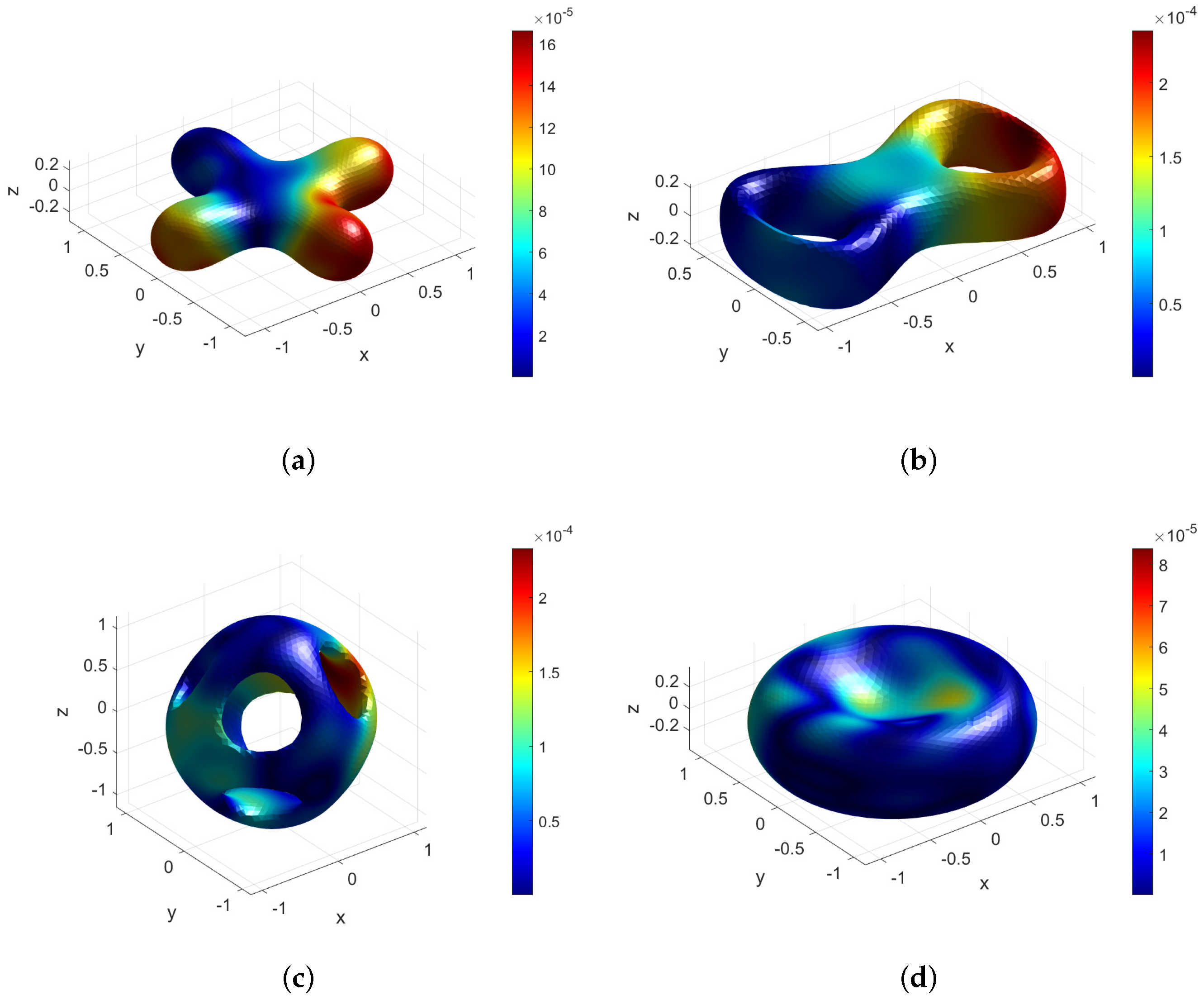
- Tours:
- (2)
- CDP:
- (3)
- Bretzel2:
- (4)
- Orthocircle:
- (5)
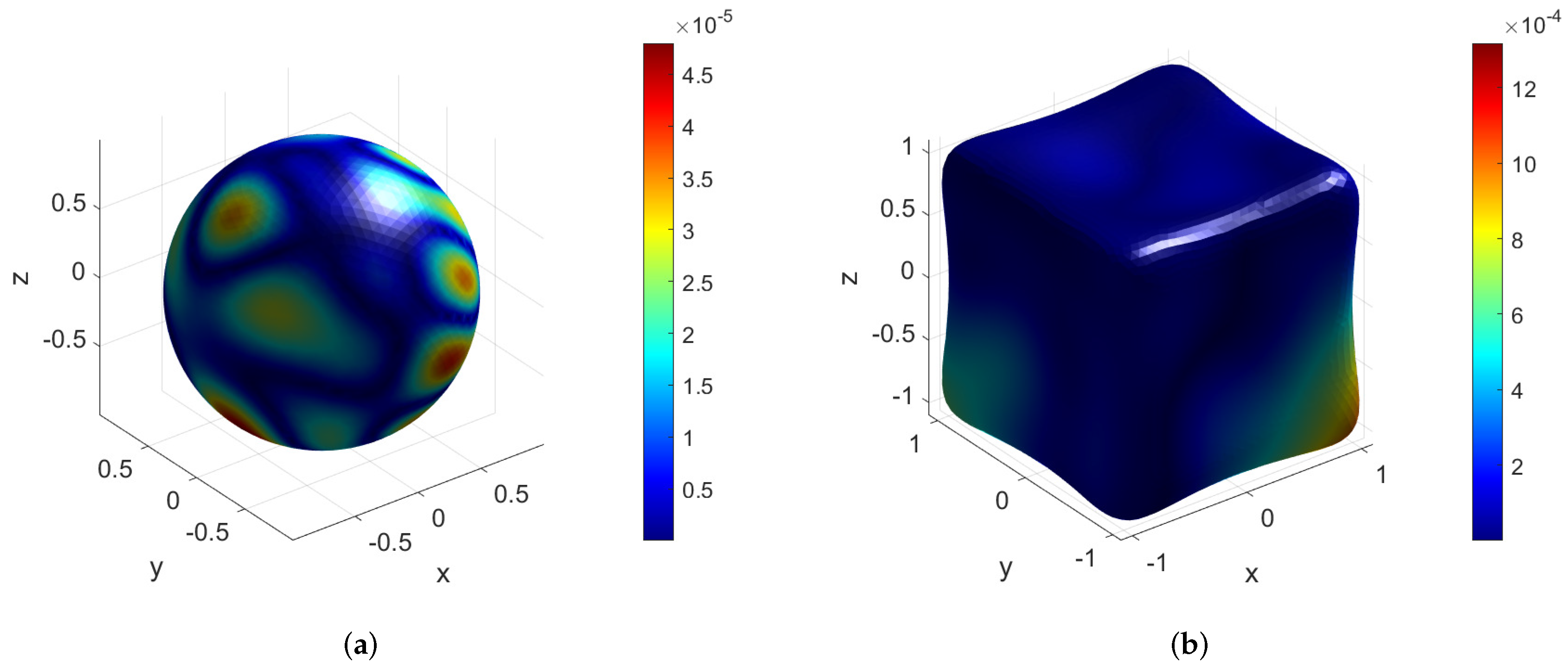
- RBC:
- (6)
- Tooth:
4. Conclusions and Discussions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Witkin, A.; Kass, M. Reaction-Diffusion Textures. ACM Siggraph Comput. Graph. 1995, 25, 299–308. [Google Scholar] [CrossRef]
- Diewald, U.; Preusser, T. Anisotropic diffusion in vector field visualization on Euclidean domains and surfaces. IEEE Trans. Vis. Comput. Graph 2000, 6, 139–149. [Google Scholar] [CrossRef] [Green Version]
- Myers, T.G.; Charpin, J.P.F. A mathematical model for atmospheric ice accretion and water flow on a cold surface. Int. J. Heat Mass Transf. 2004, 47, 5483–5500. [Google Scholar] [CrossRef]
- Xu, J.J.; Zhao, H.K. An Eulerian Formulation for Solving Partial Differential Equations Along a Moving Interface. J. Sci. Comput. 2003, 19, 573–594. [Google Scholar] [CrossRef]
- Ruuth, S.J.; Merriman, B. A simple embedding method for solving partial differential equations on surfaces. J. Comput. Phys. 2008, 227, 1943–1961. [Google Scholar] [CrossRef]
- Piret, C. The orthogonal gradients method: A radial basis functions method for solving partial differential equations on arbitrary surfaces. J. Comput. Phys. 2012, 231, 4662–4675. [Google Scholar] [CrossRef]
- Hansbo, P.; Larson, M.G.; Zahedi, S. A cut finite element method for coupled bulk-surface problems on time-dependent domains. Comput. Methods Appl. Mech. Eng. 2016, 307, 96–116. [Google Scholar] [CrossRef] [Green Version]
- Cheung, K.C.; Ling, L. A Kernel-Based Embedding Method and Convergence Analysis for Surfaces PDEs. SIAM J. Sci. Comput. 2018, 40, A266–A287. [Google Scholar] [CrossRef]
- Chen, M.; Ling, L. Kernel-based collocation methods for heat transport on evolving surfaces. J. Comput. Phys. 2019, 405, 109166. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Ling, L. Kernel-Based Meshless Collocation Methods for Solving Coupled Bulk–Surface Partial Differential Equations. J. Sci. Comput. 2019, 81, 375–391. [Google Scholar] [CrossRef] [Green Version]
- Floater, M.S.; Hormann, K. Surface Parameterization: A Tutorial and Survey; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Macdonald, C.B.; Ruuth, S.J. The implicit closest point method for the numerical solution of partial differential equations on surfaces. SIAM J. Sci. Comput. 2010, 31, 4330–4350. [Google Scholar] [CrossRef] [Green Version]
- Marcelo, B.; Li-Tien, C.; Stanley, O.; Guillermo, S. Variational Problems and Partial Differential Equations on Implicit Surfaces. J. Comput. Phys. 2001, 174, 759–780. [Google Scholar]
- Tang, Z.; Fu, Z.; Chen, M.; Ling, L. A localized extrinsic collocation method for Turing pattern formations on surfaces. Appl. Math. Lett. 2021, 122, 107534. [Google Scholar] [CrossRef]
- Tang, Z.; Fu, Z.; Sun, H.; Liu, X. An efficient localized collocation solver for anomalous diffusion on surfaces. Fract. Calc. Appl. Anal. 2021, 24, 865–894. [Google Scholar] [CrossRef]
- Tang, Z.; Fu, Z.; Chen, M.; Huang, J. An efficient collocation method for long-time simulation of heat and mass transport on evolving surfaces. J. Comput. Phys. 2022, 463, 111310. [Google Scholar] [CrossRef]
- Fu, Z.; Tang, Z.; Xi, Q.; Liu, Q.; Gu, Y.; Wang, F. Localized Collocation Schemes and Their Applications. Acta Mech. Sin. 2022, 38, 422167. [Google Scholar]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef]
- Tarkhov, D.A.; Vasilyev, A.N. New Neural Network Technique to the Numerical Solution of Mathematical Physics Problems. I: Simple Problems. Opt. Mem. Neural Netw. 2005, 14, 59–72. [Google Scholar]
- Tarkhov, D.A.; Vasilyev, A.N. New Neural Network Technique to the Numerical Solution of Mathematical Physics Problems II: Complicated and Nonstandard Problems. Opt. Mem. Neural Netw. 2005, 14, 97–122. [Google Scholar]
- Tarkhov, D.; Vasilyev, A.N. Semi-Empirical Neural Network Modeling and Digital Twins Development; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Antonov, V.; Tarkhov, D.; Vasilyev, A. Unified approach to constructing the neural network models of real objects Part 1. Math. Methods Appl. Sci. 2018, 41, 9244–9251. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-Informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations. J. Comput. Phys. 2018, 378, 686–707. [Google Scholar] [CrossRef]
- Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science 2020, 367, 1026–1030. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Kharazmi, E.; Karniadakis, G.E. Conservative physics-informed neural networks on discrete domains for conservation laws: Applications to forward and inverse problems. Comput. Methods Appl. Mech. Eng. 2020, 365, 113028. [Google Scholar] [CrossRef]
- Pang, G.; Lu, L.; Karniadakis, G.E. fPINNs: Fractional Physics-Informed Neural Networks. SIAM J. Sci. Comput. 2019, 41, A2603–A2626. [Google Scholar] [CrossRef]
- Mao, Z.; Jagtap, A.D.; Karniadakis, G.E. Physics-informed neural networks for high-speed flows. Comput. Methods Appl. Mech. Eng. 2020, 360, 112789. [Google Scholar] [CrossRef]
- Bihlo, A.; Popovych, R.O. Physics-informed neural networks for the shallow-water equations on the sphere. J. Comput. Phys. 2022, 456, 111024. [Google Scholar] [CrossRef]
- Fang, Z.; Zhan, J. A physics-informed neural network framework for PDEs on 3D surfaces: Time independent problems. IEEE Access 2019, 8, 26328–26335. [Google Scholar] [CrossRef]
- Hesse, K.; Sloan, I.H.; Womersley, R.S. Numerical integration on the sphere. In Handbook of Geomathematics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Krause, A.L.; Ellis, M.A.; Van Gorder, R.A. Influence of curvature, growth, and anisotropy on the evolution of Turing patterns on growing manifolds. Bull. Math. Biol. 2019, 81, 759–799. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.K.; Osher, S.; Fedkiw, R. Fast surface reconstruction using the level set method. In Proceedings of the IEEE Workshop on Variational and Level Set Methods in Computer Vision, Vancouver, BC, Canada, 13 July 2001; pp. 194–201. [Google Scholar]
- Liu, S.; Wang, C.C. Quasi-interpolation for surface reconstruction from scattered data with radial basis function. Comput. Aided Geom. Des. 2012, 29, 435–447. [Google Scholar] [CrossRef]
- Gorbachenko, V.I.; Lazovskaya, T.V.; Tarkhov, D.A.; Vasilyev, A.N.; Zhukov, M.V. Neural network technique in some inverse problems of mathematical physics. In Proceedings of the International Symposium on Neural Networks, St. Petersburg, Russia, 6–8 July 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 310–316. [Google Scholar]
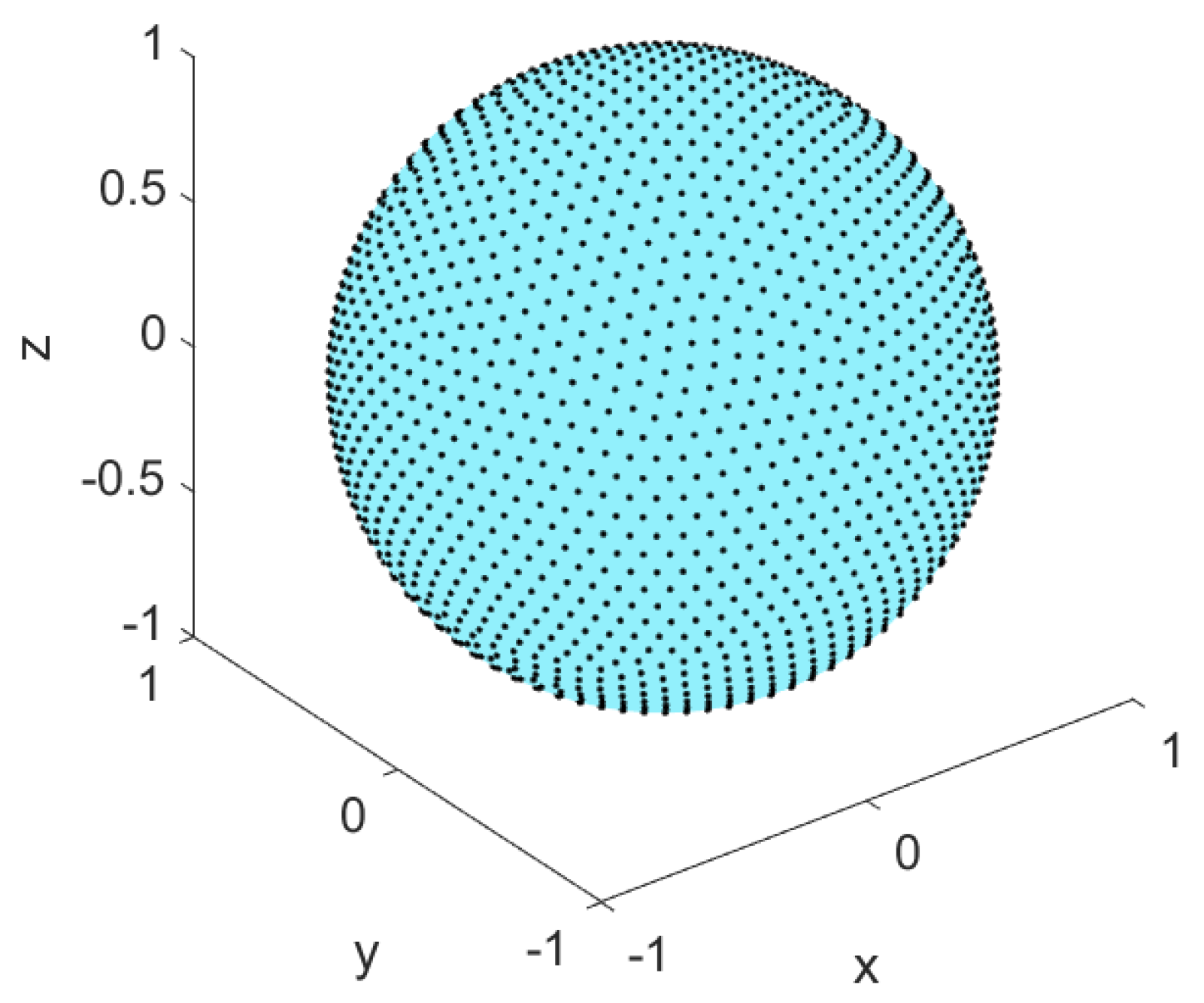
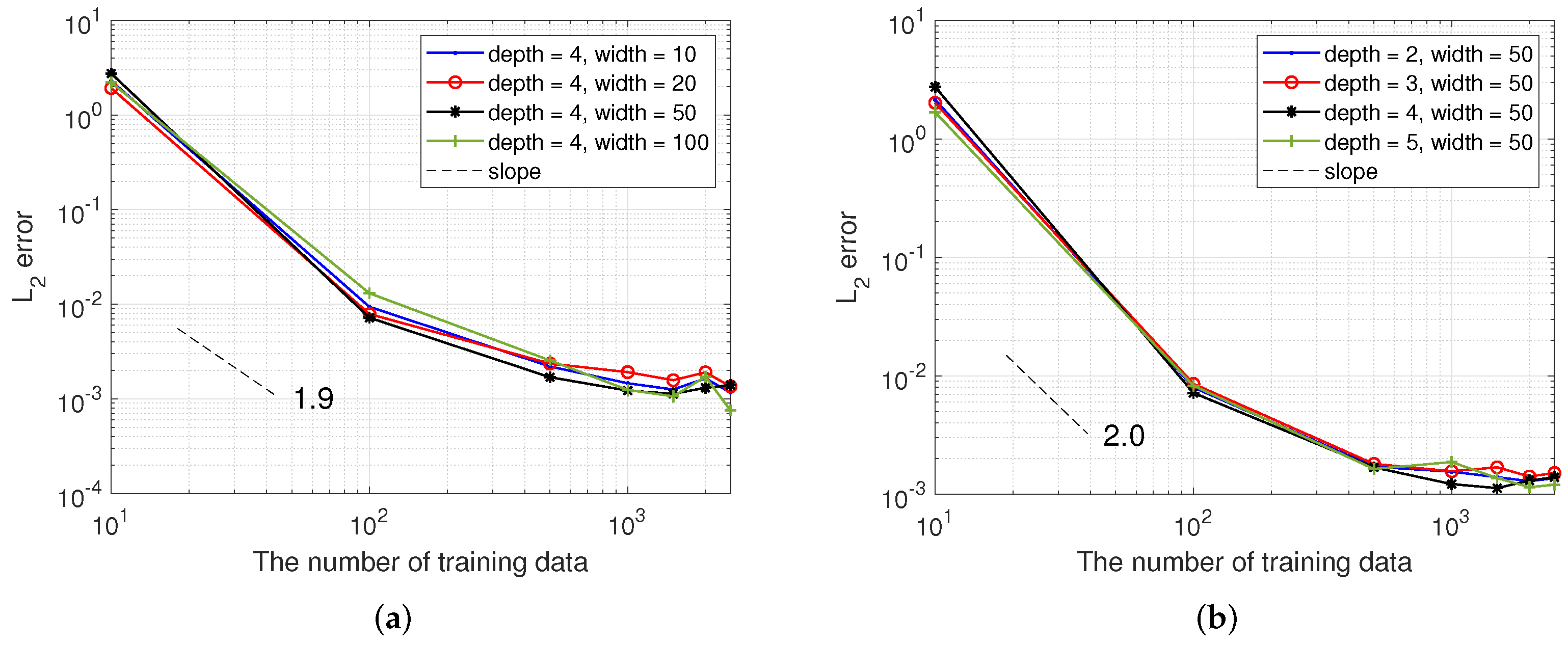
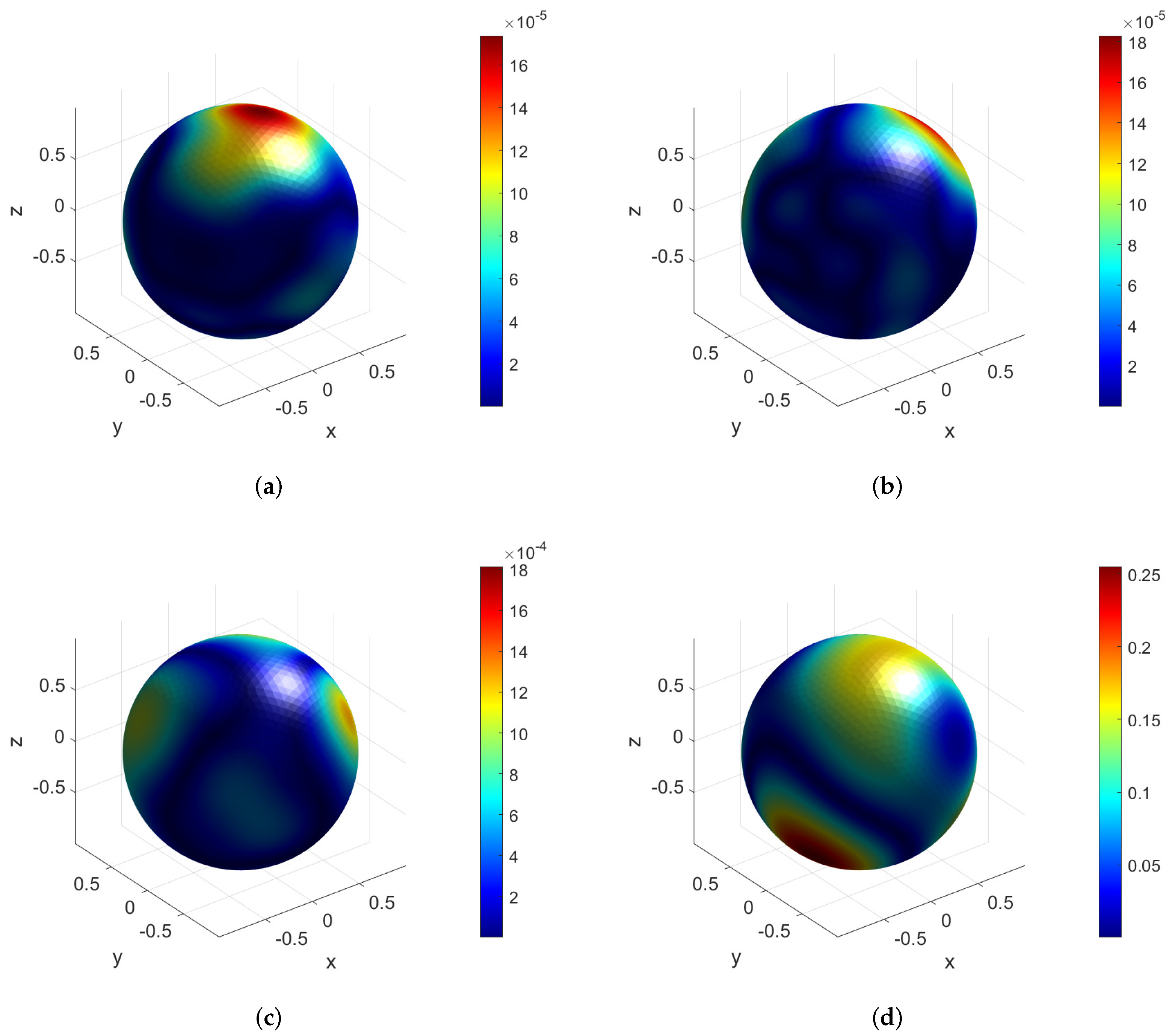

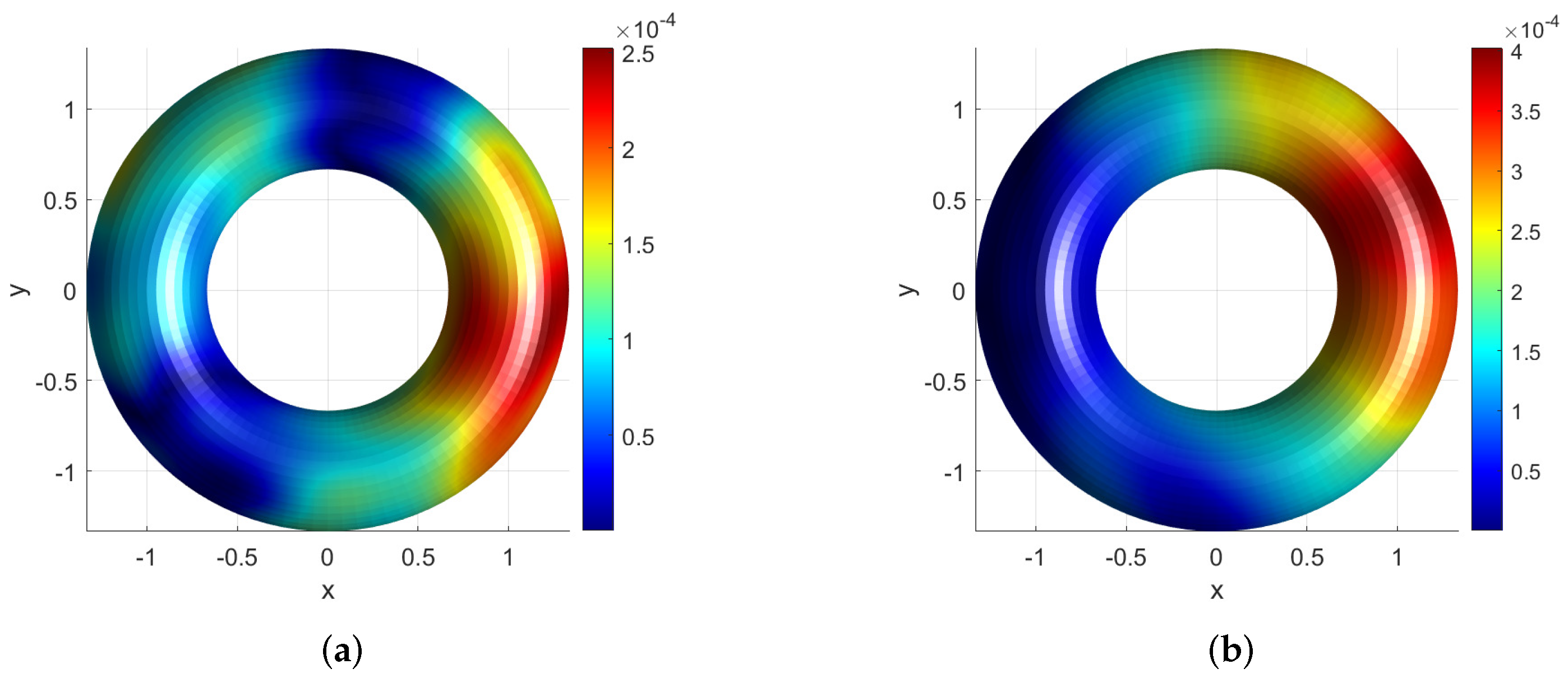


| Depth | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| error | ||||
| CPU time | 19.96 (s) | 29.42 (s) | 76.65 (s) | 102.26 (s) |
| Width | 3 | 5 | 10 | 20 | 50 | 100 |
|---|---|---|---|---|---|---|
| error | ||||||
| CPU time | 5.47 (s) | 8.54 (s) | 17.67 (s) | 34.63 (s) | 76.65 (s) | 152.72 (s) |
| N | 1000 | 1500 | 2000 | 2500 |
|---|---|---|---|---|
| Extrinsic | 1.02 × | 9.88 × | 1.49 × | 9.36 × |
| 32.70 (s) | 65.42 (s) | 102.26 (s) | 108.66 (s) | |
| Embedding | 3.51 × | 4.80 × | 2.17 × | 1.90 × |
| 113.93 (s) | 237.02 (s) | 312.26 (s) | 418.55 (s) |
| Surfaces | CDP | Bretzel2 | Orthocircle | RBC |
|---|---|---|---|---|
| error | 1.18 × | 1.51 × | 4.20 × | 2.37 × |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Z.; Fu, Z.; Reutskiy, S. An Extrinsic Approach Based on Physics-Informed Neural Networks for PDEs on Surfaces. Mathematics 2022, 10, 2861. https://doi.org/10.3390/math10162861
Tang Z, Fu Z, Reutskiy S. An Extrinsic Approach Based on Physics-Informed Neural Networks for PDEs on Surfaces. Mathematics. 2022; 10(16):2861. https://doi.org/10.3390/math10162861
Chicago/Turabian StyleTang, Zhuochao, Zhuojia Fu, and Sergiy Reutskiy. 2022. "An Extrinsic Approach Based on Physics-Informed Neural Networks for PDEs on Surfaces" Mathematics 10, no. 16: 2861. https://doi.org/10.3390/math10162861
APA StyleTang, Z., Fu, Z., & Reutskiy, S. (2022). An Extrinsic Approach Based on Physics-Informed Neural Networks for PDEs on Surfaces. Mathematics, 10(16), 2861. https://doi.org/10.3390/math10162861







