Significance of the Coriolis Force on the Dynamics of Carreau–Yasuda Rotating Nanofluid Subject to Darcy–Forchheimer and Gyrotactic Microorganisms

Abstract

In this study, the significance of the Coriolis force on the dynamics of Carreau—Yasuda flow toward a continuously stretched surface subject to the Darcy–Forchheimer law is investigated. The nanoparticles are incorporated due to their unusual characteristics (e.g., extraordinary thermal conductivity), which are significant in heat exchangers and advanced nanotechnology. To avoid possible sedimentation of tiny particles, the gyrotactic microorganisms must be incorporated. The goal of this research was to find out the dynamics of three-dimensional rotational flow for nanofluids under the influence of Darcy–Forchheimer with the thermophoresis effect and motile microorganisms. The equations governing mass, momentum, and energy equations are formalized using partial derivatives, which may subsequently be transformed into dimensionless differential shapes using the personifications of apposite similarity transformations. The MATLAB application bvp4c was used in conjunction with a shooting technique to solve a nonlinear mathematical model based on ordinary differential equations. It was observed that the base fluid velocities decreased against higher input of rotation and porosity parameters; moreover, the Brownian motion and thermophoresis increased the temperature profile.

1. Introduction

Nanofluids are widely used in a variety of sectors due to their use in heat transfer applications. Fundamental operating fluids have abysmal heat transfer efficiencies. Thus, nanofluids (in addition to conventional fluids) play critical roles in heat transmission. Choi et al. [1] introduced nanofluids in 1995; nanofluids are regarded as the most promising cooling agents in the business and are the focus of interest for researchers and the industry. A nanofluid involves an essential combination of nano-sized tiny particles in a base fluid, enhancing the base fluid’s thermal conductivity; this fluid can be useful to cool automobile engines, various types of welding systems, high flux devices, heat exchangers, and in modern nanotechnology. Key advancements in nanotechnology have opened up doors to treat brain tumors, in pharmacological treatments, cancer therapy, artificial heart surgery, artificial lungs, etc. The transportation of heat and mass through nanofluid flow has piqued the curiosity of researchers [2,3]. Mahin et al. [4] explored the significance of nanofluids and how they may be used to magnify heat transmission across a specified shape while generating entropy. Similarly, Jothia et al. [5] studied the efficacy of heat and mass transformation using the Dufour effect on unsteady MHD nanofluid flow over porous geometry. Many other researchers in similar fields have shown the usefulness of nanofluid flow in various situations [6,7,8,9].

Researchers are looking into non-Newtonian fluids due to their importance in daily life, such as mechanical and synthetic processes, biological fluids, pastes, polymeric liquids, complicated mixes, and motor oils. Many researchers elaborate on different aspects and research problems. A simulation for anaerobic digestion in flow was discussed by Wu et al. [10]. Sankar et al. [11] elaborated on the non-Newtonian fluid blood flow model through the arteries. Kumar et al. [12] discussed the laminar flow of non-Newtonian fluid in cylindrical shape geometry. Khan et al. [13] investigated the heat and mass transportation through non-Newtonian fluid over Riga plates under the influence of the Fourier and Fick law. Kumar et al. [14] explored the neural network technique for non-Newtonian fluid flow to optimize the use of energy resources. Numerous scientists [15,16,17] have elaborated on non-Newtonian under different environments. Numerous researchers in similar fields have shown the usefulness of nanofluid flow in various situations [18,19,20].

Giorgio et al. [21] initially discussed the critical factor for nanofluids and named it the nonlinear Darcy–Forchheimer flow. We utilized the Darcy–Forchheimer heating law to introduce a porous medium into the fluid zone without any dispersion. Thermal performance layout, hydrothermal, meteorology, chemical furnaces, underground water bodies, encapsulation processes, crude oil protection systems, and energy storage units have significant benefits regarding porous medium interaction. Many researchers, such as Rasool et al. [22], discussed the MHD nanofluid flow with Darcy–Forchheimer over the stretching sheet. Singh et al. [23] examined nanofluid flow in the enhancement of potential heat transportation by ’fascinating’ sunlight. It was seen that the increasing skin friction was due to the high resistance offered by the porous medium. Hayat et al. [24] discussed the entropy generation in the Darcy–Forchheimer bi-directional flow of water-based carbon nanotubes with convective boundary conditions. Shaw et al. [25] studied the impact of entropy generation and nonlinear thermal radiation on the Darcy–Forchheimer flow of MnFe₂O₄ Casson/water nanofluid due to a rotating disk application to brain dynamics. Similarly, Rasool et al. [26] examined the significance of thermal slip and convective boundary conditions in three-dimensional rotating Darcy–Forchheimer nanofluid flow. The opposite behavior was noticed in nanofluid concentration when the intensive resistance offered by the porosity factor in the flow model led to the rise of the temperature profile.

Creating an apparent fluid pattern, i.e., falling plumes causing bioconvection, the directed movements of denser microorganisms in water (self-driven) cause bioconvection. Each microbe swims at this macroscopic level, which is a physical phenomenon. Convection is caused by the extensive density gradient caused by the up-swimming of a range of microorganisms, resulting in radially periodic apparent fluid circulation. Due to the improvements in mass movement and mixing, which seem to be critical challenges in diverse microsystems, bioconvection offers a wide range of applications in bio-micro-systems [27,28]. Ali et al. [29] employed a finite element approach to investigate the bioconvection consequences of mixed convection and MHD on the dynamics of Casson nanofluid in the stagnation point of a spinning sphere. Yin et al. [30] discussed the thermal radiation issue of floating microorganisms in a bioconvection movement of Sisko nanofluid under a magnetic environment in a stretched cylinder. Nabwey et al. [31] considered the effects of bioconvection and chemical reactions on Magneto–Carreau nanofluid flow through an inclined cylinder. Many researchers also investigated the effects of bioconvection because of its numerous uses in blood flow, nuclear reactors, turbomachinery, nuclear accelerator installation, and electrical furnaces [32]. Tayebi [33] discussed the significance of the Darcy fluid flow model in the presence of thermal convection. Nima et al. [34] examined the melting boundary effects on the dynamics of non-Newtonian fluid subject to gyrotactic microorganisms.

In the above-mentioned mentioned literature, less consideration was paid toward the significance of the Coriolis force on the dynamics of the Carreau–Yasuda nanofluid over a stretch surface subject to the Lorentz force, gyrotactic microorganisms, and Darcy–Forchheimer law. To the authors’ knowledge, these aspects of the topic have not been addressed in previous research. The fundamental objective of this comprehensive work was to optimize heat transmission using nanofluids. Motivated by the above-mentioned applications of non-Newtonian fluids and nanofluids in the literature, the elaborated fluid model was selected. Geometric problems in three dimensions were reduced to ODE dimensions via a similarity transformation, and then ODEs were solved using a well-known bvp4c with a shooting approach, which was then coded and simulated in a MATLAB environment. The numerical outputs were confirmed by comparing them to previously available data. Additionally, graphical and tabular representations of these results are included. This report is related to the various applications that have manufactured plastic and metal spinning, paints, liquid material, crude oil purification, heat exchangers, polymer extrusion, etc.

2. Mathematical Model

The objective of this study was to observe the significance of the Coriolis force on the dynamics of Carreau–Yasuda rotating nanofluid subject to Darcy–Forchheimer. The energized particle’s thermal movement generates no electromagnetic radiation in fluid due to the radiation effect’s unavailability. The impact of bioconvection was explored. Further, the nanoparticles were incorporated due to their unusual characteristics (e.g., extraordinary thermal conductivity), which are significant in heat exchangers and advanced nanotechnology. The surface corresponds with the stretching plan z ≥ 0 and $\tilde{\mathsf{\Omega }}$ = k$\tilde{\mathsf{\Omega }}$, here, k is the unit vector along the z-axis, as shown in Figure 1. This figure depicts the geometry of this research problem. The Cartesian coordinate system, along with the z-axis angular velocity, existed on the rotating framework. The main objective of this study involved the enhancement of heat transportation. The agglomeration of tiny particles was ignored; the nanoparticle suspension was assumed to be a stable compound, which is very important for the presence of motile microorganisms. Furthermore, we suppose that perhaps surface concentration and warmth as well as the environmental concentration and temperature are $C_w$, $T_w$, and $C_{\infty }$, $T_{\infty }$, respectively. The governing equations of the problem are presented below [35,36,37,38].

$$u_x+u_y+u_z=0,$$

(1)

$$u{u}_x+v{v}_y+w{w}_z-2\tilde{\mathsf{\Omega }}v=\nu u{{}_z}_z+\nu \left[\frac{(n-1)(D+1)}{D}{\mathsf{\Gamma }}^D{\left(u_y\right)}^{D}u{{}_z}_z\right]-\frac{\nu }{K}u-F{u}^2,$$

(2)

$$u{u}_x+v{v}_y+w{w}_z+2\tilde{\mathsf{\Omega }}u=\nu v{{}_z}_z+\nu \left[\frac{(n-1)(D+1)}{D}{\mathsf{\Gamma }}^D{\left(v_y\right)}^{D}v{{}_z}_z\right]-\frac{\nu }{K}u-F{v}^2,$$

(3)

$$u{T}_x+v{T}_y+w{T}_z=\alpha T{{}_z}_z+[D_b{C}_z{T}_z+\frac{D_T}{T_{\infty }}{\left(T_z\right)}^2],$$

(4)

$$u{C}_x+v{C}_y+w{C}_z=\tilde{D}{\nabla }^{2}C+\frac{D_T}{D_{\infty }}T{{}_z}_z,$$

(5)

$$u{N}_x+v{N}_y+w{N}_z+\frac{b{W}_c}{C_w-C_{\infty }}.[\frac{\partial }{\partial z}\left(N{C}_z\right)]=D_{m}N{{}_z}_z$$

(6)

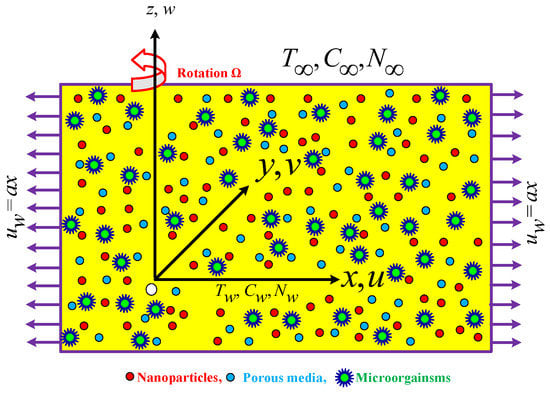
Figure 1. Darcy– Forchheimer flow geometry with bioconvection particles.

The velocity components are represented by u, v, and w, $\nu =\left(\frac{\mu }{\rho }\right)$ is the representation of kinematic viscosity, $\mu$ is used for dynamic viscosity, K is used for permeability of the porous medium, F = $\frac{C_b}{K^{\frac{1}{2}}}$ represents the coefficient of non-uniform inertia, $C_b$ indicates the drag coefficient, $\alpha$ is the thermal diffusibility of the fluid, k is the thermal conductivity, $c_p$ is a representation of the specific heat, $D_T$ is the thermophoretic coefficient, $D_m$ represents the microorganism coefficient. The boundary conditions [35,39,40] are described as,

$$\begin{array}{l}\left\{\begin{array}{c}u=ax,v=0,w=0,T=T_w,C=C_w,N=N_{w}atz=0,\hfill \\ \hfill u⟶0,v⟶0,T⟶T_{\infty },C⟶C_{\infty },N⟶N_{\infty }whenz⟶\infty ,\hfill \end{array}\right.\end{array}$$

(7)

where $T_w$ is the wall temperature, $T_{\infty }$ the ambient temperature, $C_w$ is the concentration well beyond the wall, $C_{\infty }$ is the ambient concentration [40,41]. The similarity transformations [35,40] are defined as,

$$u=ax{f}^{\prime }\left(\eta \right),v=axg\left(\eta \right),\eta =\sqrt{\frac{a}{v}.z},\chi \left(\eta \right)(N_w-N_{\infty })=N-N_{\infty },w=-{\left(a\nu \right)}^{\frac{1}{2}}.$$

(8)

By the above-mentioned similarity transformations, Equation (5) is inconsequentially verified; Equations (2)–(7) of the above-mentioned model will yield the following results

$$f{}^{‴}+\frac{(n-1)(D+1)}{D}{W}_e^{D}f{}^{″}{}^{D}f{}^{‴}+f.f{}^{″}-\lambda .f{}^{\prime }+2\beta g-(1+F_r).f{}^{\prime }{}^2=0,$$

(9)

$$g{}^{″}+\frac{(n-1)(D+1)}{D}{W}_e^{D}g{}^{\prime }{}^{D}g{}^{″}+f.g{}^{\prime }-f{}^{\prime }.g-2.\beta .f{}^{\prime }-\lambda .g-F_r{g}^2=0,$$

(10)

$$\theta {}^{″}+P_r.f\theta {}^{\prime }+P_r(N_t\theta {}^{\prime }{}^2+N_b\theta {}^{\prime }\varphi {}^{\prime })=0,$$

(11)

$$\varphi {}^{″}+S_c.f.\varphi {}^{\prime }+\frac{Nt}{Nb}\theta {}^{″}=0,$$

(12)

$$\chi {}^{″}+P_r{L}_b\chi {}^{\prime }-P_e(\varphi {}^{″}(\sigma +\chi )+\chi {}^{\prime }\varphi {}^{\prime })=0,$$

(13)

with

$$\begin{array}{c}\left\{\begin{array}{c}f=0,f{}^{\prime }=1,g=0,\theta =\varphi =1,x=0,at\eta =0,\hfill \\ \hfill f{}^{\prime }⟶0,g⟶0,x⟶0,\theta ⟶0,\varphi ⟶0,at\eta ⟶\infty ,\hfill \end{array}\right.\end{array}$$

(14)

where $\lambda =\frac{\nu }{ka}$, $\beta =\frac{\tilde{\mathsf{\Omega }}}{a}$, $F_r=\frac{C_b}{k\frac{1}{2}}$, $P_r=\frac{\nu }{\alpha }$, $S_c=\frac{\nu }{D}$, $\sigma =\frac{k^2}{a}$, $Lb$, $Nb=\tau {\tilde{D}}_B({\nu }^{-1}{\tilde{C}}_w-{\nu }^{-1}{\tilde{C}}_{\infty })$, $Nt=\frac{{\tilde{D}}_T(\tau {\tilde{T}}_w-\tau {\tilde{T}}_{\infty })}{\nu {\tilde{T}}_{\infty }}$ represent the porosity parameter, rotating parameter, inertia coefficient, the Prandtl number, Schmidt number, reaction rate, bioconvection Lewis number, Brownian motion, and thermophoresis, respectively. The skin fraction coefficient, local Nusselt numbers, and Sherwood numbers [35,39,41] are given as,

$$N{u}_x=\frac{x{q}_w}{k(T_w-T_{\infty })},S{h}_x=\frac{x{j}_w}{D(C_w-C_{\infty })},C_f=\frac{T_w}{\rho U_w^2},T_w=\mu \left(\frac{\partial u}{\partial z}\right)$$

(15)

3. Numerical Solution and Validation of Results

The exact solution to the current problem seems complicated. Therefore, MATLAB was used to solve the problem by discussing the numerical procedure (below). The bvp4c methodology was used to solve the system of Equations (13)–(17). To compute the results, a first guess was necessary to meet the boundary condition when using this approach. For implementation, the following variables are introduced:

$$\begin{array}{c}\left\{\begin{array}{c}f={\zeta }_1,f^{\prime }={\zeta }_2,f^{″}={\zeta }_3,f^{‴}=\zeta .{\zeta }_1\hfill \\ \hfill g={\zeta }_4,g^{\prime }={\zeta }_5,g^{″}=\zeta .{\zeta }_2\hfill \\ \hfill \theta ={\zeta }_6,\theta {}^{\prime }={\zeta }_7,{\theta }^{″}=\zeta .{\zeta }_3\hfill \\ \hfill \varphi ={\zeta }_8,\varphi {}^{\prime }={\zeta }_9,{\varphi }^{″}=\zeta .{\zeta }_4\hfill \\ \hfill \chi ={\zeta }_{10},\chi {}^{\prime }={\zeta }_{11},{\chi }^{″}=\zeta .{\zeta }_5\hfill \end{array}\right.\end{array}$$

(16)

$$\begin{array}{c}\left\{\begin{array}{c}\zeta .{\zeta }_1=(1+F_r).{\zeta }_2{}^2-2\beta .{\zeta }_4+\lambda .{\zeta }_2-{\zeta }_1.{\zeta }_3\hfill \\ \hfill \zeta .{\zeta }_2={\zeta }_2.{\zeta }_4+2\beta .{\zeta }_2+\lambda .{\zeta }_4+F_r{\zeta }_4{}^2-{\zeta }_1.{\zeta }_5\hfill \\ \hfill \zeta .{\zeta }_3=-P_r({\zeta }_1.{\zeta }_7+(N_b{\zeta }_7.{\zeta }_9+N_t{\zeta }_7{}^2))\hfill \\ \hfill \zeta .{\zeta }_4=-\frac{Nt}{Nb}\zeta .{\zeta }_3-S_c.{\zeta }_1.{\zeta }_9\hfill \\ \hfill \zeta .{\zeta }_5=P_e(\zeta .{\zeta }_4.(\sigma +{\zeta }_{10})+{\zeta }_{1}1.{\zeta }_9)-P_r.L_b.F.{\zeta }_{11}\hfill \end{array}\right.\end{array}$$

(17)

The boundary conditions are:

$$\left\{\begin{array}{c}{\zeta }_1={\zeta }_4={\zeta }_{10}=0,{\zeta }_2={\zeta }_6={\zeta }_8=1,at\eta =0\hfill \\ \hfill {\zeta }_2⟶0,{\zeta }_4⟶0,{\zeta }_6⟶0,{\zeta }_8⟶0,{\zeta }_{10}⟶0,at\eta ⟶0\hfill \end{array}\right.$$

(18)

Validation of Results

The reliability of the newly obtained results was established by comparing the obtained solutions for a ‘limiting’ case with already published references [42,43,44,45]. From Table 1 and Table 2, it is clearly seen that the results have excellent and reasonable correlations with the published articles.

Table 1. Computing $f^{″}\left(0\right)$ and $h^{\prime }\left(0\right)$ values with distinct values of parameters $\lambda$ and $\beta =Fr=0$.

$\mathit{\lambda }$	Nazar et al. [42]		Zaimi et al. [43]		Current Findings
	$-f^{″}\left(\mathbf{0}\right)$	$-h^{\prime }\left(\mathbf{0}\right)$	$-f^{″}\left(\mathbf{0}\right)$	$-h^{\prime }\left(\mathbf{0}\right)$	$-f^{″}\left(\mathbf{0}\right)$	$-h^{\prime }\left(\mathbf{0}\right)$
0	1.0000	0.0000	1.0000	0.0000	1.00001	0.00000
0.5	1.1384	0.5128	1.1384	0.5128	1.13839	0.51277
1	1.3250	0.8371	1.3250	0.8371	1.32503	0.83710
2	1.6523	1.2873	1.6523	1.2873	1.65232	1.28725
3	1.6523	1.2870	1.9289	1.6248	1.92894	1.62474

Table 2. Computing $f^{″}\left(0\right)$ and $h^{\prime }\left(0\right)$ values with distinct values of parameters $\lambda$ and $\beta =Fr=0$.

$\mathit{\lambda }$	Ali et al. [44]		Bagh et al. [45]		Current Findings
	$-f^{″}\left(\mathbf{0}\right)$	$-h^{\prime }\left(\mathbf{0}\right)$	$-f^{″}\left(\mathbf{0}\right)$	$-h^{\prime }\left(\mathbf{0}\right)$	$-f^{″}\left(\mathbf{0}\right)$	$-h^{\prime }\left(\mathbf{0}\right)$
0	1.0000	0.0000	1.0000	0.0000	1.00001	0.00000
0.5	1.1384	0.5128	1.1384	0.5128	1.13839	0.51277
1	1.3250	0.8371	1.3250	0.8371	1.32503	0.83710
2	1.6523	1.2873	1.6523	1.2873	1.6523 5	1.28725
3	1.6523	1.2870	1.9289	1.6248	1.92894	1.62474

4. Analysis and Discussion of Results

In this section, we analyze and discuss the results of a model used to predict the Coriolis force effects on the dynamics of Carreau–Yasuda flow toward a continuously stretched surface subject to the Darcy–Forchheimer law. The default numeric values of the parameters that are already dimensionless in the mathematical model section are: $\beta =1,\lambda =0.2,Fr=1,Pr=2,Sc=1,\sigma =0.5,Nb=0.1,Nt=0.1,Lb=1,Pe=0.5,D=0.2$, $W_e=0.3$, $D=2.0$, $n=2.0$.

4.1. Analysis of the Results

The rotating ($\beta$) and Forchheimer number $F_r$ parameter impacts on the velocities are described in Figure 2a,b. When there was an increase in the rotational parameter $\beta$, a decrease occurred in the velocity distribution along ‘a axis’, but an inverse trend was reported along the y-axis. Physically, the stretching rate of the sheet decreased as $\beta$ increased; hence, the velocity decreased. In Figure 2a,b, regarding the consequences, one can observe how the change in the $Fr$ parameter took place by the variation of velocities $f^{\prime }\left(\eta \right)$ & $g(\eta$). When one can increase, $Fr$ reduces the magnitude of the fluid flow, thus reducing the speed. Regarding the association with the porous medium, which makes the fluid more viscous and produces an opposition, this force is responsible for slowing down the fluid speed. A similar influence in Figure 3a,b against the higher strength of the porous parameter $\lambda$ is noted; we observed that the impacts of $\lambda$ on $f{}^{\prime }$($\eta$) were comparable to those of $\beta$. When $\lambda$ increased, the viscosity of fluid was elevated, creating resistance to the flow and reducing the speed of the flow. Further, the growing value of n elevated the primary $f^{\prime }\left(\eta \right)$), but an opposite curve behavior was also noted. Figure 4a,b presents the physical description of $W_e$ (Weissenberg number) and D (Carreau–Yasuda constant) on the dynamics of $f^{\prime }\left(\eta \right)$ & $g(\eta$). The $f^{\prime }\left(\eta \right)$ booted up against $W_e$; decreasing curves were reported against D, and $g(\eta$) showed an opposite trend. The rise in $W_e$ enhanced the elastic forces that were more prominent as compared to the viscous forces that boosted the fluid velocity. Further, $f^{\prime }\left(\eta \right)$ slowed down when growing the strength of D, and an inverse curve trend in $g(\eta$) was observed.

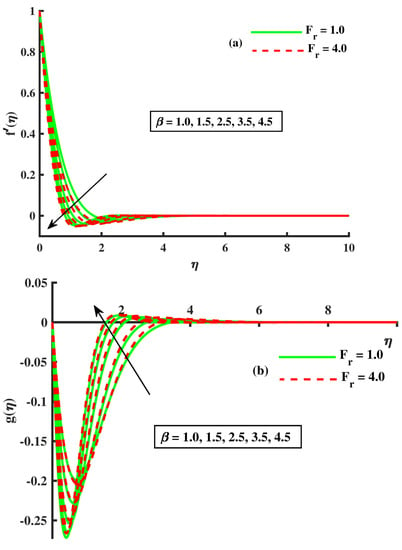
Figure 2. The effect of $\beta \&F_r$ on $f^{\prime }\left(\eta \right)\&g(\eta$).

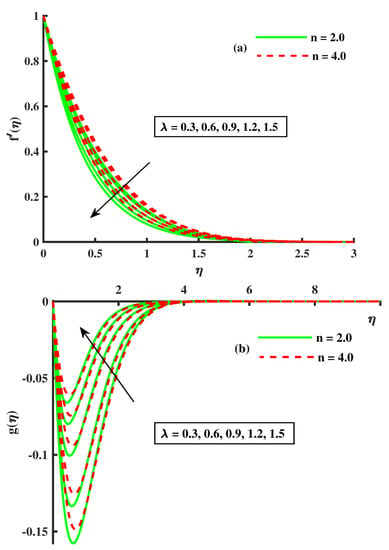
Figure 3. The effect of $\lambda \&n$ on $f^{\prime }\left(\eta \right)\&g(\eta$).

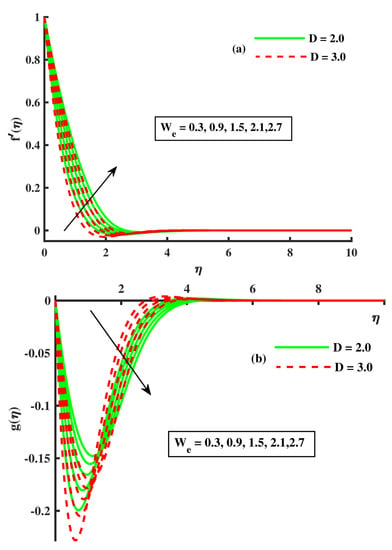
Figure 4. The effect of $W_e\&D$ on $f^{\prime }\left(\eta \right)\&g(\eta$).

In Figure 5a,b and Figure 6a,b, we describe the effects on the temperature $\theta \left(\eta \right)$ by changing $\beta ,F_r,\lambda ,n,W_e,D,N_t,\&N_b$ parameters. In these figures, we noticed that the base fluid temperature was enhanced against higher inputs of $\beta ,F_r,\lambda ,D,N_t,\&N_b$, but declined against n & $W_e$. Physically, the nanoparticle movement occurred due to the thermophoresis force, which caused nanoparticle movement from the hot region to the cooler region, which is why heat transportation was faster at the boundary region. Similarly, the tiny particle random motion was faster in the base fluid, which elevated the Brownian motion to strengthen the thermal transport. The rise in $W_e$ enhanced the elastic forces that were more prominent as compared to viscous forces, which declined the fluid temperature $\theta \left(\eta \right)$. Similarly, the drag force was produced due to the porous medium, which resulted in thermal dissipation to create extra heat.

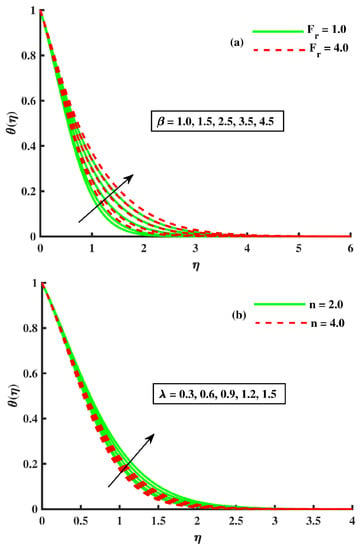
Figure 5. The effect of $\beta ,n,\lambda ,\&F_r$ on $\theta \left(\eta \right)$.

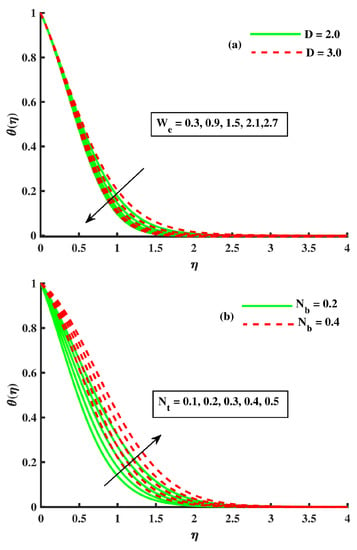
Figure 6. The effect of $W_e,D,N_b,\&N_t$ on $\theta \left(\eta \right)$.

In Figure 7a,b, we described the effects on $\varphi \left(\eta \right)$ by changing $\beta ,F_r,\lambda ,N_t,$ & $N_b$ parameters. In this figure, we noticed that the base fluid concentration of the tiny particle function $\varphi \left(\eta \right)$ was boosted against higher inputs of $\beta ,F_r,$ & $N_t$, but declined against $N_b$. In Figure 7b, we describe the effects of thermophoresis on the concentration profile by increasing thermophoresis $Nt$, the behavior of the concentration profile also increases. In Figure 7b, we also describe the effects of the Brownian motion on the concentration profile; by increasing the Brownian motion $Nb$, the behavior of the concentration profile decreases. The motile microorganism function $\chi \left(\eta \right)$ demonstrates the rising function against the input of higher value $\beta$ & $F_r$, but curves show the decline against $L_b$ & $P_e$. In Figure 8a,b and Figure 9a,b, the values of skin friction, the Nusselt number, and Sherwood number are concluded under the boosted values of $\beta ,F_r,$ & $W_e$ parameters. The values of the skin friction coefficients along the x-axis decrease with the increase of the rotatory parameter $\beta$ & $F_r$, and the values of the skin friction coefficient along the y-axis show the opposite trend but boosted values are reported against $W_e$. The Nusselt number depreciation was observed for the boosted values of $W_e$, and lower values in the case of the growing strength of $\beta$ & $F_r$. The values of the Sherwood number for the boosted values of $\beta ,F_r.$ & $W_e$ are mentioned in Figure 9b. A similar curve behavior is seen in Figure 9a.

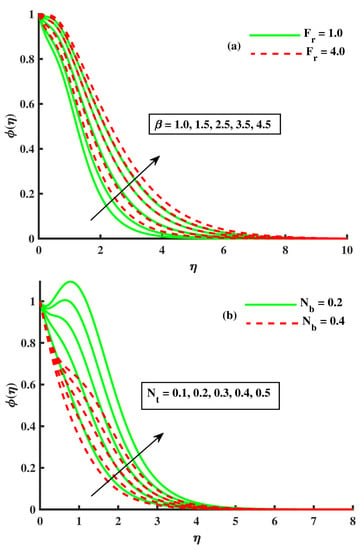
Figure 7. The effects of $W_e,D,N_b,\&N_t$ on $\varphi \left(\eta \right)$.

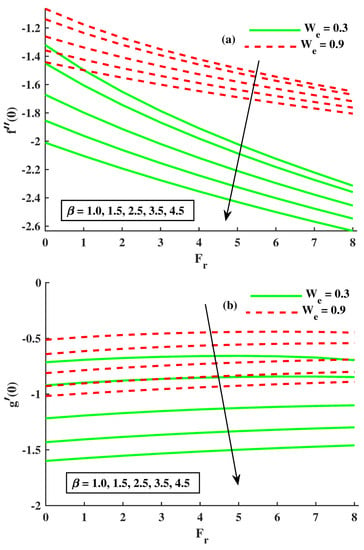
Figure 8. The effects of $\beta ,F_r,\&W_e$ on Skin friction.

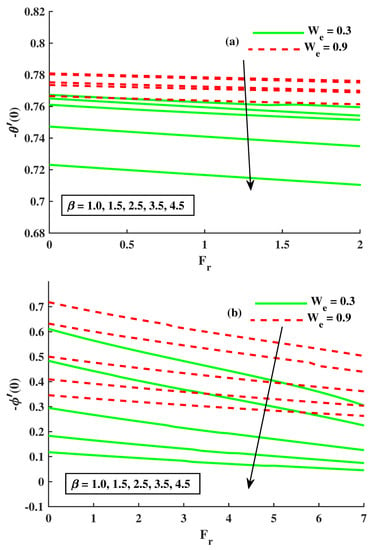
Figure 9. The effects of $\beta ,F_r,\&W_e$ on Nusselt and Sherwood numbers.

4.2. Discussion of the Results

Figure 2a,b demonstrates the influence of the rotating ($\beta$) and Forchheimer number $\left(F_r\right)$ against the growing strength of these involved parameters. The magnitudes of both velocities decreased via rising values of $\beta \&F_r$. According to Bagh et al. [45] and Tayyab et al. [39], the physical reason behind this behavior is the Coriolis force $\left(2\beta g\right)$ and $(-2\beta f{}^{\prime })$ incorporated, respectively, in Equations (9) and (10). As mentioned above, velocity g is negative, the two forces in their respective orders impart opposing impacts on $f^{\prime }\&g$. Further, the association with the porous medium, which makes the fluid more viscous, produced an opposition; this force was responsible for slowing down the fluid speed. An opposite trend was reported in the temperature and concentration distribution against rotating and the Forchheimer number (see Figure 5, Figure 6 and Figure 7a). The viscosity of the fluid elevated against the higher input of porosity, which created resistance to the flow; this resistance force slowed down the fluid velocity, which enhanced the temperature [26]. Figure 4a,b shows the variation of velocities against rinsing values of $W_e$, and the magnitudes of both the velocities boosted against $W_e$. According to Rana et al. [36] and Tayebi et al. [32], the reason for the outcomes are elastic forces, which were produced due to the growing strength of the Weissenberg number. The rise in $W_e$ enhanced the elastic forces that were more prominent as compared to viscous forces, which boosted the fluid velocity. Further, the $\theta \left(\eta \right)$ profile shows a decline against $W_e$ (see Figure 6a).

Figure 6b and Figure 7b show the implication of the Buongiorno model parameters, such as thermophoresis and the Brownian motion on the temperature field. In these figures, we noticed that the base fluid temperature was enhanced against higher input of $N_t,$ & $N_b$, but the concentration field showed similar behavior against $Nt$ and declined against $Nb$. Similar curves for the temperature and concentration field against Buongiorno’s model parameters have been reported by many other researchers, and physically, the nanoparticle movement occurred due to the thermophoresis force, which caused nanoparticle movement from the hot region to the cooler region, and that is why heat transportation was faster at the boundary region. Similarly, the tiny particle random motion was faster in the base fluid, which elevated the Brownian motion to strengthen the thermal transport [7,8]. Figure 10a,b demonstrates the decreasing motile microorganism function $\chi \left(\eta \right)$ against the input of higher value $L_b$ & $P_e$. According to Ali et al. [29], the physical reason behind this trend is explained as follows: the bioconvection Lewis number $Lb$ and Péclet number $Pe$ are declining functions. In fact, the Péclet number is the proportion of the extreme cell swimming speed to the diffusivity of microorganisms as the escalation in $Pe$ raises the speed of motile microorganisms, shrinking the motile density.

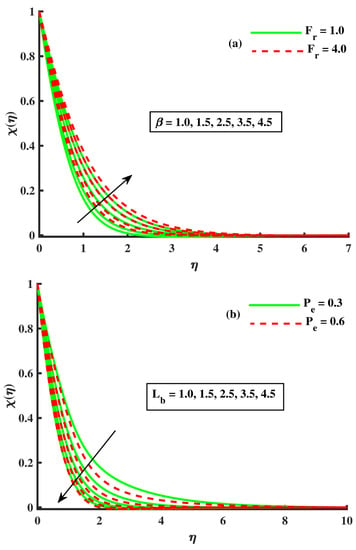
Figure 10. The effects of $\beta ,F_r,L_b,\&P_e$ on $\chi \left(\eta \right)$.

5. Conclusions

We analyzed the bioconvection 3D nanofluid Darcy–Forchheimer rotating flow in the presence of activation energy. In this manuscript, the system of PDE was solved by similarity transformations and non-linear ODE was obtained. The system of ODE was reduced to a first-order non-linear ODE; we then solved the equations with the help of the bvp4c package built in MATLAB. The main results are given below.

• The velocity profile along the x-axis $f{}^{\prime }$ has negative behavior for the boosted values of $\beta$, $Fr$, D, and $\lambda$
• The velocity profile along the y-axis $g{}^{\prime }$ has negative behavior for the boosted values of $\beta$, $Fr$, and $\lambda$
• The temperature profile of the nanofluid was enhanced for the boosted value of $Nb$ and $Nt$, with the decreasing behavior nature for the large value of $W_e$
• The concentration of the nanofluid increased for the boosted value of $F_r$, $\beta$, $Nt$, and we observed opposite behavior for $Nb$.
• Regarding the profile of the micro-motile organism, there was an ’increasing nature’ for the enhanced value of $Pe$, and we observed ’decreasing behavior’ for the boosted value of $\beta$ & $F_r$
• The values of the skin friction coefficients increased with the increase of $W_e$ and the decrease of $\beta$ & $F_r$.
• The Sherwood number increment was observed for the boosted values of $W_e$, and was opposite to $\beta$ & $F_r$.

After successful numerical computation of this elaborated fluid problem, this study could be extended to Casson nanofluid, Oldroyd-B nanofluid, Maxwell nanofluid, and tangent hyperbolic nanofluid.