Abstract
Fractional nonlinear systems have been considered in many fields due to their ability to bring memory-dependent properties into various systems. Therefore, using fractional derivatives to model real-world phenomena, such as neuronal dynamics, is of significant importance. This paper presents the fractional memristive Wilson neuron model and studies its dynamics as a single neuron. Furthermore, the collective behavior of neurons is researched when they are locally and diffusively coupled in a ring topology. It is found that the fractional-order neurons are bistable in some values of the fractional order. Additionally, complete synchronization, lag synchronization, phase synchronization, and sine-like synchronization patterns can be observed in the constructed network with different fractional orders.
MSC:
34C28; 34K23
1. Introduction
Fractional differential equations have been used for modeling different phenomena in various fields [1]. In fact, many natural dynamical behaviors are not dependent on instant time and rely on time history. This reality can be considered in certain models by changing their integer-order derivatives into fractional ones [2]. Hence, fractional-order equations are usually more successful in modeling the nonlinear behavior of memory-dependent systems [3]. For example, such fractal approaches are applicable for modeling the non-equilibrium processes [4,5]. The fractional calculus can be found in biology, electrochemistry, electromagnetism, etc. [6,7,8]. The other advantage of the fractional models is the addition of the degree of freedom by one, which lets the model exhibits more diverse and even complex behaviors [9]. In other words, the fractional-order models indicate more flexibility.
The advantages of fractional calculus have led neuroscientists to present fractional-order neuron models. It has been shown that fractional-order models result in more efficient information processing [10]. In the literature, several fractional-order neuron models have been introduced and investigated [11,12,13,14]. For example, Brandibur and Kaslik analyzed the asymptotic stability and instability of a two-dimensional fractional-order Morris-Lecar neuron model [11]. Mondal et al. [12] extended the FitzHugh-Rinzel (FH-R) model by fractional-order derivatives and reported different firing patterns such as regular spiking, fast-spiking, bursting, etc. The Izhikevich neuron model was generalized by the fractional-order derivatives in [13]. In this study, numerical techniques were applied for solving the fractional model and then their synchronization was studied. Chen et al. [14] considered a fractional-order Hodgkin–Huxley neuron model to analyze the effect of fractional order on the Hopf bifurcation and presented a control method.
Synchronization of neurons is an important problem in neuroscience. The reason is that synchronization has a substantial role in the information processing of neurons and the occurrence of pathological brain functions [15]. Consequently, it has been the focus of many pieces of research [16,17]. Generally, synchronization relies on the network structure, the dynamics of the neuron model, and the configuration of coupling between neurons. Depending on these properties and the parameters’ values, complete synchronization, phase synchronization, lag synchronization, partial synchronization, etc., can appear in the network [18]. The synchronization behaviors have also been studied among the fractional-order neuronal models [19,20,21,22,23]. Recently, Yang et al. [20] considered Hindmarsh–Rose models under electromagnetic radiation to study synchronization and burst transitions. Xin et al. [21] investigated the fractional-order neurons with memristive synapses. They reported different behaviors which were dependent on the fractional-order and the parameter of the synapse. Liu et al. [19] focused on the fractional-order extended Hindmarsh-Rose neurons exposed to a magneto-acoustical stimulation input that can represent complex firing behaviors. In this study, a control method was proposed for synchronization.
In this paper, we introduce the fractional-order memristive Wilson neuron. The dynamics of the model are investigated and bifurcation analysis is carried out. The collective behaviors of the fractional-order memristive Wilson neurons are also considered. The synchronization patterns are studied for different parameter values. The paper is organized as follows: the fractional model is proposed and analyzed in the next section; the collective behaviors of the network of the proposed model are investigated in Section 3; and the conclusions are given in Section 4.
2. Fractional Memristive Wilson Neuron
Since Hodgkin and Huxley [24] proposed a nonlinear differential equation to describe the behavior of a real neuron, many attempts have been made to model the neuron’s dynamics. For example, Wilson [25] introduced a 2-D neuron model by performing a simplification on the Hodgkin and Huxley model. Later, adding a flux-controlled memristor to the model, Xu et al. [26] presented the memristive Wilson (MW) model that is mathematically expressed as
where
Here variables , , and refer to the membrane potential, recovery, and flux variables. and are two activation functions of the membrane potantial and recovey states. Furthermore, is the membrane capacitor, is the reversal potential of channel, is the reversal potential of channel, is the maximal conductance of channel, activation time of channel, time scale of the flux changes, is the memristor inner parameter, memductance changing rate, is the electromagnetic induction coupling strength, and is the time scale coefficient.
Since fractional calculus brings memory characteristics to the models, they are more functional for modeling real-world phenomena, such as neuron behaviors [22]. Hence, we present the WM model with fractional derivatives (FMW) that can be rewritten in general form as
where denotes Caputo-type fractional derivative with the fractional order of . The Caputo-type derivative can be expressed by
Here, is an operation that rounds the inner value to the first higher integer. According to the definition in Equation (4), the derivative of is proportional to its classical derivative , for all . Thus, past times get involved in the calculations, and fractional calculus deals with memory. Furthermore, for , due to the determined distribution function, recent times have more impact than past times. Note that a Caputo-type fractional derivative mathematically includes initial and boundary conditions, and thus, such a derivative can be practical in dealing with real problems [27]. Applying the Riemann–Liouville integral operator [28], Equation (4) can be reformatted as
Equation (5) can be solved numerically by employing the Adam–Bashforth–Moulton algorithm [28]. The model exhibits different firing patterns by varying the fractional order of derivatives. Setting , , , , , , , , , and , Figure 1 shows the bifurcation diagram of the FMW neuron model as a function of fractional order , where is in the range of . In general, a period-doubling bifurcation can be seen as increases. Looking more closely at Figure 1, many saddle-node bifurcations and crises can be observed as varies. However, the most noticeable ones are at (saddle-node bifurcation), (boundary crisis), and (interior crisis). Note that the strategy for plotting the bifurcation diagrams is taken from [29]. Accordingly, the initial condition of each step ( value) is determined as the last sample of the previous step (former value) trajectory by increasing the bifurcation parameter.
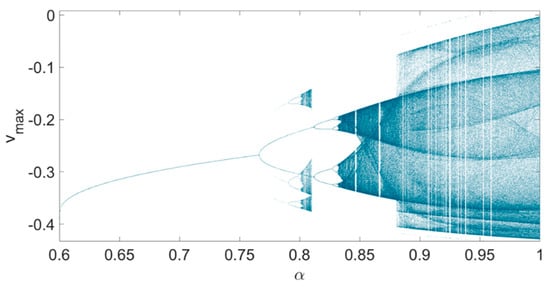
Figure 1.
The bifurcation diagram of FMW neuron as a function of fractional order . Other parameters are , , , , , , , , , and . The initial condition is .
The phase portraits of the FMW neuron in 3-D variable space by considering (period-1 region of Figure 1), (period-2 region of Figure 1), (period-4 region of Figure 1), and (chaotic region of Figure 1), are obtained and demonstrated in Figure 2. It can be seen that the model represents different periodic and chaotic patterns by varying .
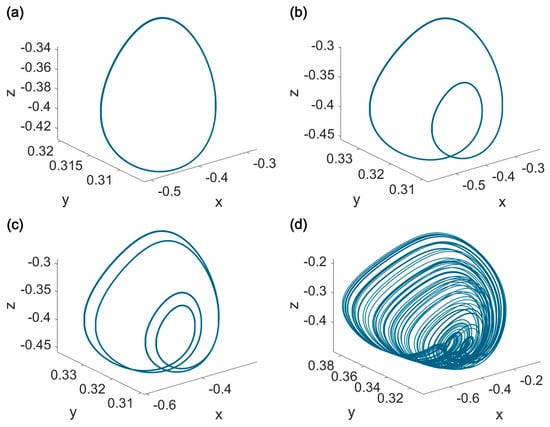
Figure 2.
The phase portraits of the FMW neuron for (a) and , (b) and , (c) and , and (d) and . Other parameters are , , , , , , , , , and .
Although the MW neuron is monostable in the determined parameter set (see [26]), more numerical investigations reveal that the FMW neuron model is bistable in all studied fractional orders (Figure 2a–d). The coexisting attractors of the FMW neuron are presented in Figure 3 for , , , and , respectively. Consequently, the period-1 limit cycle (Figure 2a) coexists with a period-2 limit cycle (Figure 3a). Similarly, the period-2 and period-4 limit cycles (Figure 2b,c) coexist with a chaotic attractor (Figure 3b,c). The coexistence of the strange attractor (Figure 2d) and a limit cycle (Figure 3d) can also be observed.
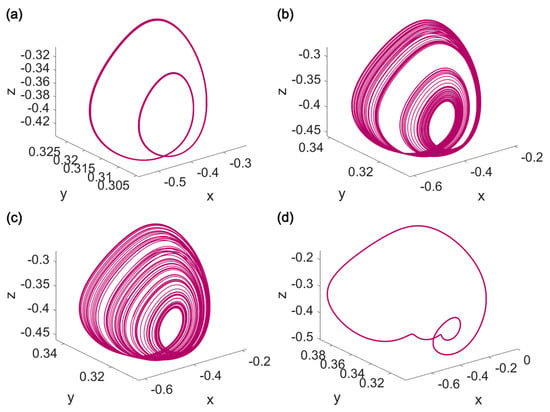
Figure 3.
The phase portraits of the FMW neuron for (a) and , (b) and , (c) and , and (d) and . Other parameters are , , , , , , , , , and .
3. Network Dynamics
This paper also investigates the collective behavior of the FMW neurons by considering its dynamics as a ring graph’s nodes. The constructed network can be mathematically formulated by
where is the coupling strength, is the connectivity matrix, and shows the network size (number of coupled oscillators). For locally coupled oscillators in an undirected ring network of size , is . Here, 100 locally coupled FMW neurons are considered in an undirected ring network. It should be noted that the same investigations can be performed considering an asymmetric graph. However, for simplicity, a symmetric ring network is considered here. The synchronization error [30] and the parameter [31] are calculated as the measures of complete synchronization and phase synchronization in the considered network. The synchronization error can be obtained by
Here, denotes averaging over time.
The parameter which is a quantification of the phase synchronization degree, can be defined as
And
where defines the phase of the th neuron at each time step and refers to the onset of the the spike of the the neuron [32].
Figure 4 shows the synchronization error and parameter values as a function of coupling strengths () at . It is observed that for , the FMW neurons become completely synchronous. Next, the network is investigated to observe other collective patterns before the neurons reach complete synchronization. Figure 5 shows the spatio-temporal patterns along with the snapshot of the last sample and the neurons’ time series for . According to Figure 5a, lag synchronization patterns can be found in the studied network. Besides, Figure 5b shows that the neurons are synchronized in the period-1 attractor shown in Figure 2a. Note that the randomly generated initial conditions in a range of are considered for values and zero initial values are assumed for and .
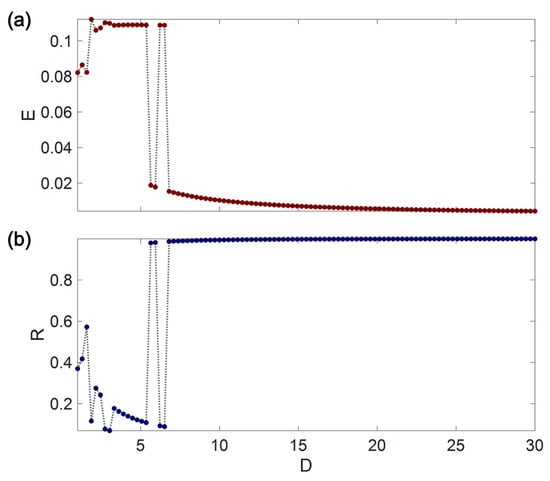
Figure 4.
(a) The synchronization error and (b) parameter values as a function of the coupling strength. The fractional-order is .
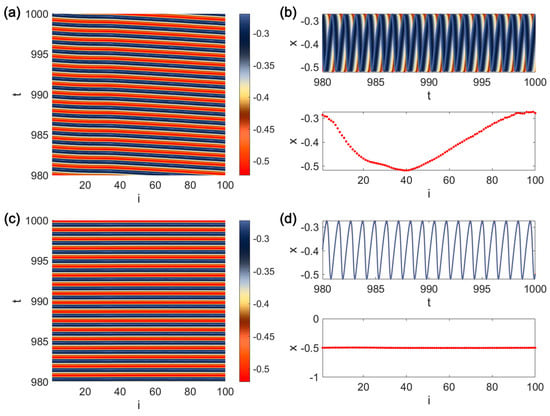
Figure 5.
(a) The spatio-temporal patterns of locally coupled FMW neurons, as well as (b) the neurons’ time series and the snapshot of the last samples for . (c) The spatio-temporal patterns of locally coupled FMW neurons, as well as (d) the neurons’ time series and the snapshot of the last samples for . is considered.
Similar to Figure 4, Figure 6 expresses the synchronization error and parameter values as a function of coupling strengths () at . Neurons’ initial conditions and the parameter set are considered the same as those in Figure 4. From Figure 6, it can be noticed that for the networks cannot get completely synchronized, although the broader range for coupling strength is investigated. However, the signs of phase synchronization can be observed in Figure 6 since, in some values, the parameter is almost equal to one, but the synchronization error has a considerable amount. The result of studying the collective patterns of the FMW network for , including the spatio-temporal patterns, the snapshot of the last sample, and the neurons’ time series, are presented in Figure 7. Phase synchronization patterns ( and ) can be observed for higher values of the coupling strength (Figure 7b). However, in lower values of , sine-like synchronization ( and ) can also be found (Figure 7a). Moreover, the neurons’ synchronization manifold is the chaotic attractor, as demonstrated in Figure 2d.
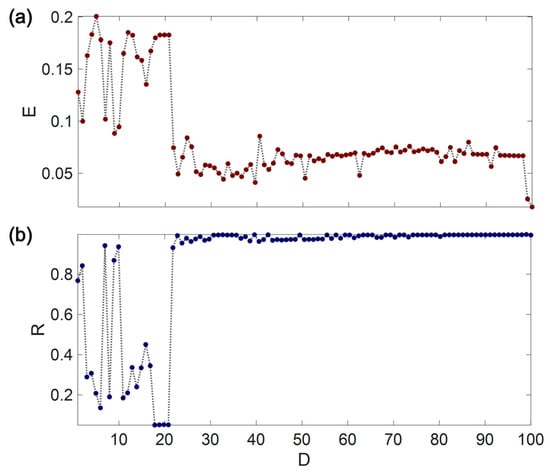
Figure 6.
(a) The synchronization error and (b) parameter values as a function of the coupling strength . The fractional-order is .
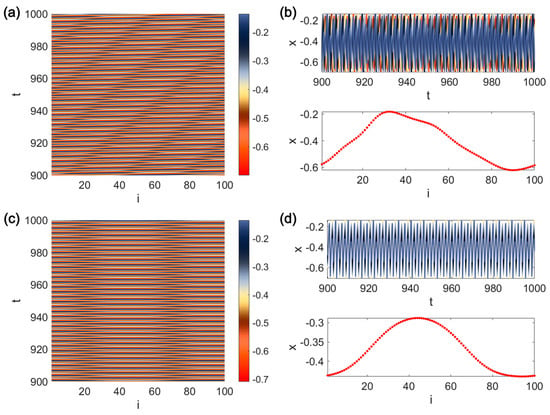
Figure 7.
(a) The spatio-temporal patterns of locally coupled FMW neurons, as well as (b) the neurons’ time series and the snapshot of the last samples for . (c) The spatio-temporal patterns of locally coupled FMW neurons, as well as (d) the neurons’ time series and the snapshot of the last samples for . is considered.
4. Conclusions
This paper presented a fractional version of the memristive Wilson neuron model described in [26], using Caputo-type fractional derivatives. As described in [27], the Caputo derivative functions well in dealing with real concerns since it involves the initial and boundary conditions in the formulation. It should be noted that applying the Caputo derivative function, the derivative of a constant is zero. However, it cannot be employed on non-differentiable functions. On the other hand, the Riemann-Liouville derivative of an arbitrary constant value is not zero, but it can be performed for non-differentiable functions. Moreover, the Jumarie fractional derivative has no solution for a function with a discontinuity at the origin, and therefore the derivative of a constant value with the Weyl derivative cannot be obtained.
Firstly, the dynamical characteristics of the FMW neuron model were investigated through a bifurcation analysis. The study of the neuron’s bifurcation diagrams showed different types of bifurcation points, including period-doubling bifurcations, interior crises, boundary crises, and saddle-node bifurcations. The original MW neuron model parameters were set to the value at which the system is monostable. However, when fractional, the numerical investigation showed the bistability of the FMW neurons in some fractional order () values. Secondly, to study the collective behavior of the FMW neurons, a ring network of 100 FMW neurons that were locally connected through diffusive couplings was constructed. The synchronization error and parameter were selected to investigate the networks from the point of complete synchronization and phase synchronization. The constructed network was explored in two fractional-order values (, wherein the FMW neuron has periodic solutions, and , wherein the FMW neuron has a chaotic solution). As a result, complete synchronization and lag synchronization was found for . Moreover, for , phase synchronization and sine-like synchronization were observed in the studied network.
A newly developed fractional derivative, namely the fractal-fractional derivative [33], is concerned to be applicable in dealing with real problems. So, as a future study, it would be interesting to investigate the dynamical properties and collective behavior of FMW neurons using the fractal-fractional derivative in an asymmetric network topology.
Author Contributions
Conceptualization, K.R. and H.N.; methodology, H.N.; software, G.V. and M.M.; validation, E.T.-C. and K.R.; investigation, G.V. and M.M.; writing—original draft preparation, M.M. and G.V.; writing—review and editing, E.T.-C. and K.R.; visualization, K.R.; supervision, E.T.-C.; All authors have read and agreed to the published version of the manuscript.
Funding
This work is funded by the Center for Nonlinear Systems, Chennai Institute of Technology, India vide funding number CIT/CNS/2022/RD/006.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Rahimy, M. Applications of fractional differential equations. Appl. Math. Sci. 2010, 4, 2453–2461. [Google Scholar]
- Atıcı, F.M.; Şengül, S. Modeling with fractional difference equations. J. Math. Anal. Appl. 2010, 369, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Naghibolhosseini, M.; Long, G.R. Fractional-order modelling and simulation of human ear. Int. J. Comput. Math. 2018, 95, 1257–1273. [Google Scholar] [CrossRef]
- Shymanskyi, V.; Sokolovskyy, Y. Finite Element Calculation of the Linear Elasticity Problem for Biomaterials with Fractal Structure. Open Bioinform. J. 2021, 14, 114–122. [Google Scholar] [CrossRef]
- Shymanskyi, V.; Sokolovskyy, Y. Variational Formulation of the Stress-Strain Problem in Capillary-Porous Materials with Fractal Structure. In Proceedings of the 2020 IEEE 15th International Conference on Computer Sciences and Information Technologies (CSIT), Zbarazh, Ukraine, 23–26 September 2020; Volume 1, pp. 1–4. [Google Scholar]
- Jesus, I.S.; Machado, J.T. Implementation of fractional-order electromagnetic potential through a genetic algorithm. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1838–1843. [Google Scholar] [CrossRef] [Green Version]
- Zou, C.; Zhang, L.; Hu, X.; Wang, Z.; Wik, T.; Pecht, M. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, H.; Dubey, V.; Kumar, R.; Singh, J.; Kumar, D.; Baleanu, D. An efficient computational approach for a fractional-order biological population model with carrying capacity. Chaos Solitons Fractals 2020, 138, 109880. [Google Scholar] [CrossRef]
- Gutiérrez, R.E.; Rosário, J.M.; Tenreiro Machado, J. Fractional order calculus: Basic concepts and engineering applications. Math. Probl. Engin. 2010, 2010, 375858. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Li, Y.; Huang, X. Stability and Hopf bifurcation of fractional-order complex-valued single neuron model with time delay. Int. J. Bifurc. Chaos 2017, 27, 1750209. [Google Scholar] [CrossRef]
- Brandibur, O.; Kaslik, E. Stability properties of a two-dimensional system involving one Caputo derivative and applications to the investigation of a fractional-order Morris–Lecar neuronal model. Nonlinear Dyn. 2017, 90, 2371–2386. [Google Scholar] [CrossRef] [Green Version]
- Mondal, A.; Sharma, S.K.; Upadhyay, R.K.; Mondal, A. Firing activities of a fractional-order FitzHugh-Rinzel bursting neuron model and its coupled dynamics. Sci. Rep. 2019, 9, 15721. [Google Scholar] [CrossRef] [PubMed]
- Tolba, M.F.; Elsafty, A.H.; Armanyos, M.; Said, L.A.; Madian, A.H.; Radwan, A.G. Synchronization and FPGA realization of fractional-order Izhikevich neuron model. Microelectron. J. 2019, 89, 56–69. [Google Scholar] [CrossRef]
- Chen, S.; Zou, Y.; Zhang, X. An efficient method for Hopf bifurcation control in fractional-order neuron model. IEEE Access 2019, 7, 77490–77498. [Google Scholar] [CrossRef]
- Abeles, M.; Prut, Y.; Bergman, H.; Vaadia, E. Synchronization in neuronal transmission and its importance for information processing. Prog. Brain Res. 1994, 102, 395–404. [Google Scholar]
- Hussain, I.; Jafari, S.; Ghosh, D.; Perc, M. Synchronization and chimeras in a network of photosensitive FitzHugh–Nagumo neurons. Nonlinear Dyn. 2021, 104, 2711–2721. [Google Scholar] [CrossRef]
- Rakshit, S.; Bera, B.K.; Ghosh, D.; Sinha, S. Emergence of synchronization and regularity in firing patterns in time-varying neural hypernetworks. Phys. Rev. E 2018, 97, 052304. [Google Scholar] [CrossRef]
- Boccaletti, S.; Pisarchik, A.N.; Del Genio, C.I.; Amann, A. Synchronization: From Coupled Systems to Complex Networks; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Liu, D.; Zhao, S.; Luo, X.; Yuan, Y. Synchronization for fractional-order extended Hindmarsh-Rose neuronal models with magneto-acoustical stimulation input. Chaos Solitons Fractals 2021, 144, 110635. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, G.; Li, X.; Wang, D. The synchronization behaviors of coupled fractional-order neuronal networks under electromagnetic radiation. Symmetry 2021, 13, 2204. [Google Scholar] [CrossRef]
- Xin, Y.; Guangjun, Z. The Synchronization Behaviors of Memristive Synapse-Coupled Fractional-Order Neuronal Networks. IEEE Access 2021, 9, 131844–131857. [Google Scholar] [CrossRef]
- Ramadoss, J.; Aghababaei, S.; Parastesh, F.; Rajagopal, K.; Jafari, S.; Hussain, I. Chimera state in the network of fractional-order fitzhugh–nagumo neurons. Complexity 2021, 2021, 2437737. [Google Scholar] [CrossRef]
- Ramakrishnan, B.; Parastesh, F.; Jafari, S.; Rajagopal, K.; Stamov, G.; Stamova, I. Synchronization in a Multiplex Network of Nonidentical Fractional-Order Neurons. Fractal Fract. 2022, 6, 169. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef] [PubMed]
- Wilson, H.R. Simplified Dynamics of Human and Mammalian Neocortical Neurons. J. Theor. Biol. 1999, 200, 375–388. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, Q.; Ju, Z.; Ding, S.; Feng, C.; Chen, M.; Bao, B. Electromagnetic induction effects on electrical activity within a memristive Wilson neuron model. Cogn. Neurodynamics 2022. [Google Scholar] [CrossRef]
- Atangana, A.; Secer, A. A note on fractional order derivatives and table of fractional derivatives of some special functions. Abstr. Appl. Anal. 2013, 2013, 279681. [Google Scholar] [CrossRef] [Green Version]
- Diethelm, K.; Freed, A.D. The FracPECE subroutine for the numerical solution of differential equations of fractional order. Forsch. Und Wiss. Rechn. 1998, 1999, 57–71. [Google Scholar]
- Sprott, J.C. A proposed standard for the publication of new chaotic systems. Int. J. Bifurc. Chaos 2011, 21, 2391–2394. [Google Scholar] [CrossRef] [Green Version]
- Sawicki, J.; Omelchenko, I.; Zakharova, A.; Schöll, E. Delay controls chimera relay synchronization in multiplex networks. Phys. Rev. E 2018, 98, 062224. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Perc, M.; Kurths, J. Effects of partial time delays on phase synchronization in Watts-Strogatz small-world neuronal networks. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 053113. [Google Scholar] [CrossRef] [PubMed]
- Shafiei, M.; Parastesh, F.; Jalili, M.; Jafari, S.; Perc, M.; Slavinec, M. Effects of partial time delays on synchronization patterns in Izhikevich neuronal networks. Eur. Phys. J. B 2019, 92, 36. [Google Scholar] [CrossRef]
- Arif, M.; Kumam, P.; Kumam, W.; Akgul, A.; Sutthibutpong, T. Analysis of newly developed fractal-fractional derivative with power law kernel for MHD couple stress fluid in channel embedded in a porous medium. Sci. Rep. 2021, 11, 20858. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).