A Novel Chaos-Based Cryptography Algorithm and Its Performance Analysis

Abstract

Data security represents an essential task in the present day, in which chaotic models have an excellent role in designing modern cryptosystems. Here, a novel oscillator with chaotic dynamics is presented and its dynamical properties are investigated. Various properties of the oscillator, like equilibria, bifurcations, and Lyapunov exponents (LEs), are discussed. The designed system has a center point equilibrium and an interesting chaotic attractor. The existence of chaotic dynamics is proved by calculating Lyapunov exponents. The region of attraction for the chaotic attractor is investigated by plotting the basin of attraction. The oscillator has a chaotic attractor in which its basin is entangled with the center point. The complexity of the chaotic dynamic and its entangled basin of attraction make it a proper choice for image encryption. Using the effective properties of the chaotic oscillator, a method to construct pseudo-random numbers (PRNGs) is proposed, then utilizing the generated PRNG sequence for designing secure substitution boxes (S-boxes). Finally, a new image cryptosystem is presented using the proposed PRNG mechanism and the suggested S-box approach. The effectiveness of the suggested mechanisms is evaluated using several assessments, in which the outcomes show the characteristics of the presented mechanisms for reliable cryptographic applications.

1. Introduction

Information security plays a significant role in our daily lives [1,2]. Information can be protected via performing one of the data security methods like information hiding [3]. The main objective of data encryption is to convert the data style from an intelligible style into an unintelligible pattern. Chaotic models are considered as a backbone of designing modern data encryption algorithms [4,5]. In [6], an encryption method based on a hyperchaotic oscillator was proposed to use the ciphertext in the pseudo-random sequences, and also the encryption method has a closed-loop form.

Chaos is one of the most mysterious dynamics that catches the attention of many researchers [7]. A critical question in this area is the generation of chaotic attractors. Previously, there was a hypothesis that chaotic attractors are linked to saddle points [8,9]. After that, two systems were presented to show chaotic oscillations without saddle point [10,11]. Thus, two groups of dynamics were investigated: self-excited and hidden. The basin of attraction of a self-excited attractor is around an unstable equilibrium, while in hidden attractors, there is not such an association [12]. It was a turning point in the study of chaotic flows. Then, investigations have been focused on various features of chaotic flows such as multistability and multi-scroll attractors. Dynamical properties of of a novel oscillator with extreme multistability was studied in [13]. A memristive oscillator with multiwing dynamics was discussed in [14]. In [15], an image encryption method based on a multi-scroll memristive system was designed. The analog implementation of Hindmarsh–Rose neuron model was discussed in [16]. Various dynamics of a fractional-order chaotic oscillator were investigated in [17]. The oscillator has three types of offset-boosting. The synchronization of flows is interesting. The synchronization of chaotic neural network with impulsive control was studied in [18]. Sliding mode and passivity method was used to investigate the synchronization of chaotic flows with perturbations [19].

Various tools can be used to investigate the properties of dynamical oscillators [20,21,22]. Plotting a bifurcation diagram is one of the most noticeable methods [23,24,25]. It shows the variations of the oscillator’s attractors by varying a parameter. Another tool is a Lyapunov exponent that reveals the chaotic behaviors [26]. Plotting the basin of attraction helps to investigate various oscillator dynamics by changing initial conditions [27]. The basin of attraction is often a two-dimensional plot that shows the attraction’s area of various attractors. Multistability is an interesting behavior of dynamical oscillators [28,29,30]. Multistability is a condition in which the system has two or more attractors in a constant set of parameters and just by changing initial conditions. Extreme multistability is a particular case of multistability [31,32]. It is a case with coexisting uncountable infinite attractors. Here, a novel chaotic flow is proposed. Dynamical behavior of the system reveals its noticeable behavior.

PRNG and S-box mechanisms are considered as the backbone of designing modern data encryption algorithms and draw in much attention from cryptographers and specialists [33], in which chaotic models are commonly used for generating PRNG sequences and constructing S-boxes due to their complex dynamics [34]. Using the effective properties of the new chaotic flow, a method to construct PRNGs is presented and then utilizes the generated PRNG sequence for designing secure S-boxes. Finally, a new image cryptosystem is proposed using the suggested PRNG method and the suggested S-box approach. The effectiveness of the suggested mechanisms is evaluated using several assessments, in which the outcomes show the vital characteristics of the presented mechanisms for reliable cryptographic applications.

We can recap the principal contributions of this work as given below:

• Presenting a novel oscillator with chaotic dynamics and investigating its dynamical properties;
• Constructing a novel PRNG method using the effective properties of the new chaotic flow;
• Utilizing the PRNG method for designing secure S-boxes;
• Due to the importance of data security in the present day, a new image cryptosystem is presented as a cryptographic application of the presented chaotic oscillator.

In the following, the chaotic oscillator system is proposed, and its features are investigated in Section 2. In Section 3, the suggested PRNG scheme is introduced including its performance analyses, while the suggested chaos-based S-box and its performance analyses are provided in Section 4. The image cryptosystem is proposed including its analyses in Section 5. Section 6 gives the concluding points and future works.

2. Chaotic Oscillator

A novel chaotic oscillator is designed and its equations are presented in Equation (1). It is a jerk system that shows chaotic dynamics in $a=-0.7,b=2.7,c=0.3$, and initial values $(0,1,0)$. Figure 1 gives the attractor of the oscillator. The oscillator is solved by runtime 800. Half of the signals are removed as the transient time:

$$\begin{array}{c}\dot{x}=y\\ \dot{y}=z\\ \dot{z}=ax-y-0.7z-0.9y^2-0.7z^2+0.3xy+cxz+byz\end{array}$$

(1)

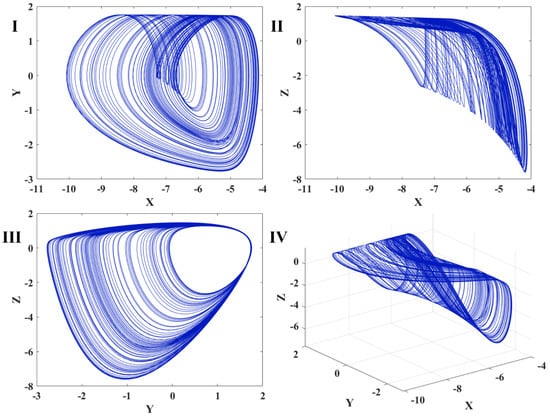
Figure 1. Chaotic behavior of the oscillator in various projections; (I) $x-y$ plane; (II) $x-z$ plane; (III) $y-z$ plane; (IV) $x-y-z$ space.

To investigate the dynamics of the oscillator, its equilibrium point is calculated as $(0,0,0)$. The characteristic equation of the oscillator at $(0,0,0)$ is $l^3+0.7l^2+l+0.7=0$. Therefore, the eigenvalues are $-0.7,\pm i$. Thus, the type of the origin cannot be revealed by the eigenvalues. Numerical examinations show that the equilibrium point is a center point. The dynamics of the oscillator around the equilibrium point are a cycle in which its amplitude changes by changing initial conditions. In this situation, which is proved by running the system for many initial conditions, the equilibrium point is called a center point. Investigation of equilibrium points and their stability is very important in the study of chaotic systems. In [35], various chaotic flows with different equilibrium points were reviewed. Chaotic flows with specific analytical solutions were discussed in [36].

Different dynamics of the oscillator can be investigated using a bifurcation diagram (BD). The BD of a continuous oscillator is schemed using a Poincare section (PS) of the attractors in each parameter by varying the bifurcation parameter gradually. Usually, the PS is selected as the peak values of the variables. Lyapunov exponent (LE) is another mechanism to investigate various dynamics of a flow. The Wolf method with runtime 20,000 is used to calculate Lyapunov exponents [37]. It is a well-known method and is very popular in the literature [38,39]. Here, the BDs of the oscillator are studied by varying three parameters, a, b and c. A period-doubling route to chaos is shown in all of the figures. The first row of Figure 2 presents a BD for changing $a\in [-0.7,-0.6]$. It presents the peaks of x. By increasing a, the oscillator’s dynamics become more orderly. Part II of Figure 2 displays the LEs of the oscillator by varying parameters a. It shows that the oscillator has chaotic dynamics in $a\in [-0.7,-0.688]$ since it has one positive LE. Then, in the interval $a\in [-0.688,-0.6]$, the largest LE is zero, which means the dynamics are limit cycles. The first row of Figure 3 presents the bifurcations by changing $b\in [2.4,2.7]$. The oscillator shows a period-doubling until it reaches the chaotic attractors. Part II of Figure 3 displays the LEs of the oscillator by varying parameters b. The results show that the oscillator has periodic dynamics in $b\in [2.4,2.653]$. In that interval, the largest LE of the oscillator is zero. Then, by increasing the parameter b, the oscillator’s dynamics become chaotic with one positive LE. Figure 4 shows the BD by varying c. The bifurcation has a wider chaotic region than bifurcation by changing a and b. Its LEs by changing c represents the chaotic regions (part II of Figure 4).

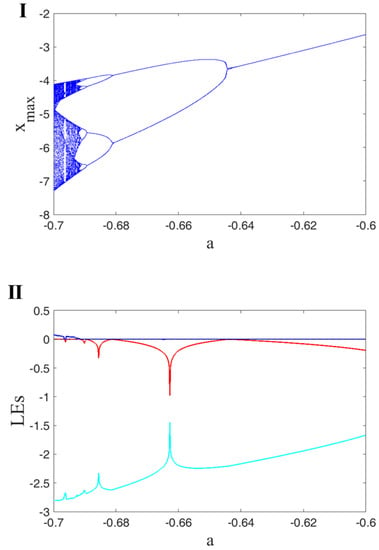
Figure 2. BD of Oscillator (1) by constant initial conditions $(0,1,0)$; (I) peaks of x by varying the parameter a; (II) three different Lyapunov exponents of the oscillator shown by different colors calculated using constant initial values $(0,1,0)$ and by changing a.

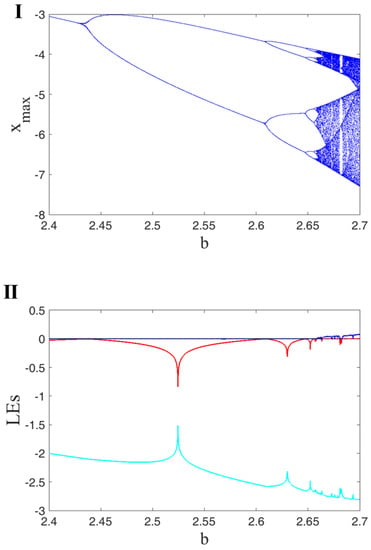
Figure 3. BD of Oscillator (1) by constant initial conditions $(0,1,0)$; (I) peaks of x by varying the parameter b; (II) three different Lyapunov exponents of the oscillator shown by different colors calculated using constant initial values $(0,1,0)$ and by changing b.

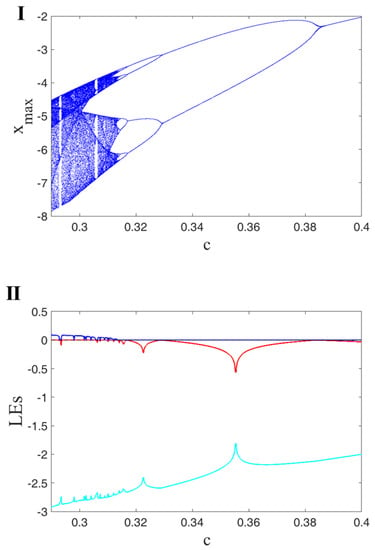
Figure 4. BD of Oscillator (1) by constant initial conditions $(0,1,0)$; (I) peaks of x by varying the parameter c; (II) three different Lyapunov exponents of the oscillator shown by different colors calculated using constant initial values $(0,1,0)$ and by changing c.

The basin of attraction of the oscillator is shown in Figure 5. The yellow region in this plot shows unbounded solutions, the cyan color is attracted to the chaotic attractors, and the red color remains around the equilibrium point. The result shows that the chaotic dynamics have a large basin of attraction entangled with center point dynamics.

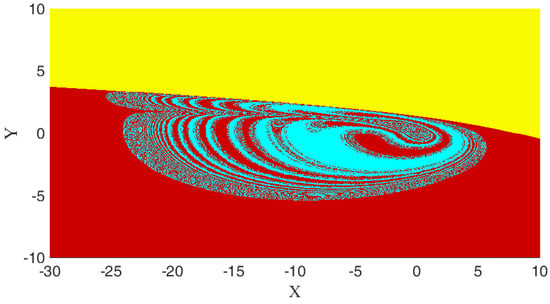
Figure 5. Basin of attraction of Oscillator (1); The yellow region in this plot shows unbounded solutions, the cyan color is attracted to the chaotic attractors, and the red color remains around the equilibrium point.

The chaotic dynamic of the oscillator shows a complex signal which can be used in encryption applications. In addition, it has a range of parameters to present chaotic dynamics, making finding the exact system hard for attackers. However, initial conditions are an essential matter if they know the exact system. In the following, the proposed oscillator is used in designing various cryptographic applications.

3. Proposed PRNG Mechanism and Its Performance

PRNG plays a vital task in designing robust cryptographic primitives [40]. It guarantees that the attackers cannot prophesy the data. In this part, the proposed PRNG mechanism and its performance analyses are presented.

3.1. PRNG Mechanism

The PRNG scheme is proposed using the presented chaotic oscillator. The itemized actions of the presented PRNG are provided in the following:

• Solve the chaotic oscillator (Equation (1)) with initial values ($x_0$,$y_0$,$z_0$) and control parameters $a=-0.7,b=2.7,c=0.3$ to obtain the signals X, Y, and Z;
• Transform signals X, Y, and Z into integer numbers in the interval $[0,255]$;

  $$\begin{array}{c}\hfill SeqX=fix(X\times {10}^{12}mod256)\hfill \\ \hfill SeqY=fix(Y\times {10}^{12}mod256)\hfill \\ \hfill SeqZ=fix(Z\times {10}^{12}mod256)\hfill \end{array}$$

  (2)

  where fix function rounds each number to the closest integer toward zero (i.e., fix(5.483) = 5) and mod function represents the modulo operation (i.e., 7.5 mod 3 = 1.5) [41].
• Obtain the PRNG sequence using SeqX, SeqY, and SeqZ as given in Equation (3).

  $$PRNG=SeqX\oplus SeqY\oplus SeqZ$$

  (3)

3.2. PRNG Performance Analyses

To guarantee the effectiveness of the presented PRNG mechanism, security analyses are carried out for the generated PRNG sequences in terms of correlation, randomness tests, histograms, key sensitivity, and entropy.

3.2.1. Correlation Performance

The correlation coefficient measures the relation between two pseudo-random sequences. The correlation coefficient of two sequences can be defined by

$$r_{xy}=\frac{{\sum }_{i=1}^M\left(x_i-\frac{1}{M}{\sum }_{i=1}^M{x}_i\right)\left(y_i-\frac{1}{M}{\sum }_{i=1}^M{y}_i\right)}{\sqrt{{\sum }_{i=1}^M{\left(x_i-\frac{1}{M}{\sum }_{i=1}^M{x}_i\right)}^2{\sum }_{i=1}^M{\left(y_i-\frac{1}{M}{\sum }_{i=1}^M{y}_i\right)}^2}}$$

(4)

where $x_i$ and $y_i$ are the ith pair of adjacent numbers, and M is the entire number of neighborhood numbers. The average outcome of correlation is 0.0001288, which refers to the absence of correlation between the two generated sequences.

3.2.2. Randomness Test

To measure the randomness of the signal, NIST SP 800-22 is employed. Its role is to highlight any non-randomness in a PRNG signal. It consists of 15 tests that are executed on different 1000 PRNG signals each of ${10}^6$ bits [42]. The outcomes are shown in Table 1, in which the successful proportion is greater than 98%. Therefore, the PRNG signal is purely random.

Table 1. NIST SP800-22 outcomes of 1000 PRNG signals each of ${10}^6$ bits.

	Test	Successful Proportion
Serial	T1	990/1000
	T2	990/1000
Cumulative sums	Forward	989/1000
	Reverse	987/1000
Approximate entropy		984/1000
Frequency		999/1000
No overlapping templates		991/1000
Runs		986/1000
Random excursions variant		986/1000
Rank		991/1000
Spectral DFT		987/1000
Linear complexity		983/1000
Overlapping templates		992/1000
Long runs of ones		986/1000
Random excursions		989/1000
Block-frequency		998/1000
Universal		996/1000

3.2.3. Key Sensitivity (KS)

The KS is a vital feature of any secure PRNG method. Any tiny modifications in the key lead to different results. To assess the KS of the PRNG, some tests are done: byte change rate and bit change rate. For two sequences with tiny modifications in the secret key, the byte change rate is 99.62745% and the bit change rate is 50.01032%, which is near the ideal bit change rate of 50%. The stated results for both byte and bit change rates proved that the PRNG mechanism is susceptible to slight modifications in the secret key.

3.2.4. Histograms

A good PRNG scheme should ensure the uniformity of histograms for distinct PRNG sequences. Figure 6 presents the histograms of four different PRNG sequences, in which the histograms are uniform.

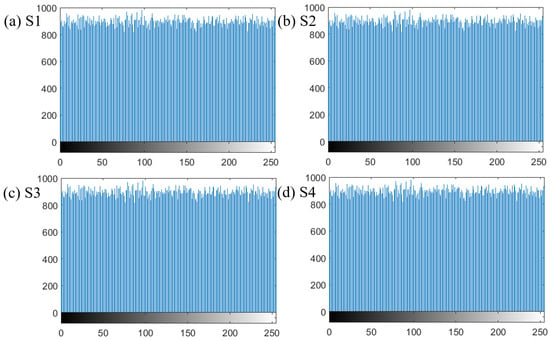
Figure 6. Histograms of four different PRNG sequences, in which the histograms are uniform. (a) Histogram of sequence S1; (b) Histogram of sequence S2; (c) Histogram of sequence S3; (d) Histogram of sequence S4.

3.2.5. Information Entropy

Information entropy is intended for computing the randomness of a specific message as Equation (5) [43]:

$$E\left(X\right)=\sum _{i=0}^{255}p\left(x_i\right){log}_2\frac{1}{p\left(x_i\right)}$$

(5)

where $p\left(x_i\right)$ signifies the probability of $x_i$. Optimal entropy value for a number with 8-bit is equal to 8. To estimate the effectiveness of the presented PRNG scheme, the information entropy test is performed on the generated PRNG sequence. The outcome value of entropy is 7.9992, which is close to 8. Therefore, the presented PRNG mechanism is reliable for various cryptographic applications.

4. Proposed S-Box Mechanism and Its Performance

S-boxes is important in designing robust cryptographic applications. Here, the S-box mechanism and its performance are provided.

4.1. S-Box Mechanism

The S-box approach is based on the presented PRNG approach. The itemized actions of the presented S-box are provided in the following steps:

• Obtain a PRNG sequence using the presented PRNG algorithm (see Section 3.1);
• Collect the first 256 dissimilar element from the PRNG sequence to construct an 8 × 8 S-box.

4.2. S-Box Performance Analyses

To guarantee the effectiveness of the presented S-box mechanism, performance analyses are carried out for the generated S-box [44,45]. The primary states and control parameters that are used to create an $8\times 8$ S-box (An $n\times n$ S-box has an $2^n$ different elements) are given as $x_0$ = −0.2851, $y_0$ = 0.7692, $z_0$ = 0.6170, a = −0.7, b = 2.7, and c = 0.3. The created S-box is provided in Table 2, while Table 3 presented a comparison of the performance for the proposed S-box besides relevant S-boxes as reported in [33,44,46,47] in terms of nonlinearity, strict avalanche criterion (SAC), bit independence (BIC), linear approximation probability (LP), and differential probability (DP), in which the stated S-box approach has good SAC, BIC, and nonlinearity properties.

Table 2. An $8\times 8$ S-box created via the proposed approach.

0	161	115	34	104	200	203	173	37	24	255	239	240	190	93	76
198	251	12	57	236	223	188	72	83	127	179	237	67	158	20	94
88	126	183	222	212	150	228	73	133	230	55	226	157	1	97	101
210	61	43	136	4	233	172	221	28	129	232	125	8	42	224	81
69	247	178	128	141	22	23	15	253	189	252	99	121	254	50	3
49	64	116	31	13	147	6	238	25	92	220	216	163	243	192	46
119	175	201	79	174	153	194	82	148	80	191	102	35	149	250	62
89	11	197	44	74	219	18	185	248	84	205	135	123	77	90	96
143	112	56	152	117	70	211	10	39	29	2	184	144	160	146	100
109	131	33	171	168	91	105	27	139	202	169	59	78	208	53	177
40	156	30	52	155	124	214	38	103	196	229	215	217	66	138	113
164	180	86	9	5	145	65	19	54	199	132	98	95	225	21	118
63	58	207	41	218	162	195	75	134	181	165	204	85	71	187	176
206	87	245	137	166	16	36	130	227	108	51	111	182	170	151	106
32	107	45	209	122	234	14	114	241	110	231	17	68	249	246	26
242	193	244	60	48	142	47	235	7	159	186	120	154	213	140	167

Table 3. Comparison of the performance for the S-box besides relevant S-boxes.

S-box Approach	Nonlinearity	BIC-NL	SAC	BIC-SAC	LP	DP
Proposed	106.5	103.1	0.5000	0.5058	0.1250	0.0391
[44]	106.00	104.2	0.4993	0.5030	0.1250	0.0391
[46]	102.00	102.9	0.5178	0.4999	0.1250	0.0313
[33]	106.00	103.9	0.4958	0.5023	0.1250	0.0313
[47]	105.25	103.8	0.4956	0.4996	0.1562	0.0391

5. Proposed Image Encryption Algorithm and Its Performance

Data security is important due to the rapid growth of internet technologies. Digital images are usually utilized for representing information [48,49]. Digital images can be protected via image encryption algorithms. Image encryption aims to convert the image from an intelligible style into an unintelligible pattern. Chaotic models are usually utilized for designing reliable image cryptosystems [50,51]. Using the effective properties of the chaotic flow, an image cryptosystem is presented. Therefore, this part is devoted to the proposed image cryptosystem and its performance analyses.

5.1. Encryption Algorithm

The proposed image cryptosystem is based on the PRNG algorithm and the suggested S-box approach. At first, the plain image is substituted using the generated PRNG sequence, then some information about the substituted image is acquired, and this information is utilized to update the initial conditions of the chaotic oscillator. Using the updated initial conditions, solve the chaotic oscillator system to generate three sequences, and utilize the first and the third sequences to construct a permutation box for shuffling the rows of the substituted image and utilize the second and the third sequences to construct a permutation box for shuffling the columns of the substituted image. Finally, construct an S-box for substituting the permutated image to generate the cipher image. The procedure of the proposed image encryption algorithm is outlined in Figure 7 and its details in Algorithm 1.

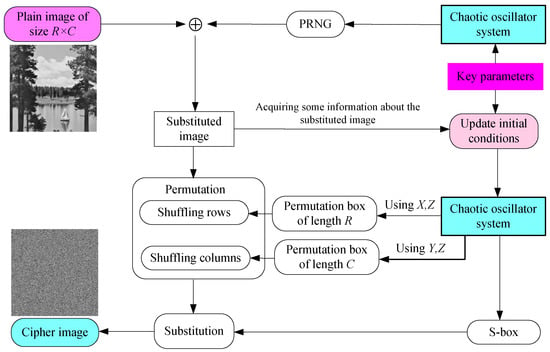
Figure 7. Outline of the image encryption algorithm for the proposed cryptosystem.

5.2. Decryption Algorithm

The decryption algorithm of the proposed cryptosystem is the inverse of the encryption algorithm. Prior to the encryption process, the key parameters utilized in the encryption process are shared between the sender and the receiver via a closed environment or by utilizing one of the appropriate asymmetric cryptography algorithms for distributing keys (i.e., 5 RSA, ECC). After the encryption process, the value of $\beta$ is shared between the sender and the receiver by utilizing one of the asymmetric cryptography algorithms, to perform the decryption algorithm on the receiver’s device. The procedure of the proposed decryption algorithm is outlined in Figure 8 and its details in Algorithm 2.

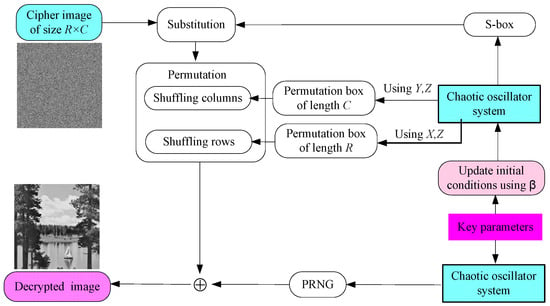
Figure 8. Outline of the decryption algorithm for the proposed cryptosystem.

5.3. Image Cryptosystem Performance Analyses

To guarantee the effectiveness of the presented image cryptosystem, performance analyses are carried out on a PC with Intel ${core}^{TM}$ 2 Duo of CPU 3.00 GHz, 4.00 GB of RAM, and preinstalled with MATLAB 2016b. The dataset of used images consists of four standard grayscale images with dimension 512 × 512 and labeled as Lake, WalkBridge, Mandrill, and JetPlane (see Figure 9). The primary key parameters are given as $x_0$ = −0.2851, $y_0$ = 0.7692, $z_0$ = 0.6170, a = −0.7, b = 2.7, and c = 0.3.

Algorithm 1: Image encryption algorithm

Algorithm 2: Image decryption algorithm

Figure 9. Experimental dataset of images, in which the top two rows represent the plain version of images and the bottom two rows indicate the cipher version of images.

The efficiency of any image encryption algorithm relies on two factors; the first one is based on encryption time, while the second factor is based on the ability to resistant manifold attacks: such as brute force, statistical cryptanalysis, differential cryptanalysis, etc. These factors are discussed in the following subsections to illustrate the efficiency of the presented image encryption algorithm.

5.3.1. Encryption Time

Encryption time is the time elapsed to encrypt one image. Table 4 provides the encryption speed in Mbits/second, in which the presented cryptosystem has good encryption time besides other related algorithms.

Table 4. Comparison of encryption speed (in Mbits/second) for the proposed cryptosystem with other corresponding methods, as stated in [52,53,54].

Cryptosystem	Encrypted MBits Per Second
Proposed	2.1744
[52]	0.5418
[53]	1.3027
[54]	2.1612

5.3.2. Correlation Performance

Each pixel value in a plain image is extremely correlated with its adjacent pixels and its correlation coefficients are close to 1 in all directions, while correlation coefficients for cipher images are very close to 0. For calculating the correlation coefficients for plain and their cipher images, we randomly picked 10,000 neighboring pixels in each direction. Table 5 stated the correlation coefficients for the plain images and their analogous cipher versions, in which the correlation coefficients of cipher images are very close to 0. In addition, the correlation distribution for the plain and cipher Lake image are plotted in Figure 10. From the declared outcomes, we can deduce that the proposed cryptosystem withstands correlation analysis.

Table 5. Correlation coefficients for the plain images and their analogous cipher versions, in which the correlation coefficients of cipher images are very close to 0.

Image	Direction
	Horizontal	Vertical	Diagonal
Lake	0.9773	0.9778	0.9638
WalkBridge	0.9396	0.9412	0.9062
Mandrill	0.9045	0.9324	0.8598
JetPlane	0.9704	0.9734	0.9501
Cipher Lake	0.0006	−0.0003	0.0009
Cipher WalkBridge	−0.0006	0.0003	0.0005
Cipher Mandrill	0.0001	−0.0003	−0.0004
Cipher JetPlane	−0.0007	0.0006	−0.0004

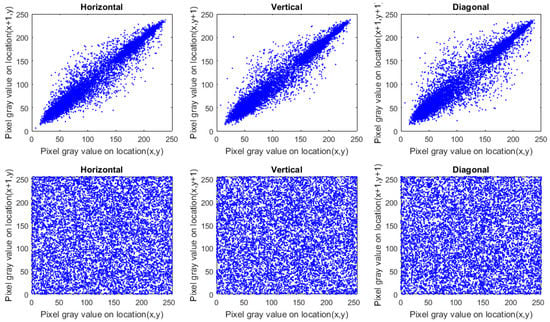
Figure 10. Correlation distribution for plain and cipher Lake image, in which the top row refers to the correlation distribution of the plain image, while the bottom row refers to the correlation distribution of the ciphered image.

5.3.3. Differential Analyses

Plain image sensitivity is a vital feature of any secure image cryptosystem, in which any tiny modifications in the plain image lead to significant different in the cipher image. To assess the plain image sensitivity of the proposed cryptosystem, some tests are done: NPCR (Number of Pixels Change Rate) and UACI (Unified Average Changing Intensity). They can be defined as follows [49]:

$$\begin{array}{c}\hfill NPCR=\frac{{\sum }_{i=1}^{N}Diff\left(i\right)}{N}\times 100\%,\hfill \\ \hfill Diff\left(i\right)=\left\{\begin{array}{c}0whenS1\left(i\right)=S2\left(i\right)\\ 1whenS1\left(i\right)\ne S2\left(i\right)\end{array}\right.\hfill \end{array}$$

(6)

$$UACI=\frac{1}{N}\left(\sum _{i=1}^N\frac{\left|S1\left(i\right)-S2\left(i\right)\right|}{255}\right)\times 100\%$$

(7)

where $S1$, $S2$ are two generated cipher images for one plain image with tiny modifications in one of its bits; N denotes the entire pixels for the image. The results are stated in Table 6, in which the stated data proved that the proposed cryptosystem is sensitive to slight modifications in the plain image.

Table 6. NPCR and UACI values for investigated images when changing one bit in one pixel in the image.

Image	UACI	NPCR
Lake	33.42641%	99.62311%
WalkBridge	33.49124%	99.62196%
Mandrill	33.48107%	99.61967%
JetPlane	33.41351%	99.62768%

5.3.4. Histogram Test

A good image cryptosystem scheme should ensure the uniformity of histograms for distinct cipher images. Figure 11 presents the histograms of the plain images and their analogous cipher versions, in which the histograms of plain images are distinct from each other’s while the histograms of their analogous cipher images are uniform with each other. To ensure the similarity of histograms for the ciphered images, we used a quantity test like variance (Var) [4], which can be defined as provided in Equation (8):

$$Var\left(T\right)=\frac{1}{{255}^2}\sum _{p=0}^{255}\sum _{q=0}^{255}\frac{{\left(t_p-t_q\right)}^2}{2}$$

(8)

where $T=\left\{t_0,t_1,\dots ,t_{255}\right\}$ is the sequence of the histogram values, and $t_p$ and $t_q$ are the pixel numbers whose grey values are equal to p and q, respectively. Table 7 provides the outcomes of histogram variance for the tested images previous and after the encryption process, in which the low values denote the high uniformity of histograms.

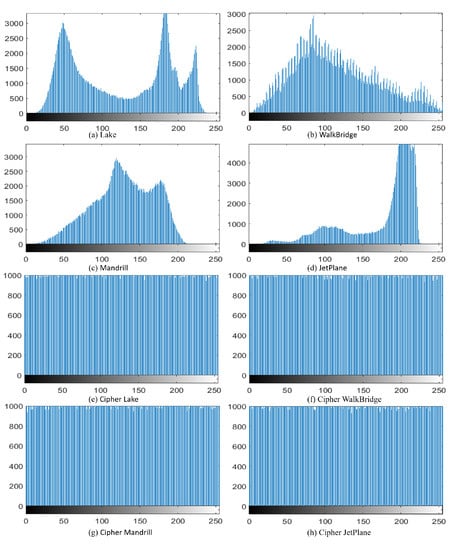
Figure 11. Histograms of images, in which the top two rows represent the histograms of plain images and the bottom two rows indicate the histograms of cipher images.

Table 7. Outcomes of histogram variance, in which low values of histogram variance denote the high uniformity of histograms.

Image	Variance Value
	Plain	Cipher
Lake	727,739.4117	966.8784
WalkBridge	428,846.3451	1020.4078
Mandrill	848,778.8784	920.8314
JetPlane	2,843,823.0823	1099.6313

5.3.5. Information Entropy

Information entropy is intended to compute the randomness of a specific message [55]. The optimal entropy value for a grayscale image is equal to 8. To estimate the effectiveness of the presented image cryptosystem, the information entropy test is performed on the plain and its analog cipher images. The outcomes of entropy are provided in Table 8, in which the entropy values for cipher images are near 8. From the stated data, we can deduce that the proposed cryptosystem withstands entropy analysis.

Table 8. Outcomes of entropy, in which the entropy values for cipher images are very close to 8.

Image	Information Entropy
	Plain	Cipher
Lake	7.48264	7.99933
WalkBridge	7.68301	7.99930
Mandrill	7.29254	7.99936
JetPlane	6.71351	7.99924

5.3.6. Key Space and Key Sensitivity

The key space refers to the diverse keys that can be used in brute force attacks which should be extensive sufficiently to resist those attacks. In the presented encryption algorithm, we utilize the primary key parameters ($x_0$, $y_0$, $z_0$, a, and b) to solve the chaotic oscillator (Equation (1)) in the encryption and decryption procedures. By assuming that the precision computation of digital devices is ${10}^{-16}$, the key space for the presented cryptosystem is ${10}^{80}$, which is enough for any cryptographic method.

Key sensitivity is a vital feature of any secure cryptosystem. Any tiny modifications in the key lead to different results. To assess the key sensitivity of the proposed image cryptosystem, we attempt to decrypt the cipher image of Lake several times utilizing tiny modifications in key parameters. The decryption effects are provided in Figure 12, in which the original image is not retrieved when making tiny changes in the key parameters. Furthermore, to test the key sensitivity in quantity terms, we execute an NPCR test on the decrypted Lake image with the actual key and other decrypted images with slight changes in the initial keys as stated in Figure 12, the outcomes are displayed in Table 9. From the outcomes given in Figure 12 and Table 9, the presented image encryption algorithm has high key sensitivity, in which any slight modifications in initial keys lead to significant modifications in the results.

Figure 12. Decryption effects of cipher Lake image when making tiny changes in the key parameters.

Table 9. NPCR values for the decrypted Lake image with the actual key and other decrypted images with slight changes in the initial keys as stated in Figure 12.

Image	NPCR
Figure 12a & Figure 12b	99.62348%
Figure 12a & Figure 12c	99.60479%
Figure 12a & Figure 12d	99.60594%
Figure 12a & Figure 12e	99.61204%
Figure 12a & Figure 12f	99.60975%

5.3.7. Data Loss Attack

During data transmission across a communication channel, the cipher data may have vulnerability to data loss attacks. Therefore, any image cryptosystem must be invincible against data loss attacks. To value the proposed image cryptosystem for withstanding data loss attacks, we cut out some blocks of the cipher image and then attempt to retrieve the secret data from the defective cipher image through the decryption algorithm. Figure 13 presents the outcomes of data loss attacks, in which the plain image is retrieved effectively from the defective cipher image.

Figure 13. Results of data loss attacks, in which the Lake image is retrieved effectively from the defective cipher image.

To assess in quantity terms the visual quality of the retrieved images from defected cipher images, we utilized peak signal-to-noise ratio (PSNR) which can be formulated mathematically as stated in Equation (9) [49]:

$$PSNR\left(P,D\right)=20{log}_{10}\left(\frac{255}{\sqrt{MSE\left(P,D\right)}}\right)$$

(9)

$$MSE\left(P,D\right)=\frac{1}{x\times y}\sum _{i=1}^x\sum _{j=1}^y{[P(i,j)-D(i,j)]}^2$$

(10)

where $x\times y$ is dimensional of the plain image P, and D indicates the retrieved image from the defective image. The outcomes of PSNR test for the plain Lake image (Figure 9a) and the retrieved images (the second row of Figure 13) are displayed in Table 10. From the outcomes given in Figure 13 and Table 10, it is seen that, when the defective image losses more data, the retrieved image has lost more of its visual quality.

Table 10. PSNR values for the plain Lake image (Figure 9a) and the retrieved images (the second row of Figure 13).

Image	PSNR
Losing data by 10%	17.6429
Losing data by 15%	15.8784
Losing data by 20%	14.6695

5.3.8. Comparative Analysis

To prove the effectiveness of the presented image cryptosystem alongside other similar image cryptosystems, Table 11 presents a comparison of the average values of information entropy, NPCR, UACI, and correlation coefficients of our encryption system with their average values reported in [54,56,57,58,59]. From the stated data, we can deduce the efficiency of the proposed image cryptosystem compared to other related approaches.

Table 11. Comparison of the average values of information entropy, NPCR, UACI, and correlation coefficients of our encryption system with their average values reported in [54,56,57,58,59].

Image Cryptosystem	Information Entropy	UACI	NPCR	Correlation Coefficient
				Horizontal	Vertical	Diagonal
Proposed	7.99931	33.453%	99.623%	−0.00015	0.00007	0.00015
[56]	7.99929	33.476%	99.611%	0.00219	0.00169	0.00186
[57]	7.99700	33.440%	99.600%	−0.00970	−0.00870	0.00650
[54]	7.99941	33.463%	99.609%	0.00265	−0.00105	0.00013
[58]	7.99923	32.620%	99.210%	0.00180	0.00053	0.00113
[59]	7.99658	33.360%	99.610%	0.01554	-	-

We can recap the principal advantages of the proposed encryption algorithm as given below:

• According to the data stated in Table 4, the presented cryptosystem has good encryption time besides other related algorithms.
• According to the data stated in Table 5, the correlation coefficients of cipher images are very close to 0, and the proposed cryptosystem has the ability to withstand correlation analysis.
• According to the data stated in Table 6, the proposed cryptosystem is sensitive to slight modifications in the plain image.
• According to the plots stated in Figure 11, the histograms of cipher images are uniform with each other.
• According to the data stated in Table 7, the cipher images have high uniformity of histograms.
• According to the data stated in Table 8, the entropy values for cipher images are near 8, and the proposed cryptosystem has the ability to withstand entropy analysis.
• According to the outcomes given in Figure 12 and Table 9, the presented image encryption algorithm has high key sensitivity, in which any slight modifications in initial keys lead to significant modifications in the results.
• From the outcomes given in Figure 13 and Table 10, it is seen that, when the defective image losses more data, the retrieved image has lost more of its visual quality.

6. Conclusions

Here, a novel chaotic oscillator was proposed, and its dynamical properties were investigated.The chaotic attractor of the system was shown. The oscillator was discussed using bifurcation diagram and Lyapunov exponents. The oscillator has fascinating bifurcations by changing three parameters, a, b and c. Lyapunov exponents of the oscillator were wholly matched with the bifurcation diagrams and present their types of dynamics. In addition, this study introduced various cryptographic applications using the effectiveness of the chaotic flow. A method is presented to construct PRNGs, and the generated PRNG algorithm is utilized for constructing secure S-boxes. Finally, a new image cryptosystem is presented using the proposed PRNG method and the suggested S-box approach. The effectiveness of the suggested mechanisms was evaluated using several assessments, in which the outcomes showed the vital characteristics of the presented mechanisms that are valuable for reliable security purposes. In the future, we aim to study applying the generated sequences from the proposed PRNG algorithm to the auxiliary classifier generative adversarial nets [60].