Almost Anti-Periodic Oscillation Excited by External Inputs and Synchronization of Clifford-Valued Recurrent Neural Networks
Abstract
:1. Introduction
2. Preliminaries
- Let , then one can easily show that f is not periodic or anti-periodic but almost anti-periodic.
- Let , then one can easily show that is almost periodic, not almost anti-periodic.
- For , , and are continuous and integrable such that .
- For , there exist positive constants , and such that for all ,
- and .
3. Almost Anti-Periodic Solutions
4. Synchronization
- For , .
- For , there exist positive constants such that for all ,
- For , denote , then
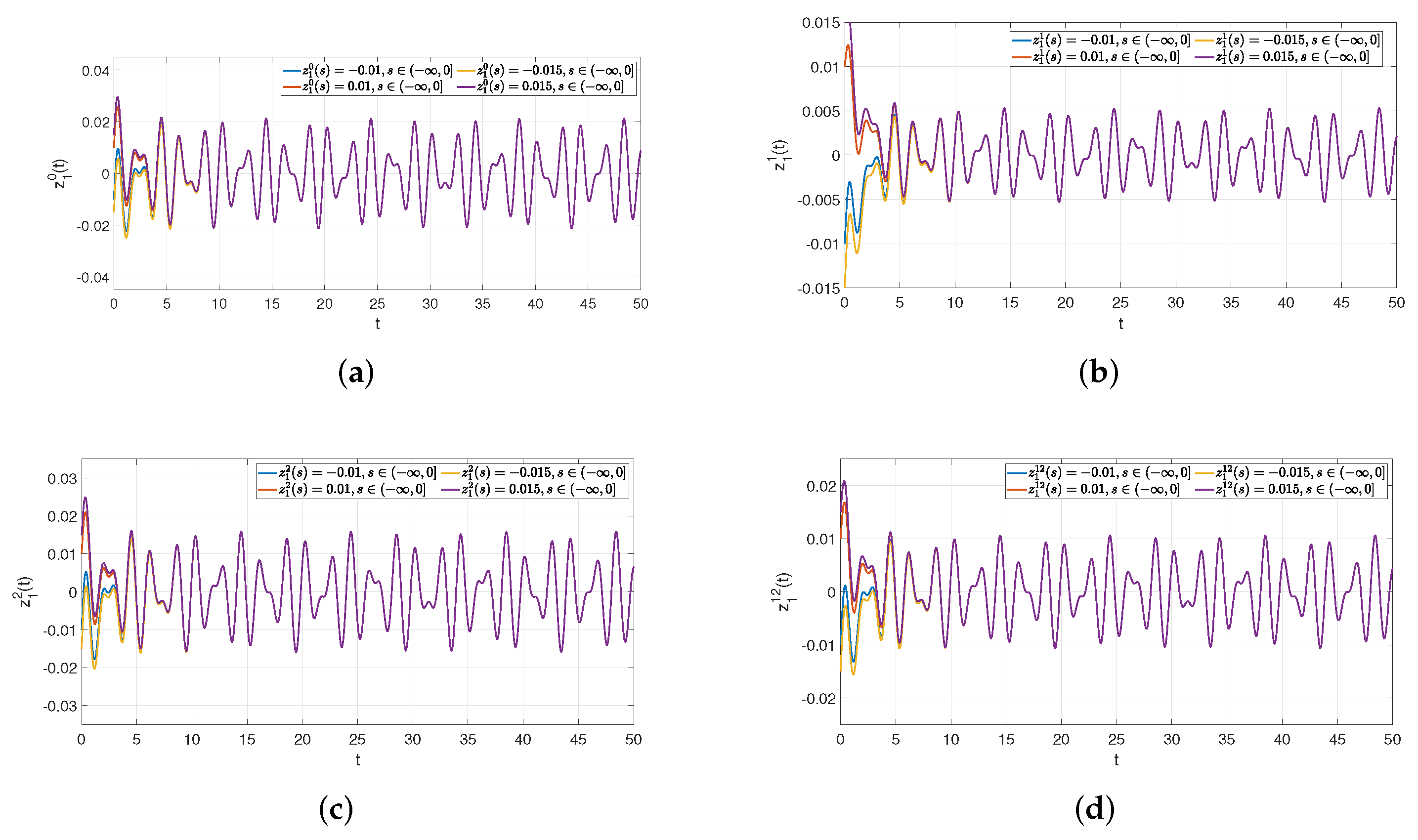
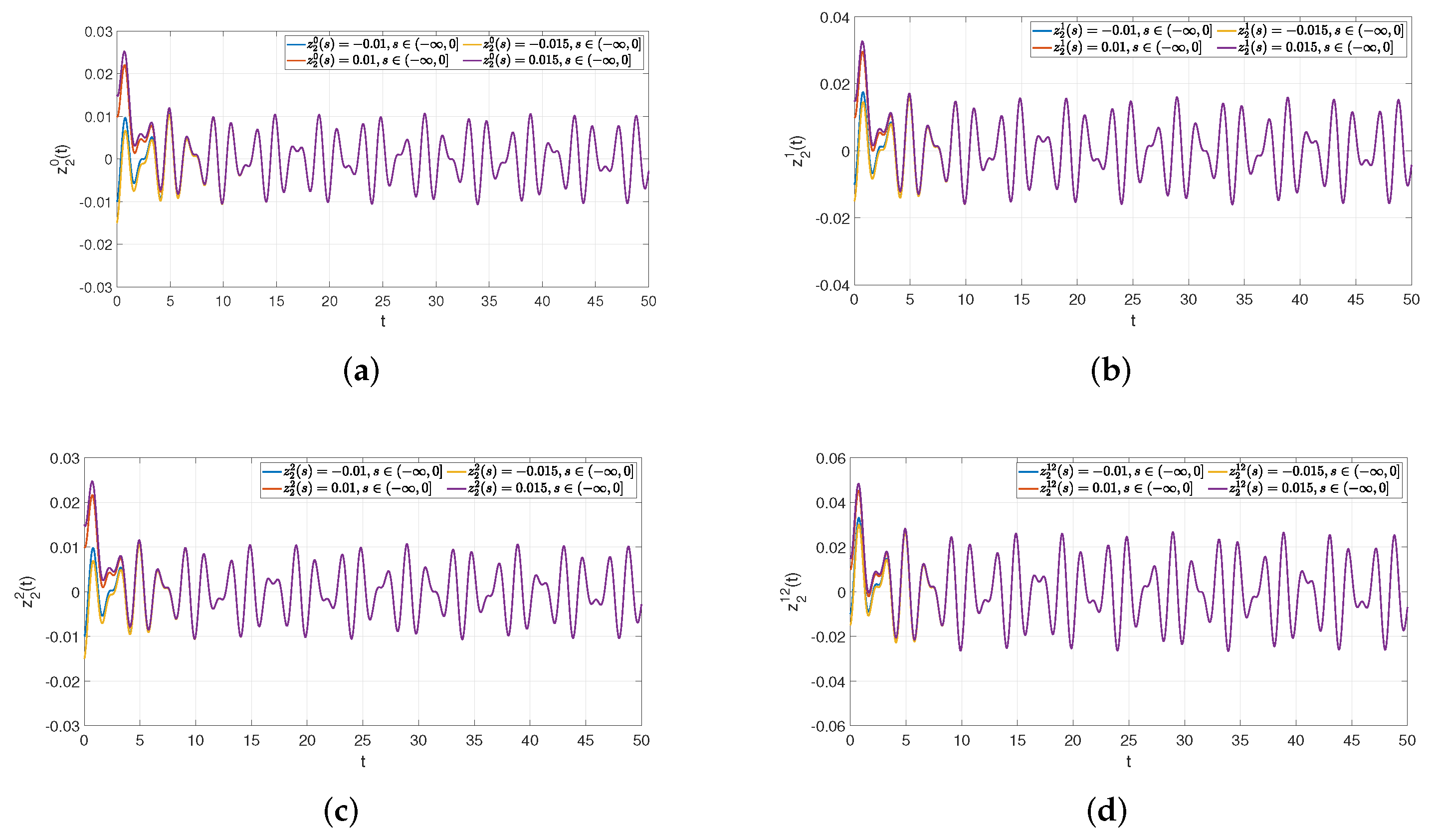
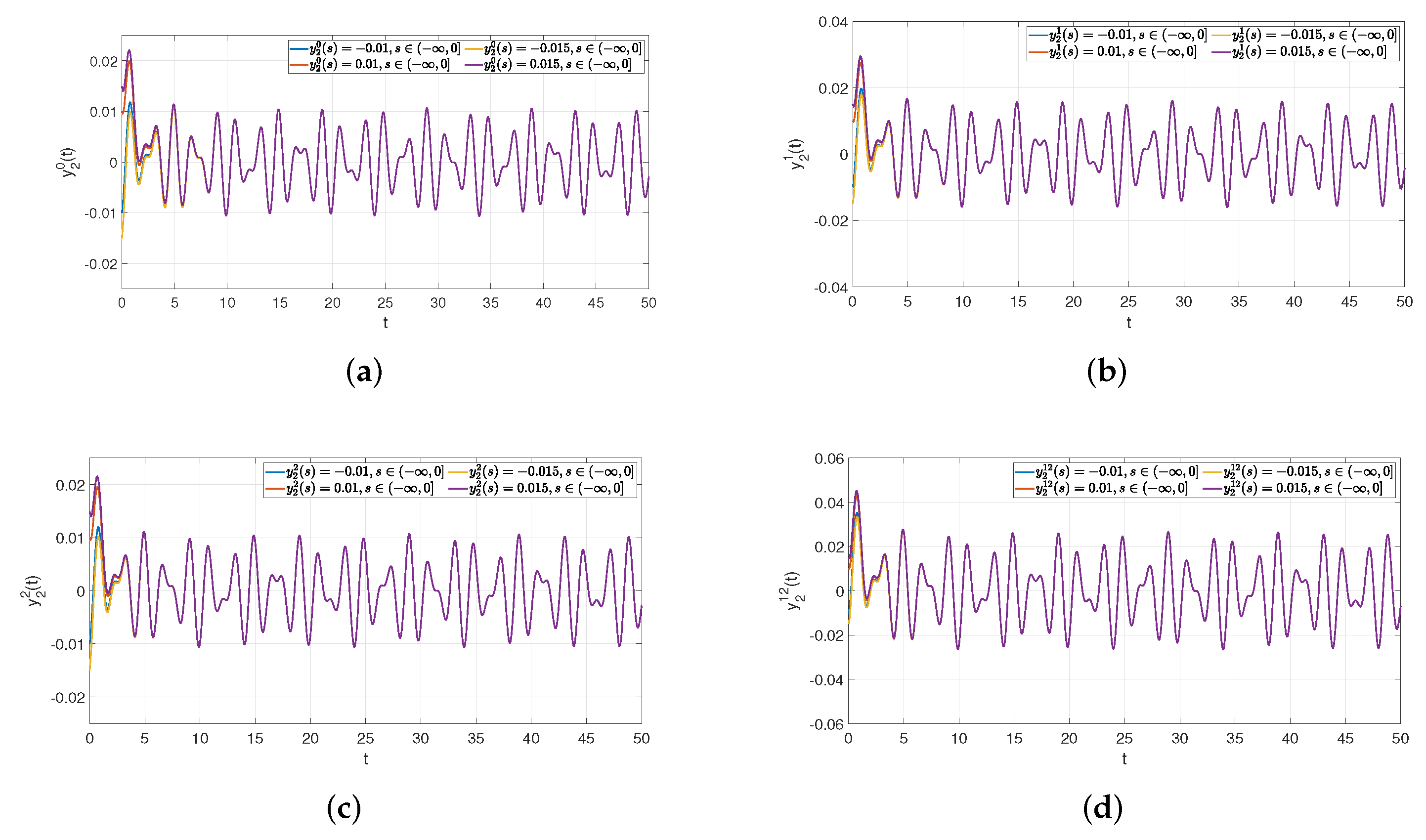
5. Illustrative Example
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [Green Version]
- Rajchakit, G.; Sriraman, R.; Vignesh, P.; Lim, C.P. Impulsive effects on Clifford-valued neural networks with time-varying delays: An asymptotic stability analysis. Appl. Math. Comput. 2021, 407, 126309. [Google Scholar] [CrossRef]
- Li, Y.; Li, B. Pseudo compact almost automorphy of neutral type Clifford-valued neural networks with mixed delays. Discrete Contin. Dyn. Syst.-B 2022, 27, 4703–4724. [Google Scholar] [CrossRef]
- Rajchakit, G.; Sriraman, R.; Lim, C.P.; Sam-ang, P.; Hammachukiattikul, P. Synchronization in finite-time analysis of Clifford-valued neural networks with finite-time distributed delays. Mathematics 2021, 9, 1163. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, P.; Lu, J.; Liang, J. Global stability of Clifford-valued recurrent neural networks with time delays. Nonlinear Dyn. 2016, 84, 767–777. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X. Almost periodic solutions in distribution of Clifford-valued stochastic recurrent neural networks with time-varying delays. Chaos Solitons Fractals 2021, 153, 111536. [Google Scholar] [CrossRef]
- Xia, Z.; Liu, Y.; Kou, K.I.; Wang, J. Clifford-valued distributed optimization based on recurrent neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Huo, N. Besicovitch almost automorphic stochastic processes in distribution and an application to Clifford-valued stochastic neural networks. Commun. Nonlinear Sci. Numer. Simul. 2022, 111, 106488. [Google Scholar] [CrossRef]
- Cao, Y.; Li, B. Existence and global exponential stability of compact almost automorphic solutions for Clifford-valued high-order Hopfield neutral neural networks with D operator. AIMS Math. 2022, 7, 6182–6203. [Google Scholar] [CrossRef]
- Rajchakit, G.; Sriraman, R.; Lim, C.P.; Unyong, B. Existence, uniqueness and global stability of Clifford-valued neutral-type neural networks with time delays. Math. Comput. Simul. 2022, 201, 508–527. [Google Scholar] [CrossRef]
- Rajchakit, G.; Sriraman, R.; Boonsatit, N.; Hammachukiattikul, P.; Lim, C.P.; Agarwal, P. Exponential stability in the Lagrange sense for Clifford-valued recurrent neural networks with time delays. Adv. Differ. Equ. 2021, 2021, 256. [Google Scholar] [CrossRef]
- Diagana, T. Almost Automorphic Type and Almost Periodic Type Functions in Abstract Spaces; Springer: New York, NY, USA, 2013. [Google Scholar]
- Kostić, M. Almost Periodic and Almost Automorphic Type Solutions to Integro-Differential Equations; W. de Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Levitan, M. Almost Periodic Functions; G.I.T.T.L.: Moscow, Russia, 1959. (In Russian) [Google Scholar]
- Aftabizadeh, A.R.; Aizicovici, S.; Pavel, N.H. On a class of second-order anti-periodic boundary value problems. J. Math. Anal. Appl. 1992, 171, 301–320. [Google Scholar] [CrossRef] [Green Version]
- Du, J.Y.; Han, H.L.; Jin, G.X. On trigonometric and paratrigonometric Hermite interpolation. J. Approx. Theory 2004, 131, 74–99. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.L. Antiperiodic wavelets. J. Comput. Math. 1996, 14, 32–39. [Google Scholar]
- Li, Y.; Qin, J.; Li, B. Existence and global exponential stability of anti-periodic solutions for delayed quaternion-valued cellular neural networks with impulsive effects. Math. Meth. Appl. Sci. 2019, 42, 5–23. [Google Scholar] [CrossRef] [Green Version]
- Shao, J. Anti-periodic solutions for shunting inhibitory cellular neural networks with time-varying delays. Phys. Lett. A 2008, 372, 5011–5016. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, Q. Existence and global exponential stability of anti-periodic solutions for BAM neural networks with inertial term and delay. Neurocomputing 2015, 153, 108–116. [Google Scholar] [CrossRef]
- Xu, C.; Li, P. On anti-periodic solutions for neutral shunting inhibitory cellular neural networks with time-varying delays and D operator. Neurocomputing 2018, 275, 377–382. [Google Scholar] [CrossRef]
- Peng, G.; Huang, L. Anti-periodic solutions for shunting inhibitory cellular neural networks with continuously distributed delays. Nonlinear Anal. Real World Appl. 2009, 10, 2434–2440. [Google Scholar] [CrossRef]
- Huang, C.; Long, X.; Cao, J. Stability of antiperiodic recurrent neural networks with multiproportional delays. Math. Meth. Appl. Sci. 2020, 43, 6093–6102. [Google Scholar] [CrossRef]
- Luo, D.; Jiang, Q.; Wang, Q. Anti-periodic solutions on Clifford-valued high-order Hopfield neural networks with multi-proportional delays. Neurocomputing 2022, 472, 1–11. [Google Scholar] [CrossRef]
- Arbi, A.; Tahri, N.; Jammazi, C.; Huang, C.; Cao, J. Almost anti-periodic solution of inertial neural networks with leakage and time-varying delays on timescales. Circuits Syst. Signal Process. 2022, 41, 1940–1956. [Google Scholar] [CrossRef]
- Arbi, A.; Tahri, N. Stability analysis of inertial neural networks: A case of almost anti-periodic environment. Math. Meth. Appl. Sci. 2022; in press. [Google Scholar] [CrossRef]
- Gao, J.; Dai, L. Anti-periodic synchronization of quaternion-valued high-order Hopfield neural networks with delays. AIMS Math. 2022, 7, 14051–14075. [Google Scholar] [CrossRef]
- Kostić, M.; Velinov, D.A. Note on almost anti-periodic functions in Banach spaces. Kragujev. J. Math. 2020, 44, 287–297. [Google Scholar] [CrossRef]
- He, W.; Luo, T.; Tang, Y.; Du, W.; Tian, Y.C.; Qian, F. Secure communication based on quantized synchronization of chaotic neural networks under an event-triggered strategy. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 3334–3345. [Google Scholar] [CrossRef]
- Wen, S.; Zeng, Z.; Huang, T.; Meng, Q.; Yao, W. Lag synchronization of switched neural networks via neural activation function and applications in image encryption. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1493–1502. [Google Scholar] [CrossRef] [Green Version]
- Wan, X.; Yang, X.; Tang, R.; Cheng, Z.; Fardoun, H.M.; Alsaadi, F.E. Exponential synchronization of semi-Markovian coupled neural networks with mixed delays via tracker information and quantized output controller. Neural Netw. 2019, 118, 321–331. [Google Scholar] [CrossRef]
- Arbi, A. Novel traveling waves solutions for nonlinear delayed dynamical neural networks with leakage term. Chaos Solitons Fractals 2021, 152, 111436. [Google Scholar] [CrossRef]
- Guo, Y.; Ge, S.S.; Arbi, A. Stability of traveling waves solutions for nonlinear cellular neural networks with distributed delays. J. Syst. Sci. Complex. 2022, 35, 18–31. [Google Scholar] [CrossRef]
- Corduneanu, C. Almost Periodic Oscillations and Waves; Springer: New York, NY, USA, 2009. [Google Scholar]

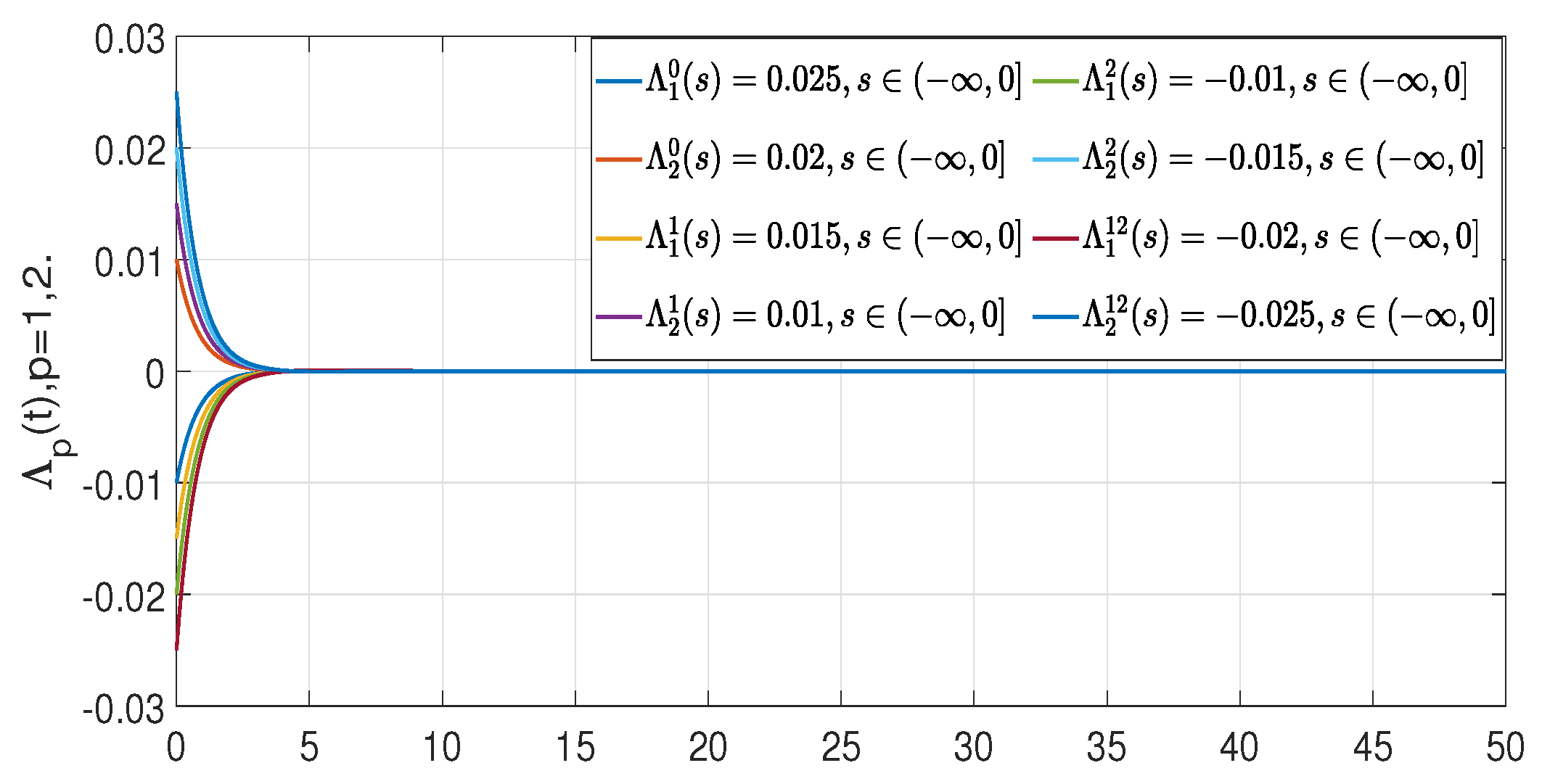
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, W.; Li, Y. Almost Anti-Periodic Oscillation Excited by External Inputs and Synchronization of Clifford-Valued Recurrent Neural Networks. Mathematics 2022, 10, 2764. https://doi.org/10.3390/math10152764
Qi W, Li Y. Almost Anti-Periodic Oscillation Excited by External Inputs and Synchronization of Clifford-Valued Recurrent Neural Networks. Mathematics. 2022; 10(15):2764. https://doi.org/10.3390/math10152764
Chicago/Turabian StyleQi, Weiwei, and Yongkun Li. 2022. "Almost Anti-Periodic Oscillation Excited by External Inputs and Synchronization of Clifford-Valued Recurrent Neural Networks" Mathematics 10, no. 15: 2764. https://doi.org/10.3390/math10152764
APA StyleQi, W., & Li, Y. (2022). Almost Anti-Periodic Oscillation Excited by External Inputs and Synchronization of Clifford-Valued Recurrent Neural Networks. Mathematics, 10(15), 2764. https://doi.org/10.3390/math10152764






