Hygrothermal Buckling of Smart Graphene/Piezoelectric Nanocomposite Circular Plates on an Elastic Substrate via DQM
Abstract
:1. Introduction
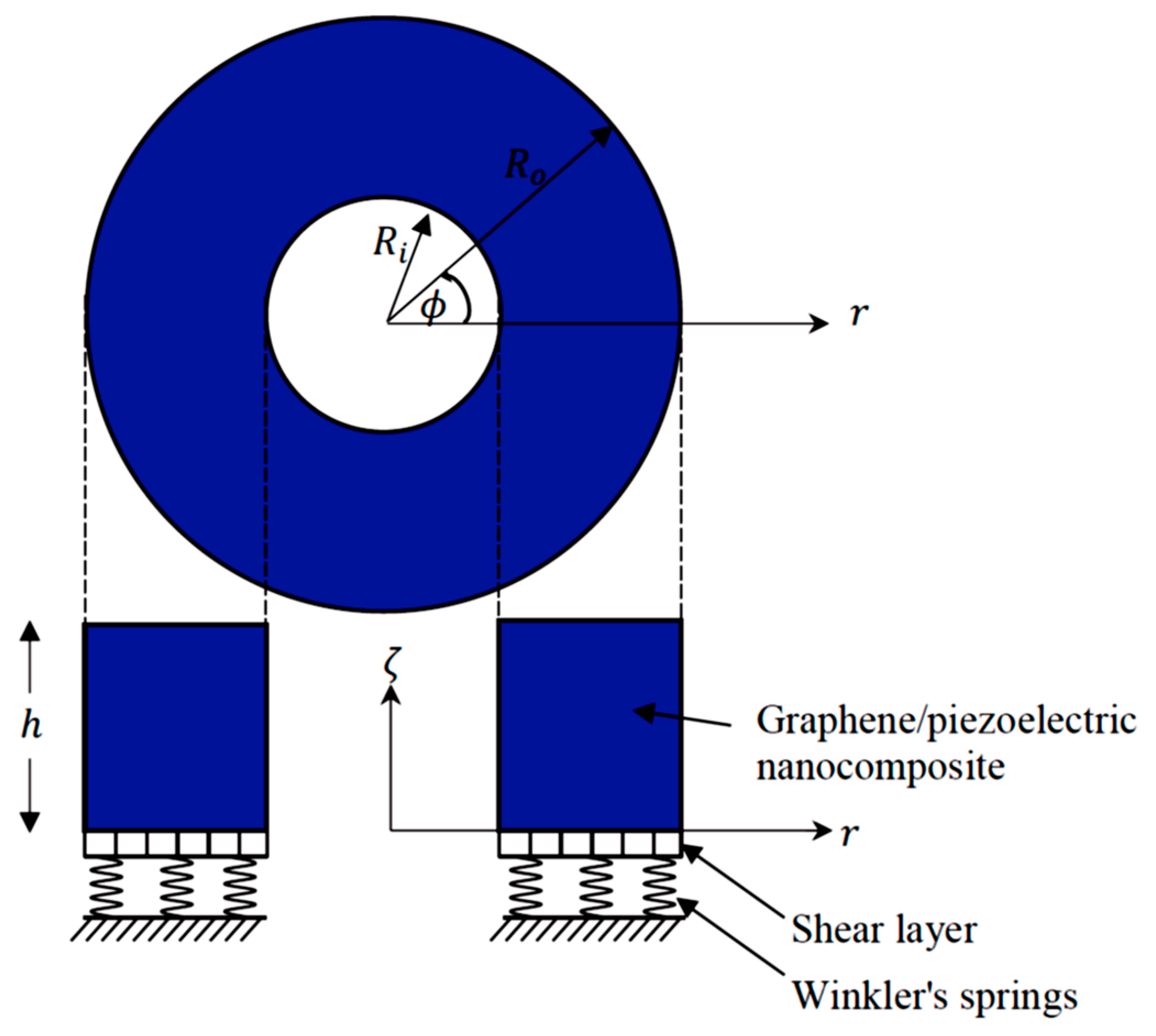
2. Nanoplate Configuration
3. Constitutive Equations
4. Stability Equations
- Differentiate Equation (30) with respect to ;
- Multiply Equation (30) by ;
- Differentiate Equation (31) with respect to and then multiply by ;
- Add the obtained equations in the three above steps;
- Multiply the obtained equation in step (4) by and then add to Equation (32).
5. Solution Procedure
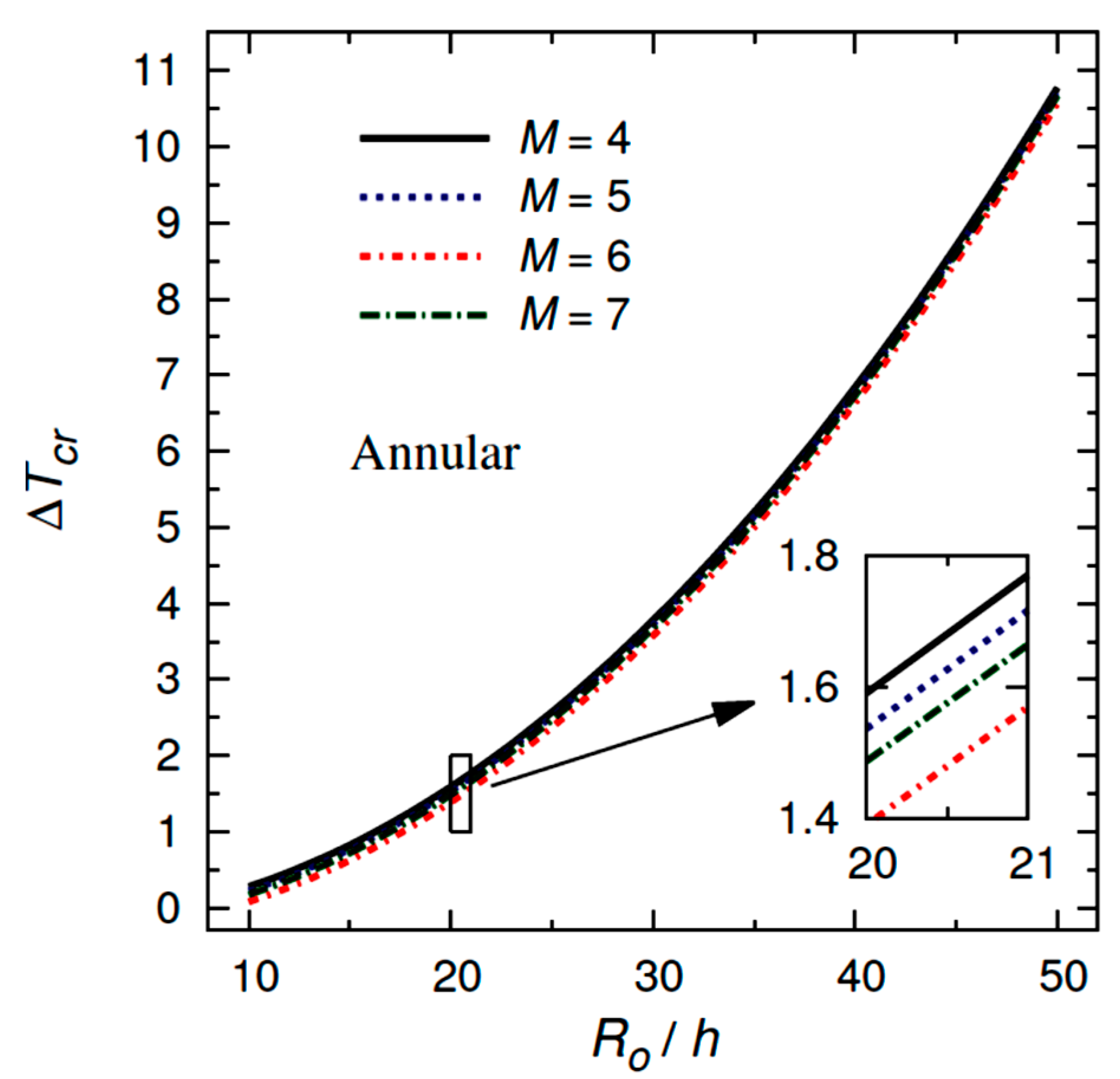
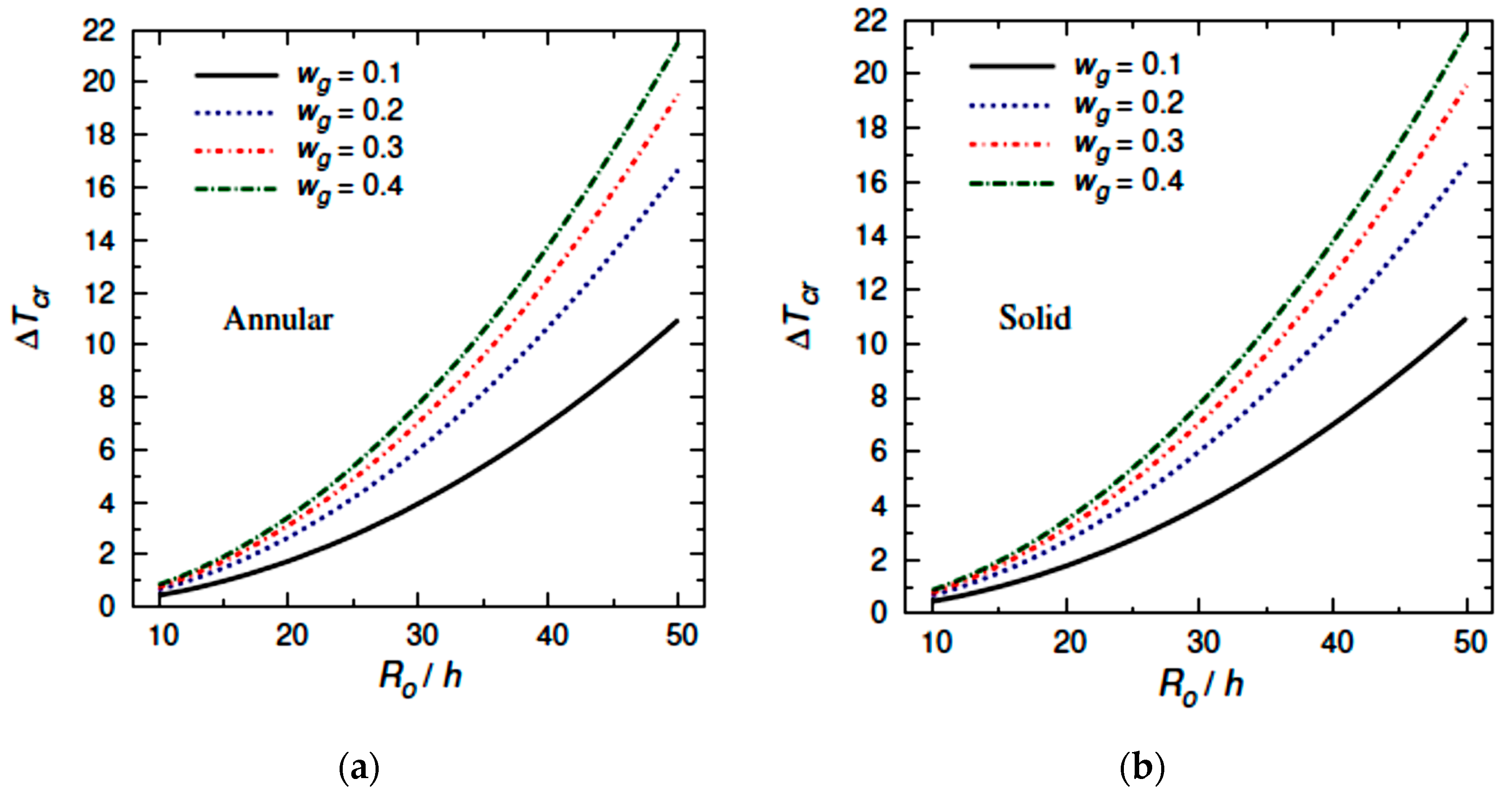
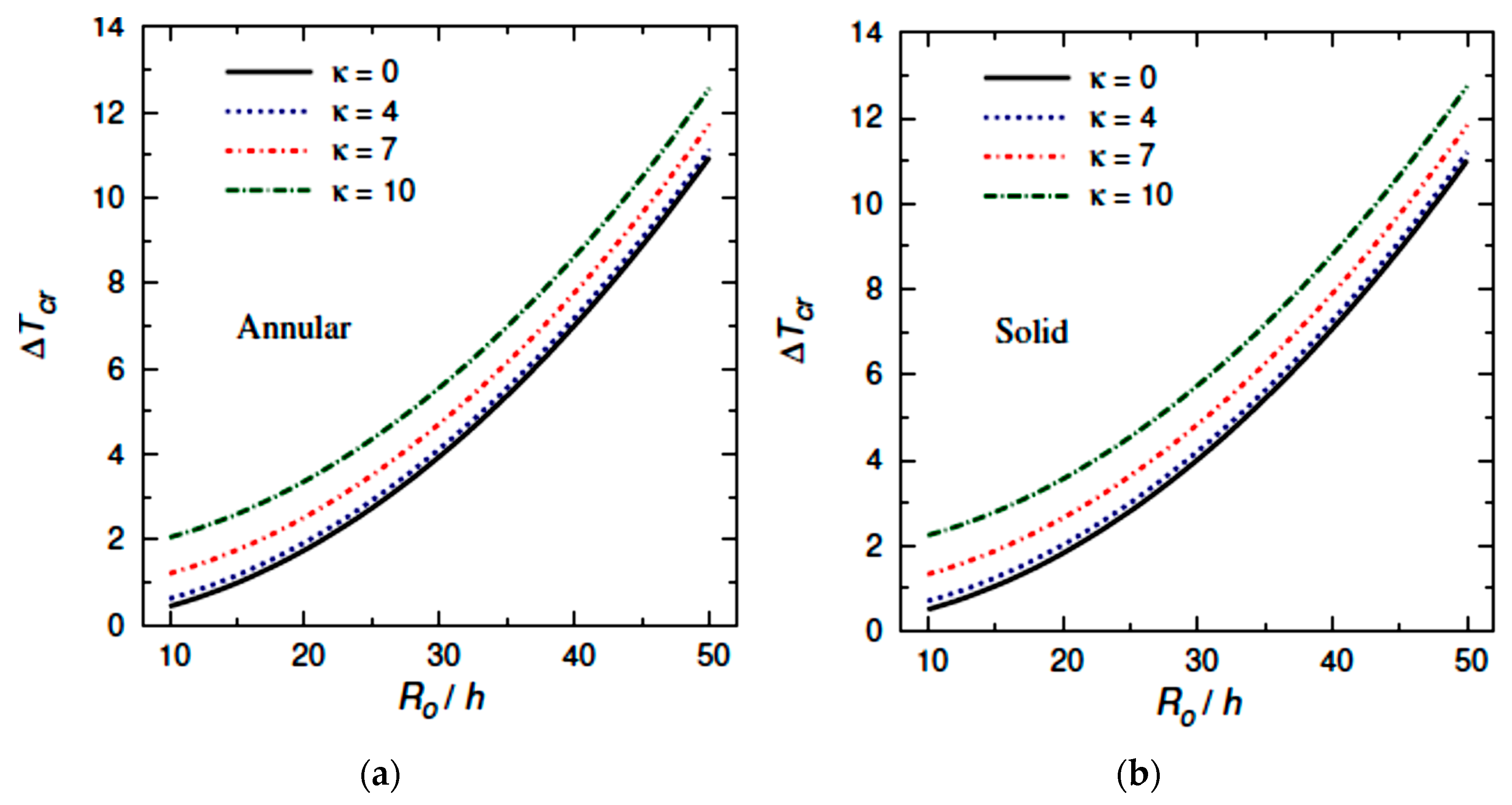
6. Numerical Results
7. Conclusions
- The differential quadrature method (DQM) showed a successful convergence;
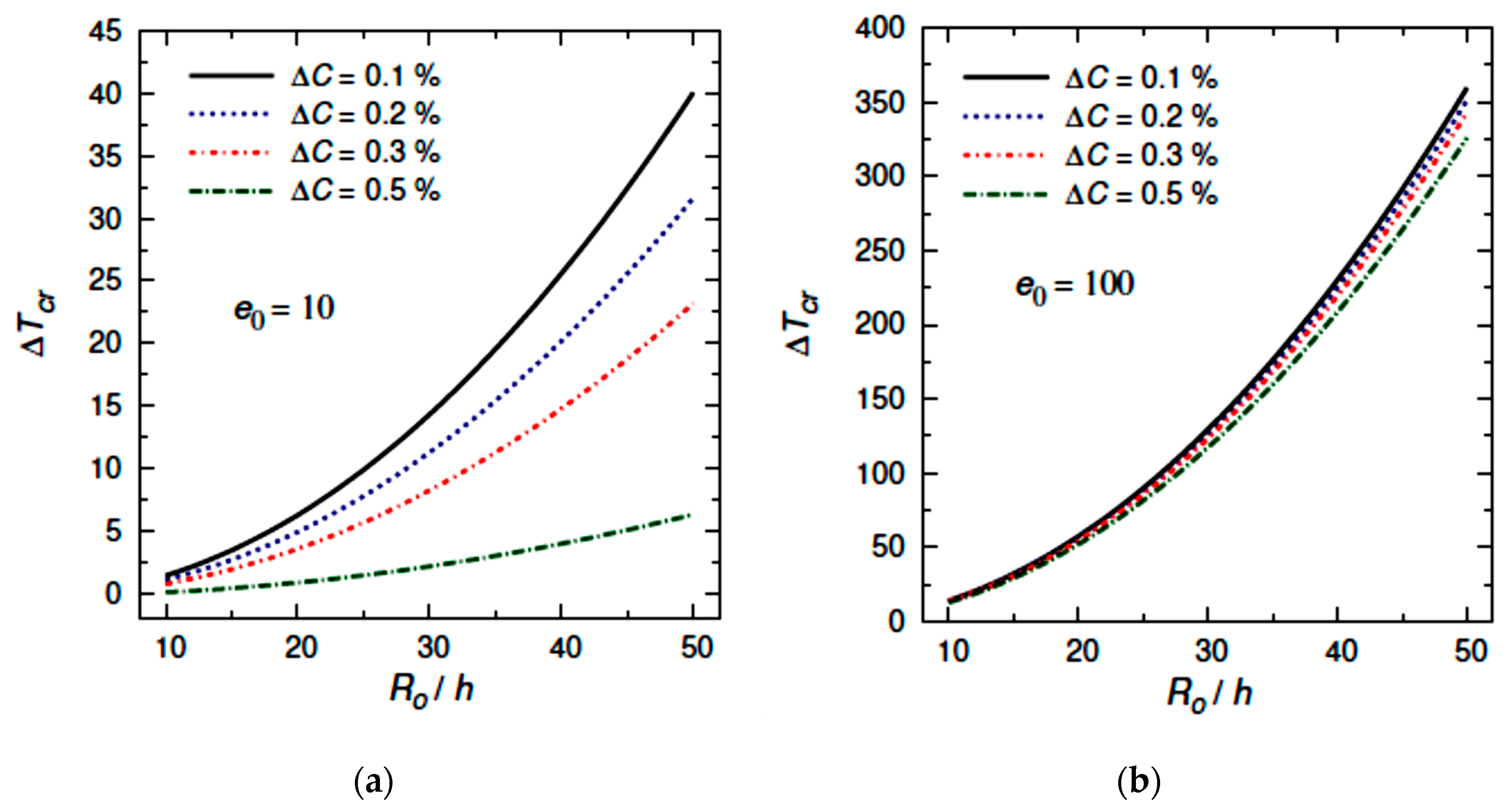
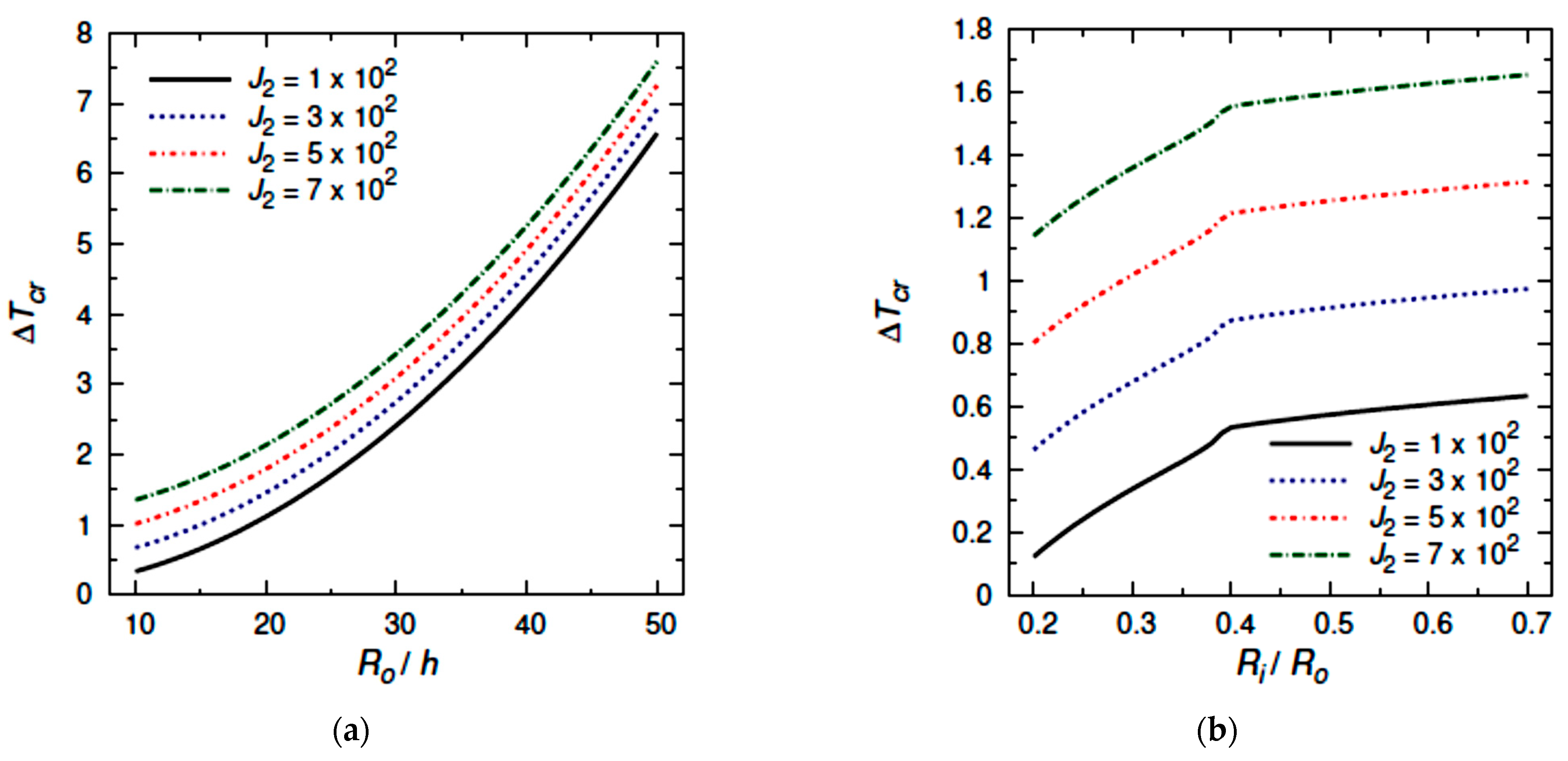
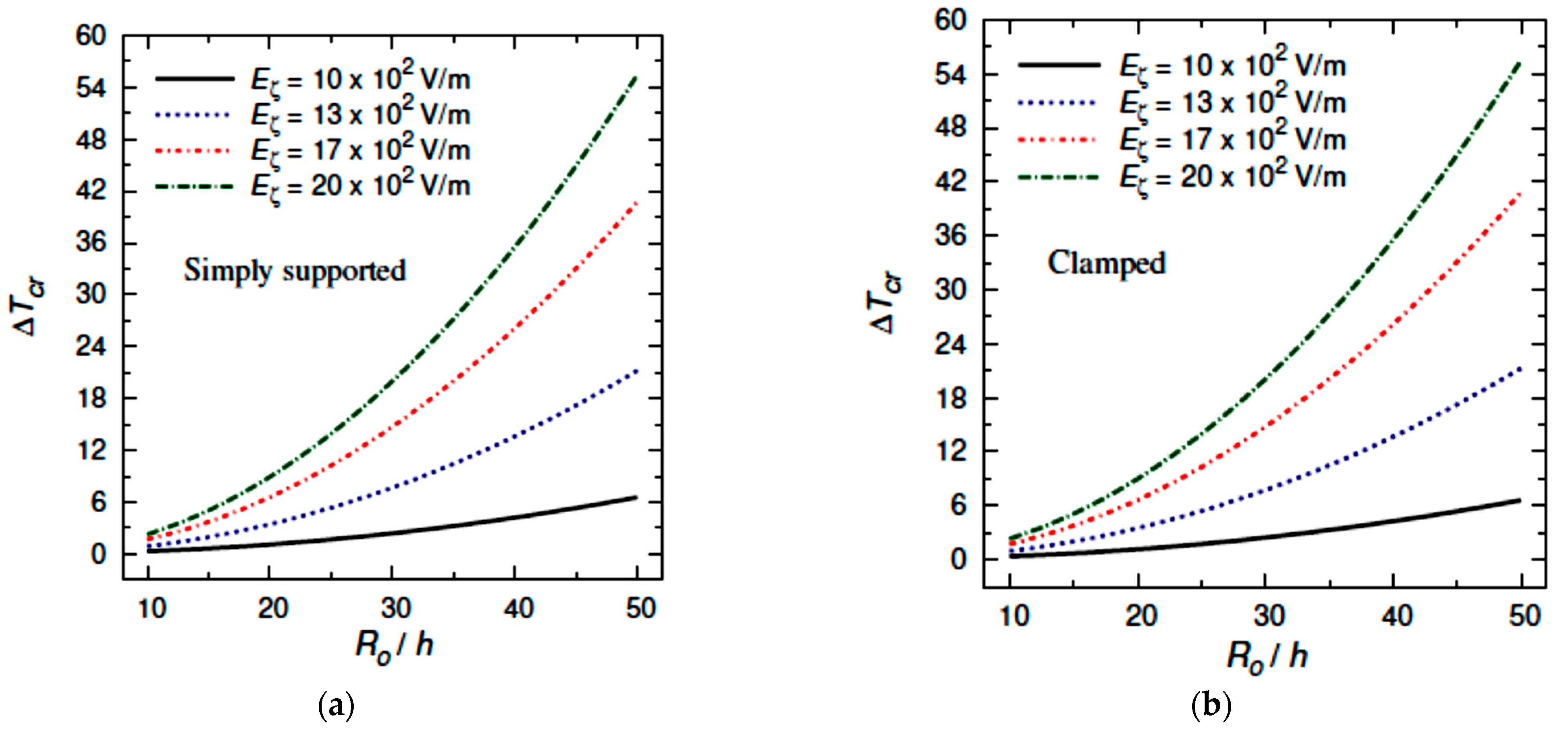
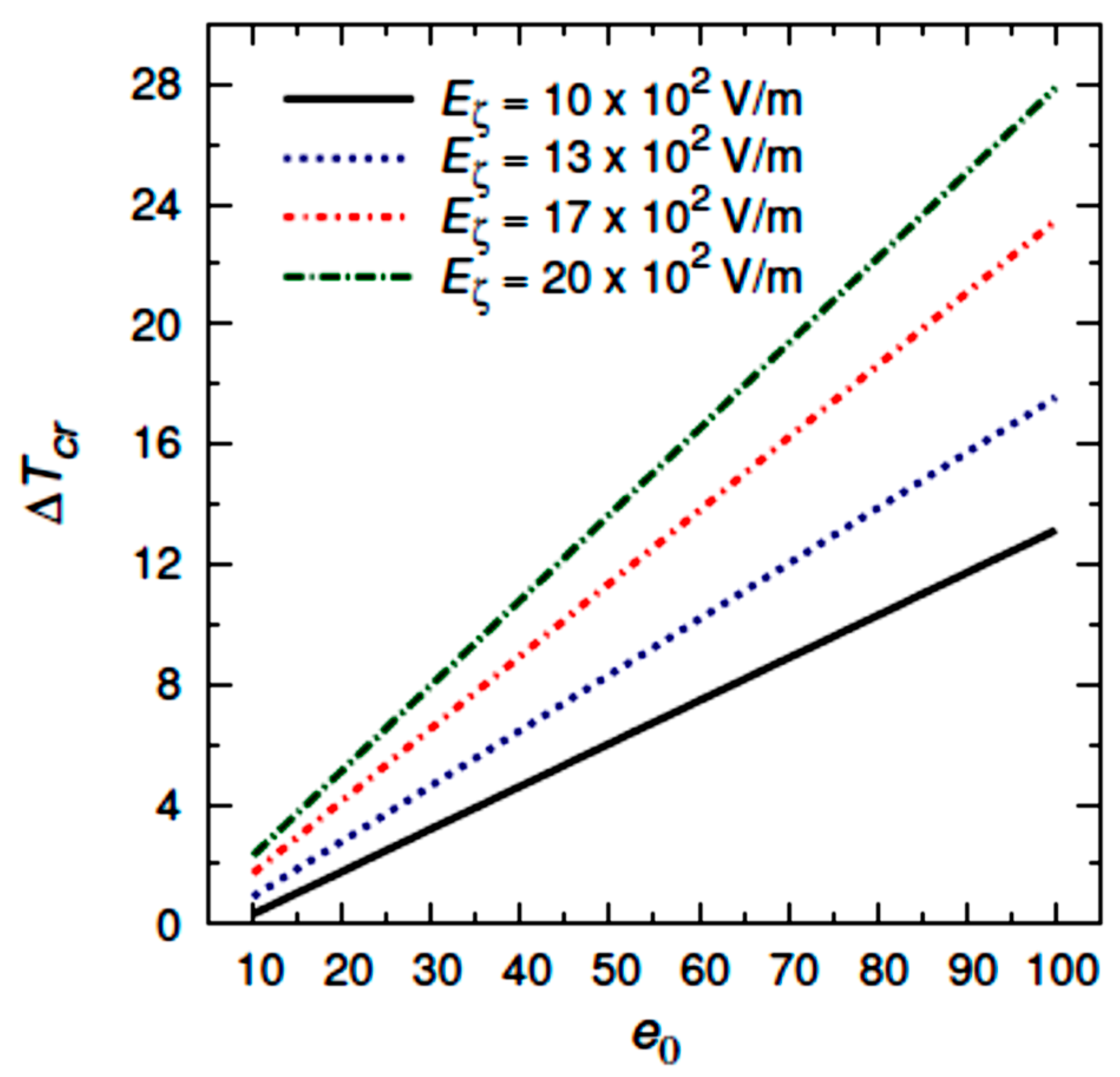
- The critical buckling temperature increases monotonically with increasing the outer radius to thickness ratio for different values of graphene weight fraction, number of nodal diameters, moisture concentration, Winkler coefficient, Pasternak coefficient, and electric field;
- The critical buckling temperature increases with a successful increase in graphene weight fraction, number of nodal diameters, Winkler coefficient, Pasternak coefficient, electric field, and piezoelectric multiple;
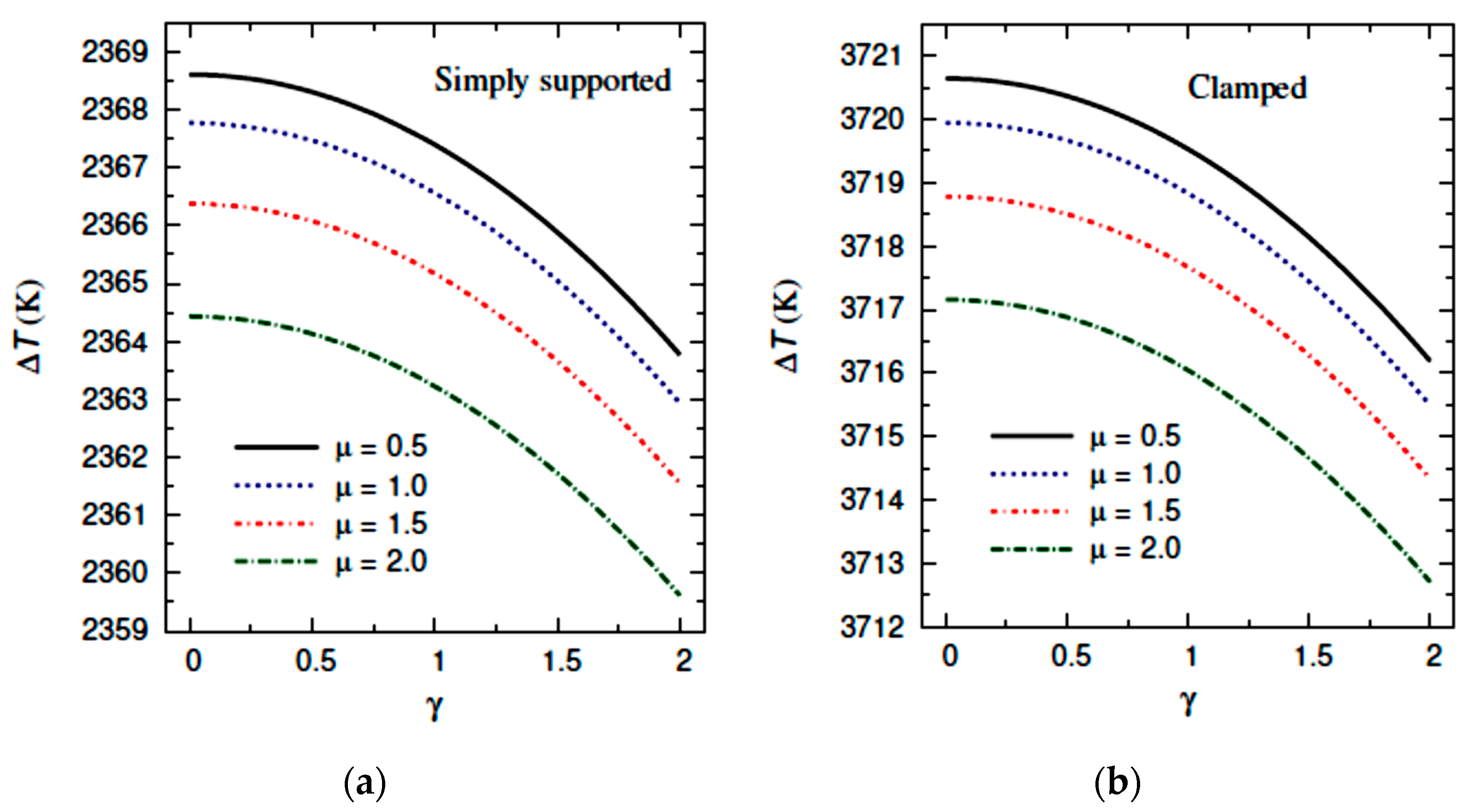
- The critical buckling temperature increases when the nonlocal coefficient decreases for simply supported SGP plates, while it increases when the nonlocal coefficient increases in the case of clamped SGP plates;
- The increment in graphene components and elastic foundation stiffness enhances the strength of the plates leading to an increment in the buckling temperature;
- While the moisture conditions weaken the plate stiffness, therefore, the buckling temperature decreases as the moisture concentration increases;
- Mechanical and thermal post-buckling analysis of sandwich circular smart graphene/piezoelectric annular plate with porous core may be considered for future work.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, J.; Xu, X.; Lim, C.W.; Zhou, Z.; Xiao, S. Accurate thermo-electro-mechanical buckling of shear deformable piezoelectric fiber-reinforced composite cylindrical shells. Compos. Struct. 2016, 141, 221–231. [Google Scholar] [CrossRef]
- Wang, G.; Tan, J.; Zhao, Z.; Cui, S.; Wu, H. Mechanical and energetic characteristics of an energy harvesting type piezoelectric ultrasonic actuator. Mech. Syst. Signal Process. 2019, 128, 110–125. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, C.; Ning, X.; Huang, J.; Zhang, J. Harmonic excitation response performance and active regulation of the high-frequency piezoelectric ultrasonic transducer used in the thermosonic bonding for microelectronics. Sens. Actuators A Phys. 2020, 304, 111839. [Google Scholar] [CrossRef]
- Jia, H.; Li, H.; Lin, B.; Hu, Y.; Peng, L.; Xu, D.; Cheng, X. Fine scale 2-2 connectivity PZT/epoxy piezoelectric fiber composite for high frequency ultrasonic application. Sens. Actuators A Phys. 2021, 324, 112672. [Google Scholar] [CrossRef]
- Laasri, I.; Bybi, A.; Mouhat, O.; Jamal, M.; Hladky, A.C.; Ettahir, A.; Kettani, K. Investigation of the electrical limit conditions effects in piezoelectric transducer arrays utilized in medical imaging. Appl. Acoust. 2020, 170, 107509. [Google Scholar] [CrossRef]
- Bußmann, A.B.; Durasiewicz, C.P.; Kibler, S.H.A.; Wald, C.K. Piezoelectric titanium based microfluidic pump and valves for implantable medical applications. Sens. Actuators A Phys. 2020, 323, 112649. [Google Scholar] [CrossRef]
- Ederer, I.; Raetsch, P.; Schullerus, W.; Tille, C.; Zech, U. Piezoelectrically driven micropump for on-demand fuel-drop generation in an automobile heater with continuously adjustable power output. Sens. Actuators A Phys. 1997, 62, 752–755. [Google Scholar] [CrossRef]
- Kulkarni, H.; Zohaib, K.; Khusru, A.; Aiyappa, K.S. Application of piezoelectric technology in automotive systems. Mater. Today Proc. 2018, 5, 21299–21304. [Google Scholar] [CrossRef]
- Mason, W.P. Piezoelectricity, its history and applications. J. Acoust. Soc. Am. 1980, 68, S39. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Zhu, J.; Liu, D. Dynamic analysis of laminated piezoelectric cylindrical shells. Eng. Struct. 2020, 209, 109945. [Google Scholar] [CrossRef]
- Moradi-Dastjerdi, R.; Behdinan, K.; Safaei, B.; Qin, Z. Buckling behavior of porous CNT-reinforced plates integrated between active piezoelectric layers. Eng. Struct. 2020, 222, 111141. [Google Scholar] [CrossRef]
- Abazid, M.A.; Sobhy, M. Thermo-electro-mechanical bending of FG piezoelectric microplates on Pasternak foundation based on a four-variable plate model and the modified couple stress theory. Microsyst. Technol. 2018, 24, 1227–1245. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Sobhy, M. Nonlocal piezo-hygrothermal analysis for vibration characteristics of a piezoelectric Kelvin–Voigt viscoelastic nanoplate embedded in a viscoelastic medium. Acta Mech. 2018, 229, 3–19. [Google Scholar] [CrossRef]
- Napole, C.; Barambones, O.; Calvo, I.; Derbeli, M.; Silaa, M.Y.; Velasco, J. Advances in tracking control for piezoelectric actuators using fuzzy logic and hammerstein-wiener compensation. Mathematics 2020, 8, 2071. [Google Scholar] [CrossRef]
- Wang, G.; Wang, B.; Zhang, C. Fixed-time third-order super-twisting-like sliding mode motion control for piezoelectric nanopositioning stage. Mathematics 2021, 9, 1770. [Google Scholar] [CrossRef]
- Liu, T.; Li, C.; Wang, C.; Lai, J.W.; Cheong, K.H. A simple-FSDT-based isogeometric method for piezoelectric functionally graded plates. Mathematics 2020, 8, 2177. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Aljadani, M.H. Buckling analysis of actuated functionally graded piezoelectric plates via a quasi-3D refined theory. Mech. Mater. 2020, 151, 103632. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Alghanmi, R.A. Static response of sandwich plates with FG core and piezoelectric faces under thermo-electro-mechanical loads and resting on elastic foundations. Thin-Walled Struct. 2020, 157, 107025. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior thermal conductivity of single-layer graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Frank, I.W.; Tanenbaum, D.M.; van der Zande, A.M.; McEuen, P.L. Mechanical properties of suspended graphene sheets. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2007, 25, 2558–2561. [Google Scholar] [CrossRef] [Green Version]
- Rafiee, M.A.; Rafiee, J.; Wang, Z.; Song, H.; Yu, Z.Z.; Koratkar, N. Enhanced mechanical properties of nanocomposites at low graphene content. ACS Nano 2009, 3, 3884–3890. [Google Scholar] [CrossRef]
- Sobhy, M. Magneto-electro-thermal bending of FG-graphene reinforced polymer doubly-curved shallow shells with piezoelectromagnetic faces. Compos. Struct. 2018, 203, 844–860. [Google Scholar] [CrossRef]
- Sobhy, M.; Zenkour, A.M. Vibration analysis of functionally graded graphene platelet-reinforced composite doubly-curved shallow shells on elastic foundations. Steel Compos. Struct. 2019, 33, 195–208. [Google Scholar]
- Arefi, M.; Bidgoli, E.M.R.; Rabczuk, T. Effect of various characteristics of graphene nanoplatelets on thermal buckling behavior of FGRC micro plate based on MCST. Eur. J. Mech.-A/Solids 2019, 77, 103802. [Google Scholar] [CrossRef]
- Thai, C.H.; Ferreira, A.J.M.; Tran, T.D.; Phung-Van, P. Free vibration, buckling and bending analyses of multilayer functionally graded graphene nanoplatelets reinforced composite plates using the NURBS formulation. Compos. Struct. 2019, 220, 749–759. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Sobhy, M. Axial magnetic field effect on wave propagation in bi-layer FG graphene platelet-reinforced nanobeams. Eng. Comput. 2022, 38, 1313–1329. [Google Scholar] [CrossRef]
- Sobhy, M. 3-D elasticity numerical solution for magneto-hygrothermal bending of FG graphene/metal circular and annular plates on an elastic medium. Eur. J. Mech.-A/Solids 2021, 88, 104265. [Google Scholar] [CrossRef]
- Mao, J.J.; Lu, H.M.; Zhang, W.; Lai, S.K. Vibrations of graphene nanoplatelet reinforced functionally gradient piezoelectric composite microplate based on nonlocal theory. Compos. Struct. 2020, 236, 111813. [Google Scholar] [CrossRef]
- Kundalwal, S.I.; Shingare, K.B.; Gupta, M. Flexoelectric effect on electric potential in piezoelectric graphene-based composite nanowire: Analytical and numerical modelling. Eur. J. Mech.-A/Solids 2020, 84, 104050. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, C.; Santiuste, C.; Zhao, Z.; Yang, J. Buckling and postbuckling of dielectric composite beam reinforced with Graphene Platelets (GPLs). Aerosp. Sci. Technol. 2019, 91, 208–218. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, C.; Yang, J.; Zhou, D.; Liu, W. Static response of functionally graded graphene platelet–reinforced composite plate with dielectric property. J. Intell. Mater. Syst. Struct. 2020, 31, 2211–2228. [Google Scholar] [CrossRef]
- Wu, H.; Zhu, J.; Kitipornchai, S.; Wang, Q.; Ke, L.L.; Yang, J. Large amplitude vibration of functionally graded graphene nanocomposite annular plates in thermal environments. Compos. Struct. 2020, 239, 112047. [Google Scholar] [CrossRef]
- Zhao, S.; Zhao, Z.; Yang, Z.; Ke, L.; Kitipornchai, S.; Yang, J. Functionally graded graphene reinforced composite structures: A review. Eng. Struct. 2020, 210, 110339. [Google Scholar] [CrossRef]
- Feng, C.; Kitipornchai, S.; Yang, J. Nonlinear free vibration of functionally graded polymer composite beams reinforced with graphene nanoplatelets (GPLs). Eng. Struct. 2017, 140, 110–119. [Google Scholar] [CrossRef]
- Affdl, J.H.; Kardos, J.L. The Halpin-Tsai equations: A review. Polym. Eng. Sci. 1976, 16, 344–352. [Google Scholar] [CrossRef]
- Song, M.; Yang, J.; Kitipornchai, S. Bending and buckling analyses of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Part B Eng. 2018, 134, 106–113. [Google Scholar] [CrossRef] [Green Version]
- Brush, D.O.; Almroth, B.O. Buckling of Bars, Plates, and Shells; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Ke, L.L.; Liu, C.; Wang, Y.S. Free vibration of nonlocal piezoelectric nanoplates under various boundary conditions. Phys. E Low-Dimens. Syst. Nanostructures 2015, 66, 93–106. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Khorshidvand, A.R.; Jabbari, M.; Eslami, M.R. Thermoelastic buckling analysis of functionally graded circular plates integrated with piezoelectric layers. J. Therm. Stresses 2012, 35, 695–717. [Google Scholar] [CrossRef]
- Meyers, C.A.; Hyer, M.W. Thermal buckling and postbuckling of symmetrically laminated composite plates. J. Therm. Stresses 1991, 14, 519–540. [Google Scholar] [CrossRef]
- Shariat, B.S.; Eslami, M.R. Buckling of thick functionally graded plates under mechanical and thermal loads. Compos. Struct. 2007, 78, 433–439. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Sobhy, M. Thermal buckling of various types of FGM sandwich plates. Compos. Struct. 2010, 93, 93–102. [Google Scholar] [CrossRef]
- Sobhy, M. Size-dependent hygro-thermal buckling of porous FGM sandwich microplates and microbeams using a novel four-variable shear deformation theory. Int. J. Appl. Mech. 2020, 12, 2050017. [Google Scholar] [CrossRef]
- Wang, C.Y. On the buckling of a circular plate on an elastic foundation. Trans. -Am. Soc. Mech. Eng. J. Appl. Mech. 2005, 72, 795. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Demir, O.; Balkan, D.; Peker, R.C.; Metin, M.; Arikoglu, A. Vibration analysis of curved composite sandwich beams with viscoelastic core by using differential quadrature method. J. Sandw. Struct. Mater. 2020, 22, 743–770. [Google Scholar] [CrossRef]
- Sobhy, M. Differential quadrature method for magneto-hygrothermal bending of functionally graded graphene/Al sandwich-curved beams with honeycomb core via a new higher-order theory. J. Sandw. Struct. Mater. 2021, 23, 1662–1700. [Google Scholar] [CrossRef]
- Mao, J.J.; Zhang, W. Buckling and post-buckling analyses of functionally graded graphene reinforced piezoelectric plate subjected to electric potential and axial forces. Compos. Struct. 2019, 216, 392–405. [Google Scholar] [CrossRef]
- Kiani, Y.; Eslami, M.R. An exact solution for thermal buckling of annular FGM plates on an elastic medium. Compos. Part B Eng. 2013, 45, 101–110. [Google Scholar] [CrossRef]


| Source | |||||
|---|---|---|---|---|---|
| 0.10 | Ref. [52] | 1 | 39.002 | 87.755 | 156.009 |
| Present | 1 | 39.043 | 87.831 | 156.436 | |
| 0.15 | Ref. [52] | 2 | 43.227 | 97.261 | 172.908 |
| Present | 2 | 43.372 | 97.486 | 173.091 |
| Annular | Solid | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.3 | 0.4 | 0.1 | 0.2 | 0.3 | 0.4 | |||
| 100 | 2.41302 | 2.07505 | 1.73709 | 1.39912 | 2.32675 | 1.98878 | 1.65081 | 1.31284 | |
| 300 | 2.75337 | 2.41541 | 2.07744 | 1.73947 | 2.66710 | 2.32913 | 1.99116 | 1.65319 | |
| 500 | 3.09373 | 2.75576 | 2.41779 | 2.07982 | 3.00745 | 2.66948 | 2.33152 | 1.99355 | |
| 700 | 3.43408 | 3.09611 | 2.75814 | 2.42017 | 3.34780 | 3.00984 | 2.67187 | 2.33390 | |
| 100 | 3.50808 | 3.17011 | 2.83214 | 2.49417 | 2.87936 | 2.54139 | 2.20342 | 1.86545 | |
| 300 | 3.84843 | 3.51046 | 3.17249 | 2.83452 | 3.21971 | 2.88174 | 2.54377 | 2.20580 | |
| 500 | 4.18878 | 3.85081 | 3.51284 | 3.17487 | 3.56006 | 3.22209 | 2.88412 | 2.54615 | |
| 700 | 4.52913 | 4.19116 | 3.85320 | 3.51523 | 3.90041 | 3.56244 | 3.22447 | 2.88651 | |
| 100 | 4.60394 | 4.26597 | 3.92800 | 3.59003 | 3.42502 | 3.08705 | 2.74908 | 2.41111 | |
| 300 | 4.94429 | 4.60632 | 4.26835 | 3.93038 | 3.76537 | 3.42740 | 3.08943 | 2.75146 | |
| 500 | 5.28464 | 4.94667 | 4.60870 | 4.27073 | 4.10572 | 3.76775 | 3.42978 | 3.09182 | |
| 700 | 5.62499 | 5.28702 | 4.94905 | 4.61109 | 4.44607 | 4.10810 | 3.77014 | 3.43217 | |
| 100 | 5.69990 | 5.36193 | 5.02396 | 4.68599 | 3.96968 | 3.63171 | 3.29374 | 2.95577 | |
| 300 | 6.04025 | 5.70228 | 5.36431 | 5.02634 | 4.31003 | 3.97206 | 3.63409 | 3.29612 | |
| 500 | 6.38060 | 6.04263 | 5.70466 | 5.36669 | 4.65038 | 4.31241 | 3.97444 | 3.63647 | |
| 700 | 6.72095 | 6.38298 | 6.04501 | 5.70705 | 4.99073 | 4.65276 | 4.31479 | 3.97682 | |
| Annular | Solid | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.3 | 0.4 | 0.1 | 0.2 | 0.3 | 0.4 | |||
| 0.1 | 1000 | 1.73149 | 1.39352 | 1.05555 | 0.71758 | 1.76672 | 1.42875 | 1.09078 | 0.75281 |
| 1200 | 2.12236 | 1.78439 | 1.44642 | 1.10845 | 2.15759 | 1.81962 | 1.48165 | 1.14368 | |
| 1400 | 2.51322 | 2.17525 | 1.83728 | 1.49932 | 2.54846 | 2.21049 | 1.87252 | 1.53455 | |
| 1600 | 2.90409 | 2.56612 | 2.22815 | 1.89018 | 2.93932 | 2.60135 | 2.26339 | 1.92542 | |
| 0.2 | 1000 | 1.42862 | 1.09953 | 0.77043 | 0.44134 | 1.48595 | 1.15686 | 0.82777 | 0.49868 |
| 1200 | 1.78909 | 1.46000 | 1.13090 | 0.80181 | 1.84642 | 1.51733 | 1.18824 | 0.85914 | |
| 1400 | 2.14956 | 1.82046 | 1.49137 | 1.16228 | 2.20689 | 1.87780 | 1.54871 | 1.21961 | |
| 1600 | 2.51002 | 2.18093 | 1.85184 | 1.52275 | 2.56736 | 2.23827 | 1.90917 | 1.58008 | |
| 0.3 | 1000 | 1.28604 | 0.96770 | 0.64935 | 0.33100 | 1.32080 | 1.00245 | 0.68411 | 0.36576 |
| 1200 | 1.63408 | 1.31573 | 0.99739 | 0.67904 | 1.66884 | 1.35049 | 1.03214 | 0.71379 | |
| 1400 | 1.98212 | 1.66377 | 1.34542 | 1.02707 | 2.01687 | 1.69853 | 1.38018 | 1.06183 | |
| 1600 | 2.33016 | 2.01181 | 1.69346 | 1.37511 | 2.36491 | 2.04656 | 1.72822 | 1.40987 | |
| 0.4 | 1000 | 1.16949 | 0.86442 | 0.55934 | 0.25427 | 1.16479 | 0.85972 | 0.55465 | 0.24957 |
| 1200 | 1.50824 | 1.20316 | 0.89809 | 0.59301 | 1.50354 | 1.19846 | 0.89339 | 0.58831 | |
| 1400 | 1.84698 | 1.54191 | 1.23683 | 0.93176 | 1.84228 | 1.53721 | 1.23213 | 0.92706 | |
| 1600 | 2.18573 | 1.88065 | 1.57558 | 1.27050 | 2.18103 | 1.87595 | 1.57088 | 1.26580 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alazwari, M.A.; Zenkour, A.M.; Sobhy, M. Hygrothermal Buckling of Smart Graphene/Piezoelectric Nanocomposite Circular Plates on an Elastic Substrate via DQM. Mathematics 2022, 10, 2638. https://doi.org/10.3390/math10152638
Alazwari MA, Zenkour AM, Sobhy M. Hygrothermal Buckling of Smart Graphene/Piezoelectric Nanocomposite Circular Plates on an Elastic Substrate via DQM. Mathematics. 2022; 10(15):2638. https://doi.org/10.3390/math10152638
Chicago/Turabian StyleAlazwari, Mashhour A., Ashraf M. Zenkour, and Mohammed Sobhy. 2022. "Hygrothermal Buckling of Smart Graphene/Piezoelectric Nanocomposite Circular Plates on an Elastic Substrate via DQM" Mathematics 10, no. 15: 2638. https://doi.org/10.3390/math10152638
APA StyleAlazwari, M. A., Zenkour, A. M., & Sobhy, M. (2022). Hygrothermal Buckling of Smart Graphene/Piezoelectric Nanocomposite Circular Plates on an Elastic Substrate via DQM. Mathematics, 10(15), 2638. https://doi.org/10.3390/math10152638






