Abstract
(1) Background: In silico approaches to rational drug design are among the fastest evolving ones. Depending on the available structural information for the biomacromolecule and the small molecule, the in silico methods are classified as ligand- and structure-based. The latter predict ligand–receptor binding using 3D structures of both molecules, whose computational simulation is referred to as molecular docking. It aims at estimating the binding affinity (approximated by scoring function) and the ligand binding pose in the receptor’s active site, which postulates a key role of the scoring functions in molecular docking algorithms. This study focuses on the performance of different types of scoring functions implemented in molecular modelling software packages. (2) Methods: An InterCriteria analysis (ICrA) was applied to assess the performance of the scoring functions available in MOE, GOLD, SeeSAR, and AutoDock Vina software platforms. The InterCriteria analysis was developed to distinguish possible relations between pairs of criteria when multiple objects are considered. All 12 investigated scoring functions were tested by docking a set of protease inhibitors in the binding sites of two protein targets. The dataset consisted of 88 benzamidine-type compounds with experimentally measured inhibitory constants for thrombin and trypsin, which allows for the objective assessment of the scoring functions performance. The results generated by the molecular docking were subjected to ICrA in order to analyze both docking energies as approximations of the binding affinities and RMSDs (root-mean-square deviation) as measures of the experimental binding pose proximity between the compounds and the co-crystalized ligand, based on the atoms in the common scaffold. (3) Results: The results obtained for the best poses, the average of the best 5 or 30 poses retained after docking, were analyzed. A comparison with the experimentally observed inhibitory effects was also performed. The InterCriteria analysis application confirms that the performance of the scoring functions for the same dataset of ligands depends on the studied protein. The analysis reveals that none of the studied scoring functions is a good predictor of the compounds’ binding affinities for the considered protein targets. (4) Conclusion: In terms of this analysis, the investigated scoring functions do not produce equivalent results, which suggests the necessity for their combined use in consensus docking studies.
MSC:
92-08; 92-10; 62C86
1. Introduction
Computer-aided drug design (CADD, or in silico drug design) stands for a collection of computational approaches aiming at optimization and speed-up of the time-consuming and costly process of drug design. The in silico methods are classified as ligand- and structure-based according to the available structural information. Among the structure-based approaches, molecular docking is the most commonly used one. It is a computational simulation that places the structure of the small molecule (ligand) in different orientations and conformations within the biomacromolecule (usually protein) active site, aiming to find the optimal binding mode through the calculation of the ligand–receptor binding energy. Molecular docking results in the generation of different poses of the ligand within the protein binding pocket. The simulation follows the complementarity principle in the protein–ligand interaction and estimates the change in the free energy of their binding using a scoring function [1]. The best poses subjected to further investigations are selected based on the calculated scores.
A variety of docking algorithms exists and their performance strongly depends on the implemented scoring functions. In the scientific literature, there are comparative studies on scoring functions as well [2,3,4,5,6]; however, the selection of a suitable one for a particular ligands’ dataset bound to a particular receptor or receptors is not a trivial task. The authors of [2] performed a comparative assessment of 16 scoring functions implemented in commercial software or software with free access and later [3,4] on more scoring functions and revealed that the investigated scoring functions did not perform well on the ligands’ ranking. The authors of [5] proposed 12 scoring functions based on a wide range of machine learning techniques and compared them to results obtained in [3]. Eight docking programs and 16 scoring functions were compared in [6] and none of the used programs was effective for all six protein–ligand datasets. A number of studies performed a systematic comparative investigation of the available docking programs (with commercial license or with free access) and concluded that the predictive docking aiming to rank the binding affinities for the explored datasets does not perform well in most docking programs [7,8]. In addition, the results depend on the protein families that are investigated [7]. Thus, the question of which molecular docking software and protocol perform better is still open. Facing this problem, the present study explores the capability of InterCriteria analysis (ICrA), developed as a new multicriteria decision-making approach [9], to assess the performance of various scoring functions on a given set of compounds and protein targets. In addition, the chosen dataset includes a large number of compounds with a common scaffold and various substituents and with binding affinities experimentally measured by the same methodology. These facts provide a good basis for a more objective and detailed analysis of the performance of the scoring functions.
InterCriteria analysis aims at discerning possible similarities in the behavior of pairs of criteria when considering multiple objects [9]. Depending on the research topics, ICrA could be applied to compare predefined criteria and the objects estimated by them or to discover some dependencies between the criteria themselves. Bringing together two fundamental concepts of the index matrices [10,11] and the intuitionistic fuzzy sets [12], an extension of Zadeh’s fuzzy sets [13], ICrA pursues at obtaining new information based on the criteria involved in evaluation processes. Once the existing relations between the criteria themselves are outlined, the decision-making process can be strongly facilitated. Due to its successful applications in different research areas, ICrA has gained more attention and its theory has been further developed and upgraded in parallel with its continuously rising number of applications. InterCriteria analysis has been applied in many challenging fields, among them, medicine [14], ecology [15], artificial intelligence and metaheuristics algorithms performance [16], and e-learning [17], all of them illustrating the ability of the analysis to reveal new relations and dependencies between the studied criteria and a new view on the analyzed data. The approach has been successfully tested in computer-aided drug design and computational toxicology [18]. Using ICrA, the authors explored, in particular, the docking results from a dataset of 160 tyrosine-based agonists in the active site of peroxisome proliferator-activated nuclear receptor gamma. For two of the Molecular Operating Environment (MOE) scoring functions (London dG and Alpha HB), a positive consonance was demonstrated, while none of the functions were outlined as a good predictor of binding affinity.
In the current study, we present the ICrA application aiming to assess the performance of the scoring functions implemented in commercial and free-access software. Twelve scoring functions were used in the molecular docking of a dataset of benzamidine-type inhibitors in the active sites of thrombin and trypsin.
2. Materials and Methods
2.1. InterCriteria Analysis Approach
The ICrA approach was proposed by Atanassov et al. in 2014 [9]. It combines fundamental concepts of two mathematical formalisms: index matrices (IM) [10,11] and intuitionistic fuzzy sets (IFS) [12]. To facilitate the exposition, a brief overview of the theoretical background of ICrA is outlined below.
Intuitionistic fuzzy sets, introduced by Atanassov [12], are an extension of Zadeh’s fuzzy sets [13]. Fuzzy sets generalize the notion of characteristic function for each element to a set (equaling 0 when an element does not belong to the set and 1 when it does) by introducing a membership function, taking values in the interval [0, 1] for each element. The intuitionistic fuzzy sets further extend this idea by adding a degree of non-membership, also in the closed unit interval, adding the requirement the sum of the two degrees to fall in the closed unit interval. The IFS A* is formally defined as:
where E is a universe set, ; and the mappings are the degree of membership and the degree of non-membership for each element to the fixed subset A of E, respectively, satisfying .
An intuitionistic fuzzy pair (IFP) is an ordered pair , such that and [19]. The intuitionistic fuzzy pairs are one of the basic elements of ICrA, where they are obtained as an evaluation of the similarity of behavior of two criteria over a set of objects.
The input of the ICrA is a two-dimensional IM. Each 2D IM is represented by a set of row indexes (labels), column indexes (labels), and elements corresponding to the combination of the said indexes. Due to this fact, swapping two rows or columns does not result in a different IM.
Each 2D IM may be written as [K, L, ], where K is the set of row indexes (labels); L is the set of column indexes (labels), k ∈ K, l ∈ L; and is the element corresponding to row index k and column index l. In general, not all elements need to be of the same type. In ICrA, the input IM consists of objects evaluated by different criteria and, thus, may be denoted as [O, C, ], where the index set of rows O corresponds to the distinct evaluated objects and the index set of columns C corresponds to different evaluating criteria, while corresponds to the evaluation assigned to the object “O” under the criterion “C”. If we have n criteria and m objects, this can be represented as the following IM:
| C1 | … | Ck | … | Cn | |
| O1 | … | … | |||
| … | … | … | … | … | … |
| Oi | … | … | |||
| … | … | … | … | … | … |
| Om | … | … |
In such a manner, ICrA starts with an m × n table and, after processing, the ICrA outputs an n × n table of IFPs corresponding to InterCriteria relationships. ICrA performs a comparison between every two criteria over multiple evaluated objects considering the relation between the respective elements, as shown in Figure 1.
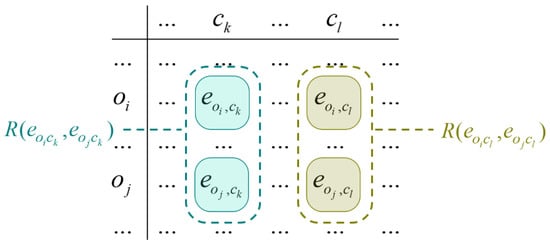
Figure 1.
Pairwise comparisons of the objects’ evaluations against the criteria.
We have several possible cases depending on the nature of the input elements. When the two relations (R1, R2 ∈ {<, =, >}) coincide, this adds to the score of IF agreement (or similarity). If they differ, depending on the fact of whether one of the relations is the dual of the other, e.g., R1 is the relation “<” and R2 is the relation “>” or vice versa, this contributes to the score of IF disagreement (dissimilarity).
Otherwise, the contribution is assigned to the score of uncertainty (indeterminacy). The detailed mathematical considerations may be found in [9]. Both counters and are formed and incremented, based on the following rules:
- −
- counts the cases where the relations and are identical.
- −
- counts cases where the relation is the one dual to the relation .
The pairwise comparisons between the objects total to m(m − 1)/2; therefore, it holds true that . For every k, l (1 ≤ k ≤ l ≤ m and m ≥ 2), the following normalized values are obtained from and as follows:
- , called, in terms of ICrA, degree of agreement;
- , called degree of disagreement.
The degrees of agreement/disagreement between two criteria need to be calculated only once, since and .
Obviously, is an IFP. The value corresponds to the degree of uncertainty.
The output IM has all the collected IFPs , which may be viewed as an intuitionistic fuzzy evaluation of the relations between any two criteria Ck and Cl:
| C1 | … | Ck | … | Cn | |
| C1 | … | … | |||
| … | … | … | … | … | … |
| Ck | … | … | |||
| … | … | … | … | … | … |
| Cn | … | … |
In practice, it is easier to consider two distinct index matrices IMμ and IMν, rather than the IM of IFPs above.
The result of the ICrA algorithm provides a classification of the InterCriteria relations, based on the thresholds for and , which are chosen by the user or algorithmically determined. Let α, β ∈ [0, 1] (with α > β) be the thresholds to which the values of and are compared. Then, the criteria Ck and Cl are said to be in:
- Positive consonance, whenever > α and < β;
- Negative consonance, whenever < β and > α;
- Dissonance, otherwise.
Figure 2 presents the intuitionistic fuzzy triangle with the zones of positive consonance and negative consonance with α = 0.75 and β = 0.25.
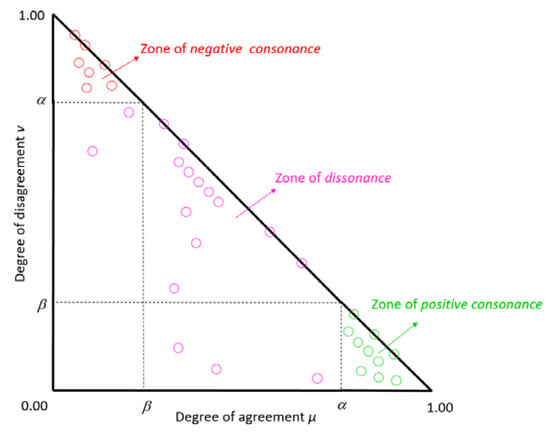
Figure 2.
Intuitionistic fuzzy triangle with zones of positive consonance, dissonance, and negative consonance for α = 0.75 and β = 0.25.
A finer scale for determining types of consonance or dissonance between criteria pairs, as well as the results’ interpretation with respect to the degrees of agreement, disagreement, and uncertainty, are presented in [20]. In [21], the rules from [20] are formulated and presented (with their pseudo-code) as different algorithms for the calculation of ICrA relations, called μ-biased, balanced, ν-biased, unbiased, and weighted.
2.2. Software Implementation of ICrA
A software implementation of ICrA, named ICrAData [22], is freely available at http://intercriteria.net/software/ (accessed on 3 June 2022). Figure 3 presents the user interface, with the left panel showing the input data, the central panel showing the result of the ICrA implementation in the form of a table with colored values, and the right panel showing the graphical visualization of the results in the intuitionistic fuzzy interpretation triangle with points (circles) colored as in the central panel.
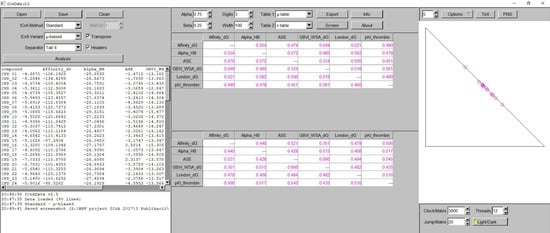
Figure 3.
An exemplary view of ICrAData.
Imposed by its use for the specific tasks of this study, the following additions were implemented in ICrAData:
- ✓
- The ability to load comma-separated value (CSV) files with headers by row and column, which are taken as object and criteria names, respectively. This allows loading data from any computer program able to output tables in CSV format.
- ✓
- A functionality that allows a user definition of the thresholds α and β. The default values set in ICrAData are α = 0.75 and β = 0.25 and they were used in the current investigation.
- ✓
- To visualize the results better, cell colors were introduced in accordance with the rules below and the user-defined thresholds α and β:
- −
- In the case of positive consonance, the results are colored in green;
- −
- In the case of negative consonance, the results are colored in red;
- −
- Otherwise, when there is dissonance, the results are colored in magenta.
- ✓
- ICrAData automatically records the results every 15 min and when exiting the program in order to prevent overwriting or accidental loss of data.
All the aforementioned functionalities improve the automation in the ICrAData workflow.
2.3. Dataset
For the purposes of the current investigation, a dataset of protease inhibitors, as described in [23], was used. The dataset consists of a benzamidine-type compounds, whose parent structure (structural variations at positions R1 and R2) is presented in Figure 4.
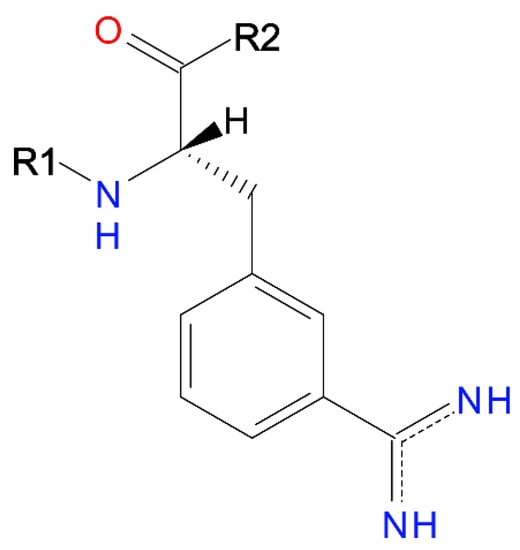
Figure 4.
Parent structure of the compounds in the dataset.
The dataset consists of a large number of small drug-like compounds with a common scaffold—88 protease inhibitors derived from 3-amidinophenylalanine, with experimentally defined Ki values for their inhibition of the enzymes trypsin and thrombin [23]. This dataset was chosen due to the fact that it has been employed as a benchmark set in the validation of molecular modelling methodologies [23]. This is a good attestation of the quality of the data, in particular the available experimental data. These features make the dataset very useful for the purposes of the current research, enabling not only the assessment of the interrelations between the scoring functions themselves, but also their interrelations with the available experimental data. As such, it could allow for an objective evaluation of the performance of the scoring functions.
The 2D structures of the benzamidine-type inhibitors were built in MOE, according to Boehm et al. [23]. All structures were energetically minimized with an MMFF94x force field.
Thrombin and trypsin are representatives of serine proteases, known to play a significant role in a number of physiological and pathophysiological processes.
Thrombin (coagulation factor II) is a serine protease, a key enzyme of blood coagulation. At the same time, it plays an important role in a number of physiological and pathophysiological processes related to blood coagulation and fibrinolysis, tissue repair and wound healing, platelet and endothelial cell activation, progression of neoplasia, inflammation, etc. [24]. For the purposes of this study, the X-ray crystal structure of thrombin complex with the ligand 1-[N-(naphthalen-2-ylsulfonyl)glycyl-4-carbamimidoyl-D-phenylalanyl]piperidine (NAPAP) was retrieved from the Protein Data Bank (PDB, https://www.rcsb.org (accessed on 3 June 2022) PDB ID 1ETS).
Trypsin is a serine protease found in the digestive system of many vertebrates serving both digestive and regulatory functions. As a digestive agent, it degrades large polypeptides into smaller fragments. As a regulatory protease, it activates other proteins through proteolysis at specific lysine and arginine bonds [25]. For the purposes of this study, the X-ray crystal structure of the trypsin complex with the ligand 3-[(2S)-2-[(4-methylphenyl)sulfonyl]amino-3-oxo-3-piperidin-1-ylpropyl]benzenecarboximidamide (4-TAPAP) was retrieved from PDB (PDB ID 1PPH).
Prior to docking, both protein structures were appropriately prepared for the subsequent molecular docking. The protein structures were protonated using the Protonate3D tool in MOE. The tool applies the Generalized Born electrostatics model and, following the optimal free energy proton geometry and the ionization states of titratable protein groups, assigns hydrogens to the structures. The water molecules were removed.
2.4. Investigated Scoring Functions
The scoring functions available in both commercial and free molecular docking software packages were explored. Representatives of all three main types of scoring functions were studied—empirical, force-field, and knowledge-based, shortly described below:
- ➢
- Empirical: Use training sets of X-ray protein–ligand complexes and multiple linear regression as a statistical method to derive the equation. The equation terms describe important binding interactions, such as hydrogen bonds (H-bonds), ionic, hydrophobic, loss in the ligand flexibility (entropy), etc.
- ➢
- Force-field based: Based on classical force fields for proteins and use Lennard-Jones and Coulomb potentials to describe the enthalpy terms. The entropy terms are often missing.
- ➢
- Knowledge-based (known also as Potential of Mean Force): Involve distance-dependent interaction potentials derived through the statistical analyses of a large number of crystal structures of protein–ligand complexes. Such functions describe the interactions between each pair of ligand–protein atoms based on the structural information of the X-ray protein–ligand coordinates. In contrast to the above-mentioned two types, knowledge-based functions do not have physical interpretation.
Among the commercial software packages for molecular docking, MOE, GOLD, and SeeSAR were chosen due to the fact that they are widely used by the research community in the field of in silico drug design. In addition, the scoring functions included in these software packages represent different types (empirical, force-field, and knowledge-based, or their combinations; see Table 1) that makes them a good representative sample of scoring functions broadly used in the contemporary docking studies.

Table 1.
Brief description of the investigated scoring functions.
- ✓
- MOE v. 2016.08 (Molecular Operating Environment, The Chemical Computing Group http://www.chemcomp.com (accessed on 3 June 2022)) operates with five scoring functions, four of which are empirical (London dG, ASE, Affinity dG, and Alpha HB) and one is a force-field scoring function (GBVI/WSA dG) [26].
- ✓
- GOLD v. 5.6.3 (Genetic Optimization for Ligand Docking, The Cambridge Crystallographic Data Center https://www.ccdc.cam.ac.uk/solutions/csd-discovery/components/gold/ (accessed on 3 June 2022)) operates with four scoring functions, two of which are empirical (ChemPLP and ChemScore), one is knowledge-based (ASP), and one is force-field scoring function (GoldScore) [26].
- ✓
- SeeSAR v. 4.3 (BioSolveIT, https://www.biosolveit.de/SeeSAR (accessed on 3 June 2022)) operates with two empirical scoring functions—HYDE [27,28] and FlexX [29].
Among the molecular modelling software packages with free access, AutoDock Vina was used (as Smina, Vina [30]).
- ✓
- AutoDock Vina v. 1.2.0. (The Scripps Research Institute, https://vina.scripps.edu (accessed on 3 June 2022)) implements a scoring function of a mixed type (knowledge-based and empirical) [30,31].
The above-mentioned scoring functions are briefly described in Table 1.
The rigid protein/flexible ligand approach was used in all molecular docking studies. No water molecules were left in the binding sites of the studied proteins. The default placement algorithm for every molecular docking package was used. Up to 30 poses were kept after docking.
During data processing, we relied on the general understanding that docking results are considered good if: (i) the docking scores of the studied bioactive compounds are in agreement with the experimental data on their binding affinities; and (ii) the docking poses are close to the experimentally observed of the co-crystalized ligand in the complex. The first one is usually estimated by correlating the docking scores with the binding affinities, such as, for example, the inhibitory constants expressed as pKi (−log Ki)—the higher the correlation coefficient, the better the docking scores approximate the binding affinities. The second one is estimated by the RMSD (root-mean-square deviation) values between the positions of the corresponding atoms of the ligand in the co-crystalized and the docked poses—the lower the RMSD, the better the correspondence is. These two metrics were used to estimate the performance of the scoring functions.
The results from the performed molecular docking studies were processed depending on the particular metric and were prepared as spreadsheets, in a format suitable for the subsequent application of ICrA.
All spreadsheets were constructed in an identical way: the compounds (protease inhibitors) were considered as objects in terms of ICrA, while the docking scores calculated by the scoring functions, as well as the experimental binding affinity data (pKi), were considered as criteria. An exemplary view of a spreadsheet serving as an input for ICrA is shown in Figure 5, reporting the results from the docking of the first 10 compounds (column compound, CPD_01 to CPD_10) in the active site of thrombin by the five MOE scoring functions (columns Affinity dG, Alpha HB, ASE, GBVI/WSA dG, and London dG) as the docking energies of the best poses, and the experimental inhibitory pKi values.
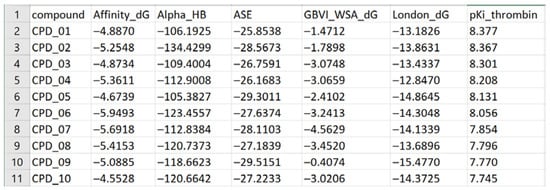
Figure 5.
An exemplary view of a spreadsheet used as ICrAData input.
3. Results and Discussion
3.1. Applied ICrA to Assess the Performance of the Scoring Functions in MOE
The docking results were assessed based on the following docking outputs:
- (i)
- Binding energies calculated by different scoring functions as an indicator of protein–ligand binding affinity (for all scoring functions, lower scores indicate more favorable poses; the unit is kcal/mol):
- −
- The value of the binding energy for the best out of 30 saved docking poses, for each of the tested compounds;
- −
- The average value of the binding energies of the best 5 and 10 poses (having in mind that the pose with the lowest energy is not always the bioactive one), for each of the tested compounds;
- −
- The average values of the binding energies of the 30 saved docking poses, for each of the tested compounds.
- (ii)
- RMSD between the atoms in the benzamidine substructure (nine heavy atoms) of the docked ligands and the matching atoms in the co-crystalized ligands (NAPAP in 1ETS and 4-TAPAP in 1PPH) in the crystallographic structures of the PDB complexes, as an indicator of the geometric proximity in the pose prediction.
In view of the best docking poses, the ICrA results did not outline any significant relations neither for the scoring energies of the different scoring functions nor for the experimental binding affinity data of both protein targets. Similar results were obtained when ICrA was applied on the average values of the binding energies of the best 5 and 10 poses. Figure 6 illustrates the ICrAData view for the average values of the binding energies of all 30 saved docking poses together with the experimental binding affinity data, showing the matrices for the degrees of agreement µ in the cases of thrombin (Figure 6a) and trypsin (Figure 6b). As it can be observed, in this case, ICrA does not outline any of the scoring functions to reliably predict the binding affinities for any of the two proteins. A positive consonance was only reported between the Affinity dG and GBVI/WSA dG scoring functions in the case of thrombin. This observation might be considered valuable, since the simulations employing GBVI/WSA dG scoring are significantly more time-consuming than those employing Affinity dG or any other scoring function. Another noteworthy observation is the negative consonance between the scoring function ASE, on the one hand, and the scoring functions Affinity dG and GBVI/WSA dG, on the other hand, again in the case of thrombin. This observation suggests that, with the increase in the number of considered poses, the scoring functions show a tendency to greater distinction. Thus, in the case of thrombin, the scoring functions do not produce equivalent results for the best 5 and 10 poses after docking, which are commonly taken into account in the virtual screening.
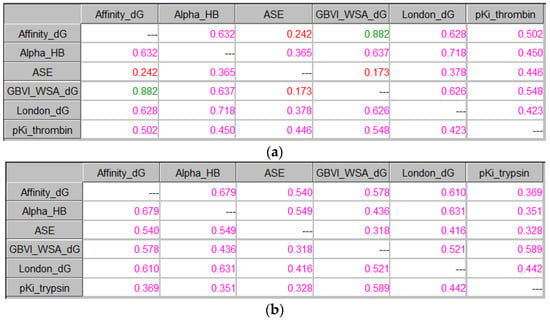
Figure 6.
ICrA implementation based on the averaged docking scores of the 30 saved poses. (a) Thrombin. (b) Trypsin.
Figure 7 presents the use of ICrA when the results from docking are examined based on RMSDs calculated between the benzamidine substructure of the corresponding ligand in the X-ray structure and in the docking poses: firstly, based on the average RMSD values of the 30 saved docking poses (Figure 7a,c), and later on, based on the scores of the docking poses with the lowest RMSD (Figure 7b,d).
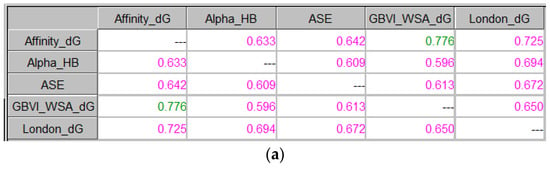
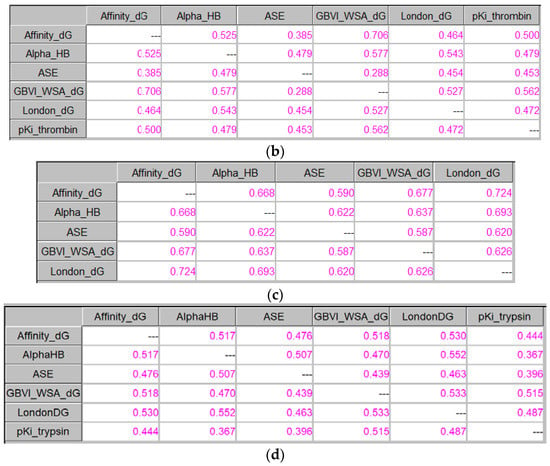
Figure 7.
ICrA implementation based on RMSDs. (a) Thrombin, based on the RMSD values averaged over the 30 saved poses. (b) Thrombin, based on the scores of the docking poses with the lowest RMSD. (c) Trypsin, based on the RMSD values averaged over the 30 saved poses. (d) Trypsin, based on the scores of the docking poses with the lowest RMSD.
As it can be observed from Figure 7a, a positive consonance between Affinity dG and GBVI/WSA dG is present. As mentioned above, the thresholds α and β are set according to the user’s choice; so, if one considers a lower value of the threshold α (0.7 or 0.65), a positive consonance will be identified between the following pairs of scoring functions: Affinity dG–London dG, Alpha HB–London dG, ASE–London dG, and GBVI/WSA dG–London dG (Figure 7a); Affinity dG–GBVI/WSA dG (Figure 7b); and Affinity dG–Alpha HB, Affinity dG–GBVI/WSA dG, Affinity dG–London dG, and Alpha HB–London dG (Figure 7c).
3.2. Applied ICrA to Assess the Performance of the Scoring Functions in GOLD
Due to the stochastic nature of the algorithm implemented in GOLD, up to five runs were performed for each scoring function and the average scores were calculated and used for further analysis. Considering this stochasticity of the genetic algorithms, the observed ICrA relations for the GOLD scoring functions could not be directly compared due to the random starting points, but they may outline some trends.
The results obtained with the GOLD scoring functions were assessed by ICrA based on the following docking outputs:
- (i).
- Binding energies calculated by different scoring functions as an indicator of protein–ligand binding affinity:
- −
- For the best docking poses for each of the tested compounds;
- −
- The average values of the binding energies of the best 5 and 10 poses;
- −
- The average values of the binding energies of the 30 saved docking poses.
- (ii).
- Three running modes concerning the GOLD algorithm’s speed:
- −
- Slow—the slowest, but the most accurate one;
- −
- Fast—the fastest, but the least accurate one;
- −
- The medium one.
Figure 8 presents the results from ICrA utilization for thrombin and trypsin, based on the binding energies calculated by the scoring function GoldScore in GOLD at the three running modes—slow, medium, and fast. The impact of the algorithm’s speed was explored for the best pose (with the lowest binding energy, top1), for the average values of the binding energy of the first 5 poses (top5), and for the average values of the binding energy of the first 10 poses (top10), for each compound in the dataset.
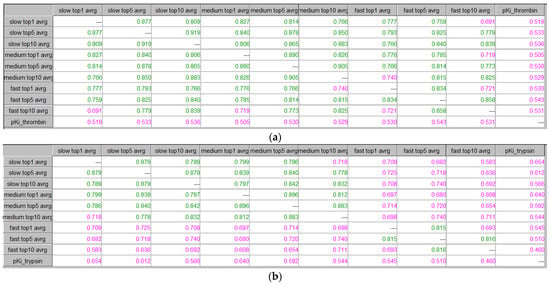
Figure 8.
ICrA implementation to assess the running modes regarding the GoldScore scoring function in GOLD. (a) Thrombin. (b) Trypsin.
In the case of thrombin, the analysis outlines that, the three running modes are in a positive consonance, revealing that there is a high degree of reliability between the fast, medium, and slow modes. In the case of trypsin, however, there is no consonance between the fast and the two other modes of algorithms’ performance. Based on the results obtained for trypsin, the medium mode might be considered as the most appropriate, since showing results closer to the most precise slow mode than to the fastest one for the particular dataset. Moreover, the medium mode represents a good compromise between execution time and accuracy.
The investigation of the three modes concerning the GOLD algorithm’s speed was extended to all available scoring functions in GOLD, namely ChemScore (CS), ASP, and ChemPLP (CPLP), only for the best docking score out of the 30 saved docking poses for each of the tested compounds. As a demonstration, Figure 9a represents the ICrA implementation for thrombin for all scoring functions in GOLD, in all three modes of GOLD algorithm’s speed. As it can be seen, almost no significant relations (except two pairs in GoldScore (GS) and one pair in ChemScore in positive consonance) might be outlined among the scoring functions themselves or among the different running modes concerning the algorithm’s speed in GOLD. Figure 9b represents the ICrA use for trypsin for all scoring functions in GOLD for the medium mode only. The results confirm that each scoring function brings unique and independent information. Again no significant relations in terms of ICrA might be outlined—neither among the scoring functions themselves nor between them and the experimental binding affinities.
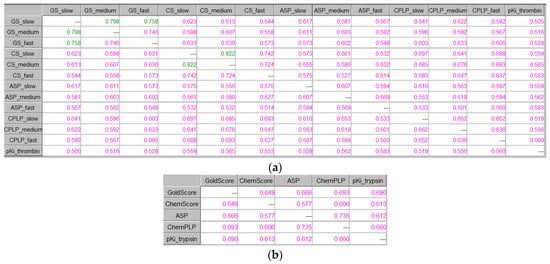
Figure 9.
ICrA implementation to assess the running modes regarding all scoring functions available in GOLD. (a) Thrombin. (b) Trypsin.
3.3. Applied ICrA to Assess the Performance of the Scoring Functions in SeeSAR
The binding energies of the best poses for each compound in the dataset were subjected to ICrA along with the experimental pKi values. The obtained results are shown in Figure 10a for thrombin, and in Figure 10b for trypsin.
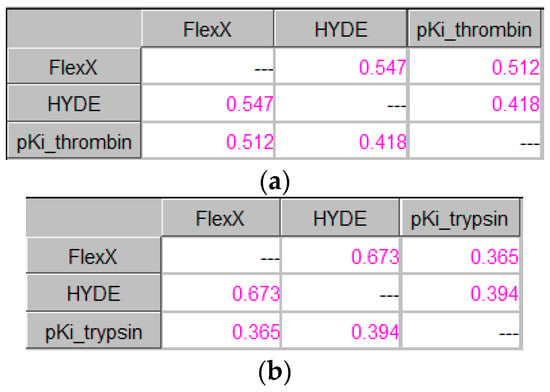
Figure 10.
ICrA implementation based on the binging energies of the best poses. (a) Thrombin. (b) Trypsin.
As seen from Figure 10, identical results were obtained for both targets, showing no significant relations among the scoring functions themselves or for the experimental pKi values, as already observed for most of the studied scoring functions.
3.4. Applied ICrA to Assess the Performance of the Scoring Function in AutoDock Vina
ICrA was applied to the following results: (1) binding energies of the best poses for each compound in the dataset (top_score); (2) RMSDs of the best poses (rmsd_of_top_score); (3) binding energies of the poses with the best RMSDs (score_of_top_rmsd); (4) the best RMSDs (top_rmsd); and (5) experimental pKi values. The results obtained after ICrA application are shown in Figure 11a for thrombin and in Figure 11b for trypsin.
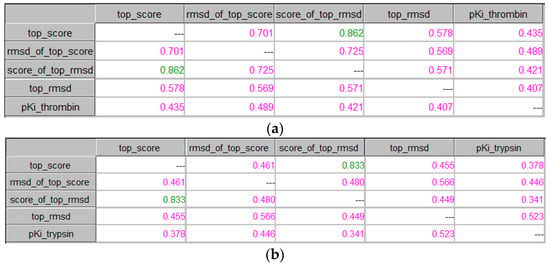
Figure 11.
ICrA implementation based on the binding energies and RMSDs. (a) Thrombin. (b) Trypsin.
As it can be observed from Figure 11, similar results were obtained for both targets, showing positive consonance between the binding energies of the best poses and the binding energies of the poses with the best RMSD. Although no significant relations were noticed between the applied scoring functions and the experimental pKi values for any of the proteins, it is worth noting that the values calculated for thrombin are, in most cases, slightly higher than those for trypsin. A further analysis of the results showed that the best docking score pose coincides with the best RMSD pose for 20 of 88 compounds in the case of thrombin and only for 6 of 88 compounds in the case of trypsin.
Considering the fact that the comparison between the scoring functions of different software packages is not straightforward due to the differences in the implemented docking protocols, we summarized the ICrA results for all scoring functions used in this study in relation to the experimental pKi data only, which is the constantly present validation criterion in all comparisons. Table 2 shows them for the top score poses of the ligands within the binding sites of the two studied proteins.

Table 2.
ICrA relations between investigated scoring functions and experimental pKi data.
Obviously, as reported above, no significant relations are observed between the docking scores and the experimental inhibitory effects and none of the scoring functions can be given any preference. In addition, the results illustrate the dependence of the ICrA relations on the studied protein. In the case of thrombin, the relations are closer to each other, covering an interval from 0.418 (HYDE) to 0.565 (ChemScore). In the case of trypsin, there is an almost two-fold difference between the highest (0.690 by GoldScore) and the lowest (0.347 by Vina) values. It is worth noting that GoldScore and ChemPLP produce results that approach the positive consonance threshold.
4. Conclusions
In this investigation, the capability of ICrA to assess the performance of 12 scoring functions available in MOE, GOLD, SeeSAR, and AutoDock Vina was explored by docking simulations on a set of 88 protease inhibitors in the binding sites of thrombin and trypsin. The performance of the scoring functions was evaluated based on the docking energies as approximations of the binding affinities and on the RMSDs as measures of the experimental binding pose proximity.
As expected, the ICrA application confirmed that the performance of the scoring functions for the same dataset of ligands depends on the studied protein used for docking.
The InterCriteria analysis also revealed that none of the studied scoring functions is a good predictor of the binding affinities of the compounds to the investigated proteins. The lack of a good correlation between the docking scores and the experimental binding affinity data is a question of debate. In terms of ICrA, no significant relations were recorded between the docking scores of any of the studied scoring functions and the experimental binding affinities.
In general, ICrA does not outline any significant relations between the investigated scoring functions applied either. Thus, in terms of ICrA, the scoring functions do not produce equivalent results. This fact, together with the observation about the lack of good correlations with the experimental data, suggest the necessity for a combined use of the scoring functions in consensus docking studies.
To the best of our knowledge, this is the first systemic investigation of ICrA as a tool to support decision making in the molecular docking studies of small drug-like molecules in the binding sites of different biomacromolecules. As with any analysis of such a kind, the results are limited by the data with which the analysis operates. In this investigation, the limitations are related to the extrapolation of the conclusions from the ICrA application to other structural information (different structural classes of ligands) and different protein families. Thus, the capability of ICrA will be further explored to assess the performance of scoring functions for a larger dataset of protein–ligand complexes broadly used as benchmark dataset in contemporary docking studies.
Author Contributions
Conceptualization, K.A., I.P. and T.P.; methodology, P.A., I.T., K.A., I.P. and T.P.; software development, V.A., P.V. and N.I.; validation, D.J., P.A., I.T., I.P. and T.P.; formal analysis, D.J., P.A., I.T., M.A., V.A., P.V., K.A., I.P. and T.P.; investigation, D.J., P.A., I.T., I.P. and T.P.; data curation, D.J., P.A., I.T. and T.P.; writing—original draft, P.A., I.T., I.P. and T.P.; writing—review and editing, D.J., P.A., I.T., M.A., V.A., P.V., N.I., K.A., I.P. and T.P.; visualization, P.A., V.A. and T.P.; supervision, K.A., I.P. and T.P.; project administration, T.P.; funding acquisition, K.A. and T.P. All authors have read and agreed to the published version of the manuscript.
Funding
This investigation is supported by National Science Fund of Bulgaria, grant number DN 17/06 “A New Approach, Based on an Intercriteria Data Analysis, to Support Decision Making in in silico Studies of Complex Biomolecular Systems”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Höltje, H.-D. (Ed.) Molecular Modeling: Basic Principles and Applications, 3rd ed.; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar]
- Cheng, T.; Li, X.; Li, Y.; Liu, Z.; Wang, R. Comparative Assessment of Scoring Functions on a Diverse Test Set. J. Chem. Inf. Model. 2009, 49, 1079–1093. [Google Scholar] [CrossRef]
- Li, Y.; Han, L.; Liu, Z.; Wang, R. Comparative Assessment of Scoring Functions on an Updated Benchmark: 2. Evaluation Methods and General Results. J. Chem. Inf. Model. 2014, 54, 1717–1736. [Google Scholar] [CrossRef] [PubMed]
- Su, M.; Yang, Q.; Du, Y.; Feng, G.; Liu, Z.; Li, Y.; Wang, R. Comparative Assessment of Scoring Functions: The CASF-2016 Update. J. Chem. Inf. Model. 2019, 59, 895–913. [Google Scholar] [CrossRef] [PubMed]
- Khamis, M.A.; Gomaa, W. Comparative Assessment of Machine-learning Scoring Functions on PDBbind 2013. Eng. Apll. Artif. Intell. 2015, 45, 136–151. [Google Scholar] [CrossRef]
- Xu, W.; Lucke, A.J.; Fairlie, D.P. Comparing Sixteen Scoring Functions for Predicting Biological Activities of Ligands for Protein Targets. J. Mol. Graph. Model. 2015, 57, 76–88. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Sun, H.; Yao, X.; Li, D.; Xu, L.; Li, Y.; Tiand, S.; Hou, T. Comprehensive Evaluation of Ten Docking Programs on a Diverse Set of Protein-ligand Complexes: The Prediction Accuracy of Sampling Power and Scoring Power. Phys. Chem. Chem. Phys. 2016, 18, 12964–12975. [Google Scholar] [CrossRef]
- Stanzione, F.; Giangreco, I.; Cole, J.C. Use of Molecular Docking Computational Tools in Drug Discovery. Prog. Med. Chem. 2021, 60, 273–343. [Google Scholar] [CrossRef]
- Atanassov, K.; Mavrov, D.; Atanassova, V. Intercriteria Decision Making: A New Approach for Multicriteria Decision Making, Based on Index Matrices and Intuitionistic Fuzzy Sets. In Issues in Intuitionistic Fuzzy Sets and Generalized Nets; Wydawnictwo WIT: Piwniczna-Zdrój, Poland, 2014; Volume 11, pp. 1–8. [Google Scholar]
- Atanassov, K. Generalized index matrices. C. R. Acad. Bulg. Sci. 1987, 40, 15–18. [Google Scholar]
- Atanassov, K. Index Matrices: Towards an Augmented Matrix Calculus; Studies in Computational Intelligence; Springer International Publishing: Cham, Switzerland, 2014; Volume 573. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic Fuzzy Logics; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Jekova, I.; Vassilev, P.; Stoyanov, T.; Pencheva, T. InterCriteria Analysis: Application for ECG Data Analysis. Mathematics 2021, 9, 854. [Google Scholar] [CrossRef]
- Ilkova, T.; Petrov, M. InterCriteria analysis for evaluation of the pollution of the Struma River in the Bulgarian section. Notes IFSs 2016, 22, 120–130. [Google Scholar]
- Roeva, O.; Fidanova, S. Comparison of Different Metaheuristic Algorithms Based on InterCriteria Analysis. J. Comput. Appl. Math. 2018, 340, 615–628. [Google Scholar] [CrossRef]
- Krawczak, M.; Bureva, V.; Sotirova, E.; Szmidt, E. Application of the intercriteria decision making method to universities ranking. Adv. Intell. Syst. Comput. 2016, 401, 365–372. [Google Scholar]
- Tsakovska, I.; Alov, P.; Ikonomov, N.; Atanassova, V.; Vassilev, P.; Roeva, O.; Jereva, D.; Atanassov, K.; Pajeva, I.; Pencheva, T. Intercriteria analysis implementation for exploration of the performance of various docking scoring functions. Stud. Comput. Intell. 2021, 902, 88–98. [Google Scholar]
- Atanassov, K.; Szmidt, E.; Kacprzyk, J. On intuitionistic fuzzy pairs. Notes Intuit. Fuzzy Sets 2013, 19, 1–13. [Google Scholar]
- Atanassov, K.; Atanassova, V.; Gluhchev, G. Intercriteria analysis: Ideas and problems. Notes Intuit. Fuzzy Sets 2015, 21, 81–88. [Google Scholar]
- Roeva, O.; Vassilev, P.; Ikonomov, N.; Angelova, M.; Su, J.; Pencheva, T. On Different Algorithms for InterCriteria Relations Calculation. In Intuitionistic Fuzziness and Other Intelligent Theories and Their Applications; Hadjiski, M., Atanassov, K., Eds.; Studies in Computational Intelligence; Springer: Berlin, Germany, 2019; Volume 757, pp. 143–160. [Google Scholar]
- Ikonomov, N.; Vassilev, P.; Roeva, O. ICrAData—Software for InterCriteria Analysis. Int. J. Bioautom. 2018, 22, 1–10. [Google Scholar] [CrossRef]
- Boehm, M.; Stürzebecher, J.; Klebe, G. Three-Dimensional Quantitative Structure-Activity Relationship Analyses Using Comparative Molecular Field Analysis and Comparative Molecular Similarity Indices Analysis to Elucidate Selectivity Differences of Inhibitors Binding to Trypsin, Thrombin, and Factor Xa. J. Med. Chem. 1999, 42, 458–477. [Google Scholar] [CrossRef]
- Licari, L.G.; Kovacic, J.P. Thrombin Physiology and Pathophysiology. J. Vet. Emerg. Crit. Care 2009, 19, 11–22. [Google Scholar] [CrossRef]
- Maloy, S.R.; Hughes, K.T. (Eds.) Brenner’s Encyclopedia of Genetics, 2nd ed.; Academic Press: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Kalinowsky, L.; Weber, J.; Balasupramaniam, S.; Baumann, K.; Proschak, E. A Diverse Benchmark Based on 3D Matched Molecular Pairs for Validating Scoring Functions. ACS Omega 2018, 3, 5704–5714. [Google Scholar] [CrossRef]
- Reulecke, I.; Lange, G.; Albrecht, J.; Klein, R.; Rarey, M. Towards an Integrated Description of Hydrogen Bonding and Dehydration: Decreasing False Positives in Virtual Screening with the HYDE Scoring Function. ChemMedChem 2008, 3, 885–897. [Google Scholar] [CrossRef] [PubMed]
- Schneider, N.; Lange, G.; Hindle, S.; Klein, R.; Rarey, M. A Consistent Description of HYdrogen Bond and DEhydration Energies in Protein–Ligand Complexes: Methods behind the HYDE Scoring Function. J. Comput. Aided Mol. Des. 2013, 27, 15–29. [Google Scholar] [CrossRef] [PubMed]
- Rarey, M.; Kramer, B.; Lengauer, T.; Klebe, G. A Fast Flexible Docking Method Using an Incremental Construction Algorithm. J. Mol. Biol. 1996, 261, 470–489. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koes, D.R.; Baumgartner, M.P.; Camacho, C.J. Lessons Learned in Empirical Scoring with Smina from the CSAR 2011 Benchmarking Exercise. J. Chem. Inf. Model. 2013, 53, 1893–1904. [Google Scholar] [CrossRef] [PubMed]
- Trott, O.; Olson, A.J. AutoDock Vina: Improving the Speed and Accuracy of Docking with a New Scoring Function, Efficient Optimization, and Multithreading. J. Comput. Chem. 2010, 31, 455–461. [Google Scholar] [CrossRef] [Green Version]
- Molecular Operating Environment (MOE); Version 2020.09; Chemical Computing Group ULC: Montreal, QC, Canada, 2022.
- Jones, G.; Willett, P.; Glen, R.C. Molecular Recognition of Receptor Sites Using a Genetic Algorithm with a Description of Desolvation. J. Mol. Biol. 1995, 245, 43–53. [Google Scholar] [CrossRef]
- Jones, G.; Willett, P.; Glen, R.C.; Leach, A.R.; Taylor, R. Development and Validation of a Genetic Algorithm for Flexible Docking 1 1Edited by F. E. Cohen. J. Mol. Biol. 1997, 267, 727–748. [Google Scholar] [CrossRef] [Green Version]
- Eldridge, M.D.; Murray, C.W.; Auton, T.R.; Paolini, G.V.; Mee, R.P. Empirical Scoring Functions: I. The Development of a Fast Empirical Scoring Function to Estimate the Binding Affinity of Ligands in Receptor Complexes. J. Comput. Aided Mol. Des. 1997, 11, 425–445. [Google Scholar] [CrossRef]
- Baxter, C.A.; Murray, C.W.; Clark, D.E.; Westhead, D.R.; Eldridge, M.D. Flexible Docking Using Tabu Search and an Empirical Estimate of Binding Affinity. Proteins 1998, 33, 367–382. [Google Scholar] [CrossRef]
- Mooij, W.T.M.; Verdonk, M.L. General and Targeted Statistical Potentials for Protein-Ligand Interactions. Proteins 2005, 61, 272–287. [Google Scholar] [CrossRef]
- Verdonk, M.L.; Berdini, V.; Hartshorn, M.J.; Mooij, W.T.M.; Murray, C.W.; Taylor, R.D.; Watson, P. Virtual Screening Using Protein−Ligand Docking: Avoiding Artificial Enrichment. J. Chem. Inf. Comput. Sci. 2004, 44, 793–806. [Google Scholar] [CrossRef] [PubMed]
- Boehm, H.-J. The Development of a Simple Empirical Scoring Function to Estimate the Binding Constant for a Protein-Ligand Complex of Known Three-Dimensional Structure. J. Comput. Aided Mol. Des. 1994, 8, 243–256. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).