Abstract
Attribute-based credentials (ABCs) provide an efficient way to transfer custody of personal and private data to the final user, while minimizing the risk of sensitive data revelation and thus granting anonymity. Nevertheless, this method cannot detect whether one attribute has been used more than once without compromising anonymity when the emitter and consumer collude with one another. The protocol proposed in this article deals with this issue by using a modification of ZSS pairing-based short signatures over elliptic curves and Verheul’s self-blinded credentials scheme. Each user can generate an identifier (pseudonym) that is unique and verifiable by everyone in a given scope, without compromising anonymity. However, the identifier cannot be reused in the same scope, since such reuse would be detected.
Keywords:
attribute-based credentials; pseudonyms; privacy-preserving credentials; self-blinded scheme; security proofs; user-centered system MSC:
94A62
1. Introduction
The ongoing digitalization of our daily lives pushes users towards the creation of multiple online identities, both for informal interactions, such as social networks and entertainment, and more formal ones, such as digital banking or digital citizenship. Citizens have to be identified and such identification can be performed using a credential, i.e., a passport, an identity card, or a driving licence. The personal information these legal documents provide is usually more than what is needed. Institutions holding citizens’ data therefore have access to personal data that they do not need for their intended purposes. Furthermore, most of this information is often repeated and scattered all over the Internet, beyond the user’s control, and, even worse, with little to no guarantee regarding its access and safeguarding.
Identity providers (IDP) were developed to prevent the spread of such personal information, acting as a trusted third party (TTP). They centralize and verify the identities and give out credentials. Nevertheless, TTPs may have issues with privacy and security, and may also exhibit the single-point-of-failure problem [1]. To overcome these issues, researchers have developed solutions that involve the use of blockchain technologies, which shift the control of digital activities over to users [2,3]. Blockchains rely on cryptographic algorithms to provide properties such as tampering resistance, pseudo-anonymity, fault-tolerance, auditability, and resilience. However, blockchains have to deal with several inconveniences related to privacy, confidentiality, and efficiency [4].
The main contribution of this paper is a credential protocol to protect personal attributes efficiently. The protocol, based on a proposal by Singh et al. [4], is user-centered and provides privacy-preserving features. The main characteristic of the protocol is the capacity to link different uses of the same attribute in a given scope when it is performed by the same user, so anonymous identities can only be used once within a given scope. More precisely, the protocol provides:
- Unlinkability between scopes, i.e., the same user with the same credential cannot be linked between scopes.
- Reusability detection within the same scope, i.e., it prevents misbehavior by the user, who, thanks to their anonymity, could try to authenticate more than once.
One of the most interesting and obvious applications of the protocol proposed in this article could be in an e-voting system to ensure the ”one voter one vote”concept.
The rest of the paper is organized as follows. Section 2 introduces the state of the art on attribute-based credentials [5,6]. Section 3 provides the cryptographic background needed to ensure the security and feasibility of the protocol presented in Section 4. Section 5 evaluates how secure the protocol is, and finally, Section 6 deals with conclusions and future lines of research.
2. State of the Art
Anonymous credentials [5,6] are designed to assert an identity and, at the same time, maintain privacy. Idemix [7] and U-Prove [8] are two well-known privacy-oriented attribute-based credentials schemes. In [4], the authors exposed the shortcomings of these schemes in regard to their anonymity, untraceability, and unlinkability. Furthermore, the authors proposed a protocol that enables efficient and user-centered features using the pairing-based short signature of modified-ZSS (Zhang, Safavi-Naini and Susilo) scheme [9] and the self-blinding scheme developed by Verheul [10]. In a more recent paper [11], Teodor Dahl Knutsen at al. demonstrated the practicality of implementing two protocols and extended them with hidden public metadata.
An anonymous credential system usually involves the following roles: issuers, recipients, provers, and verifiers. The credential owner, or recipient, acts as the prover when presenting the credential to a verifier. To achieve this purpose, the credential consists of cryptographic information that allows the owner of the credential to create a proof, as well as the set of values of attributes to be proven.
The Idemix protocol, based on the Camenisch–Lysyanskaya (CL) signature scheme, uses this scheme to issue credentials [12]. The distinguishing feature of a CL signature is that it allows a user to prove the possession of a signature without revealing the original message, or even the signature itself, using zero-knowledge proofs (ZKP). The protocol uses XML and XSD to specify objects and build messages. It works using the RSA crypto-system that implies the use of 2048 or 4096 key lengths.
The downside of the Idemix protocol is the use of RSA cryptography, which uses long keys and requires resources to compute exponentiation. At the same time, the use of XML and XSD to codify messages adds an important overhead in both the setup and message exchange. Finally, the setup of the system can be difficult [13] to accomplish.
U-Prove is another anonymous credential system. It can be defined for a group in which it is unfeasible to compute a discrete logarithm. Proof-of-possession of the private key is the foundation of U-Prove. Every U-Prove token has the unique private key that signs it. It is a container of attributes of any kind, and this container is signed. The prover, using an issuance protocol, obtains the issuer parameters needed to build a token and convince a verifier using the presentation protocol. The prover then signs the issuer parameters to create a presentation proof.
In the case of U-Prove, the downside is that, even if it is more efficient than other alternatives, it does not provide unlinkability. In addition, the security of the protocol has not been fully proven [8].
In the protocol based on pairing-based short signatures and a self-blinding scheme introduced in [4], the authors provided proof of inefficiency and security in both Idemix and U-Prove. In the proposed protocol, to enforce unlinkability, the architecture splits the issuer into two actors: (1) the identity validator, who verifies the identity of the recipient and signs the commitment of values to allow the identification of the recipient in a blockchain; and (2) the Certificate provider, who provides a credential to the recipient for each service. This is accomplished after having verified the signature of an identity validator on the recipient’s anonymized attributes and proof of these anonymized attributes.
This protocol is based on: (1) pairings, (2) short signatures, (3) commitments, (4) zero-knowledge proofs, and (5) elliptic-curve cryptography. An additional privacy feature to protect the recipient’s activities on the blockchain is implemented using a self-blinding scheme [10].
This protocol is more efficient than others, but it is not suitable in applications where user actions need to be restricted to a single authentication, since the unlinkability property it offers does not detect whether someone has been authenticated more than once.
In order to obtain proof of authorization of an action or resource, many researchers propose the use of anonymous tokens. Davidson et al. [14] introduced a concept of an anonymous token named Privacy Pass [15,16,17,18] in order to avoid the use of CAPTCHAS for human proofs in the Tor network.
On the other hand, Moe, Silde and Strand [19] reimplemented the Privacy Pass for use in the COVID-19 digital contact tracing app Smittestopp [20]. The same Silde and Strand [21] extended their work with the construction of a new system of anonymous tokens with both private and public metadata.
Independently, Tyagi et al. [22] presented the same construction, along with a complete security proof.
Finally, Teodor Dahl Knutsen et al. [11] demonstrated the practicality of implementing two protocols and extending them with hidden public metadata.
These protocols, primarily focused on the pairing-based instantiation, are more generally known as verifiable (partially) oblivious pseudo-random functions. Pseudo-random functions (PRF) produce an output that will seem random unless one knows the secret key material.
Oblivious PRFs [23,24] are protocols that can compute a PRF without any of the parties learning the other party’s secret input, and with one of the parties learning the output of the function. In addition, verifiable oblivious PRFs (VOPRF) [24] guarantee that a correct input has been used. The output from the VOPRF is used as the anonymous token since the user’s private input is unknown to the issuer. The protocols use two mechanisms for creating this verifiability. The first set of protocols uses non-interactive zero-knowledge proofs to enable an issuer to prove that the correct private key was used to generate the function output. However, this proof cannot be updated by the receiver, so the resulting token can only be verified by a party holding the private key. Considering this disadvantage, Silde and Strand suggested a second set of protocols, named VOPRF instantiation, which allows verification without using zero-knowledge proofs, but with bilinear pairings instead.
Other anonymous authentication protocols have been developed in order to guarantee security in communications. In Internet of Things (IoT) systems, Alzahrani et al. [25] proposed an anonymous protocol with untraceability, resilience to physical device capture attacks, node impersonation, desynchronisation, and forward secrecy. Chien-Ming et al. [26] enhanced the previous protocol with the prevention of privileged insider attacks and stolen verification attacks. Nevertheless, none of these systems offers the traceability needed to implement e-voting systems.
In the field of vehicular ad hoc networks (VANETs), Ahmed et al. [27] presented a protocol that ensures message verification and integrity, resistance to unauthorized access, he preservation of privacy with pseudonyms, resistance to replay attacks, and traceability. Nonetheless, by only allowing traceability by a trusted authority, pseudonyms could be linked to real identities. This is inadmissible in a real election process. On the other hand, Waheeb et al. [28] developed a protocol with authentication, integrity, and non-repudiation, with conditional privacy, which was efficient and robust. However, conditional privacy is again an issue with this system.
In healthcare applications, Jangseok et al. [29] introduced a protocol with forgery attack prevention, perfect forward secrecy, patient anonymity, and insider or privileged insider attack prevention. The issue in this case is the complexity of the three-way login and authentication processes, which overloads communications and is not suitable for high-load systems such as national elections.
In the drone communications field, Tsuyang et al. [30] detailed a protocol with mutual authentication, replay attack prevention, physical device capture, and user anonymity and untraceability. Again, untraceability is the main issue with this protocol regarding its potential use in e-voting systems.
In public cloud servers, Naveed et al. [31] charted a protocol that provides user anonymity, untraceability, perfect forward secrecy, and resistance to replay attacks. Again, non-traceability is the problem, as one-voter-one-vote cannot be assured.
In the study of smart cities [32] and RFID [33], similar issues to the ones presented above can also be found.
3. Preliminaries
The protocol presented in this article uses pairings, short signatures, and zero-knowledge proofs over elliptic curves (EC). In this section, an overview of the primitives and the cryptographic problems upon which the security relies are provided.
Throughout this section, we consider a cyclic group of prime order q with a generator P, and a cyclic multiplicative group of the same order. We also denote by a cryptographic hash function.
3.1. Bilinear Pairings
As stated in [9], a bilinear pairing is defined by , , and is a map with the following properties:
- Bilineality: for all ,
- Non-degeneracy: There exists such that , that is, mapping does not send all pairs in to identity in
- Computability: Computing for all can be achieved with an efficient algorithm.
We also need e to be an admissible bilinear map, that is, must generate to ensure that if P is a generator of , then is a generator of .
3.2. Cryptographic Problems in Additive Groups
The following cryptographic computational problems in the additive group are considered (against an adversary ):
- Problem 1: Discrete logarithm problem (DLP): it is hard for , given , to find such that .
- Problem 2: Computational Diffie–Hellman Problem (CDHP): it is hard for , given with to compute .
- Problem 3: decisional Diffie–Hellman problem (DDHP): it is hard for , given with to decide whether mod q israndomly chosen from .
- Problem 4: Inverse computational Diffie–Hellman problem (Inv-CDHP): For and given , it is hard to compute .
- Problem 5: The bilinear Diffie–Hellman problem (BDHP) in : givenfor some , it is hard for to compute such that .
3.3. A Short Signature Scheme from Pairings
Nowadays, the most efficient short signature scheme in the current literature is the well-known short signature scheme ZSS [9].
- Parameter generation: {, , e, q, P, H} will be the system parameters.
- Key generation: the key generation is performed by randomly selecting and computing , where will be the public key and x will be the secret key.
- Signature: the signature will betaking the secret key x and a message m.
- Verification: we will verify the signature, taking the public key , a message m, and a signature S and computing
3.4. Non-Interactive Zero-Knowledge Proofs
Using zero-knowledge proofs, a prover is able to convince a verifier that a statement is true without revealing any additional information other than that the statement is true [34]. Schnorr proofs of knowledge are normally interactive. To overcome this issue, the Fiat–Shamir transformation that converts a traditional ZPK into a non-interactive one (NI-Schnorr ZKP) is used. The protocol has to satisfy two properties: (1) completeness—if the protocol is run by an honest prover and an honest verifier, the verifier always accepts the proof; and (2) soundness—an honest verifier accepts the proof of a dishonest prover for a false statement with a probability not greater than a certain bound (e.g., 1/2).
The prover knows the secret v, so the necessary steps are the following:
- chooses a random and calculatesand sends the tuple to ; the proof is the tuple .
- computes and verifies
In [4], the authors present the use of this technique to prove correctness on committed data over the blockchain, in this case applied to elliptic curves.
4. The Proposed Protocol
4.1. Overview
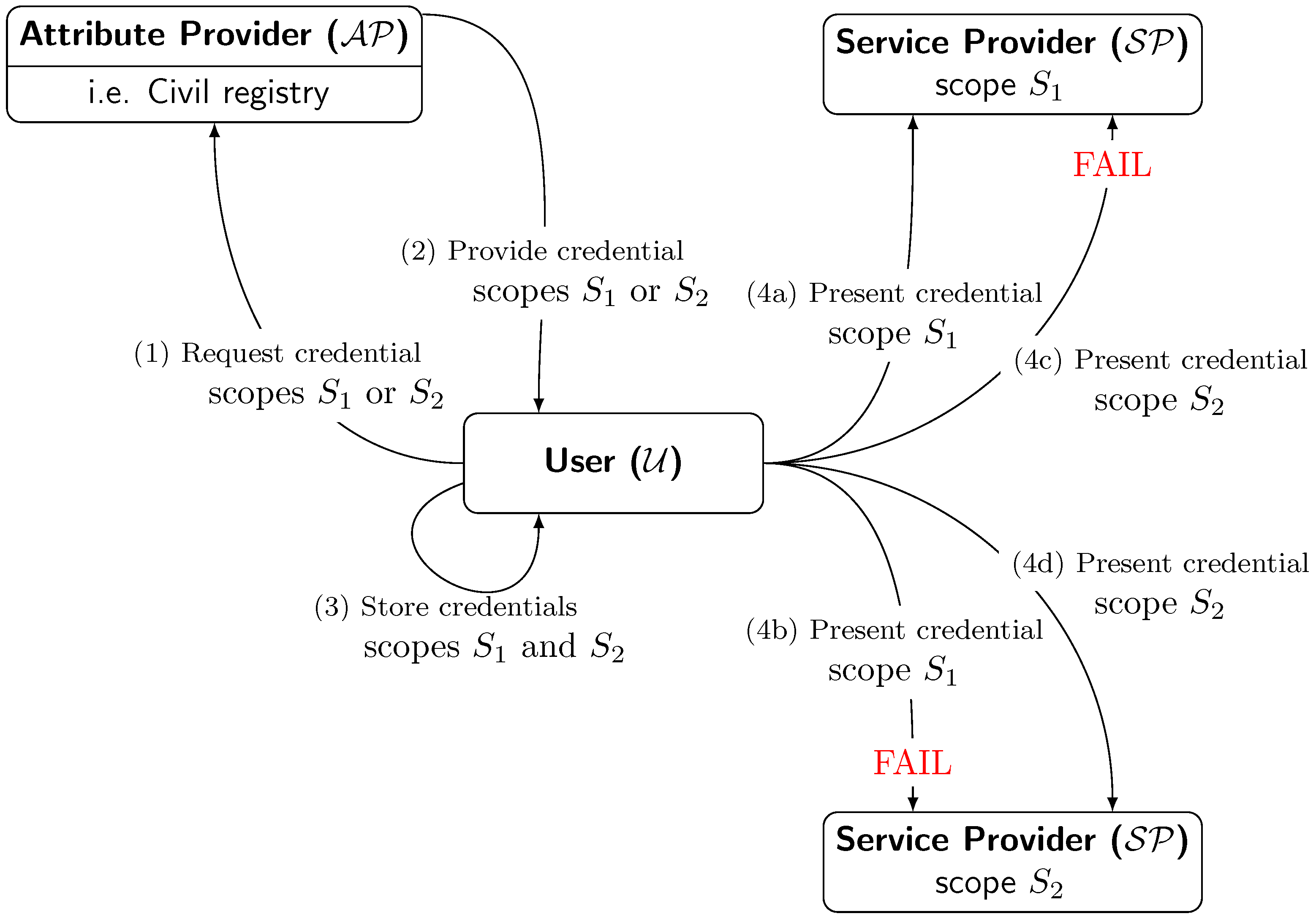
The proposed protocol presented in this section aims to provide credentials to users in a given scope and ensure that they can use this credential only in the given scope in a linkable manner. This means that anybody can link two credentials and detect their reuse, but no one can link the credentials with the identity owner of said credential. We define scope as an arbitrary string acting as an identifier of the scope. Figure 1 shows a high-level diagram of the proposed scenario and the information exchange.
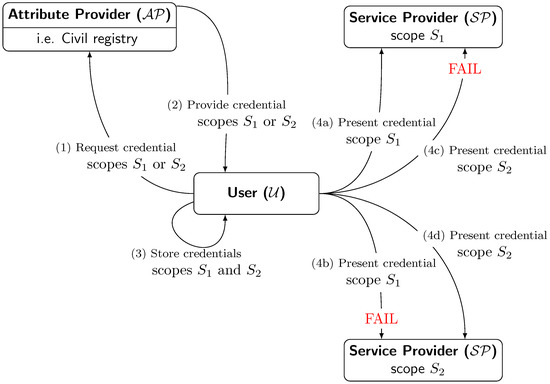
Figure 1.
Overview of the information exchange between roles. (1) begins the protocol by requesting for a credential for a given scope S. In this case, this is carried out two times, one for scope and one for scope . (2) After user identity verification, provides the user with a credential. This credential is only valid for within the request. (3) stores both credentials. (4) presents the credentials to . The figure illustrates four cases: (4a) presents the credential for to of scope , verification succeeds and accepts the credential (4b) presents the credential for to of scope , verification fails and rejects the credential. (4c) presents credential for to of scope , verification fails and rejects the credential. (4d) presents credential for to of scope , verification succeeds and accepts the credential.
Table 1 presents a guide to the specific notation used.

Table 1.
Notation guide.
In the following we present a case in which we use and follow this protocol:
- A service provider, known as , offers a service only if the user is of legal age.
- needs to know that the user is of legal age, and nothing else.
- needs to be able to identify through different interactions because the provided service should be accessed only once.
- An attribute provider , for instance, the civil registry, has all the information of all users and can provide anonymous credentials in the form of verifiable attributes. This anonymous credential is verifiable since it contains the signature of .
- To overcome linkability, blinds the credentials using Verheul’s algorithm. This allows the verification of a blinded attribute with a blinded signature. Once blinded, the linkability between the attribute and the real user is broken.
- could blind one attribute in different ways, with different final values, without losing the verifiable characteristic, which makes it impossible to link different uses of the same attribute. To overcome this, the use of a universal identifier is proposed. Computed for a given scope S, it includes the values of S and the attribute. will not be blinded; it will be anonymous and unique, and used together with the blinded attribute. It enables anonymous authentication with linkability.
- acts as a consumer of anonymous credentials and can identify the use of one credential with the associated with a given scope S.
Below is the full description of the protocol, including the involved actors, the definitions regarding information, and the information exchanges.
4.2. Actors
Three different actors take part in the protocol:
- The user, , obtains and uses an anonymous credential.
- The attribute provider, , provides with a verifiable attribute in a given scope S by signing the hash S and the public key provided by .
- The service provider, , grants access to a particular service to identified users with a verifiable attribute and their universal identifier , after verifying both.
4.3. Key Generation
Let be a cyclic group of prime order q and the elliptic point be a generator. Every actor chooses a random value as a private key, and computes the scalar product over the fixed point of the elliptic curve to obtain the corresponding public key . Thus, the scheme deals with three different key pairs: , , and . These keys correspond to , , and , respectively.
4.4. Issuance of Anonymous Credentials:
Before any protocol interaction, verifies the identity of by any means necessary, involving, for instance, physical documents or face-to-face verification. It then registers as an authorized member for a given scope S and provides the scope credential to .
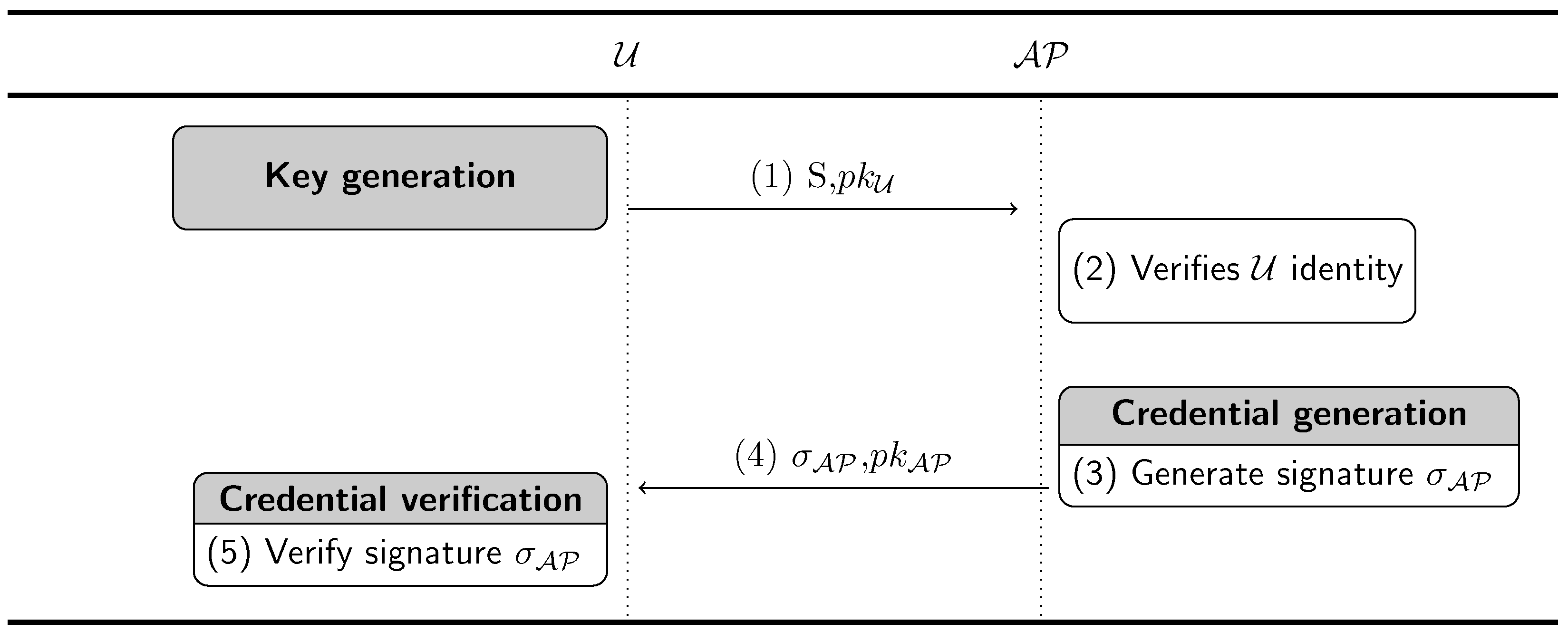
The messages exchanged between the two parties are as follows (see Figure 2):
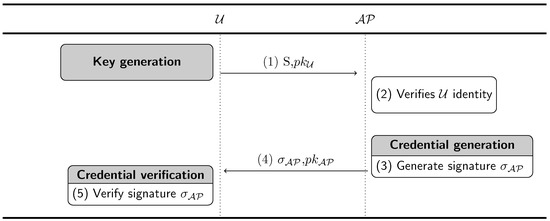
Figure 2.
Message exchange between and during the credential issuance phase.
- requests authorization for a given scope S.
- reliably checks the identity and possible attributes requested to belong to the scope S.
- generates the signature with the modified short signature scheme for bilinear pairing
- sends to .
- verifies the received signature:
After the successful verification of the signature, the credential is stored for future use by . is the credential that grants access to a service in the given scope S.
4.5. Presentation of Credentials:
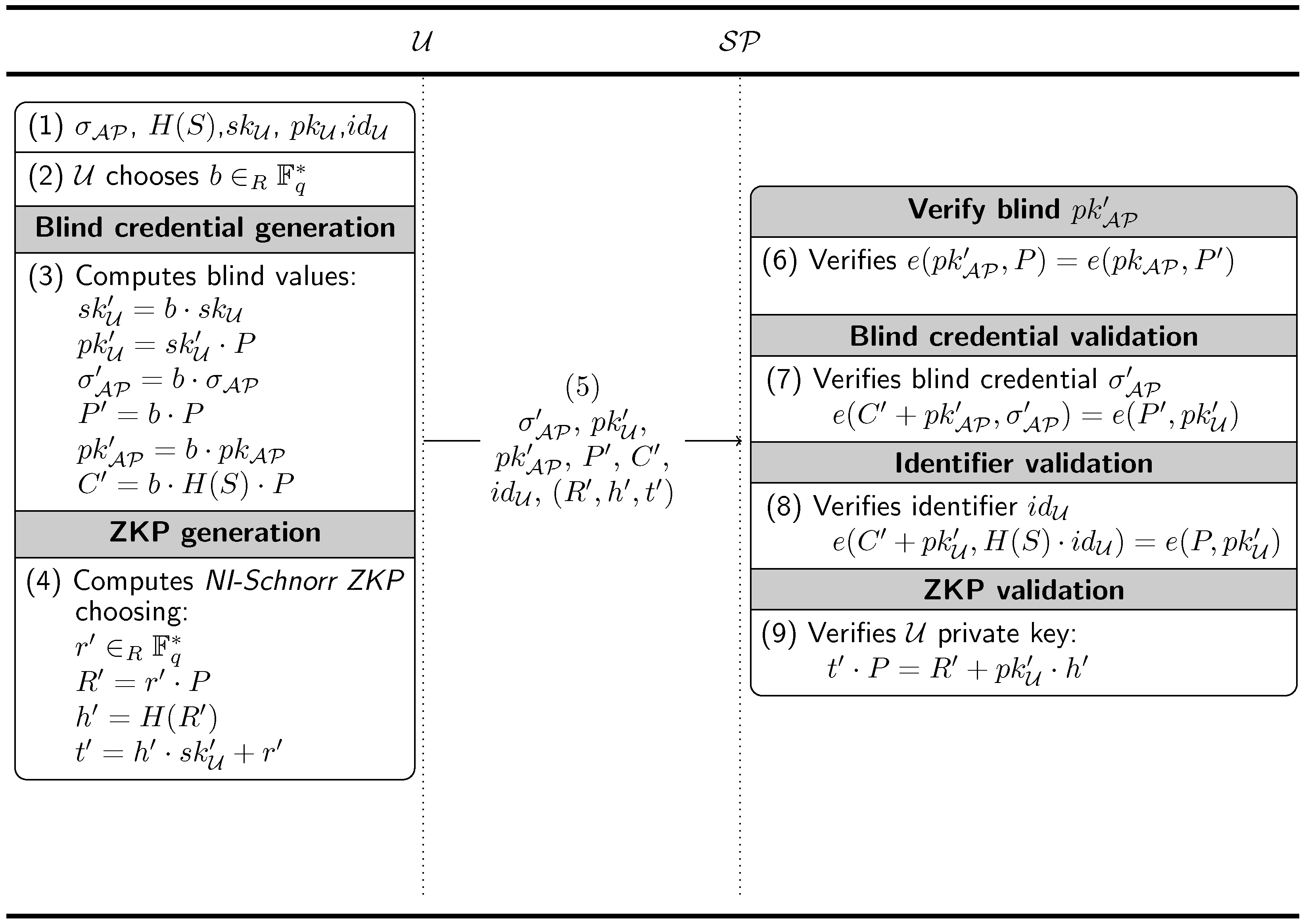
A privacy feature to protect the activities performed by based on a self-blinding scheme has been added into this protocol. A diagram of the exchanged messages and processes is shown in Figure 3.
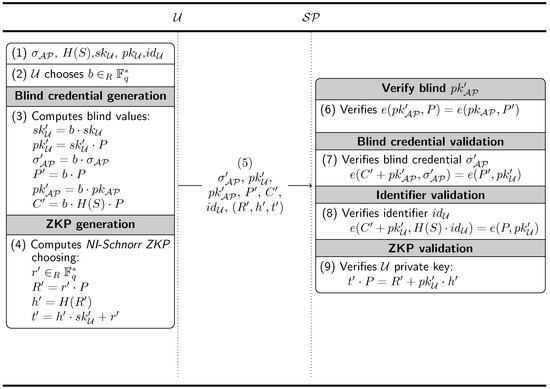
Figure 3.
Message exchange between and during the credential presentation phase.
We use a modified short signature and Verheul’s self-credentials with the aim of blinding the keys delivered by . Furthermore, will never be blinded, allowing the linking of different presentations.
, in order to compute their unique identifier, generates the signature using a signature scheme for bilinear pairing
These blind credentials are still verifiable and retain the signature of .
The steps needed to obtain these values are:
- has , , , , and .
- chooses as a blind factor.
- computes:
- also computes a NI-Schnorr ZKP, choosing and finds:
- sends the anonymous credential , , , , . also sends the universal identifier , and the NI-Schnorr ZKP proof-of-possession of the private key (), to allow the verification of the credentials and the universal identifier.
- needs to verify that is really after being blinded. To accomplish this, can test the following equality:
- If is correct, can verify the following:
- can also verify the universal identifier following this process:
- Finally, can also verify that has the correct private key:
5. Security Analysis
A security analysis of the proposed protocol is provided in this section. First, we analyze its robustness when faced with a malicious user who tries to forge fake credentials. Then, the anonymous properties of the proposed scheme are verified.
Two main threats have been analyzed. The user fair-play caseand the possible collusion between and .
The assumptions that we made about the abilities of are summarized below:
- can forge fake credentials.
- can blind credentials many times with different results to use credentials more than once.
In both cases, we demonstrate that this malicious behaviour will be detected.
The assumptions that we made about the abilities of and are summarized below:
- knows the real identity of .
- and collude and collect all messages exchanged with .
We demonstrate that in any case, cannot obtain ’s real identity, and cannot know when uses their credential.
5.1. Unforgeability
First, a malicious user cannot generate fake credentials that are not blindly signed by . This property is ensured by the use of the ZZS short signature, which has the property of unforgeability. More precisely, in the case in which generates a fake credential, such a credential would not be properly signed using the , and the fake ZSS signature would not pass the validation performed by in the credential presentation phase; verifying that
would fail. If this did not fail, this would mean that the short signature ZSS did not have the property of unforgeability, which would be false in this case.
Secondly, a malicious user cannot generate an that is not associated with an for a given scope , since such an identifier would not pass the validation performed by . More precisely, in the credential issuance phase, the computation of ,
provides a unique identifier for the given scope, , and a private key, . In the case in which generates a different identifier,
must verify and with the same ; however, if sends in the credential presentation phase, the verification performed by of will fail because . On the other hand, if sends , can detect the attack since .
Finally, a malicious user cannot generate a fake blinded public key associated with a fake in the scope , since this would not pass the validation performed by .
5.2. User Anonymity
The proposed protocol protects the identity of in such a way that it cannot be obtained by an adversary who has access to a number of messages and/or credentials generated by or processed by from the same user. In fact, the identity of is protected even if and collude.
In the credential issuance phase, does not know the value of generated by in the last step of the protocol since it is computed using the private key of .
In the credential presentation phase, uses a blinding factor b to protect the information sent to , so cannot obtain ’s identity based on the received blinded values. The use of short ZZS signatures allows for the proper security verification when using blinded data.
Regarding the value, it cannot be used to obtain ’s identity based on since, as discussed for the case of , is generated by using the private key of .
Note, as well, that collusion between and cannot compromise the anonymity of . As only receives blinded values, even if it colludes with it has no chance of obtaining the user’s identity, due to the assumptions of DLP, CDHP, and DDHP (problems 1, 2, and 3, respectively, in Section 3.2).
5.3. Identifier Unlinkability between Scopes
Given n different scopes, , an adversary who has knowledge of the corresponding identifiers for a particular user , denoted by , cannot link these identifiers nor obtain the identity of .
This property is ensured by the identifier definition:
since obtaining either or , even with the knowledge of , is not possible due to the DLP (problem 1 in Section 3.2).
5.4. Identifier Reusability Detection within the Same Scope
The proposed protocol is able to detect user identifier reuse within the same scope. This property is based on how is defined.
Note that all the terms in the expression
are fixed for a given scope ; thus, the resulting will be the same for a given and . only needs to store to detect its reuse. Moreover, as does not depend on the blinded value , will be the same for different blinded versions of C.
A malicious user cannot generate an that is not associated with an and , since this identifier will not pass the validation performed by . In the same way as in Section 5.1, generates a different identifier:
must verify and with the same ; however, if sends in the credential presentation phase, the verification performed by of will fail, because . On the other hand, if sends , can detect the attack since .
6. Conclusions and Future Line of Research
A new protocol that defines attribute-based pseudonyms has been proposed in this paper, which is based on a proposal by Singh et al. [4]. The concept of scopes has been added to provide reusability detection within a given scope, without the loss of anonymity, even in cases with collusion between participants. The concept of scope determines the cases wherein the pseudonym will be linkable, and we have defined a user identifier, , that represents the pseudonym for a given scope. This identifier will be unique in the given scope, and is linked to an anonymous credential.
We reinforce the fact that only knows the personal user data, preventing the spread of personal data over the network. gives the user a verifiable credential that is anonymous but grants rights in the formof a to obtain a service. It is important to highlight that the user is the one who stores those credentials and is responsible for their custody. By blinding the credentials before their presentation, the user knows that it is not possible to link any credentials to the real identity, even if and collude with one another. With the use of bilinear pairings over elliptic-curves that allow signature verification even when credentials are blinded, we establish a mechanism to validate anonymous credentials. In order to allow linkability in a given scope, the user must present the identifier, together with the associated blinded anonymous credential. The identifier is unique and is associated with an anonymous credential before blinding, and the can detect its reuse, thanks to its uniqueness, by storing the .
Future works could focus on the application of the proposed protocol in environments where both anonymity and uniqueness of the user are essential properties that need to be preserved. One of these scenarios could be a blockchain-based e-voting scheme. The vast majority of blockchain-based e-voting proposals do not deal with the problem of user identification, so we plan to include our protocol in an existing blockchain voting scheme to evaluate its use in a large-scale scenario such as a national voting deployment, in which the election process is stored in a blockchain and can be fully verifiable.
Author Contributions
Writing—original draft preparation: F.G.-G.; writing—review and editing: F.G.-G., J.H.-J. and A.D.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Berkowsky, J.A.; Hayajneh, T. Security issues with certificate authorities. In Proceedings of the 2017 IEEE 8th Annual Ubiquitous Computing, Electronics and Mobile Communication Conference (UEMCON), New York, NY, USA, 19–21 October 2017; pp. 449–455. [Google Scholar]
- Khan, M.A.; Salah, K. IoT security: Review, blockchain solutions, and open challenges. Future Gener. Comput. Syst. 2018, 82, 395–411. [Google Scholar] [CrossRef]
- Dib, O.; Huyart, C.; Toumi, K. A novel data exploitation framework based on blockchain. Pervasive Mob. Comput. 2020, 61, 101104. [Google Scholar] [CrossRef]
- Singh, K.; Dib, O.; Huyart, C.; Toumi, K. A novel credential protocol for protecting personal attributes in blockchain. Comput. Electr. Eng. 2020, 83, 106586. [Google Scholar] [CrossRef]
- Camenisch, J.; Lysyanskaya, A. An Efficient System for Non-transferable Anonymous Credentials with Optional Anonymity Revocation. In Advances in Cryptology—EUROCRYPT 2001; Pfitzmann, B., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 93–118. [Google Scholar]
- Bogatov, D.; Caro, A.D.; Elkhiyaoui, K.; Tackmann, B. Anonymous Transactions with Revocation and Auditing in Hyperledger Fabric. Cryptology ePrint Archive, Report 2019/1097. 2019. Available online: https://eprint.iacr.org/2019/1097 (accessed on 1 June 2022).
- IBM. Specification of the Identity Mixer Cryptographic Library. In Information Security; IBM: Armonk, NY, USA, 2010; pp. 1–52. [Google Scholar]
- Paquin, C.; Zaverucha, G. U-Prove Cryptographic Specification V1.1 (Revision 3). 2013. Available online: https://www.microsoft.com/en-us/research/publication/u-prove-cryptographic-specification-v1-1-revision-3/ (accessed on 1 June 2022).
- Zhang, F.; Safavi-Naini, R.; Susilo, W. An Efficient Signature Scheme from Bilinear Pairings and Its Applications. In Public Key Cryptography—PKC 2004; Bao, F., Deng, R., Zhou, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 277–290. [Google Scholar]
- Verheul, E.R. Self-Blindable Credential Certificates from the Weil Pairing. In Advances in Cryptology—ASIACRYPT 2001; Boyd, C., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 533–551. [Google Scholar]
- Knutsen, T.D.; Manum, T.; Strand, M. FFI-NOTAT Anonymous Tokens-Implementation and Development; FFI/NOTAT: Kjeller, Norway, 2022. [Google Scholar]
- Camenisch, J.; Lysyanskaya, A. A Signature Scheme with Efficient Protocols. In Security in Communication Networks; Cimato, S., Persiano, G., Galdi, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 268–289. [Google Scholar]
- Camenisch, J.; Herreweghen, E. Design and Implementation of the idemix Anonymous Credential System. In Proceedings of the ACM Conference on Computer and Communications Security, Washington, DC, USA, 27–30 October 2003. [Google Scholar] [CrossRef]
- Davidson, A.; Goldberg, I.; Sullivan, N.; Tankersley, G.; Valsorda, F. Privacy Pass: Bypassing Internet Challenges Anonymously. Proc. Priv. Enhancing Technol. 2018, 2018, 164–180. [Google Scholar] [CrossRef] [Green Version]
- Internet Engineering Task Force. Privacy Pass Datatracker. 2021. Available online: https://datatracker.ietf.org/wg/privacypass (accessed on 26 March 2022).
- Davidson, A.; Internet Engineering Task Force. Privacy Pass: The Protocol. Internet-Draft Draft-Davidson-pp-Protocol-01. 2020. Available online: https://datatracker.ietf.org/doc/html/draft-davidson-pp-protocol-01 (accessed on 26 March 2022).
- Celi, S.; Davidson, A.; Faz-Hernández, A.; Valdez, S.; Wood, C.A.; Internet Engineering Task Force. Privacy Pass Issuance Protocol. Internet-Draft draft-ietf-privacypass-protocol-03. 2022. Available online: https://datatracker.ietf.org/doc/html/draft-ietf-privacypass-protocol-03 (accessed on 26 March 2022).
- Davidson, A.; Iyengar, J.; Wood, C.A.; Internet Engineering Task Force. Privacy Pass Architectural Framework. Internet-Draft Draft-Ietf-Privacypass-Architecture-03. 2022. Available online: https://datatracker.ietf.org/doc/html/draft-ietf-privacypass-architecture-03 (accessed on 26 March 2022).
- Moe, H.W.; Silde, T.; Strand, M. Anonymous Tokens. 2021. Available online: https://github.com/HenrikWM/anonymous-tokens/ (accessed on 26 March 2022).
- Norwegian Institute of Public Health. The Smittestopp App—Helsenorge.no. Available online: https://www.helsenorge.no/en/smittestopp/ (accessed on 26 March 2022).
- Silde, T.; Strand, M. Anonymous Tokens with Public Metadata and Applications to Private Contact Tracing. Cryptology ePrint Archive, Report 2021/203. 2021. Available online: https://ia.cr/2021/203 (accessed on 26 March 2022).
- Tyagi, N.; Celi, S.; Ristenpart, T.; Sullivan, N.; Tessaro, S.; Wood, C.A. A Fast and Simple Partially Oblivious PRF, with Applications. Cryptology ePrint Archive, Report 2021/864. 2021. Available online: https://ia.cr/2021/864 (accessed on 26 March 2022).
- Casacuberta, S.; Hesse, J.; Lehmann, A. SoK: Oblivious Pseudorandom Functions. Cryptology ePrint Archive, Report 2022/302. 2022. Available online: https://ia.cr/2022/302 (accessed on 26 March 2022).
- Davidson, A.; Faz-Hernández, A.; Sullivan, N.; Wood, C.A.; Internet Engineering Task Force. Oblivious Pseudorandom Functions (OPRFs) using Prime-Order Groups. Internet-Draft draft-irtf-cfrg-voprf-09. 2022. Available online: https://datatracker.ietf.org/doc/html/draft-irtf-cfrg-voprf-09 (accessed on 26 March 2022).
- Alzahrani, B.A.; Mahmood, K. Provable Privacy Preserving Authentication Solution for Internet of Things Environment. IEEE Access 2021, 9, 82857–82865. [Google Scholar] [CrossRef]
- Chen, C.M.; Li, X.; Liu, S.; Wu, M.E.; Kumari, S. Enhanced Authentication Protocol for the Internet of Things Environment. Secur. Commun. Netw. 2022, 2022, 8543894. [Google Scholar] [CrossRef]
- Ahmed, W.; Di, W.; Mukathe, D. Privacy-preserving blockchain-based authentication and trust management in VANETs. IET Netw. 2022. [Google Scholar] [CrossRef]
- Goudarzi, S.; Soleymani, S.A.; Anisi, M.H.; Azgomi, M.A.; Movahedi, Z.; Kama, N.; Rusli, H.M.; Khan, M.K. A privacy-preserving authentication scheme based on Elliptic Curve Cryptography and using Quotient Filter in fog-enabled VANET. Ad Hoc Netw. 2022, 128, 102782. [Google Scholar] [CrossRef]
- Ryu, J.; Oh, J.; Kwon, D.; Son, S.; Lee, J.; Park, Y.; Park, Y. Secure ECC-Based Three-Factor Mutual Authentication Protocol for Telecare Medical Information System. IEEE Access 2022, 10, 11511–11526. [Google Scholar] [CrossRef]
- Wu, T.; Guo, X.; Chen, Y.; Kumari, S.; Chen, C. Amassing the Security: An Enhanced Authentication Protocol for Drone Communications over 5G Networks. Drones 2022, 6, 10. [Google Scholar] [CrossRef]
- Khan, N.; Zhang, J.; Jan, S.U. A Robust and Privacy-Preserving Anonymous User Authentication Scheme for Public Cloud Server. Secur. Commun. Netw. 2022, 2022, 1943426. [Google Scholar] [CrossRef]
- Xie, Q.; Li, K.; Tan, X.; Han, L.; Tang, W.; Hu, B. A secure and privacy-preserving authentication protocol for wireless sensor networks in smart city. Eurasip J. Wirel. Commun. Netw 2021, 119. [Google Scholar] [CrossRef]
- Wei, G.h.; Qin, Y.l.; Fu, W. An Improved Security Authentication Protocol for Lightweight RFID Based on ECC. J. Sens. 2022, 7516010. [Google Scholar] [CrossRef]
- Schnorr, C.P. Efficient signature generation by smart cards. J. Cryptol. 1991, 4, 161–174. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).