Abstract
In this paper, we present a numerical approach to solving singularly perturbed semilinear convection-diffusion problems. The nonlinear part of the problem is linearized via the quasilinearization technique. We then design and implement a fitted operator finite difference method to solve the sequence of linear singularly perturbed problems that emerges from the quasilinearization process. We carry out a rigorous analysis to attest to the convergence of the proposed procedure and notice that the method is first-order uniformly convergent. Some numerical evaluations are implemented on model examples to confirm the proposed theoretical results and to show the efficiency of the method.
Keywords:
singularly perturbed problems; semilinear differential equation; quasilinearization; boundary layer; fitted operator finite difference method; uniform convergence MSC:
65L10; 65L11; 65L12
1. Introduction
Differential problems in which a small parameter, often referred to as a perturbation parameter, multiply the highest derivatives are called singularly perturbed differential problems. These problems arise in different fields of study such as fluid dynamics, magnetohydrodynamics, aerodynamics, oceanography, quantum mechanics, plasma dynamics, chemical reactions, and liquid crystal modeling [1,2,3]. As an example, the heat and mass transport phenomena [4] are described by singularly perturbed differential equations in which the diffusion coefficient is regarded as a perturbation parameter.
Classical numerical methods have often failed to solve singularly perturbed problems. This is because one or more boundaries or interior layers may arise as the perturbation parameter approaches zero, thereby give undesirable results. To overcome this problem, constructed numerical methods such as finite difference methods, in the form of fitted mesh and fitted operator finite difference methods, finite element methods, and spline methods are adopted. These methods are used on layer-adapted meshes such as the Shishkin mesh, which is easy to construct, the Bakhvalov mesh, which gives superior accuracy, the Bakhvalov–Shishkin mesh, and the Vulanovic–Shishkin mesh (see [5,6,7,8,9,10]). In this paper, we consider the singularly perturbed semilinear convection-diffusion problems
subject to the following boundary conditions:
where is the perturbation parameter such that , A and B are given constants, and the functions and are sufficiently smooth in the intervals and , respectively, satisfying
where is a positive constant.
We obtain the reduced problem of Equation (1) by setting to zero, given as
Under these conditions, Equations (1) and (2) and the reduced problem in Equation (4) have a unique solution. This unique solution to Equations (1) and (2) exhibits a boundary layer at the origin of the interval as the perturbation parameter approaches zero (i.e., at ) (see [11,12,13,14]).
Not much work has been conducted on convection-diffusion semilinear singularly perturbed problems related to Equation (1). Cimen and Amiraliyev [15] constructed an exponential finite difference scheme, which flourishes by the method of integral identities to solve a singularly perturbed semilinear delay differential equation. They obtained a first-order uniform convergence in the discrete maximum norm. Niijima and Stynes [16,17] separately solved a singularly perturbed boundary value problem of the form in Equation (1). They adopted the use of finite difference schemes, and each obtained an almost first-order uniform accuracy in a discrete norm. Cakir and Arslan [18] used a fitted mesh finite difference scheme constructed on a Shishkin mesh to solve a singularly perturbed semilinear problem with integral boundary conditions. Their proposed scheme was found to be first-order uniformly convergent in the discrete maximum norm. Cakir and Amiraliyev [19] constructed a uniform finite difference scheme on a Shishkin-type mesh to solve a singularly perturbed semilinear convection-diffusion three-point boundary value problem. This method was shown to be first-order uniform convergent in the discrete maximum norm. Igor and Pack [20] solved a singularly perturbed semilinear convection-diffusion problem with discontinuous data using a difference scheme on local Green’s functions. The authors achieved a first-order uniform convergent scheme on arbitrary meshes.
Linß [21] constructed a fitted mesh finite difference scheme on a Shishkin mesh to solve singularly perturbed convection-diffusion with a boundary layer of attractive turning points. He achieved an almost first-order convergence. Shishkin and Shishkina [22] examined a Dirichlet problem on a vertical strip for a singularly perturbed semilinear convection-diffusion problem. The authors used an iterative monotone difference scheme to solve the problem and obtained a first-order uniform convergent results. They then improved the order of convergence to second-order uniform (and improved the accuracy) using a Richardson scheme. Linß and Vulanović [23] solved a semilinear convection-diffusion problem with attractive boundary turning points by constructing a fitted mesh finite difference method on a Shishkin mesh type. This method was established to be of first-order uniform convergence.
More recently, further works were completed on semilinear singularly perturbed scalar boundary value problems [24], scalar parabolic problems [25], or on systems of such problems [26,27,28,29]. Again, the methods adopted in these works are essentially the fitted finite difference methods based on Shishkin meshes.
Based on the literature, we observed that authors have mostly exploited the fitted mesh finite difference schemes as well as some other methods to solve singularly perturbed semilinear convection-diffusion problems. However, none of them, to the best of our knowledge, have proposed a numerical method in the framework of nonstandard finite difference (NSFD) methods to solve such problems.
In this paper, we propose an NSFD scheme to solve singularly perturbed semilinear convection-diffusion problems. This scheme falls under the category of fitted operator finite difference methods (FOFDMs), as they are known in previously published works such as [30,31,32]. We transform the semilinear problem into a sequence of linear equations via the quasilinearization technique. We then construct a fitted operator finite difference scheme on the transformed problem. We show that the proposed method is -uniform convergent to the first order. Unlike its fitted mesh counterpart, not only do the fitted operator finite difference methods provide a simpler platform for analysis owing to their use of a uniform mesh, but their error bounds are not adversely affected by a logarithmic factor, as pointed out in [33].
The rest of this paper is structured as follows. In Section 2, we transform the semilinear problem into a system of linear singularly perturbed problems by the quasilinearization technique. In Section 3, we analyze some properties of the system of linear problems. In Section 4, we construct a fitted operator finite difference scheme, which is analyzed in Section 5. In Section 6, we present numerical examples to demonstrate the -uniformity of the proposed method. Finally, we present the conclusion in Section 7.
2. Quasilinearization
We use the quasilinearization technique to transform the semilinear singularly perturbed convection-diffusion problem into a sequence of linear equations. We choose a reliable initial approximation for the function in , and by a Taylor series, we expand around the chosen initial approximation and obtain
Notice that Equation (6) is linear in . Therefore, we solve the sequence of linear Equations (6) and (7) in place of the semilinear problem in Equations (1) and (2) by the fitted operator finite difference method that will be introduced in Section 4.
For the solution of the semilinear boundary value problem, we require that
where is the solution of the semilinear problem. Numerically, we require that
where is a small tolerance chosen by us. Then, is the approximate solution of the semilinear problem.
3. Some Properties of the Linear Problem
We present some important properties for the solution of Equations (10) and (11) which will be useful in the subsequent section for the analysis of relevant numerical solutions. Without a loss of generality, we assume that f is a decreasing function of y:
Lemma 1.
Continuous minimum principle: Assume that is a sufficiently smooth function which satisfies and . Then, implies that .
Proof.
Let be a value such that , and assume that . Clearly, , and therefore and Moreover, there is
which is a contradiction. It follows that , and thus . □
Lemma 2.
Proof.
We construct two barrier functions defined by
Then, it can be said that
It follows that
Through Lemma 1, we obtain . □
Lemma 3.
The proof can be seen in [7].
4. Construction of the FOFDM
In this section, we design a fitted operator finite different scheme base on the Mickens rules [34,35]. We denote the approximations of at the grid point by the unknown . We partitioned the domain into N subintervals of a length h such that
We denote the set of these mesh points by . We then discretized Equations (10) and (11) as
with the boundary condition
where
and is the denominator function given by
The difference equations consist of equations for unknowns where and are given boundary conditions. We write Equations (14) and (15) in matrix form as
where U = and A is a tridiagonal matrix whose entries are of the form
where
and G is obtained as
Thus, the unknown is solved. The following lemma are relevant in the convergence analysis of this method:
Lemma 4.
Discrete minimum principle: Let be a discrete function defined on and satisfying . Then, implies
Proof.
Let k be a value such that , and assume . Clearly, 0, , , and . It follows that
Thus, which is a contradiction. Hence, . □
Lemma 5.
Uniform stability estimate: If is in any mesh function such that , then
Proof.
Put for Introduce two mesh functions defined by
Clearly, and :
Since , Lemma 4 implies that and this completes the proof. □
5. Convergence Analysis
In this section, we analyze the convergence property of the proposed method described in the previous section. The truncation error at the grid point is
By taking the Taylor series expansion of and and the truncated Taylor series expansion of we obtain
where . By applying the boundary of the solution and its derivative (see Lemma 3) along with Lemma 5.2 in [36], we obtain
From the relation , we have
By applying the uniform stability estimate (Lemma 5), we obtain
Theorem 1.
Let u(x) be the solution of Equations (10) and (11) and U(x) be the numerical approximation of Equations (14) and (15). If and are sufficiently smooth functions, then the truncation error is given by
where C is a constant independent of ε and h. This establishes that the numerical method developed is first-order uniformly convergent.
6. Numerical Results
In this section, we consider four test examples of singularly perturbed semilinear convection-diffusion problems to confirm our theoretical findings and to illustrate the performance of the proposed method in practice. We compute the maximum error and the rate of convergence and display the results in tables for different values of N and . Because the exact solution of Example 3 does not behave well for values close to 1, we chose and for and . In the case where the exact solution is known, the point-wise maximum error is given by
where U is the approximate solution and u is the exact solution. In cases where the exact solution is unknown, we compute the maximum point-wise error using the double mesh principle [37]:
where and are the numerical solutions computed on the meshes and , respectively.
The rates of convergence are computed using the formula
In the iteration process, the initial guess is , and the stopping criterion is
Example 1.
Consider the following singularly perturbed semilinear problem [38]:
The exact solution is
In this case, the exact value is known, the maximum error, and the rate of convergence are obtained with the formula described in Equations (30) and (32).
The quasilinearization process equations are
Example 2.
Consider the following singularly perturbed semilinear problem [39]:
In this case, the exact value is unknown, and mthe aximum error and rate of convergence are obtained with the formula describe in Equations (31) and (32). The quasilinearization process equations are
Example 3.
Consider the following singularly perturbed semilinear problem [40]:
The exact value is unknown, and the maximum error and rate of convergence are obtained with the formula described in Equations (31) and (32). The quasilinearization process equations are
Example 4.
Consider the following singularly perturbed semilinear problem [41]:
The exact value is unknown, and the maximum error and rate of convergence are also obtained with the formula described in Equations (31) and (32). The quasilinear process equations are
In each of the four examples, the solution has a boundary layer at the left side of the interval . Table 1, Table 2, Table 3 and Table 4 present the point-wise maximum error and the rate of convergence for different values of and N. The results shown in the tables reveal that the proposed method is of first-order uniform convergence, as projected by the theoretical analysis. Figure 1 provides the plots of the exact and numerical solutions of Example 1 for and , intuitively showing that this numerical solution is a “good” approximation of the exact solution. In Figure 2, for the fixed number of subintervals , we plot the numerical solution for Example 1 for different values of , showing that the impact of on the numerical solution disappears as approaches 0, thus confirming the -uniform aspect of the proposed method. These conclusions were arrived at when observing the tabulated results. When is small, the nodal maximum errors and the rate of convergence remain unaffected by the change in value of this parameter.

Table 1.
Results for Example 1: maximum errors and convergence rates for FOFDM.

Table 2.
Results for Example 2: maximum errors and convergence rate for FOFDM.

Table 3.
Results for Example 3: maximum errors and convergence rate for FOFDM.

Table 4.
Results for Example 4: maximum errors and convergence rates for FOFDM.
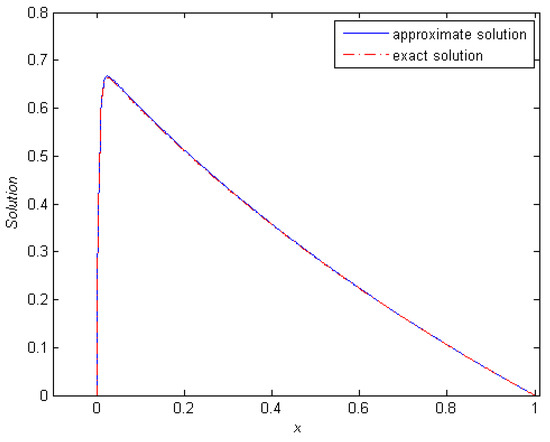
Figure 1.
Comparison of the exact and approximate solutions of Example 1 for and .
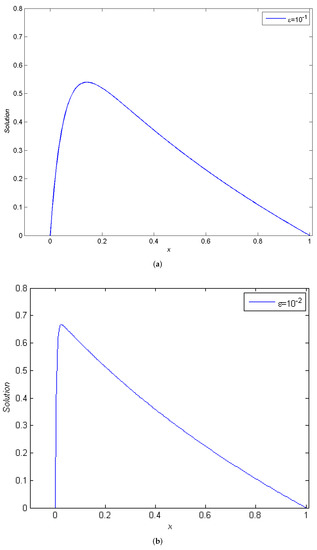
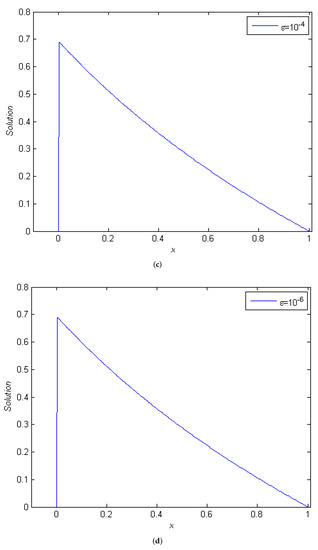
Figure 2.
Plots of the approximate solution of Example 1 for (a) , and (d) with .
7. Conclusions
We designed a fitted operator finite difference method for the numerical solution of a singularly perturbed semilinear convection-diffusion problem. The semilinear problem is transformed into a system of linear problems via the quasilinearization technique. The analysis and the numerical illustration conform to an agreement of a first-order -uniform convergence rate independent of the perturbation parameter. We present the maximum error and rate of convergence for different values of and N in tables. This work presents an alternative to numerical approaches for this class of problems. This is, to the best of our knowledge, the first time that singularly perturbed semilinear convection-diffusion two-point boundary value problems are solved using fitted operator finite difference methods.
The few previous works on singularly perturbed semilinear problems considered majorly fitted mesh methods based on Shishkin meshes. Although uniformly convergent, these methods suffer the drawback of presenting error bounds that depend on a logarithmic factor. This factor contributes to lowering both the accuracy and the rate of convergence. A further advantage of fitted operator finite difference methods is the simplicity of their analysis due to their use of uniform meshes.
Author Contributions
Conceptualization, J.B.M.; Methodology, J.B.M. and O.O.K.; Supervision, J.B.M.; Visualization, O.O.K.; Writing—original draft, O.O.K.; Writing—review & editing, J.B.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Carusotto, I.; Ciuti, C. Quantum fluids of light. Rev. Mod. Phys. 2013, 85, 299. [Google Scholar] [CrossRef] [Green Version]
- Malchow, A.K.; Azhand, A.; Knoll, P.; Engel, H.; Steinbock, O. From nonlinear reaction-diffusion processes to permanent microscale structures. Chaos. Interdiscip. J. Nonlinear Sci. 2019, 29, 53–129. [Google Scholar]
- Shyy, W.; Udaykumar, H.S.; Rao, M.M. Computational Fluid Dynamics with Moving Boundaries; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Nagy, A.; Saleh, M.; Omle, I.; Kareem, H.; Kovács, E. New Stable, Explicit, Shifted-Hopscotch Algorithms for the Heat Equation. Math. Comput. Appl. 2021, 26, 61. [Google Scholar] [CrossRef]
- Farrell, P.; Hegarty, A.; Miller, J.M.; O’Riordan, E.; Shishkin, G.I. Robust Computational Techniques for Boundary Layers; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Linß, T. Layer-adapted meshes for convection-diffusion problems. Comput. Methods Appl. Mech. Eng. 2003, 192, 1061–1105. [Google Scholar] [CrossRef] [Green Version]
- Miller, J.J.; O’riordan, E.; Shishkin, G.I. Fitted Numerical Methods for Singular Perturbation Problems: Error Estimates in the Maximum Norm for Linear Problems in One and Two Dimensions; World Scientific: Singapore, 1996. [Google Scholar]
- O’Malley, R.E. Historical Developments in Singular Perturbations; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Roos, H.G.; Stynes, M.; Tobiska, L.; Kellogg, R.B. Numerical methods for singularly perturbed differential equations. SIAM Rev. 1997, 39, 535. [Google Scholar]
- Roos, H.G.; Stynes, M.; Tobiska, L. Robust Numerical Methods for Singularly Perturbed Differential Equations: Convection-Diffusion-Reaction and Flow Problems; Springer Science & Business Media: Cham, Switzerland, 2008; p. 24. [Google Scholar]
- Gracia, J.L.; O’Riordan, E. A defect-correction parameter-uniform numerical method for ia singularly perturbed convection-diffusion problem in one dimension. Numer. Algorithms 2006, 41, 359–385. [Google Scholar] [CrossRef]
- Kopteva, N.; O’Riordan, E. Shishkin meshes in the numerical solution of singularly perturbed differential equations. Int. J. Numer. Anal. Modeling 2010, 7, 393–415. [Google Scholar]
- Mo, J.Q. Quasilinear singularly perturbed problem with boundary perturbation. J. Zhejiang Univ.-Sci. A 2004, 5, 1144–1147. [Google Scholar] [CrossRef]
- Vulanovic, R.; Teofanov, L. On the quasilinear boundary-layer problem and its numerical solution. J. Comput. Appl. Math. 2014, 268, 56–67. [Google Scholar] [CrossRef]
- Cimen, E.; Amiraliyev, G.M. A uniform convergent method for singularly perturbed nonlinear differential-difference equation. J. Inform. Math. Sci. 2017, 9, 191–199. [Google Scholar]
- Niijima, K. A uniformly convergent difference scheme for a semilinear singular perturbation problem. Numer. Math. 1984, 43, 175–198. [Google Scholar] [CrossRef]
- Stynes, M. An adaptive uniformly convergent numerical method for a semilinear singular perturbation problem. SIAM J. Numer. Anal. 1989, 26, 442–455. [Google Scholar] [CrossRef] [Green Version]
- Cakir, M.; Arslan, D. Finite difference method for nonlocal singularly perturbed problem. Int. J. Mod. Res. Eng. Technol. 2016, 1, 25–39. [Google Scholar]
- Cakir, M.; Amiraliyev, G.M. Numerical solution of a singularly perturbed three-point boundary value problem. Int. J. Comput. Math. 2007, 84, 1465–1481. [Google Scholar] [CrossRef]
- Boglaev, I.; Pack, S. A uniformly convergent method on arbitrary meshes for a semilinear convection-diffusion problem with discontinuous data. Int. J. Numer. Anal. Model 2008, 5, 24–39. [Google Scholar]
- Linß, T. Robustness of an upwind finite difference scheme for semilinear convection-diffusion problems with boundary turning points. J. Comput. Math. 2003, 21, 401–410. [Google Scholar]
- Shishkin, G.I.; Shishkina, L.P. A higher order richardson scheme for a singularly perturbed semilinear elliptic convection-diffusion equation. Comput. Math. Math. Phys. 2010, 50, 437–456. [Google Scholar] [CrossRef]
- Linss, T.; Vulanović, R. Uniform methods for semilinear problems with attractive boundary turning points. PAMM Proc. Appl. Math. Mech. 2002, 1, 518–519. [Google Scholar] [CrossRef]
- Yamac, K.; Erdogan, F. A Numerical scheme for semilinear singularly perturbed reaction-diffusion problems. Appl. Math. Nonlinear Sci. 2020, 5, 405–412. [Google Scholar] [CrossRef]
- Kabeto, M.J.; Duressa, G.F. Robust numerical method for singularly perturbed semilinear parabolic differential difference equations. Math. Comput. Simul. 2021, 188, 537–547. [Google Scholar] [CrossRef]
- Clavero, C.; Jorge, J.C. An efficient and uniformly convergent scheme for one-dimensional parabolic singularly perturbed semilinear systems of reaction-diffusion type. Numer. Algorithms 2020, 85, 1005–1027. [Google Scholar] [CrossRef]
- Kumar, S.; Rao, S.C.S. A robust domain decomposition algorithm for singularly perturbed semilinear systems. Int. J. Comput. Math. 2017, 94, 1108–1122. [Google Scholar] [CrossRef]
- Mariappan, M.; Tamilselvan, A. Higher order numerical method for a semilinear system of singularly perturbed differential equations. Math. Commun. 2021, 26, 41–52. [Google Scholar]
- Rao, S.C.S.; Chaturvedi, A.K. Analysis of an almost fourth-order parameter-uniformly convergent numerical method for singularly perturbed semilinear reaction-diffusion system with non-smooth source term. Appl. Math. Comput. 2022, 421, 126944. [Google Scholar]
- Munyakazi, J.B. A robust finite difference method for two-parameter parabolic convection-diffusion problems. Appl. Math. Inf. Sci. 2015, 9, 2877–2883. [Google Scholar]
- Munyakazi, J.B. A uniformly convergent nonstandard finite difference scheme for a system of convection-diffusion equations. Comput. Appl. Math. 2015, 34, 1153–1165. [Google Scholar] [CrossRef]
- Patidar, K.C. High order fitted operator numerical method for self-adjoint singular perturbation problems. Appl. Math. Comput. 2005, 171, 547–566. [Google Scholar] [CrossRef]
- Munyakazi, J.B.; Patidar, K.C. A fitted numerical method for singularly perturbed parabolic reaction-diffusion problems. Comput. Appl. Math. 2013, 32, 509–519. [Google Scholar] [CrossRef] [Green Version]
- Mickens, R.E. Nonstandard Finite Difference Models of Differential Equations; World Scientific: Singapore, 1994. [Google Scholar]
- Micken, R.E. Applications of Nonstandard Finite Difference Schemes; World Scientific: Singapore, 2000. [Google Scholar]
- Kadalbajoo, M.K.; Patidar, K.C. ε-uniformly convergent fitted mesh finite difference methods for general singular perturbation problems. Appl. Math. Comput. 2006, 179, 248–266. [Google Scholar] [CrossRef]
- Doolan, E.P.; Miller, J.J.; Schilders, W.H.A. Uniform Numerical Methods for Problems with Initial and Boundary Layers; Boole Press: Dublin, Ireland, 1980. [Google Scholar]
- Bender, C.M.; Orszag, S.A. Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Cash, J.R.; Wright, M.H. A deferred correction method for nonlinear two-point boundary value problems: Implementation and numerical evaluation. SIAM J. Sci. Stat. Comput. 1991, 12, 971–989. [Google Scholar] [CrossRef]
- Kadalbajoo, M.K.; Patidar, K.C. Numerical solution of singularly perturbed non-linear two point boundary value problems by spline in compression. Int. J. Comput. Math. 2002, 79, 271–288. [Google Scholar] [CrossRef]
- Tikhovskaya, S.V.; Zadorin, A.I. A two-grid method with Richardson extrapolation for a semilinear convection-diffusion problem. AIP Conf. Proc. 2015, 1684, 090007. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).