Revisiting the Polynomial-Time Equivalence of Computing the CRT-RSA Secret Key and Factoring

Abstract

The Rivest–Shamir–Adleman (RSA) cryptosystem is currently the most influential and commonly used algorithm in public-key cryptography. Whether the security of RSA is equivalent to the intractability of the integer factorization problem is an interesting issue in mathematics and cryptography. Coron and May solved the above most fundamental problem and proved the polynomial-time equivalence of computing the RSA secret key and factoring. They demonstrated that the RSA modulus $N=pq$ can be factored in polynomial time when given RSA key information $(N,e,d)$. The CRT-RSA variant is a fast technical implementation of RSA using the Chinese Remainder Theorem (CRT), which aims to speed up the decryption process. We focus on the polynomial-time equivalence of computing the CRT-RSA secret key and factoring in this paper. With the help of the latest partial key exposure attack on CRT-RSA, we demonstrate that there exists a polynomial-time algorithm outputting the factorization of $N=pq$ for $e{d}_p,e{d}_q<N^{3/2}$ when given the CRT-RSA key information $(N,e,d_p,d_q)$. We apply Coppersmith’s lattice-based method as a basic mathematical tool for finding the small root solutions of modular polynomial equations. Furthermore, we provide validation experiments to illustrate the correctness of the CRT-RSA modulus factorization algorithm, and show that computing the CRT-RSA secret key and factoring its modulus is polynomial-time equivalent by using concrete numerical examples.

1. Introduction

Rivest, Shamir, and Adleman proposed the first practical public-key cryptosystem named the RSA algorithm [1]. This algorithm just involves the elementary number-theoretic operations and is easy to compute and implement. Thus, RSA is widely studied in the field of information security and serves as an influential public-key cryptographic algorithm utilized by international standardization organizations. The RSA cryptosystem consists of a key generation algorithm, an encryption algorithm, and a decryption algorithm, which are described as follows.

Key Generation. 

Randomly select two prime numbers $p,q$ of the same bit-size and compute the modulus $N=pq$ along with its Euler’s totient function $\phi \left(N\right)=(p-1)(q-1)$. Randomly select $0<e<\phi \left(N\right)$ satisfying $gcd(e,\phi (N\left)\right)=1$ as the public key and compute $d\equiv e^{-1}mod\phi \left(N\right)$ as the private key.

Encryption. 

Alice transforms a plaintext message into $m\in {\mathbb{Z}}_N$ and computes $c\equiv m^{e}modN$ as the corresponding ciphertext.

Decryption. 

Bob receives a ciphertext c and calculates $c^{d}modN$. Bob extracts the transformed m and recovers the original plaintext message.

The correctness of the encryption and decryption algorithms is ensured by Euler’s Totient Theorem. Since both the public key e and the private key d are calculated in the exponent position, they are mentioned as the public and private exponents, respectively.

The hardness assumption of the RSA algorithm is the intractability of the integer factorization problem [2]. There is still no known polynomial-time algorithm that can factor sufficiently large integers using current classical computers. So there is no known effective attack against the RSA algorithm. However, on the other hand, RSA with small private exponents have been proven to be insecure when using Wiener’s continued fraction-based attack [3] and Coppersmith’s lattice-based attack [4]. A series of cryptanalytic researches on RSA and its variants were subsequently developed based on the lattice-based method, see the literature [5,6,7,8,9,10,11,12]. One of these works related to the hardness assumption of RSA is the polynomial-time equivalence proof of computing the RSA secret key and factoring [8,13]. The main contribution is applying the lattice-based method to prove that there exists an algorithm that can output the factorization of the modulus $N=pq$ in polynomial time when given $(N,e,d)$.

In fact, in the public key cryptography standard PKCS #1 [14], the CRT-RSA algorithm is a fast technical implementation of RSA. Here CRT-RSA refers to the RSA variant using the Chinese Remainder Theorem, which was proposed in [15]. The Chinese Remainder Theorem formulates the solution to simultaneous linear congruences and is specified as follows.

Theorem 1.

Let $m_1,m_2,\dots ,m_k$ be mutually coprime positive integers, and let $a_1,\dots ,a_k$ be integers. Then the following system of linear congruences

$$x\equiv a_{i}mod{m}_i$$

has a unique solution in the sense of modulo $M={\prod }_{i=1}^k{m}_i$. Let $M_i=M/m_i$ for $i=1,\dots ,k$, then the unique solution is

$$x=\sum _{i=1}^k{a}_i{M}_i(M_i^{-1}mod{m}_i)modM.$$

Since the RSA modulus $N=pq$ is the product of two prime numbers, we consider the case of $k=2$, i.e., the system of linear congruences is $x\equiv a_{1}modp$ and $x\equiv a_{2}modq$. In this case, the solution expression is more concise.

$$x=(a_1+((a_2-a_1)\times (p^{-1}modq)modq)\times p)modpq.$$

(1)

For a ciphertext $c=m^{e}modN$, the decryption algorithm works in the following strategy. One first does a partial decryption operation to recover $m_p=c^{d}modp$, $m_q=c^{d}modq$, and then use the Chinese Remainder Theorem to combine the above two parts to recover m. Since p and q are coprime, one applies the Formula (1) that yields

$$m=(m_p+((m_q-m_p)\times (p^{-1}modq)modq)\times p)modpq.$$

It can be further simplified as

$$m=(m_p+p((m_q-m_p)p^{-1}modq))modN.$$

(2)

Let $d_p\equiv e^{-1}mod(p-1)$ and $d_q\equiv e^{-1}mod(q-1)$, by Fermat’s Little Theorem we have

$$m_p=c^{d_p}\equiv c^{d}modp,m_q=c^{d_q}\equiv c^{d}modq.$$

Thus, $d_p,d_q$ are called CRT exponents and used as private exponents instead of d. The above Formula (2) is known as Garner’s algorithm [16]. Theoretically speaking, the decryption efficiency of the modular operations can be accelerated by a factor of four due to the reduction of the modulus from N to p or q. We summarize the CRT-RSA cryptosystem as follows.

Key Generation. 

Randomly select two prime numbers $p,q$ of the same bit-size and compute the modulus $N=pq$ and its Euler’s totient function $\phi \left(N\right)=(p-1)(q-1)$. Randomly select $0<e<\phi \left(N\right)$ satisfying $gcd(e,\phi (N\left)\right)=1$ as the public key and compute $d_p\equiv e^{-1}mod(p-1)$, $d_q\equiv e^{-1}mod(q-1)$ as the private key.

Encryption. 

Alice transforms a plaintext message into $m\in {\mathbb{Z}}_N$ and computes $c\equiv m^{e}modN$ as the corresponding ciphertext.

Decryption. 

Bob receives a ciphertext c and calculates $m_p=c^{d_p}modp,m_q=c^{d_q}modq$. Bob extracts $m=(m_p+p((m_q-m_p)p^{-1}modq))modN$ and recovers the original plaintext message.

Cryptanalysis of the CRT-RSA algorithm also attracts many researchers. The small CRT-exponent attack was originally presented as an open problem in Wiener’s attack [3]. The first cryptanalytic result was given in [6], which was effective for unbalanced primes p and q. Subsequently, Jochemsz and May [17] proposed the small CRT-exponent attack for balanced primes when the attack range is $d_p,d_q<N^{0.073}$. It was further improved to $d_p,d_q<N^{0.091}$ in [12] and shortly afterwards to $d_p,d_q<N^{0.122}$ [18]. In addition, the partial-key-exposure attacks such as [19,20,21,22,23] were studied due to the consideration of partial leakage of the CRT-RSA private key. From the implementation aspect, side-channel attacks such as [24,25,26,27,28] were proposed by exploiting the side-channel information leakage during the running process of the CRT-RSA algorithm.

Unlike the above attacks, we focus on the intrinsic security of CRT-RSA, i.e., its mathematical hardness assumption. From the theoretical research aspect, it is interesting to investigate the polynomial-time equivalence of computing the CRT-RSA secret key and factoring its modulus. Therefore, the research problem is stated as follows.

If the CRT-RSA key information $(N,e,d_p,d_q)$ is given as input, does there exist a polynomial-time algorithm that can output the factorization of N? Furthermore, is it possible that the CRT-exponents reach the natural constraint $d_p,d_q<N^{1/2}$ for $e\approx N$?

It is well known that $d_p$ and $d_q$ can be efficiently inferred from the factorization of $N=pq$ and the public exponent e. Hence, it suffices to show that the above problem is solvable to conclude that computing the CRT-RSA secret key and factoring the modulus are polynomial-time equivalent. Our main goal is to demonstrate and design a polynomial-time algorithm outputting the factorization of N for given CRT-RSA key information $(N,e,d_p,d_q)$. The specific goal is to further enlarge the attack range of CRT exponents $d_p,d_q$. We study how to use improved analysis techniques to carry out attacks on CRT-RSA from the perspective of its intrinsic security, namely the polynomial-time equivalence of computing the CRT-RSA secret key and factoring its modulus.

Inspired by the latest partial key exposure attack on CRT-RSA [23], we show an optimized polynomial-time equivalence of computing the CRT-RSA secret key and factoring. To be specific, we give a positive answer to the above research problem based on the partial key exposure attack on CRT-RSA. A polynomial-time factoring algorithm is presented for the given CRT-RSA key information $(N,e,d_p,d_q)$, which outputs the factorization result of $N=pq$. Technically speaking, the factoring algorithm involves an error term $gcd(N-1,2^{t}e)$ for $t:=\lceil {log}_2(max(d_p,d_q))\rceil$. This term may equal to $O\left(1\right)$, which is negligible compared to $e,d_p,d_q$ in the most favorable case, and asymptotically leads to the natural constraint $d_p,d_q<N^{1/2}$ for $e\approx N$. Moreover, we provide validation experiments in the form of numerical examples.

Our contribution mainly includes a new factoring algorithm and an improved attack result, which are summarized as follows.

• We study the security of CRT-RSA concerning its mathematical hardness assumption and propose an improved polynomial-time algorithm of factoring the CRT-RSA modulus.
• We verify the correctness and validity of the proposed CRT-RSA modulus factorization algorithm with numerical computer experiments and always successfully obtain the factorization results.
• We further discuss the advantages and disadvantages of our approach with several comparisons to properly assess the proposed factoring attack.

The rest of this paper is organized as follows. Section 2 introduces the lattice-based method, which is used as a basic mathematical tool to solve the research problem. Section 3 first reviews the latest partial key exposure attack on CRT-RSA and gives a refined theorem with more flexible parameters. Then we propose an improved polynomial-time equivalence of computing the CRT-RSA secret key and factoring. Both the CRT-RSA key computation algorithm and the CRT-RSA modulus factorization algorithm are presented. Finally, the validation experiments are provided in the form of numerical examples. We compare our results with previous studies and discuss the advantages and disadvantages of the proposed algorithms in Section 4. Section 5 concludes this paper.

2. Materials and Methods

We introduce the lattice-based method, which consists of the lattice reduction algorithm [29] and Coppersmith’s techniques [4]. Generally speaking, a lattice is a discrete additive subgroup in ${\mathbb{R}}^n$ that is defined as follows.

Definition 1.

Let $1\le \omega \le n$ and ${\overrightarrow{b}}_1,\dots ,{\overrightarrow{b}}_{\omega }\in {\mathbb{R}}^n$ be a set of linearly independent vectors. The lattice $\mathcal{L}$ generated by ${\overrightarrow{b}}_1,\dots ,{\overrightarrow{b}}_{\omega }$ is the set containing all linear combinations of the vectors with integer coefficients.

$$\mathcal{L}:=\mathbb{Z}{\overrightarrow{b}}_1+\cdots +\mathbb{Z}{\overrightarrow{b}}_{\omega }=\left\{\sum _{i=1}^{\omega }{z}_i{\overrightarrow{b}}_i:z_i\in \mathbb{Z}\right\}.$$

The vector set ${\overrightarrow{b}}_1,\dots ,{\overrightarrow{b}}_{\omega }$ is called a basis of the lattice $\mathcal{L}$. Further, n is the lattice dimension, ω is the lattice rank, and $\mathcal{L}$ is full-rank if $\omega =n$. For $i=1,\dots ,\omega$, each basis vector can be written as ${\overrightarrow{b}}_i=(b_{i1},\dots ,b_{in})$ in the form of row vectors, thus forming a basis matrix $\mathbf{B}={\left(b_{ij}\right)}_{\omega \times n}$.

Definition 2.

The fundamental parallelepiped of $\mathcal{L}$ is defined as $\mathcal{P}\left(\mathcal{L}\right):=\left\{\mathbf{B}\overrightarrow{x}:\overrightarrow{x}\in {[0,1)}^n\right\}$, where $\mathbf{B}$ is any basis matrix of the lattice $\mathcal{L}$. The lattice determinant is defined as the volume of the fundamental parallelepiped.

$$det\left(\mathcal{L}\right):=\sqrt{det\left(\mathbf{B}{\mathbf{B}}^{\mathsf{T}}\right)},$$

where ${\mathbf{B}}^{\mathsf{T}}$ is the transpose matrix of $\mathbf{B}$. Thus, it follows that the determinant of a full-rank lattice $\mathcal{L}$ is

$$det\left(\mathcal{L}\right)=\sqrt{det\left(\mathbf{B}{\mathbf{B}}^{\mathsf{T}}\right)}=\sqrt{det\left(\mathbf{B}\right)det\left({\mathbf{B}}^{\mathsf{T}}\right)}=|det\left(\mathbf{B}\right)|,$$

where $det\left(\mathbf{B}\right)$ is the determinant of the basis matrix $\mathbf{B}$.

The lattice determinant does not depend on a particular basis matrix since it is an invariant of the lattice itself. A lattice can usually be generated by many different basis matrices. More concretely, any two basis matrices of the same lattice can be converted to each other using a unimodular matrix. Unless otherwise specified, the lattices in this paper are full-rank.

The famous Lenstra–Lenstra–Lovász (LLL) lattice reduction algorithm was proposed in [29]. Though this algorithm cannot directly output the shortest lattice vector, it outputs the approximately shortest basis vectors in polynomial time. In other words, the length of the output vectors does not exceed a certain multiple of the shortest vector, and the LLL algorithm usually works better in practice. The works [29,30] show the following lemma for the upper bound estimation of the approximately shortest vectors output by the LLL algorithm.

Lemma 1

(LLL). Let ${\overrightarrow{v}}_1,\dots ,{\overrightarrow{v}}_{\omega }$ be a set of basis vectors output by the LLL algorithm running on the lattice $\mathcal{L}$. We have

$$|{\overrightarrow{v}}_1|,\dots ,|{\overrightarrow{v}}_i|\le 2^{\frac{\omega (\omega -1)}{4(\omega +1-i)}}{\left(det\left(\mathcal{L}\right)\right)}^{\frac{1}{\omega +1-i}},i=1,\dots ,\omega .$$

Its time complexity is $O\left({\omega }^6{(logB)}^3\right)$ that is polynomial in the lattice dimension ω and the length of the input vectors B.

Coppersmith presented how to solve modular or integer polynomial equations based on the LLL algorithm [31,32]. The core idea is to construct solvable equations over the integers, which are represented as short basis vectors in the lattice. Meanwhile, the short basis vectors can be efficiently found by the LLL algorithm.

We describe the specific problem of solving modular polynomial equations as follows. Let R be a known positive integer, and let $v(x_1,\dots ,x_k)$ be a multivariate polynomial. The goal is to find small root solutions of $v(x_1,\dots ,x_k)modR$, i.e., to solve $v(x_1^{\prime },\dots ,x_k^{\prime })\equiv 0modR$ under $|x_i^{\prime }|\le X_i$, where $X_i$ is the upper bound on the absolute value of the variable $x_i^{\prime }$ related to the small root solution. It is required is to maximize the upper bound $X_i$ on the unknown variables, while keeping the time complexity polynomial in the input parameters.

Before describing the strategy of solving modular polynomial equations, we define the polynomial norm. For a certain k-variable polynomial $v(x_1,\dots ,x_k)=\sum a_{i_1,\dots ,i_k}{x}_1^{i_1}\cdots x_k^{i_k}$, the non-zero coefficients $a_{i_1,\dots ,i_k}$ are related to the corresponding monomials $x_1^{i_1}\cdots x_k^{i_k}$. The polynomial norm is defined as follows.

Definition 3.

Let $v(x_1,\dots ,x_k)=\sum a_{i_1,\dots ,i_k}{x}_1^{i_1}\cdots x_k^{i_k}$ with $a_{i_1,\dots ,i_k}\ne 0$ be a k-variable polynomial. Its norm is defined as

$$\parallel v(x_1,\dots ,x_k)\parallel :={\left(\sum a_{i_1,\dots ,i_k}^2\right)}^{1/2}.$$

Howgrave-Graham [33] further improved on Coppersmith’s original techniques. The following lemma is used for determining whether the small root solution of a modular polynomial equation also holds on the integers, i.e., whether the modular condition can be eliminated.

Lemma 2

(Howgrave-Graham). Let $v(x_1,\dots ,x_k)\in \mathbb{Z}[x_1,\dots ,x_k]$ be a k-variable integer polynomial containing ω monomials. When the following conditions are satisfied, $v(x_1^{\prime },\dots ,x_k^{\prime })=0$ also holds over the integers.

1. 

$v(x_1^{\prime },\dots ,x_k^{\prime })\equiv 0modR,|x_1^{\prime }|\le X_1,\dots ,\left|x_k^{\prime }\right|\le X_k$,

2. 

$\parallel v(X_1{x}_1,\dots ,X_k{x}_k)\parallel <R/\sqrt{\omega }$.

The basic idea of solving k-variable polynomials is to construct $\ell \ge k$ algebraically with independent polynomials sharing the same small root over the integers. Hence, one can extract the final solution by the Gröbner basis computation [34]. By applying Lemma 2, the problem of solving modular polynomial equations can be turned to solving integer equations. Further, by combining Lemma 1, one can solve a given modular polynomial equation under certain conditions. The lattice-based method constructs a set of shift polynomials sharing the same root modulo R and then transforms the derived polynomials into integer equations in a specific way. Technically speaking, a lattice-basis matrix is generated from the coefficient vectors of the shift polynomials, which spans an $\omega$-dimensional lattice. The LLL algorithm is applied to obtain the approximately shortest basis vectors, which are later transformed into polynomial equations. If the corresponding polynomial norm is small enough, then the derived equation also holds over the integers. We summarize the process of solving k-variable polynomial equations using the lattice-based method as follows.

• The first step is to construct the set of shift polynomials $\mathcal{P}$ for given modular polynomials $f_1(x_1,\dots ,x_k),\dots ,f_n(x_1,\dots ,x_k)$ containing k unknown variables and a given modulus M. For $0\le i_1,\dots ,i_n\le m\in \mathbb{N}$ and $j_1,\dots ,j_k\in \mathbb{N}$, the basic form of a shift polynomial is defined as

  $$p_i(x_1,\dots ,x_k):=f_1^{i_1}\cdots f_n^{i_n}·x_1^{j_1}\cdots x_k^{j_k}·M^{m-(i_1+\cdots +i_n)},1\le i\le \omega .$$

  Thus, all polynomials in $\mathcal{P}$ have the same root $(x_1^{\prime },\dots ,x_k^{\prime })mod{M}^m$, where the modulus is $R=M^m$.
• The second step is to use ${\overrightarrow{b}}_i$ denoting the row vector transformed from the coefficient vectors of the shift polynomial $p_i(X_1{x}_1,\dots ,X_k{x}_k)$ when substituting $X_i{x}_i$ for $x_i$. The lattice $\mathcal{L}=\left\{{\sum }_{i=1}^{\omega }{z}_i{\overrightarrow{b}}_i:z_i\in \mathbb{Z}\right\}$ is constructed by the lattice basis matrix $\mathbf{B}={\left(b_{ij}\right)}_{\omega \times \omega }$. Then apply the LLL algorithm to the lattice $\mathcal{L}$ and extract the first ℓ many approximately shortest vectors ${\overrightarrow{v}}_1,\dots ,{\overrightarrow{v}}_{\ell }$ from the output. The output vectors are transformed into a system $\mathcal{V}$ of integer equations $v_1(x_1,\dots ,x_k),\dots ,v_{\ell }(x_1,\dots ,x_k)$, whose roots also hold over the integers.
• The third step is extract the desired small root solution. If the derived polynomials $v_i(x_1,\dots ,x_k)$ are mutually algebraically independent, the system of integer equations $\mathcal{V}$ can be solved by applying the Gröbner basis computation. At this point, the small root solution $(x_1^{\prime },\dots ,x_k^{\prime })$ of the original modular polynomials is obtained.

When obtaining the first ℓ number of basis vectors using the LLL algorithm, to ensure that the polynomial equations related to the basis vectors satisfy the solvable conditions, we have $2^{\frac{\omega (\omega -1)}{4(\omega +1-\ell )}}det{\left(\mathcal{L}\right)}^{\frac{1}{\omega +1-\ell }}<R/\sqrt{\omega }$. Since we always have $\ell \ll \omega \ll R$, the following simplified condition is obtained by omitting the lower error terms,

$$det\left(\mathcal{L}\right)<R^{\omega }.$$

(3)

To make the lattice determinant $det\left(\mathcal{L}\right)$ easy to compute, it is generally required that the basis matrix $\mathbf{B}$ is of lower or upper triangular form. Therefore, during the construction of shift polynomials, it is necessary to ensure that each new shift polynomial $p_i$ introduces exactly one new monomial ${\lambda }_i$. Hence, the lattice determinant is calculated by accumulating the monomials on the diagonal of the lattice basis matrix. We have $det\left(\mathcal{L}\right)=|det\left(\mathbf{B}\right)|={\prod }_{i=1}^{\omega }\left|{\lambda }_i(X_1,\dots ,X_k)\right|$.

The solution of multivariate polynomials using the lattice-based method is heuristic, so we note that its feasibility relies on the following heuristic assumption. Although the LLL algorithm guarantees that the reduced basis vectors are linearly independent, it cannot guarantee the algebraic independence of the transformed polynomials. On the other hand, similar to other cryptanalytic researches on RSA and its variants using the lattice-based method, the following assumption always holds in the validation experiments.

Assumption 1.

The system of integer equations related to the approximately shortest basis vectors output by the LLL algorithm can be efficiently solved. The small root solution can be extracted in polynomial time by the Gröbner basis computation.

3. Results

We aim to propose a polynomial-time algorithm outputting the factorization of N for given CRT-RSA key information $(N,e,d_p,d_q)$ by using the latest partial key exposure attack. To do so, we modify solving the factoring problem into conducting the partial key exposure attack. In other words, we extract two primes p and q for known LSB components of the CRT-exponents (i.e., the LSB components are exactly $d_p,d_q$ themselves if let the MSB components be 0). We follow the lattice-based method and briefly review the partial key exposure attack on CRT-RSA.

The partial key exposure attack on CRT-RSA [23] implicitly shows the existence of a factoring algorithm, which takes given CRT-RSA key information $(N,e,d_p,d_q)$ as input and outputs the factorization of $N=pq$ for $d_p,d_q<N^{1/2}$ and $e\approx N$. Therefore, we explicitly design a polynomial-time algorithm that outputs the factorization of N for $d_p,d_q<N^{1/2}$ and $e\approx N$. From a mathematical standpoint, we simplify the complicated and redundant attack analysis in [23] and further present a refined theorem in order to fit the factoring problem on CRT-RSA. To be specific, we concentrate on the error term that appears in the mathematical derivation process. We carefully analyze and reduce the influence of this error term and hence obtain attack results that are better than previous studies [23,35].

3.1. Partial Key Exposure Attack on CRT-RSA

Recently, May, Nowakowski, and Sarkar [23] proposed an improved partial key exposure attack on CRT-RSA, which is based on the small CRT exponent attack working for $d_p,d_q<N^{0.122}$ of [18]. This attack applies to the range $N^{0.122}<d_p,d_q<N^{0.5}$, which smoothly covers the full interval of the CRT exponents. Let $N=pq$ be the CRT-RSA modulus, where p and q are prime numbers of the same bit-size. Assume that the public exponent is $e\approx N^{\alpha }$, the CRT-exponents are $d_p,d_q\approx N^{\beta }$. The CRT-exponents can be written as $d_p=d_p^{*}{2}^t+{\tilde{d}}_p,d_q=d_q^{*}{2}^t+{\tilde{d}}_q$, where $t\in \mathbb{N}$ and the LSB components ${\tilde{d}}_p,{\tilde{d}}_q\approx N^{\beta -\delta }$ are known, whereas the MSB components $d_p^{*},d_q^{*}\approx N^{\delta }$ are unknown. Then, there exists a polynomial-time algorithm that outputs the secret information $p,q$ using the given partial key exposure.

According to $d_p\equiv e^{-1}mod(p-1)$ and $d_q\equiv e^{-1}mod(q-1)$, we have

$$\begin{array}{cc}\hfill & e{d}_p=k(p-1)+1\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & e{d}_q=\ell (q-1)+1\hfill \end{array}$$

(5)

for two positive integers $k,\ell \in \mathbb{N}$. Since the sizes of e, $d_p$, $d_q$, p, and q are known, the upper bounds on k and ℓ are estimated as

$$k,\ell <max\left(\frac{e{d}_p}{p-1},\frac{e{d}_q}{q-1}\right)=\Theta \left(\frac{N^{\alpha }{N}^{\beta }}{N^{1/2}}\right)=\Theta \left(N^{\alpha +\beta -1/2}\right).$$

(6)

Applying the Formula (4), we have $f\left(x_p,y_p\right):=x_p\left(y_p-1\right)+1=x_p{y}_p-x_p+1$, whose root is $(k,p)mode$. In addition, multiplying the Formula (5) by p and rearranging it gives

$$pe{d}_q=p\ell (q-1)+p=N\ell -p\ell +p=N(\ell -1)+N-p(\ell -1).$$

Similarly, we have $g\left(y_p,z_p\right):=y_p{z}_p-N{z}_p-N$, whose root is $(p,\ell -1)mode$. Moreover, the Equations (4) and (5) can be rewritten as $kp=k-1+e{d}_p$ and $\ell q=\ell -1+e{d}_q$. Multiplying them together gives $k\ell N=(k-1)(\ell -1)+(k-1)e{d}_q+e{d}_p(\ell -1)+e^2{d}_p{d}_q$, and we obtain

$$(N-1)k(\ell -1)+Nk+(\ell -1)=e\left(d_q(k-1)+d_p(\ell -1)+e{d}_p{d}_q\right).$$

Therefore, we have $h\left(x_p,z_p\right):=(N-1)x_p{z}_p+N{x}_p+z_p$, whose root is $(k,\ell -1)mode$. Combining the above modular polynomials, we obtain the following system of polynomial equations,

$$\left\{\begin{array}{cc}\hfill f\left(x_p,y_p,z_p\right)& =x_p{y}_p-x_p+1=0,\hfill \\ \hfill g\left(x_p,y_p,z_p\right)& =y_p{z}_p-N{z}_p-N=0,\hfill \\ \hfill h\left(x_p,y_p,z_p\right)& =(N-1)x_p{z}_p+N{x}_p+z_p=0.\hfill \end{array}\right.$$

Their common root is $(k,p,\ell -1)mode$.

Considering the special algebraic relationship between the unknown variables, we use six variables, namely $x_p,x_q,y_p,y_q,z_p,z_q$ instead of three variables. In this case, the relevant elements in certain monomials of the original polynomials need to be converted algebraically as follows.

$$y_p{y}_q⟷N,x_p-1⟷x_q,x_q+1⟷x_p,z_p+1⟷z_q,z_q-1⟷z_p.$$

(7)

Thus, we obtain linear polynomials after the conversion,

$$\left\{\begin{array}{cc}& f\left(x_p,x_q,y_p,y_q,z_p,z_q\right):=x_p{y}_p-x_q,\hfill \\ & g\left(x_p,x_q,y_p,y_q,z_p,z_q\right):=y_p{z}_p-N{z}_q,\hfill \\ & h\left(x_p,x_q,y_p,y_q,z_p,z_q\right):=N{x}_p{z}_q-x_q{z}_p.\hfill \end{array}\right.$$

Combining known values ${\tilde{d}}_p$ and ${\tilde{d}}_q$, the polynomials involved in the partial key exposure attack are as follows.

$$\left\{\begin{array}{cc}\hfill & \tilde{f}\left(x_p,x_q,y_p,y_q,z_p,z_q\right):=x_p{y}_p-x_q-e{\tilde{d}}_p\hfill \\ \hfill & \tilde{g}\left(x_p,x_q,y_p,y_q,z_p,z_q\right):=y_p{z}_p-N{z}_q+e{\tilde{d}}_q{y}_p\hfill \\ \hfill & \tilde{h}\left(x_p,x_q,y_p,y_q,z_p,z_q\right):=N{x}_p{z}_q-x_q{z}_p-e^2{\tilde{d}}_p{\tilde{d}}_q-e{\tilde{d}}_p{z}_p-e{\tilde{d}}_q{z}_q.\hfill \end{array}\right.$$

(8)

The root is $(x_p^{\prime },x_q^{\prime },y_p^{\prime },y_q^{\prime },z_p^{\prime },z_q^{\prime })=(k,k-1,p,q,\ell -1,\ell )mod{2}^{t}e$, and the corresponding upper bounds are $x_p^{\prime },x_q^{\prime },z_p^{\prime },z_q^{\prime }\le X=N^{\alpha +\beta -1/2},$ and $y_p^{\prime },y_q^{\prime }\le Y=N^{1/2}$.

We apply the lattice-based method to extract $(x_p^{\prime },x_q^{\prime },y_p^{\prime },y_q^{\prime },z_p^{\prime },z_q^{\prime })$. The first step is to construct the shift polynomials. Before that, we need to define the monomial set, whose elements are contained in the shift polynomials. The monomial set is closely related to the columns of the lattice basis matrix in the second step, and directly affects the alignment of the matrix rows.

Definition 4.

Let $m\in {\mathbb{Z}}_{+}$. The monomial set $\tilde{\mathcal{M}}$ is defined as

$$\tilde{\mathcal{M}}=\left\{x_p^a{y}_p^b{z}_p^c\mid 0\le a\le m,0\le c\le m,0\le b\le 2m\right\}.$$

To facilitate the exposition of the lattice construction, it is additional to define $\mathcal{M}\subseteq \tilde{\mathcal{M}}$ as

$$\mathcal{M}=\left\{x_p^a{y}_p^b{z}_p^c\mid 0\le a\le m,0\le c\le m,0\le b\le a+c\right\}.$$

Furthermore, $\tilde{\mathcal{M}}={\mathcal{M}}_1\cup {\mathcal{M}}_2\cup {\mathcal{M}}_3\cup {\mathcal{M}}_4\cup {\mathcal{M}}_5$ is partitioned using five disjoint subsets as follows.

$$\begin{array}{cc}& {\mathcal{M}}_1:=\left\{x_p^a{y}_p^b{z}_p^c\in \mathcal{M}\mid a\le c,b\le c-a\right\},\hfill \\ & {\mathcal{M}}_2:=\left\{x_p^a{y}_p^b{z}_p^c\in \mathcal{M}\mid a>c,b<a-c\right\},\hfill \\ & {\mathcal{M}}_3:=\left\{x_p^a{y}_p^b{z}_p^c\in \mathcal{M}\mid x_p^a{y}_p^b{z}_p^c\notin \left({\mathcal{M}}_1\cup {\mathcal{M}}_2\right),a+b+c\equiv 0mod2\right\},\hfill \\ & {\mathcal{M}}_4:=\left\{x_p^a{y}_p^b{z}_p^c\in \mathcal{M}\mid x_p^a{y}_p^b{z}_p^c\notin \left({\mathcal{M}}_1\cup {\mathcal{M}}_2\cup {\mathcal{M}}_3\right)\right\},\hfill \\ & {\mathcal{M}}_5:=\left\{x_p^a{y}_p^b{z}_p^c\in \tilde{\mathcal{M}}\mid x_p^a{y}_p^b{z}_p^c\notin \mathcal{M}\right\}.\hfill \end{array}$$

The shift functions and the corresponding shift polynomials are defined based on the monomial sets $\tilde{\mathcal{M}}$ and $\mathcal{M}$.

Definition 5.

The shift functions are defined as follows.

$$\begin{array}{cc}\hfill & E_f(a,b,c):=\left\{\begin{array}{cc}0,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_1\hfill \\ b,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_2\hfill \\ (a+b-c)/2,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_3\hfill \\ (a+b-c+1)/2,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_4\hfill \\ a,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_5\hfill \end{array}\right.\hfill \\ \hfill & E_g(a,b,c):=\left\{\begin{array}{cc}b,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_1\hfill \\ 0,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_2\hfill \\ (-a+b+c)/2,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_3\hfill \\ (-a+b+c-1)/2,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_4\hfill \\ c,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_5\hfill \end{array}\right.\hfill \\ \hfill & E_h(a,b,c):=\left\{\begin{array}{cc}a,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_1\hfill \\ c,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_2\hfill \\ (a-b+c)/2,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_3\hfill \\ (a-b+c-1)/2,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_4\hfill \\ 0,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_5\hfill \end{array}\right.\hfill \\ \hfill & E_x(a,b,c):=\left\{\begin{array}{cc}a-b-c,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_2\hfill \\ 0,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_1\cup {\mathcal{M}}_3\cup {\mathcal{M}}_4\cup {\mathcal{M}}_5\hfill \end{array}\right.\hfill \\ \hfill & E_z(a,b,c):=\left\{\begin{array}{cc}-a-b+c,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_1\hfill \\ 0,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_2\cup {\mathcal{M}}_3\cup {\mathcal{M}}_5.\hfill \\ 1,\hfill & x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_4\hfill \end{array}\right.\hfill \end{array}$$

For a given monomial $x_p^a{y}_p^b{z}_p^c\in \tilde{\mathcal{M}}$, the corresponding shift polynomial is determined as

$${\tilde{p}}_{[a,b,c]}\left(x_p,x_q,y_p,y_q,z_p,z_q\right):={\tilde{f}}^{E_f}{\tilde{g}}^{E_g}{\tilde{h}}^{E_h}{x}_p^{E_x}{z}_p^{E_z}{\left(2^{t}e\right)}^{2m-\left(E_f+E_g+E_h\right)}.$$

(9)

It is known that all the shift polynomials ${\tilde{p}}_{[a,b,c]}\left(x_p,x_q,y_p,y_q,z_p,z_q\right)$ have the common root $(k,k-1,p,q,\ell -1,\ell )mod{\left(2^{t}e\right)}^{2m}$. The shift polynomials are further adapted by using the algebraic relation Formula (7). We construct the updated shift polynomials under the following induced transformation rules.

Definition 6.

Let u be a polynomial defined over $x_p,x_q,y_p,y_q,z_p,z_q$. $\mathsf{tr}\left(u\right)$ is defined as the updated polynomial after the following transformation rules.

1. 

For all monomials, $y_p{y}_q$ are converted to N,

2. 

For monomials without $y_p$, $x_p$ are converted to $x_q+1$ and $z_p$ are converted to $z_q-1$,

3. 

For monomials with $y_p$, $x_q$ are converted to $x_p-1$ and $z_q$ are converted to $z_p+1$.

• Thus, $\mathsf{tr}\left(u\right)$ contains only monomials of the form $x_p^a{y}_p^b{z}_p^c$ and $x_q^a{y}_q^b{z}_q^c$, i.e., variables with subscripts p and q do not appear in a monomial at the same time.

The second step is to construct the lattice-basis matrix $\mathbf{B}$. To do this, we need to define the monomial order and the polynomial order, which are used to arrange the order of columns and rows in the lattice-basis matrix. When we generate the lattice-basis matrix, a polynomial ${\tilde{p}}_{[a,b,c]}\left(x_p,x_q,y_p,y_q,z_p,z_q\right)$ is first multiplied by some extra variables and then transformed by Definition 6. Finally, the upper bounds on the unknown variables are substituted and the polynomials are arranged in a one-to-one correspondence with the monomial order.

Definition 7.

The monomial order is defined as follows.

$$x_p^{a_1}{y}_p^{b_1}{z}_p^{c_1}\prec x_p^{a_2}{y}_p^{b_2}{z}_p^{c_2}⟺\left\{\begin{array}{c}{c}_1<c_2\hfill \\ c_1=c_2,a_1<a_2\hfill \\ c_1=c_2,a_1=a_2,b_1<b_2\hfill \end{array}\right.$$

The lattice basis matrix $\mathbf{B}$ and the polynomial order (namely the matrix row) are defined in the following way. The i-th column is related to the monomial ${\lambda }_{[a,b,c]}$, which is $x_q^a{y}_q^{b/2}{z}_q^c$ for even b and $x_p^a{y}_p^{\lceil b/2\rceil }{z}_p^c$ for odd b. The parameters $a,b,c$ are taken from the i-th smallest monomial $x_p^a{y}_p^b{z}_p^c$ in $\tilde{\mathcal{M}}$. For $x_p^a{y}_p^b{z}_p^c\in \mathcal{M}$, the i-th row is associated with the coefficient vector of polynomial $\mathsf{tr}\left({\tilde{p}}_{[a,b,c]}·y_q^{\lfloor b/2\rfloor }\right)\left(X{x}_p,X{x}_q,Y{y}_p,Y{y}_q,X{z}_p,X{z}_q\right)$. For $x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_5$ with even b, the i-th row takes $\mathsf{tr}\left({\tilde{p}}_{[a,b,c]}·y_q^{\lfloor (a+c)/2\rfloor }·y_q^{\lceil (b-a-c)/2\rceil }\right)\left(X{x}_p,X{x}_q,Y{y}_p,Y{y}_q,X{z}_p,X{z}_q\right)$. For $x_p^a{y}_p^b{z}_p^c\in {\mathcal{M}}_5$ with odd b, it takes $\mathsf{tr}\left({\tilde{p}}_{[a,b,c]}·y_q^{\lfloor (a+c)/2\rfloor }·y_p^{\lceil (b-a-c)/2\rceil }\right)\left(X{x}_p,X{x}_q,Y{y}_p,Y{y}_q,X{z}_p,X{z}_q\right)$. Then the lattice basis matrix $\mathbf{B}$ is lower triangular.

We then apply the lattice reduction algorithm to $\mathcal{L}$ generated by the basis matrix $\mathbf{B}$. The first few approximately shortest basis vectors ${\overrightarrow{v}}_i$ of the output are converted to polynomial form $v_i$, which make up the system of integer equations $\mathcal{V}$. The third step is to solve the above system of integer equations. We apply the Gröbner basis computation to extract $(k,k-1,p,q,\ell -1,\ell )$. At this point, we finally obtain the secret information p and q. Under the above lattice-based solution process, we present the following theorem.

Theorem 2.

Let $N=pq$ be a sufficiently large CRT-RSA modulus, where p and q are prime numbers of the same bit-size. Assume that the public exponent is $e\approx N^{\alpha }$, the CRT exponents are $d_p,d_q\approx N^{\beta }$. The CRT exponents are written as $d_p=d_p^{*}{2}^t+{\tilde{d}}_p$ and $d_q=d_q^{*}{2}^t+{\tilde{d}}_q$, where $t\in \mathbb{N}$ and the LSB components ${\tilde{d}}_p,{\tilde{d}}_q\approx N^{\beta -\delta }$ are known, whereas the MSB components $d_p^{*},d_q^{*}\approx N^{\delta }$ are unknown. Then given $(N,e,{\tilde{d}}_p,{\tilde{d}}_q)$ and ensuring $gcd(N-1,2^{t}e)=O\left(1\right)$, if the condition

$$\delta <\frac{3-2\alpha -2\beta }{10}$$

(10)

holds then p and q can be computed in polynomial time in $logN$.

Proof. 

We construct the lattice-basis matrix $\mathbf{B}$ and generate the $\omega$-dimensional full-rank lattice $\mathcal{L}$. Hence, each diagonal element $b_{i,i}$ of $\mathbf{B}$ contains the powers of $2^{t}e$, X, Y, and N, $(N-1)$, which are expressed as

$$b_{i,i}={\left(2^{t}e\right)}^{E_{1,i}}{X}^{E_{2,i}}{Y}^{E_{3,i}}{N}^{E_{4,i}}{(N-1)}^{E_{5,i}}.$$

To simplify the computation of the lattice determinant, we should multiply the polynomials of the rows by the following appropriate multiplicative inverse

$${\left(N^{E_{4,i}}{\left(\frac{N-1}{gcd(2^{t}e,N-1)}\right)}^{E_{5,i}}\right)}^{-1}mod{\left(2^{t}e\right)}^{2m}$$

(11)

to eliminate the effect of powers of N and $(N-1)$. The updated diagonal elements are $b_{i,i}^{*}={\left(2^{t}e\right)}^{E_{1,i}}{X}^{E_{2,i}}{Y}^{E_{3,i}}{gcd(2^{t}e,N-1)}^{E_{4,i}^{*}}$. Meanwhile, the root solution remains $(k,k-1,p,q,\ell -1,\ell )mod{\left(2^{t}e\right)}^{2m}$. Since it is assumed that $gcd(2^{t}e,N-1)=O\left(1\right)$ in the most favorable case, its influence can be ignored. The lattice determinant is calculated asymptotically as $det\left(\mathcal{L}\right)=|det\left(\mathbf{B}\right)|={\left(2^{t}e\right)}^{s_e}{X}^{s_X}{Y}^{s_Y}$, where the corresponding exponents are calculated as follows.

$$\begin{array}{cc}\hfill s_e& =\sum _{i=1}^{\omega }{E}_{1,i}=\sum _{x_p^a{y}_p^b{z}_p^c\in \tilde{\mathcal{M}}}\left(2m-E_f(a,b,c)-E_g(a,b,c)-E_h(a,b,c)\right)=\frac{7}{3}{m}^4+o\left(m^4\right),\hfill \\ \hfill s_X& =\sum _{i=1}^{\omega }{E}_{2,i}=\sum _{x_p^a{y}_p^b{z}_p^c\in \tilde{\mathcal{M}}}(a+c)=2m^4+o\left(m^4\right),\hfill \\ \hfill s_Y& =\sum _{i=1}^{\omega }{E}_{3,i}=\sum _{x_p^a{y}_p^b{z}_p^c\in \tilde{\mathcal{M}}}\frac{b}{2}=m^4+o\left(m^4\right).\hfill \end{array}$$

On the other hand, the dimension of the lattice $\mathcal{L}$ is

$$\omega =\sum _{x_p^a{y}_p^b{z}_p^c\in \tilde{\mathcal{M}}}1={(m+1)}^2(2m+1)=2m^3+o\left(m^3\right).$$

We apply the condition (3), i.e., $det\left(\mathcal{L}\right)<{\left(2^{t}e\right)}^{2m\omega }$. By substituting $2^t=N^{\beta -\delta }$, $e=N^{\alpha }$, $X=N^{\alpha +\beta -1/2}$ and $Y=N^{1/2}$, we have

$$(\alpha +\beta -\delta )·\frac{7}{3}{m}^4+\left(\alpha +\beta -\frac{1}{2}\right)·2m^4+\frac{1}{2}·m^4<(\alpha +\beta -\delta )·4m^4+o\left(m^4\right).$$

After simplification, we obtain $\delta <(3-2\alpha -2\beta )/10$. The running time mainly depends on the LLL algorithm, while the running time of the Gröbner basis computation is negligible in comparison. Thus, its time complexity is $O\left({\omega }^6{(logB)}^3\right)=O\left(m^{21}{(logN)}^3\right)$. Because m is a fixed number for generating the lattice, the time complexity is polynomial in $logN$.    □

We elaborate on the details of the lattice-basis matrix in the partial key exposure attack on CRT-RSA and present the specific attack algorithm. Furthermore, to understand Theorem 2 and the order of columns and rows in the lattice construction more intuitively, we give a toy example of the lattice basis matrix for $m=1$.

Example 1.

According to Definition 7, the lattice basis matrix $\mathbf{B}$ for $m=1$ is shown in

Table 1. A toy example of the lattice basis matrix for $m=1$.

1

$y_p$

$y_q$

$x_q$

$x_p{y}_p$

$x_q{y}_q$

$z_q$

$y_p{z}_p$

$y_q{z}_q$

$x_q{z}_q$

$x_p{y}_p{z}_p$

$x_q{y}_q{z}_q$

${\tilde{e}}^2$

${\tilde{e}}^2$

$y_p{\tilde{e}}^2$

–

${\tilde{e}}^{2}Y$

$y_q{\tilde{e}}^2$

–

–

${\tilde{e}}^{2}Y$

$x_q{\tilde{e}}^2$

–

–

–

${\tilde{e}}^{2}X$

$\tilde{f}\tilde{e}$

–

–

–

–

$\tilde{e}XY$

$\tilde{f}{y}_q\tilde{e}$

–

–

–

–

–

$\tilde{e}XY$

$z_p{\tilde{e}}^2$

–

–

–

–

–

–

${\tilde{e}}^{2}X$

$\tilde{g}\tilde{e}$

–

–

–

–

–

–

–

$\tilde{e}XY$

$\tilde{g}{y}_q\tilde{e}$

–

–

–

–

–

–

–

–

$\tilde{e}XY$

$\tilde{h}\tilde{e}$

–

–

–

–

–

–

–

–

–

$\tilde{e}XY$

$\tilde{f}{z}_p\tilde{e}$

–

–

–

–

–

–

–

–

–

–

$\tilde{e}{X}^{2}Y$

$\tilde{f}\tilde{g}{z}_p$

–

–

–

–

–

–

–

–

–

–

–

$X^{2}Y$

, where $\tilde{e}:=2^{t}e$ and $\tilde{f},\tilde{g},\tilde{h}$ are the derived polynomials to be solved.

It is clear that the lattice basis matrix $\mathbf{B}$ is indeed a lower triangular matrix, and that each new shift polynomial ${\tilde{p}}_i$ introduces only one new monomial ${\lambda }_i$.

We present the partial key exposure attack on CRT-RSA in Algorithm 1, which is denoted by $\mathcal{A}(N,e,2^t,{\tilde{d}}_p,{\tilde{d}}_q)$.

Algorithm 1 The partial key exposure attack algorithm $\mathcal{A}(N,e,2^t,{\tilde{d}}_p,{\tilde{d}}_q)$.
Input:  CRT-RSA modulus N, public exponent e, $2^t$ and known LSBs ${\tilde{d}}_p,{\tilde{d}}_q$ 1: $\tilde{f}\left(x_p,x_q,y_p,y_q,z_p,z_q\right)\leftarrow x_p{y}_p-x_q-e{\tilde{d}}_p$ 2: $\tilde{g}\left(x_p,x_q,y_p,y_q,z_p,z_q\right)\leftarrow y_p{z}_p-N{z}_q+e{\tilde{d}}_q{y}_p$ 3: $\tilde{h}\left(x_p,x_q,y_p,y_q,z_p,z_q\right)\leftarrow N{x}_p{z}_q-x_q{z}_p-e^2{\tilde{d}}_p{\tilde{d}}_q-e{\tilde{d}}_p{z}_p-e{\tilde{d}}_q{z}_q$
4: $\tilde{\mathcal{M}}\Leftarrow m\in {\mathbb{Z}}_{+}$	{construct the monomial set}
5: $E_f,E_g,E_h,E_x,E_z\Leftarrow \tilde{\mathcal{M}}$	{generate shift exponents}
6: ${\tilde{p}}_{[a,b,c]}\left(x_p,x_q,y_p,y_q,z_p,z_q\right)\leftarrow {\tilde{f}}^{E_f}{\tilde{g}}^{E_g}{\tilde{h}}^{E_h}{x}_p^{E_x}{z}_p^{E_z}{\left(2^{t}e\right)}^{2m-\left(E_f+E_g+E_h\right)}$
7: $\mathbf{B}\Leftarrow {\tilde{p}}_{[a,b,c]}\left(x_p,x_q,y_p,y_q,z_p,z_q\right)$	{generate the lattice basis matrix}
8: ${\overrightarrow{v}}_i\Leftarrow \mathbf{B}$	{compute reduced basis vectors}
9: $\mathcal{V}\Leftarrow {\overrightarrow{v}}_i$	{construct the equation system}
10: $(k,k-1,p,q,\ell -1,\ell )\Leftarrow \mathcal{V}$	{extract the desired root}
11: return p and q Output:  The factorization of $N=pq$

3.2. Polynomial Time Equivalence of Computing the CRT-RSA Secret Key and Factoring

We show an explicit demonstration on the polynomial-time equivalence of computing the CRT-RSA secret key and factoring by invoking the partial key exposure attack algorithm $\mathcal{A}(N,e,2^t,{\tilde{d}}_p,{\tilde{d}}_q)$. It is specified in the following theorem.

Theorem 3.

Let $N=pq$ be a sufficiently large CRT-RSA modulus, where p and q are prime numbers of the same bit size. Let e be the public exponent and $d_p,d_q$ be the corresponding CRT-exponents. Then the following statements hold under the condition $e{d}_p,e{d}_q<N^{3/2}$ and ensuring $gcd(N-1,2^{t}e)=O\left(1\right)$.

• Given $(N,e,p,q)$, $d_p$ and $d_q$ can be computed in polynomial time,
• Given $(N,e,d_p,d_q)$, p and q can be computed in polynomial time.

When $e\approx N$ is close to the CRT-RSA modulus, the CRT-exponents satisfies the natural constraint $d_p,d_q<N^{1/2}$ (or $d_p{d}_q<N$).

Note that the error term $gcd(N-1,2^{t}e)$ is derived from the proof of Theorem 2. To simplify the lattice determinant computation, we multiply each row polynomial by an appropriate multiplicative inverse, i.e., (11) to eliminate the effect of powers of N and $(N-1)$. However, $gcd(N-1,2^{t}e)$ is at least equal to 2 and hence its influence cannot be completely eliminated. We further check whether the assumption $gcd(N-1,2^{t}e)=O\left(1\right)$ holds in Section 4. From an algorithmic perspective, this error term $gcd(N-1,2^{t}e)$ affects the computation efficiency. To achieve the same attacking effect, a larger error term requires lattices with higher dimension and hence the corresponding factoring attack takes more time.

Proof. 

We divide the proof into two parts. One part proves that knowing $(N,e,p,q)$ is sufficient to compute $d_p$ and $d_q$ in polynomial time. The other part proves that known $(N,e,d_p,d_q)$ is sufficient to compute p and q in polynomial time. According to the key generation algorithm, we have $d_p\equiv e^{-1}mod(p-1)$, $d_q\equiv e^{-1}mod(q-1)$. When $(N,e,p,q)$ is known, the values of $e^{-1}mod(p-1)$ and $e^{-1}mod(q-1)$ can be computed by applying the extended Euclidean algorithm. It is shown in Algorithm 2 and denoted by $\mathcal{E}(e,p-1,q-1)$.

Algorithm 2 The CRT-RSA key computation algorithm $\mathcal{E}(e,p-1,q-1)$

Input:  CRT-RSA public exponent e, modulus factorization p and q 1: $(u_1,u_2,u_3)\leftarrow (0,1,p-1)$ 2: $(v_1,v_2,v_3)\leftarrow (1,0,e)$ 3: while$v_3>0$do 4:    $r\leftarrow \lfloor u_3/v_3\rfloor$ 5:    $(u_1,u_2,u_3)\leftarrow (u_1,u_2,u_3)-r·(v_1,v_2,v_3)$ 6:    $(u_1,u_2,u_3)⟷(v_1,v_2,v_3)$ 7: end while 8: $(u_1,u_2,u_3)\leftarrow (0,1,q-1)$ 9: $(w_1,w_2,w_3)\leftarrow (1,0,e)$ 10: while$v_3>0$do 11:    $r\leftarrow \lfloor u_3/w_3\rfloor$ 12:    $(u_1,u_2,u_3)\leftarrow (u_1,u_2,u_3)-r·(w_1,w_2,w_3)$ 13:    $(u_1,u_2,u_3)⟷(w_1,w_2,w_3)$ 14: end while 15: return$v_1$ and $w_1$ Output:  CRT-exponents $d_p=e^{-1}mod(p-1)$ and $d_q=e^{-1}mod(q-1)$

It is known that the time complexity of the modular inverse computation is $O(logN)$, so the CRT-RSA secret key computation algorithm $\mathcal{E}(e,p-1,q-1)$ can be done in polynomial time. To prove that knowing $(N,e,d_p,d_q)$ is sufficient to compute p and q in polynomial time, we slightly modify the original problem into the form of the partial key exposure attack on CRT-RSA. Denoting $t:=\lceil {log}_2(max(d_p,d_q))\rceil$ and letting $d_p^{*}=d_q^{*}=0$, we have leaked LSBs ${\tilde{d}}_p:=d_p,{\tilde{d}}_q:=d_q$. By calling the partial key exposure attack algorithm $\mathcal{A}(N,e,2^t,{\tilde{d}}_p,{\tilde{d}}_q)$, we can extract p and q in polynomial time. The specific algorithm is shown in Algorithm 3 and denoted by $\mathcal{F}(N,e,d_p,d_q)$.

Algorithm 3 The CRT-RSA modulus factorization algorithm $\mathcal{F}(N,e,d_p,d_q)$
Input:  CRT-RSA modulus N, public exponent e, CRT-exponents $d_p$ and $d_q$ 1: $t\leftarrow \lceil {log}_2(max(d_p,d_q))\rceil$ 2: $d_p^{*}\leftarrow 0,d_q^{*}\leftarrow 0$ 3: ${\tilde{d}}_p\leftarrow d_p,{\tilde{d}}_q\leftarrow d_q$ 4: $\tilde{f}\left(x_p,x_q,y_p,y_q,z_p,z_q\right)\leftarrow x_p{y}_p-x_q-e{\tilde{d}}_p$ 5: $\tilde{g}\left(x_p,x_q,y_p,y_q,z_p,z_q\right)\leftarrow y_p{z}_p-N{z}_q+e{\tilde{d}}_q{y}_p$ 6: $\tilde{h}\left(x_p,x_q,y_p,y_q,z_p,z_q\right)\leftarrow N{x}_p{z}_q-x_q{z}_p-e^2{\tilde{d}}_p{\tilde{d}}_q-e{\tilde{d}}_p{z}_p-e{\tilde{d}}_q{z}_q$
7: $\tilde{\mathcal{M}}\Leftarrow m\in {\mathbb{Z}}_{+}$	{construct the monomial set}
8: $E_f,E_g,E_h,E_x,E_z\Leftarrow \tilde{\mathcal{M}}$	{generate shift exponents}
9: ${\tilde{p}}_{[a,b,c]}\left(x_p,x_q,y_p,y_q,z_p,z_q\right)\leftarrow {\tilde{f}}^{E_f}{\tilde{g}}^{E_g}{\tilde{h}}^{E_h}{x}_p^{E_x}{z}_p^{E_z}{\left(2^{t}e\right)}^{2m-\left(E_f+E_g+E_h\right)}$
10: $\mathbf{B}\Leftarrow {\tilde{p}}_{[a,b,c]}\left(x_p,x_q,y_p,y_q,z_p,z_q\right)$	{generate the lattice basis matrix}
11: ${\overrightarrow{v}}_i\Leftarrow \mathbf{B}$	{compute reduced basis vectors}
12: $\mathcal{V}\Leftarrow {\overrightarrow{v}}_i$	{construct the equation system}
13: $(k,k-1,p,q,\ell -1,\ell )\Leftarrow \mathcal{V}$	{extract the desired root}
14: return p and q Output:  The factorization of $N=pq$

The time complexity of the CRT-RSA modulus factorization algorithm depends mainly on the partial key exposure attack, which can be done in $O\left({(logN)}^3\right)$ according to Theorem 2. Thus, $\mathcal{F}(N,e,d_p,d_q)$ runs in polynomial time in $logN$. However, Algorithm 3 partially answers the research problem. It remains to show that the CRT exponents satisfy the natural constraint, i.e., $d_p,d_q<N^{1/2}$ for $e\approx N$. For this purpose, we further apply the judgment condition (10) in Theorem 2. Assume that $e\approx N^{\alpha }$, $d_p,d_q\approx N^{\beta }$, $d_p^{*},d_q^{*}\approx N^{\delta }$, the partial key exposure attack on CRT-RSA works if

$$\delta <\frac{3-2\alpha -2\beta }{10}.$$

In Algorithm 3, we have the implication $\delta =0$, which shows that

$$0<\frac{3-2\alpha -2\beta }{10}.$$

Hence, it follows that $\alpha +\beta <3/2$, i.e., $e{d}_p,e{d}_q<N^{3/2}$. The CRT-RSA modulus factorization algorithm $\mathcal{F}(N,e,d_p,d_q)$ is feasible for $e\approx N$, and the CRT-exponents are in the range of $d_p,d_q<N^{1/2}$. So far, our research goal is achieved. □

3.3. Validation Experiments

We implement the CRT-RSA key computation algorithm $\mathcal{E}(e,p-1,q-1)$ and the CRT-RSA modulus factorization algorithm $\mathcal{F}(N,e,d_p,d_q)$ based on SageMath [36]. The experimental platform is a personal computer running Windows 10 with Intel(R) Core(TM) i5-10500 CPU 3.10 GHz and 8 GB RAM. All numbers in the validation experiments are randomly selected. We summarize the experimental results as follows. The CRT-RSA key computation algorithm $\mathcal{E}(e,p-1,q-1)$ outputs the modular inverse values $e^{-1}mod(p-1)$ and $e^{-1}mod(q-1)$ quite efficiently. The CRT-RSA modulus factorization algorithm $\mathcal{F}(N,e,d_p,d_q)$ runs with enough integer equations for solving the unknown variables and finally factors the modulus N. To be specific, after running the LLL algorithm, we can obtain a sufficient number of approximately shortest basis vectors to meet the requirements in the lattice-based method. The desired root can be efficiently extracted by transforming the lattice vectors into a system of integer equations and then applying the Gröbner basis computation.

As the CRT-RSA key computation algorithm is a direct call to the extended Euclidean algorithm, we focus on the CRT-RSA modulus factorization algorithm. In the experiments, we first choose an appropriate m to control the construction of the shift polynomials. We then construct the lattice basis matrix $\mathbf{B}$ and the $\omega$-dimensional full-rank lattice $\mathcal{L}$. The LLL algorithm is applied to $\mathcal{L}$, and we transform the first few output vectors into a system of integer equations. We finally solve the system of integer equations using the Gröbner basis computation and extract the desired root.

The detailed experimental results are given in

Table 2. Experimental results of our proposed factoring attack on CRT-RSA.

${log}_2\mathit{N}$	$\mathit{\alpha }{log}_2\mathit{N}$	$\mathit{\beta }{log}_2\mathit{N}$	m	$\mathit{\omega }$	Time
512	40	384	2	45	3
512	512	20	2	53	4
512	512	30	3	132	424
1024	100	512	2	45	11
1024	200	768	3	112	2482
1024	1024	103	4	245	84,221
2048	250	2000	2	45	39
2048	2048	80	2	53	51
2048	2048	200	3	130	7412

. The ${log}_{2}N$ column provides the bit size of the CRT-RSA modulus of the generated instance. The $\alpha {log}_{2}N$ column provides the bit size of the public exponent e. The $\beta {log}_{2}N$ column provides the bit size of the CRT exponents in our attacks. The lattice settings for conducting the factoring algorithms are indicated by the m and $\omega$ columns. The time consumption (recorded in seconds) of the LLL algorithm and the Gröbner basis computation are given in the Time-column. Two particular numerical CRT-RSA examples are given in Examples 2 and 3.

Example 2.

In order to check the correctness and validity of the CRT-RSA modulus factorization algorithm, we choose the following specific parameters and generate the test example.

1. 

Randomly generate 512-bit prime numbers p, q and the modulus $N=pq$,

2. 

Randomly generate 103-bit CRT exponents $d_p$ and $d_q$,

3. 

Generate the public exponent e based on above p, q and $d_p$, $d_q$,

4. 

Denote the CRT-RSA key information as $(N,e,d_p,d_q)$.

The values of the numerical CRT-RSA example are as follows.

$$\begin{array}{cc}\hfill N=& 114347036081803578673339388300699529343751209241907643180876\hfill \\ \hfill & 458206667330922848834036065664761789957008250918211860604774\hfill \\ \hfill & 566584479411936175341623770289022043707073762248864386282628\hfill \\ \hfill & 990346540436123901362681015966801988295462057535857497607361\hfill \\ \hfill & 768945381482239937653004859004894600582582900917446891506894\hfill \\ \hfill & 263052143,\hfill \\ \hfill e=& 223240854903959329163056785473769020659799535319489715586782\hfill \\ \hfill & 390754702103216662596028424458821582218235232577019255075762\hfill \\ \hfill & 125125183259281313726576508416053530713656742151040100413422\hfill \\ \hfill & 917401393760099325929355604572256120456696898516220623395554\hfill \\ \hfill & 309873831847027002512654955273158052172095928389224394251597\hfill \\ \hfill & 30187731,\hfill \\ \hfill d_p=& 6793718331323137434420097081795,\hfill \\ \hfill d_q=& 5689304626278643905322268826251.\hfill \end{array}$$

In the CRT-RSA modulus factorization algorithm $\mathcal{F}(N,e,d_p,d_q)$, we choose $m=4$, which means that we need to apply the LLL algorithm to the lattice $\mathcal{L}$ with $\omega =245$. After running for almost 84221 s, the approximately shortest basis vectors that meet the solvable condition are obtained. The system of integer equations to be solved is then derived by transforming vectors into polynomials. We finally solve it by applying the Gröbner basis computation in less than one second and recover

$$\begin{array}{cc}\hfill p=& 108638302771434350392709121078675710123453598877100622797142\hfill \\ \hfill & 999156910491518974867800775506243747756303770936993791366549\hfill \\ \hfill & 71732967591897327085997551822606809,\hfill \\ \hfill q=& 105254807158005691967534136739997233691243442214073820398841\hfill \\ \hfill & 619002989698022942925837218623347529765489194410746175686245\hfill \\ \hfill & 27351967084444332562641383615278727.\hfill \end{array}$$

One may check that $N=pq$ does hold, so the CRT-RSA modulus factorization algorithm $\mathcal{F}(N,e,d_p,d_q)$ successfully outputs the factorization of $N=pq$.

To show that the CRT-RSA key computation algorithm $\mathcal{E}(e,p-1,q-1)$ also runs in polynomial time, we use the above CRT-RSA example and apply extended Euclidean algorithm. It runs in less than one second and outputs

$$\begin{array}{cc}\hfill d_p=& 6793718331323137434420097081795,\hfill \\ \hfill d_q=& 5689304626278643905322268826251.\hfill \end{array}$$

Example 3.

In order to further check the correctness and validity of the CRT-RSA modulus factorization algorithm for smaller e and larger CRT exponents, we choose the following specific parameters and generate the test example.

1. 

Randomly generate 512-bit prime numbers p, q, and the modulus $N=pq$,

2. 

Randomly generate 200-bit public exponent e,

3. 

Generate 768-bit CRT-exponents $d_p$ and $d_q$ based on above p, q, and e,

4. 

Denote the CRT-RSA key information as $(N,e,d_p,d_q)$.

The values of the numerical CRT-RSA example are as follows.

$$\begin{array}{cc}\hfill N=& 156512694533516563511957875673047248424661607738276291458198\hfill \\ \hfill & 561587305961477716057755389974955796966826998822273532598444\hfill \\ \hfill & 073354133765045009506842533224118977797362970342863277332916\hfill \\ \hfill & 054340774252180351940497697856282577719012074116639472745869\hfill \\ \hfill & 837430174148381260146968287423827682202356316536216812133505\hfill \\ \hfill & 242483721,\hfill \\ \hfill e=& 870234913689148331430538521742157308545604222372763981584709,\hfill \\ \hfill d_p=& 105054920889694313236643515475986229698560379691663463225512\hfill \\ \hfill & 302039400442603589508021349904320178302089471845434045075084\hfill \\ \hfill & 406806664103314275213793412703224020726768063140359644831769\hfill \\ \hfill & 2200027809366346806478596786324049639383282415416033,\hfill \\ \hfill d_q=& 148571987412482932015696111740202311634967482494902349345138\hfill \\ \hfill & 137535116614527333185153973996870696864633712947488523072563\hfill \\ \hfill & 209530823364587205330955760387748864552847890724262288611841\hfill \\ \hfill & 4037628097962124364926249633316687480099589768273565.\hfill \end{array}$$

In the CRT-RSA modulus factorization algorithm $\mathcal{F}(N,e,d_p,d_q)$, we choose $m=3$, which means that we need to apply the LLL algorithm to the lattice $\mathcal{L}$ with $\omega =112$. After running for almost 2482 s, the approximately shortest basis vectors that meet the solvable condition are obtained. The system of integer equations to be solved is then derived by transforming vectors into polynomials. We finally solve it by applying the Gröbner basis computation in less than one second and recover

$$\begin{array}{cc}\hfill p=& 117661909776482824125451009716243933710550298018498329113532\hfill \\ \hfill & 519144170968368272845860632479094497702166147221073340778054\hfill \\ \hfill & 06168249462396739783087920487938303,\hfill \\ \hfill q=& 133018998952878525725128760686837839812976256555609678813921\hfill \\ \hfill & 757867209306278453420877763154370943445528651863267874726515\hfill \\ \hfill & 62727232145095808167865245044585207.\hfill \end{array}$$

One may check that $N=pq$ does hold, so the CRT-RSA modulus factorization algorithm $\mathcal{F}(N,e,d_p,d_q)$ successfully outputs the factorization of $N=pq$.

To show that the CRT-RSA key computation algorithm $\mathcal{E}(e,p-1,q-1)$ also runs in polynomial time, we use the above CRT-RSA example and apply extended Euclidean algorithm. It runs in less than one second and outputs $d_p$ and $d_q$.

4. Discussion

To solve the proposed research problem, we apply the lattice-based method and present an improved CRT-RSA modulus factorization algorithm in Section 3.2. The correctness and validity of our factoring algorithm have been verified in Section 3.3. Our validation experiments always output the desired modulus factorization for small CRT-exponents. The running time depends on the particular lattice dimension and is in the range of 1 s to ${10}^6$ s. Hence, the accuracy and speed of our factoring algorithm have been evaluated. Next, we discuss the difference between previous studies and ours and show the superiority of our approach.

Maitra and Sarkar [35] have proposed a factorization attack using lattice-based method when $(N,e,d_p,d_q)$ are known. Assume that one has $e\approx N^{\alpha }$, $d_p<N^{{\delta }_1}$, $d_q<N^{{\delta }_2}$ and $g:=gcd(N-1,e{d}_p-1,e{d}_q-1)\approx N^{\gamma }$. They demonstrated that N can be factored in polynomial time in $logN$ when $2\alpha +{\delta }_1+{\delta }_2+2\gamma <3$. For $e\approx N$, i.e., $\alpha \approx 1$, we have ${\delta }_1+{\delta }_2<1-2\gamma$. It implies that the above approach cannot reach the natural constraint since $\gamma$ is not a negligible term.

Relatively speaking, our factoring algorithm involves an error term $gcd(N-1,2^{t}e)$ instead of $gcd(N-1,e{d}_p-1,e{d}_q-1)$ and hence our result seems superior. To illustrate the superiority, we examine and compare $gcd(N-1,e{d}_p-1,e{d}_q-1)$ in [35] and $gcd(N-1,2^{t}e)$ of ours. We choose 1024-bit CRT-RSA moduli and the corresponding CRT exponents of various bit sizes. The comparison results are given in

Table 3. The comparison of previous error term and ours.

CRT-Exponents Bit-Size	$gcd(\mathit{N}-1,{\mathit{ed}}_{\mathit{p}}-1,{\mathit{ed}}_{\mathit{q}}-1)$	$gcd(\mathit{N}-1,2^{\mathit{t}}\mathit{e})$
192	53	6.18
256	16.18	6.78
320	19.22	3.9
384	13.62	8.8
448	14.08	2.26
512	16.74	4.38
576	18.5	3.1
640	61.78	4.5
704	18.52	7
768	16.46	8.28
832	26.02	5
896	17.52	4.16
960	21.4	4.76
1024	27.94	3.22

. For the bit size of each CRT exponent, we randomly take 100 trials and calculate the average value.

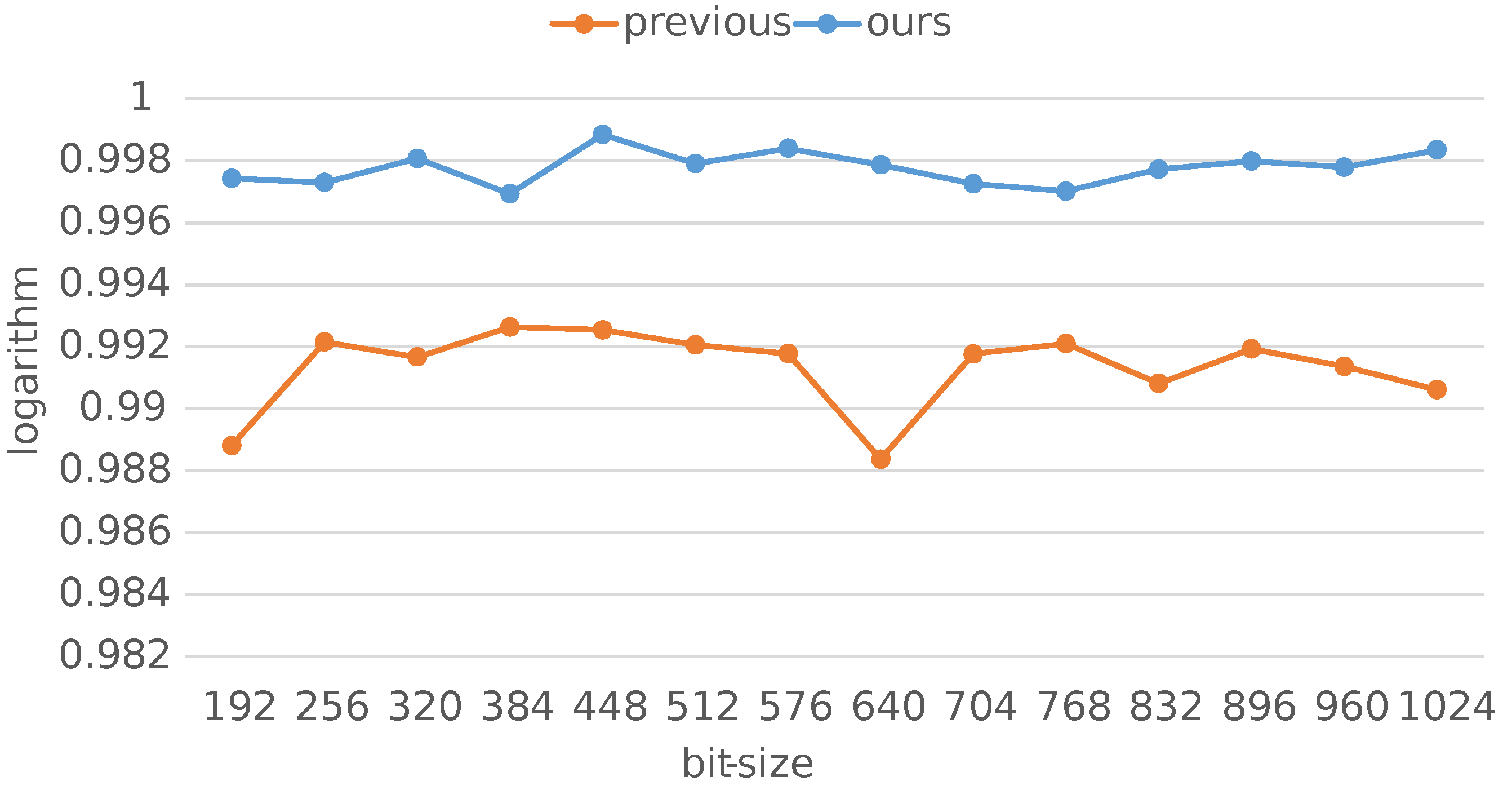
We observe that our error term $gcd(N-1,2^{t}e)$ equals to $O\left(1\right)$, i.e, negligible compared to $e,d_p,d_q$ in most cases. Further, our error term is always less than the previous one $gcd(N-1,e{d}_p-1,e{d}_q-1)$. Hence, our approach performs better than the previous work [35]. As shown in Figure 1, the attack upper bound ${log}_N{d}_p{d}_q$ of ours is closer to 1. Thus, our improvement further strengthens the modulus factoring attack on CRT-RSA when its key information is known.

To illustrate the relation of our work to the field of attacking CRT-RSA, we compare and classify recent related works as shown in

Table 4. The comparison and classification of related works and ours on cryptanalysis of CRT-RSA.

Related Works	Attack Type	Used Method
ours, [35]	factoring attack	lattice-based method
[37]	factoring attack	elliptic curve method
[6,12,17,18,38]	small CRT-exponent attack	lattice-based method
[19,20,21,22,23]	partial key exposure attack	lattice-based method
[24,25,26,27,28]	side-channel attack	power-based method
[39,40,41]	key recovery attack	tree-based method

. Our work further enriches cryptanalyses of CRT-RSA. To be specific, the work not only makes further improvements on factoring attacks, but also reveals the importance and correctness of the polynomial-time equivalence of computing the CRT-RSA secret key and factoring. It can be seen that factoring attack is a more essential security threat.

Notice that we experimentally verify our CRT-RSA modulus factorization algorithm for small CRT exponents. A limiting factor in achieving large CRT exponents is that we need to perform the lattice reduction algorithm with large lattice dimension in such cases. The running time increases rapidly, which leads to decreased attack efficiency, and is practically infeasible. This disadvantage can be eliminated with optimized lattice reduction algorithms and enhanced computing capability.

5. Conclusions

In this paper, we positively answer the research problem whether there exists a polynomial-time algorithm outputting the modulus factorization if given the CRT-RSA key information. Our work is summarized as follows.

• We study the security of CRT-RSA concerning its mathematical hardness assumption. We propose the improved polynomial-time algorithm of factoring the CRT-RSA modulus with the help of partial key exposure attack on CRT-RSA.
• Our asymptotic attack upper bound is superior to previous work [35]. Our factoring attack is a more essential security threat compared to others.
• We verify the correctness and validity of the proposed CRT-RSA modulus factorization algorithm with numerical experiments. Our validation experiments always successfully output the factorization results for small CRT-exponents.
• We discuss our results with several comparisons to properly assess the proposed factoring attack. Furthermore, we discuss the advantages and disadvantages of the proposed algorithm.

More concretely, under the condition that $e{d}_p,e{d}_q<N^{3/2}$, the factoring algorithm takes the given CRT-RSA key information $(N,e,d_p,d_q)$ as input and outputs the factorization of modulus $N=pq$ in polynomial time. We transform the original factorization problem into a modular polynomial solution problem. We apply Coppersmith’s lattice-based method to find the root solution, which contains the prime factors of the modulus. Notice that the polynomial-time equivalence of CRT-RSA key computation and factorization is still not completely solved. One open problem is whether there exists a polynomial-time algorithm for factoring the CRT-RSA modulus in the case of $e{d}_p,e{d}_q>N^{3/2}$.

Future research should be devoted to the development of optimized lattice-reduction algorithm in order to enhance the efficiency of the proposed factoring attack. In addition, hybrid attacks based on the proposed CRT-RSA modulus factorization algorithm is an interesting topic for future work.