1. Introduction
The application of space technologies is the theme of this era. Growing uncontrolled space debris and satellites greatly increase the possibility of collisions year by year. The collision of Iridium 33 and Cosmos 2251 is believed to be the first accidental hypervelocity collision of two intact satellites [
1]. In August 2016, significant orbit and attitude changes occurred to the Sentinel-1A, which were later proved to be the result of a 1 cm space debris impact [
2]. Therefore, there have been many efforts to calculate collision probabilities [
3], for collision avoidance [
4] and to design space debris removal missions [
5]. Above all, cataloging space objects with precise orbits is needed for the good performance of collision avoidance operations and space debris removal missions.
Restricted to the characteristics of current optical or radar surveys for space debris, only short-arc observations, also called as tracklets, can be obtained. If a tracklet can be correlated to one of the cataloged orbits, the tracklet can be used to update the orbit. The left tracklets that are uncorrelated (UCT) are either newly generated debris or an operational satellite after maneuvering. For UCTs, tracklet correlation is usually first needed to accomplish cataloging.
Milani [
6] suggested the method of an admissible region (AR) using attributables to solve the observation correlation of asteroids. Tommei and Milani [
7] applied the AR method to space debris in Earth orbit and generalized the method to radar cases. Fujimoto [
8] gave circular and zero-inclination solutions to the AR method. Farnocchia [
9] proposed a virtual debris algorithm based on the AR method. For many correlation works, only two-body integrals were considered. However, Reihs [
10] showed that correlation without considering
perturbation is effective only when the time interval between two measurements is very limited. Rehis [
11] suggested a solution of the AR method considering
perturbation.
The Gaussian and Laplacian methods are the most classical IOD algorithms, and they are used in this work. IOD algorithms such as Gibbs are used to deal with radar observations. Details of these algorithms can be found in Escobal [
12], Vallado [
13], and Liu [
14]. Hill [
15] took the IOD result as an initial value for an unscented Kalman filter. The calculated orbits and covariances are propagated to a common epoch to accomplish the comparison of orbits. A numerical integral has good precision in propagating orbits and covariances, but the computation requirements are heavy. It is not quite good at dealing with massive amount of tracklets considering the cost of time.
The Air Force Space Surveillance System (AFSSS) has achieved great success in the past few decades because of the wide coverage and its ability to detect high-speed LEO objects. Therefore, continuous attention is being paid to fencelike radar systems. Huang [
16] investigated a large-scale distributed space surveillance radar system, and a tracklet association scheme for LEO space debris observed by the double fence radar system was produced [
17].
At one step further than other UCTs correlation algorithms, analytic solutions are not only used in orbit calculation but also used in covariance propagation in this work. With analytic solutions, the lack of accuracy by Keplerian integrals can be compensated for, and the cost of time is still much less than that of the numerical integral. For monostatic radars, traditional IOD methods are accurate enough when dealing with a single tracklet. However, the same IOD methods are not quite suitable for the sum of ranges by bistatic radars; thus, an extra OD step is added, and a direct correlation criterion to the observations is raised. The effect of the weight of different observation types in the OD process is analyzed. The criteria can eliminate beforehand outliers that might lead to an error in the correlation process. Lastly, the variation in and evolution of the error of bistatic radar ranging are discussed.
2. Initial Orbit Determination for Tracklets Observed by Bistatic Radar
Given the geocentric position
of a transmitting station, the geocentric position
of the receiving station and the corresponding topocentric position of the space debris
,
, the geocentric position
of space debris can be expressed as
or
. As shown in
Figure 1, there are two types of observation for bistatic radars.
angles observed by the receiving station, usually azimuth and elevation in topocentric horizontal coordinate system for radars;
the sum of ranges by the transmitting station and receiving station, . and , and are the unit vector of and , and are the length of and . Sum of ranges can be measured directly, but and are unknown.
Radar ranging is based on the measurement of signal transmission time, and angles are based on the mechanical measurements of an antenna. Different measurement principles and equipment capabilities result in a difference in accuracy. In normalized units in which the unit of distance is the radius of Earth, and the unit of angles is radian, the error of angles is dozens of times larger than the error of radar ranging.
Traditional IOD methods can deal with monostatic radar ranging, but they are not quite suitable for a sum of ranges by a bistatic radar. Two approximate approaches can be used to obtain an initial orbit from bistatic radar observations.
Angles only: Since a series of angle observations is sufficient for IOD, a sum of ranges can be temporarily put aside. With Equation (
1),
from the receiving station to the space debris can be eliminated; therefore, only azimuth and elevation observed by the receiving station are used. The defect of this approach is that low-accuracy measurements are used, and high-accuracy measurements are rejected.
calculation: Since , and are known with a simple geometric calculation, can be obtained. Then, the position of space debris can be calculated. The problem of this approach is that the errors of angles are transferred to .
Since a tracklet is usually short-arc with initial geocentric position and velocity (
,
) at
and prediction duration
, the geocentric position
of the space debris at
t could be calculated by series expansion:
where
F and
G are the polynomial function of
. For the
calculation approach, Equation (
2) has 6 unknown variables (
,
) and a known vector
. With at least 2 groups of measurements
, (
,
) would be solvable.
By substituting Equation (
2) into Equation (
1),
For the angles-only approach, Equation (
3) has 6 unknown variables (
,
) and 2 known observations
. With at least 3 groups of measurements
, (
,
) would be solvable.
3. Orbit Improvement with Weighted Least Square Method
The angles-only and calculation approaches can both provide a set of the estimated state, but the accuracies of the two approaches much depend on the quality of angle measurements. For the angles-only approach, the random noise of is directly absorbed by the estimated state. For the calculation approach, the random noise of is absorbed by and also leads to a huge error in the estimated state.
With the weighted least-squares method (WLSM) and an accurate measurement model, the effects of the random noise of measurements can be reduced, measurements with large error can be stripped out, and can be appropriately calculated. Therefore, the accuracy of the orbit can be improved.
3.1. Weighted Least-Squares Method
Suppose that
is the observation at
,
is the calculated state at
, and
is the observation equation. The loss function is defined as
the result
should satisfy
where
is the state-space of
. For the least-squares method, either the position and velocity or orbital elements could form the state vector of space debris. For analytic solutions, the state of the space debris is usually expressed by orbital elements.
The loss function can also be expressed as
Supposing that
where
is the actual state at
, we have
If
is nonsingular, there exists a solution
which leads to
.
As mentioned in
Section 2, the accuracies of
and
are different. Equal treatment with different types of observations would lower the accuracy of the results, and a proper weight is essential to data fusion. Thus, measurement errors
are put into Equation (
11) and form Equation (
12).
where
Since observation equation
is an equation with respect to
, to calculate
, the state transition matrix
is needed:
3.2. Effect of Weight
Theoretical weight in WLSM is the accuracy of observation, as shown in Equation (
13). In practice, it is not easy to obtain the exact error of each observation while tracking and observing. The errors of observations are different since the error is affected by multiple factors. Usually, a composite weight from experience and equipment performance is set for each type of observation.
In this work, the relative weight between different types of observations could affect the accuracy of a certain orbital element. Two stations, as shown in
Table 1, and a satellite, as shown in
Table 2, were simulated to demonstrate the effect of observation weight. The duration of the simulated tracklet was 1 min.
As discussed in
Section 2, there are mainly two types of observation for bistatic radar, and the accuracy of radar ranging is usually better than that of angles. From Equation (
12), the results of estimation change with the relative weight between different observations, instead of the absolute weight of observations. In normalized units which the unit of distance is the radius of Earth, and the unit of angles is radian, variation in the relative error between the sum of ranges and azimuth (
) was set from 0.1 to 0.02, and variation in the relative error between elevation and azimuth (
) was set from 0.5 to 2.0. Like the relative errors of observations being used to describe weight, the relative error between different orbital elements is used to describe the accuracy of certain orbital element. By setting the error of the estimated eccentricity as the reference, the relative error between the semimajor axis and eccentricity (
) can represent the accuracy of the estimated semimajor axis, and the relative error between inclination and eccentricity (
) can represent the accuracy of the estimated inclination. The effects of weight on the accuracy of estimated orbital elements are shown in
Figure 2.
Figure 2 shows that the accuracy of the estimated semimajor axis increases with the weight of radar ranging. This effect becomes stronger when
. On the other hand, the accuracy of inclination decreases with the weight of radar ranging, and increases with the weight of elevation.
4. Correlation Considering Perturbation
The motion of space debris in terrestrial space is affected by all kinds of perturbations, such as drag, solar radiation pressure, and the gravitational perturbations of the Sun and Moon. Among all, the term of Earth’s nonspherical perturbation has the strongest influence.
The
term represents the perturbation caused by the oblateness of Earth. The acceleration of
perturbation is shown in Equation (
16),
G is the gravitational constant,
is the mass of Earth,
is the radius of Earth, and
is the position of space debris in an Earth-centered fixed coordinate system.
perturbation is not only considered in orbit prediction, but also in covariance propagation in this work.
4.1. Orbit Propagation with Perturbation
perturbation causes a secular variation in the orbital plane (right ascension of ascending node,
) and argument of perigee (
) as shown in Equations (
17) and (
18):
where
is the radius of Earth,
n is the mean motion of a satellite, and
. Equation (
19) shows that the mean motion (
n) of space debris is affected by
perturbation, but has no secular variation:
Since
, variation in
n leads to extra secular variation in mean anomaly (
M). Equation (
20) gives the expression of
:
With Equations (
17)–(
20), analytic state transition matrix
,
where
is a function of (
,
), and
are functions of (
,
,
,
).
represents the state transition of Keplerian motion, and
represents the effect of
perturbation.
4.2. Correlation of Tracklets
Assuming that there are n tracklets (), and each tracklet has more than 3 groups of measurements, the correlation between the jth tracklet and one of the measurements in the kth tracklet is taken as an example.
After IOD and OD with WLSM, an improved state () could be obtained for the jth tracklet. Propagating and the error of to the kth tracklet, observation (, , ) and the error of observation (, , ) can be calculated. The error of by OD with only one tracklet was much smaller than the actual deviation of . In order to more accurately calculate (, , ), the empirical error of the estimated orbit with one tracklet is needed.
Since the observation error (
,
,
) of the receiving station was pairwise orthogonal, (
A,
E,
) should conform to the restriction of the error ellipsoid as shown in
Figure 3.
If the
jth and
kth tracklets belong to the same satellite,
should satisfy Equation (
23):
m is the coefficient absorbing the inaccuracy of dynamic models and the error growth in propagation.
The error of bistatic radar ranging () is affected by three factors:
the error produced by the receiving station;
the error produced by the transmitting station;
the systematic error between the receiving station and the transmitting station.
is mainly decided by the performance of time synchronization between different stations. According to Guo [
18], timing with a global navigation satellite system (GNSS) is about 0.1 ns. Thus,
at present. Assuming that the variation in
and
is mainly affected by
perturbation, and Equation (
24) can be approximated to Equation (
25) in one tracklet:
Equation (
23) can be transformed into Equation (
26),
Different from calculating the Mahalanobis distance of two orbits [
11,
19], each group of observations was tested with Equation (
26). If 70% measurements of the tracklet were successfully correlated, the tracklet was successfully correlated. For tracklets with clean data, the effect of the proposed approach is similar to that of calculating Mahalanobis distance. However, tracklets with mixed measurements of different space debris appear now and then, and mixed measurements could lead to a failure in an OD process or an estimated orbit with huge error. With the proposed approach, correlation and data cleansing can be accomplished in one step.
There were quite a few miscorrelations only with Equation (
26). Orbit determination with WLSM can also be used to screen out miscorrelations. Two tracklets were insufficient for confirmation. Tests with real data were reported by Tommei [
20], who found that the correctness of correlation would be largely increased when at least 3 tracklets are confirmed by the least-square method. In this work, only correlated observations, instead of the entire tracklet, were used to implement the confirmation.
5. Discussion
Since the properties of azimuth and elevation observed by a receiving station are the same with those observed by monostatic radars, which was discussed by Cordelli [
21],
and
are not discussed in the following. Two issues are discussed in detail:
- (1)
the performance of orbit determination with WLSM for a single bistatic radar tracklet;
- (2)
the effect of orbital elements’ accuracy and prediction duration on .
5.1. Accuracy of Orbit Determination
In order to test the performance of orbit determination, 4298 tracklets of 3538 LEO satellites were simulated. Detailed simulation strategies are shown in
Table 3.
For the initial orbit determination demonstration, the
calculation approach was selected.
Figure 4 gives the deviation between the estimated orbit elements by IOD and the true orbital elements (TLE).
is the mathematical expectation of the deviation which represents the systematic bias of the estimated orbital elements.
The estimated inclination by IOD barely had systematic bias, and the error reached . On the other hand, the systematic bias of the estimated semimajor axis by IOD was as large as several kilometers, and the standard deviation was even larger.
Figure 5 gives the deviation between the estimated orbital elements by WLSM and the true orbital elements (TLE).
The accuracy of the estimated inclination by OD was only slightly higher than that of the estimated inclination by IOD. However, the estimated semimajor axis was significantly improved by OD with WLSM. The systematic bias of the estimated semimajor axis dropped to the order of magnitude of ten meters, and the accuracy of the estimated semimajor axis increased several dozens of times. This improvement was largely due to the proper use of
.
had a strong restriction on the estimation of the semimajor axis, and this phenomenon corresponded to the effect of weight discussed in
Section 3.2.
Two more things were also noticed from the results of orbit determination:
Orbit improvement with WLSM is indispensable. Since the error of the estimated orbit elements by IOD was too large, the number of miscorrelations would grow rapidly as the interval between tracklets increased. At the same time, the systematic bias of the estimated semimajor axis would render the orbit propagation wrong.
As mentioned in
Section 4.2, an empirical error of the estimated orbit is needed to calculate (
,
,
) in Equation (
26). From
Figure 5, the empirical error can be obtained.
5.2. Variation in and Evolution of
is mainly affected by the accuracy of orbit determination and the prediction duration. In order to test the effect of different factors, the two stations in
Table 1 and the satellite in
Table 2 were chosen to accomplish the experiment. Assuming that the prediction duration was 1 day,
Figure 6 shows the variation in
with respect to the estimated orbit element and its accuracy.
was easily found to always be positively associated with the absolute error of an orbital element. This feature can substantially simplify the calculation because the extreme value is sufficient for calculating the confidence zone of
instead of traversing all possible errors of orbital elements.
Figure 6 also shows that
became smaller for the satellites of a higher altitude with the same semimajor axis error. The effect of the right ascension of the ascending node (
) was almost identical to that of inclination, which demonstrates that the orbit plane had no direct relationship with
.
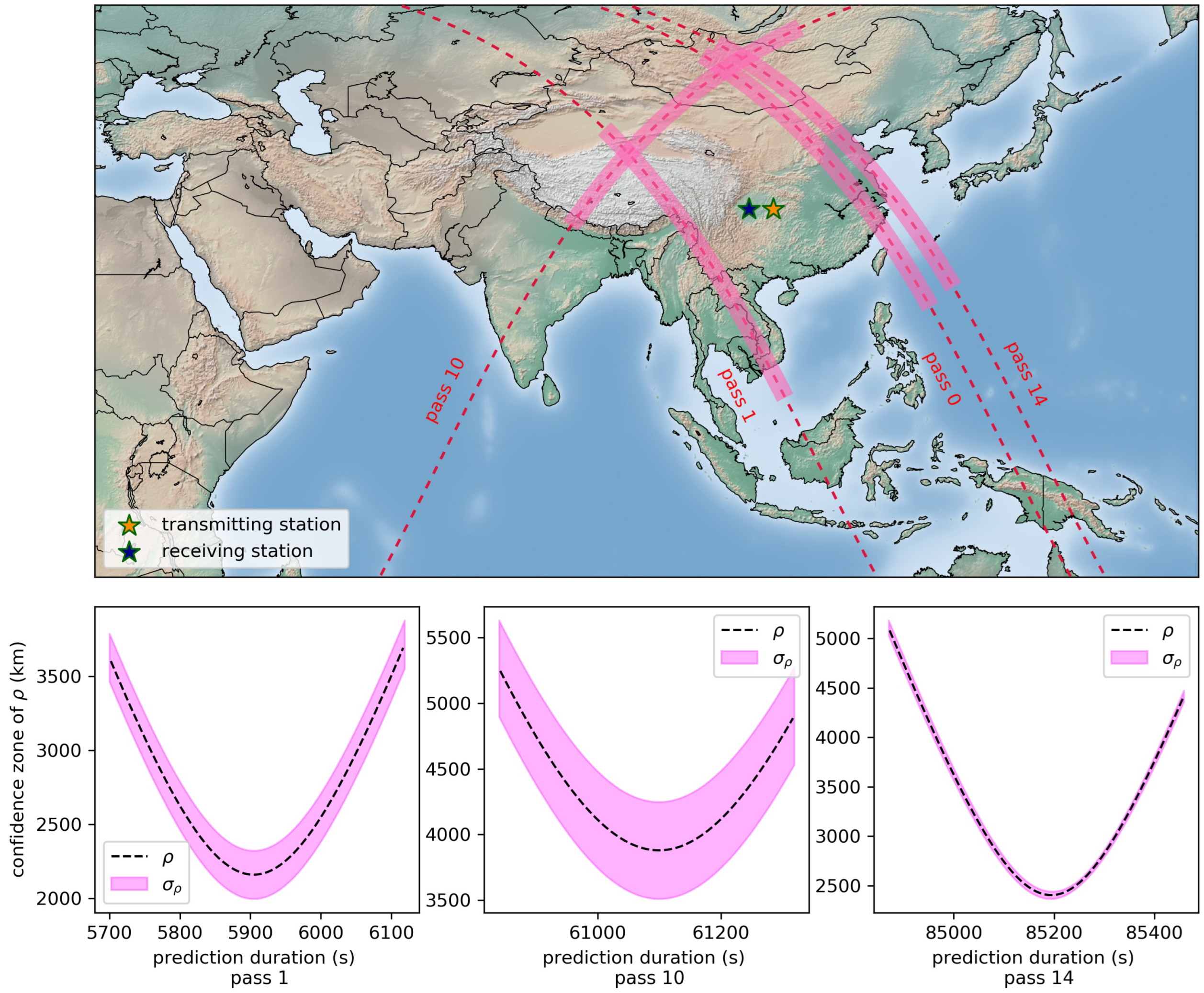
Assuming that the orbit was calculated with the tracklet in Pass 0, the orbit and its error propagated to tracklets in Passes 1, 10, and 14. The evolution of
and
is shown in
Figure 7.
Figure 7 shows that
in one tracklet could vary by several thousand kilometers for a satellite with an altitude of 500 km, while
only varies little. This shows that
barely had a relationship with
.
is not always positively associated with prediction duration. If
drops, either the error of velocity or the error of azimuth and elevation grows.
6. Conclusions
In this work, an efficient algorithm was presented to deal with the UCT correlation problem. The algorithm was based on analytic solutions for orbit and covariance propagation. The lack of accuracy of Keplerian integral can be compensated to a certain level by taking perturbation into consideration.
The process of correlation starts with the IOD of a tracklet, followed by obtaining an improved orbit with WLSM. An empirical error of the estimated state is used to form the covariance. The OD with an analytic orbit and covariance propagation runs fast for sparse data, which also significantly decreases the systematic bias of the estimated semimajor axis, and the accuracy of the estimated semimajor axis increases several dozens of times. The orbit and covariance are propagated to the epoch of the second tracklet, and Equation (
26) was used to perform the correlation. Instead of OD for the second tracklet and comparing the estimated orbit, each pair of observations in the second tracklet were separately correlated. If 70% observations of the tracklet were successfully correlated, the tracklet was successfully correlated. With the proposed approach, correlation and data cleansing can be accomplished in one step. However, only the correlated observations in the tracklet are used in the next step to implement the confirmation, and update the orbit and covariance. The accuracy of the semimajor axis increased with the weight of radar ranging. This effect became stronger when
. On the other hand, the accuracy of inclination decreased with the weight of radar ranging, and increased with the weight of elevation. The error of bistatic radar ranging also became smaller for space debris of higher altitude with the same semimajor axis error, and the orbit plane had no direct relationship with the error of bistatic radar ranging.
Author Contributions
Conceptualization, Z.H. and P.M.; Data curation, D.Z.; Formal analysis, H.L.; Funding acquisition, Y.J.; Investigation, Z.H., Y.J. and H.L.; Methodology, Z.H. and Y.J.; Project administration, Y.J. and H.L.; Resources, Y.J.; Software, Z.H. and D.Z.; Supervision, H.L.; Validation, Y.J. and P.M.; Visualization, Z.H.; Writing—original draft, Z.H.; Writing—review & editing, Z.H., Y.J., H.L. and P.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China grant number U21B2050.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Anselmo, L.; Pardini, C. Analysis of the consequences in low Earth orbit of thecollision between Cosmos 2251 and Iridium 33. In Proceedings of the 21st International Symposium on Space Flight Dynamics (ISSFD-2009), Toulouse, France, 28 September–2 October 2009. [Google Scholar]
- Krag, H.; Serrano, M.; Braun, V.; Kuchynka, P.; Catania, M.; Siminski, J.; Schimmerohn, M.; Marc, X.; Kuijper, D.; Shurmer, I.; et al. A 1 cm space debris impact onto the Sentinel-1A solar array. Acta Astronaut. 2017, 137, 434–443. [Google Scholar] [CrossRef]
- Wen, C.; Qiao, D. Calculating collision probability for long-term satellite encounters through the reachable domain method. Astrodynamics 2022, 6, 141–159. [Google Scholar] [CrossRef]
- Uriot, T.; Izzo, D.; Simões, L.F.; Abay, R.; Einecke, N.; Rebhan, S.; Martinez-Heras, J.; Letizia, F.; Siminski, J.; Merz, K. Spacecraft collision avoidance challenge: Design and results of a machine learning competition. Astrodynamics 2021, 6, 121–140. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, Z.; Baoyin, H. Timeline Club: An optimization algorithm for solving multiple debris removal missions of the time-dependent traveling salesman problem model. Astrodyn 2021, 6, 219–234. [Google Scholar] [CrossRef]
- Milani, A.; Gronchi, G.F.; Vitturi, M.d.M.; Knezevic, Z. Orbit determination with very short arcs. i admissible regions. Celestial Mech. Dyn. Astron. 2004, 90, 57–85. [Google Scholar] [CrossRef]
- Tommei, G.; Milani, A.; Rossi, A. Orbit determination of space debris: Admissible regions. Celestial Mech. Dyn. Astron. 2004, 97, 289–304. [Google Scholar] [CrossRef] [Green Version]
- Fujimoto, K.; Maruskin, J.M.; Scheeres, D.J. Circular and zero-inclination solutions for optical observations of Earth-orbiting objects. Celestial Mech. Dyn. Astron. 2010, 106, 157–182. [Google Scholar] [CrossRef]
- Farnocchia, D.; Tommei, G.; Milani, A.; Rossi, A. Innovative methods of correlation and orbit determination for space debris. Celestial Mech. Dyn. Astron. 2010, 107, 169–185. [Google Scholar] [CrossRef] [Green Version]
- Reihs, B.; Vananti, A.; Schildknecht, T. Comparison of new methods for the correlation of short radar tracklets. In Proceedings of the 69th International Astronautical Congress, Bremen, Germany, 1–5 October 2018. [Google Scholar]
- Reihs, B.; Vananti, A.; Schildknecht, T. A method for perturbed initial orbit determination and correlation of radar measurements. Adv. Space Res. 2020, 66, 426–443. [Google Scholar] [CrossRef]
- Escobal, P. Methods of Orbit Determination; R.E. Krieger Pub., Co.: Huntington, NY, USA, 1976. [Google Scholar]
- Vallado, D. Fundamentals of Astrodynamics and Applications; Microcosm Press: Hawthorne, CA, USA, 2013. [Google Scholar]
- Liu, L.; Tang, J.S. Theory and Application of Satellite Orbit; Publishing House of Electronics Industry: Beijing, China, 2015. [Google Scholar]
- Hill, K.; Sabol, C.; Alfriend, K.T. Comparison of covariance based track association approaches using simulated radar data. J. Astron. Sci. 2012, 59, 281–300. [Google Scholar] [CrossRef]
- Huang, J.; Wang, D.; Xia, S. An Optimal Beam Alignment Method for Large-scale Distributed Space Surveillance Radar System. Adv. Space Res. 2018, 61, 2777–2786. [Google Scholar] [CrossRef]
- Huang, J.; Hu, W.D.; Xin, Q.; Guo, W.W. A novel data association scheme for LEO space debris surveillance based on a double fence radar system. Adv. Space Res. 2012, 50, 1451–1461. [Google Scholar] [CrossRef]
- Guo, F.; Li, X.X.; Zhang, X.H.; Wang, J.L. Assessment of precise orbit and clock products for Galileo, BeiDou, and QZSS from IGS Multi-GNSS Experiment (MGEX). GPS Solut. 2017, 21, 279–290. [Google Scholar] [CrossRef]
- Mahalanobis, P. On the generalised distance in statistics. Proc. Natl. Inst. Sci. India 1936, 2, 49–55. [Google Scholar]
- Tommei, G.; Milani, A.; Farnocchia, D.; Rossi, A. Correlation of space debris observations by the virtual debris algorithm. In Proceedings of the Fifth European Conference on Space Debris, Darmstadt, Germany, 30 March–2 April 2009. [Google Scholar]
- Cordelli, E.; Vananti, A.; Schildknecht, T. Analysis of Laser Ranges and Angular Measurements Data Fusion for Space Debris Orbit Determination. Adv. Space Res. 2019, 65, 419–434. [Google Scholar] [CrossRef]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).