Containment Control for Discrete-Time Multi-Agent Systems with Nonconvex Control Input and Position Constraints

Abstract

With increasing attention on containment control problems in several areas, we investigate this specific problem which can be more practical. Systems with nonconvex input and position constraints are common but can be strongly nonlinear. A distribute algorithm using a projection operator is proposed to ensure that the control input of every follower remains in a nonconvex set and that all followers stay in the closed set given by leaders. In analysis, a model transformation is proposed, and then we introduce a method utilizing two similar triangles to prove the acceptability of the algorithm. The findings of the research could be pragmatic in robotics, astronautics, and so on. At last, numerical simulations are provided to show the contrast and results.

1. Introduction

Over the past few years, containment control has attracted widespread attention due to its potential applications in robotics, astronautics, biology, traffic engineering, etc. The potential of containment control for different areas such as game theory and cyberattack is significant. Numerous works on containment control have been conducted, as in [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. Containment control problem is associated with systems composed of follower agents and multiple leaders. The purpose of containment control is to drive all followers into the convex hull spanned by some static leaders. In [7], the containment control problem was studied when the communication graph was fixed, while containment control with switching topologies where the communication graphs were strongly connected was discussed in [9]. In [16], communication delays for containment control were taken into consideration.

Most of the above works focused on problems in which states and control input of agents had no constraints. In practical situations, agents are always subject to constraints due to physical limitations. For instance, the velocities of vehicles and satellites are constrained to lie in a certain zone. In [27], the consensus problem with convex constraints were studied; the nonconvex constraints of velocity and control input were discussed in [28]. In [29], switching topologies were taken into consideration, which are different from a consensus problem, since the final positions of followers do not converge to one point but a convex hull. The above methods cannot be directly applied to the containment problem with constraints. In [30], the projection operator was used to solve the containment problem with nonconvex control input constraints; the containment problem with position constraints was studied in [31].

In this work, the main task is to take into consideration the control input and position constraints for a containment control problem with switching topologies. A distributed algorithm is proposed to ensure that every follower in the multiagent system can converge into the convex hull spanned by the given leaders. Meanwhile, the position of every follower stays in a closed set given before and the control input does not need to keep lying in a hypercube. In the following, by using model transformation and analyzing the distance from each follower to the convex hull formed by given points, it is shown that the containment control problem can be solved when the directed spanning tree exists in the union of the graphs. In Section 2, the graph theory and multiagent dynamic model id introduced. In Section 3, we describe the main algorithm of the containment control system and the analysis of the main result when applied to a system with nonconvex control input and position constraints. In Section 4, we provide some simulation examples to confirm the feasibility of the algorithm. Finally, concluding notes and further works are remarked in Section 5.

2. Model and Statement

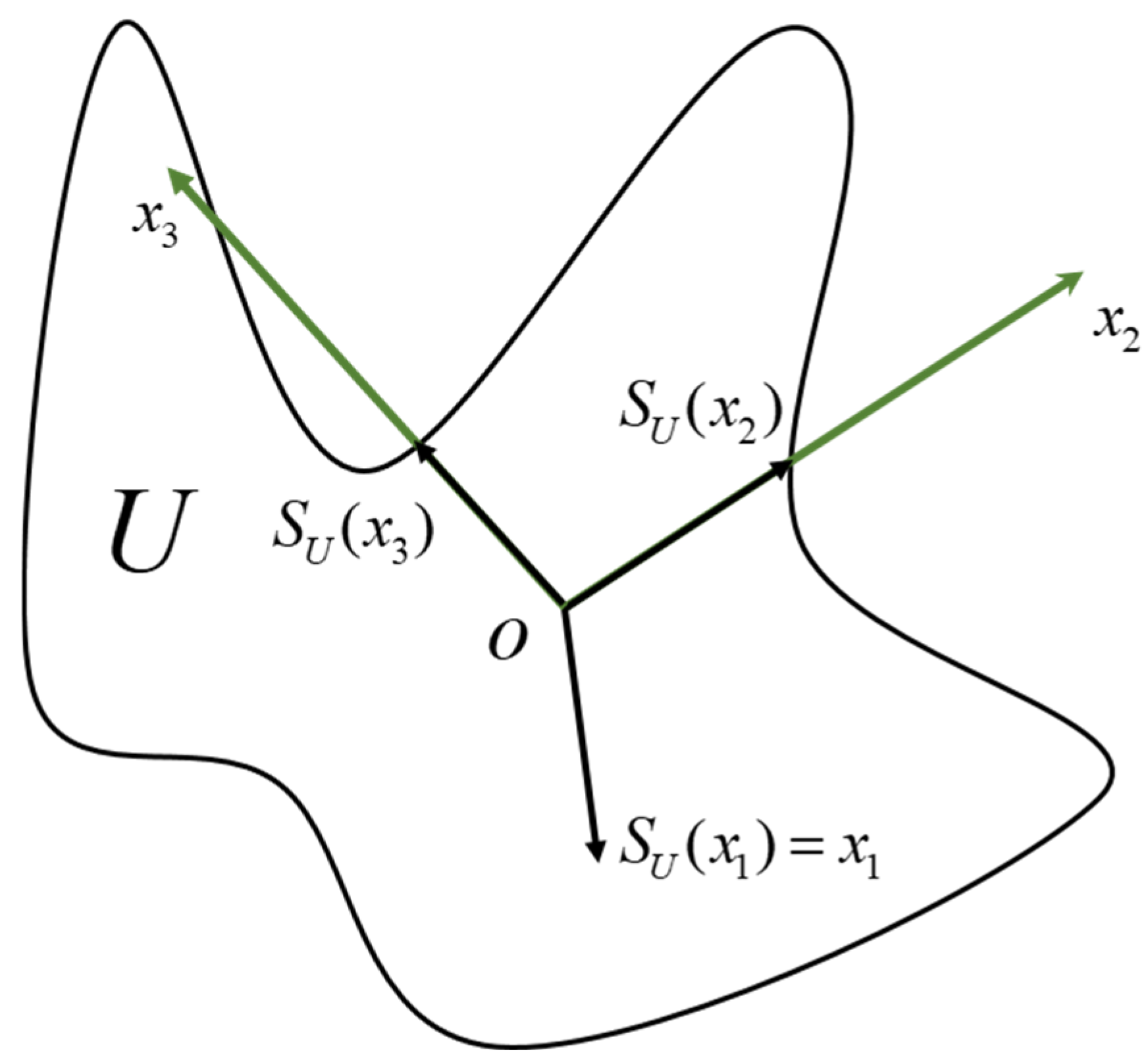
2.1. Preliminaries and Notations

Let $G(\mathcal{V},\mathcal{E},\mathcal{A})$ represent a directed graph, where $\mathcal{V}=\{1,2,\dots ,n+m\}$ is the set of nodes, $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$ is the set of edges, and $\mathcal{A}=[a_{ij}]$ is the weighted adjacency matrix. Each $a_{ij}$ is nonnegative and $a_{ii}=0$ holds for every agent $i$. Suppose that $(j,i)\in \mathcal{E}$ is an edge of the directed graph, and a directed path is a sequence of edges of the form $(i_1,i_2),(i_2,i_3),\dots$, otherwise, $a_{ij}(k)>0$ if the agent $i$ can get information from agent $j$ at time $k$ and $a_{ij}(k)=0$.

Notations: The set of r-dimensional real column vectors is represented by ${ℝ}^r$; $ℝ$, $\mathbb{N}$, and ${\mathbb{N}}_{+}$ represent the set of positive real numbers, nonnegative integers, and positive integers, respectively; $\parallel x\parallel$ and $x^T$ denote the Euclidean norm and transpose of the vector $x$, respectively; the projection of vector $x$ onto a closed convex set $X$ is represented by $P_Y(x)$, where $P_Y(x)=\arg \underset{\tilde{x}\in X}{\min }\parallel >\parallel x-\tilde{x}\parallel$.

2.2. Description of Model

Consider a multiagent system with $n+m$ agents, i.e., $n$ followers and $m$ leaders. The set of all followers and leaders can be denoted, respectively, by ${\mathcal{N}}_f=\{1,2,..,n\}$ and ${\mathcal{N}}_l=\{n+1,n+2,..,n+m\}$. Let $y_{n+1},y_{n+2},\dots y_{n+m}\in {ℝ}^r$ be the $m$ static points of the leaders, which forms the convex hull denoted by $Y=\{{\displaystyle \sum _{i=n+1}^{n+m}{\alpha }_i{y}_i}|{\alpha }_i\ge 0,{\displaystyle \sum _{i=n+1}^{n+m}{\alpha }_i}=1\}$.

Each follower is constrained to lie in a convex constraint set that is denoted by $X_i$. The dynamics of follower is:

$$\begin{array}{l}{x}_i((k+1)T)=P_{X_i}[x_i(kT)+v_i(kT)T]\\ v_i((k+1)T)=v_i(kT)+u_i(kT)T\end{array}$$

(1)

where $x_i(kT)\in {ℝ}^r$, $v_i(kT)\in {ℝ}^r$, and $u_i(kT)\in {ℝ}^r$ denote the position, the velocity, and the control input of the follower $i$, respectively. In many practical systems, the control input and position state of the agents are always constrained. Next, we give Assumption 1:

Assumption 1.

Let$0\in U_i\subseteq {ℝ}^r$for$i=1,2,..,n$be the bounded nonempty closed sets, $\underset{x\in U_i}{\max }\parallel S_{U_i}(x)\parallel ={\overline{\lambda }}_i$ and $\underset{x\notin U_i}{\min }\parallel S_{U_i}(x)\parallel ={\underset{\_}{\lambda }}_i$, where${\overline{\lambda }}_i$and${\underset{\_}{\lambda }}_i$are both positive constants. Then,$S_{U_i}(·)$is a constrained operator defined by$S_{U_i}(x)=\frac{x}{\parallel x\parallel }\underset{0\le \delta \le \parallel x\parallel }{\max }\{\delta |\frac{\delta \gamma x}{\parallel x\parallel }\in U_i,\forall 0\le \gamma \le 1\}$where$x\ne 0$and$S_{U_i}(0)=0$, as shown in Figure 1.

Remark 1.

Assumption 1 aims to find a new vector$S_{U_i}(x)$which has the same direction as vector$x$and satisfies$\gamma S_{U_i}(x)\in U_i$for all$0\le \gamma \le 1$and$\parallel S_{U_i}(x)\parallel \le \parallel x\parallel$for the bounded nonempty closed set$U_i$. This assumption shows that every follower can move in all directions. Moreover, the control input of agents are constrained. We suppose each follower to be available in every direction in this paper.

In this paper, our objective is to propose a proper algorithm to drive each follower, whose position and control input are constrained, to move into the convex hull $Y$ formed by the leaders, that is, $\underset{k\to \infty }{\lim }\parallel x_i(k)-P_Y(x_i(k))\parallel =0$ for $i\in {\mathcal{N}}_f$.

3. Main Results

3.1. Containment Control Algorithm

In this section, we would give a nonlinear algorithm to solve the containment control problem with nonconvex control input and position constraints and switching topologies.

$$\begin{array}{l}{u}_i=S_{U_i}[-p_i{v}_i(k)-c_i(k)(x_i(k)-P_{Y_i(k)}(x_i(k)))\\ \hspace{1em}\hspace{1em}+{\displaystyle \sum _{j\in N_i(k)}{a}_{ij}(k)(x_j(k)-x_i(k))}]\end{array}$$

(2)

for $i\in {\mathcal{N}}_f$, where $p_i>0$ represents the velocity damping gain of follower $i$, $c_i(k)=c>0$ when follower $i$ can receive information directly from one or more leaders at time $k$, and $c_i(k)=0$ otherwise, and $N_i(k)$ is the set of neighbors of agent $i$. $a_{ij}(k)$ is the edge weight of edge $(j,i)$, and it is assumed that if $a_{ij}(k)>0$, then $a_{ij}(k)$ is lower bounded by a positive constant. $Y_i(k)\subseteq Y$ is the convex hull formed by leaders whose information can be received by follower $i$ directly at time $k$.

3.2. Analysis of Algorithm

In this section, we provide some necessary assumptions and lemmas to analyze the algorithm given in Section 3.1.

Assumption 2.

Give an infinite sequence of time$k_0,k_1,k_2,k_3,\dots$satisfying$k_0>0$and$0<k_{q+1}-k_q\le C$where$q\in N$and$C\in N_{+}$. For every follower, it can be found at least one directed path from given static points to this follower in the union of the graphs in each time interval$[k_q,k_{q+1})$.

Remark 2.

This assumption ensures that each follower can receive information from the given static leaders directly or indirectly in every time interval.

It is clear that System (1) with (2) has strong nonlinearities due to the existence of the nonconvex control input and position constraints. For this reason, we first introduce a model transformation as follows:

Define

$$\begin{array}{ll}\hfill {\theta }_i(k)=& -c_i(k)[x_i(k)-P_{Y_i(k)}(x_i(k))]\hfill \\ & +{\displaystyle \sum _{j\in N_i(k)}{a}_{ij}(k)(x_j(k)-x_i(k))}\hfill \end{array}$$

and

$$h_i(k)=\left\{\begin{array}{c}1,\hspace{1em}if -p_i{v}_i(k)+{\theta }_i(k)=0\\ \frac{\parallel S_{U_i}[-p_i{v}_i(k)+{\theta }_i(k)]\parallel }{\parallel -p_i{v}_i(k)+{\theta }_i(k)\parallel },\hspace{1em}else\hfill \end{array}\right.$$

Then, System (2) can be rewritten as:

$$u_i(k)=h_i(k)(-p_i{v}_i(k)+{\theta }_i(k))$$

(3)

Define

$${\tilde{v}}_i(k)=x_i(k)+\frac{2}{p_i}{v}_i(k)$$

and

$$\begin{array}{l}{e}_i(k)=P_{X_i}[x_i(k)+\frac{p_i}{2}({\tilde{v}}_i(k)-x_i(k)T)]\\ \hspace{1em}\hspace{1em}\hspace{1em}-[x_i(k)+\frac{p_i}{2}({\tilde{v}}_i(k)-x_i(k)T)]\end{array}$$

(4)

for $i\in {\mathcal{N}}_f$.

Systems (1) and (2) can be transformed into:

$$\begin{array}{l}{x}_i(k+1)=P_{X_i}[x_i(k)+\frac{p_i}{2}({\tilde{v}}_i(k)-x_i(k)T)]\\ {\tilde{v}}_i(k+1)=P_{X_i}[x_i(k)+\frac{p_i}{2}({\tilde{v}}_i(k)-x_i(k)T)]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+(1-p_i{h}_i(k)T)({\tilde{v}}_i(k)-x_i(k))\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{2h_i(k)T}{p_i}{\displaystyle \sum _{j\in N_i(k)}{a}_{ij}(k)(x_j(k)-x_i(k))}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{2h_i(k)c_{i}T}{p_i}(x_i(k)-P_{Y_i(k)}(x_i(k)))\end{array}$$

(5)

for $i\in {\mathcal{N}}_f$.

Put the definition of (4) into equation, System (5) could be rewritten as:

$$\begin{array}{l}{x}_i(k+1)=(1-\frac{p_{i}T}{2})x_i(k)+\frac{p_i}{2}{\tilde{v}}_i(k)T+e_i(k)\\ {\tilde{v}}_i(k+1)=[p_i(h_i(k)-\frac{1}{2})T-\frac{2h_i(k)T}{p_i}({\displaystyle \sum _{j\in N_i}{a}_{ij}(k)}+c_i)]x_i(k)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+(1-p_i(h_i(k)-\frac{1}{2})T){\tilde{v}}_i(k)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{2h_i(k)T}{p_i}{\displaystyle \sum _{j\in N_i}{a}_{ij}(k)x_j(k)}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{2h_i(k)c_{i}T}{p_i}{P}_{Y_i(k)}(x_i(k))+e_i(k)\end{array}$$

(6)

for $i\in {\mathcal{N}}_f$.

From System (6), it can be easily found that the sum of the coefficients of $x_i(k)$ and ${\tilde{v}}_i(k)$ in the first equation and the coefficients of $x_i(k)$, ${\tilde{v}}_i(k)$, $x_j(k)$, and $P_{Y_i(k)}(x_i(k))$ in the other equation are both equal to 1, which means the existence of $e_i(k)$ destroys the linearity of $x_i(k+1)$ with $x_i(k)$ and ${\tilde{v}}_i(k)$, ${\tilde{v}}_i(k+1)$ with $x_i(k)$, ${\tilde{v}}_i(k)$, $x_j(k)$, and $P_{Y_i(k)}(x_i(k))$. Hence, the next step is to remove $e_i(k)$ when $k\to \infty$. Give the following definition:

$$\begin{array}{l}{g}_i(k)={\displaystyle \sum _{j\in N_i(k)}{a}_{ij}(k)}+c_i(k)\\ {\tau }_{ia}(k)=[p_{i}T(h_i-\frac{1}{2})-\frac{2h_{i}T}{p_i}{g}_i(k)]/(1-\frac{2h_{i}T}{p_i}{g}_i(k))\\ {\tau }_{ib}(k)=[1-p_{i}T(h_i-\frac{1}{2})]/(1-\frac{2h_{i}T}{p_i}{g}_i(k))\\ {\tau }_{ic}(k)=1-\frac{2h_{i}T}{p_i}{g}_i(k)\end{array}$$

(7)

and

$$q_{ia}(k)={\tau }_{ia}(k)x_i(k)+{\tau }_{ib}(k){\tilde{v}}_i(k)+\frac{1}{{\tau }_{ic}(k)}{e}_i(k)$$

(8)

for $i\in {\mathcal{N}}_f$. Then, (6) could be transformed as:

$$\begin{array}{l}{\tilde{v}}_i(k+1)={\tau }_{ic}(k)q_{ia}(k)+\frac{2h_i(k)T}{p_i}{\displaystyle \sum _{j\in N_i}{a}_{ij}(k)x_j(k)}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{2h_i(k)c_{i}T}{p_i}{P}_Y(x_i(k))\end{array}$$

(9)

for $i\in {\mathcal{N}}_f$.

Assumption 3.

$\parallel {\displaystyle \sum _{j\in N_i(k)}{a}_{ij}(k)(x_j(k)-x_i(k))}\parallel \le Q_i/2$and$\parallel c_i(k)[x_i(k)-P_{Y_i(k)}(x_i(k))]\parallel \le Q_i/2$for some constant$Q_i>0$.

Remark 3.

This assumption could be satisfied easily. By using the operator$S_{U_i}(x)$defined in Assumption 1, the terms${\displaystyle \sum _{j\in N_i(k)}{a}_{ij}(k)(x_j(k)-x_i(k))}$and$c_i(k)[x_i(k)-P_{Y_i(k)}(x_i(k))]$can be redefined as$S_{V_i}[{\displaystyle \sum _{j\in N_i(k)}{a}_{ij}(k)(x_j(k)-x_i(k))}]$and$S_{V_i}[c_i(k)[x_i(k)-P_{Y_i(k)}(x_i(k))]]$, where$V_i=\{y|\parallel y\parallel \le \frac{1}{2}{Q}_i\}$. As the definition of$h_i(k)$, we define that${\overline{h}}_i(k)=\frac{\parallel S_{V_i}[{\displaystyle \sum _{j\in N_i(k)}{a}_{ij}(k)(x_j(k)-x_i(k))}]\parallel }{\parallel {\displaystyle \sum _{j\in N_i(k)}{a}_{ij}(k)(x_j(k)-x_i(k))}\parallel }$and${\tilde{h}}_i(k)=\frac{\parallel S_{V_i}[c_i(k)[x_i(k)-P_{Y_i(k)}(x_i(k))]]\parallel }{\parallel c_i(k)[x_i(k)-P_{Y_i(k)}(x_i(k))]\parallel }$. It is clear that the two terms can be expressed as${\displaystyle \sum _{j\in N_i(k)}{\overline{h}}_i(k)a_{ij}(k)(x_j(k)-x_i(k))}$and$c_i(k){\tilde{h}}_i(k)[x_i(k)-P_{Y_i(k)}(x_i(k))]$, where$0<{\overline{h}}_i(k),{\tilde{h}}_i(k)\le 1$. Then, it can be similarly proven that${\overline{h}}_i(k)$and${\tilde{h}}_i(k)$are lower bounded by a positive constant with the discussion in Lemma 1.

Lemma 1.

Under Assumption 4 and the definition of operator$S_{U_i}(·)$, we have that if$0\le Q_i\le {\underset{\_}{\lambda }}_i/2$, there exists$k_m>0$such that:

$${\sigma }_i\le h_i(k)\le 1$$

for$i\in {\mathcal{N}}_f$and$k\ge k_m$, where${\sigma }_i=({\underset{\_}{\lambda }}_i-Q_i)/(2Q_i)$.

Proof of Lemma 1.

From the definition of $h_i(k)$, it is apparently that $0<h_i(k)<1$ and $\parallel -p_i{v}_i(k)+{\theta }_i(k)\parallel >{\underset{\_}{\lambda }}_i$ when $-p_i{v}_i(k)+{\theta }_i(k)\ne S_{U_i}[-p_i{v}_i(k)+{\theta }_i(k)]$, and $h_i(k)=1$ otherwise. Define ${\mathsf{\Phi }}_i(k)=\frac{1}{2}\parallel v_i(k){\parallel }^2$. From the definition of difference, there is:

$$\begin{array}{ll}\Delta {\mathsf{\Phi }}_i(k)& ={\mathsf{\Phi }}_i(k+1)-{\mathsf{\Phi }}_i(k)\\ & =(\parallel v_i{}^T(k+1){\parallel }^2-\parallel v_i{}^T(k){\parallel }^2)/2\\ & \le -2p_i{h}_i(k){\mathsf{\Phi }}_i(k)+Q_i\sqrt{2{\mathsf{\Phi }}_i(k)}\\ & =-\sqrt{2{\mathsf{\Phi }}_i(k)}(p_i{h}_i(k)\sqrt{2{\mathsf{\Phi }}_i(k)}-Q_i)\end{array}$$

Considering the property of $h_i(k)$, it can be easily deduced that ${\underset{\_}{\lambda }}_i/(p_i\parallel v_i(k)\parallel +Q_i)\le h_i(k)<1$. Given all this and the condition of Lemma 1, we have:

$$\begin{array}{l}\parallel v_i(k)\parallel \le -\sqrt{2{\mathsf{\Phi }}_i(k)}(\frac{p_i{\underset{\_}{\lambda }}_i}{p_i\parallel v_i(k)\parallel +Q_i}\sqrt{2{\mathsf{\Phi }}_i(k)}-Q_i)\\ \hspace{1em}\hspace{1em}\hspace{1em}\le -\sqrt{2{\mathsf{\Phi }}_i(k)}(\frac{p_i{\underset{\_}{\lambda }}_i}{p_i+Q_i/\parallel v_i(k)\parallel }-Q_i)\end{array}$$

When $p_i{\underset{\_}{\lambda }}_i/(p_i+Q_i/\parallel v_i(k)\parallel )-Q_i>{\epsilon }_0$, which is $\parallel v_i(k)\parallel >Q_i({\epsilon }_0+Q_i)/[p_i({\underset{\_}{\lambda }}_i-Q_i-{\epsilon }_0)]$, ${\epsilon }_0>0$ is a sufficiently small constant, $\parallel v_i(k)\parallel \le -Q_i({\epsilon }_0+Q_i){\epsilon }_0/[p_i({\underset{\_}{\lambda }}_i-Q_i-{\epsilon }_0)]$ can be obtained under the condition of this lemma. Therefore, there exists a constant $k_m>0$ such that $\parallel v_i(k)\parallel >Q_i({\epsilon }_0+Q_i)/[p_i({\underset{\_}{\lambda }}_i-Q_i-{\epsilon }_0)]$ for all $k\ge k_m$. From the assumption of Lemma 1 that $0\le Q_i\le {\underset{\_}{\lambda }}_i/2$, we have $Q_i{}^2/[p_i({\underset{\_}{\lambda }}_i-Q_i)]>({\underset{\_}{\lambda }}_i-Q_i)/p_i$. Then, we get $({\underset{\_}{\lambda }}_i-Q_i-{\epsilon }_0)/Q_i\le h_i(k)\le 1$ for all $k\ge k_m$. Since that ${\epsilon }_0$ can be arbitrarily small, $({\underset{\_}{\lambda }}_i-Q_i)/2Q_i\le h_i(k)\le 1$ holds, for all $k\ge k_m$. □

Assumption 4.

Suppose that$0<p_{i}T<1$,$p_i^2-4d_{im}>{\alpha }_1$,$d_{im}>{\displaystyle \sum _{j\in N_i}{a}_{ij}(k)}+c_i(k)$for${\alpha }_i>0$,$d_{im}>0$, for all$i\in \mathcal{F}$ and $k$.

Remark 4.

This assumption gives the design rules of the algorithm parameters. The parameter$p_i$can be selected by the following steps:

(1) 

Select the value of$p_i$such that$0<p_{i}T<1$and$p_i^2-4d_{im}>{\alpha }_1$for two constants${\alpha }_i>0$and$d_{im}>0$.

(2) 

Select the values of each nonzero$a_{ij}(k)$and$c$such that${\displaystyle \sum _{j\in N_i}{a}_{ij}(k)}+c_i(k)<d_{im}$for each$k$.

Lemma 2

[32].Let$X\subseteq {ℝ}^r$denote a nonempty closed convex set.$x_i\in {ℝ}^r$and scalars$a_i\ge 0$satisfying${\displaystyle \sum _{i=1}^n{a}_i}=1$. It follows$\parallel {\displaystyle \sum _{i=1}^n{a}_i{x}_i}-P_X({\displaystyle \sum _{i=1}^n{a}_i{x}_i})\parallel \le {\displaystyle \sum _{i=1}^n{a}_i\parallel x_i-P_X(x_i)\parallel }$.

Lemma 3

[33].Considering a closed convex set$0\ne \mathrm{Z}\subseteq R^r$, for any$x,y\in R^r$and all$z\in Z$, inequalities${[x-P_Z(x)]}^T(x-z)\ge 0$,$\parallel P_Z(x)-z{\parallel }^2\le \parallel x-z{\parallel }^2-\parallel P_Z(x)-x{\parallel }^2$and$\parallel P_Z(x)-P_Z(y)\parallel \le \parallel x-y\parallel$hold.

In order to eliminate $e_i(k)$, we present the following lemmas.

Lemma 4.

Under Assumption 4, the following statements stand for all$i\in {\mathcal{N}}_f$and all$k$:

(1) 

${\tau }_{ia}(k)+{\tau }_{ib}(k)=1$and${\tau }_{ic}(k)+\frac{2h_i(k)T}{p_i}{\displaystyle \sum _{j\in N_i}{a}_{ij}(k)}+\frac{2h_i(k)c_{i}T}{p_i}=1$;

(2) 

${\alpha }_2<{\tau }_{ia}(k)<\frac{1}{2}$,$\frac{1}{2}<{\tau }_{ib}(k)<1-{\alpha }_2$,$\frac{1}{2}<{\tau }_{ic}(k)<1$.

Proof of Lemma 4.

(1)

As the definition in (7), ${\tau }_{ic}(k)=1-\frac{2h_{i}T}{p_i}{g}_i(k)$ and $g_i(k)={\displaystyle \sum _{j\in N_i(k)}{a}_{ij}(k)}+c_i(k)$, for all $i\in \mathcal{F}$ and all $k$. It follows that

$$\begin{array}{l}\hspace{1em}{\tau }_{ic}(k)+\frac{2h_i(k)T}{p_i}{\displaystyle \sum _{j\in N_i}{a}_{ij}(k)}+\frac{2h_i(k)c_{i}T}{p_i}\\ =1-\frac{2h_i(k)T}{p_i}({\displaystyle \sum _{j\in N_i(k)}{a}_{ij}(k)}+c_i(k))\\ \hspace{1em}+\frac{2h_i(k)T}{p_i}{\displaystyle \sum _{j\in N_i}{a}_{ij}(k)}+\frac{2h_i(k)c_i(k)T}{p_i}\\ =1\end{array}$$

Note that ${\tau }_{ia}(k)=[p_{i}T(h_i-\frac{1}{2})-\frac{2h_{i}T}{p_i}{g}_i(k)]/(1-\frac{2h_{i}T}{p_i}{g}_i(k))$ and ${\tau }_{ib}(k)=[1-p_{i}T(h_i-\frac{1}{2})]/(1-\frac{2h_{i}T}{p_i}{g}_i(k))$, it is obviously that ${\tau }_{ia}(k)+{\tau }_{ib}(k)=1$.

(2)

Under Assumption 4, $0<p_{i}T<1$ and $p_i^2-4d_{im}>0$. It can be deduced that $\frac{1}{2}>\frac{1}{2}{p}_{i}T>2d_{im}T/p_i>2g_{i}T/p_i\ge 2c_{i}T/p_i\ge 0$. According to the definition of ${\tau }_{ib}$, we have $1/2<{\tau }_{ib}<1-{\alpha }_2$ for some constant $0<{\alpha }_2<1/2$. In the proof of Lemma 4(1), ${\tau }_{ia}(k)+{\tau }_{ib}(k)=1$. Thus, ${\alpha }_2<{\tau }_{ia}(k)<1/2$; also under $0\le 2g_{i}T/p_i<1/2$ and Lemma 1, it shows that $\frac{1}{2}<{\tau }_{ic}(k)=1-\frac{2h_{i}T}{p_i}{g}_i(k)<1$. □

Lemma 5.

Under Assumptions 4 and 5, the following two inequalities hold for all$i\in {\mathcal{N}}_f$and all$k$:

Proof of Lemma 5.

(1)

Let $q_{ib}(k)=(1-\frac{p_{i}T}{2})x_i(k)+\frac{p_i}{2}{\tilde{v}}_i(k)T$ for $i\in {\mathcal{N}}_f$. Since $P_Y(q_{ib}(k))\in X_i$, we have

$$\begin{array}{l} \parallel x_i(k+1)-P_Y(x_i(k+1))\parallel \\ =\parallel P_{X_i}(q_{ib}(k))-P_Y(P_{X_i}(q_{ib}(k)))\parallel \\ \le \parallel P_{X_i}(q_{ib}(k))-P_Y(q_{ib}(k))\parallel \end{array}$$

for $i\in {\mathcal{N}}_f$.

From Lemma 3, we have

$$\begin{array}{l} \parallel x_i(k+1)-P_Y(x_i(k+1)){\parallel }^2\\ \le \parallel P_{X_i}(q_{ib}(k))-P_Y(q_{ib}(k)){\parallel }^2\\ \le \parallel q_{ib}(k)-P_Y(q_{ib}(k)){\parallel }^2-\parallel P_{X_i}(q_{ib}(k))-q_{ib}(k){\parallel }^2\\ =\parallel q_{ib}(k)-P_Y(q_{ib}(k)){\parallel }^2-\parallel e_i(k){\parallel }^2\end{array}$$

for $i\in {\mathcal{N}}_f$.

Then, we use Lemma 2. It can transform to:

$$\begin{array}{l} \parallel x_i(k+1)-P_Y(x_i(k+1))\parallel \\ \le \parallel q_{ib}(k)-P_Y(q_{ib}(k))\parallel \\ =\parallel (1-\frac{p_{i}T}{2})x_i(k)+\frac{p_i}{2}{\tilde{v}}_i(k)T\\ \hspace{1em}-P_Y((1-\frac{p_{i}T}{2})x_i(k)+\frac{p_i}{2}{\tilde{v}}_i(k)T)\parallel \\ \le (1-\frac{p_{i}T}{2})\parallel x_i(k)-P_Y(x_i(k))\parallel \\ \hspace{1em}+\frac{p_{i}T}{2}\parallel {\tilde{v}}_i(k)-P_Y({\tilde{v}}_i(k))\parallel \end{array}$$

for $i\in {\mathcal{N}}_f$.

(2)

Notice that $2c_i{h}_i(k)T/p_i\ge 0$, $2a_{ij}(k)h_i(k)T/p_i\ge 0$, ${\tau }_{ic}(k)>1/2$ and ${\tau }_{ic}(k)+(2h_i(k)T/p_i){\displaystyle \sum _{j\in N_i}{a}_{ij}(k)}+2h_i(k)c_{i}T/p_i=1$. It follows that

$$\begin{array}{l} \parallel {\tilde{v}}_i(k+1)-P_Y({\tilde{v}}_i(k+1))\parallel \\ \le {\tau }_{ic}(k)\parallel q_{ia}(k)-P_Y(q_{ia}(k))\parallel +\frac{2h_i(k)T}{p_i}\\ \times {\displaystyle \sum _{j\in N_i}{a}_{ij}(k)}\parallel x_j(k)-P_Y(x_j(k))\parallel +\frac{2h_i(k)c_{i}T}{p_i}\\ \times \parallel P_{Y_i(k)}(x_i(k))-P_Y(P_{Y_i(k)}(x_i(k)))\parallel \end{array}$$

for $i\in {\mathcal{N}}_f$.

Because $Y_i(k)\subseteq Y$, it follows that

$$\begin{array}{l}\parallel {\tilde{v}}_i(k+1)-P_Y({\tilde{v}}_i(k+1))\parallel \\ \le {\tau }_{ic}(k)\parallel q_{ia}(k)-P_Y(q_{ia}(k))\parallel +\frac{2h_i(k)T}{p_i}\\ \times {\displaystyle \sum _{j\in N_i}{a}_{ij}(k)}\parallel x_j(k)-P_Y(x_j(k))\parallel \end{array}$$

for $i\in {\mathcal{N}}_f$. □

Lemma 6.

Under Assumption 4, the following inequality:

$$\parallel q_{ia}(k)-P_Y(q_{ia}(k))\parallel \le {\tau }_{ia}(k)\parallel x_i(k)-P_Y(x_i(k))\parallel +{\tau }_{ib}(k)\parallel {\tilde{v}}_i(k)-P_Y({\tilde{v}}_i(k))\parallel$$

holds for all$i\in {\mathcal{N}}_f$and all$k$.

Proof of Lemma 6.

Let $q_{ic}(k)={\tau }_{ia}(k)x_i(k)+{\tau }_{ib}(k){\tilde{v}}_i(k)$ for $i\in {\mathcal{N}}_f$. It can be easily observed that $\parallel q_{ia}(k)-P_Y(q_{ia}(k))\parallel \le \parallel q_{ia}(k)-P_Y(q_{ic}(k))\parallel$ for $i\in {\mathcal{N}}_f$.

• When $e_i(k)=0$, $\parallel q_{ia}(k)-P_Y(q_{ic}(k))\parallel =\parallel q_{ic}(k)-P_Y(q_{ic}(k))\parallel$ for $i\in {\mathcal{N}}_f$. Now, it should be proven that when $e_i(k)\ne 0$, $\parallel q_{ia}(k)-P_Y(q_{ic}(k))\parallel \le \parallel q_{ic}(k)-P_Y(q_{ic}(k))\parallel$ for $i\in {\mathcal{N}}_f$.
• Define $q_{id}(k)=P_{X_i}(q_{ib}(k))$ for convenience, and it is clear that $e_i(k)=q_{id}(k)-q_{ib}(k)$.

Now, define two hyperplanes ${\mathsf{\Psi }}_1$ and ${\mathsf{\Psi }}_2$, shown in Figure 2, that $e_i(k)$ is perpendicular to them, $q_{id}(k)\in {\mathsf{\Psi }}_1$ and $q_{ia}(k)\in {\mathsf{\Psi }}_2$. Meanwhile, it is clear that $e_i(k)/{\tau }_{ic}(k)=q_{ia}(k)-q_{ic}(k)$ is perpendicular to the hyperplanes. Then, define ${\beta }_{ia}(k)$ and ${\beta }_{ib}(k)$, as shown in Figure 2.

$$\begin{gathered} {\beta }_{ia}(k)=(1-{\delta }_{i1})x_i(k)+{\delta }_{i1}{\tilde{v}}_i(k)\in {\mathsf{\Psi }}_1 \\ {\beta }_{ib}(k)=(1-{\delta }_{i2})x_i(k)+{\delta }_{i2}{\tilde{v}}_i(k)\in {\mathsf{\Psi }}_2 \end{gathered}$$

for the constants $0<{\delta }_{i1}<1$ and $0<{\delta }_{i2}<1$.

It follows that there exist two similar triangles constituted by points ${\beta }_{ia}(k)$, $q_{id}(k)$, $q_{ib}(k)$ and points ${\beta }_{ib}(k)$, $q_{ia}(k)$, $q_{ic}(k)$. Now, the characters of similar triangles can be applied.

As shown in Figure 2, define $a_{i1}=p_{i}T/2-{\delta }_{i1}>0$. It follows that $q_{ib}(k)-{\beta }_{ia}=a_{i1}({\tilde{v}}_i(k)-x_i(k))$. Since the similarity of triangles, it can be obtained that $q_{ic}(k)-{\beta }_{ib}=a_{i1}({\tilde{v}}_i(k)-x_i(k))/{\tau }_{ic}(k)$, i.e., ${\beta }_{ib}=q_{ic}(k)-a_{i1}({\tilde{v}}_i(k)-x_i(k))/{\tau }_{ic}(k)$. ${\delta }_{i2}=(1-p_{i}T+{\delta }_{i1})/{\tau }_{ic}>{\delta }_{i1}$ can be obtained in the same way. Moreover, ${\mathsf{\Psi }}_2$ and $X$ are at the different sides of ${\mathsf{\Psi }}_1$. Given all this, it follows that the angle between vectors $q_{ia}(k)-q_{ic}(k)$ and $q_{ia}(k)-P_Y(q_{ic}(k))$ is an obtuse angle, which means $\parallel q_{ia}(k)-P_Y(q_{ic}(k))\parallel \le \parallel q_{ic}(k)-P_Y(q_{ic}(k))\parallel$. Notice Lemma 2 and 4(1), it can be seen that $\parallel q_{ic}(k)-P_Y(q_{ic}(k))\parallel \le {\tau }_{ia}(k)\parallel x_i(k)-P_Y(x_i(k))\parallel +{\tau }_{ib}(k)\parallel {\tilde{v}}_i(k)-P_Y({\tilde{v}}_i(k))\parallel$. Above all, it follows that

$$\begin{array}{ll}\parallel q_{ia}(k)-P_Y(q_{ia}(k))\parallel & \le \parallel q_{ia}(k)-P_Y(q_{ic}(k))\parallel \\ & \le \parallel q_{ic}(k)-P_Y(q_{ic}(k))\parallel \\ & \le {\tau }_{ia}(k)\parallel x_i(k)-P_Y(x_i(k))\parallel \\ & \hspace{1em}+{\tau }_{ib}(k)\parallel {\tilde{v}}_i(k)-P_Y({\tilde{v}}_i(k))\parallel \end{array}$$

for $i\in {\mathcal{N}}_f$. □

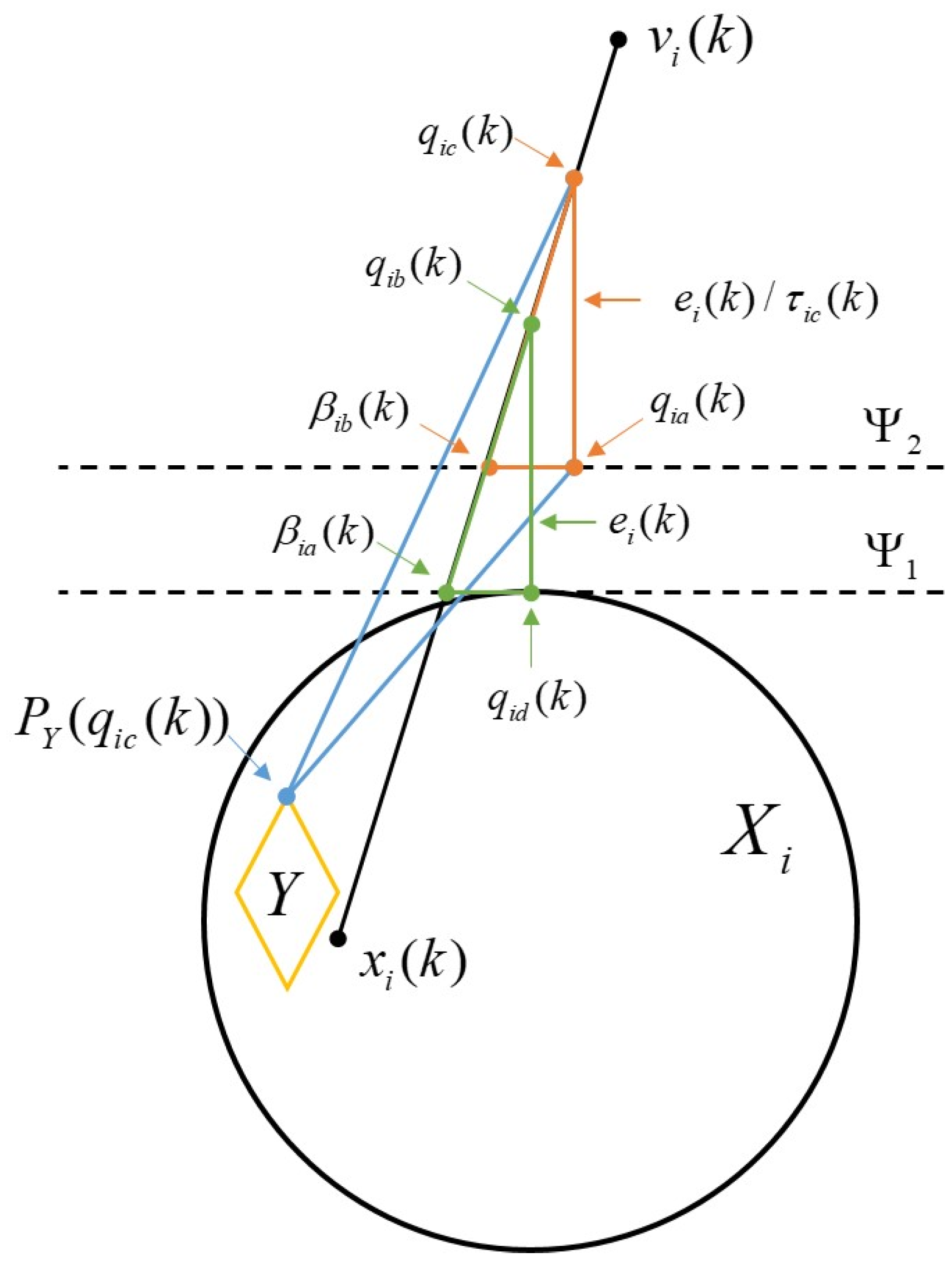
3.3. Analysis of Result

In this section, the result of containment control using the given algorithm would be analyzed. First, we design a Lyapunov function.

Let $\xi (k)=[x_1^T(k),{\tilde{v}}_1^T(k),\dots \dots x_n^T(k),{\tilde{v}}_n^T(k)]$. Design a Lyapunov function as:

$$V(k)=\underset{i\in \left\{1,2,\dots 2n\right\}}{\max }\{\Vert {\xi }_i(k)-P_Y({\xi }_i(k))\Vert \}$$

Summarizing the above lemma and analysis, it follows that

$$\parallel x_i(k+1)-P_Y(x_i(k+1))\parallel \le \underset{i\in F}{\max }\{\parallel x_i(k)-P_Y(x_i(k))\parallel ,\parallel {\tilde{v}}_i(k)-P_Y({\tilde{v}}_i(k))\parallel \}$$

and

$$\parallel {\tilde{v}}_i(k+1)-P_Y({\tilde{v}}_i(k+1))\parallel \le \underset{i\in F}{\max }\{\parallel x_i(k)-P_Y(x_i(k))\parallel ,\parallel {\tilde{v}}_i(k)-P_Y({\tilde{v}}_i(k))\parallel \}$$

for all $i\in {\mathcal{N}}_f$.

Next, we analyze the convergence of containment control problem under the given algorithm in the time interval $[k_l,k_{l+1})$.

Case A. Assuming that there is an agent $i_q$ that can get information from one of the static leaders at $k_{l0}\in [k_l,k_{l+1})$. Clearly, $c_{i_q}>0$ and ${\tau }_{i_{q}c}(k)+2h_{i_q}(k)T/p_{i_q}{\displaystyle \sum _{j\in N_{i_q}}{a}_{i_{q}j}(k)}=1-2h_{i_q}(k)c_{i_q}T/p_{i_q}<1$. Note that

$$\begin{array}{ll}\parallel {\tilde{v}}_i(k+1)-P_Y({\tilde{v}}_i(k+1))\parallel \le & {\tau }_{ic}(k)\parallel q_{ia}(k)-P_Y(q_{ia}(k))\parallel \\ & +\frac{2h_i(k)T}{p_i}{\displaystyle \sum _{j\in N_i}{a}_{ij}(k)}\parallel x_j(k)-P_Y(x_j(k))\parallel \end{array}$$

and

$$\begin{array}{ll}\parallel {\tilde{v}}_{i_q}(k_{l0}+1)-P_Y({\tilde{v}}_{i_q}(k_{l0}+1))\parallel & \le (1-\frac{2h_{i_q}(k_{l0})c_{i_q}T}{p_{i_q}})V(k_{l0})\\ & \le (1-\frac{2h_{i_q}(k_{l0})c_{i_q}T}{p_{i_q}})V(k_l)\triangleq m_{1}V(k_l)\end{array}$$

where $0<m_1<1$.

Moreover, there is

$$\begin{array}{l}\parallel x_{i_q}(k_{l0}+1)-P_Y(x_{i_q}(k_{l0}+1))\parallel \le (1-\frac{1}{2}{p}_{i_q}T)V(k_{l0})+\frac{1}{2}{p}_{i_q}T\\ \times (1-\frac{2h_{i_q}(k_{l0})c_{i_q}T}{p_{i_q}})V(k_{l0})\\ \le (1-h_{i_q}(k_{l0})c_{i_q}{T}^2)V(k_l)\triangleq m_{2}V(k_l)\end{array}$$

where $0<m_2<1$.

Case B. Suppose that there exists an agent $i_q$ that satisfies $\parallel {\tilde{v}}_{i_q}(k_{l0})-P_Y({\tilde{v}}_{i_q}(k_{l0}))\parallel \le (1-m_3)V(k_l)$ at time $k_{l0}\in [k_l,k_{l+1})$. It can be deduced from Lemmas 4 and 5 that

$$\begin{array}{ll}\parallel x_{i_q}(k_{l0}+1)-P_Y(x_{i_q}(k_{l0}+1))\parallel \le & (1-\frac{1}{2}{p}_{i_q}T)V(k_l)+\frac{1}{2}{p}_{i_q}T(1-m_3)V(k_l)\\ & \le (1-m_3{h}_{i_q}(k_{l0})c_{i_q}T)V(k_l)\triangleq m_{4}V(k_l)\end{array}$$

where $0<m_4<1$.

Moreover, it follows that

$$\begin{array}{l}\hspace{1em}\parallel {\tilde{v}}_{i_q}(k_{l0}+1)-P_Y({\tilde{v}}_{i_q}(k_{l0}+1))\parallel \\ \le {\tau }_{i_{q}c}(k_{l0}){\tau }_{i_{q}a}(k_{l0})V(k_l)+m_3{\tau }_{i_{q}c}(k_{l0}){\tau }_{i_{q}b}(k_{l0})V(k_l)\\ \hspace{1em}+\frac{2h_{i_q}(k_{l0})T}{p_{i_q}}{\displaystyle \sum _{j\in N_{i_q},j\ne i_q}{a}_{i_{q}j}(k_{l0})}V(k_l)\\ \le [1-(1-\frac{1}{2}{p}_{i_q}{h}_{i_q}(k_{l0})T)(1-m_3)]V(k_l)\\ \le m_4(k_{l0}+1)V(k_l)\end{array}$$

Then, after recursive calculations, we can obtain $\parallel x_{i_q}(k_l+1)-P_Y(x_{i_q}(k_l+1))\parallel \le m_{4}V(k_l)$ and $\parallel {\tilde{v}}_{i_q}(k_l+1)-P_Y({\tilde{v}}_{i_q}(k_l+1))\parallel \le m_{4}V(k_l)$ where $0<m_4<1$.

Case C. Suppose that there exist 2 agents $i_q$ and $i_s$ that satisfy $\parallel x_{i_q}(k_{l0})-P_Y(x_{i_q}(k_{l0}))\parallel \le m_{5}V(k_l)$ for some constant $0\le m_5<1$ and $a_{i_s{i}_q}>\gamma$ for some constant $\gamma >0$ at time $k_{l0}\in [k_l,k_{l+1})$, which means agent $i_s$ can receive information from agent $i_q$ at $k_{l0}$. It follows that

$$\begin{array}{cc}\hfill \parallel {\tilde{v}}_{i_s}(k_{l0}+1)-P_Y({\tilde{v}}_{i_s}(k_{l0}+1))\parallel & \le {\tau }_{i_{s}c}(k_{l0})V(k_l)+\frac{2h_{i_s}(k_{l0})T}{p_{i_s}}\hfill \\ & \times {\displaystyle \sum _{j\in N_{i_s},j\ne i_s}{a}_{i_{s}j}(k_{l0})}V(k_l)+\frac{2h_{i_s}(k_{l0})T{m}_5}{p_{i_s}}{a}_{i_s{i}_q}(k_{l0})V(k_l)\hfill \\ & \le [1-(1-m_5)\frac{2h_{i_s}(k_{l0})T}{p_{i_s}}\gamma ]V(k_l)\triangleq m_{6}V(k_l)\hfill \end{array}$$

where $0<m_6<1$.

From $p_{i_s}T<1$, it can be obtained that

$$0<1-(1-m_5)\frac{2h_{i_s}(k_{l0})T}{p_{i_s}}\gamma <1-(1-m_5)\gamma 2h_{i_s}(k_{l0})T^2<1$$

Hence, by using Lemma 5, it follows that

$$\begin{array}{ll}\parallel x_{i_s}(k_{l0}+1)& -P_Y(x_{i_s}(k_{l0}+1))\parallel \le (1-\frac{1}{2}{p}_{i_s}T)V(k_l)+\frac{1}{2}{p}_{i_s}T\\ & \hspace{1em}\times [1-(1-m_5)\frac{2h_{i_s}(k_{l0})T}{p_{i_s}}\gamma ]V(k_l)\\ & \le [1-(1-m_5)\gamma 2h_{i_s}(k_{l0})T^2]V(k_l)=m_{6}V(k_l)\end{array}$$

where $0<m_6<1$.

Theorem 1.

Based on Assumptions 1–4, applying constrained control input algorithm (2) to System (1), all followers are driven into the convex hull spanned by leaders, i.e., $\underset{k\to +\infty }{\lim }\parallel x_i(k)-P_Y(x_i(k))\parallel =0$ for $i\in {\mathcal{N}}_f$.

Proof of Theorem 1.

As shown in Assumption 2, it can always find one or more follower that can receive information from one of the static leaders directly in every time interval $[k_l,k_{l+1})$, which guarantees the condition of Case A. That is, $\parallel {\tilde{v}}_{i_q}(k_{l0}+1)-P_Y({\tilde{v}}_{i_q}(k_{l0}+1))\parallel \le m_{1}V(k_l)$ and $\parallel x_{i_q}(k_{l0}+1)-P_Y(x_{i_q}(k_{l0}+1))\parallel \le m_{2}V(k_l)$ hold, where $0<m_1<1$ and $0<m_2<1$; then, consider Case B, it follows that $\parallel x_{i_q}(k)-P_Y(x_{i_q}(k))\parallel \le m_{4}V(k_l)$ and $\parallel {\tilde{v}}_{i_q}(k)-P_Y({\tilde{v}}_{i_q}(k))\parallel \le m_{4}V(k_l)$ works for $0<m_4<1$ and all $k\in [k_{l+1},k_{l+n+1})$. It is clear that agent $i_s\ne i_q$ which could get information from agent $i_q$ or one of the static leaders at $k\in [k_{l+1},k_{l+2})$ exists. Hence, by using the calculation of Cases A, B, and C, it could be obtained that $\parallel {\tilde{v}}_{i_s}(k)-P_Y({\tilde{v}}_{i_s}(k))\parallel \le {\tilde{m}}_{6}V(k_l)$ and $\parallel x_{i_s}(k)-P_Y(x_{i_s}(k))\parallel \le {\tilde{m}}_{6}V(k_l)$ for $0<{\tilde{m}}_6<1$ and all $k\in [k_{l+2},k_{l+n})$. Recall that the constants $m_1$, $m_2$, $m_4$, and ${\tilde{m}}_6$ are only affected by constants $c_i$, $T$, $p_i$, $h_i$, $\gamma$, and topologies in the time interval. Therefore, it can certainly find a constant $0<\eta <1$ satisfying $\eta >m_i$, where $i=1,2,4,6$. Given all this, $V(k_{m+n})<{\eta }^{n}V(k_m)$ holds. To summarize all the calculations, we have $\underset{k\to +\infty }{\lim }\parallel x_i(k)-P_Y(x_i(k))\parallel =\underset{k\to +\infty }{\lim }V(k)=0$ for $i\in {\mathcal{N}}_f$. □

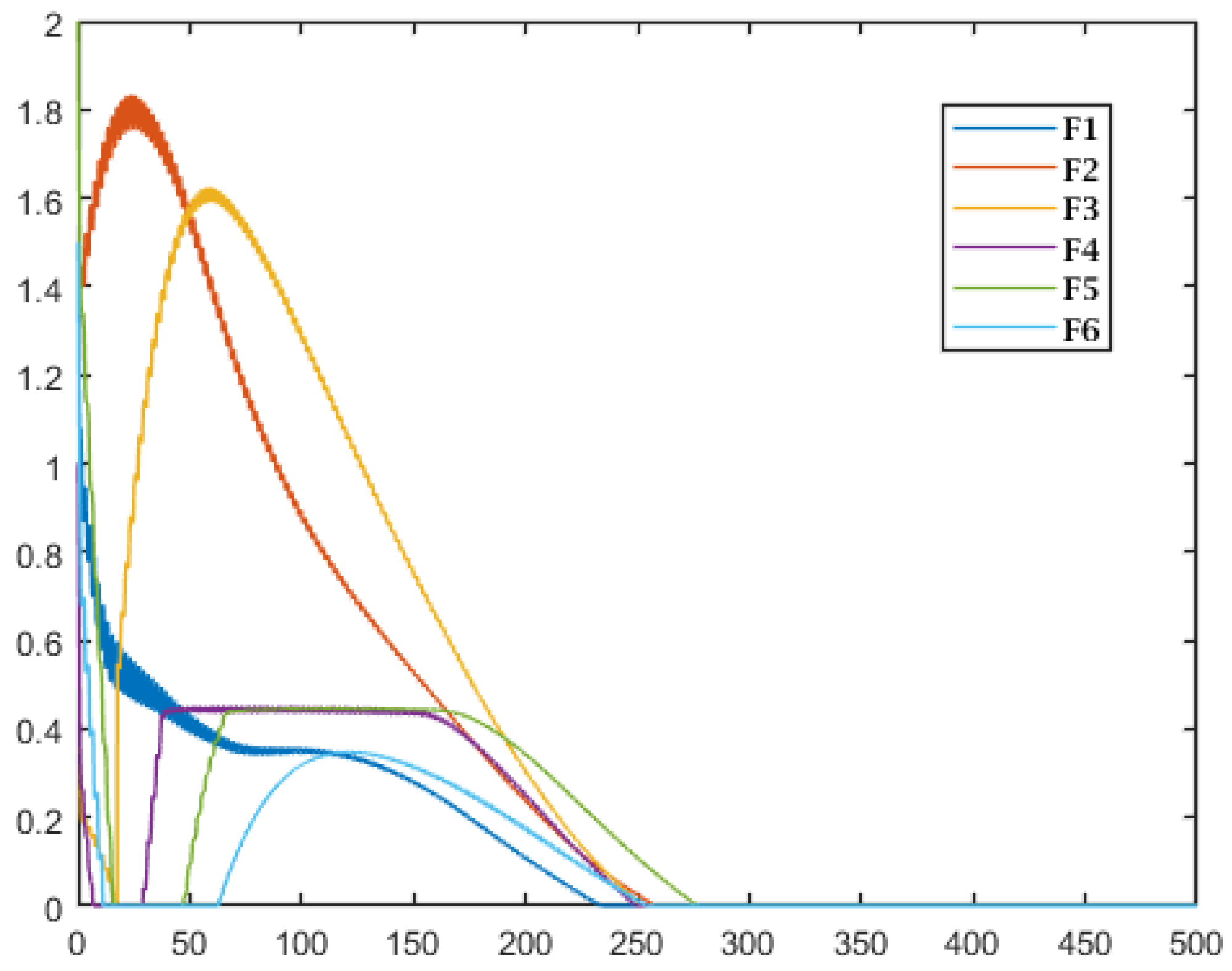
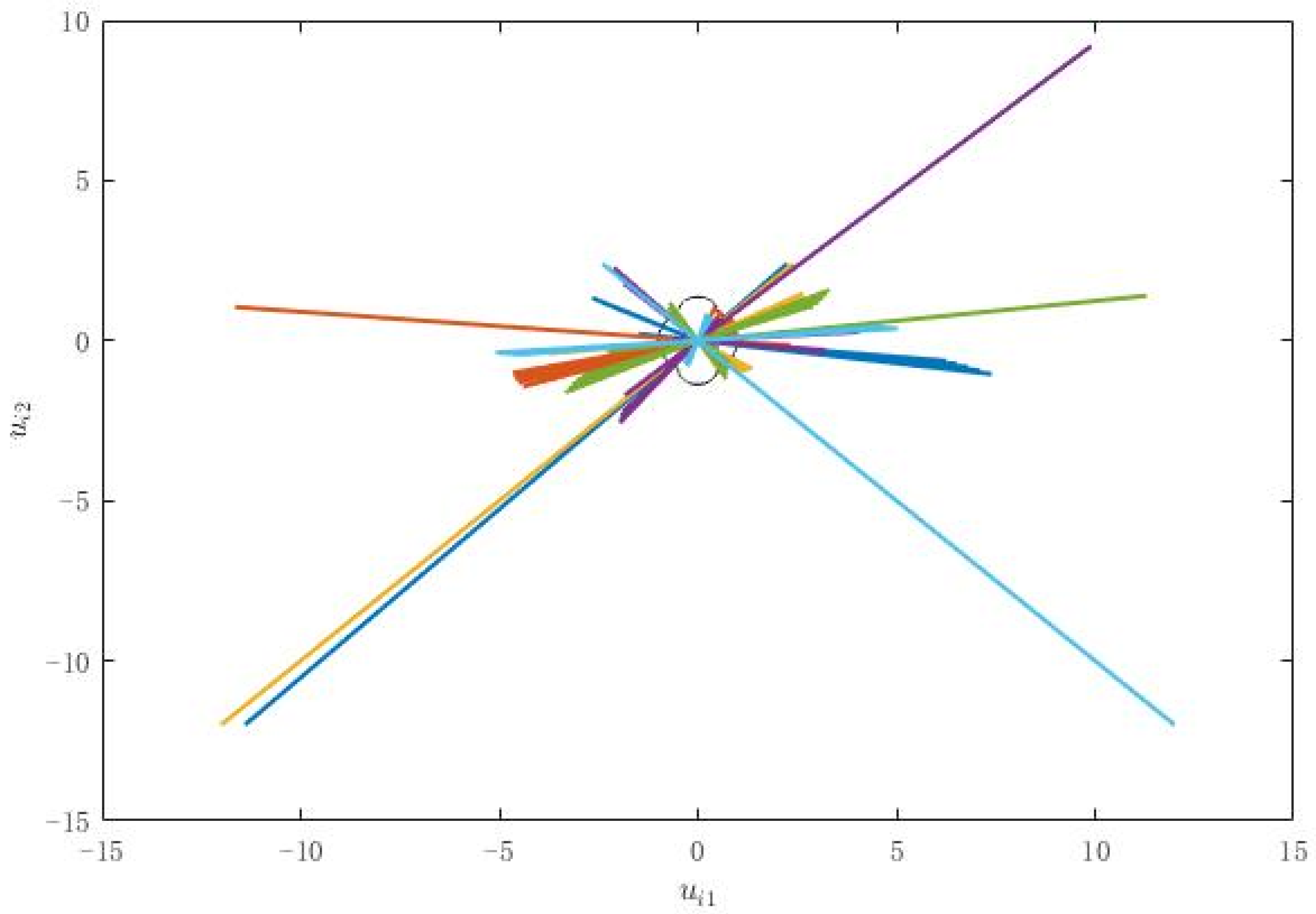
4. A Numerical Example

4.1. Simulation Parament Configuration

Give a multiagent system composed of 6 followers and 4 leaders. The graphs of switching topologies are shown in Figure 3. The switching step of the system is 0.5 s and the sequence of the graphs is $\{G_a,G_b\}$, $\{G_b,G_c\}$, $\{G_c,G_d\}$, $\{G_d,G_a\}$. The weights of all edges $a_{ij}=0.7$. The parameters are $c_i=0.3$ and $p_i=12$ for $i\in {\mathcal{N}}_f$ and the sampling time is $T=0.1 \mathrm{s}$. The control input constraint set is $U_i=\{x|\parallel x-{[0,-\sqrt{3}/2]}^T\parallel \le 0.5\}\cup \{x|\parallel x\parallel \le 1\}\cup \{x|\parallel x-{[0,\sqrt{3}/2]}^T\parallel \le 0.5\}$. The position constraint sets of the followers are $X_1=\{x|\parallel x-{[0,1]}^T\parallel \le \sqrt{6}\}$ and $X_2=\{x|\parallel x-{[2,1]}^T\parallel \le \sqrt{6}\}$. For followers, the initial states of position are ${[-1.5,2;-2,0.5;0,-1;3,3;4,1;3.5,0]}^T$ and the initial states of velocity states are ${[1,1;1,0;1,1;-1,-1;-1,0;-1,1]}^T$. For leaders, the initial states of position is ${[0,2;2,2;2,0;0,0]}^T$.

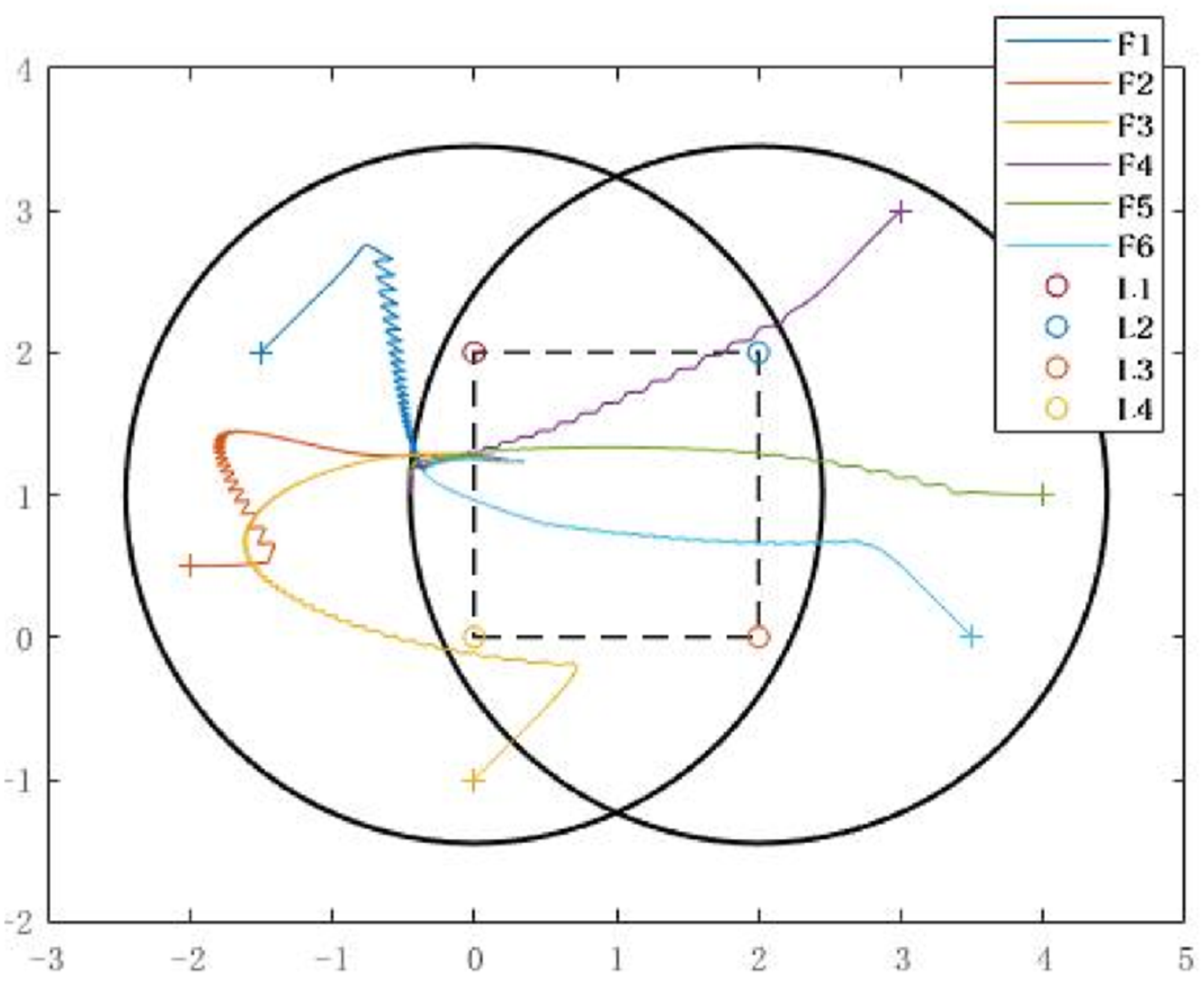
4.2. Simulation Result

The convex hull is spanned by static points, as illustrated in Figure 4. Figure 5 shows the control input of followers. The containment errors of followers are shown in Figure 6.

The switching graphs are illustrated in Figure 3 which satisfy the assumption that each follower could get information from at least one leader directly or indirectly in every time interval. In Figure 4, Followers 1, 2, and 3 stay in the left circle which illustrates the constraint of position, while Followers 4, 5, and 6 stay in the right circle. The convex region spread by the 4 leaders is the target region. Figure 5 gives the constraints of control input that is a nonconvex hull. It shows the containment errors of followers by using the distance form every follower to the target region in Figure 6.

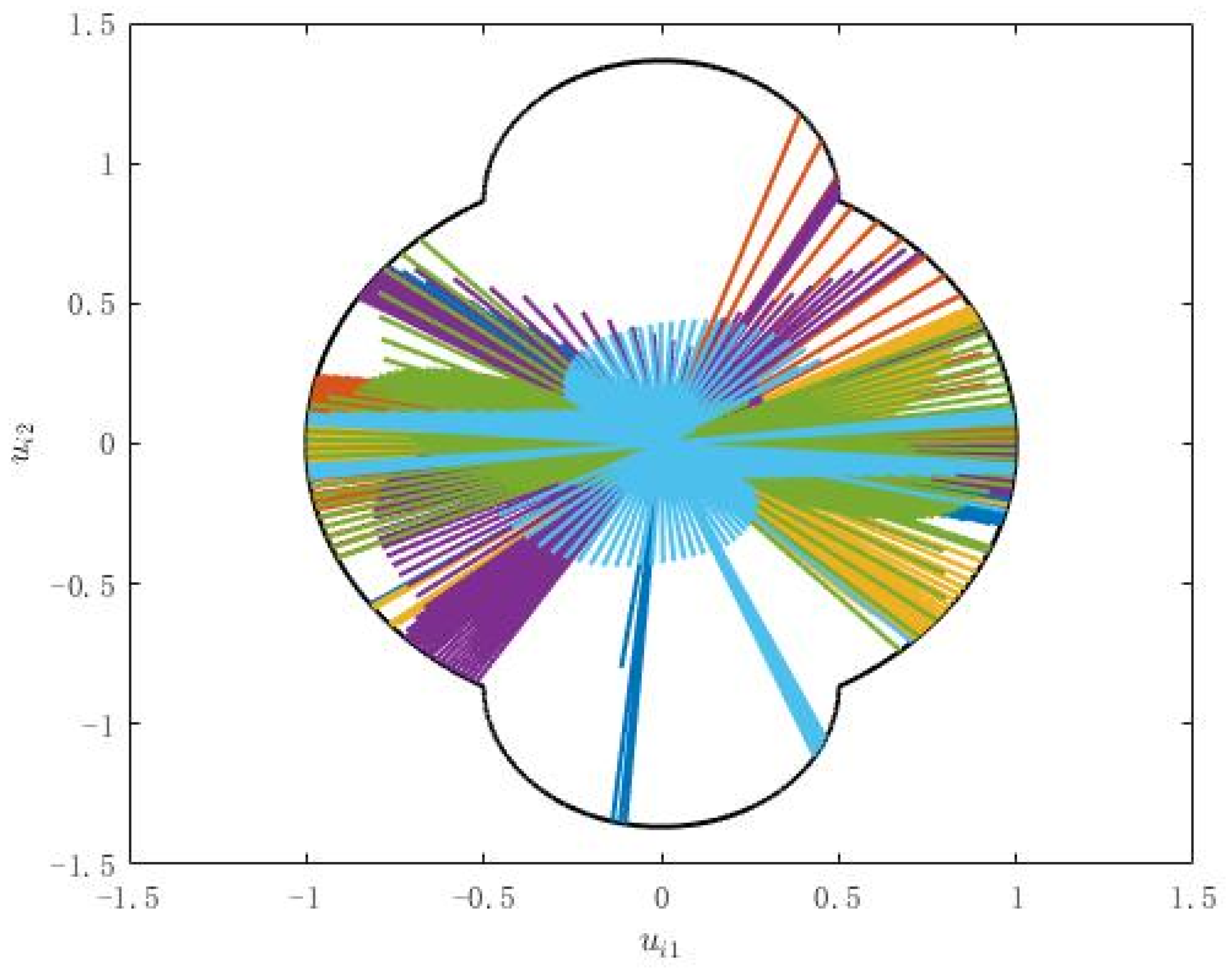
4.3. Simulation Comparison

In this section, we provide some simulation comparison results.

As compared with Figure 5, Figure 7 shows the control input without constraints. It is clear that our algorithm could be more practical in reality. In Figure 8, we can see that the algorithm can still achieve containment control when a sudden interference happens, which means the algorithm has stability to some extent.

5. Conclusions

In the above work, containment control for a multiagent system with nonconvex control input and position constraints was discussed. To solve the problem, a nonlinear algorithm with projection operator for followers was proposed. After the analysis of the distance from every follower to the convex hull spanned by static leaders, it is found that all followers could be driven into the convex hull formed by leaders and the position states of followers remain in the constraint set. Finally, a numerical example is given to guarantee the theoretical results.

Under analysis of the algorithm and simulation results, our work has the following advantages:

(1)

The projection operator we introduced can ensure the control input of every follower to lie in a nonconvex set which is useful in practice. It has apparent superiority as compared with other algorithms which can be seen in the simulation.

(2)

With the existence of constraints both in control input and position, the system has strong nonlinearity. By model transformation and introducing new error variable, we successfully remove the nonlinearity and achieve containment control.

(3)

In the process of analysis, we introduce a geometrical method which uses two similar triangles. This method solves the problem in the proof of effectiveness of our algorithm.

Of course, there are still many shortcomings in our current work. In future study, we will take the dynamic situation of leaders into consideration. Meanwhile, we hope to make better analysis and results against interference, and therefore, the algorithm may get closer to practical application.