Advances in Parameter Estimation and Learning from Data for Mathematical Models of Hepatitis C Viral Kinetics
Abstract
:1. Introduction
2. The Models Description
2.1. The Biphasic Model
2.2. The Multiscale Model
3. Sensitivity Analysis
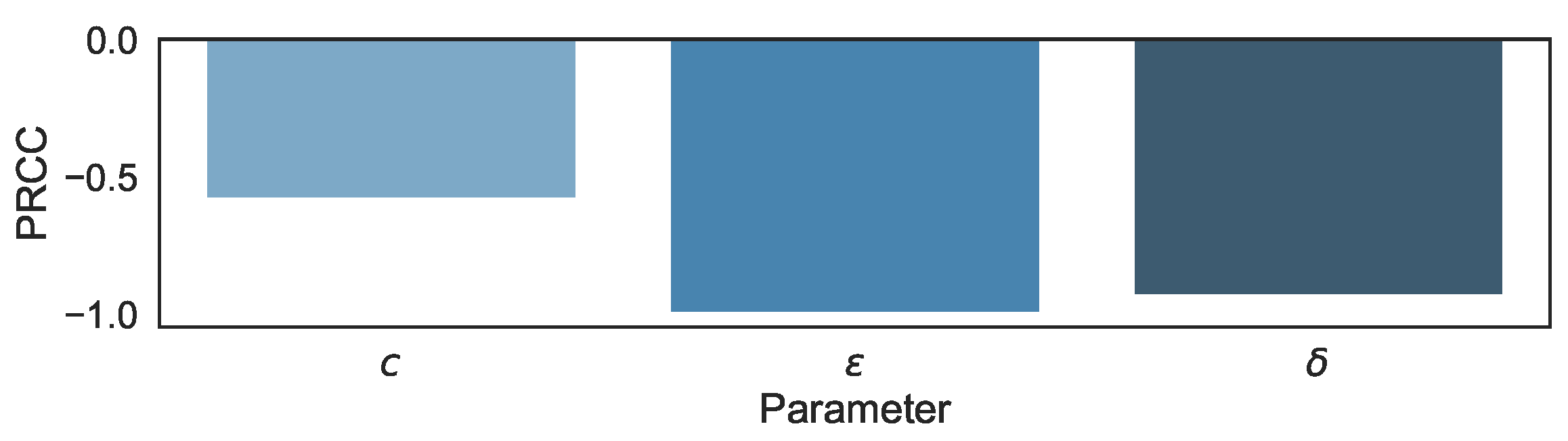
3.1. Sensitivity Analysis in the Biphasic Model
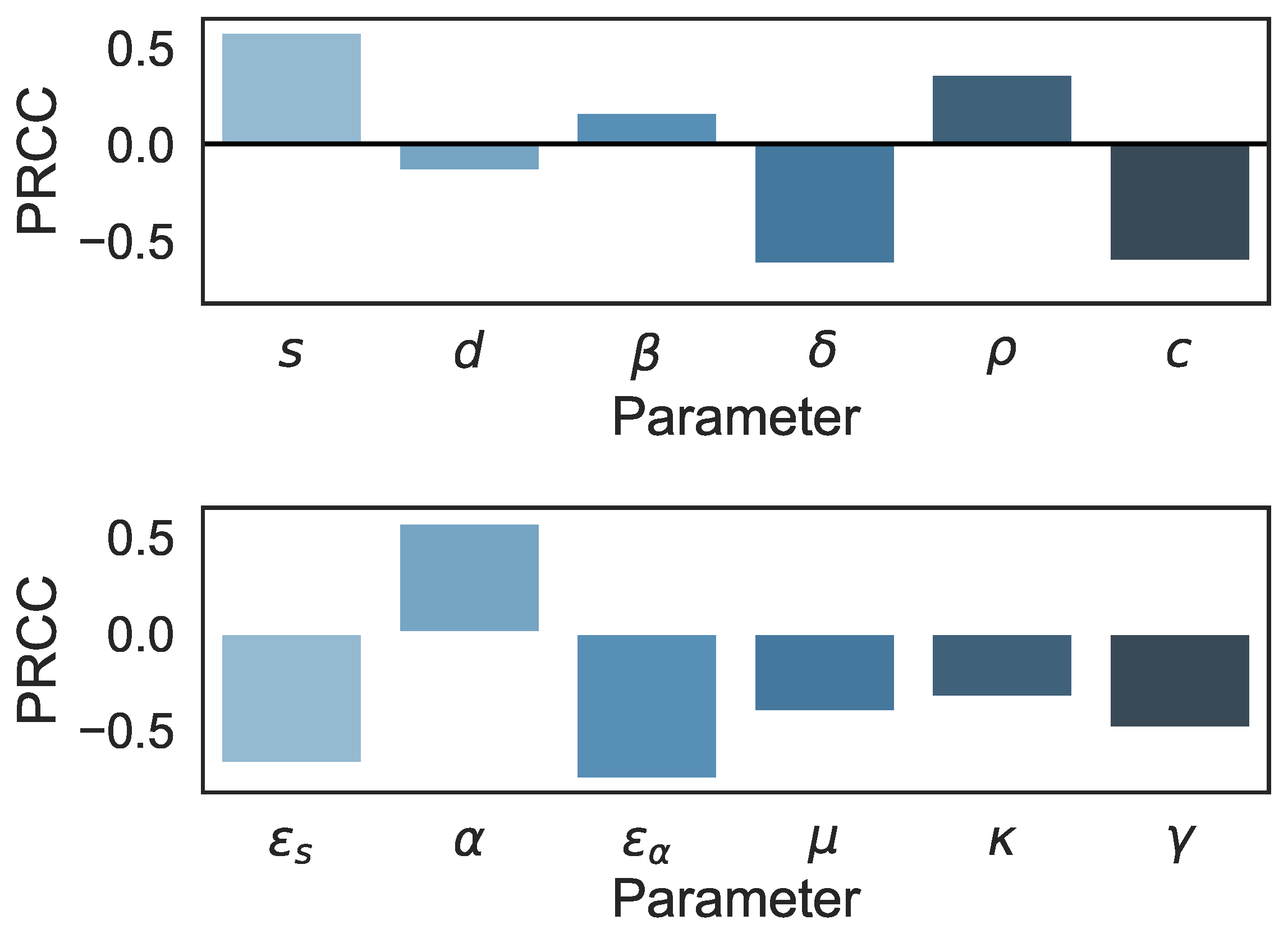
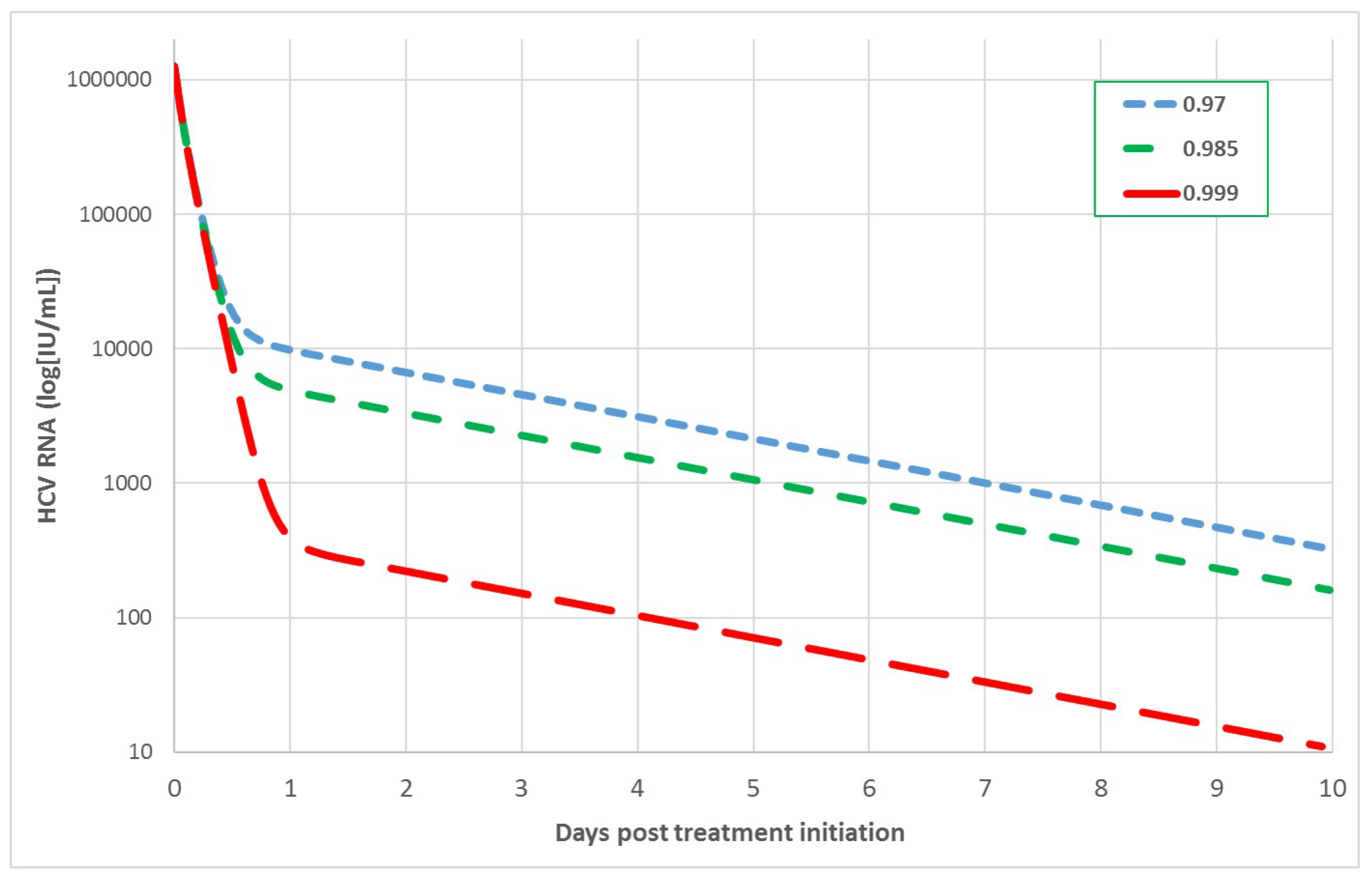
3.2. Sensitivity Analysis in the Multiscale Model
4. Machine Learning
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
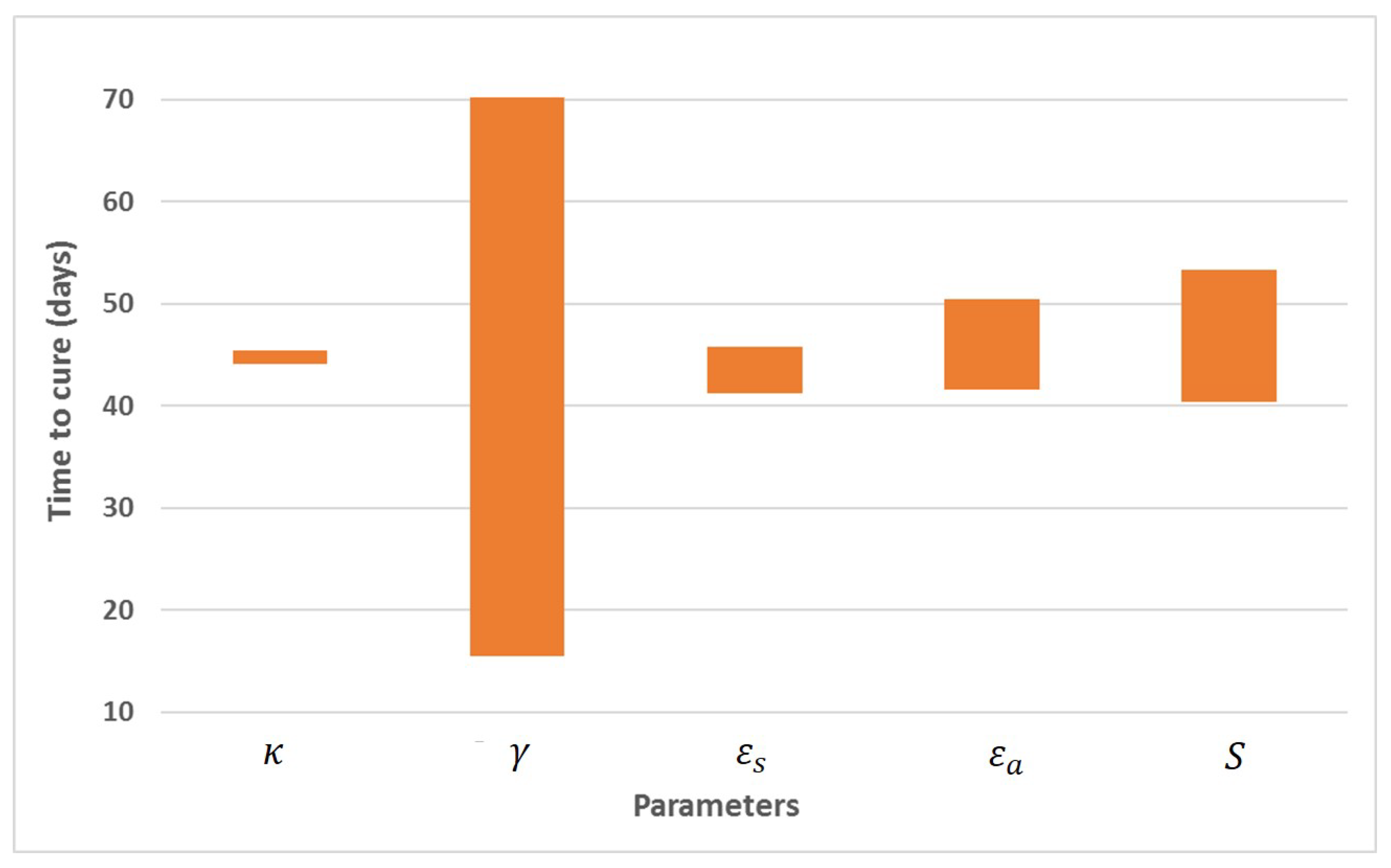
Appendix A. Influence of Multiscale Model Parameters on Time-to-Cure
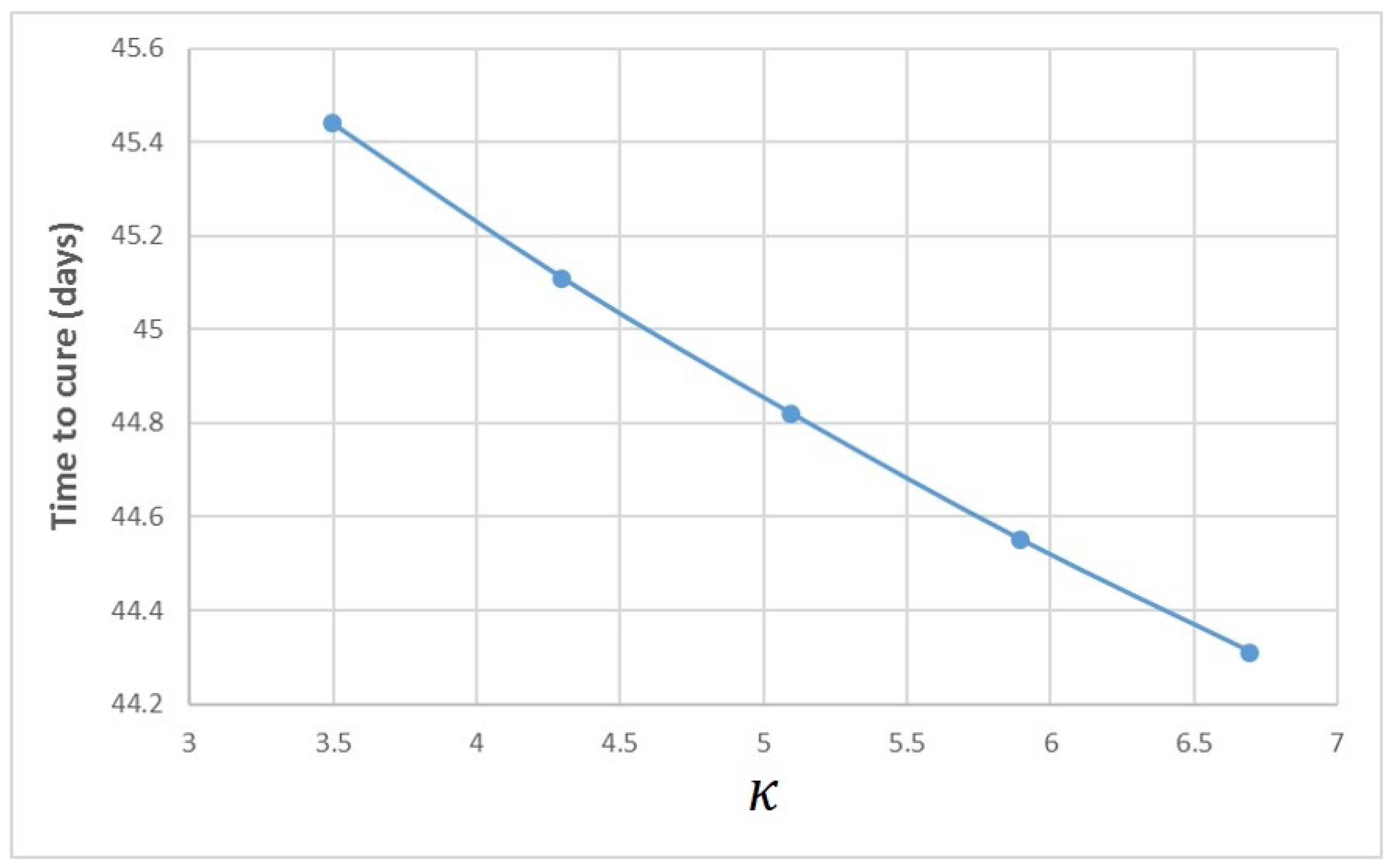

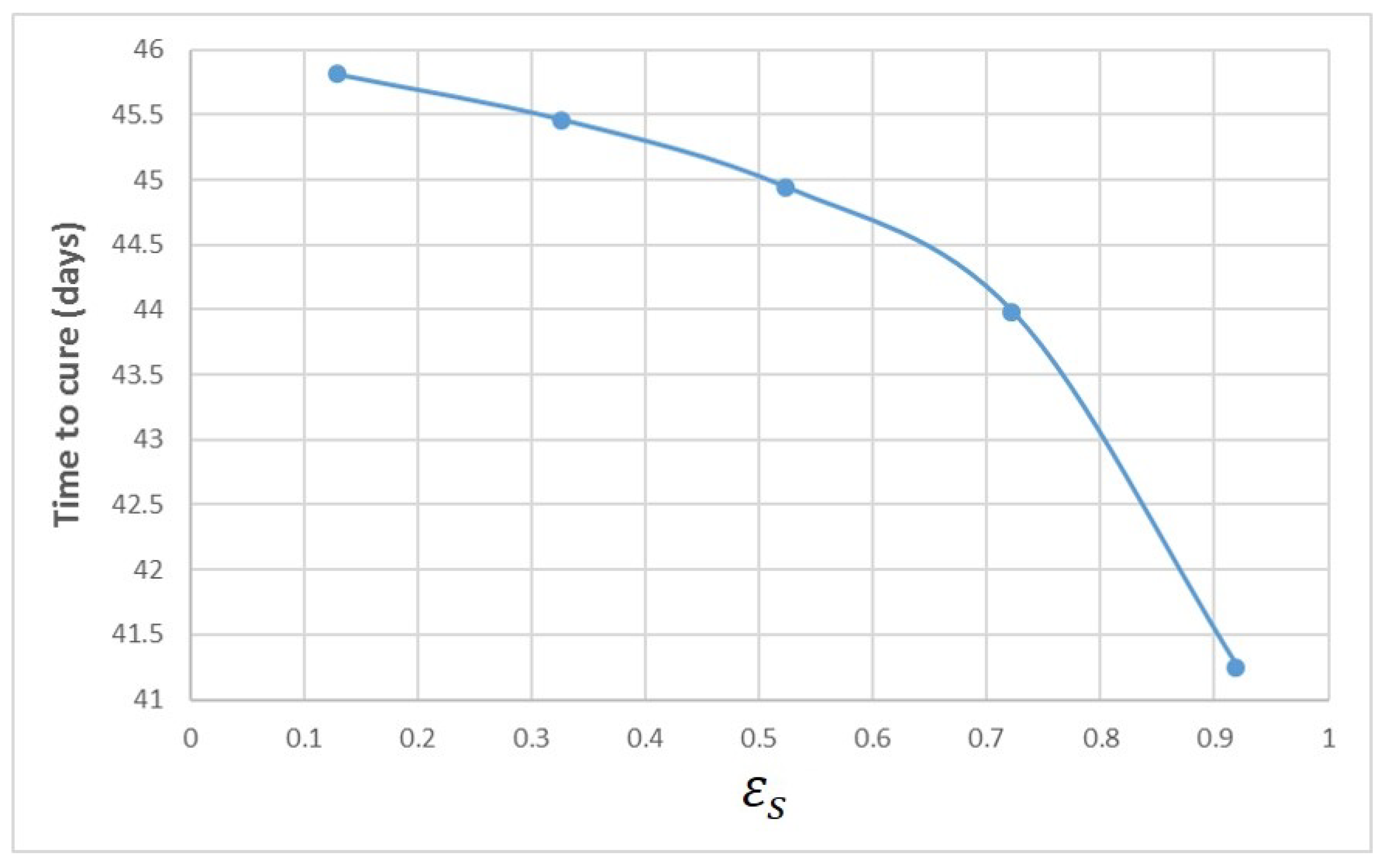
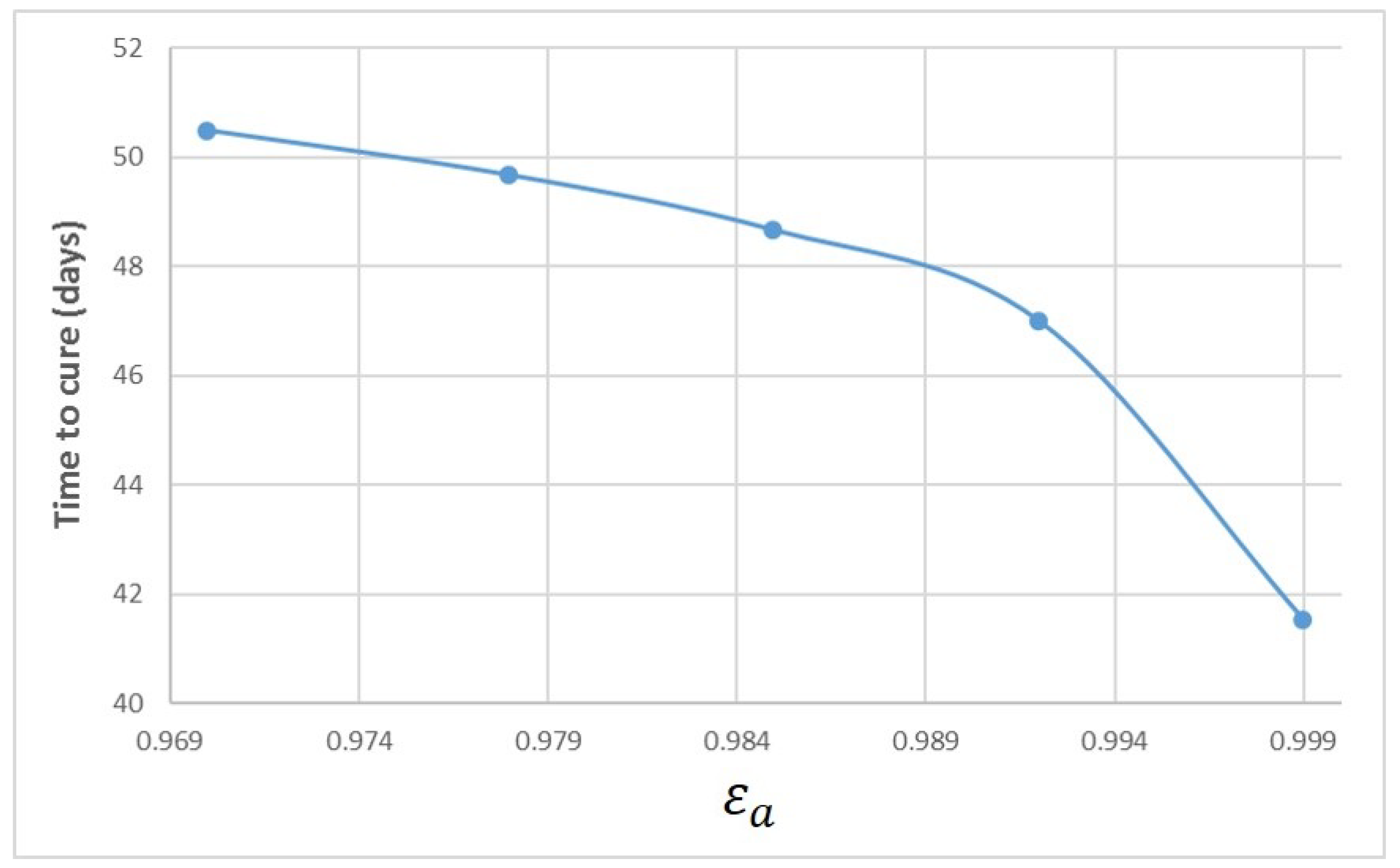
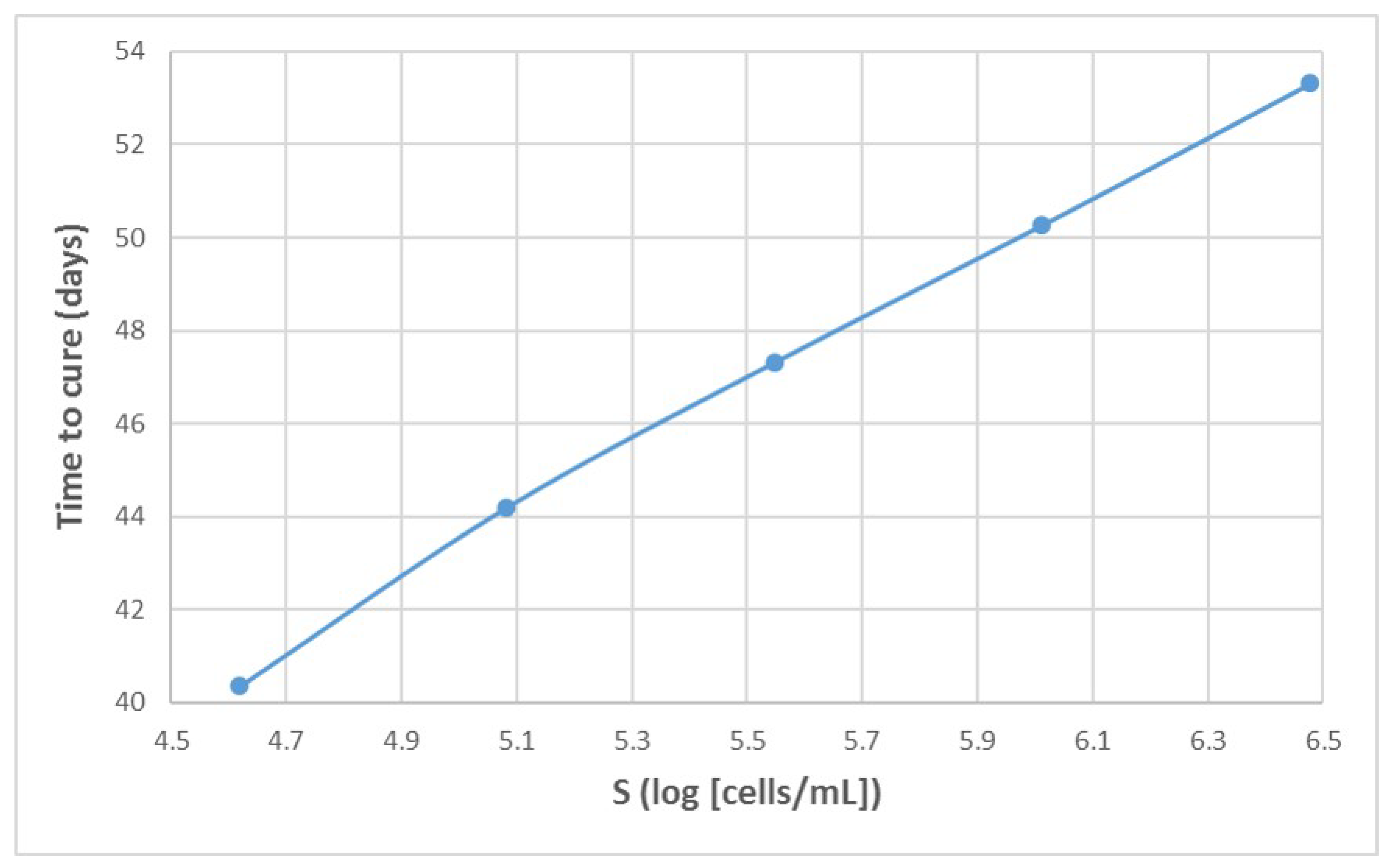
References
- Perelson, A.S. Modelling viral and immune system dynamics. Nat. Rev. Immunol. 2002, 2, 28–36. [Google Scholar] [CrossRef] [PubMed]
- Ho, D.D.; Neumann, A.U.; Perelson, A.S.; Chen, W.; Leonard, J.M.; Markowitz, M. Rapid turnover of plasma virions and CD4 lymphocytes in HIV-1 infection. Nature 1995, 373, 123. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.S.; Neumann, A.U.; Markowitz, M.; Leonard, J.M.; Ho, D.D. HIV-1 dynamics in vivo: Virion clearance rate, infected cell life-span, and viral generation time. Science 1996, 271, 1582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Burg, D.; Rong, L.; Neumann, A.U.; Dahari, H. Mathematical modeling of viral kinetics under immune control during primary HIV-1 infection. J. Theor. Biol. 2009, 259, 751–759. [Google Scholar] [CrossRef] [PubMed]
- Aviran, A.; Shah, P.S.; Schaffer, D.P.; Arkin, P.A. Computational Models of HIV-1 Resistance to Gene Therapy Elucidate Therapy Design Principles. PLoS Comput. Biol. 2010, 6, e1000883. [Google Scholar] [CrossRef]
- Ciupe, S.M.; Ribeiro, R.M.; Nelson, P.W.; Dusheiko, G.; Perelson, A.S. The role of cells refractory to productive infection in acute hepatitis B viral dynamics. Proc. Natl. Acad. Sci. USA 2007, 104, 5050–5055. [Google Scholar] [CrossRef] [Green Version]
- Ribeiro, R.M.; Germanidis, G.; Powers, K.A.; Pellegrin, B.; Nikolaidis, P.; Perelson, A.S.; Pawlotsky, J.M. Hepatitis B Virus Kinetics under Therapy Sheds Light on Differences Between e-antigen Positive and Negative Infection. J. Infect. Dis. 2010, 202, 1309–1318. [Google Scholar] [CrossRef]
- Nowak, M.A.; Bonhoeffer, S.; Hill, A.M.; Boehme, R.; Thomas, H.C.; McDade, H. Viral dynamics in hepatitis B virus infection. Proc. Natl. Acad. Sci. USA 1996, 93, 4398–4402. [Google Scholar] [CrossRef] [Green Version]
- Koh, C.; Canini, L.; Dahari, H.; Zhao, X.; Uprichard, S.L.; Haynes-Williams, V.; Winters, M.A.; Subramanya, G.; Cooper, S.L.; Pinto, P.; et al. Oral prenylation inhibition with lonafarnib in chronic hepatitis D infection: A proof-of-concept randomised, double-blind, placebo-controlled phase 2A trial. Lancet Infect. Dis. 2015, 15, 1167–1174. [Google Scholar] [CrossRef] [Green Version]
- Guedj, J.; Rotman, Y.; Cotler, S.J.; Koh, C.; Schmid, P.; Albrecht, J.; Haynes-Williams, V.; Liang, T.J.; Hoofnagle, J.H.; Heller, T.; et al. Understanding early serum hepatitis D virus and hepatitis B surface antigen kinetics during pegylated interferon-alpha therapy via mathematical modeling. Hepatology 2014, 60, 1902–1910. [Google Scholar] [CrossRef]
- Shekhtman, L.; Cotler, S.J.; Hershkovich, L.; Uprichard, S.L.; Bazinet, M.; Pantea, V.; Cebotarescu, V.; Cojuhari, L.; Jimbei, P.; Krawczyk, A.; et al. Modelling hepatitis D virus RNA and HBsAg dynamics during nucleic acid polymer monotherapy suggest rapid turnover of HBsAg. Sci. Rep. 2020, 10, 7837. [Google Scholar] [CrossRef] [PubMed]
- Shekhtman, L.; Cotler, S.J.; Ploss, A.; Dahari, H. Mathematical modeling suggests that entry-inhibitor bulevirtide may interfere with hepatitis D virus clearance from circulation. J. Hepatol. 2022, 76, 1229–1231. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Lipton, H.L.; Perelson, A.S.; Dahari, H. Modeling the acute and chronic phases of Theiler murine encephalomyelitis virus infection. J. Virol. 2013, 87, 4052–4059. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schiffer, J.T.; Abu-Raddad, L.; Mark, K.E.; Zhu, J.; Selke, S.; Magaret, A.; Wald, A.; Corey, L. Frequent release of low amounts of herpes simplex virus from neurons: Results of a mathematical model. Sci. Transl. Med. 2009, 1, 7ra16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Neumann, A.U.; Lam, N.P.; Dahari, H.; Gretch, D.R.; Wiley, T.E.; Layden, T.J.; Perelson, A.S. Hepatitis C viral dynamics in vivo and the antiviral efficacy of interferon-α therapy. Science 1998, 282, 103–107. [Google Scholar] [CrossRef]
- Shekhtman, L.; Navasa, M.; Sansone, N.; Crespo, G.; Subramanya, G.; Chung, T.L.; Cardozo-Ojeda, E.F.; Pérez-del Pulgar, S.; Perelson, A.S.; Cotler, S.J.; et al. Modeling hepatitis C virus kinetics during liver transplantation reveals the role of the liver in virus clearance. Elife 2021, 10, e65297. [Google Scholar] [CrossRef]
- Wasik, S.; Jackowiak, P.; Figlerowicz, M.; Blazewicz, J. Multi-agent model of hepatitis C virus infection. Artif. Intell. Med. 2014, 60, 123–131. [Google Scholar] [CrossRef] [Green Version]
- Boianelli, A.; Nguyen, V.K.; Ebensen, T.; Schulze, K.; Wilk, E.; Sharma, N.; Stegemann-Koniszewski, S.; Bruder, D.; Toapanta, F.R.; Guzmán, C.A.; et al. Modeling influenza virus infection: A roadmap for influenza research. Viruses 2015, 7, 5274–5304. [Google Scholar] [CrossRef] [Green Version]
- Madelain, V.; Oestereich, L.; Graw, F.; Nguyen, T.H.T.; De Lamballerie, X.; Mentré, F.; Günther, S.; Guedj, J. Ebola virus dynamics in mice treated with favipiravir. Antivir. Res. 2015, 123, 70–77. [Google Scholar] [CrossRef] [Green Version]
- Chertow, D.S.; Shekhtman, L.; Lurie, Y.; Davey, R.T.; Heller, T.; Dahari, H. Modeling challenges of Ebola virus–host dynamics during infection and treatment. Viruses 2020, 12, 106. [Google Scholar] [CrossRef] [Green Version]
- Dahari, H.; Canini, L.; Graw, F.; Uprichard, S.L.; Araujo, E.S.A.; Penaranda, G.; Coquet, E.; Chiche, L.; Riso, A.; Renou, C.; et al. HCV kinetic and modeling analyses indicate similar time to cure among sofosbuvir combination regimens with daclatasvir, simeprevir or ledipasvir. J. Hepatol. 2016, 54, 1232–1239. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dasgupta, S.; Imamura, M.; Gorstein, E.; Nakahara, T.; Tsuge, M.; Churkin, A.; Yardeni, D.; Etzion, O.; Uprichard, S.L.; Barash, D.; et al. Modeling-Based Response-Guided Glecaprevir-Pibrentasvir Therapy for Chronic Hepatitis C to Identify Patients for Ultrashort Treatment Duration. J. Infect. Dis. 2020, 222, 1165–1169. [Google Scholar] [CrossRef] [PubMed]
- Dahari, H.; Shteingart, S.; Gafanovich, I.; Cotler, S.J.; D’Amato, M.; Pohl, R.T.; Weiss, G.; Ashkenazi, Y.J.; Tichler, T.; Goldin, E.; et al. Sustained virological response with intravenous silibinin: Individualized IFN-free therapy via real-time modelling of HCV kinetics. Liver Int. 2015, 35, 289–294. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Etzion, O.; Dahari, H.; Yardeni, D.; Issachar, A.; Nevo-Shor, A.; Cohen-Naftaly, M.; Ashur, Y.; Uprichard, S.L.; Sneh Arbib, O.; Munteanu, D.; et al. Response guided therapy for reducing duration of direct acting antivirals in chronic hepatitis C infected patients: A Pilot study. Sci. Rep. 2020, 10, 17820. [Google Scholar] [CrossRef] [PubMed]
- Rong, L.; Dahari, H.; Ribeiro, R.M.; Perelson, A.S. Rapid emergence of protease inhibitor resistance in hepatitis C virus. Sci. Transl. Med. 2010, 2, 30ra32. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goyal, A.; Lurie, Y.; Meissner, G.; Major, M.; Sansone, N.; Uprichard, S.; Cotler, S.; Dahari, H. Modeling HCV cure after an ultra-short duration of therapy with direct acting agents. Antivir. Res. 2017, 30, 281–285. [Google Scholar] [CrossRef]
- Rong, L.; Guedj, J.; Dahari, H.; Coffield, D.J.J.; Levi, M.; Smith, P.; Perelson, A.S. Analysis of hepatitis C virus decline during treatment with the protease inhibitor danoprevir using a multiscale model. PLoS Comput. Biol. 2013, 9, e1002959. [Google Scholar] [CrossRef]
- Guedj, J.; Dahari, H.; Rong, L.; Sansone, N.D.; Nettles, R.E.; Cotler, S.J.; Layden, T.J.; Uprichard, S.L.; Perelson, A.S. Modeling shows that the NS5A inhibitor daclatasvir has two modes of action and yields a shorter estimate of the hepatitis C virus half-life. Proc. Natl. Acad. Sci. USA 2013, 110, 3991–3996. [Google Scholar] [CrossRef] [Green Version]
- Reinharz, V.; Churkin, S.; Dahari, H.; Barash, D. A Robust and Efficient Numerical Method for RNA-Mediated Viral Dynamics. Front. Appl. Math. Stat. 2017, 3, 20. [Google Scholar] [CrossRef] [Green Version]
- Rong, L.; Perelson, A.S. Mathematical analysis of multiscale models for hepatitis C virus dynamics under therapy with direct-acting antiviral agents. Math. Biosci. 2013, 245, 22–30. [Google Scholar] [CrossRef] [Green Version]
- Reinharz, V.; Dahari, H.; Barash, D. Numerical schemes for solving and optimizing multiscale models with age of hepatitis C Virus Dynamics. Math. Biosci. 2018, 300, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Weickert, J.; Romeny, B.T.H.; Viergever, M. Efficient and reliable schemes for nonlinear diffusion filtering. IEEE Trans. Imag. Proc. 1998, 7, 398–410. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barash, D. Nonlinear Diffusion Filtering on Extended Neighborhood. Appl. Num. Math. 2005, 52, 1–11. [Google Scholar] [CrossRef]
- Rosenbrock, H. Some general implicit processes for the numerical solution of differential equations. Comput. J. 1963, 5, 329–330. [Google Scholar] [CrossRef] [Green Version]
- Reinharz, V.; Churkin, A.; Lewkiewicz, S.; Dahari, H.; Barash, D. A Parameter Estimation Method for Multiscale Models of hepatitis C Virus Dynamics. Bull. Math. Biol. 2019, 81, 3675–3721. [Google Scholar] [CrossRef] [PubMed]
- Churkin, A.; Kriss, S.; Uziel, A.; Goyal, R.; Zakh, R.; Cotler, S.J.; Etzion, O.; Shlomai, A.; Rotstein, H.G.; Dahari, H.; et al. Machine Learning for Mathematical Models of HCV Kinetics During Antiviral Therapy. Math. Biosci. 2022, 343, 108756. [Google Scholar] [CrossRef]
- Dahari, H.; Lo, A.; Ribeiro, R.M.; Perelson, A.S. Modeling hepatitis C virus dynamics: Liver regeneration and critical drug efficacy. J. Theor. Biol. 2007, 247, 371–381. [Google Scholar] [CrossRef] [Green Version]
- Quintela, B.; Conway, J.; Hyman, J.; Reis, R.; dos Santos, R.; Lobosco, M.; Perelson, A. An Age-based Multiscale Mathematical Model of the Hepatitis C Virus Life-cycle during Infection and Therapy: Including Translation and Replication. In Proceedings of the VII Latin American Congress on Biomedical Engineering CLAIB 2016, Bucaramanga, Colombia, 26–28 October 2016; Springer: Berlin/Heidelberg, Germany, 2017; pp. 508–511. [Google Scholar]
- Kitagawa, K.; Nakaoka, S.; Asai, Y.; Watashi, K.; Iwami, S. A PDE Multiscale Model of hepatitis C virus infection can be transformed to a system of ODEs. J. Theor. Biol. 2018, 267, 330–340. [Google Scholar] [CrossRef]
- Kitagawa, K.; Kuniya, T.; Nakaoka, S.; Asai, Y.; Watashi, K.; Iwami, S. Mathematical analysis of a transformed ODE from a PDE multiscale model of hepatitis C virus infection. Bull. Math. Biol. 2019, 81, 1427–1441. [Google Scholar] [CrossRef]
- Goncalves, A.; Lemenuel-Diot, A.; Cosson, V.; Jin, Y.; Feng, S.; Bo, Q.; Guedj, J. What drives the dynamics of HBV RNA during treatment? J. Viral Hepat. 2021, 28, 383–392. [Google Scholar] [CrossRef]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bazan, E.; Dokladal, P.; Dokladalova, E. Quantitative Analysis of Similarity Measures and Distributions. In Proceedings of the 30th British Machine Vision Conference, Cardiff, UK, 9–12 September 2019. [Google Scholar]
- Ivry, T.; Michal, S.; Avihoo, A.; Sapiro, G.; Barash, D. An Image Processing Approach to Computing Distances Between RNA Secondary Structures Dot Plots. Algorithms Mol. Biol. 2009, 4, 4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Prentice Hall PTR: Hoboken, NJ, USA, 1998. [Google Scholar]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pall, C.J. Data Mining: Practical Machine Learning Tools and Techniques, 3rd ed.; Morgan Kaufmann: Burlington, MA, USA, 2011. [Google Scholar]
- Strang, G. Linear Algebra and Learning from Data, 1st ed.; Wellesley-Cambridge Press: Wellesley, MA, USA, 2019. [Google Scholar]
- Goyal, A.; Churkin, A.; Barash, D.; Cotler, S.J.; Shlomai, A.; Etzion, O.; Dahari, H. Modeling-Based Response-Guided DAA Therapy for Chronic Hepatitis C to Identify Individuals for Shortening Treatment Duration. Open Forum Infec. Dis. 2022, 9, ofac157. [Google Scholar] [CrossRef] [PubMed]

| c | ||
|---|---|---|
| s | d | c | |||
|---|---|---|---|---|---|
| 130,000 (65,000, 260,000) | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reinharz, V.; Churkin, A.; Dahari, H.; Barash, D. Advances in Parameter Estimation and Learning from Data for Mathematical Models of Hepatitis C Viral Kinetics. Mathematics 2022, 10, 2136. https://doi.org/10.3390/math10122136
Reinharz V, Churkin A, Dahari H, Barash D. Advances in Parameter Estimation and Learning from Data for Mathematical Models of Hepatitis C Viral Kinetics. Mathematics. 2022; 10(12):2136. https://doi.org/10.3390/math10122136
Chicago/Turabian StyleReinharz, Vladimir, Alexander Churkin, Harel Dahari, and Danny Barash. 2022. "Advances in Parameter Estimation and Learning from Data for Mathematical Models of Hepatitis C Viral Kinetics" Mathematics 10, no. 12: 2136. https://doi.org/10.3390/math10122136
APA StyleReinharz, V., Churkin, A., Dahari, H., & Barash, D. (2022). Advances in Parameter Estimation and Learning from Data for Mathematical Models of Hepatitis C Viral Kinetics. Mathematics, 10(12), 2136. https://doi.org/10.3390/math10122136







