Impulsive Stabilization on Hyper-Chaotic Financial System under Neumann Boundary
Abstract
:1. Introduction
- □
- The newly obtained stability criterion admits big impulse, reducing some conservatism of criteria. Particularly, one of numerical examples shows that the new stability criterion allows the impulse strength to be bigger than 1. In fact, impulse was actually required to be less than 1 in some of the literature ([25,26]).
- □
- The financial system is stable with positive interest rates and other economic indicators, which is in line with the national conditions of most countries. Particularly, in previous research papers ([5,6,9]), for example, in [6], the equilibrium point only involves positive interest rate , but other economic indicators are negative. However, positive stationary solution in this paper implies that all economic indicators are not negative. Particularly, Examples 1 and 2 in this article illustrate that all economic indicators are bigger than , which means newly derived criteria really have some advantages over those in previous articles.
- □
- Diffusion leads to more complexity and chaos on the dynamic behavior of the system, and hence we have to adopt new methods, which are different from the known literature without diffusion, to solve the stabilization of reaction-diffusion financial system. In fact, it is the first article to employ Laplacian semigroup together with two different fixed point theorems to get the existence of PSS and its global stabilization for the hyper-chaotic financial system.
2. Preliminaries
- (A1)
- , where constants .
- (A2)
- there are positive constants such that
3. Main Results
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- ⋄
- Denote by a bounded domain in with smooth boundary ;
- ⋄
- Denote by the external normal direction of ;
- ⋄
- ;
- ⋄
- ;
- ⋄
- Denote by the norm of the Sobolev space ;
- ⋄
- Denote by Laplace operator, and by the Laplacian semigroup;
- ⋄
References
- Chen, S.; Lu, J. Synchronization of an uncertain unified chaotic system via adaptive control. Chaos Solitons Fractals 2022, 14, 643–647. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Chen, Y. Study for the bifurcation topological structure and the global complicated character of a kind of nonlinear finance system (II). Appl. Math. Mech. 2001, 22, 1375–1382. [Google Scholar] [CrossRef]
- Chen, W. Dynamics and control of a financial system with time-delayed feedbacks. Chaos Solitons Fractals 2008, 37, 1198–1207. [Google Scholar] [CrossRef]
- Bhalekar, S.; Daftardar-Gejji, V. Synchronization of different fractional order chaotic systems using active control. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 3536–3546. [Google Scholar] [CrossRef]
- Zheng, S. Impulsive stabilization and synchronization of uncertain financial hyperchaotic systems. Kybernetika 2016, 52, 241–257. [Google Scholar] [CrossRef] [Green Version]
- Rao, R.; Zhu, Q. Exponential synchronization and stabilization of delayed feedback hyperchaotic financial system. Adv. Diff. Equ. 2021, 2021, 216. [Google Scholar] [CrossRef]
- Yu, H.; Cai, G.; Li, Y. Dynamic analysis and control of a new hyperchaotic finance system. Nonlinear Dyn. 2012, 67, 2171–2182. [Google Scholar] [CrossRef]
- Stelios, B.; Hadi, J.; Frank, B.; Aly Ayman, A. A novel fuzzy mixed H2/H∞ optimal controller for hyperchaotic financial systems. Chaos Solitons Fractals 2021, 146, 110878. [Google Scholar]
- Yao, H.; Pan, H.; Qi, L. Global exponential stability of a financial system with impulses and time-delayed feedbacks. J. Jiangsu Univ. 2011, 32, 241–244. (In Chinese) [Google Scholar]
- Nazarimehr, F.; Sheikh, J.; Ahmadi, M.M.; Pham, V.T.; Jafari, S. Fuzzy predictive controller for chaotic flows based on continuous signals. Chaos Solitons Fractals 2018, 106, 349–354. [Google Scholar] [CrossRef]
- Rajagopal, K.; Li, C.; Nazarimehr, F.; Karthikeyan, A.; Duraisamy, P.; Jafari, S. Chaotic dynamics of modified Wien bridge oscillator with fractional order memristor. Radioengineering 2019, 28, 165–174. [Google Scholar] [CrossRef]
- Xu, C.; Duan, Z. A delayed feedback control method for fractional-order chaotic financial models. Appl. Math. Mech. 2020, 41, 1392–1404. (In Chinese) [Google Scholar]
- Chen, W. Nonlinear dynamics and chaos in a fractional-order financial system. Chaos Solitons Fractals 2008, 36, 1305–1314. [Google Scholar] [CrossRef]
- Abd-Elouahab, M.S.; Hamri, N.E.; Wang, J. Chaos control of a fractional-order financial system. Math. Probl. Eng. 2010, 2010, 270646. [Google Scholar] [CrossRef]
- Pan, J.; Liu, X.; Zhong, S. Stability criteria for impulsive reaction-diffusion Cohen-Grossberg neural networks with time-varying delays. Math. Comput. Model. 2010, 51, 1037–1050. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, J. H∞ control of a chaotic finance system in the presence of external disturbance and input time-delay. Appl. Math. Comput. 2014, 233, 320–327. [Google Scholar] [CrossRef]
- Valls, C. Darboux integrability of a nonlinear financial system. Appl. Math. Comput. 2011, 218, 3297–3302. [Google Scholar] [CrossRef]
- Du, J.; Huang, T.; Sheng, Z.; Zhang, H. A new method to control chaos in an economic system. Appl. Math. Comput. 2010, 217, 2370–2380. [Google Scholar] [CrossRef]
- Yang, X.; Li, X.; Lu, J.; Cheng, Z. Synchronization of time-delayed complex networks with switching topology via hybrid actuator fault and impulsive effects control. IEEE Trans. Cybern. 2020, 50, 4043–4052. [Google Scholar] [CrossRef]
- Sun, J. Impulsive control of a new chaotic system. Math. Comput. Simul. 2004, 64, 669–677. [Google Scholar] [CrossRef]
- Xu, H.; Zhu, Q. Stability analysis of impulsive stochastic delayed differential systems with infinite delay or finite delay and average-delay impulses. J. Franklin Inst. 2021, 358, 8593–8608. [Google Scholar] [CrossRef]
- Ji, Y.; Cao, J. Parameter estimation algorithms for hammerstein finite impulse response moving average systems using the data filtering theory. Mathematics 2022, 10, 438. [Google Scholar] [CrossRef]
- Bai, Q.; Zhu, W. Event-triggered impulsive optimal control for continuous-time dynamic systems with input time-delay. Mathematics 2022, 10, 279. [Google Scholar] [CrossRef]
- Tang, R.; Su, H.; Zou, Y.; Yang, X. Finite-time synchronization of Markovian coupled neural networks with delays via intermittent quantized control: Linear programming approach. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q.; Cao, J. Robust exponential stability of Markovian jump impulsive stochastic Cohen-Grossberg neural networks with mixed time delays. IEEE Trans. Neural Netw. 2010, 21, 1314–1325. [Google Scholar]
- Dong, M.; Zhang, H.; Wang, Y. Dynamics analysis of impulsive stochastic Cohen-Grossberg neural networks with Markovian jumping and mixed time delays. Neurocomputing 2009, 72, 1999–2004. [Google Scholar] [CrossRef]
- Deimling, K. Nonlinear Functional Analysis; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Istratescu, V.I. Fixed Point Theory: An Introduction; Reidel, D., Ed.; Springer Science and Business Media: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Gilbarg, D.; Trudinger, N.S. Elliptic Partial Differential Equations of Second Order; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
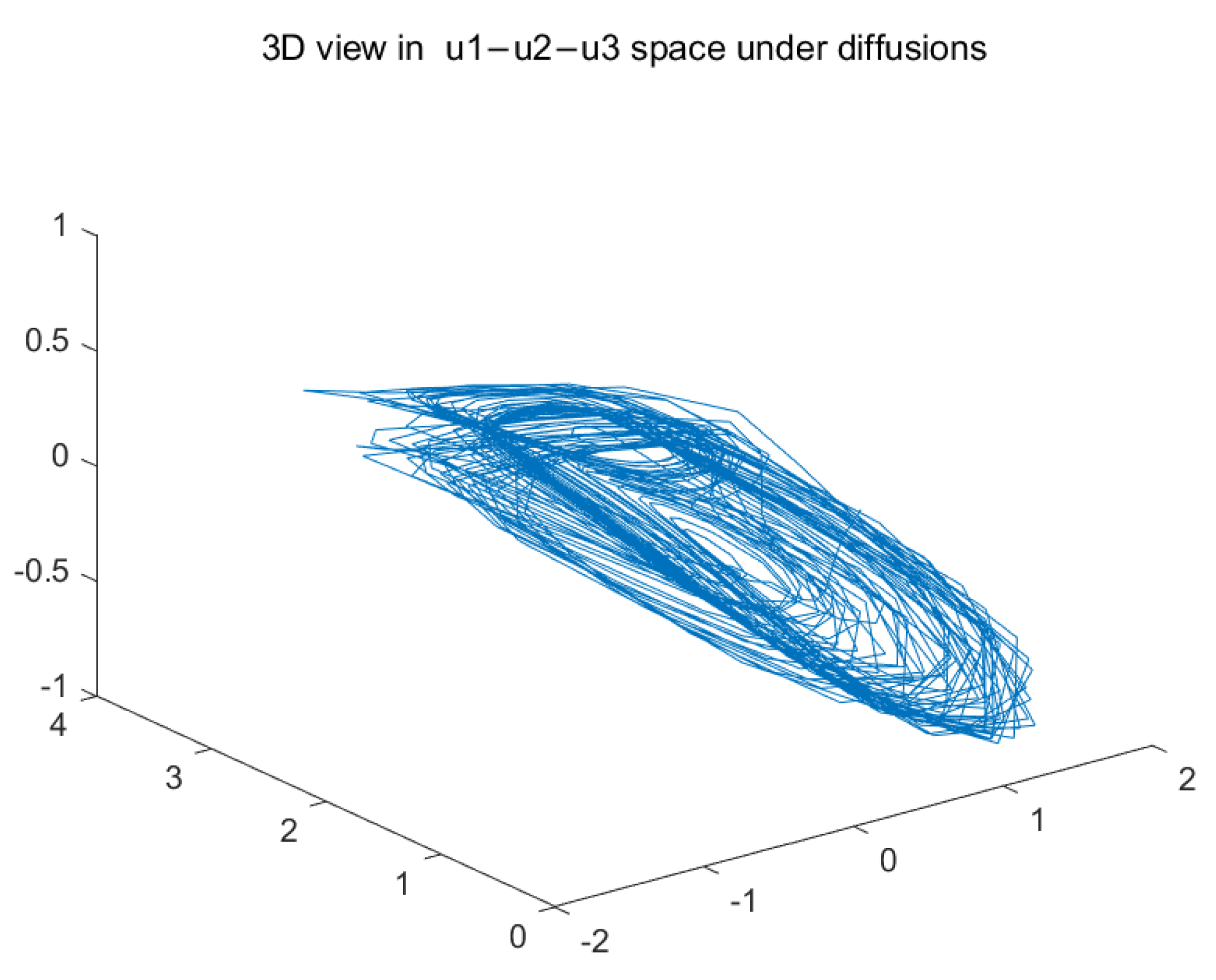


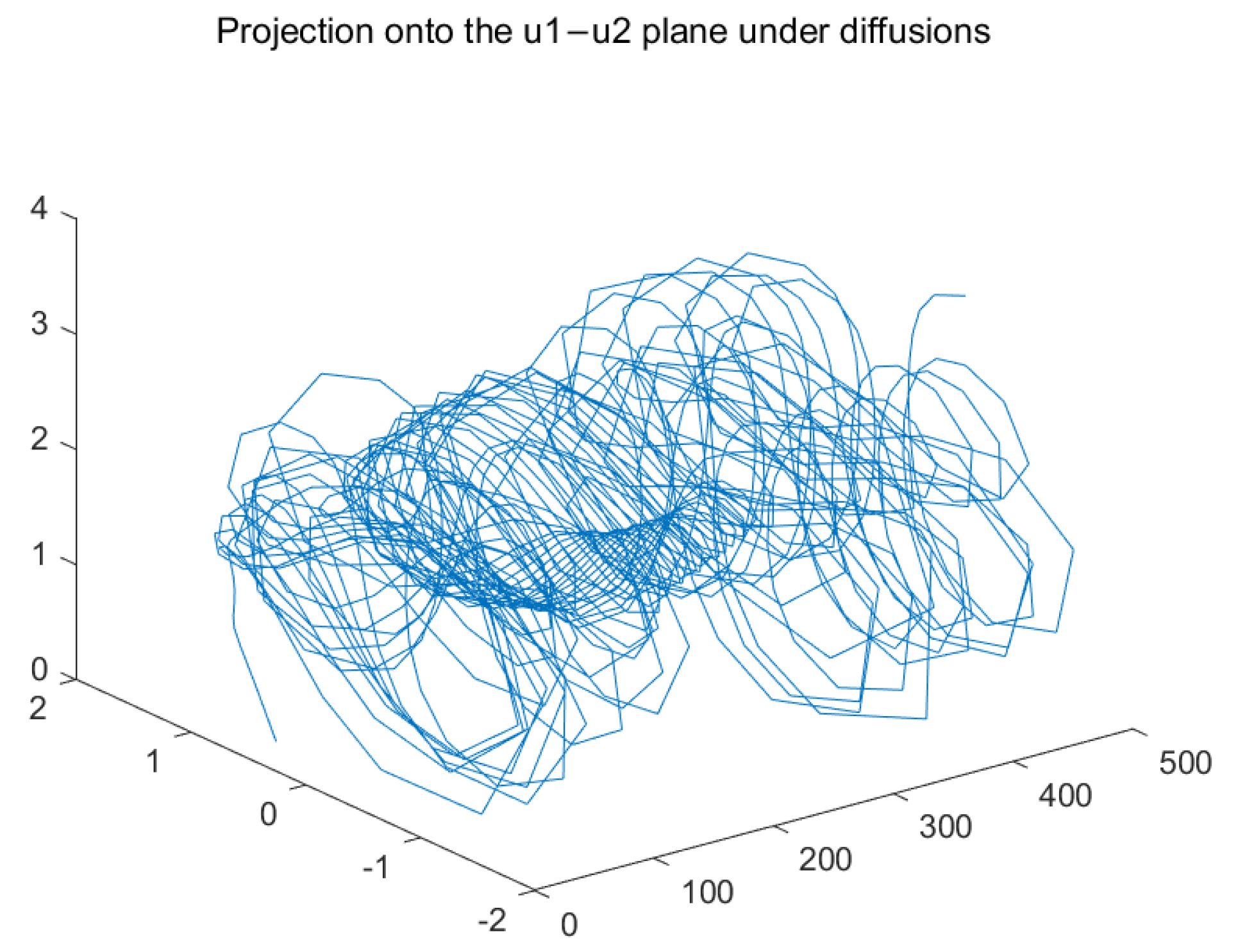

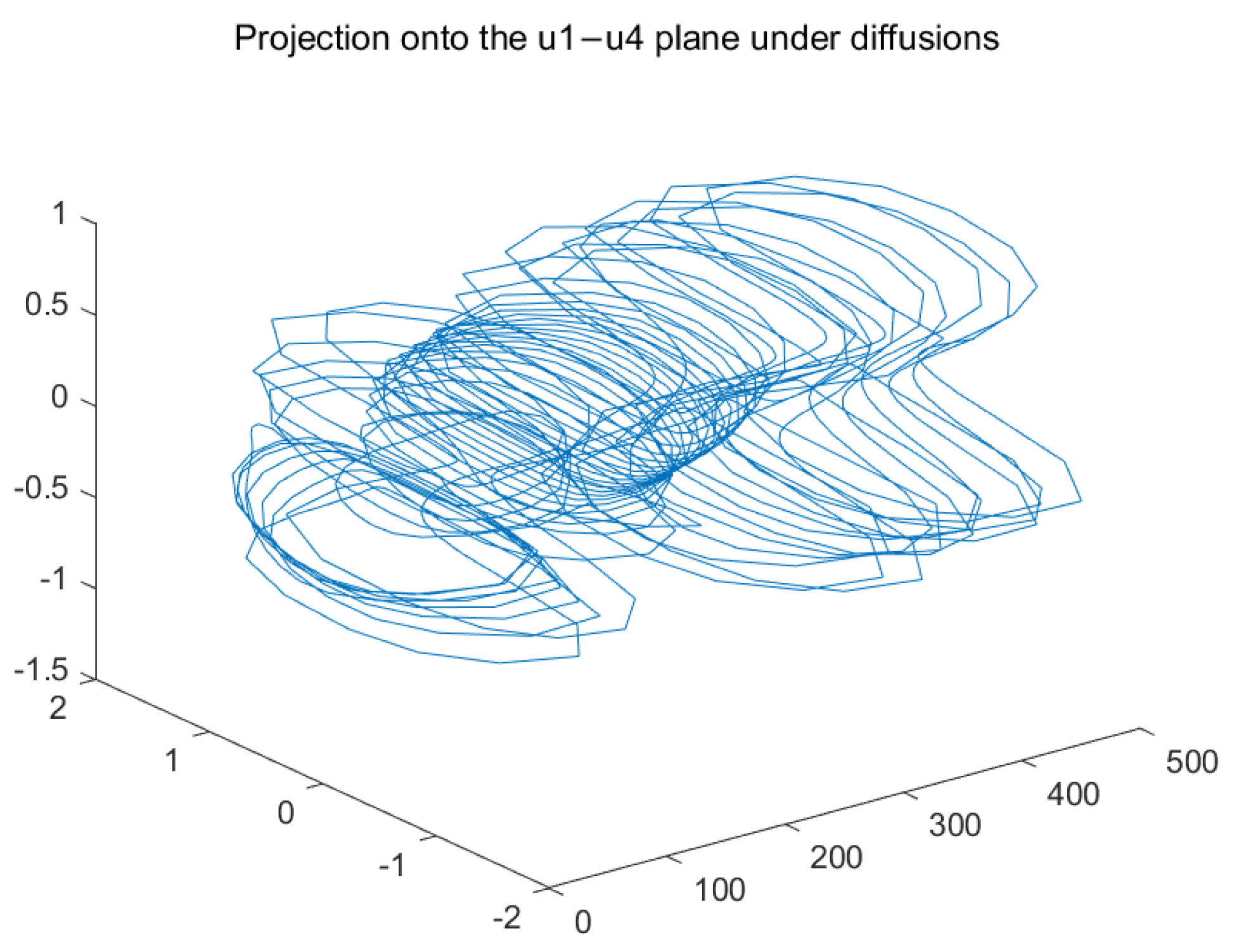


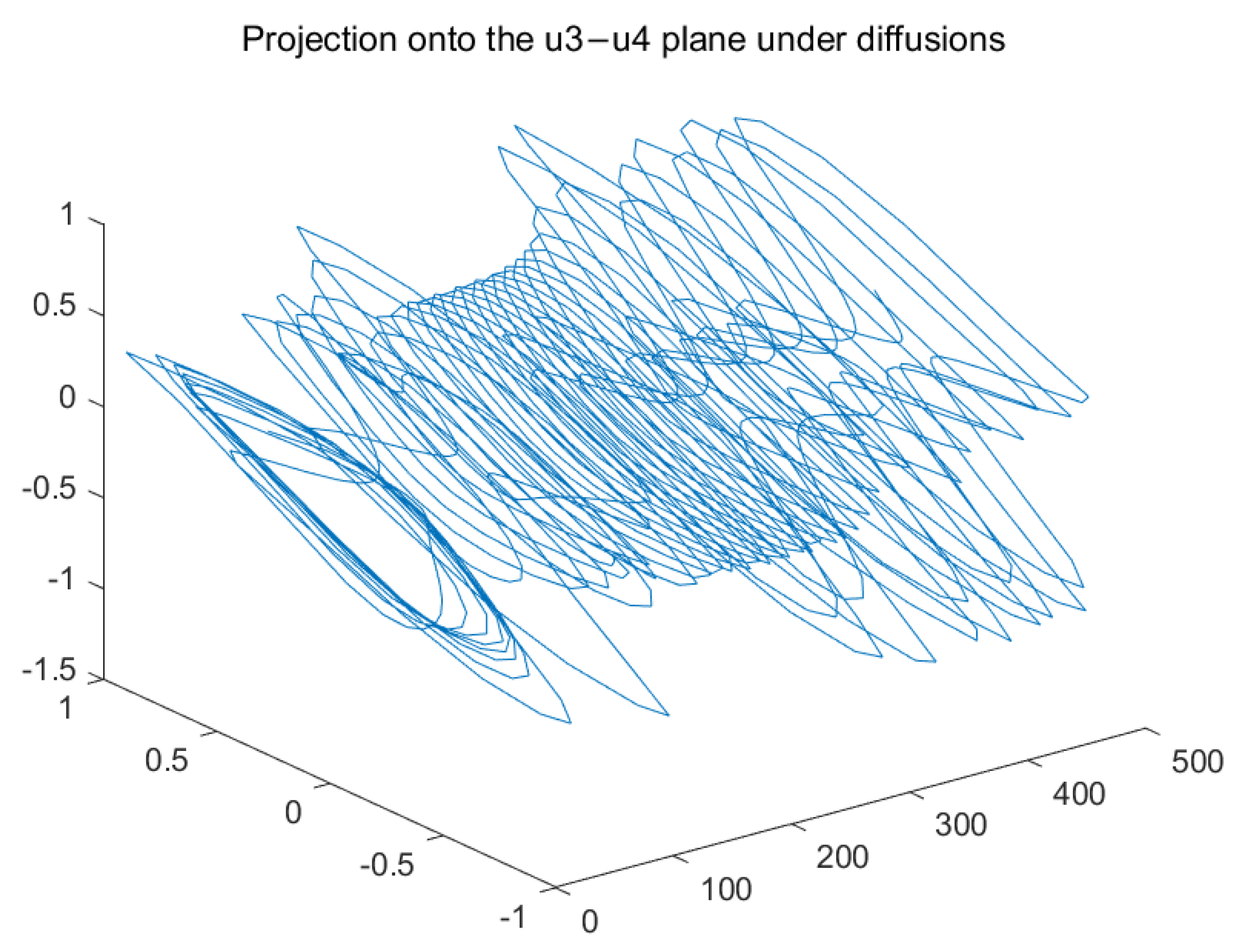



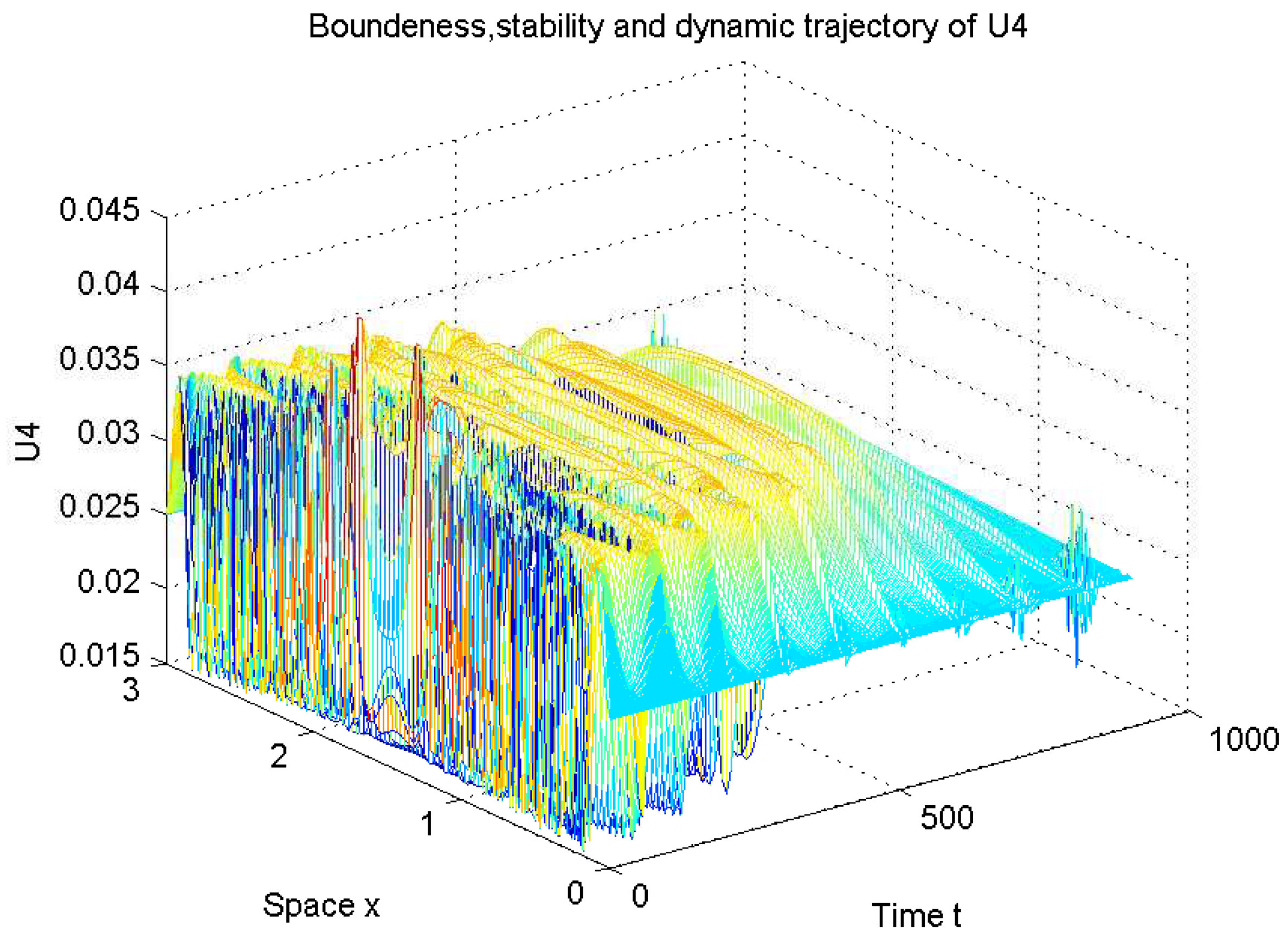

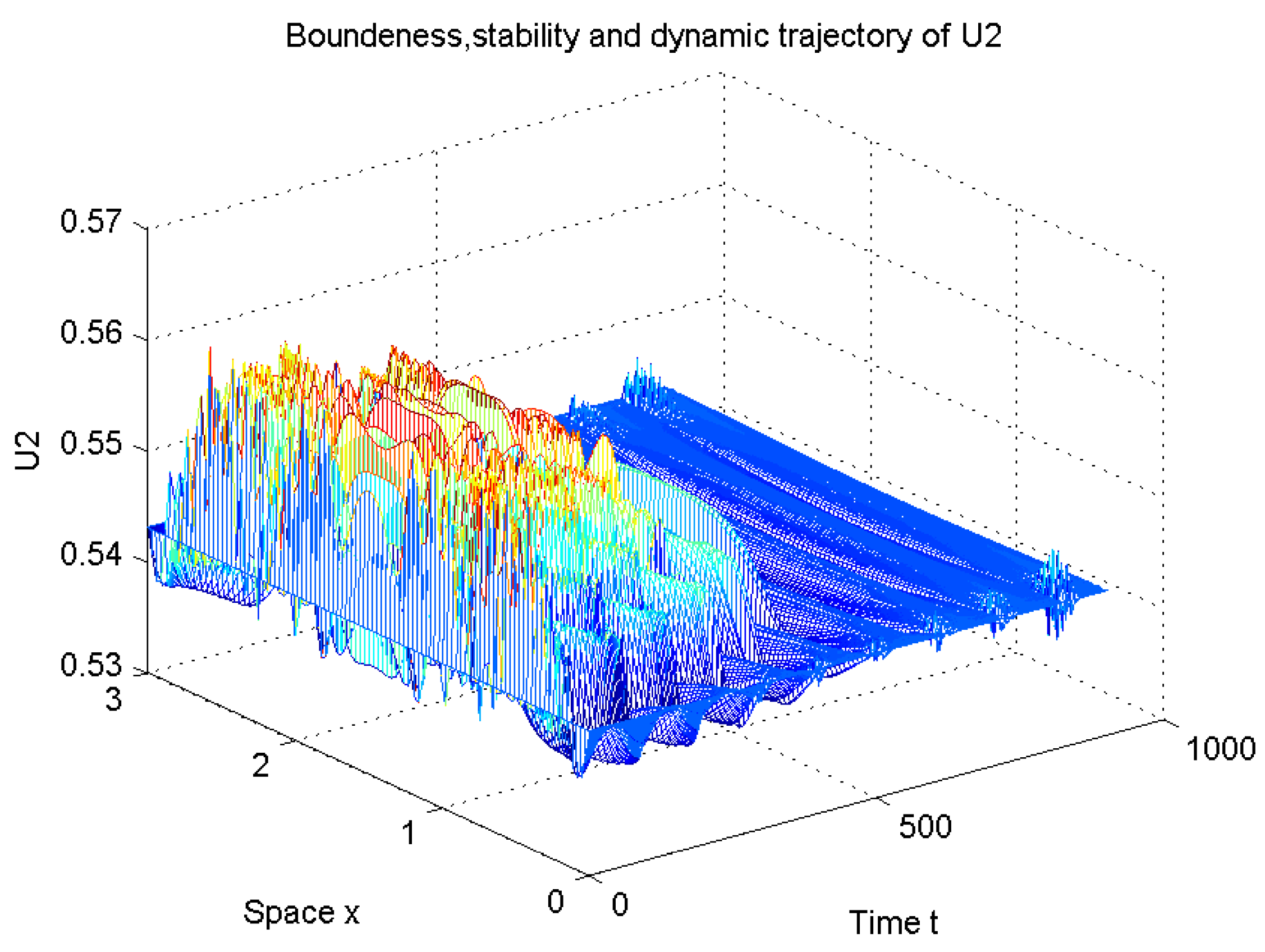
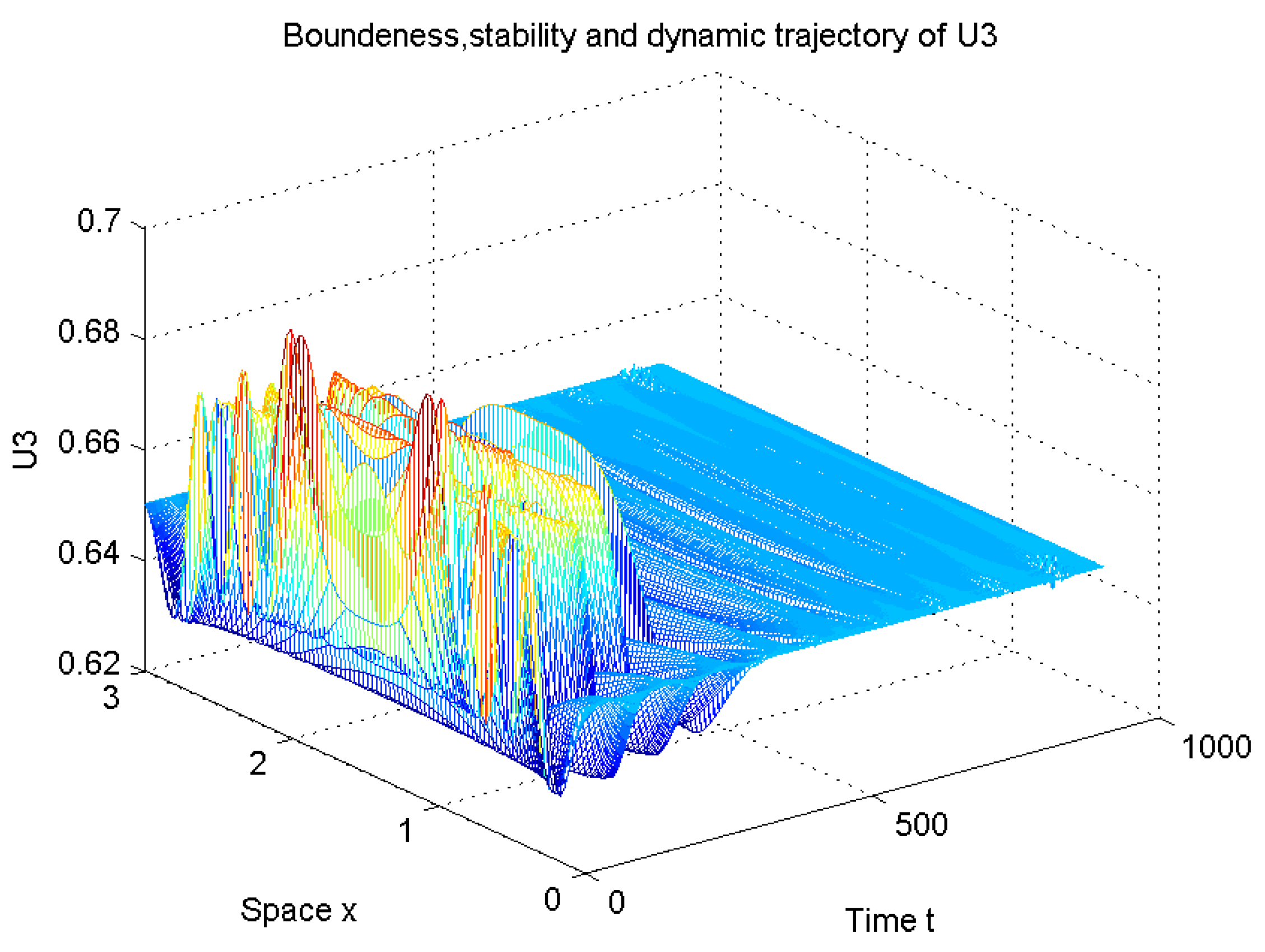

| Case 1: | Case 2: | |
|---|---|---|
| 0.9210 | 0.9210 | |
| 0.6607 | 0.6607 | |
| 0.8943 | 0.8943 | |
| 0.5937 | 0.5937 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Rao, R.; Yang, X. Impulsive Stabilization on Hyper-Chaotic Financial System under Neumann Boundary. Mathematics 2022, 10, 1866. https://doi.org/10.3390/math10111866
Li X, Rao R, Yang X. Impulsive Stabilization on Hyper-Chaotic Financial System under Neumann Boundary. Mathematics. 2022; 10(11):1866. https://doi.org/10.3390/math10111866
Chicago/Turabian StyleLi, Xinggui, Ruofeng Rao, and Xinsong Yang. 2022. "Impulsive Stabilization on Hyper-Chaotic Financial System under Neumann Boundary" Mathematics 10, no. 11: 1866. https://doi.org/10.3390/math10111866
APA StyleLi, X., Rao, R., & Yang, X. (2022). Impulsive Stabilization on Hyper-Chaotic Financial System under Neumann Boundary. Mathematics, 10(11), 1866. https://doi.org/10.3390/math10111866







