An Approach to Assessing Spatial Coherence of Current and Voltage Signals in Electrical Networks
Abstract
:1. Introduction
2. Proposed Method for Assessing Spatial Coherence of Current and Voltage Signals in Electrical Networks
3. Influence of Spatial Coherence of Current and Voltage Signals on the Accuracy of Double-Ended Fault Location in Power Transmission Lines
3.1. Determination of the Value of the Complex Correlation Coefficient
3.2. Description of Fault Location in the Power Transmission Line
- additive current and voltage components in the form of interharmonics of various intensities and spectral ranges;
- a component in the form of white noise in the analyzed frequency spectrum.
4. Investigation of the Influence of Interharmonics and Noise on Errors in DTLFL, in the Case of Violations of the Spatial Coherence of Signals
- errors in DTLFL depend on violations of sinusoidality of current and voltage signals, and the amplitude–phase relationships of interharmonics that are part of the distorted signals. The amplitude–phase relationships of interharmonics can both decrease and increase the values of the amplitudes of current I″ and voltage U″. With the same amplitude relationships, changes in the phase ratios lead to significant differences in errors in DTLFL. A 1.5-fold decline in the amplitudes of interharmonics at the same phase relationships results in a disproportionate decrease in the error in DTLFL;
- the discrete Fourier transform, in measuring elements of digital devices, provides complete suppression of multiple harmonics. However, when analyzing the spatial coherence of discrete currents and voltages, one should take into account the influence of interharmonics, the aperiodic component, and noise on the process of digital signal processing;
- the cross-correlation coefficient can be chosen as a numerical characteristic that makes it possible to estimate the magnitude of the distortion of the current and voltage signals of power frequency and to characterize a violation of spatial coherence. The smaller the cross-correlation coefficient, the greater the error in DTLFL will be;
- the nature of the influence of violations of spatial coherence on errors in DTLFL depends on the expression used to calculate the distance to the site of a power line fault. Consequently, different algorithms designed for DTLFL have their own inherent robustness to violations of spatial coherence.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| fD | sampling frequency |
| TD | sampling time (step) |
| f0 | power frequency of the network |
| |Xj|, fj, φj | amplitude, frequency and phase of the j-th interharmonic component |
| N | observation interval |
| Ρ | absolute value of the correlation coefficient |
| Β | argument of the correlation coefficient |
| yn | discrete random signal |
| mwR, mwI | mathematical expectations of random variables wR and wI |
| σ2wR, σ2wI | variances of random variables wR and wI |
| δ | white noise |
| E | signal energy |
| I0(·) | zero-order Bessel function of the first kind |
| I′, U′ | measured current and voltage magnitudes at the beginning of the power line |
| I″, U″ | measured current and voltage magnitudes at the end of the power line |
| Im, Um | current and voltage magnitudes obtained by simulation modeling |
| L | power transmission line length |
| z0 | zero sequence resistance of the power line |
| USC | phase voltage at the fault site |
| lSC | distance to the short circuit site |
| M | number of interharmonics in the spectrum of a sinusoidal current or voltage signal |
| g(n) | random instantaneous values of a noise component |
References
- Khan Shabbir, M.N.S.; Liang, X. A DFFT and Coherence Analysis-Based Fault Diagnosis Approach for Induction Motors Fed by Variable Frequency Drives. In Proceedings of the 2020 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), London, ON, Canada, 26–29 April 2020. [Google Scholar]
- Graham, M.T.; Lediju Bell, M.A. Photoacoustic Spatial Coherence Theory and Applications to Coherence-Based Image Contrast and Resolution. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 67, 2069–2084. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.S.; Lee, M.T. Multi-channel post-filtering based on spatial coherence measure. Signal Process. 2014, 105, 338–349. [Google Scholar] [CrossRef]
- Li, F.; Zou, L.; Songa, J.; Liang, S.; Chen, Y. Investigation of the spatial coherence function of wind loads on lattice frame structures. J. Wind Eng. Ind. Aerodyn. 2021, 215, 104675. [Google Scholar] [CrossRef]
- Mehigana, L.; Deanea, J.P.; Gallachóira, B.P.Ó.; Bertsch, V. A review of the role of distributed generation (DG) in future electricity systems. Energy 2018, 163, 822–836. [Google Scholar] [CrossRef]
- Ilyushin, P.V.; Kulikov, A.L.; Suslov, K.V.; Filippov, S.P. Consideration of Distinguishing Design Features of Gas-Turbine and Gas-Reciprocating Units in Design of Emergency Control Systems. Machines 2021, 9, 47. [Google Scholar] [CrossRef]
- Buchholz, B.M.; Styczynski, Z. Smart Grids-Fundamentals and Technologies in Electricity Networks; Springer: Berlin/Heidelberg, Germany; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2014; p. 396. [Google Scholar]
- Arranz-Gimon, A.; Zorita-Lamadrid, A.; Morinigo-Sotelo, D.; Duque-Perez, O. A review of total harmonic distortion factors for the measurement of harmonic and interharmonic pollution in modern power systems. Energies 2021, 14, 6467. [Google Scholar] [CrossRef]
- Silva, E.N.M.; Rodrigues, A.B.; Da Guia Da Silva, M. Stochastic assessment of the impact of photovoltaic distributed generation on the power quality indices of distribution networks. Electr. Power Syst. Res. 2016, 135, 59–67. [Google Scholar] [CrossRef]
- Savina, N.V.; Myasoedov, Y.V.; Myasoedova, L.A. Influence of quality of the electric energy on reliability of electrical supply systems. In Proceedings of the 2018 International Multi-Conference on Industrial Engineering and Modern Technologies (FarEastCon), Vladivostok, Russia, 2–4 October 2018; p. 8602690. [Google Scholar]
- Phadke, A.G.; Thorp, J.S. Synchronized Phasor Measurements and Their Applications; Springer: New York, NY, USA, 2008. [Google Scholar]
- Kezunovic, M.; Meliopoulos, S.; Venkatasubramanian, V.; Vittal, V. Application of Time-Synchronized Measurements in Power System Transmission Networks; Springer: New York, NY, USA, 2014. [Google Scholar]
- Wide Area Protection & Control Technologies; CIGRE Working Group B5.14; CIGRE: Paris, France, 2016.
- Arghandeh, R.; Brady, K.; Brown, M.; Cotter, G.R.; Deka, D.; Hooshyar, H.; Jamei, M.; Kirkham, H.; McEachern, A.; Mehrmanesh, L.; et al. Synchrophasor Monitoring for Distribution Systems: Technical Foundations and Applications; A White Paper by the NASPI Distribution Task Team NASPI-2018-TR-001; U.S. Department of Energy: Washington, DC, USA, 2018.
- Ribeiro, P.F.; Duque, C.A.; da Silveira, P.M.; Cerqueira, A.S. Power Systems Signal Processing for Smart Grids; John Wiley & Sons: Michigan, MI, USA, 2014. [Google Scholar]
- Marple, S.L. Digital Spectral Analysis: With Applications; Prentice Hall: Englewood Cliffs, NJ, USA, 1987. [Google Scholar]
- Gardner, W.A. Introduction to Random Processes with applications to Signal and Systems. In With Applications to Signals & Systems; McGraw Hill: New York, NY, USA, 1990; p. 560. [Google Scholar]
- Shushpanov, I.; Suslov, K.; Ilyushin, P.; Sidorov, D. Towards the flexible distribution networks design using the reliability performance metric. Energies 2021, 14, 6193. [Google Scholar] [CrossRef]
- Shalyt, G.M.; Aizenfeld, A.I.; Maly, A.S. Power Line Fault Location Based on the Emergency Parameters; Energoatomizdat: Moscow, Russia, 1983; p. 208. [Google Scholar]
- Saha, M.M.; Izykowski, J.; Rosolowski, E. Fault Location on Power Networks; Springer: London, UK, 2010; p. 437. [Google Scholar]
- Izykowsky, J. Fault Location on Power Transmission Line; Springer: Berlin/Heidelberg, Germany, 2008; p. 221. [Google Scholar]
- Visyashchev, A.N. Devices and Methods for Locating Faults on Power Lines: Textbook in 2 Parts—Part 1; ISTU Publishing House: Irkutsk, Russia, 2001; p. 188. [Google Scholar]
- Schweitzer, E.O. A review of impedance-based fault locating experience. In Proceedings of the 14th Annual Iowa–Nebraska System Protection Seminar, Omaha, NE, USA, 16 October 1990; pp. 1–31. [Google Scholar]
- Kezunovic, M.; Perunicic, B. Fault Location: Wiley Encyclopedia of Electrical and Electronics Terminology; John Wiley & Sons: New York, NY, USA, 1999; Volume 7, pp. 276–285. [Google Scholar]
- Rebizant, W.; Szafran, J.; Wiszniewski, A. Digital Signal Processing in Power System Protection and Control; Springer: New York, NY, USA, 2011; p. 316. [Google Scholar]
- Shirman, Y.D.; Baghdasaryan, S.T.; Malyarenko, A.S. Radioelectronic Systems: Fundamentals of Construction and Theory: Handbook. Radioengineering 2007, 512. (In Russian) [Google Scholar]
- Shneerson, E.M. Digital Relay Protection; Energoatomizdat: Moscow, Russia, 2007; p. 549. (In Russian) [Google Scholar]
- Falshina, V.A.; Kulikov, A.L. Algorithms for simplified digital filtering of electrical signals of industrial frequency. Ind. Energy 2012, 5, 39–46. (In Russian) [Google Scholar]
- Ilyushin, P.V. Analysis of the specifics of selecting relay protection and automatic (RPA) equipment in distributed networks with auxiliary low-power generating facilities. Power Technol. Eng. 2018, 51, 713–718. [Google Scholar] [CrossRef]
- Arzhannikov, E.A.; Lukoyanov, V.Y.; Misrikhanov, M.S. Determining the Location of a Short Circuit on High-Voltage Power Lines; Shuin, V.A., Ed.; Energoatomizdat: Moscow, Russia, 2003; p. 272. (In Russian) [Google Scholar]
- Obalin, M.D.; Kulikov, A.L. Application of adaptive procedures in algorithms for determining the location of damage to power lines. Ind. Energy 2013, 12, 35–39. (In Russian) [Google Scholar]
- Sheta, A.N.; Abdulsalam, G.M.; Eladl, A.A. Online tracking of fault location in distribution systems based on PMUs data and iterative support detection. Int. J. Electr. Power Energy Syst. 2021, 128, 106793. [Google Scholar] [CrossRef]
- Abbas, A.K.; Hamad, S.; Hamad, N.A. Single line to ground fault detection and location in medium voltage distribution system network based on neural network. Indones. J. Electr. Eng. Comput. Sci. 2021, 23, 621. [Google Scholar] [CrossRef]
- Shabalov, M.Y.; Zhukovskiy, Y.L.; Buldysko, A.D.; Gil, B.; Starshaia, V.V. The influence of technological changes in energy efficiency on the infrastructure deterioration in the energy sector. Energy Rep. 2021, 7, 2664–2680. [Google Scholar] [CrossRef]
- Kulikov, A.L.; Loskutov, A.A.; Ilyushin, P.V. High-performance sequential analysis in grid automated systems of distributed-generation areas. Russ. Electr. Eng. 2021, 92, 90–96. [Google Scholar] [CrossRef]
- Cook, C.E.; Bernfeld, M. Radar Signals; Academic Press: Cambridge, MA, USA, 1967; p. 531. [Google Scholar]
- Lavrik, A.; Zhukovskiy, Y.; Tcvetkov, P. Optimizing the Size of Autonomous Hybrid Microgrids with Regard to Load Shifting. Energies 2021, 14, 5059. [Google Scholar] [CrossRef]
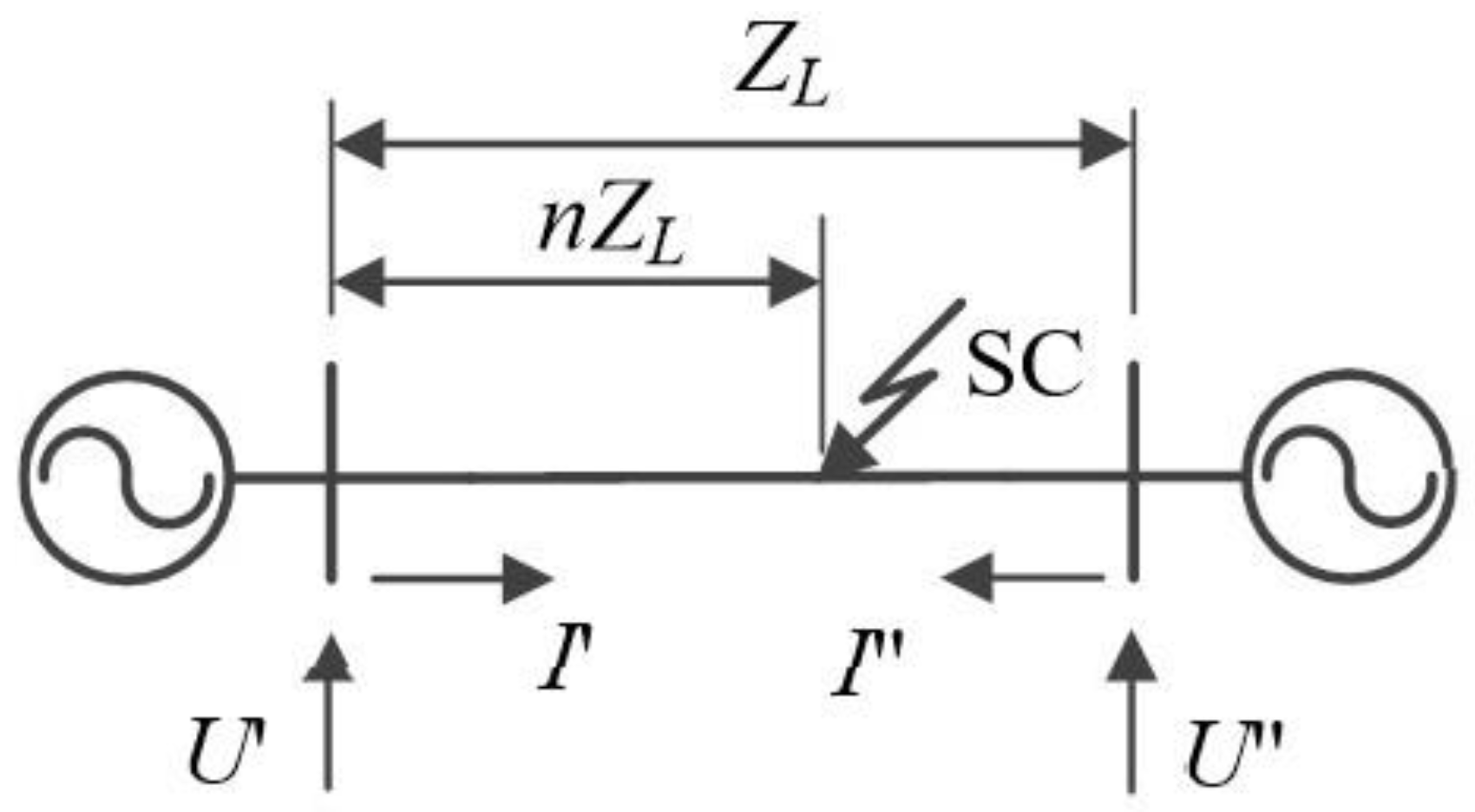
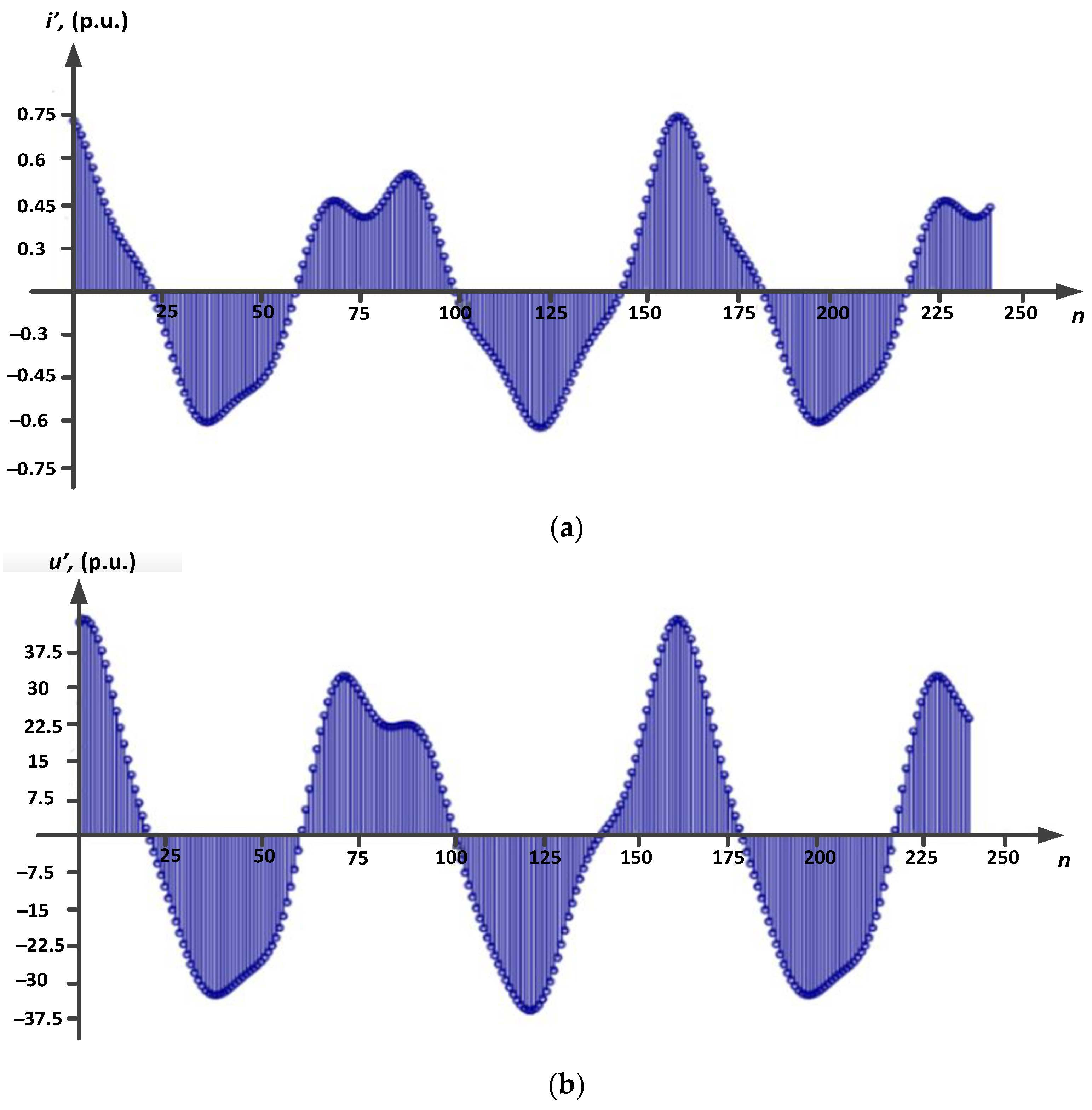
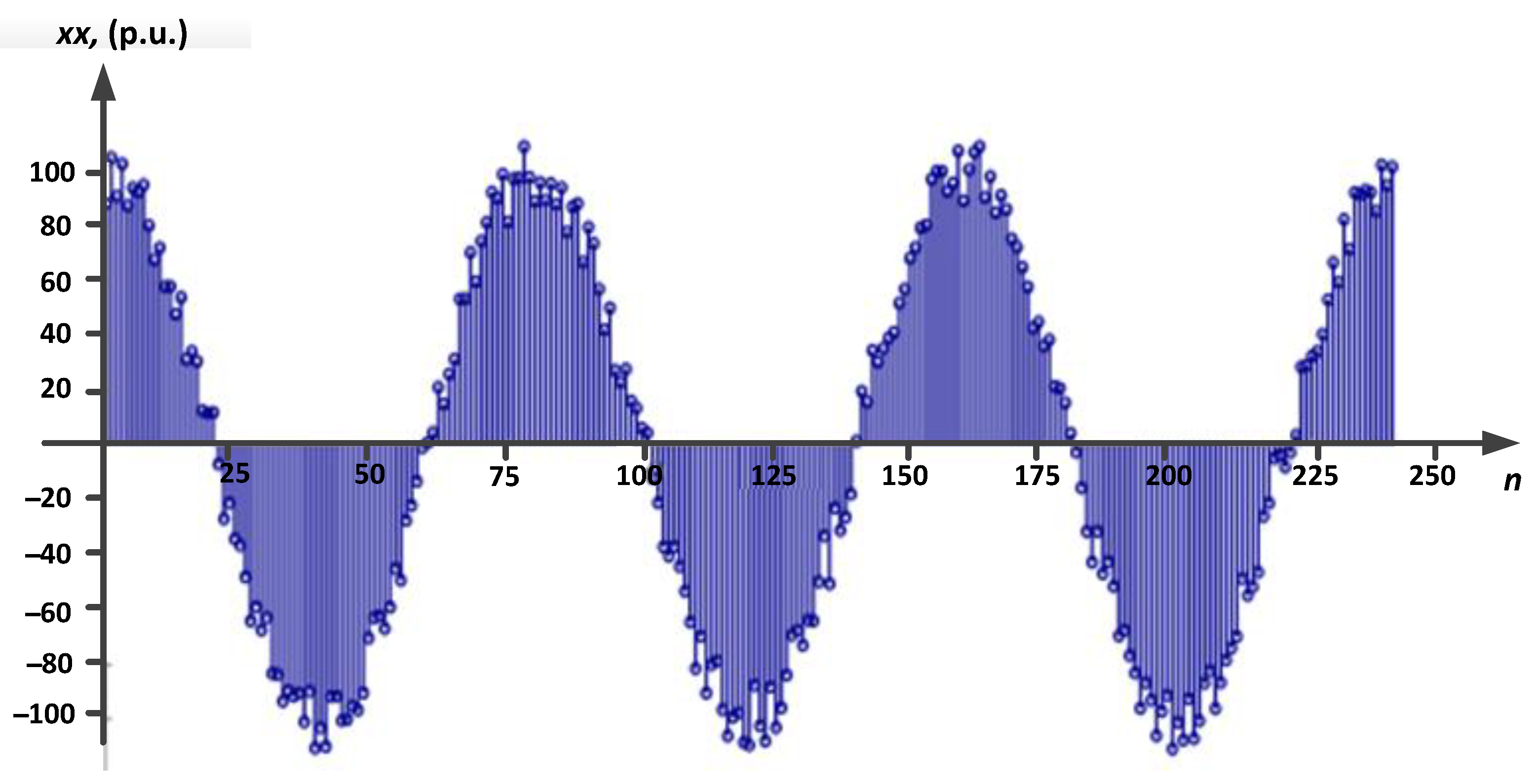
| Calculation Options | Amplitude–Phase Relationships of Current and Voltage Interharmonics | Normalized Current (Voltage) Correlation Coefficient | Error in Power Line Fault Location Δ under Violated Spatial Coherence | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |Xi1| (I″) | |Xi2| (I″) | |Xi3| (I″) | φi1 | φi2 | φi3 | |Xu1| (U″) | |Xu2| (U″) | |Xu3| (U″) | φu1 | φu2 | φu3 | |||
| 1. | 0.15 | 0.1 | 0.15 | 0 | π/6 | π/4 | 0.1 | 0.15 | 0.1 | −π/6 | −π/4 | 0 | 0.973 (0.985) | −0.19 km (0.16%) |
| 2. | 0.15 | 0.15 | 0.15 | π | π | π | 0.15 | 0.15 | 0.15 | −π | −π | −π | 0.967 (0.967) | 0.176 km (0.15%) |
| 3. | 0.15 | 0.15 | 0.15 | π | π | π | 0.15 | 0.15 | 0.15 | 0 | 0 | 0 | 0.967 (0.969) | −0.0165 km (0.014%) |
| 4. | 0.15 | 0.15 | 0.15 | 0 | 0 | 0 | 0.15 | 0.15 | 0.15 | 0 | 0 | 0 | 0.969 (0.969) | −0.491 km (0.41%) |
| 5. | 0.15 | 0.15 | 0.15 | π/2 | π/2 | π/2 | 0.15 | 0.15 | 0.15 | 0 | 0 | 0 | 0.977 (0.969) | 4.063 km (3.39%) |
| 6. | 0.15 | 0.15 | 0.15 | −π/2 | −π/2 | −π/2 | 0.15 | 0.15 | 0.15 | 0 | 0 | 0 | 0.989 (0.969) | −4.011 km (3.34%) |
| 7. | 0.1 | 0.1 | 0.1 | −π/2 | −π/2 | −π/2 | 0.1 | 0.1 | 0.1 | 0 | 0 | 0 | 0.995 (0.986) | −2.701 km (2.25%) |
| 8. | 0.1 | 0.1 | 0.1 | −π/2 | −π/2 | −π/2 | 0.1 | 0.1 | 0.1 | π/2 | π/2 | π/2 | 0.995 (0.991) | −1.567 km (1.31%) |
| 9. | 0.1 | 0. | 0.1 | −π/2 | −π/2 | −π/2 | 0.1 | 0.1 | 0.1 | 3π/2 | 3π/2 | 3π/2 | 0.995 (0.995) | −3.67 km (3.06%) |
| 10. | 0.1 | 0.1 | 0.1 | −π/2 | −π | −3π/2 | 0.1 | 0.1 | 0.1 | 3π/2 | 3π/2 | 3π/2 | 0.988 (0.995) | −2.21 km (1.84%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ilyushin, P.; Kulikov, A.; Suslov, K.; Filippov, S. An Approach to Assessing Spatial Coherence of Current and Voltage Signals in Electrical Networks. Mathematics 2022, 10, 1768. https://doi.org/10.3390/math10101768
Ilyushin P, Kulikov A, Suslov K, Filippov S. An Approach to Assessing Spatial Coherence of Current and Voltage Signals in Electrical Networks. Mathematics. 2022; 10(10):1768. https://doi.org/10.3390/math10101768
Chicago/Turabian StyleIlyushin, Pavel, Aleksandr Kulikov, Konstantin Suslov, and Sergey Filippov. 2022. "An Approach to Assessing Spatial Coherence of Current and Voltage Signals in Electrical Networks" Mathematics 10, no. 10: 1768. https://doi.org/10.3390/math10101768
APA StyleIlyushin, P., Kulikov, A., Suslov, K., & Filippov, S. (2022). An Approach to Assessing Spatial Coherence of Current and Voltage Signals in Electrical Networks. Mathematics, 10(10), 1768. https://doi.org/10.3390/math10101768








