Joint Optimization of Ticket Pricing Strategy and Train Stop Plan for High-Speed Railway: A Case Study
Abstract
:1. Introduction
- (1)
- Few studies consider the joint problem of HSR pricing, seat allocation, and train stop planning. This is one of the limited number of papers that jointly optimize pricing, seat allocation, and stop planning for HSR.
- (2)
- Considering the impact of the stop plan on the travel time, an elastic passenger demand function related to the ticket price and travel time is constructed.
- (3)
- Based on the simulated annealing theory, an efficient solution algorithm is designed for the combinatorial optimization problem of ticket pricing, seat allocation, and train stop planning for HSR.
2. Literature Review
3. Mathematical Formulation
3.1. Problem Analysis
- (1)
- All ODs have the same demand elasticity in the same ticket pre-sale period.
- (2)
- For the same OD and same train, the ticket price will not be reduced as the train departure time approaches.
- (3)
- Passengers who fail to obtain tickets in a certain period will continue to buy the tickets in the next period.
- (4)
- Different seat classes, ticket overbooking, and cancellations are not considered.
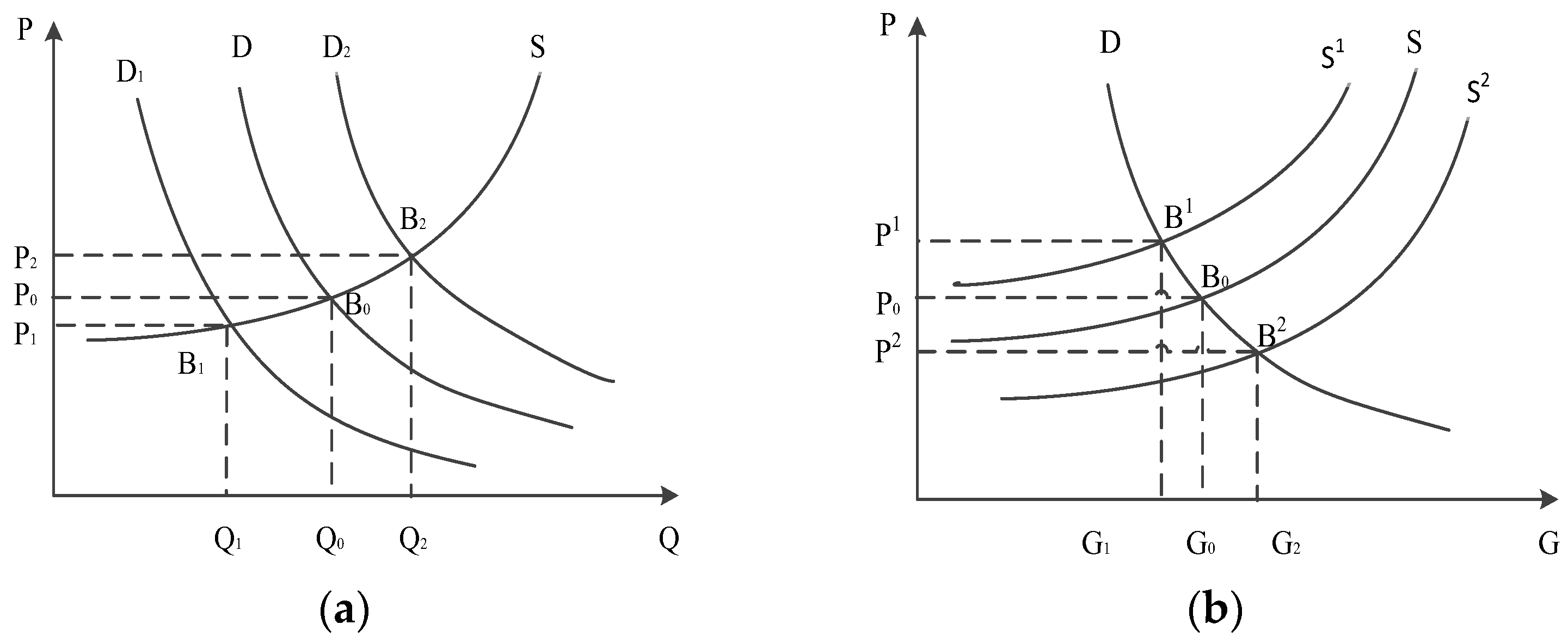
3.2. Elastic Passenger Demand and Choice Behavior
3.3. Integrated Optimization Model of Ticket Pricing and Stop Planning
3.3.1. Objective Function
- (1)
- Transport revenue
- (2)
- Time loss of passengers
3.3.2. Constraints
- (1)
- Price constraints
- (2)
- Ticket (seat) constraints
- (3)
- Capacity constraints
- (4)
- Reachability constraints
4. Solution Method
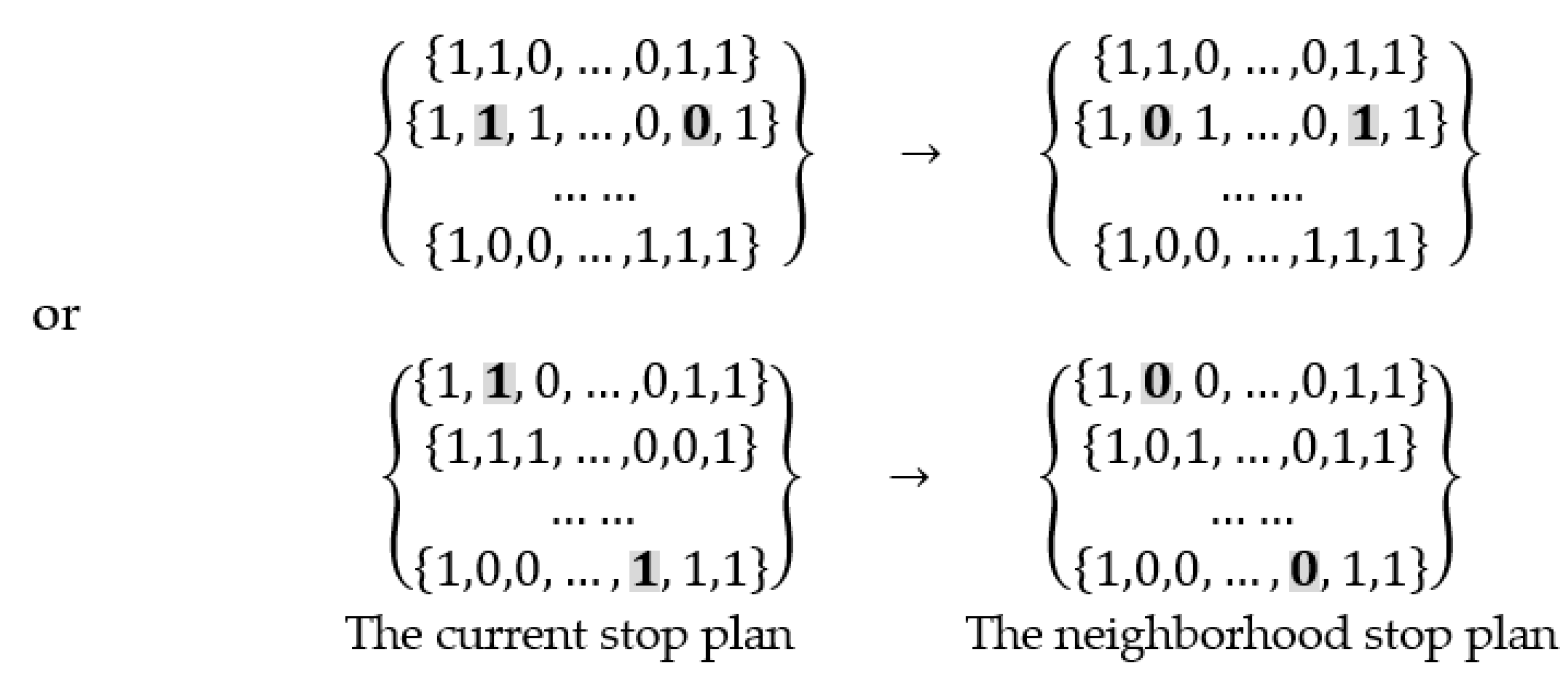
4.1. Neighborhood Structure
4.1.1. Outer Neighborhood
4.1.2. Inner Neighborhood
4.2. Implementation Process
5. Empirical Analysis
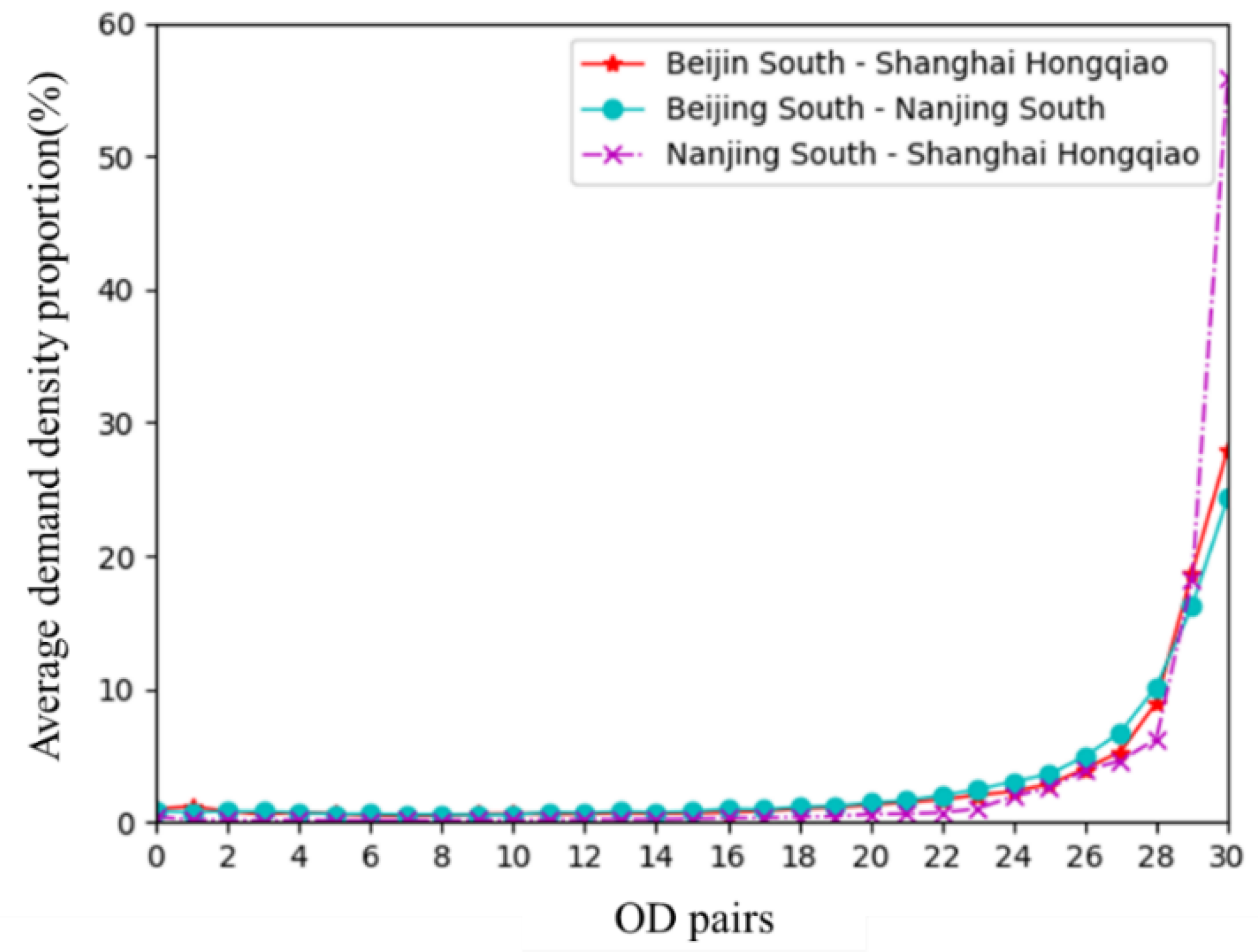
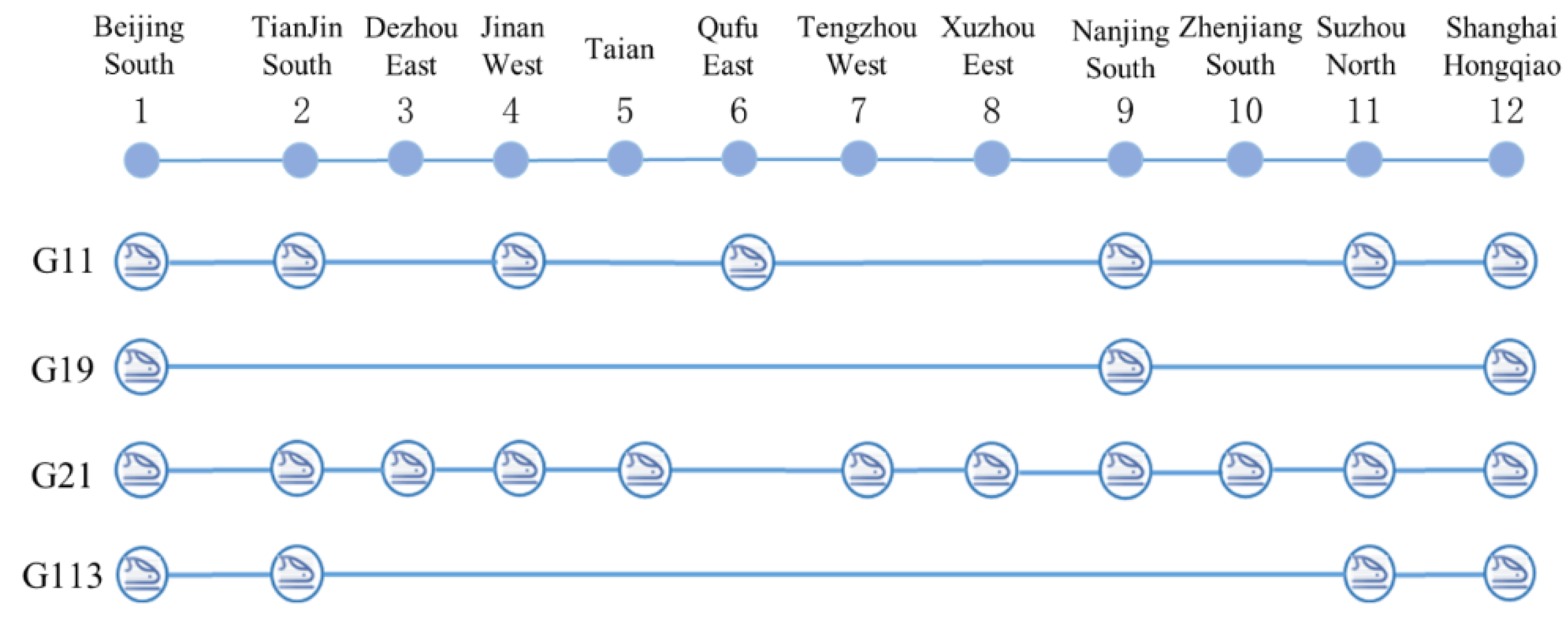
5.1. Basic Data
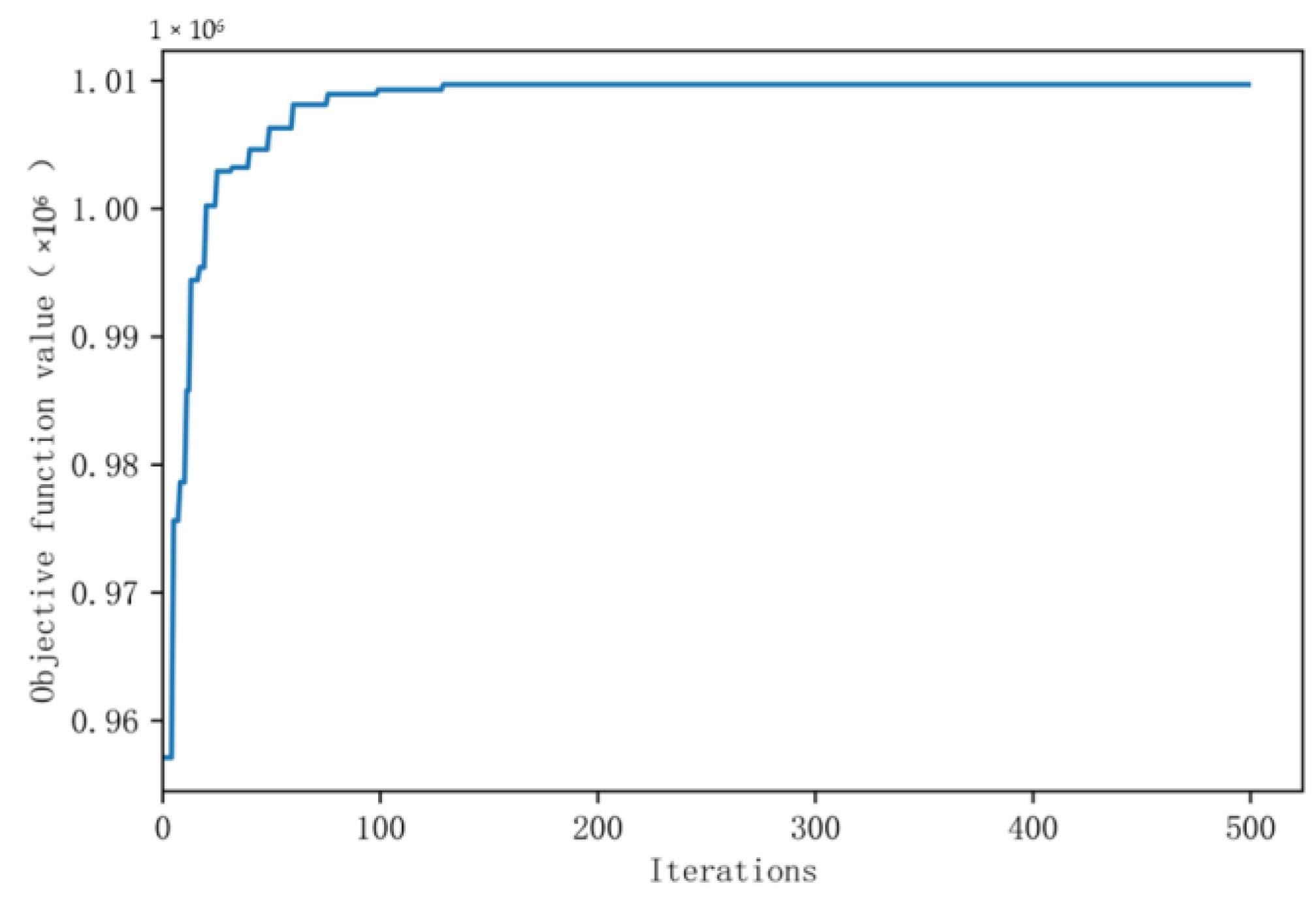
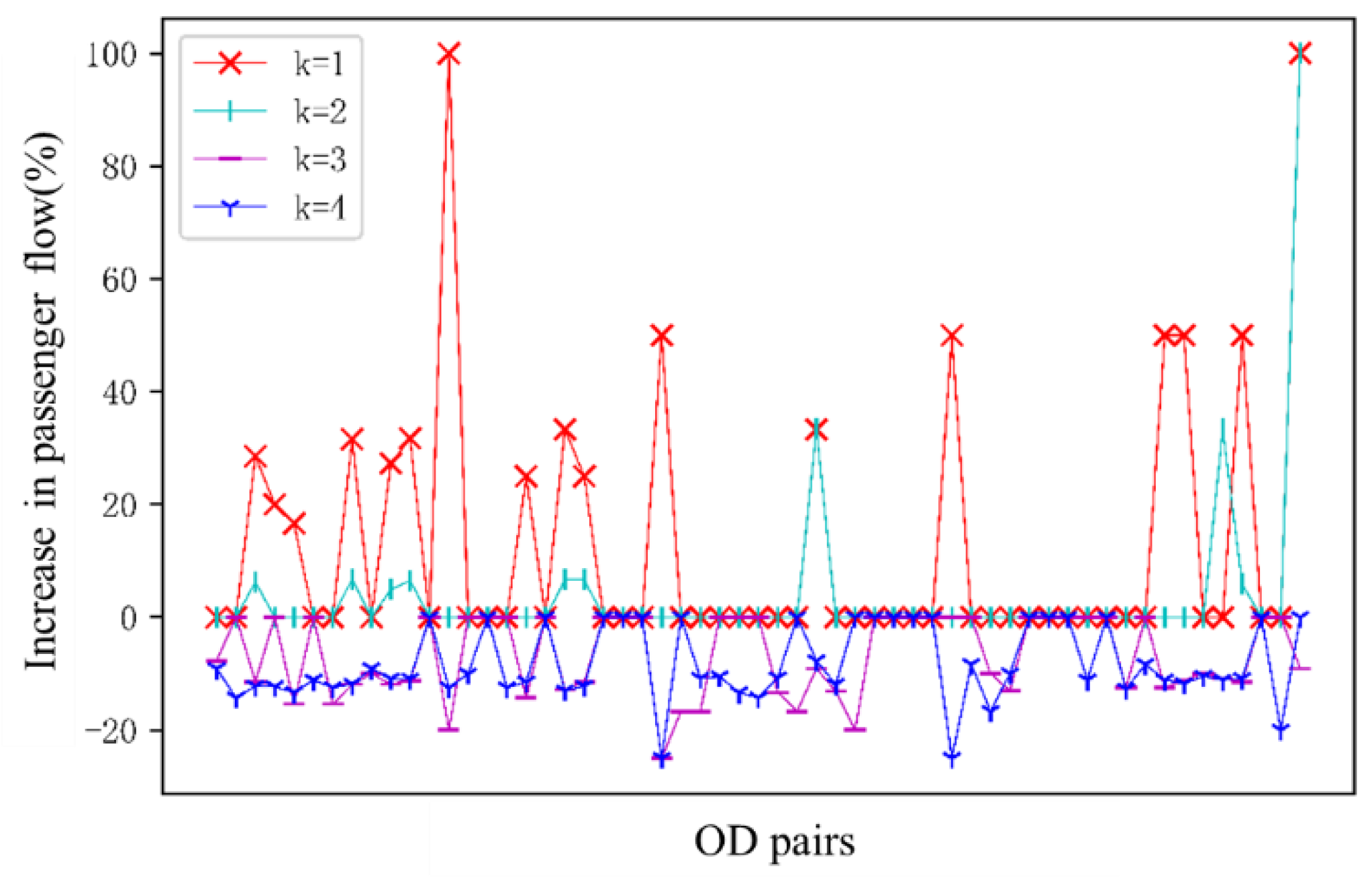
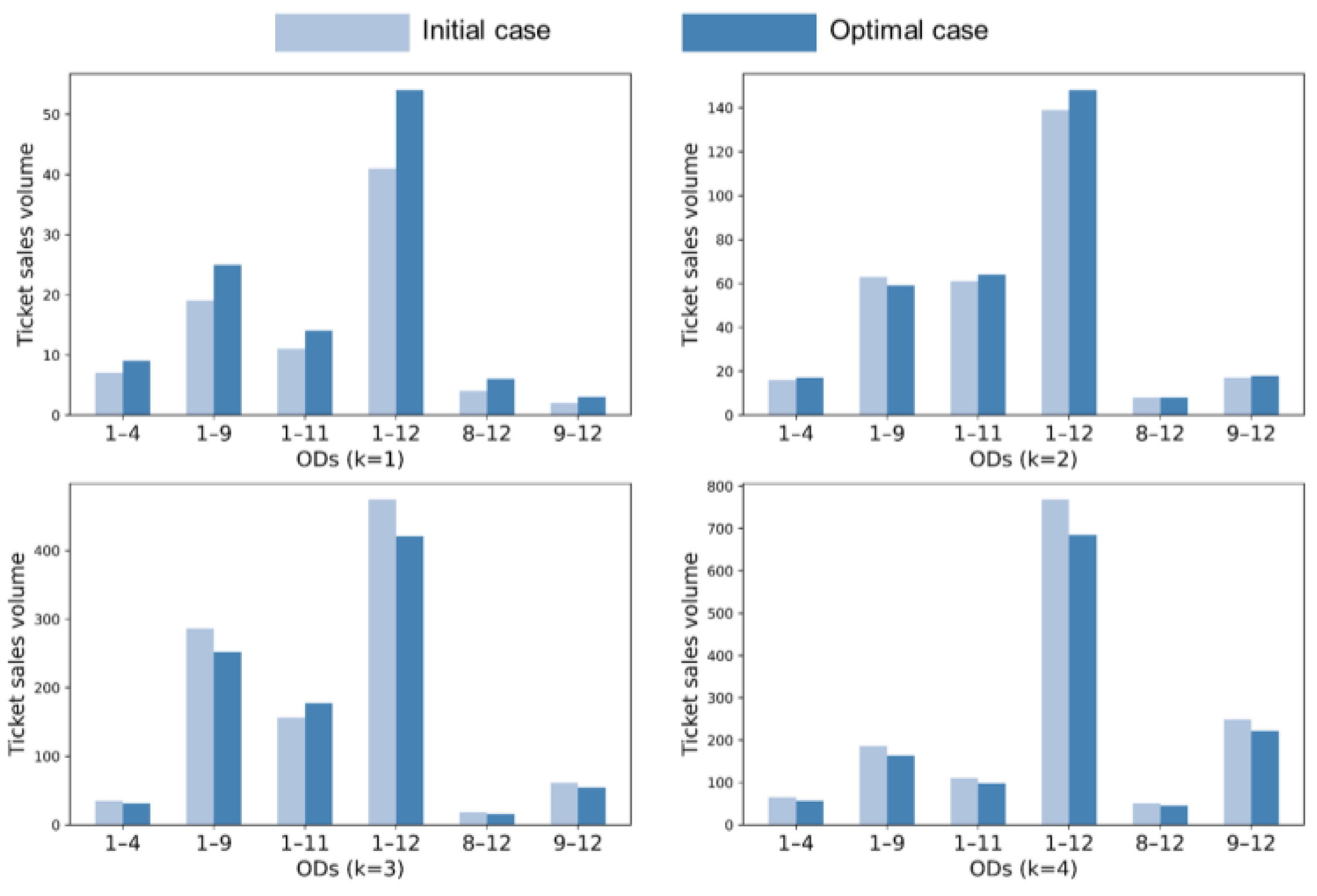
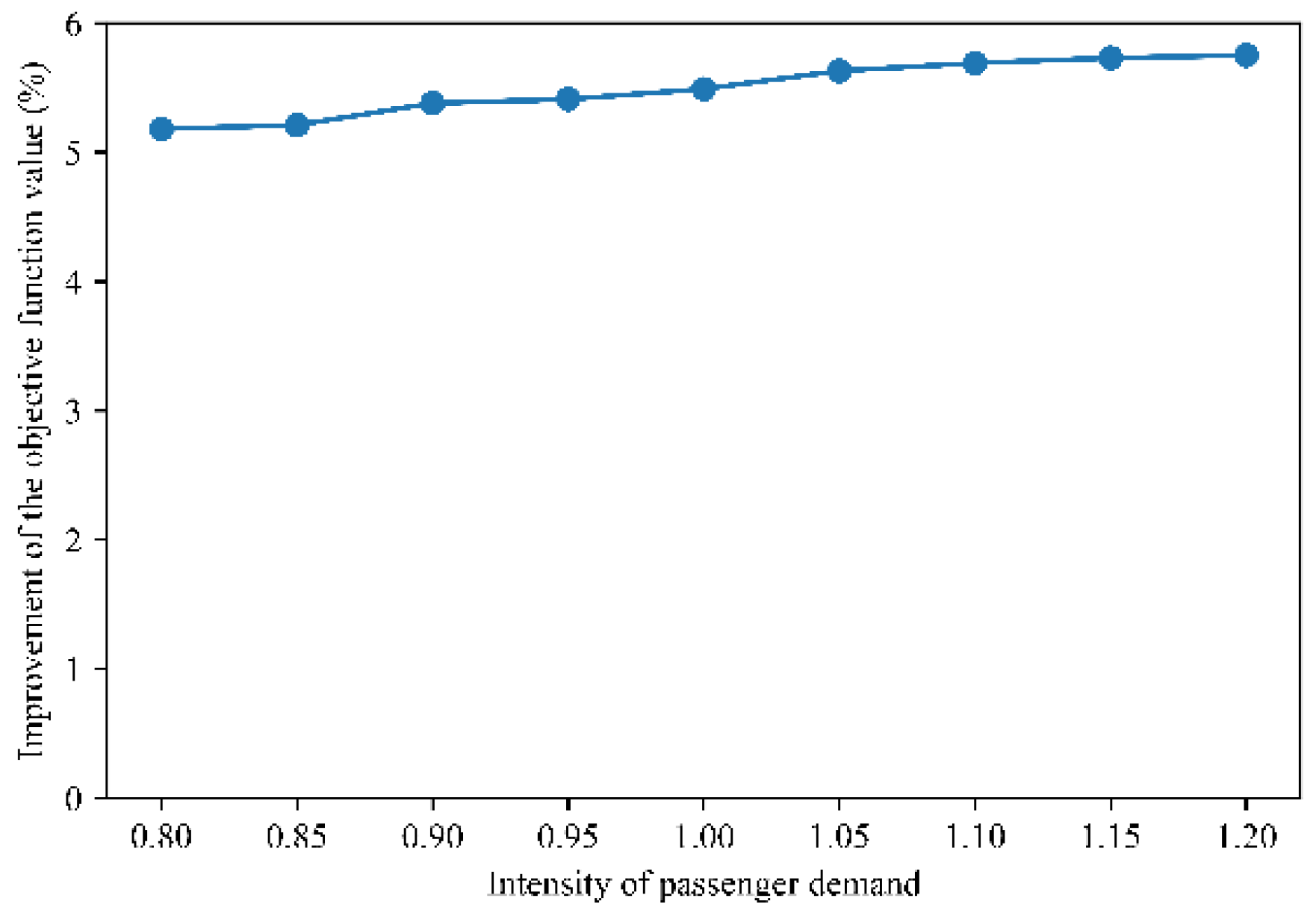
5.2. Results and Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weatherford, L.R.; Kimes, S.E. A comparison of forecasting methods for hotel revenue management. Int. J. Forecast. 2003, 19, 401–415. [Google Scholar] [CrossRef] [Green Version]
- Noone, B.M.; Mattila, A.S. Hotel revenue management and the internet: The effect of price presentation strategies on customers’ willingness to book. Int. J. Hosp. Manag. 2009, 28, 272–279. [Google Scholar] [CrossRef]
- Heo, C.Y.; Lee, S. Influences of consumer characteristics on fairness perceptions of revenue management pricing in the hotel industry. Int. J. Hosp. Manag. 2011, 30, 243–251. [Google Scholar] [CrossRef]
- Grauberger, W.; Kimms, A. Airline revenue management games with simultaneous price and quantity competition. Comput. Oper. Res. 2016, 75, 64–75. [Google Scholar] [CrossRef]
- Lawhead, R.J.; Gosavi, A. A Bounded Actor-Critic Reinforcement Learning Algorithm Applied to Airline Revenue Management. Eng. Appl. Artif. Intell. 2019, 82, 252–262. [Google Scholar] [CrossRef]
- Selcuk, A.M.; Avar, Z.M. Dynamic pricing in airline revenue management. J. Math. Anal. Appl. 2019, 478, 1191–1217. [Google Scholar] [CrossRef]
- Kyparisis, G.J.; Koulamas, C. Optimal pricing and seat allocation for a two-cabin airline revenue management problem. Int. J. Prod. Econ. 2018, 201, 18–25. [Google Scholar] [CrossRef]
- Armstrong, A.; Meissner, J. Railway Revenue Management: Overview and Models; Lancaster University Management School: Lancaster, UK, 2010. [Google Scholar]
- Abe, I. Revenue Management in the Railway Industry in Japan and Portugal: A Stakeholder Approach. Technology and Policy Program. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2007. [Google Scholar]
- Bharill, R.; Rangaraj, N. Revenue management in railway operations: A study of the Rajdhani Express, Indian Railways. Transp. Res. Part A Policy Pract. 2008, 42, 1195–1207. [Google Scholar] [CrossRef]
- Riss, M.; Côté, J.P.; Savard, G. A new revenue optimization tool for high-speed railway: Finding the right equilibrium between revenue growth and commercial objectives. In Proceedings of the 8th World Congress on Railway Research, Seoul, Korea, 18–22 May 2008. [Google Scholar]
- Crevier, B.; Cordeau, J.F.; Savard, G. Integrated operations planning and revenue management for rail freight transportation. Transp. Res. Part B Methodol. 2012, 46, 100–119. [Google Scholar] [CrossRef]
- Vuuren, D.V. Optimal pricing in railway passenger transport: Theory and practice in the Netherlands. Transp. Policy 2002, 9, 95–106. [Google Scholar] [CrossRef]
- Jarocka, M.; Ryciuk, U. Pricing in the railway transport. In Proceedings of the 9th International Scientific Conference “Business and Management 2016”, Vilnius, Lithuania, 12–13 May 2016. [Google Scholar]
- Zhang, J.; Yang, X.; Du, G. Research on High-speed Railway Fare Optimization based on Change of Passenger Flow. In Proceedings of the 3rd International Conference on Mechatronics Engineering and Information Technology (ICMEIT 2019), Dalian, China, 29–30 March 2019. [Google Scholar]
- Dargay, J.M.; Clark, S.; Rose, J. The determinants of long distance travel in Great Britain. Transp. Res. Part A Policy Pract. 2012, 46, 576–587. [Google Scholar] [CrossRef]
- Georggi, N.L.; Pendyala, R.M. Analysis of long-distance travel behavior of the elderly and the low-income. Transp. Res. Rec. 2012, E-C026, 121–150. [Google Scholar]
- Sato, K.; Sawaki, K. Dynamic pricing of high-speed rail with transport competition. J. Revenue Pricing Manag. 2011, 11, 548–559. [Google Scholar] [CrossRef]
- Chen, J.H.; Gao, Z.Y. Optimal Railway Passenger-ticket Pricing. J. China Railw. Soc. 2005, 27, 16–19. [Google Scholar]
- Wang, X.C.; Wang, H.; Zhang, X.N. Stochastic seat allocation models for passenger rail transportation under customer choice. Transp. Res. Part E 2016, 96, 95–112. [Google Scholar] [CrossRef]
- Jiang, X.S.; Chen, X.Q.; Zhang, L.; Zhang, R. Dynamic Demand Forecasting and Ticket Assignment for High-Speed Rail Revenue Management in China. Transp. Res. Rec. 2015, 2475, 37–45. [Google Scholar] [CrossRef]
- Yan, Z.Y.; Li, X.J.; Zhang, Q.; Han, B.M. Seat allocation model for high-speed railway passenger transportation based on flexible train composition. Comput. Ind. Eng. 2020, 142, 106383. [Google Scholar] [CrossRef]
- Hetrakul, P.; Cirillo, C. A latent class choice based model system for railway optimal pricing and seat allocation. Transp. Res. Part E 2014, 61, 68–83. [Google Scholar] [CrossRef]
- Hu, X.L.; Shi, F.; Xu, G.M.; Qin, J. Joint optimization of pricing and seat allocation with multiperiod and discriminatory strategies in high-speed rail networks. Comput. Ind. Eng. 2020, 148, 106690. [Google Scholar] [CrossRef]
- Wu, X.K.; Qin, J.; Qu, W.X.; Zeng, Y.J.; Yang, X. Collaborative Optimization of Dynamic Pricing and Seat Allocation for High-speed Railways: An Empirical Study from China. IEEE Access 2019, 7, 139409–139419. [Google Scholar] [CrossRef]
- Qin, J.; Zeng, Y.J.; Yang, X.; He, Y.X.; Wu, X.K.; Qu, W.X. Time-Dependent Pricing for High-Speed Railway in China Based on Revenue Management. Sustainability 2019, 11, 4272. [Google Scholar] [CrossRef] [Green Version]
- Deng, L.B.; Zeng, N.X.; Chen, Y.X.; Xiao, L.W. A divide-and-conquer optimization method for dynamic pricing of high-speed railway based on seat allocation. J. Railw. Sci. Eng. 2019, 16, 2407–2413. [Google Scholar]
- Vuchic, V.R. Urban Transit; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Chang, Y.H.; Ye, C.H.; Shen, C.C. A multi-objective model for passenger train services planning: Application to taiwan’s high-speed rail line. Transp. Res. Part B 2000, 34, 91–106. [Google Scholar] [CrossRef]
- Bussieck, M.R.; Lindner, T.; Lübbecke, M.E. A fast algorithm for near cost optimal line plans. Math. Methods Oper. Res. 2004, 59, 205–220. [Google Scholar] [CrossRef]
- Yang, L.X.; Qi, J.G.; Li, S.K.; Gao, Y. Collaborative optimization for train scheduling and train stop planning on high-speed railways. Omega 2016, 64, 57–76. [Google Scholar] [CrossRef]
- Jin, G.W.; He, S.W.; Li, J.B.; Guo, X.L.; Li, Y.B. An Approach for Train Stop Planning with Variable Train Length and Stop Time of High-speed Rail Under Stochastic Demand. IEEE Access 2019, 7, 129690–129708. [Google Scholar] [CrossRef]
- Dong, X.L.; Li, D.W.; Yin, Y.H.; Ding, S.X.; Cao, Z.C. Integrated optimization of train stop planning and timetabling for commuter railways with an extended adaptive large neighborhood search metaheuristic approach. Transp. Res. Part C Emerg. Technol. 2020, 117, 102681. [Google Scholar] [CrossRef]
- Qi, J.G.; Li, S.K.; Gao, Y.; Yang, K.; Liu, P. Joint optimization model for train scheduling and train stop planning with passengers distribution on railway corridors. J. Oper. Res. Soc. 2018, 69, 556–570. [Google Scholar] [CrossRef]
- Xu, G.M.; Zhong, L.H.; Hu, X.L.; Liu, W. Optimal pricing and seat allocation schemes in passenger railway systems. Transp. Res. Part E Logist. Transp. Rev. 2022, 157, 102580. [Google Scholar] [CrossRef]


| Reference | Competitor | Optimization Aspects | |||
|---|---|---|---|---|---|
| Pricing | Seat Allocation | Stop Plan | Timetable | ||
| [13,14,15] | × | √ | × | × | × |
| [18,19] | √ | ||||
| [20,21,22] | × | × | √ | × | × |
| [23,24,25,26,27,35] | × | √ | √ | × | × |
| [28,29,30,31,32] | × | × | × | √ | × |
| [33,34] | × | × | × | √ | √ |
| This research | × | √ | √ | √ | × |
| OD | Availability of Transportation | OD Service Frequency | Possible Maximum Number of Tickets | |
|---|---|---|---|---|
| Train 1 | Train 2 | |||
| (1,2) | √ | × | 1 | 1000 |
| (1,3) | × | √ | 1 | 1000 |
| (1,4) | √ | × | 1 | 1000 |
| (1,5) | √ | √ | 2 | 2000 |
| (2,3) | × | × | 0 | 0 |
| (2,4) | √ | × | 1 | 1000 |
| (2,5) | √ | × | 1 | 1000 |
| (3,4) | × | × | 0 | 0 |
| (3,5) | × | √ | 1 | 1000 |
| (4,5) | √ | × | 1 | 1000 |
| Notation | Definition | Unit |
|---|---|---|
| Set of all OD in a certain direction on an HSR line, any OD and . | - | |
| Set of all trains that depart on a certain day on the line, any train . | - | |
| Set of predetermined price discounts, and . | - | |
| The carrying capacity of train . | passengers | |
| The number of ticket pre-sale periods, . | - | |
| The published ticket price (ceiling price) of train on . | ||
| The ticket price of train on in pre-sale period . | yuan | |
| The generalized travel cost of the train on in pre-sale period . | yuan | |
| The travel time of train on when train cannot provide transport service for . | minutes | |
| The sharing rate of train for the passenger flow on in pre-sale period . | % | |
| The elastic passenger flow demand of train on in pre-sale period . | passengers | |
| The stopping cost of train at station . | yuan | |
| The stopping time of train at station . | minutes | |
| The passenger flow that is rejected in pre-sale period and continues to choose train in period . | passengers | |
| Parameters | ||
| The elastic demand function coefficient in pre-sale period . | - | |
| The time value conversion coefficient. | yuan/min | |
| The utility conversion coefficient. | - | |
| Decision variables | ||
| The price discount of train on in pre-sale period and is a discrete variable. | - | |
| when train stops at station ; otherwise is a binary variable. | - | |
| The number of seats that train allocates to in pre-sale period is an integer variable. | tickets | |
| Item | Type | Size | Characteristic |
|---|---|---|---|
| Variable | Discrete | ||
| Variable | Binary | ||
| Variable | Integer | ||
| Variable | Binary | ||
| Constraint (10) | Constraint | Linear | |
| Constraint (11) | Constraint | Linear | |
| Constraint (12) | Constraint | Linear | |
| Constraint (14) | Constraint | Linear | |
| Constraint (15) | Constraint | Nonlinear | |
| Constraint (16) | Constraint | Linear | |
| Constraint (18) | Constraint | Linear | |
| Constraint (19) | Constraint | Linear | |
| Constraint (20) | Constraint | Linear | |
| Constraint (21) | Constraint | Linear | |
| Constraint (22) | Constraint | Linear |
| Solid Annealing | Combinatorial Optimization |
|---|---|
| State | Solution |
| System energy | The objective function |
| The lowest energy state | The optimal solution |
| Heating to melt | Setting the initial temperature |
| Isothermal process | Generating and accepting (or rejecting) new solutions |
| Cooling process | Changing the current temperature |
| OD Pairs | Dynamic Prices (Yuan) | Public Prices (Yuan) | Current Prices (Yuan) | |||
|---|---|---|---|---|---|---|
| = 1 | = 2 | = 3 | = 4 | |||
| 1–4 | 129 | 175.5 | 203 | 221.5 | 230.5 | 184.5 |
| 1–9 | 310.5 | 421.5 | 488 | 532 | 554.5 | 443.5 |
| 1–11 | 366.5 | 497.5 | 576 | 628 | 654.5 | 523.5 |
| 1–12 | 387 | 525.5 | 608.5 | 663.5 | 691 | 553.0 |
| 8–12 | 195.5 | 265 | 307 | 335 | 349 | 279.0 |
| 9–12 | 94 | 128 | 148 | 161.5 | 168 | 134.5 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 57/63 | 10/9 | 189/174 | 79/74 | 53/55 | 9/11 | 58/53 | 550/521 | 33/29 | 359/345 | 1422/1334 |
| 2 | 5/5 | 22/20 | 13/15 | - | 3/3 | 12/12 | 50/46 | 7/7 | 86/87 | 140/137 | |
| 3 | 5/5 | - | - | - | 3/3 | 0/0 | - | 10/10 | 12/11 | ||
| 4 | 43/38 | 21/23 | 16/14 | 22/19 | 53/48 | 11/12 | 30/28 | 110/97 | |||
| 5 | - | 9/10 | 0/0 | 5/5 | 0/0 | 0/0 | 11/14 | ||||
| 6 | - | - | 15/10 | 0/0 | 16/19 | 42/45 | |||||
| 7 | 1/1 | /0 | /0 | 9/8 | /0 | ||||||
| 8 | 83/74 | 14/17 | 49/45 | 81/75 | |||||||
| 9 | 59/65 | 139/126 | 329/299 | ||||||||
| 10 | 2/2 | 9/8 | |||||||||
| 11 | 145/129 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, J.; Li, X.; Yang, K.; Xu, G. Joint Optimization of Ticket Pricing Strategy and Train Stop Plan for High-Speed Railway: A Case Study. Mathematics 2022, 10, 1679. https://doi.org/10.3390/math10101679
Qin J, Li X, Yang K, Xu G. Joint Optimization of Ticket Pricing Strategy and Train Stop Plan for High-Speed Railway: A Case Study. Mathematics. 2022; 10(10):1679. https://doi.org/10.3390/math10101679
Chicago/Turabian StyleQin, Jin, Xiqiong Li, Kang Yang, and Guangming Xu. 2022. "Joint Optimization of Ticket Pricing Strategy and Train Stop Plan for High-Speed Railway: A Case Study" Mathematics 10, no. 10: 1679. https://doi.org/10.3390/math10101679
APA StyleQin, J., Li, X., Yang, K., & Xu, G. (2022). Joint Optimization of Ticket Pricing Strategy and Train Stop Plan for High-Speed Railway: A Case Study. Mathematics, 10(10), 1679. https://doi.org/10.3390/math10101679






