Asymptotic Normality in Linear Regression with Approximately Sparse Structure

Abstract

In this paper, we study the asymptotic normality in high-dimensional linear regression. We focus on the case where the covariance matrix of the regression variables has a KMS structure, in asymptotic settings where the number of predictors, p, is proportional to the number of observations, n. The main result of the paper is the derivation of the exact asymptotic distribution for the suitably centered and normalized squared norm of the product between predictor matrix, $\mathbb{X}$, and outcome variable, Y, i.e., the statistic $\parallel {\mathbb{X}}^{\prime }{Y\parallel }_2^2$, under rather unrestrictive assumptions for the model parameters ${\beta }_j$. We employ variance-gamma distribution in order to derive the results, which, along with the asymptotic results, allows us to easily define the exact distribution of the statistic. Additionally, we consider a specific case of approximate sparsity of the model parameter vector $\beta$ and perform a Monte Carlo simulation study. The simulation results suggest that the statistic approaches the limiting distribution fairly quickly even under high variable multi-correlation and relatively small number of observations, suggesting possible applications to the construction of statistical testing procedures for the real-world data and related problems.

1. Introduction

Consider a linear regression model

$$\begin{array}{c}\hfill Y=\mathbb{X}\beta +\epsilon ,\end{array}$$

(1)

where $Y:={(y_1,\dots ,y_n)}^{\prime }\in {\mathbb{R}}^{n\times 1}$ are n observations of outcome and $\mathbb{X}={(X_1,\dots ,X_n)}^{\prime }\in {\mathbb{R}}^{n\times p}$ are p-dimensional predictors with $X_1,\dots ,X_n$ being i.i.d. $p\times 1$ random vectors $X_i={(X_{1,i},\dots ,X_{p,i})}^{\prime }$, which are normally distributed with zero mean and the covariance matrix $\mathsf{\Sigma }$, denoted $X_i\stackrel{d}{=}{\mathcal{N}}_p(0,\mathsf{\Sigma })$. We assume that the covariance matrix $\mathsf{\Sigma }$ has a form

$$\begin{array}{ccc}\hfill \mathsf{\Sigma }& =& {\left({\varrho }^{|i-j|}\right)}_{i,j=1}^p=\left[\begin{array}{cccc}1& \varrho & \cdots & {\varrho }^{p-1}\\ \varrho & 1& \cdots & {\varrho }^{p-2}\\ ⋮& ⋮& \ddots & ⋮\\ {\varrho }^{p-1}& {\varrho }^{p-2}& \cdots & 1\end{array}\right],\hfill \end{array}$$

(2)

if $0<\left|\varrho \right|<1$ and $\mathsf{\Sigma }=I_p$ if $\varrho =0$ (here and below $I_p$ denotes the $p\times p$ identity matrix). This matrix is often called the Kac–Murdock–Szego (KMS) matrix, originally introduced in [1]. As the autocorrelation matrix of corresponding causal AR(1) processes, the KMS matrix is positive definite and is considered due to the wide array of applications in the literature and its well known spectral properties (see, e.g., [2] for a thorough literature review). When carefully chosen, such a structure could well-approximate a wide array of possible covariance structures (see, e.g., [3] for a more general approach with various Toeplitz covariance structures). Furthermore, $\epsilon :={({\epsilon }_1,\dots ,{\epsilon }_n)}^{\prime }\in {\mathbb{R}}^{n\times 1}\stackrel{d}{=}{\mathcal{N}}_n(0,{\sigma }_{\epsilon }^2{I}_n)$ are unobserved i.i.d. errors with $\mathbb{E}{\epsilon }_i=0$, $Var\left({\epsilon }_i\right)={\sigma }_{\epsilon }^2>0$, and $\beta :={({\beta }_1,\dots ,{\beta }_p)}^{\prime }\in {\mathbb{R}}^{p\times 1}$ is an unknown p-dimensional parameter. In practice, the assumption is that $\mathbb{E}{X}_i=0$ can be untenable, and it may be appropriate to add an intercept to the linear model (1); however, for simplicity, throughout this paper we will assume that the intercept is known and the variables are centered. Similar settings are considered when dealing with certain geospatial data, longitudinal studies, microarray data, and research on approximate message passing algorithms (see, e.g., [4,5,6,7,8,9]).

This paper is concerned with the derivation of the exact asymptotic distribution for the suitably centered and normalized squared norm $\parallel {\mathbb{X}}^{\prime }{Y\parallel }_2^2$ under the assumption of the KMS type covariance structure in (2), where p and n are assumed to be large. Throughout the paper, we assume that $p,n\to \infty$ and $p/n\to c\in (0,\infty )$. We are particularly interested in cases where $p>n$. Statistics of such form arise in various applications in the context of high-dimensional linear regression, and under normality assumptions general results can be derived using random matrix theory through Wishart distributions (see, e.g., [7,10,11,12]). Dealing with such statistics typically require strong restrictions on the model parameters $\beta$; however, in this paper, we only require that ${\parallel \beta \parallel }_2^2<\infty$ is satisfied. Moreover, our results could be extended by using $\beta$-generating functions (e.g., parameters of FARIMA models). In comparison to the related papers, ref. [12] assumes exact sparsity, while [7,10] require approximate sparsity.

We approach the problem following an observation by [13] that the distribution of product of Gaussian random variables admits a variance-gamma distribution, which results in a set of attractive properties. We contribute to the literature on variance-gamma distribution by extending the results by [14,15,16]. We demonstrate that, along with the derivation of the asymptotic distribution of $\parallel {\mathbb{X}}^{\prime }{Y\parallel }_2^2$, this approach allows us to define the exact distribution of the statistic given any fixed values $p,n$, which can be expressed through a combination of gamma and normal random variables. In the related literature we were not able to find results for the exact distribution and asymptotic analysis of the statistic $\parallel {\mathbb{X}}^{\prime }{Y\parallel }_2^2$ based on the variance-gamma distribution. Furthermore, we deem that such a result is much easier to work with than when considering the characteristic or density functions of $\parallel {\mathbb{X}}^{\prime }{Y\parallel }_2^2$ straightforwardly. Therefore, in addition to the ${\ell }_2$-norm statistic, we argue that the obtained results can be easily extended towards alternative forms of the statistic, e.g., by using a different norm, which would reduce the problem to manipulating variance-gamma distribution, thus suggesting possible further research cases and useful extensions.

Additionally, we examine a specific case of parameter $\beta$ by considering ${\beta }_j=j^{-1}$, $j\ge 1$. Similar structures of the vector $\beta$ are often found in the literature when approximate sparsity of the coefficients in the linear regression model (1) is assumed. See, e.g., [17,18] for a broader view towards sparsity requirements and its implications to specific high-dimensional algorithms; refs. [19,20] for model selection problems in autoregressive time series models; refs. [21,22,23,24,25,26,27,28] for applications on inference of high-dimensional models and high-dimensional instrumental variable (IV) regression models; or [29,30,31,32,33] for recent applications of high-dimensional and sparse methods with financial and economic data. Performing Monte Carlo simulations, we find that the empirical distributions of the corresponding statistic approach the limiting distribution reasonably quickly even for large values of $\varrho$ and c. These results suggest that the assumption of sparse structure can be included in the applications and statistical tests, thus, could be further extended following the literature on testing for sparsity or construction of signal-to-noise ratio estimators (see, e.g., [7,10,11,12]).

In this paper, $\stackrel{d}{=}$, $\stackrel{d}{\to }$ and $\stackrel{\mathbb{P}}{\to }$ denote the equality of distributions, convergence of distributions and convergence in probability, respectively. The notation of C represents a generic positive constant which may assume different values at various locations, and ${\mathbf{1}}_A$ denotes the indicator function of a set A.

The structure of the paper is as follows. In Section 2, we present the main results of the paper. In Section 3, we present useful properties of variance-gamma distribution, which are used in Section 4 in order to prove some auxiliary results. In Section 5, we present the proof of the main result. Finally, in Section 6, we provide an example of the main result under imposed approximate sparsity assumption for the parameter $\beta$ of the model (1). Technical results are presented in Appendix A, while, for brevity, some straightforward yet tedious proofs are presented in the Supplementary Material.

2. Main Results

In this section we formulate the main results on the normality of statistic $\parallel {\mathbb{X}}^{\prime }{Y\parallel }_2^2$. Introduce the notations:

$$\begin{array}{ccc}\hfill {\kappa }_{1,p}& :=& \sum _{k=1}^p\sum _{l=1}^p{\beta }_k{\beta }_l{\varrho }^{|k-l|},\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill {\kappa }_{2,p}& :=& \sum _{k=1}^p{\left(\sum _{l=1}^p{\beta }_l{\varrho }^{|k-l|}\right)}^2,\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill {\kappa }_{3,p}& :=& \sum _{k,l,j,j^{\prime }=1}^p{\beta }_j{\beta }_{j^{\prime }}{\varrho }^{|k-j|}{\varrho }^{|l-j^{\prime }|}{\varrho }^{|k-l|}.\hfill \end{array}$$

(5)

It can be observed that under ${\sum }_{j=1}^{\infty }{\beta }_j^2<\infty$, there exist limits

$$\begin{array}{ccc}\hfill {\kappa }_i& =& \underset{p\to \infty }{lim}{\kappa }_{i,p},i=1,2,3.\hfill \end{array}$$

Additionally, ${\kappa }_{2,p}\ge 0$. Since ${\left({\varrho }^{|i-j|}\right)}_{i,j=1}^p$ is positive semi-definite, ${\kappa }_{i,p}\ge 0$, $i=1,3$. Indeed, ${\sum }_{k,l=1}^p{\varrho }^{|k-l|}{a}_k{a}_l\ge 0$, thus it suffices to take $a_k={\beta }_k$ for $i=1$ and $a_k={\sum }_{j=1}^p{\beta }_j{\varrho }^{|k-j|}$ for $i=3$.

Our first main result is the following theorem.

Theorem 1.

Assume the model in (1) with covariance structure in (2). Let $n\to \infty$ and let $p=p_n$ satisfy

$$\begin{array}{ccc}\hfill p\to \infty ,& & \frac{p}{n}\to c\in (0,\infty ).\hfill \end{array}$$

(6)

Let also the ${\beta }_j$ satisfy

$$\begin{array}{ccc}\hfill \sum _{j=1}^{\infty }{\beta }_j^2& <& \infty .\hfill \end{array}$$

(7)

Then

$$\begin{array}{ccc}\hfill \frac{\parallel {\mathbb{X}}^{\prime }{Y\parallel }_2^2-n^2{\kappa }_{2,p}-pn({\kappa }_{1,p}+{\sigma }_{\epsilon }^2)}{n^{3/2}}& \stackrel{d}{\to }& \mathcal{N}(0,s^2),\hfill \end{array}$$

(8)

where variance $s^2$ has the structure

$$\begin{array}{ccc}\hfill s^2& =& 4{\kappa }_2^2+4({\kappa }_1+{\sigma }_{\epsilon }^2)\left(2{\kappa }_{2}c+{\kappa }_3\right)+2c{({\kappa }_1+{\sigma }_{\epsilon }^2)}^2\left(c+\frac{1+{\varrho }^2}{1-{\varrho }^2}\right).\hfill \end{array}$$

(9)

Our second main result deals with the case where the centering sequence in (8) is modified to include the limiting values of ${\kappa }_{i,p}$, $i=1,2$.

Theorem 2.

Let the assumptions of Theorem 1 hold. In addition, assume that ${\sum }_{j=p+1}^{\infty }{\beta }_j^2=o\left(p^{-1/2}\right)$ and ${sup}_{j\ge 1}\left|{\beta }_j\right|j^{\alpha }<\infty$ with $\alpha >1/2$. Then,

$$\begin{array}{ccc}\hfill \frac{\parallel {\mathbb{X}}^{\prime }{Y\parallel }_2^2-n^2\left({\kappa }_2+c({\kappa }_1+{\sigma }_{\epsilon }^2)\right)}{n^{3/2}}& \stackrel{d}{\to }& \mathcal{N}(0,s^2).\hfill \end{array}$$

(10)

The proofs of these theorems are given in Section 5.

Remark 1.

For alternative expressions of ${\kappa }_1$, ${\kappa }_2$ and ${\kappa }_3$, see Lemma 5 below.

Define

$$\begin{array}{ccc}\hfill \beta \left(x\right)& :=& \sum _{j=1}^{\infty }{\beta }_j^2{x}^j,\left|x\right|\le 1.\hfill \end{array}$$

The following corollary deals with the case when $\varrho =0$, i.e., $\mathsf{\Sigma }=I_p$. The result follows from Theorem 2, noting that in this case ${\kappa }_i=\beta \left(1\right)$, $i=1,2,3$.

Corollary 1.

Assume a model (1) with covariance structure $\mathsf{\Sigma }=I_p$. Let assumptions (6) and (7) be satisfied. In addition, assume that ${\sum }_{j=p+1}^{\infty }{\beta }_j^2=o\left(p^{-1/2}\right)$ and ${sup}_{j\ge 1}\left|{\beta }_j\right|j^{\alpha }<\infty$ with $\alpha >1/2$. Then,

$$\begin{array}{ccc}\hfill \frac{\parallel {\mathbb{X}}^{\prime }{Y\parallel }_2^2-n^2(\beta \left(1\right)(1+c)+c{\sigma }_{\epsilon }^2)}{n^{3/2}}& \stackrel{d}{\to }& \mathcal{N}(0,s^2),\hfill \end{array}$$

(11)

where

$$\begin{array}{ccc}\hfill s^2& =& 2\beta {\left(1\right)}^2\left(4+5c+c^2\right)+4\beta \left(1\right){\sigma }_{\epsilon }^2\left(1+3c+c^2\right)+2{\sigma }_{\epsilon }^4(c+c^2).\hfill \end{array}$$

(12)

3. Properties of the Variance-Gamma Distribution

In this section, we provide some properties of the variance-gamma distribution, which will be used in the following proofs.

Recall that the variance-gamma distribution with parameters $r>0$, $\theta \in \mathbb{R}$, $\sigma >0$ and $\mu \in \mathbb{R}$ has density

$$\begin{array}{c}\hfill f^{\mathrm{VG}}\left(x\right)=\frac{1}{\sigma \sqrt{\pi }\mathsf{\Gamma }(r/2)}{\mathrm{e}}^{\theta (x-\mu )/{\sigma }^2}{\left(\frac{|x-\mu |}{2\sqrt{{\theta }^2+{\sigma }^2}}\right)}^{(r-1)/2}{K}_{(r-1)/2}\left(\frac{\sqrt{{\theta }^2+{\sigma }^2}}{{\sigma }^2}|x-\mu |\right),\end{array}$$

(13)

where $x\in \mathbb{R}$, $K_{\nu }\left(x\right)$ is the modified Bessel function of the second kind. For a random variable Q with density (13), we write $Q\stackrel{d}{=}\mathrm{VG}(r,\theta ,\sigma ,\mu )$. Let $\mathsf{\Gamma }(a,b)$, $a>0$, $b>0$, denote the gamma distribution with density

$$\begin{array}{ccc}\hfill f^{\mathrm{G}}\left(x\right)& =& \frac{b^a}{\mathsf{\Gamma }\left(a\right)}{x}^{a-1}{\mathrm{e}}^{-bx},x>0.\hfill \end{array}$$

It holds that

$$\begin{array}{ccc}\hfill Q& \stackrel{d}{=}& \mu +\theta W_r+\sigma \sqrt{W_r}U,\hfill \end{array}$$

(14)

where $W_r\stackrel{d}{=}\mathsf{\Gamma }(r/2,1/2)$, $U\stackrel{d}{=}\mathcal{N}(0,1)$, $W_r$ and U are independent. The characteristic function of $Q\stackrel{d}{=}\mathrm{VG}(r,\theta ,\sigma ,\mu )$ has a form (see, e.g., [34,35])

$$\begin{array}{ccc}\hfill {\phi }_Q\left(t\right)& =& \frac{{\mathrm{e}}^{\mathrm{i}\mu t}}{{(1+{\sigma }^{2}t-2\mathrm{i}\theta t)}^{r/2}},t\in \mathbb{R}.\hfill \end{array}$$

(15)

We note the following properties of the variance-gamma distribution.

(i)

If $Q_1\stackrel{d}{=}\mathrm{VG}(r_1,\theta ,\sigma ,{\mu }_1)$ and $Q_2\stackrel{d}{=}\mathrm{VG}(r_2,\theta ,\sigma ,{\mu }_2)$ are independent random variables then

$$\begin{array}{ccc}\hfill Q_1+Q_2& \stackrel{d}{=}& \mathrm{VG}(r_1+r_2,\theta ,\sigma ,{\mu }_1+{\mu }_2).\hfill \end{array}$$

(ii)

If $Q\stackrel{d}{=}\mathrm{VG}(r,\theta ,\sigma ,\mu )$, then for any $a>0$

$$\begin{array}{ccc}\hfill aQ& \stackrel{d}{=}& \mathrm{VG}(r,a\theta ,a\sigma ,a\mu ).\hfill \end{array}$$

The following proposition is crucial for our purposes.

Proposition 1.

(i) If ${({\xi }_1,{\xi }_2)}^{\prime }\stackrel{d}{=}{\mathcal{N}}_2(0,\mathsf{\Sigma })$, where $\mathsf{\Sigma }=\left(\begin{array}{cc}{\sigma }_1^2& \varrho {\sigma }_1{\sigma }_2\\ \varrho {\sigma }_1{\sigma }_2& {\sigma }_2^2\end{array}\right)$, then

$$\begin{array}{ccc}\hfill {\xi }_1{\xi }_2& \stackrel{d}{=}& \mathrm{VG}(1,\varrho {\sigma }_1{\sigma }_2,\sqrt{1-{\varrho }^2}{\sigma }_1{\sigma }_2,0).\hfill \end{array}$$

(ii) If ${({\xi }_{1j},{\xi }_{2j})}^{\prime }$, $j=1,\dots ,n$, are i.i.d. random vectors with common distribution ${\mathcal{N}}_2(0,\mathsf{\Sigma })$, then

$$\begin{array}{ccc}\hfill \sum _{j=1}^n{\xi }_{1j}{\xi }_{2j}& \stackrel{d}{=}& \mathrm{VG}(n,\varrho {\sigma }_1{\sigma }_2,\sqrt{1-{\varrho }^2}{\sigma }_1{\sigma }_2,0)\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \sum _{j=1}^n{\xi }_{1j}{\xi }_{2j}& \stackrel{d}{=}& {\sigma }_1{\sigma }_2(\varrho W_n+\sqrt{1-{\varrho }^2}\sqrt{W_n}U),\hfill \end{array}$$

where $W_n\stackrel{d}{=}\mathsf{\Gamma }(n/2,1/2)$ and $U\stackrel{d}{=}\mathcal{N}(0,1)$ are independent random variables.

(iii) Assume that ${({\xi }_{1j}^{\left(1\right)},\dots ,{\xi }_{1j}^{\left(p\right)},{\xi }_{2j})}^{\prime }$, $j=1,\dots ,n$, are i.i.d. copies of ${({\xi }_1^{\left(1\right)},\dots ,{\xi }_1^{\left(p\right)},{\xi }_2)}^{\prime }\stackrel{d}{=}{\mathcal{N}}_{p+1}(0,{\mathsf{\Sigma }}^{\left(p\right)})$ and let ${\varrho }^{\left(kl\right)}:=\mathrm{Corr}({\xi }_1^{\left(k\right)},{\xi }_1^{\left(l\right)})$, ${\varrho }^{\left(k\right)}:=\mathrm{Corr}({\xi }_1^{\left(k\right)},{\xi }_2)$, ${\left({\sigma }_1^{\left(k\right)}\right)}^2:=\mathrm{Var}\left({\xi }_1^{\left(k\right)}\right)$, ${\sigma }_2^2:=\mathrm{Var}\left({\xi }_2\right)$, $k,l=1,\dots ,p$. Then

$$\left(\begin{array}{c}\sum _{j=1}^n{\xi }_{1j}^{\left(1\right)}{\xi }_{2j}\\ ⋮\\ \sum _{j=1}^n{\xi }_{1j}^{\left(p\right)}{\xi }_{2j}\end{array}\right)\hspace{1em}\stackrel{d}{=}\hspace{1em}\left(\begin{array}{c}{\sigma }_1^{\left(1\right)}{\sigma }_2({\varrho }^{\left(1\right)}{W}_n+\sqrt{1-{\left({\varrho }^{\left(1\right)}\right)}^2}\sqrt{W_n}{U}_1)\\ ⋮\\ {\sigma }_1^{\left(p\right)}{\sigma }_2({\varrho }^{\left(p\right)}{W}_n+\sqrt{1-{\left({\varrho }^{\left(p\right)}\right)}^2}\sqrt{W_n}{U}_p)\end{array}\right),$$

where ${(U_1,\dots ,U_p)}^{\prime }\stackrel{d}{=}{\mathcal{N}}_p(0,{\mathsf{\Sigma }}_U)$, ${\mathsf{\Sigma }}_U=\left({\sigma }_U^{\left(kl\right)}\right)$ with

$$\begin{array}{ccc}\hfill {\sigma }_U^{(k,l)}& =& \mathbb{E}{U}_k{U}_l=\frac{{\varrho }^{\left(kl\right)}-{\varrho }^{\left(k\right)}{\varrho }^{\left(l\right)}}{\sqrt{1-{\left({\varrho }^{\left(k\right)}\right)}^2}\sqrt{1-{\left({\varrho }^{\left(l\right)}\right)}^2}},k,l=1,\dots ,p.\hfill \end{array}$$

(16)

Proof. 

The statements in (i), (ii) are well known, see e.g., [16]. The proof of part (iii) follows from Lemma 1. □

Lemma 1.

Assume that ${({\xi }_1^{\left(1\right)},\dots ,{\xi }_1^{\left(p\right)},{\xi }_2)}^{\prime }$ has distribution ${\mathcal{N}}_{p+1}(0,{\mathsf{\Sigma }}^{\left(p\right)})$ and let ${\varrho }^{\left(kl\right)}:=\mathrm{Corr}({\xi }_1^{\left(k\right)},{\xi }_1^{\left(l\right)})$, ${\varrho }^{\left(k\right)}:=\mathrm{Corr}({\xi }_1^{\left(k\right)},{\xi }_2)$, ${\left({\sigma }_1^{\left(k\right)}\right)}^2:=\mathrm{Var}\left({\xi }_1^{\left(k\right)}\right)$, ${\sigma }_2^2:=\mathrm{Var}\left({\xi }_2\right)$, $k,l=1,\dots ,p$. Then

$$\left(\begin{array}{c}{\xi }_1^{\left(1\right)}{\xi }_2\\ ⋮\\ {\xi }_1^{\left(p\right)}{\xi }_2\end{array}\right)\hspace{1em}\stackrel{d}{=}\hspace{1em}\left(\begin{array}{c}{\sigma }_1^{\left(1\right)}{\sigma }_2\left({\varrho }^{\left(1\right)}{W}_1+\sqrt{1-{\left({\varrho }^{\left(1\right)}\right)}^2}\sqrt{W_1}{U}_1\right)\\ ⋮\\ {\sigma }_1^{\left(p\right)}{\sigma }_2\left({\varrho }^{\left(p\right)}{W}_1+\sqrt{1-{\left({\varrho }^{\left(p\right)}\right)}^2}\sqrt{W_1}{U}_p\right)\end{array}\right),$$

where $W_1\stackrel{d}{=}\mathsf{\Gamma }(1/2,1/2)$, ${(U_1,\dots ,U_p)}^{\prime }$ is, independent of $W_1$, zero mean normal vector with covariances in (16).

Proof. 

It suffices to prove that for any $(t_1,\dots ,t_p)\in {\mathbb{R}}^p$ it holds

$$\begin{array}{ccc}\hfill \left(\sum _{k=1}^p{t}_k{\xi }_1^{\left(k\right)}\right){\xi }_2& \stackrel{d}{=}& {\sigma }_2\sum _{k=1}^p{t}_k{\sigma }_1^{\left(k\right)}\left({\varrho }^{\left(k\right)}{W}_1+\sqrt{1-{\left({\varrho }^{\left(k\right)}\right)}^2}\sqrt{W_1}{U}_k\right).\hfill \end{array}$$

(17)

Since

$$\begin{array}{ccc}\hfill \sum _{k=1}^p{t}_k{\xi }_1^{\left(k\right)}& \stackrel{d}{=}& \mathcal{N}\left(0,\sum _{k,l=1}^p{t}_k{t}_l{\varrho }^{\left(kl\right)}{\sigma }_1^{\left(k\right)}{\sigma }_1^{\left(l\right)}\right),{\xi }_2\stackrel{d}{=}\mathcal{N}(0,{\sigma }_2^2),\hfill \end{array}$$

by Proposition 1(i) we obtain that

$$\begin{array}{ccc}\hfill \left(\sum _{k=1}^p{t}_k{\xi }_1^{\left(k\right)}\right){\xi }_2& \stackrel{d}{=}& \mathrm{VG}\left(1,{\sigma }_2\sum _{k=1}^p{t}_k{\varrho }^{\left(k\right)}{\sigma }_1^{\left(k\right)},{\sigma }_2\sqrt{\sum _{k,l=1}^p{t}_k{t}_l{\sigma }_1^{\left(k\right)}{\sigma }_1^{\left(l\right)}({\varrho }^{\left(kl\right)}-{\varrho }^{\left(k\right)}{\varrho }^{\left(l\right)})},0\right).\hfill \end{array}$$

(18)

For the right-hand side of (17) write

$$\begin{array}{ccc}& & {\sigma }_2\sum _{k=1}^p{t}_k{\sigma }_1^{\left(k\right)}\left({\varrho }^{\left(k\right)}{W}_1+\sqrt{1-{\left({\varrho }^{\left(k\right)}\right)}^2}\sqrt{W_1}{U}_k\right)\hfill \\ & =& \left({\sigma }_2\sum _{k=1}^p{t}_k{\sigma }_1^{\left(k\right)}{\varrho }^{\left(k\right)}\right)W_1+\left({\sigma }_2\sum _{k=1}^p{t}_k{\sigma }_1^{\left(k\right)}\sqrt{1-{\left({\varrho }^{\left(k\right)}\right)}^2}{U}_k\right)\sqrt{W_1}.\hfill \end{array}$$

Here, by (16),

$$\begin{array}{ccc}\hfill {\sigma }_2\sum _{k=1}^p{t}_k{\sigma }_1^{\left(k\right)}\sqrt{1-{\left({\varrho }^{\left(k\right)}\right)}^2}{U}_k& \stackrel{d}{=}& {\sigma }_2{\left(\sum _{k,l=1}^p{t}_k{t}_l{\sigma }_1^{\left(k\right)}{\sigma }_1^{\left(l\right)}\sqrt{1-{\left({\varrho }^{\left(k\right)}\right)}^2}\sqrt{1-{\left({\varrho }^{\left(l\right)}\right)}^2}\mathbb{E}\left(U_k{U}_l\right)\right)}^{1/2}{U}_1\hfill \\ & =& {\sigma }_2{\left(\sum _{k,l=1}^p{t}_k{t}_l{\sigma }_1^{\left(k\right)}{\sigma }_1^{\left(l\right)}({\varrho }^{\left(kl\right)}-{\varrho }^{\left(k\right)}{\varrho }^{\left(l\right)})\right)}^{1/2}{U}_1.\hfill \end{array}$$

Note that $U_1\stackrel{d}{=}\mathcal{N}(0,1)$. So that,

$$\begin{array}{ccc}& & {\sigma }_2\sum _{k=1}^p{t}_k{\sigma }_1^{\left(k\right)}\left({\varrho }^{\left(k\right)}{W}_1+\sqrt{1-{\left({\varrho }^{\left(k\right)}\right)}^2}\sqrt{W_1}{U}_k\right)\hfill \\ & \stackrel{d}{=}& \left({\sigma }_2\sum _{k=1}^p{t}_k{\sigma }_1^{\left(k\right)}{\varrho }^{\left(k\right)}\right)W_1+{\sigma }_2{\left(\sum _{k,l=1}^p{t}_k{t}_l{\sigma }_1^{\left(k\right)}{\sigma }_1^{\left(l\right)}({\varrho }^{\left(kl\right)}-{\varrho }^{\left(k\right)}{\varrho }^{\left(l\right)})\right)}^{1/2}\sqrt{W_1}{U}_1,\hfill \end{array}$$

which, by representation (14), has the same VG distribution as that in (18). This proves (17). □

4. Some Auxiliary Lemmas

In this section we establish some auxiliary results that will be used in the proofs of Theorems 1 and 2. Here and throughout the paper we remove the upper indices when working with triangular schemes of random variables, e.g., $(V_1,\dots ,V_p)\equiv (V_1^{\left(p\right)},\dots ,V_p^{\left(p\right)})$, whenever it is clear from the context.

Lemma 2.

Let $V={(V_1,\dots ,V_p)}^{\prime }\stackrel{d}{=}{\mathcal{N}}_p(0,{\mathsf{\Sigma }}_V^{\left(p\right)})$, where ${\mathsf{\Sigma }}_V^{\left(p\right)}$ is positive definite covariance matrix and $tr\left({\left({\mathsf{\Sigma }}_V^{\left(p\right)}\right)}^2\right)=o\left(p^2\right)$, $p\to \infty$. Then

$$\begin{array}{ccc}\hfill \frac{1}{p}\sum _{k=1}^p\left(V_k^2-\mathbb{E}{V}_k^2\right)& \stackrel{\mathbb{P}}{\to }& 0asp\to \infty .\hfill \end{array}$$

(19)

If, in addition, $p^{-1}tr\left({\mathsf{\Sigma }}_V^{\left(p\right)}\right)\to 1$, then

$$\begin{array}{ccc}\hfill \frac{1}{p}\sum _{k=1}^p{V}_k^2& \stackrel{\mathbb{P}}{\to }& 1asp\to \infty .\hfill \end{array}$$

(20)

Proof. 

Due to the Spectral Theorem, we have

$$\begin{array}{ccc}\hfill V^{\prime }V& =& \sum _{k=1}^p{V}_k^2\stackrel{d}{=}\sum _{j=1}^p{\lambda }_j^{\left(p\right)}{\tilde{Z}}_j^2,\hfill \end{array}$$

(21)

where ${\tilde{Z}}_j$ are i.i.d. standard normal variables and ${\lambda }_1^{\left(p\right)},\dots ,{\lambda }_p^{\left(p\right)}$ are the eigenvalues of ${\mathsf{\Sigma }}_V^{\left(p\right)}$. Observe from (21) that

$$\begin{array}{ccc}\hfill \mathbb{E}{V}^{\prime }V& =& \sum _{j=1}^p{\lambda }_j^{\left(p\right)}=tr\left({\mathsf{\Sigma }}_V^{\left(p\right)}\right),\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill Var\left(V^{\prime }V\right)& =& Var\left(\sum _{j=1}^p{\lambda }_j^{\left(p\right)}{\tilde{Z}}_j^2\right)=2\sum _{j=1}^p{\left({\lambda }_j^{\left(p\right)}\right)}^2=2tr\left({\left({\mathsf{\Sigma }}_V^{\left(p\right)}\right)}^2\right).\hfill \end{array}$$

(23)

Thus, by (22) and (23), for any $ϵ>0$

$$\begin{array}{ccc}\hfill \mathbb{P}\left(\left|\frac{1}{p}\left(V^{\prime }V-\mathbb{E}{V}^{\prime }V\right)\right|>ϵ\right)& \le & \frac{Var\left(V^{\prime }V\right)}{p^2{ϵ}^2}\to 0,p\to \infty ,\hfill \end{array}$$

and the relation in (19) follows due to assumption $\mathrm{tr}\left({\left({\mathsf{\Sigma }}_V^{\left(p\right)}\right)}^2\right)=o\left(p^2\right)$. Finally, if $p^{-1}tr\left({\mathsf{\Sigma }}_V^{\left(p\right)}\right)\to 1$, by (22), the result (19) leads to (20). □

Remark 2.

The assumption on matrix ${\mathsf{\Sigma }}_V={\mathsf{\Sigma }}_V^{\left(p\right)}$ in Lemma 2, requiring that $tr\left({\mathsf{\Sigma }}_V^2\right)=o\left(p^2\right)$, is not overly restrictive: assume, for example, that ${\mathsf{\Sigma }}_V=\left({\sigma }^{(i,j)}\right)$ is any KMS type covariance matrix, as in (2). Then, it can be seen that

$$\begin{array}{ccc}\hfill tr\left({\mathsf{\Sigma }}_V^2\right)& =& \sum _{i,j=1}^p{\left({\sigma }^{(i,j)}\right)}^2=\sum _{i,j=1}^p{\varrho }^{2|i-j|}\hfill \\ & =& \sum _{\left|m\right|<p}(p-|m\left|\right){\varrho }^{2\left|m\right|}\le p\sum _{\left|m\right|<p}\left|m\right|{\varrho }^{2\left|m\right|}=\mathcal{O}\left(p\right).\hfill \end{array}$$

Lemma 3.

Assume that ${\tilde{Z}}_1,{\tilde{Z}}_2,\dots$ are i.i.d. $\mathcal{N}(0,1)$ random variables. For any $p\in \mathbb{N}$ define

$$\begin{array}{ccc}\hfill {\zeta }_j^{\left(p\right)}& :=& {\nu }_j^{\left(p\right)}({\tilde{Z}}_j^2-1)+{\gamma }_j^{\left(p\right)}\sqrt{p}{\tilde{Z}}_j,j=1,\dots ,p,\hfill \end{array}$$

(24)

where ${\nu }_j^{\left(p\right)},j=1,\dots ,p$, are positive scalars, and ${\gamma }_j^{\left(p\right)}$, $j=1,\dots ,p$, are real scalars, such that

$$\begin{array}{ccc}\hfill \sum _{j=1}^p{\left({\nu }_j^{\left(p\right)}\right)}^3& =& o\left({\left(\sum _{j=1}^p\mathrm{Var}\left({\zeta }_j^{\left(p\right)}\right)\right)}^{3/2}\right),\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill p\sum _{j=1}^p{\left({\gamma }_j^{\left(p\right)}\right)}^2{\nu }_j^{\left(p\right)}& =& o\left({\left(\sum _{j=1}^p\mathrm{Var}\left({\zeta }_j^{\left(p\right)}\right)\right)}^{3/2}\right)\hfill \end{array}$$

(26)

with $\mathrm{Var}\left({\zeta }_j^{\left(p\right)}\right)=2{\left({\nu }_j^{\left(p\right)}\right)}^2+p{\left({\gamma }_j^{\left(p\right)}\right)}^2.$ Then, as $p\to \infty$,

$$\begin{array}{ccc}\hfill \frac{{\sum }_{j=1}^p{\zeta }_j^{\left(p\right)}}{\sqrt{{\sum }_{j=1}^p\mathrm{Var}\left({\zeta }_j^{\left(p\right)}\right)}}& \stackrel{d}{\to }& \mathcal{N}(0,1).\hfill \end{array}$$

(27)

Proof. 

The proof uses the method of cumulants and is structured as follows:

(i)

We establish the moment-generating function of ${\zeta }_j^{\left(p\right)}$, $M_{{\zeta }_j^{\left(p\right)}}\left(t\right):=\mathbb{E}{\mathrm{e}}^{t{\zeta }_j^{\left(p\right)}}$, and $log(M_{{\zeta }_j^{\left(p\right)}}\left(t\right))$;

(ii)

We find $G(t;p)$ which corresponds to the cumulant generating function of the sum ${\sum }_{j=1}^p{\zeta }_j^{\left(p\right)}$;

(iii)

We find ${\displaystyle K(t;p):=G(\frac{t}{\sqrt{{\sum }_{j=1}^p(2{\left({\nu }_j^{\left(p\right)}\right)}^2+p{\left({\gamma }_j^{\left(p\right)}\right)}^2)}};p)}$, which corresponds to the cumulant generating function of the left hand side of (27);

(iv)

Finally, in order to prove (27), we show that the cumulants ${\varkappa }_j^{\left(p\right)}$, generated by $K(t;p)$, satisfy ${\varkappa }_1^{\left(p\right)}=0$, ${\varkappa }_2^{\left(p\right)}=1$ and ${\varkappa }_d^{\left(p\right)}\to 0,d=3,4,\dots$, as $p\to \infty$.

Step 1. First, rewrite

$$\begin{array}{ccc}\hfill {\zeta }_j^{\left(p\right)}& =& {\nu }_j^{\left(p\right)}{\left({\tilde{Z}}_j+\frac{{\gamma }_j^{\left(p\right)}\sqrt{p}}{2{\nu }_j^{\left(p\right)}}\right)}^2-{\nu }_j^{\left(p\right)}-\frac{{\left({\gamma }_j^{\left(p\right)}\right)}^{2}p}{4{\nu }_j^{\left(p\right)}}.\hfill \end{array}$$

(28)

Here, ${\psi }_j^{\left(p\right)}:={\left({\tilde{Z}}_j+\frac{{\gamma }_j^{\left(p\right)}\sqrt{p}}{2{\nu }_j^{\left(p\right)}}\right)}^2$ has a noncentral chi-squared distribution with the following moment-generating function:

$$\begin{array}{ccc}\hfill M_{{\psi }_j^{\left(p\right)}}\left(t\right)& :=& \mathbb{E}{\mathrm{e}}^{t{\psi }_j^{\left(p\right)}}={(1-2t)}^{-1/2}exp\left\{{\left(\frac{{\gamma }_j^{\left(p\right)}}{2{\nu }_j^{\left(p\right)}}\right)}^{2}tp{(1-2t)}^{-1}\right\},\left|t\right|<\frac{1}{2}.\hfill \end{array}$$

(29)

Therefore, by (28) and (29),

$$\begin{array}{ccc}\hfill M_{{\zeta }_j^{\left(p\right)}}\left(t\right)& =& M_{{\psi }_j^{\left(p\right)}}\left({\nu }_j^{\left(p\right)}t\right)exp\left\{-t{\nu }_j^{\left(p\right)}-tp{\left(\frac{{\gamma }_j^{\left(p\right)}}{2{\nu }_j^{\left(p\right)}}\right)}^2\right\}\hfill \\ & =& {\left(1-2{\nu }_j^{\left(p\right)}t\right)}^{-\frac{1}{2}}exp\left\{\frac{{\left({\gamma }_j^{\left(p\right)}\right)}^2}{4{\nu }_j^{\left(p\right)}}tp{\left(1-2{\nu }_j^{\left(p\right)}t\right)}^{-1}-t\left({\nu }_j^{\left(p\right)}+\frac{{\left({\gamma }_j^{\left(p\right)}\right)}^{2}p}{4{\nu }_j^{\left(p\right)}}\right)\right\},\hfill \end{array}$$

for $\left|t\right|<{\left(2{\nu }_j^{\left(p\right)}\right)}^{-1}$, and

$$\begin{array}{ccc}\hfill log\left(M_{{\zeta }_j^{\left(p\right)}}\left(t\right)\right)& =& {\left(\frac{{\gamma }_j^{\left(p\right)}}{2{\nu }_j^{\left(p\right)}}\right)}^{2}pt{\nu }_j^{\left(p\right)}{\left(1-2{\nu }_j^{\left(p\right)}t\right)}^{-1}-\frac{1}{2}log\left(1-2{\nu }_j^{\left(p\right)}t\right)-t\left({\nu }_j^{\left(p\right)}+\frac{{\left({\gamma }_j^{\left(p\right)}\right)}^{2}p}{4{\nu }_j^{\left(p\right)}}\right)\hfill \\ & & =\frac{1}{2}\left({\left({\gamma }_j^{\left(p\right)}\right)}^{2}p+2{\left({\nu }_j^{\left(p\right)}\right)}^2\right)t^2+\frac{{\left({\gamma }_j^{\left(p\right)}\right)}^{2}p}{2}\sum _{k=3}^{\infty }{t}^k{2}^{k-2}{\left({\nu }_j^{\left(p\right)}\right)}^{k-2}+\frac{1}{2}\sum _{k=3}^{\infty }\frac{2^k{\left({\nu }_j^{\left(p\right)}\right)}^k{t}^k}{k}.\hfill \end{array}$$

Step 2. Since ${\zeta }_1^{\left(p\right)},\dots ,{\zeta }_j^{\left(p\right)}$ are independent, we have that

$$\begin{array}{ccc}\hfill G(t;p)& =& \sum _{j=1}^{p}log{M}_{{\zeta }_j^{\left(p\right)}}\left(t\right)=\frac{t^2}{2}\sum _{j=1}^p\left({\left({\gamma }_j^{\left(p\right)}\right)}^{2}p+2{\left({\nu }_j^{\left(p\right)}\right)}^2\right)\hfill \\ & & +\frac{p}{2}\sum _{k=3}^{\infty }{2}^{k-2}{t}^k\sum _{j=1}^p{\left({\gamma }_j^{\left(p\right)}\right)}^2{\left({\nu }_j^{\left(p\right)}\right)}^{k-2}+\frac{1}{2}\sum _{k=3}^{\infty }\frac{2^k}{k}{t}^k\sum _{j=1}^p{\left({\nu }_j^{\left(p\right)}\right)}^k.\hfill \end{array}$$

Step 3. It can be observed that

$$\begin{array}{ccc}\hfill K(t;p)& =& G\left(\frac{t}{\sqrt{{\sum }_{j=1}^p\left(2{\left({\nu }_j^{\left(p\right)}\right)}^2+p{\left({\gamma }_j^{\left(p\right)}\right)}^2\right)}};p\right)\hfill \\ & =& \frac{t^2}{2}+\frac{1}{2}\sum _{k=3}^{\infty }{2}^{k-2}{t}^k\frac{p{\sum }_{j=1}^p{\left({\gamma }_j^{\left(p\right)}\right)}^2{\left({\nu }_j^{\left(p\right)}\right)}^{k-2}}{{\left({\sum }_{j=1}^p(2{\left({\nu }_j^{\left(p\right)}\right)}^2+{\left({\gamma }_j^{\left(p\right)}\right)}^{2}p)\right)}^{k/2}}\hfill \\ & & +\frac{1}{2}\sum _{k=3}^{\infty }\frac{2^k}{k}{t}^k\frac{{\sum }_{j=1}^p{\left({\nu }_j^{\left(p\right)}\right)}^k}{{\left({\sum }_{j=1}^p(2{\left({\nu }_j^{\left(p\right)}\right)}^2+{\left({\gamma }_j^{\left(p\right)}\right)}^{2}p)\right)}^{k/2}}=\sum _{k=1}^{\infty }{\varkappa }_k^{\left(p\right)}\frac{t^k}{k!},\hfill \end{array}$$

where ${\varkappa }_1^{\left(p\right)}=0$, ${\varkappa }_2^{\left(p\right)}=1$, and for $k\ge 3$,

$$\begin{array}{ccc}\hfill {\varkappa }_k^{\left(p\right)}& =& \frac{k!2^{k-3}p{\sum }_{j=1}^p{\left({\gamma }_j^{\left(p\right)}\right)}^2{\left({\nu }_j^{\left(p\right)}\right)}^{k-2}+(k-1)!2^{k-1}{\sum }_{j=1}^p{\left({\nu }_j^{\left(p\right)}\right)}^k}{{\left({\sum }_{j=1}^p(2{\left({\nu }_j^{\left(p\right)}\right)}^2+{\left({\gamma }_j^{\left(p\right)}\right)}^{2}p)\right)}^{k/2}}.\hfill \end{array}$$

(30)

Step 4. In order to prove that (27) holds, it remains to show that, as $p\to \infty$, ${\varkappa }_d^{\left(p\right)}\to 0$ for all $d\ge 3$. By (30), it is equivalent to showing that for any fixed $k\ge 3$, as $p\to \infty$,

$$\begin{array}{ccc}\hfill \frac{{\sum }_{j=1}^p{\left({\nu }_j^{\left(p\right)}\right)}^k}{{\left({\sum }_{j=1}^p\left(2{\left({\nu }_j^{\left(p\right)}\right)}^2+{\left({\gamma }_j^{\left(p\right)}\right)}^{2}p\right)\right)}^{k/2}}& \to & 0,\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\hfill \frac{p{\sum }_{j=1}^p{\left({\gamma }_j^{\left(p\right)}\right)}^2{\left({\nu }_j^{\left(p\right)}\right)}^{k-2}}{{\left({\sum }_{j=1}^p\left(2{\left({\nu }_j^{\left(p\right)}\right)}^2+{\left({\gamma }_j^{\left(p\right)}\right)}^{2}p\right)\right)}^{k/2}}& \to & 0.\hfill \end{array}$$

(32)

In order to prove (31) we use induction. The case for $k=3$ holds by assumption. Assuming that (31) holds for fixed $k\ge 3$, we have

$$\begin{array}{ccc}\hfill \frac{{\sum }_{j=1}^p{\left({\nu }_j^{\left(p\right)}\right)}^{k+1}}{{\left({\sum }_{j=1}^p\left(2{\left({\nu }_j^{\left(p\right)}\right)}^2+{\left({\gamma }_j^{\left(p\right)}\right)}^{2}p\right)\right)}^{(k+1)/2}}& \le & \frac{{\left({\sum }_{j^{\prime }=1}^p{\left({\nu }_{j^{\prime }}^{\left(p\right)}\right)}^2\right)}^{1/2}{\sum }_{j=1}^p{\left({\nu }_j^{\left(p\right)}\right)}^k}{{\left({\sum }_{j=1}^p\left(2{\left({\nu }_j^{\left(p\right)}\right)}^2+{\left({\gamma }_j^{\left(p\right)}\right)}^{2}p\right)\right)}^{(k+1)/2}}\hfill \\ & \le & \frac{{\left({\sum }_{j^{\prime }=1}^p\left(2{\left({\nu }_{j^{\prime }}^{\left(p\right)}\right)}^2+{\left({\gamma }_{j^{\prime }}^{\left(p\right)}\right)}^{2}p\right)\right)}^{1/2}{\sum }_{j=1}^p{\left({\nu }_j^{\left(p\right)}\right)}^k}{{\left({\sum }_{j=1}^p\left(2{\left({\nu }_j^{\left(p\right)}\right)}^2+{\left({\gamma }_j^{\left(p\right)}\right)}^{2}p\right)\right)}^{(k+1)/2}}\hfill \\ & =& \frac{{\sum }_{j=1}^p{\left({\nu }_j^{\left(p\right)}\right)}^k}{{\left({\sum }_{j=1}^p\left(2{\left({\nu }_j^{\left(p\right)}\right)}^2+{\left({\gamma }_j^{\left(p\right)}\right)}^{2}p\right)\right)}^{k/2}}\to 0,\hfill \end{array}$$

concluding that (31) holds for all $k\ge 3$. The proof for (32) is analogous: the case for $k=3$ holds by assumption; thus, we repeat the same arguments as with (31) and conclude that (32) holds for all $k\ge 3$. This concludes the proof of the lemma. □

5. Proof of the Main Results

In this section we give the proofs of Theorems 1 and 2. Throughout the proofs, we express corresponding constants in terms of ${\kappa }_{i,p}$ and ${\kappa }_i$, $i=1,2,3$, introduced in (3)–(5). Recall that ${\kappa }_{i,p}\ge 0$, and, by Remark 3, ${\kappa }_i<\infty$, for $i=1,2,3$.

Proof of Theorem 1. 

Write

$$\begin{array}{ccc}\hfill \parallel {\mathbb{X}}^{\prime }{Y\parallel }_2^2& =& H_1^2+\cdots +H_p^2=:H,\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill H_k& :=& \sum _{j=1}^n{X}_{k,j}\left(\sum _{l=1}^p{\beta }_l{X}_{l,j}+{\epsilon }_j\right),k=1,\dots ,p.\hfill \end{array}$$

Denote $Z_j:={\sum }_{l=1}^p{\beta }_l{X}_{l,j}+{\epsilon }_j$, $j=1,\dots ,n$. By covariance structure (2) and $X_{k,j}\stackrel{d}{=}\mathcal{N}(0,1)$, ${\epsilon }_j\stackrel{d}{=}\mathcal{N}(0,{\sigma }_{\epsilon }^2)$, we have $Z_j\stackrel{d}{=}\mathcal{N}(0,{\sigma }_Z^2)$, where ${\sigma }_Z^2={\sum }_{l,l^{\prime }=1}^p{\beta }_l{\beta }_{l^{\prime }}{\varrho }^{|l-l^{\prime }|}+{\sigma }_{\epsilon }^2$ and $\mathrm{Cov}(X_{k,j},Z_j)={\sum }_{l=1}^p{\beta }_l{\varrho }^{|k-l|}$.

Applying Proposition 1(iii) with ${\xi }_{1j}^{\left(k\right)}=X_{k,j}$, ${\xi }_{2j}=Z_j$, and ${\sigma }_1^{\left(k\right)}=1$, ${\sigma }_{2,p}={\sigma }_Z$, ${\theta }_k^{\left(p\right)}:={\varrho }^{\left(k\right)}={\sigma }_Z^{-1}{\sum }_{l=1}^p{\beta }_l{\varrho }^{|k-l|}$, where ${\varrho }^{\left(kl\right)}={\varrho }^{|k-l|}$, we obtain that

$$\begin{array}{ccc}\hfill \parallel {\mathbb{X}}^{\prime }{Y\parallel }_2^2& \stackrel{d}{=}& {\sigma }_{2,p}^2\sum _{k=1}^p{\left({\theta }_k^{\left(p\right)}{W}_n+\sqrt{1-{\left({\theta }_k^{\left(p\right)}\right)}^2}\sqrt{W_n}{U}_k\right)}^2,\hfill \end{array}$$

where $W_n\stackrel{d}{=}\mathsf{\Gamma }(n/2,1/2)$ and ${(U_1,\dots ,U_p)}^{\prime }\stackrel{d}{=}{\mathcal{N}}_p(0,{\mathsf{\Sigma }}_U^{\left(p\right)})$ with ${\mathsf{\Sigma }}_U^{\left(p\right)}=\left({\sigma }_U^{(k,l)}\right)$ defined as (see (16)):

$$\begin{array}{ccc}\hfill {\sigma }_U^{(k,l)}& =& \frac{{\varrho }^{|k-l|}-{\theta }_k^{\left(p\right)}{\theta }_l^{\left(p\right)}}{\sqrt{1-{\left({\theta }_k^{\left(p\right)}\right)}^2}\sqrt{1-{\left({\theta }_l^{\left(p\right)}\right)}^2}},k,l=1,\dots ,p.\hfill \end{array}$$

(33)

By expanding the square we can write

$$\begin{array}{ccc}\hfill \parallel {\mathbb{X}}^{\prime }{Y\parallel }_2^2& \stackrel{d}{=}& {\sigma }_{2,p}^2({(W_n-\mathbb{E}{W}_n+\mathbb{E}{W}_n)}^2\sum _{k=1}^p{\left({\theta }_k^{\left(p\right)}\right)}^2+2W_n^{3/2}\sum _{k=1}^p{\theta }_k^{\left(p\right)}\sqrt{1-{\left({\theta }_k^{\left(p\right)}\right)}^2}{U}_k\hfill \\ & & +(W_n-\mathbb{E}{W}_n)\sum _{k=1}^p\left(1-{\left({\theta }_k^{\left(p\right)}\right)}^2\right)U_k^2+\mathbb{E}{W}_n\sum _{k=1}^p\left(1-{\left({\theta }_k^{\left(p\right)}\right)}^2\right)U_k^2).\hfill \end{array}$$

By further rearranging the right-hand side, we have

$$\begin{array}{ccc}\hfill \frac{\parallel {\mathbb{X}}^{\prime }{Y\parallel }_2^2}{n^{3/2}}& \stackrel{d}{=}& I_1+I_2+I_3+I_4,\hfill \end{array}$$

(34)

where

$$\begin{array}{ccc}\hfill I_1& :=& \frac{{\sigma }_{2,p}^2}{n^{3/2}}{(W_n-\mathbb{E}{W}_n)}^2\sum _{k=1}^p{\left({\theta }_k^{\left(p\right)}\right)}^2,\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill I_2& :=& \frac{{\sigma }_{2,p}^2}{n^{3/2}}(W_n-\mathbb{E}{W}_n)\left(2\mathbb{E}{W}_n\sum _{k=1}^p{\left({\theta }_k^{\left(p\right)}\right)}^2+\sum _{k=1}^p(1-{\left({\theta }_k^{\left(p\right)}\right)}^2)U_k^2\right),\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill I_3& :=& \frac{{\sigma }_{2,p}^2}{n^{3/2}}2W_n^{3/2}\sum _{k=1}^p{\theta }_k^{\left(p\right)}\sqrt{1-{\left({\theta }_k^{\left(p\right)}\right)}^2}{U}_k+\frac{{\sigma }_{2,p}^2}{n^{3/2}}\mathbb{E}{W}_n\sum _{k=1}^p\left((1-{\left({\theta }_k^{\left(p\right)}\right)}^2)U_k^2-1\right),\hfill \end{array}$$

(37)

$$\begin{array}{ccc}\hfill I_4& :=& \frac{{\sigma }_{2,p}^2}{n^{3/2}}\left(p\mathbb{E}{W}_n+{\left(\mathbb{E}{W}_n\right)}^2\sum _{k=1}^p{\left({\theta }_k^{\left(p\right)}\right)}^2\right).\hfill \end{array}$$

(38)

We will show that, as $p,n\to \infty$, $p/n\to c\in (0,\infty )$, the term $I_1=o_P\left(1\right)$, while the terms $I_2$ and $I_3$ are asymptotically normal. More precisely, we will show that $I_2\stackrel{d}{\to }\mathcal{N}(0,s_1^2)$ and $I_3\stackrel{d}{\to }\mathcal{N}(0,s_2^2)$, where $s_1^2$ and $s_2^2$ are given by (44) and (62) below. Here, since $W_n$ and ${(U_1,\dots ,U_p)}^{\prime }$ are mutually independent for each n, it follows that $I_2+I_3\stackrel{d}{\to }\mathcal{N}(0,s_1^2+s_2^2)$. Finally, the term $I_4$ defines the mean of the statistic, i.e.,

$$\begin{array}{ccc}\hfill \frac{\parallel {\mathbb{X}}^{\prime }{Y\parallel }_2^2}{n^{3/2}}-I_4& \stackrel{d}{\to }& \mathcal{N}(0,s_1^2+s_2^2).\hfill \end{array}$$

(39)

Thus, we will conclude by establishing that $I_4=\sqrt{n}({\kappa }_{2,p}+p{n}^{-1}({\kappa }_{1,p}+{\sigma }_{\epsilon }^2))$, while $s_1^2+s_2^2=s^2$, as in the statement of the theorem.

First, consider $I_1$ defined in (35). We will show that $I_1=o_P\left(1\right)$. Denote

$$\begin{array}{ccc}\hfill c_2& :=& \underset{p\to \infty }{lim}\sum _{k=1}^p{\left({\theta }_k^{\left(p\right)}\right)}^2={({\kappa }_1+{\sigma }_{\epsilon }^2)}^{-1}{\kappa }_2,{\sigma }_2^2:=\underset{p\to \infty }{lim}{\sigma }_{2,p}^2={\kappa }_1+{\sigma }_{\epsilon }^2.\hfill \end{array}$$

(40)

It is clear that $c_2<\infty$ and ${\sigma }_2^2<\infty$. Recall that, by CLT,

$$\begin{array}{ccc}\hfill \frac{W_n-\mathbb{E}{W}_n}{n^{1/2}}& \stackrel{d}{\to }& \mathcal{N}(0,2).\hfill \end{array}$$

(41)

Therefore,

$$\begin{array}{ccc}\hfill I_1& =& \mathcal{O}\left(1\right)n^{-1/2}{\left(\frac{W_n-\mathbb{E}{W}_n}{n^{1/2}}\right)}^2=o\left(1\right){\mathcal{O}}_P\left(1\right)=o_P\left(1\right).\hfill \end{array}$$

(42)

Second, consider $I_2$, defined in (36). We will show that

$$\begin{array}{c}\hfill I_2\stackrel{d}{\to }\mathcal{N}(0,s_1^2)\end{array}$$

(43)

with $s_1^2$ given by

$$\begin{array}{ccc}\hfill s_1^2& =& 2{\sigma }_2^4{(2c_2+c)}^2=8{\kappa }_2^2+8c({\kappa }_1+{\sigma }_{\epsilon }^2){\kappa }_2+2c^2{({\kappa }_1+{\sigma }_{\epsilon }^2)}^2.\hfill \end{array}$$

(44)

Rewrite

$$\begin{array}{ccc}\hfill I_2& =& {\sigma }_{2,p}^2\frac{W_n-\mathbb{E}{W}_n}{n^{1/2}}\left(\frac{2\mathbb{E}{W}_n}{n}\sum _{k=1}^p{\left({\theta }_k^{\left(p\right)}\right)}^2+\frac{1}{n}\sum _{k=1}^p(1-{\left({\theta }_k^{\left(p\right)}\right)}^2)U_k^2\right).\hfill \end{array}$$

(45)

Applying (40) and (41) for the outer term of (45), we obtain

$$\begin{array}{ccc}\hfill {\sigma }_{2,p}^2\frac{W_n-\mathbb{E}{W}_n}{n^{1/2}}& \stackrel{d}{\to }& \mathcal{N}(0,2{\sigma }_2^4).\hfill \end{array}$$

We will show that the inner term of (45) approaches $2c_2+c$. Since $\mathbb{E}{W}_n=n$, by (40) and assumption $p/n\to c$ it suffices to prove the convergence

$$\begin{array}{ccc}\hfill \frac{1}{p}\sum _{k=1}^p(1-{\left({\theta }_k^{\left(p\right)}\right)}^2)U_k^2& \stackrel{\mathbb{P}}{\to }& 1.\hfill \end{array}$$

(46)

Denote matrix

$$\begin{array}{ccc}\hfill A& :=& diag\left(1-{\left({\theta }_1^{\left(p\right)}\right)}^2,\dots ,1-{\left({\theta }_p^{\left(p\right)}\right)}^2\right).\hfill \end{array}$$

(47)

To prove (46), we apply Lemma 2 with $V_j=\sqrt{1-{\left({\theta }_j^{\left(p\right)}\right)}^2}{U}_j$, $j=1,\dots ,p$, and ${\mathsf{\Sigma }}_V^{\left(p\right)}=A^{1/2}{\mathsf{\Sigma }}_U{A}^{1/2}$. The conditions of Lemma 2 will hold if $tr\left({\left(A^{1/2}{\mathsf{\Sigma }}_U{A}^{1/2}\right)}^2\right)=\mathcal{O}\left(p\right)$ and $p^{-1}tr\left(A^{1/2}{\mathsf{\Sigma }}_U{A}^{1/2}\right)\to 1$, as $p\to \infty$. Observe, that

$$\begin{array}{ccc}\hfill tr\left({\left(A^{1/2}{\mathsf{\Sigma }}_U{A}^{1/2}\right)}^2\right)& =& tr\left({\left(A{\mathsf{\Sigma }}_U\right)}^2\right)\hfill \\ & =& \sum _{k=1}^p\sum _{k^{\prime }=1}^p(1-{\left({\theta }_k^{\left(p\right)}\right)}^2)(1-{\left({\theta }_{k^{\prime }}^{\left(p\right)}\right)}^2){\left({\sigma }_U^{(k,k^{\prime })}\right)}^2\hfill \\ & =& \sum _{k=1}^p\sum _{k^{\prime }=1}^p\left({\varrho }^{2|k-k^{\prime }|}-2{\varrho }^{|k-k^{\prime }|}{\theta }_k^{\left(p\right)}{\theta }_{k^{\prime }}^{\left(p\right)}+{\left({\theta }_k^{\left(p\right)}\right)}^2{\left({\theta }_{k^{\prime }}^{\left(p\right)}\right)}^2\right)\hfill \\ & =& \sum _{k=1}^p\sum _{k^{\prime }=1}^p{\varrho }^{2|k-k^{\prime }|}-2{\left({\kappa }_{1,p}+{\sigma }_{\epsilon }^2\right)}^{-1}{\kappa }_{3,p}+{\left({\kappa }_{1,p}+{\sigma }_{\epsilon }^2\right)}^{-2}{\kappa }_{2,p}^2\hfill \\ & =& \sum _{k=1}^p\sum _{k^{\prime }=1}^p{\varrho }^{2|k-k^{\prime }|}+o\left(p\right)\sim p\frac{1+{\varrho }^2}{1-{\varrho }^2},\hfill \end{array}$$

(48)

since ${\kappa }_i<\infty$, $i=1,2,3$ and ${\kappa }_{1,p}\ge 0$. Here we used (40) and the observation that

$$\begin{array}{ccc}\hfill \sum _{k=1}^p\sum _{k^{\prime }=1}^p{\varrho }^{|k-k^{\prime }|}{\theta }_k^{\left(p\right)}{\theta }_{k^{\prime }}^{\left(p\right)}& =& \frac{{\kappa }_{3,p}}{{\kappa }_{1,p}+{\sigma }_{\epsilon }^2}\to \frac{{\kappa }_3}{{\kappa }_1+{\sigma }_{\epsilon }^2},\mathrm{as}p\to \infty .\hfill \end{array}$$

(49)

Similarly, we have

$$\begin{array}{ccc}\hfill \frac{1}{p}tr\left(A^{1/2}{\mathsf{\Sigma }}_U{A}^{1/2}\right)& =& \frac{1}{p}\sum _{k=1}^p(1-{\left({\theta }_k^{\left(p\right)}\right)}^2)=1-\frac{{\kappa }_{2,p}}{p({\kappa }_{1,p}+{\sigma }_{\epsilon }^2)}\to 1,\hfill \end{array}$$

since, by Lemma A4, ${\kappa }_{2,p}=o\left(p\right)$, while ${\kappa }_{1,p}\ge 0$, ${\kappa }_1<\infty$. This concludes the proof of (46).

Next, consider $I_3$, defined by (37). We will show that

$$\begin{array}{ccc}\hfill I_3& \stackrel{d}{\to }& \mathcal{N}(0,s_2^2),\hfill \end{array}$$

(50)

with $s_2^2$ defined in (62). Write

$$\begin{array}{ccc}\hfill I_3& =& {\sigma }_{2,p}^2\left(2\frac{W_n^{3/2}}{n^{3/2}}{\mathbf{b}}^{\prime }U+n^{-1/2}(U^{\prime }AU-p)\right),\hfill \end{array}$$

where $U={\left(U_1,\dots ,U_p\right)}^{\prime }$, A is defined by (47), and

$$\begin{array}{ccc}\hfill \mathbf{b}& =& {\left({\theta }_1^{\left(p\right)}\sqrt{1-{\left({\theta }_1^{\left(p\right)}\right)}^2},\dots ,{\theta }_p^{\left(p\right)}\sqrt{1-{\left({\theta }_p^{\left(p\right)}\right)}^2}\right)}^{\prime }.\hfill \end{array}$$

Observe that $n^{-3/2}{W}_n^{3/2}\stackrel{P}{\to }1$ due to the Law of Large Numbers. Thus, since $W_n$ and U are independent for any n and $p/n\to c$, it follows that

$$\begin{array}{ccc}\hfill I_3& =& {\sigma }_{2,p}^2\left(2{\mathbf{b}}^{\prime }U+\sqrt{\frac{c}{p}}\left(U^{\prime }AU-p\right)\right)+o_P\left(1\right).\hfill \end{array}$$

(51)

First, we consider the inner term of (51) and show that as $p\to \infty$,

$$\begin{array}{ccc}\hfill 2{\mathbf{b}}^{\prime }U+\sqrt{\frac{c}{p}}(UA{U}^{\prime }-p)& \stackrel{d}{\to }& V_2,\hfill \end{array}$$

(52)

where $V_2\stackrel{d}{=}\mathcal{N}(0,{\sigma }_2^{-4}{s}_2^2)$. Then, (50) readily follows from (51).

Recall, that $U\stackrel{d}{=}{\mathcal{N}}_p(0,{\mathsf{\Sigma }}_U)$, ${\mathsf{\Sigma }}_U>0$. Further, let $\tilde{Z}\stackrel{d}{=}{\mathcal{N}}_p(0,I_p)$. Clearly, one has that $U\stackrel{d}{=}{\mathsf{\Sigma }}_U^{1/2}\tilde{Z}$, where ${\mathsf{\Sigma }}_U^{1/2}$ denotes the symmetric square root of ${\mathsf{\Sigma }}_U$. By the Spectral Theorem, we construct $V:=P^{\prime }\tilde{Z}$, where $V\stackrel{d}{=}{\mathcal{N}}_p(0,I_p)$ and P is an orthogonal matrix that diagonalizes ${\mathsf{\Sigma }}_U^{1/2}A{\mathsf{\Sigma }}_U^{1/2}$, such that $P^{\prime }{\mathsf{\Sigma }}_U^{1/2}A{\mathsf{\Sigma }}_U^{1/2}P=\mathsf{\Lambda }$, with $\mathsf{\Lambda }=diag({\lambda }_1^{\left(p\right)},\dots ,{\lambda }_p^{\left(p\right)})$ comprised of the eigenvalues of ${\mathsf{\Sigma }}_U^{1/2}A{\mathsf{\Sigma }}_U^{1/2}$. Then,

$$\begin{array}{ccc}\hfill \frac{\sqrt{c}}{\sqrt{p}}\left(U^{\prime }AU-p\right)+2{\mathbf{b}}^{\prime }U& \stackrel{d}{=}& \frac{\sqrt{c}}{\sqrt{p}}\left(V^{\prime }\mathsf{\Lambda }V-p\right)+2{\mathbf{b}}^{\prime }{\mathsf{\Sigma }}_U^{1/2}PV\hfill \\ & =& \frac{\sqrt{c}}{\sqrt{p}}\left(\sum _{j=1}^p\left({\lambda }_j^{\left(p\right)}(V_j^2-1)+g_j^{\left(p\right)}\sqrt{p}{V}_j\right)\right)\hfill \\ & =:& \frac{\sqrt{c}}{\sqrt{p}}\sum _{j=1}^p{\tilde{V}}_j^{\left(p\right)},\hfill \end{array}$$

(53)

where $(g_1^{\left(p\right)},\dots ,g_p^{\left(p\right)})=2c^{-1/2}{\mathbf{b}}^{\prime }{\mathsf{\Sigma }}_U^{1/2}P$, and

$$\begin{array}{ccc}\hfill {\tilde{V}}_j^{\left(p\right)}& :=& {\lambda }_j^{\left(p\right)}(V_j^2-1)+g_j^{\left(p\right)}\sqrt{p}{V}_j,j=1,\dots ,p.\hfill \end{array}$$

(54)

Clearly, $\mathbb{E}{\tilde{V}}_j^{\left(p\right)}=0$ and $\mathbb{E}{\left({\tilde{V}}_j^{\left(p\right)}\right)}^2=2{\left({\lambda }_j^{\left(p\right)}\right)}^2+{\left(g_j^{\left(p\right)}\right)}^{2}p$. Therefore, proving the result (52) is equivalent to showing:

$$\begin{array}{ccc}\hfill \frac{\sqrt{c}}{\sqrt{p}}\sum _{j=1}^p{\tilde{V}}_j^{\left(p\right)}& \stackrel{d}{\to }& \mathcal{N}(0,{\sigma }_2^{-4}{s}_2^2),\hfill \end{array}$$

(55)

where

$$\begin{array}{c}\hfill {\sigma }_2^{-4}{s}_2^2=c\underset{p\to \infty }{lim}{p}^{-1}\sum _{j=1}^p\mathbb{E}{\left({\tilde{V}}_j^{\left(p\right)}\right)}^2=2c\underset{p\to \infty }{lim}{p}^{-1}\sum _{j=1}^p{\left({\lambda }_j^{\left(p\right)}\right)}^2+c\underset{p\to \infty }{lim}\sum _{j=1}^p{\left(g_j^{\left(p\right)}\right)}^2.\end{array}$$

(56)

We prove (55) by applying Lemma 3 with ${\nu }_j^{\left(p\right)}={\lambda }_j^{\left(p\right)}$ as the eigenvalues of ${\mathsf{\Sigma }}_U^{1/2}A{\mathsf{\Sigma }}_U^{1/2}$ and ${\gamma }_j^{\left(p\right)}=g_j^{\left(p\right)}$. By the conditions of Lemma 3, we need to show that the following holds

$$\begin{array}{ccc}\hfill \sum _{j=1}^p{\left({\lambda }_j^{\left(p\right)}\right)}^3+p\sum _{j=1}^p{\left(g_j^{\left(p\right)}\right)}^2{\lambda }_j^{\left(p\right)}& =& o\left({\left(\sum _{j=1}^p\left(2{\left({\lambda }_j^{\left(p\right)}\right)}^2+{\left(g_j^{\left(p\right)}\right)}^{2}p\right)\right)}^{3/2}\right).\hfill \end{array}$$

(57)

First, observe that $p^{-1}{\sum }_{j=1}^p(2{\left({\lambda }_j^{\left(p\right)}\right)}^2+{\left(g_j^{\left(p\right)}\right)}^{2}p)\to C\in (0,\infty )$. Indeed, we have that ${\sum }_{j=1}^p{\left(g_j^{\left(p\right)}\right)}^2\to C_g\in (0,\infty )$, since

$$\begin{array}{ccc}\hfill \sum _{j=1}^p{\left(g_j^{\left(p\right)}\right)}^2& =& 4c^{-1}\left({\mathbf{b}}^{\prime }{\mathsf{\Sigma }}_U^{1/2}P\right){\left({\mathbf{b}}^{\prime }{\mathsf{\Sigma }}_U^{1/2}P\right)}^{\prime }=4c^{-1}{\mathbf{b}}^{\prime }{\mathsf{\Sigma }}_U\mathbf{b}\hfill \\ & =& 4c^{-1}\sum _{j=1}^p\sum _{j^{\prime }=1}^p{\theta }_j^{\left(p\right)}{\theta }_{j^{\prime }}^{\left(p\right)}\sqrt{1-{\left({\theta }_j^{\left(p\right)}\right)}^2}\sqrt{1-{\left({\theta }_{j^{\prime }}^{\left(p\right)}\right)}^2}{\sigma }_U^{(j,j^{\prime })}\hfill \\ & =& 4c^{-1}\sum _{j=1}^p\sum _{j^{\prime }=1}^p{\theta }_j^{\left(p\right)}{\theta }_{j^{\prime }}^{\left(p\right)}\left({\varrho }^{|j-j^{\prime }|}-{\theta }_j^{\left(p\right)}{\theta }_{j^{\prime }}^{\left(p\right)}\right)\hfill \\ & \to & 4c^{-1}{\left({\kappa }_1+{\sigma }_{\epsilon }^2\right)}^{-1}{\kappa }_3-4c^{-1}{\left({\kappa }_1+{\sigma }_{\epsilon }^2\right)}^{-2}{\kappa }_2^2=C_g\hfill \end{array}$$

(58)

by (40) and (49).

Next, by (48), we find that $p^{-1}{\sum }_{j=1}^p{\left({\lambda }_j^{\left(p\right)}\right)}^2\to C_{\lambda }\in (0,\infty )$. Indeed, by (48), we have

$$\begin{array}{ccc}\hfill \sum _{j=1}^p{\left({\lambda }_j^{\left(p\right)}\right)}^2& =& tr\left({\left({\mathsf{\Sigma }}_U^{1/2}A{\mathsf{\Sigma }}_U^{1/2}\right)}^2\right)=tr\left({\left({\mathsf{\Sigma }}_{U}A\right)}^2\right)\hfill \\ & =& \sum _{j=1}^p\sum _{j^{\prime }=1}^p{\varrho }^{2|j-j^{\prime }|}+o\left(p\right)\sim p\frac{1+{\varrho }^2}{1-{\varrho }^2}.\hfill \end{array}$$

(59)

Thus, by (58) and (59), it follows that $p^{-1}{\sum }_{j=1}^p(2c{\left({\lambda }_j^{\left(p\right)}\right)}^2+{\left(g_j^{\left(p\right)}\right)}^{2}p)\to C\in (0,\infty )$ and condition (57) reduces to:

$$\begin{array}{c}\hfill \sum _{j=1}^p{\left({\lambda }_j^{\left(p\right)}\right)}^3+p\sum _{j=1}^p{\left(g_j^{\left(p\right)}\right)}^2{\lambda }_j^{\left(p\right)}=o\left(p^{3/2}\right).\end{array}$$

(60)

We show that (60) holds. For the first term of (60), we have

$$\begin{array}{ccc}\hfill \sum _{j=1}^p{\left({\lambda }_j^{\left(p\right)}\right)}^3& =& tr\left({\left({\mathsf{\Sigma }}_U^{1/2}A{\mathsf{\Sigma }}_U^{1/2}\right)}^3\right)=tr\left({\left({\mathsf{\Sigma }}_{U}A\right)}^3\right)\hfill \\ & =& \sum _{i,j,k=1}^p\left(1-{\left({\theta }_i^{\left(p\right)}\right)}^2\right)\left(1-{\left({\theta }_k^{\left(p\right)}\right)}^2\right)\left(1-{\left({\theta }_j^{\left(p\right)}\right)}^2\right){\sigma }_U^{(i,j)}{\sigma }_U^{(i,k)}{\sigma }_U^{(k,j)}\hfill \\ & =& \sum _{i,j,k=1}^p\left({\varrho }^{|i-j|}+{\theta }_i^{\left(p\right)}{\theta }_j^{\left(p\right)}\right)\left({\varrho }^{|i-k|}+{\theta }_i^{\left(p\right)}{\theta }_k^{\left(p\right)}\right)\left({\varrho }^{|k-j|}+{\theta }_k^{\left(p\right)}{\theta }_j^{\left(p\right)}\right)\hfill \\ & =& o\left(p^{3/2}\right),\hfill \end{array}$$

(61)

where the last equality follows from Lemma A5. For the second term of (60), observe that by Hölder’s inequality and (61),

$$\begin{array}{ccc}\hfill p\sum _{j=1}^p{\left(g_j^{\left(p\right)}\right)}^2{\lambda }_j^{\left(p\right)}& \le & p{\left(\sum _{j=1}^p{\left|g_j^{\left(p\right)}\right|}^3\right)}^{2/3}{\left(\sum _{j=1}^p{\left({\lambda }_j^{\left(p\right)}\right)}^3\right)}^{1/3}\hfill \\ & =& p^{3/2}\mathcal{O}\left(1\right){\left(\frac{{\sum }_{j=1}^p{\left({\lambda }_j^{\left(p\right)}\right)}^3}{p^{3/2}}\right)}^{1/3}=o\left(p^{3/2}\right).\hfill \end{array}$$

This concludes with (60), ensuring that the conditions of Lemma 3 hold.

Now we can establish the expression for $s_2^2$. By (40), (56), (58) and (59),

$$\begin{array}{ccc}\hfill s_2^2& =& {\sigma }_2^4\underset{p\to \infty }{lim}\sum _{j=1}^p\left(2p^{-1}c{\left({\lambda }_j^{\left(p\right)}\right)}^2+c{\left(g_j^{\left(p\right)}\right)}^2\right)\hfill \\ & =& {\sigma }_2^4\underset{p\to \infty }{lim}\frac{2c}{p}\left(\sum _{k=1}^p\sum _{k^{\prime }=1}^p{\varrho }^{2|k-k^{\prime }|}+o\left(p\right)\right)+4{\sigma }_2^4{\left({\kappa }_1+{\sigma }_{\epsilon }^2\right)}^{-1}{\kappa }_3-4{\sigma }_2^4{\left({\kappa }_1+{\sigma }_{\epsilon }^2\right)}^{-2}{\kappa }_2^2\hfill \\ & =& 2c\frac{1+{\varrho }^2}{1-{\varrho }^2}{({\kappa }_1+{\sigma }_{\epsilon }^2)}^2+4({\kappa }_1+{\sigma }_{\epsilon }^2){\kappa }_3-4{\kappa }_2^2.\hfill \end{array}$$

(62)

By (44) and (62), recalling that $s^2=s_1^2+s_2^2$, we have that

$$\begin{array}{ccc}\hfill s^2& =& 4{\kappa }_2^2+4({\kappa }_1+{\sigma }_{\epsilon }^2)\left(2{\kappa }_{2}c+{\kappa }_3\right)+2c{({\kappa }_1+{\sigma }_{\epsilon }^2)}^2\left(c+\frac{1+{\varrho }^2}{1-{\varrho }^2}\right).\hfill \end{array}$$

(63)

Finally, consider $I_4$, defined by (38). Since $\mathbb{E}{W}_n=n$, we have that

$$\begin{array}{ccc}\hfill I_4& =& \frac{{\kappa }_{1,p}+{\sigma }_{\epsilon }^2}{n^{3/2}}\left(n^2\frac{{\kappa }_{2,p}}{{\kappa }_{1,p}+{\sigma }_{\epsilon }^2}+pn\right)=\sqrt{n}\left({\kappa }_{2,p}+\frac{p}{n}({\kappa }_{1,p}+{\sigma }_{\epsilon }^2)\right).\hfill \end{array}$$

(64)

By (34), having established four parts by (35)–(38), we proved that (39) holds due to (42), (43), (50), (62), with terms (63) and (64), as in the statement of the theorem, thus concluding the proof. □

Before proceeding with the proof of Theorem 2, we establish the following lemma that ensures $\mathcal{O}\left(p^{-1/2}\right)$ convergence rate for ${\kappa }_{1,p}$ and ${\kappa }_{2,p}$, appearing in Theorem 1, under additional restrictions for the parameters ${\beta }_j$.

Lemma 4.

Assume that ${\sum }_{j=p+1}^{\infty }{\beta }_j^2=o\left(p^{-1/2}\right)$ and ${sup}_{j\ge 1}\left|{\beta }_j\right|j^{\alpha }<\infty$, $\alpha >1/2$, and $\left|\varrho \right|<1$. Then,

(i)

$\begin{array}{c}\hfill {\kappa }_1={\kappa }_{1,p}+o\left(p^{-1/2}\right),\end{array}$

(ii)

$\begin{array}{c}\hfill {\kappa }_2={\kappa }_{2,p}+o\left(p^{-1/2}\right).\end{array}$

Proof. 

For the proof see Supplementary Materials, Section S1. □

Proof of Theorem 2. 

Rewrite the left-hand side of (10) as follows:

$$\begin{array}{ccc}\hfill \frac{\parallel {\mathbb{X}}^{\prime }{Y\parallel }_2^2-n^2({\kappa }_2+c({\kappa }_1+{\sigma }_{\epsilon }^2))}{n^{3/2}}& =& \frac{\parallel {\mathbb{X}}^{\prime }{Y\parallel }_2^2-n^2{\kappa }_{2,p}-pn({\kappa }_{1,p}+{\sigma }_{\epsilon }^2)}{n^{3/2}}\hfill \\ & & +\sqrt{n}({\kappa }_{2,p}-{\kappa }_2)+\sqrt{n}c({\kappa }_{1,p}-{\kappa }_1)+o\left(1\right).\hfill \end{array}$$

It remains to apply Lemma 4 and Theorem 1 in order to conclude the proof of the theorem. □

We end this section by deriving two supporting results that allows us to derive convenient alternative expressions for the terms ${\kappa }_1,{\kappa }_2$ and ${\kappa }_3$. For this, we introduce functions $\beta (·)$ and $b(·)$ by Definition 3 below, which, under the assumptions of Theorem 1 and a given structure of ${\beta }_j$’s, requires only to evaluate the terms $\beta \left(1\right),\beta \left(\varrho \right),\beta \left({\varrho }^2\right)$ and $b_1\left(\varrho \right),b_2\left(\varrho \right)$. Then, due to Lemma 5 below, the expressions for ${\kappa }_1$, ${\kappa }_2$ and ${\kappa }_3$ easily follow.

Definition 3.

Assume that ${\sum }_{j=1}^{\infty }{\beta }_j^2<\infty$ and $\left|\varrho \right|\le 1$. Define,

$$\begin{array}{ccc}\hfill \beta \left(\varrho \right)& :=& \sum _{j=1}^{\infty }{\beta }_j^2{\varrho }^j,\hfill \end{array}$$

(65)

$$\begin{array}{ccc}\hfill b_1\left(\varrho \right)& :=& \sum _{j^{\prime }=2}^{\infty }\sum _{j=1}^{j^{\prime }-1}{\beta }_j{\beta }_{j^{\prime }}{\varrho }^{j^{\prime }-j},\hfill \end{array}$$

(66)

$$\begin{array}{ccc}\hfill b_2\left(\varrho \right)& :=& \sum _{j=2}^{\infty }\sum _{j^{\prime }=1}^{j-1}{\beta }_j{\beta }_{j^{\prime }}{\varrho }^{j+j^{\prime }},\hfill \end{array}$$

(67)

and define the following quantities which involve derivatives of (65)–(67):

$$\begin{array}{ccc}\hfill {\beta }^{\left(1\right)}\left(\varrho \right)& :=& \varrho \frac{\mathrm{d}\beta \left(\varrho \right)}{\mathrm{d}\varrho }=\sum _{j=1}^{\infty }j{\beta }_j^2{\varrho }^j,\hfill \end{array}$$

(68)

$$\begin{array}{ccc}\hfill b_1^{\left(1\right)}\left(\varrho \right)& :=& \varrho \frac{\mathrm{d}{b}_1\left(\varrho \right)}{\mathrm{d}\varrho }=\sum _{j^{\prime }=2}^{\infty }\sum _{j=1}^{j^{\prime }-1}{\beta }_j{\beta }_{j^{\prime }}{\varrho }^{j^{\prime }-j}(j^{\prime }-j),\hfill \end{array}$$

(69)

$$\begin{array}{ccc}\hfill b_2^{\left(1\right)}\left(\varrho \right)& :=& \varrho \frac{\mathrm{d}{b}_2\left(\varrho \right)}{\mathrm{d}\varrho }=\sum _{j^{\prime }=2}^{\infty }\sum _{j=1}^{j^{\prime }-1}{\beta }_j{\beta }_{j^{\prime }}{\varrho }^{j^{\prime }+j}(j^{\prime }+j),\hfill \end{array}$$

(70)

$$\begin{array}{ccc}\hfill b^{\left(2\right)}\left(\varrho \right)& :=& {\varrho }^2\frac{{\mathrm{d}}^2{b}_1\left(\varrho \right)}{\mathrm{d}{\varrho }^2}+b_1^{\left(1\right)}\left(\varrho \right)=\sum _{j^{\prime }=2}^{\infty }\sum _{j=1}^{j^{\prime }-1}{\beta }_j{\beta }_{j^{\prime }}{\varrho }^{j^{\prime }-j}{(j^{\prime }-j)}^2.\hfill \end{array}$$

(71)

Note that, by the rules of differentiation of power series, the functions (68)–(71) are well defined.

Lemma 5.

Let the assumptions of Theorem 1 hold. Let ${\kappa }_1$, ${\kappa }_2$ and ${\kappa }_3$ be given by (3)–(5), respectively. Then, under notation in Definition 3, the following identities hold:

(i)

$\begin{array}{cc}\hfill {\kappa }_1& =\beta \left(1\right)+2b_1\left(\varrho \right),\hfill \end{array}$

(ii)

$\begin{array}{cc}\hfill {\kappa }_2& =\beta \left(1\right)\frac{1+{\varrho }^2}{1-{\varrho }^2}-\beta \left({\varrho }^2\right)\frac{1}{1-{\varrho }^2}+2\left(b_1^{\left(1\right)}\left(\varrho \right)+b_1\left(\varrho \right)\frac{1+{\varrho }^2}{1-{\varrho }^2}-b_2\left(\varrho \right)\frac{1}{1-{\varrho }^2}\right),\hfill \end{array}$

(iii)

$\begin{array}{cc}\hfill {\kappa }_3& =\frac{1}{{(1-{\varrho }^2)}^2}\left((1+4{\varrho }^2+{\varrho }^4)(\beta \left(1\right)+2b_1\left(\varrho \right))-(1+3{\varrho }^2)(\beta \left({\varrho }^2\right)+2b_2\left(\varrho \right))\right)\hfill \\ & +\frac{1}{1-{\varrho }^2}\left(3b_1^{\left(1\right)}\left(\varrho \right)(1+{\varrho }^2)-2\left(b_2^{\left(1\right)}\left(\varrho \right)+{\beta }^{\left(1\right)}\left({\varrho }^2\right)\right)\right)+b^{\left(2\right)}\left(\varrho \right).\hfill \end{array}$

Proof. 

See the proof in Appendix A.2. □

Remark 3.

From the assumptions of Definition 3 it follows that $\beta \left(1\right),\left|\beta \left(\varrho \right)\right|,|b_1\left(\varrho \right)|$, $|b_2\left(\varrho \right)|<\infty$ for $\left|\varrho \right|<1$. Thus, it follows from Lemma 5 that ${\kappa }_i<\infty$, $i=1,2,3$.

Proof of Remark 3. 

Cases for $\beta \left(1\right)$ and $\beta \left(\varrho \right)$ follow straightforwardly from the assumptions. Consider $b_1\left(\varrho \right)$. Note that for any p,

$$\begin{array}{ccc}\hfill |b_1\left(\varrho \right)|& \le & \sum _{l_1,l_2=1}^{\infty }|{\beta }_{l_1}\left|\right|{\beta }_{l_2}{\left|\right|\varrho |}^{|l_1-l_2|}=\sum _{l_1,l_2=1}^{\infty }\left(|{\beta }_{l_1}{\left|\right|\varrho |}^{|l_1-l_2|/2}\right)\left(|{\beta }_{l_2}{\left|\right|\varrho |}^{|l_1-l_2|/2}\right)\hfill \\ & \le & (1/2)\sum _{l_1,l_2=1}^{\infty }\left({\beta }_{l_1}^2{\left|\varrho \right|}^{|l_1-l_2|}+{\beta }_{l_2}^2{\left|\varrho \right|}^{|l_1-l_2|}\right)\hfill \\ & =& \sum _{l_1=1}^{\infty }{\beta }_{l_1}^2\sum _{l_2=1}^{\infty }{\left|\varrho \right|}^{|l_1-l_2|}\le \beta \left(1\right)\frac{1+\left|\varrho \right|}{1-\left|\varrho \right|}<\infty \hfill \end{array}$$

by (S9). In a similar manner, it can be seen that $|b_2\left(\varrho \right)|\le \beta \left(1\right)\frac{\left|\varrho \right|}{1-\left|\varrho \right|}$. □

6. Approximate Sparsity: An Example

In this section, we study the case when coefficients ${\beta }_j$ decay hyperbolically, i.e., ${\beta }_j=j^{-1},j\ge 1$. This assumption is analogous to the assumption of approximate sparsity, as defined by [21]. The authors of the aforementioned paper note that for approximately sparse models, the regression function can be well approximated by a linear combination of relatively few important regressors, which is one of the reasons of popularity of variable selection approaches such as LASSO ([36]) and its modifications (see, e.g., [37,38,39]). At the same time, approximate sparsity allows all coefficients ${\beta }_j$ to be nonzero, which is a more plausible assumption in many real world settings.

In order to derive the quantities in Theorem 2, we apply the results of Lemma 5. For this, we establish the expressions for the quantities in Definition 3.

Define the real dilogarithm function (see, e.g., [40]):

$$\begin{array}{ccc}\hfill {Li}_2\left(x\right)& =& -{\int }_0^x\frac{log(1-u)}{u}\mathrm{d}u,x\le 1,x\in \mathbb{R}.\hfill \end{array}$$

(72)

(Here and below, ${\int }_0^x=-{\int }_x^0$ if $x\le 0$.) For $\left|x\right|\le 1$ the real dilogarithm has a series representation,

$$\begin{array}{ccc}\hfill {Li}_2\left(x\right)& =& \sum _{k=1}^{\infty }\frac{x^k}{k^2}.\hfill \end{array}$$

(73)

Then,

$$\begin{array}{ccc}\hfill \beta \left(1\right)=\sum _{j=1}^{\infty }\frac{1}{j^2}=\frac{{\pi }^2}{6},& & \beta \left(\varrho \right)=\sum _{j=1}^{\infty }\frac{{\varrho }^j}{j^2}={\mathrm{Li}}_2\left(\varrho \right).\hfill \end{array}$$

Additionally, we have

$$\begin{array}{ccc}\hfill \frac{\mathrm{d}}{\mathrm{d}\varrho }{Li}_2\left(\varrho \right)& =& -\frac{log(1-\varrho )}{\varrho }.\hfill \end{array}$$

(74)

Thus, by (68) and (74), we establish

$$\begin{array}{ccc}\hfill {\beta }^{\left(1\right)}\left(\varrho \right)& =& \varrho \frac{\mathrm{d}}{\mathrm{d}\varrho }\beta \left(\varrho \right)=\varrho \frac{\mathrm{d}}{\mathrm{d}\varrho }{Li}_2\left(\varrho \right)=-log(1-\varrho ).\hfill \end{array}$$

Next, note that

$$\begin{array}{ccc}\hfill b_1\left(\varrho \right)& =& \sum _{i=2}^{\infty }\sum _{j=1}^{i-1}\frac{{\varrho }^{i-j}}{ij}=\sum _{i=2}^{\infty }\sum _{k=1}^{i-1}\frac{{\varrho }^k}{i(i-k)}\hfill \\ & =& \sum _{k=1}^{\infty }{\varrho }^k\sum _{i=k+1}^{\infty }\frac{1}{i(i-k)}=\sum _{k=1}^{\infty }\frac{{\varrho }^k}{k}\sum _{l=1}^k\frac{1}{l}\hfill \\ & =& \sum _{l=1}^{\infty }\frac{1}{l}\sum _{k=l}^{\infty }\frac{{\varrho }^k}{k}=\sum _{l=1}^{\infty }\frac{1}{l}{\int }_0^{\varrho }\frac{x^{l-1}}{1-x}\mathrm{d}x\hfill \\ & =& -{\int }_0^{\varrho }\frac{log(1-x)}{x(1-x)}\mathrm{d}x=\frac{{log}^2(1-\varrho )}{2}+{\mathrm{Li}}_2\left(\varrho \right),\hfill \end{array}$$

(75)

where we have used identities

$$\begin{array}{ccc}\hfill \sum _{i=k+1}^{\infty }\frac{1}{i(i-k)}& =& \frac{1}{k}\sum _{l=1}^k\frac{1}{l},k\ge 1,\sum _{k=l}^{\infty }\frac{{\varrho }^k}{k}={\int }_0^{\varrho }\frac{x^{l-1}}{1-x}\mathrm{d}x\hfill \end{array}$$

and (72). Then, by (69), (74) and (75),

$$\begin{array}{ccc}\hfill b_1^{\left(1\right)}\left(\varrho \right)& =& \varrho \frac{\mathrm{d}}{\mathrm{d}\varrho }{b}_1\left(\varrho \right)=-\frac{log(1-\varrho )}{1-\varrho },\hfill \end{array}$$

whereas by (71),

$$\begin{array}{ccc}\hfill b^{\left(2\right)}\left(\varrho \right)& =& {\varrho }^2\frac{{\mathrm{d}}^2{b}_1\left(\varrho \right)}{\mathrm{d}{\varrho }^2}+b_1^{\left(1\right)}\left(\varrho \right)=\frac{\varrho -\varrho log(1-\varrho )}{{(1-\varrho )}^2}.\hfill \end{array}$$

Furthermore, note that

$$\begin{array}{ccc}\hfill b_2\left(\varrho \right)& =& \sum _{i=2}^{\infty }\sum _{j=1}^{i-1}\frac{{\varrho }^{i+j}}{ij}=\sum _{i=2}^{\infty }\frac{{\varrho }^i}{i}\sum _{j=1}^{i-1}\frac{{\varrho }^j}{j}=\sum _{i=2}^{\infty }\frac{{\varrho }^i}{i}{\int }_0^{\varrho }\sum _{j=1}^{i-1}{x}^{j-1}\mathrm{d}x\hfill \\ & =& \sum _{i=1}^{\infty }\frac{{\varrho }^{i+1}}{i+1}{\int }_0^{\varrho }\frac{1-x^i}{1-x}\mathrm{d}x\hfill \\ & =& -log(1-\varrho )\left(\sum _{i=1}^{\infty }\frac{{\varrho }^i}{i}-\varrho \right)-{\int }_0^{\varrho }\left(\sum _{i=1}^{\infty }\frac{{\varrho }^i}{i}\frac{x^{i-1}}{1-x}-\varrho \frac{1}{1-x}\right)\mathrm{d}x\hfill \\ & =& -log(1-\varrho )\sum _{i=1}^{\infty }\frac{{\varrho }^i}{i}-{\int }_0^{\varrho }\sum _{i=1}^{\infty }\frac{{\left(\varrho x\right)}^i}{i}\frac{1}{x(1-x)}\mathrm{d}x\hfill \\ & =& {log}^2(1-\varrho )+{\int }_0^{\varrho }\frac{log(1-\varrho x)}{x(1-x)}\mathrm{d}x\hfill \\ & =& \frac{1}{2}\left({log}^2(1-\varrho )-{Li}_2\left({\varrho }^2\right)\right),\hfill \end{array}$$

(76)

where the last equality follows from Lemma A1. Next, by (69), (74) and (76) we have

$$\begin{array}{ccc}\hfill b_2^{\left(1\right)}\left(\varrho \right)& =& log\left(1-{\varrho }^2\right)-\frac{\varrho log(1-\varrho )}{1-\varrho }.\hfill \end{array}$$

Thus, we can apply Lemma 5(i) and arrive at the following expression for ${\kappa }_1$:

$$\begin{array}{ccc}\hfill {\kappa }_1& =& \frac{{\pi }^2}{6}+{log}^2(1-\varrho )+2{\mathrm{Li}}_2\left(\varrho \right).\hfill \end{array}$$

(77)

Similarly, for ${\kappa }_2$, by collecting and simplifying the terms, by Lemmas 5(ii) and A1, we have

$$\begin{array}{ccc}\hfill {\kappa }_2& =& \frac{1+{\varrho }^2}{1-{\varrho }^2}\left(\frac{{\pi }^2}{6}+2{\mathrm{Li}}_2\left(\varrho \right)\right)-\frac{2log(1-\varrho )}{1-\varrho }+{log}^2(1-\varrho )\frac{{\varrho }^2}{1-{\varrho }^2}\hfill \\ & =& \frac{1}{1-{\varrho }^2}((1+{\varrho }^2){\kappa }_1-{log}^2(1-\varrho )-2(1+\varrho )log(1-\varrho )).\hfill \end{array}$$

(78)

Lastly, for ${\kappa }_3$, by Lemma 5(iii), through simplification of terms, we get

$$\begin{array}{ccc}\hfill {\kappa }_3& =& \frac{1}{{(1-{\varrho }^2)}^2}((1+4{\varrho }^2+{\varrho }^4)\left(\frac{{\pi }^2}{6}+2{\mathrm{Li}}_2\left(\varrho \right)\right)+{log}^2(1-\varrho ){\varrho }^2(1+{\varrho }^2)\hfill \\ & & -(3-\varrho +4{\varrho }^2)(1+\varrho )log(1-\varrho )+\varrho {(1+\varrho )}^2)\hfill \\ & =& {\kappa }_2\frac{1+3{\varrho }^2}{1-{\varrho }^2}+\frac{1}{{(1-{\varrho }^2)}^2}\left((-1+\varrho +2{\varrho }^2)(1+\varrho )log(1-\varrho )+\varrho {(1+\varrho )}^2-2{\varrho }^4{\kappa }_1\right).\hfill \end{array}$$

(79)

This allows us to apply Theorem 2 under the considered specification of the parameter $\beta$ and conclude with the following corollary.

Corollary 2.

Assume a model (1) with (2) covariance structure and consider ${\beta }_j:=j^{-1}$, $j=1,\dots ,p$. Let $p=p_n$ satisfies

$$\begin{array}{ccc}\hfill p\to \infty ,& & \frac{p}{n}\to c\in (0,\infty ).\hfill \end{array}$$

Then

$$\begin{array}{ccc}\hfill \frac{\parallel {\mathbb{X}}^{\prime }{Y\parallel }_2^2-n^2\left({\kappa }_2+c({\kappa }_1+{\sigma }_{\epsilon }^2)\right)}{n^{3/2}}& \stackrel{d}{\to }& \mathcal{N}(0,s^2),\hfill \end{array}$$

(80)

where

$$\begin{array}{ccc}\hfill s^2& =& 4{\kappa }_2^2+4({\kappa }_1+{\sigma }_{\epsilon }^2)\left(2{\kappa }_{2}c+{\kappa }_3\right)+2c{({\kappa }_1+{\sigma }_{\epsilon }^2)}^2\left(c+\frac{1+{\varrho }^2}{1-{\varrho }^2}\right),\hfill \end{array}$$

(81)

and ${\kappa }_1$, ${\kappa }_2$ and ${\kappa }_3$ are defined by (77)–(79), respectively.

In order to illustrate the results of Corollary 2, we end this section with a Monte Carlo simulation study where we generate 1000 independent replications of the statistic $\parallel {\mathbb{X}}^{\prime }{Y\parallel }_2^2$. The data is generated following the assumptions of Corollary 2. We consider the following parameter values: $p=100,500,1000,1500,2000,3000$, $c=1,2,5,10$, ${\sigma }_{\epsilon }^2=1,2,4,10$. Due to the large number of resulting figures, we present only selected cases in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, which demonstrate certain disparities in greater detail. Figures show the empirical cumulative distribution function (CDF) and the empirical probability density function (PDF), together with the limiting CDF and PDF of $\mathcal{N}(0,s^2)$ by (80) for different parameter combinations. In addition, we present the corresponding Q-Q plots in order to inspect the tails of the resulting distributions in greater detail.

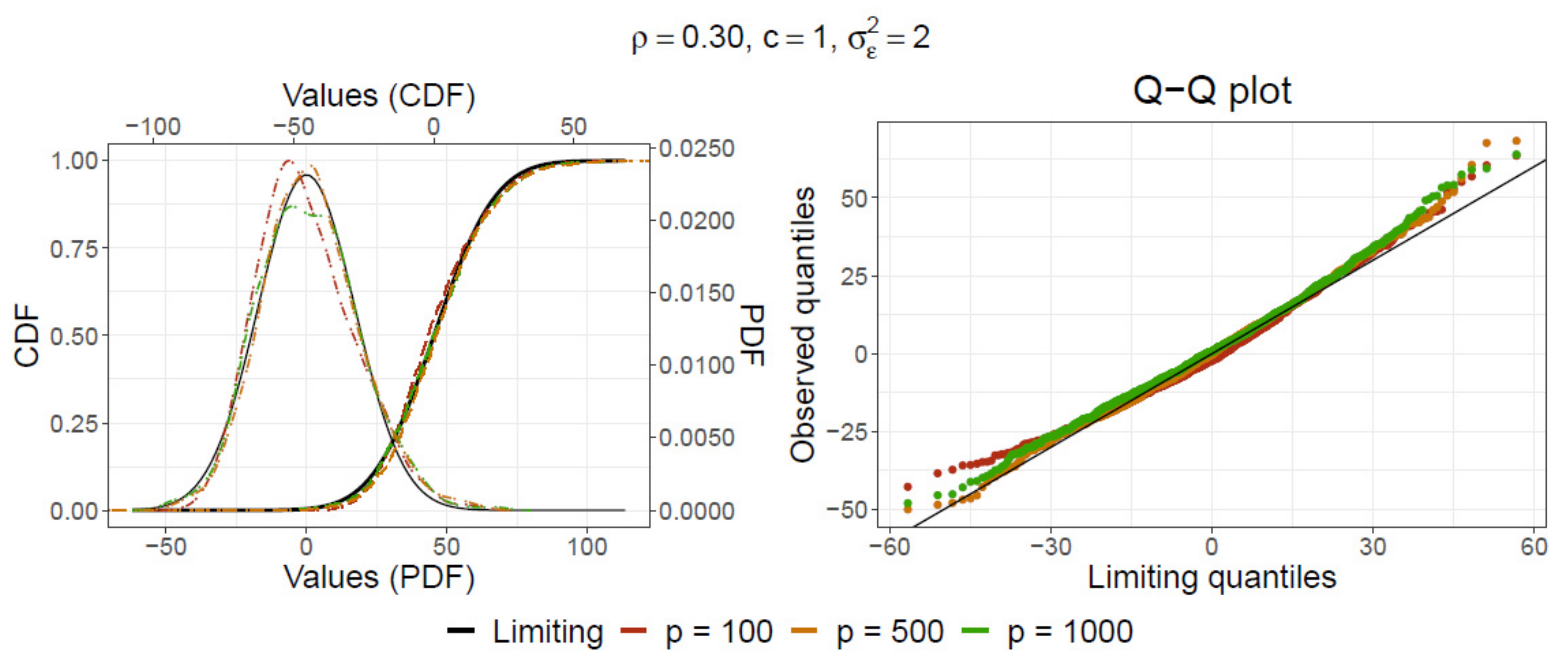
We find that for relatively small values of $\varrho$, the observed distribution of the statistic is fairly close to the limiting distribution even for small values of $p,n$ and larger ${\sigma }_{\epsilon }^2,c$ (see, e.g., Figure 1, Figure 2, Figure 3 and Figure 4). However, slower convergence is more evident with increasing values of $\varrho$. Furthermore, for moderate values of $\varrho ,c,{\sigma }_{\epsilon }^2$, only with larger values of p we observe adequate convergence towards the limiting distribution (see Figure 5 and Figure 6). Similar behaviour is observed when the relation between the parameters $\varrho ,c,{\sigma }_{\epsilon }^2$ is appropriately controlled: e.g., in Figure 7, we see comparable results to those presented by Figure 6, where the effect of the increase in parameter value $\varrho$ is countered by a smaller value of ${\sigma }_{\epsilon }^2$. Alternatively, analogous effects can be achieved when reducing the values of c, instead.

Figure 2. Comparison of the PDF and CDF (left) and the corresponding Q-Q plots (right) after 1000 replications from the Monte Carlo simulation of the statistic (80) with the limiting distribution $\mathcal{N}(0,s^2)$ by the Corollary 2 (in black) for $\varrho =0.3$, $c=1$, ${\sigma }_{\epsilon }^2=2$ and $p=1500,2000,3000$.

Figure 2. Comparison of the PDF and CDF (left) and the corresponding Q-Q plots (right) after 1000 replications from the Monte Carlo simulation of the statistic (80) with the limiting distribution $\mathcal{N}(0,s^2)$ by the Corollary 2 (in black) for $\varrho =0.3$, $c=1$, ${\sigma }_{\epsilon }^2=2$ and $p=1500,2000,3000$.

Figure 3. Comparison of the PDF and CDF (left) and the corresponding Q-Q plots (right) after 1000 replications from the Monte Carlo simulation of the statistic (80) with the limiting distribution $\mathcal{N}(0,s^2)$ by the Corollary 2 (in black) for $\varrho =0.3$, $c=1$, ${\sigma }_{\epsilon }^2=10$ and $p=100,500,1000$.

Figure 3. Comparison of the PDF and CDF (left) and the corresponding Q-Q plots (right) after 1000 replications from the Monte Carlo simulation of the statistic (80) with the limiting distribution $\mathcal{N}(0,s^2)$ by the Corollary 2 (in black) for $\varrho =0.3$, $c=1$, ${\sigma }_{\epsilon }^2=10$ and $p=100,500,1000$.

Figure 4. Comparison of the PDF and CDF (left) and the corresponding Q-Q plots (right) after 1000 replications from the Monte Carlo simulation of the statistic (80) with the limiting distribution $\mathcal{N}(0,s^2)$ by the Corollary 2 (in black) for $\varrho =0.3$, $c=1$, ${\sigma }_{\epsilon }^2=10$ and $p=1500,2000,3000$.

Figure 4. Comparison of the PDF and CDF (left) and the corresponding Q-Q plots (right) after 1000 replications from the Monte Carlo simulation of the statistic (80) with the limiting distribution $\mathcal{N}(0,s^2)$ by the Corollary 2 (in black) for $\varrho =0.3$, $c=1$, ${\sigma }_{\epsilon }^2=10$ and $p=1500,2000,3000$.

Figure 5. Comparison of the PDF and CDF (left) and the corresponding Q-Q plots (right) after 1000 replications from the Monte Carlo simulation of the statistic (80) with the limiting distribution $\mathcal{N}(0,s^2)$ by the Corollary 2 (in black) for $\varrho =0.7$, $c=5$, ${\sigma }_{\epsilon }^2=4$ and $p=100,500,1000$.

Figure 5. Comparison of the PDF and CDF (left) and the corresponding Q-Q plots (right) after 1000 replications from the Monte Carlo simulation of the statistic (80) with the limiting distribution $\mathcal{N}(0,s^2)$ by the Corollary 2 (in black) for $\varrho =0.7$, $c=5$, ${\sigma }_{\epsilon }^2=4$ and $p=100,500,1000$.

Figure 6. Comparison of the PDF and CDF (left) and the corresponding Q-Q plots (right) after 1000 replications from the Monte Carlo simulation of the statistic (80) with the limiting distribution $\mathcal{N}(0,s^2)$ by the Corollary 2 (in black) for $\varrho =0.7$, $c=5$, ${\sigma }_{\epsilon }^2=4$ and $p=1500,2000,3000$.

Figure 6. Comparison of the PDF and CDF (left) and the corresponding Q-Q plots (right) after 1000 replications from the Monte Carlo simulation of the statistic (80) with the limiting distribution $\mathcal{N}(0,s^2)$ by the Corollary 2 (in black) for $\varrho =0.7$, $c=5$, ${\sigma }_{\epsilon }^2=4$ and $p=1500,2000,3000$.

Figure 7. Comparison of the PDF and CDF (left) and the corresponding Q-Q plots (right) after 1000 replications from the Monte Carlo simulation of the statistic (80) with the limiting distribution $\mathcal{N}(0,s^2)$ by the Corollary 2 (in black) for $\varrho =0.9$, $c=5$, ${\sigma }_{\epsilon }^2=1$ and $p=1500,2000,3000$.

Figure 7. Comparison of the PDF and CDF (left) and the corresponding Q-Q plots (right) after 1000 replications from the Monte Carlo simulation of the statistic (80) with the limiting distribution $\mathcal{N}(0,s^2)$ by the Corollary 2 (in black) for $\varrho =0.9$, $c=5$, ${\sigma }_{\epsilon }^2=1$ and $p=1500,2000,3000$.

Finally, slow convergence is observed for large values of $\varrho ,c,{\sigma }_{\epsilon }^2$, as expected (see Figure 8 and Figure 9). In such cases, the simulation results suggest that even larger values of $p,n$ would be needed for more accurate results.

Figure 8. Comparison of the PDF and CDF (left) and the corresponding Q-Q plots (right) after 1000 replications from the Monte Carlo simulation of the statistic (80) with the limiting distribution $\mathcal{N}(0,s^2)$ by the Corollary 2 (in black) for $\varrho =-0.95$, $c=10$, ${\sigma }_{\epsilon }^2=4$ and $p=100,500,1000$.

Figure 8. Comparison of the PDF and CDF (left) and the corresponding Q-Q plots (right) after 1000 replications from the Monte Carlo simulation of the statistic (80) with the limiting distribution $\mathcal{N}(0,s^2)$ by the Corollary 2 (in black) for $\varrho =-0.95$, $c=10$, ${\sigma }_{\epsilon }^2=4$ and $p=100,500,1000$.

Figure 9. Comparison of the PDF and CDF (left) and the corresponding Q-Q plots (right) after 1000 replications from the Monte Carlo simulation of the statistic (80) with the limiting distribution $\mathcal{N}(0,s^2)$ by the Corollary 2 (in black) for $\varrho =-0.95$, $c=10$, ${\sigma }_{\epsilon }^2=4$ and $p=1500,2000,3000$.

Figure 9. Comparison of the PDF and CDF (left) and the corresponding Q-Q plots (right) after 1000 replications from the Monte Carlo simulation of the statistic (80) with the limiting distribution $\mathcal{N}(0,s^2)$ by the Corollary 2 (in black) for $\varrho =-0.95$, $c=10$, ${\sigma }_{\epsilon }^2=4$ and $p=1500,2000,3000$.

7. Discussion

In this paper, we consider a specific KMS covariance structure due to its attractive properties and wide application possibilities for working with real world datasets. Moreover, our results could be extended further by considering a wider family of Toeplitz covariance structures. For instance, under specific constraints, one could employ the approaches proposed in [3] in order to extend the application of our results towards more complex covariance structures of the data.

Furthermore, for future work, it would be interesting to expand and examine the results by removing the assumption of independence between the observations $X_i$, $i=1,\dots ,n$.

Finally, in this paper we have established both the exact and the asymptotic distributions of the statistic $\parallel {\mathbb{X}}^{\prime }{Y\parallel }_2^2$ (see (8), (10) and (34)). Both distributions could be used for estimating $\beta$, ${\sigma }_{\epsilon }^2$ or related measures (e.g., by applying the method of moments or maximum likelihood estimation) in future research. Such research direction could open up interesting avenues when compared with popular LASSO type methods in high-dimensional linear regression. Similar approach is taken by [10], who construct maximum likelihood estimators for the signal strength ${\parallel \beta \parallel }_2^2$ in a high-dimensional regression context. Note that the results by [10] are achieved under certain strong restrictions, which are consistent with the related literature (see, e.g., [7,41,42]). In our case, we impose weaker assumptions; therefore, both our asymptotic or exact results could be used in order to extend the approaches in the aforementioned literature.