A Creative Design Framework for Math Exam Questions Concerning Inequalities and Zeros of Functions with an Unknown Parameter in China National College Entrance Examination

Abstract

The annual exam questions in China National College Entrance Examination (CNCEE, commonly known as Gaokao) have attracted wide attention from the entire society in China. This paper analyzes an important math exam question related to always holding inequalities with an unknown parameter from the 2020 CNCEE and builds different solutions via parameter separation or classified discussion, and then gives a systematic and effective design framework for questions related to problems of always holding inequalities and zeros of functions with an unknown parameter for the CNCEE. The framework reveals the internal mechanism of designing the math exam questions in the CNCEE. According to the design framework, two simulated math exam questions with reference solutions will be proposed.

1. Introduction

The college (university) entrance examinations are important examinations for high school graduates to obtain college admission qualifications, and the study of college entrance examinations plays a positive and important role in improving high school teaching and college teaching. China has had an outstanding performance in previous international tests, such as the test results of PISA and TIMSS; therefore, China’s mathematics education has attracted global attention. Among the countries with outstanding test results in PISA and TIMSS, in addition to China, there is also Singapore, South Korea, etc. These countries have a common feature that there is a national unified college entrance examination. Therefore, studying the China National College Entrance Examination (CNCEE, commonly known as Gaokao) is of significance to improving educational quality and testing evaluation worldwide. The college entrance examinations establish an essential link between high school education and college education. Therefore, it is necessary to examine the exam questions in the college entrance examinations and the design methods or frameworks. The College Scholastic Ability Test (CSAT) is a scientific test designed to measure students’ performance and academic abilities in accordance with the national standards of the college education curriculum in South Korea. The Advanced Level (A-Level) is the qualification used by British universities to assess the eligibility of students for a bachelor’s degree. The Scholastic Assessment Test (SAT) and the American College Test (ACT) are the main college entrance examinations in the United States as selective tests for high school graduates. The CNCEE is an academic testing event held each summer in mainland China and is joined by millions of participants, a majority of whom are senior high school students [1]. Some researchers have conducted international comparative research on the exam questions of the college entrance examinations in different countries. For example, the international comparative studies of mathematics exam questions between China and South Korea [2], China and France [3], China and Britain [4], China and U.S. [5]. However, there are rarely studies into how mathematics questions are designed for college entrance examinations. Therefore, in the current research, we will investigate the design framework of mathematics examination questions for the CNCEE as an example.

Recently, some important Chinese education policies have put forward new requirements and guidelines for the CNCEE. In 2014, the “Implementation Opinions on Deepening the Reform of the Examination and Enrollment System” proposed scientifically designing the exam questions under the requirements of the talent selection of colleges and universities and the national curriculum standards, enhancing the basic and comprehensive, and focusing on examining students’ ability to independently think, analyze, and solve problems applying the knowledge learned by the candidates [6]. Among them, scientifically designing the content of exam questions and enhancing the basic and comprehensiveness to a certain extent to reflect the direction and dynamics of the reform of the national college entrance examination in the future.

The general model “one core, four layers and four wings” in the latest national college entrance examination evaluation system reflects the requirements of the selection of talent in colleges and universities (see Figure 1). The “one core” shows the general designing framework of exam questions and answers the question of “why examine”. The “four layers” show the content of the exam questions, which contains “subject literacy, key abilities, necessary knowledge and core values” to answer the question of “what to examine”. The “four wings” shows the examination requirements, which contains “basic, comprehensive, applied and innovative”, to answer the question of “how to test”. The “one core” is the commander, the “four layers” and “four wings” are the specific routes to achieve the “one core”, and the three components together constitute a theoretical system for realizing the evaluation function of the CNCEE [7].

In 2020, the “Overall Plan for Deepening the Reform of Education Evaluation in the New Era” pointed out that it is necessary to steadily promote the reform of entrance examinations for senior schools and universities, and build an examination system to guide the comprehensive development of students’ morality, intellectual, physical, aesthetic and labor, change the relatively inflexible form of exam questions, enhance the openness of exam questions and reduce rote memorization and “mechanical solving problem” [8]. For mathematics, the construction basis of the new designing framework of exam questions in the CNCEE is based on the latest college entrance examination evaluation system, the requirements for the selection of talent in universities and the national curriculum standards [9]. Therefore, to promote the reform of the college entrance examination and implement the policy, it is important to study the methods of solving and designing the framework of the mathematical exam questions in the CNCEE.

The General High School Math Curriculum Standards (2017 edition) highlight four main content lines, of which functions are one of the most important [10]. In high school mathematics, learning and the CNCEE, functions, derivatives and their applications occupy an extremely important position. In recent years, the math exam questions in the CNCEE have involved functions, derivatives and their applications; the inspection of the core literacy of mathematics is relatively comprehensive [11]. Math exam questions concerning always holding inequality and poles of functions with an unknown parameter are two frequently examined types of derivative problems in the CNCEE, and the basic strategy for solving the problems is to transform the problems to examine the monotonicity of the functions, the maximum or minimum, and compare the value of functions. The two kinds of problems are usually solved using the separation parameter method and the classification discussion method, or the definition of maximum and minimum. When using the classification discussion method, the solving process is usually complicated and lengthy, and it is also easy to make errors, such as repeating or missing data. By using the separation parameter method, when the inequality contains an unknown parameter, one can change the terms until the unknown parameter stands alone on one side of the new inequality. Then, the parameter and the variable will be separated, and the original problem can be solved by discussing the monotonicity of the function and the range on another side of the new inequality [12]. When using the parameter separation, one should consider the direction of the inequality, discuss it if necessary and clarify whether the maximum or minimum of the related function needs to be investigated. If the inequality $a\ge f\left(x\right)$ always holds, then $f{\left(x\right)}_{max}$ should be calculated, and if the inequality $a\le f\left(x\right)$ always holds, then $f{\left(x\right)}_{min}$ should be calculated, where a is the unknown parameter. Although some literature focuses on solving strategies for related problems of always holding inequalities and zeros of functions with an unknown parameter, such as [13,14,15,16], there is little research on the design framework of the two kinds of questions in the CNCEE.

To study math exam questions related to always holding inequalities and zeros of functions with an unknown parameter, we select the 21st question in the 2020 CNCEE (Science-Mathematics I) as an example to explore the design framework. The design framework can reveal the internal mechanism of the two kinds of math exam questions in the CNCEE. We give two simulated exam questions for the CNCEE. The two questions can reflect the characteristics of basic and comprehensive, concentrate on the essence of the exam questions and match the new exam orientation of rational thinking and scientific spirit in the reform of the CNCEE.

2. Question Analysis and Problem Solving

The 21st question in the 2020 CNCEE (Science-Mathematics I) reads as follows:

Question 1. Given a function $f\left(x\right)=e^x+a{x}^2-x$.

(1)

When $a=1$, discuss the monotonicity of $f\left(x\right)$;

(2)

When $x\ge 0$, $f\left(x\right)\ge \frac{1}{2}{x}^3+1$, find the range of a.

2.1. Question Analysis

Question 1 investigates the monotonicity of functions $f\left(x\right)$ and always holding inequalities. The core literacy of mathematics examined involves logical reasoning and mathematical operations. The mathematical thinking and methods examined include function and equation thinking, classification discussion thinking, transformation thinking and separation of parameter thinking.

For Question (1), the monotonicity of the function $f\left(x\right)$ can be determined by derivation. When $a=1$, $f\left(x\right)=e^x+x^2-x$,$f^{\prime }\left(x\right)=e^x+2x-1$. Since $e^x,2x-1$ are increasing functions on R, so $f^{\prime }\left(x\right)$ is also increasing. According to the continuity of $f^{\prime }\left(x\right)$, we know that $x=0$ is the only root of $f^{\prime }\left(x\right)$. Further, when $x<0$, $f^{\prime }\left(x\right)<0$, when $x>0$, $f^{\prime }\left(x\right)>0$, so the decreasing interval of $f\left(x\right)$ is $(-\infty ,0)$, the increasing interval is $(0,\infty )$. Another method is to use the second-order derivative $f^{″}\left(x\right)$. Setting $h\left(x\right)=f^{\prime }\left(x\right)=e^x+2x-1$, $h^{\prime }\left(x\right)=f^{″}\left(x\right)=e^x+2>2$ always holds, therefore, $f^{\prime }\left(x\right)$ is an increasing function. Furthermore, $f^{\prime }\left(0\right)=0$. Therefore, when $x<0$, $f^{\prime }\left(x\right)<0$, when $x>0$, $f^{\prime }\left(x\right)>0$, so the decreasing interval of $f\left(x\right)$ is $(-\infty ,0)$ and the increasing interval is $(0,\infty )$.

In addition, because $f^{″}\left(x\right)=e^x+2>0$, $f\left(x\right)$ is an up convex function. Since $x=0$ is the unique zero of $f\left(x\right)$, then $f{\left(x\right)}_{min}=f\left(0\right)=1$, so the decreasing interval of $f\left(x\right)$ is $(-\infty ,0)$, the monotone increasing range is $(0,\infty )$. Because (1) is trivial, we do not consider its design framework.

Question (2) is an inequality always holding with an unknown parameter a that must be investigated by the separation parameter method. We need to extract the unknown parameter a in the given inequality $f\left(x\right)\ge \frac{1}{2}{x}^3+1$, change the terms about a until a stands alone on one side of the new inequality and then obtain a new inequality that the other side does not involve any terms about a. The solving steps of (2) are as follows.

• Extract the unknown parameter a given in the always holding inequality, convert the right-hand side of the inequality into an expression without parameter and the left-hand side into an expression with a parameter and no independent variables as:

  $$a\ge \left(\frac{1}{2}{x}^3+x+1-e^x\right)x^{-2}(x\ge 0).$$
• Build the auxiliary function:

  $$g\left(x\right)=\left(\frac{1}{2}{x}^3+x+1-e^x\right)x^{-2}(x\ge 0).$$
  Determine the monotonicity, monotone interval, and $g{\left(x\right)}_{max}$.
• Let $a\ge g{\left(x\right)}_{max}$ and give the conclusion of the question.

2.2. The Problem Solving

2.2.1. Solution 1

If $x=0$, we have $a\in R$.

If $x>0$, $f\left(x\right)\ge \frac{1}{2}{x}^3+1$ is always holds, then $e^x+a{x}^2-x\ge \frac{1}{2}{x}^3+1$. By separating the parameter a, we obtain the following inequality:

$$a\ge \left(\frac{1}{2}{x}^3+x+1-e^x\right)x^{-2}.$$

Then, the original problem can be converted to find the maximum of the following auxiliary function:

$$g\left(x\right)=\left(\frac{1}{2}{x}^3+x+1-e^x\right)x^{-2}.$$

Differentiating $g\left(x\right)$, we obtain:

$$g^{\prime }\left(x\right)=\frac{1}{2}-\frac{1}{x^2}-\frac{2}{x^3}-\frac{(x-2)e^x}{x^3}=\left(\frac{1}{2}{x}^3-x-2-(x-2)e^x\right)x^{-3}.$$

Obviously, $g^{\prime }\left(2\right)=0$, then we have:

$$g^{\prime }\left(x\right)=(2-x)(e^x-\frac{1}{2}{x}^2-x-1)x^{-3}.$$

Letting,

$$h\left(x\right)=e^x-\frac{1}{2}{x}^2-x-1,$$

It follows that,

$$h^{\prime }\left(x\right)=e^x-x-1$$

Since $x>0$, then:

$$h^{″}\left(x\right)=e^x-1>0,$$

then when $x>0$, $h^{\prime }\left(x\right)$ is an increasing function and $h^{\prime }\left(x\right)>h^{\prime }\left(0\right)=0$. Therefore, when $x>0$, $h\left(x\right)$ is increasing, so $h\left(x\right)>h\left(0\right)=0$.

Therefore, when $0<x<2$, $g^{\prime }\left(x\right)>0$, and when $x>2$, $g^{\prime }\left(x\right)<0$. Obviously, $g{\left(x\right)}_{max}=g\left(2\right)=\frac{7-e^2}{4}$. Hence, $a\in [\frac{7-e^2}{4},\infty )$.

2.2.2. Solution 2

If $x=0$, then $a\in R$.

If $x>0$, $f\left(x\right)\ge \frac{1}{2}{x}^3+1$, it follows that:

$$a\ge \left(\frac{1}{2}{x}^3+1+x-e^x\right)x^{-2}=:g\left(x\right).$$

Therefore,

$$g^{\prime }\left(x\right)=\left(\frac{1}{2}{x}^3-x-2-(x-2)e^x\right)x^{-3},$$

Letting,

$$h\left(x\right)=\frac{1}{2}{x}^3-x-2-(x-2)e^x,$$

we have,

$$h^{\prime }\left(x\right)=\frac{3}{2}{x}^2-1-(x-1)e^x,$$

$$h^{″}\left(x\right)=3x-x{e}^x=x(3-e^x).$$

Letting $h^{″}\left(x\right)=0$, then $3-e^x=0$, it follows that $x=ln3$. Therefore, if $0<x<ln3$, $h^{″}\left(x\right)>0$, $h^{\prime }\left(x\right)$ is increasing. If $x>ln3$, $h^{″}\left(x\right)<0$, $h^{\prime }\left(x\right)$ is decreasing.

Since,

$$h^{\prime }\left(0\right)=0,$$

$$h^{\prime }(ln3)=\frac{3}{2}{(ln3)}^2-1-3(ln3-1)=\frac{3}{2}{(ln3)}^2-3ln3+2=\frac{3}{2}{(ln3-1)}^2+\frac{1}{2}>0,$$

and,

$$h^{\prime }\left(2\right)=5-e^2<0,$$

then, $h\left(x\right)$ increases first and decreases later on $(0,+\infty )$.

Since $h\left(0\right)=0$ and $h\left(2\right)=0$, so if $0<x<2$, $h\left(x\right)>0$ and if $x\in (2,+\infty )$, $h\left(x\right)<0$. Therefore, if $0<x<2$, $g^{\prime }\left(x\right)=x^{-3}h\left(x\right)>0$ and if $x\in (2,+\infty )$, $g^{\prime }\left(x\right)=x^{-3}h\left(x\right)<0$. Therefore, $g\left(x\right)$ increases on $(0,2)$, decreasing on $(2,+\infty )$. It follows that $g{\left(x\right)}_{max}=g\left(2\right)=\frac{7-e^2}{4}$, so $a\ge \frac{7-e^2}{4}$.

2.2.3. Solution 3

When $x\ge 0$, by $f\left(x\right)\ge \frac{1}{2}{x}^3+1$, we obtain $g\left(x\right):=(\frac{1}{2}{x}^3-a{x}^2+x+1)e^{-x}\le 1$. Then, $g^{\prime }\left(x\right)=-(\frac{1}{2}{x}^3-a{x}^2+x+1-\frac{3}{2}{x}^2+2ax-1)e^{-x}=-\frac{1}{2}x\left(x^2-(2a+3)x+4a+2\right)e^{-x}=-\frac{1}{2}x(x-2a-1)(x-2)e^{-x}$. We will discuss in three cases as the following:

If $2a+1\le 0$, then $a\le -\frac{1}{2}$. Then, if $x\in (0,2)$, $g^{\prime }\left(x\right)>0$, $g\left(x\right)$ increases. Further, if $x\in (0,2)$, $g\left(x\right)>g\left(0\right)=1$. It is contradicting with $g\left(x\right)\le 1$.

If $0<2a+1<2$, then $-\frac{1}{2}<a<\frac{1}{2}$. Then, if $x\in (0,2a+1)\cup (2,+\infty )$, $g^{\prime }\left(x\right)<0$, $g\left(x\right)$ decreases on $(0,2a+1)$ and $(2,+\infty )$, and increase on $(2a+1,2)$. Because $g\left(0\right)=1$, $g\left(x\right)\le 1$ if and only if $g\left(2\right)=(7-4a)e^{-2}\le 1$, it follows that $a\ge \frac{7-e^2}{4}>-\frac{1}{2}$. It means that when $\frac{7-4e^2}{4}\le a<\frac{1}{2}$, $g\left(x\right)\le 1$.

If $2a+1\ge 2$, then $a\ge \frac{1}{2}$. For arbitrary $x\ge 0$, we have $g\left(x\right)=(\frac{1}{2}{x}^3-a{x}^2+x+1)e^{-x}$$\le (\frac{1}{2}{x}^3+x+1)e^{-x}$. Because $0\in [\frac{7-e^2}{4},\frac{1}{2}]$; hence, when $a=0$, from the above discussion, we have $(\frac{1}{2}{x}^3+x+1)e^{-x}\le 1$. Hence, when $a\ge \frac{1}{2}$, $g\left(x\right)\le 1$.

Therefore, $a\in [\frac{7-e^2}{4},+\infty )$.

2.2.4. Solution 4

If $x=0$, then $a\in R$.

From $g\left(x\right)=(\frac{1}{2}{x}^3-a{x}^2+x+1)e^{-x}(x>0)$, we have $g^{\prime }\left(x\right)=-\frac{1}{2}x(x-2a-1)(x-2)e^{-x}$. Letting $g^{\prime }\left(x\right)=0$, we have $x=2,2a+1$, $g\left(0\right)=1$, $g(+\infty )=0$, $g\left(2\right)=\frac{7-e^2}{4}$.

If $a>-\frac{1}{2}$, then $h\left(a\right):=g(2a+1)=(2a^2+4a+\frac{5}{2})e^{-2a-1}$, we have $h^{\prime }\left(a\right)=-{(2a+1)}^2{e}^{-2a-1}\le 0$; therefore, $h\left(a\right)$ decreases on $(-\frac{1}{2},+\infty )$, so $h\left(a\right)\le h(-\frac{1}{2})=1$. When $x>0$, we have $g{\left(x\right)}_{max}=max\{g\left(0\right),g(+\infty ),g\left(2\right),1\}=max\{1,\frac{7-e^2}{4},1,0\}=\frac{7-e^2}{4}$.

If $a<-\frac{1}{2}$, then $h\left(a\right):=g(2a+1)=(2a^2+4a+\frac{5}{2})e^{-2a-1}$, we have $h^{\prime }\left(a\right)=-{(2a+1)}^2{e}^{-2a-1}>0$; therefore, $h\left(a\right)$ increases on $(-\infty ,-\frac{1}{2})$, so $h\left(a\right)\le h(-\frac{1}{2})=1$. When $x>0$, we have $g{\left(x\right)}_{max}=max\{1,\frac{7-e^2}{4},1,0\}=\frac{7-e^2}{4}$.

If $a=-\frac{1}{2}$, then $g^{\prime }\left(x\right)=-\frac{1}{2}{x}^2(x-2)e^{-x}$. Letting $g^{\prime }\left(x\right)=0$, we have $x=2$. Furthermore, $g{\left(x\right)}_{max}=g\left(2\right)=\frac{7-e^2}{4}$.

Hence, $a\in [\frac{7-e^2}{4},+\infty )$.

Remark 1.

Solutions 1 and 2 apply the separation parameter method to solve Question (2), and Solutions 3 and 4 apply the classification discussion method. After separating the parameter, it is necessary to discuss the monotonicity of the auxiliary function $g\left(x\right)$, and then calculate the extreme value of $g\left(x\right)$. However, for a complicated function, factorization can be applied first (for example, 2 is a special root of $g^{\prime }\left(x\right)$ in Solution 1, $g^{\prime }\left(x\right)$ can be factorized using $g^{\prime }\left(2\right)=0$). In Solution 2, without factoring $g^{\prime }\left(x\right)$, in contrast, to study $h^{\prime }\left(x\right)$, which increases the times of derivation and computational complexity. It should be noted that the auxiliary function $g\left(x\right)$ is very complicated. To find zeros of $g\left(x\right)$, it is required to first factorize $g\left(x\right)$ using factorization and basic inequalities.

3. Research on Always Holding Inequalities with an Unknown Parameter

3.1. Designing Framework of Math Exam Questions Concerning Always Holding Inequalities with an Parameter

According to the solutions of Question (2), we can propose the following inverse steps.

• Starting from $e^x-\frac{1}{2}{x}^2-x-1\ge 0$, multiplying by $\left(2-x\right)x^{-3}$, then letting $g^{\prime }\left(x\right)=(2-x)(e^x-\frac{1}{2}{x}^2-x-1)x^{-3}$;
• If $0<x<2$, $g^{\prime }\left(x\right)>0$ and if $x>2$, $g^{\prime }\left(x\right)<0$;
• Integrating $g^{\prime }\left(x\right)$, we have $g\left(x\right)=\left(\frac{1}{2}{x}^3+x+1-e^x\right)x^{-2}(x>0)$. It follows that $g\left(x\right)$ increases on $0<x<2$, and decreases on $(2,+\infty )$, therefore, $g{\left(x\right)}_{max}=g\left(2\right)=\frac{7-e^2}{4}$.
• Letting

  $$a\ge \left(\frac{1}{2}{x}^3+x+1-e^x\right)x^{-2},$$

  it follows that $f\left(x\right)\ge \frac{1}{2}{x}^3+1\left(x\ge 0\right)$.

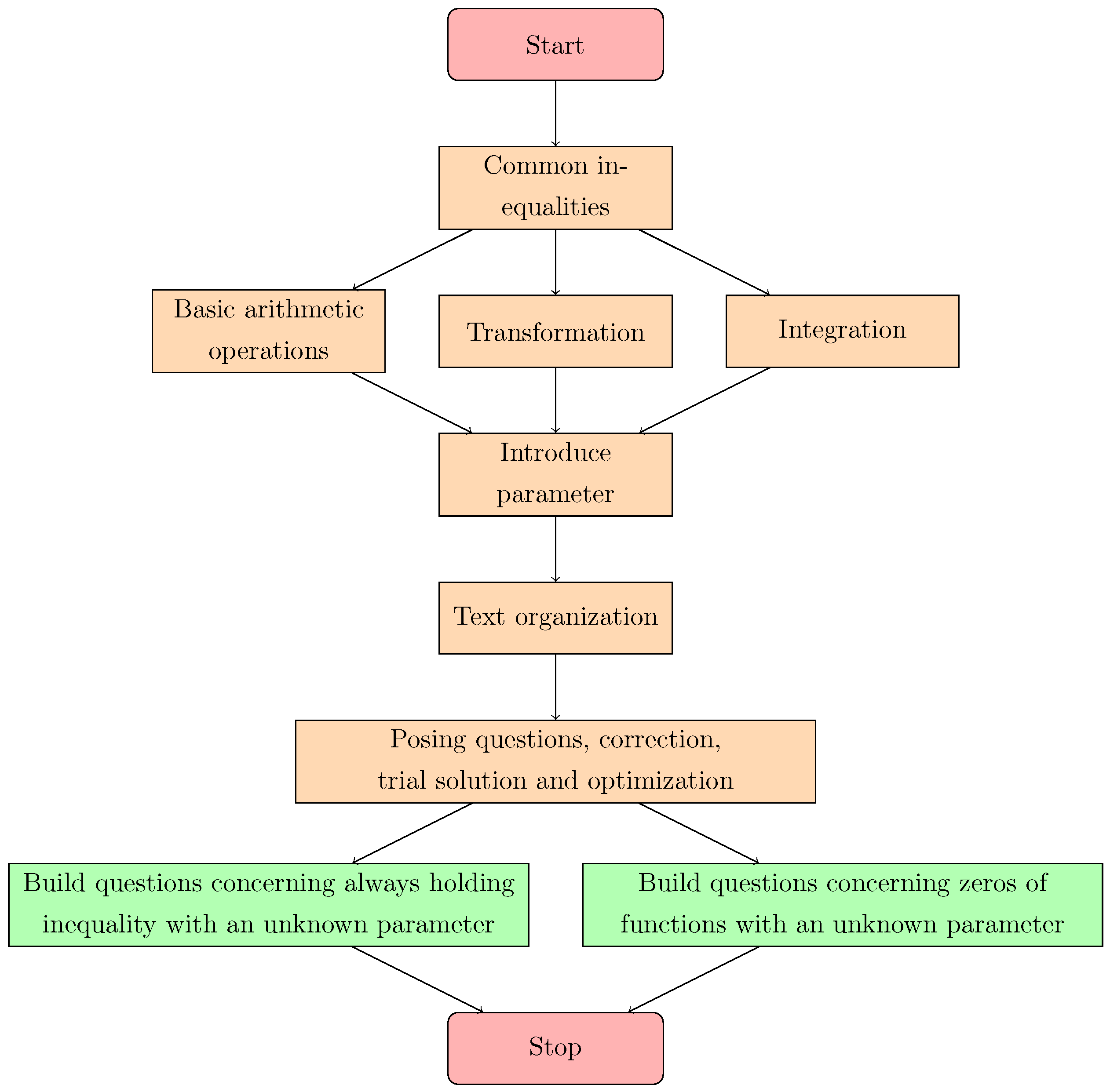
Therefore, starting from a common inequality, by simple transformation, basic arithmetic operations, integration and introducing an unknown parameter, text organization, posing questions, correction, trial solution and optimization, etc., we can build a math exam question of always holding inequalities with an unknown parameter. The design framework is shown in Figure 2.

3.2. Designing a Simulated Math Exam Question Concerning Always Holding Inequalities with an Unknown Parameter

According to the above discussion and Figure 2, we give the following discussion.

Assuming $x\ge e$, then $lnx+x+1>0$, multiplying $(x-4)x^2$, then we have $g^{\prime }\left(x\right):=(x-4)(lnx+x+1)x^{-2}$. Therefore, if $e<x<4$, $g^{\prime }\left(x\right)<0$ and if $x>4$, $g^{\prime }\left(x\right)>0$.

Integrating $g^{\prime }\left(x\right)$, we have $g\left(x\right)=\frac{{\left(lnx\right)}^2}{2}-3lnx+\frac{4lnx}{x}+x+\frac{8}{x}$, so $g\left(x\right)$ decreases on $(e,4)$ and increases on $(4,\infty )$. Therefore, $g{\left(x\right)}_{min}=g\left(4\right)$, $x=4$ is the minimum point of $g\left(x\right)$. Therefore, we build the following inequality:

$$a\le \frac{{\left(lnx\right)}^2}{2}-3lnx+\frac{4lnx}{x}+x+\frac{8}{x}.$$

Changing the terms, we have:

$$\frac{x{\left(lnx\right)}^2}{2}-3xlnx+4lnx+x^2-ax\ge -8.$$

According to the above discussion, we will put forth the following question.

3.3. Simulation Exam Questions 1

Given a function $f\left(x\right)=x^2-ax+4lnx-3xlnx$.

(1)

If $a=3$, investigate the monotonicity of $f\left(x\right)$ on $x\in (0,e)$;

(2)

If $x\ge e$, $f\left(x\right)+8\ge -\frac{1}{2}x{(lnx)}^2$, investigate the range of a.

Solutions:

(1)

If $a=3$, $f\left(x\right)=x^2-3x+4lnx-3xlnx$, $x\in (0,e)$, differential it, we have $f^{\prime }\left(x\right)=2x-3lnx+\frac{4}{x}-6$. Letting $f^{\prime }\left(x\right)=0$, we have $x=1$, and when $0<x<1$, $f^{\prime }\left(x\right)>0$, when $1<x<e$, $f^{\prime }\left(x\right)<0$. Therefore, for $f\left(x\right)$, the increasing interval is $(0,1)$, and the decreasing interval is $(1,e)$.

(2)

If $x\ge e$, $f\left(x\right)+8\ge -\frac{1}{2}x{(lnx)}^2$, then $x^2-ax+4lnx-3xlnx+8+\frac{1}{2}x{(lnx)}^2\ge 2$, then:

$$a\le \frac{{\left(lnx\right)}^2}{2}-3lnx+\frac{4lnx}{x}+x+\frac{8}{x}.$$

If $x>e$, the original problem becomes

$$a\le min\left(\frac{{\left(lnx\right)}^2}{2}-3lnx+\frac{4lnx}{x}+x+\frac{8}{x}\right).$$

Now, letting $g\left(x\right)=\frac{{\left(lnx\right)}^2}{2}-3lnx+\frac{4lnx}{x}+x+\frac{8}{x}(x>e)$. We investigate the minimum value of $g\left(x\right)$. Differential $g\left(x\right)$, then $g^{\prime }\left(x\right)=(x-4)(lnx+x+1)x^{-2}$. Letting $g^{\prime }\left(x\right)=0$, we have $x=4$. Therefore, when $e<x<4$, $g^{\prime }\left(x\right)<0$, and when $x>4$, $g^{\prime }\left(x\right)>0$. Therefore, $g{\left(x\right)}_{min}=g\left(4\right)=\frac{1}{2}{\left(ln4\right)}^2-2ln4+6$. Hence, $a\le \frac{1}{2}{\left(ln4\right)}^2-2ln4+6$.

Remark 2.

The answer to this question can be summarized as follows: separating the parameter, building an auxiliary function, obtaining the minimum of the auxiliary function by using derivative and obtaining the range of the parameter. Therefore, we successfully design a simulated math exam problem of always holding inequalities with an unknown parameter in the CNCEE.

4. Research on Math Exam Questions Concerning Zeros of Functions with an Unknown Parameter

4.1. Designing Framework of Math Exam Questions Concerning Zeros of Functions with an Unknown Parameter

The distribution or numbers of zeros is a bridge between functions, equations and graphs, and plays an important role in the knowledge of elementary functions and derivatives in the CNCEE. The theorem of the existence of zero of the continuous function is often used to solve math exam questions concerning zeros of functions, with the assistance of mathematical thinking such as the symbolic-graphic combination, derivative, transformation and normalization and classification discussion. These questions in the CNCEE mainly examine students’ key mathematical competencies, such as mathematical abstraction, intuitive imagination, mathematical modelling, logical reasoning and mathematical operations. The basic steps of solving this kind of question are: separating the parameter of the given function, using derivatives to obtain the monotonicity of the given function, investigating the extreme value and related properties of the auxiliary function by using symbolic-graphic combination thinking and obtaining the range of the unknown parameter. Although some researchers have obtained related results regarding how to solve math exam questions concerning the zeros of functions with an unknown parameter via different methods [15,16], the design framework is still unknown. Thus, the following case discussion will build the design framework (also see Figure 2).

For any $x\in R$, we have $e^x\ge x+1$. Therefore, $e^{x-1}\ge x$. Integrating it, we have inequality $e^{x-1}\ge \frac{1}{2}{x}^2$. Letting $f\left(x\right)=e^{x-1}-m{x}^2$, where $m=\frac{1}{2}$. After reasonable questions, text arrangement and other procedures, the following questions can be put forward.

4.2. Simulation Exam Questions 2

Given a function $f\left(x\right)=e^{x-1}-m{x}^2$.

(1)

If $m=\frac{1}{2}$, prove that if $x\ge 1$, then $f\left(x\right)\ge \frac{1}{2}$;

(2)

If $m\le \frac{1}{2}$, compute the number of zeros of $f\left(x\right)$.

Solutions:

(1)

If $m=\frac{1}{2}$, we have $f\left(x\right)=e^{x-1}-\frac{1}{2}{x}^2$ and $f^{\prime }\left(x\right)=e^{x-1}-x$. Letting $h\left(x\right)=f^{\prime }\left(x\right)=e^{x-1}-x$, we have $h^{\prime }\left(x\right)=e^{x-1}-1$. Obviously, if $x>1$, $e^{x-1}>0$, $h^{\prime }\left(x\right)>0$, so $h\left(x\right)=f^{\prime }\left(x\right)=e^{x-1}-x$ increases, $h\left(x\right)>h\left(1\right)=0$, then $f^{\prime }\left(x\right)>f^{\prime }\left(1\right)=0$, so $f\left(x\right)$ increases on $x\in [1,+\infty )$, so $f\left(x\right)\ge f\left(1\right)=\frac{1}{2}$.

(2)

If $f\left(x\right)=0$, then $x\ne 0$. According to $f\left(x\right)=e^{x-1}-m{x}^2=0$, we have $m=\frac{e^{x-1}}{x^2}$. Setting an auxiliary function $g\left(x\right)=\frac{e^{x-1}}{x^2}$. Then, $g^{\prime }\left(x\right)=\frac{e^{x-1}\left(x^2-2x\right)}{x^4}=\frac{e^{x-1}(x-2)}{x^3}$. For any arbitrary real number x, we have $g\left(x\right)>0$, and when $x\to \infty$, $g\left(x\right)\to +\infty$. Letting $h\left(x\right)=\frac{x-2}{x^3}$.

If $x<0$, $h\left(x\right)>0$, then $g^{\prime }\left(x\right)>0$. Then $g\left(x\right)$ increases on $x\in (-\infty ,0)$ and if $x\to 0$, $g\left(x\right)\to +\infty$.

If $x\in (0,2)$, $h\left(x\right)<0$, $g^{\prime }\left(x\right)<0$, then $g\left(x\right)$ decreases on $x\in (0,2)$.

If $x\in (2,+\infty )$, $h\left(x\right)>0$, $g^{\prime }\left(x\right)>0$, so $g\left(x\right)$ increases on $x\in (2,+\infty )$.

Therefore, if $x>0$, $g{\left(x\right)}_{min}=g\left(2\right)=\frac{e}{4}>\frac{1}{2}$. Consequently, when $m<0$, the number of zeros of $f\left(x\right)$ equals 0, and when $0<m\le \frac{1}{2}$, the number of $f\left(x\right)$ equals 1 (see Figure 3).

Remark 3.

Question (2) mainly examines mathematical thinking, such as classified discussion and symbolic-graphic combination where the interval $-\infty <x<\infty$ was divided into three parts $(-\infty ,0),(0,2)$ and $(2,+\infty )$. Question (2) can be changed as follows:

Question: When $m\le \frac{e}{4}$, calculate the numbers of $f\left(x\right)$.

While designing an exam problem of the number of zeros of a function, it is necessary to pay attention to the coefficient of the variable when the inequality takes “=”, to design the first subquestion. Then, we replace constants with a parameter, to design the second subquestion. The key to designing an exam question on the number of zeros of a function is to find the critical values for the inequality and replace the critical value with a parameter. If necessary, mathematical software can be used to draw graphics of the function to assist in designing exam questions for the CNCEE.

Remark 4.

We would like to give some useful advice for senior high school students who will participate in the CNCEE, they should be familiar with some useful inequalities, such as $e^x\ge x+1$, $e^x\ge ex$, $lnx\le x-1\left(x>0\right),ln(x+1)\le x\left(x>-1\right)$; the derivation formula, factorization; some basic knowledge of calculus, such as higher-order derivatives, stagnation points, inflection points, convex functions and concave functions; Fermat’s theorem, Rolle’s theorem, Lagrange’s mean value theorem, Taylor’s expansion of functions, etc.

5. Discussion and Future Work

5.1. Disscussion

This study reveals the knowledge and competency goals of the CNCEE mathematics and is consistent with the direction of mathematics education reform around the world. Furthermore, based on the goals of knowledge and competency, this study confirms the characteristics of math exam problems such as multi-solution of one question and general solutions of the same category of questions, which also inspire other countries’ college entrance examinations. The results reveal the different solutions to the selected exam question from the 2020 CNCEE mathematics, propose a creative design framework concerning inequalities and zeros of functions with an unknown parameter and design two new questions. Taken together, these results give a systematic and flexible design framework for mathematics college entrance examinations and are not limited to the CNCEE.

The design framework for questions related to problems of always holding inequalities and zeros of functions with an unknown parameter is constructed based on the recent national exam policies in China and the selected questions from the 2020 CNCEE mathematics. Moreover, the expressions, questions and solutions of the two simulated questions are very similar to the selected questions from the 2020 CNCEE mathematics. Therefore, we hope that our design framework can be used effectively to design math exam questions for the CNCEE.

Clearly, mathematicians, teachers and test experts can read or refer to the creative design framework, and current research has the following characteristics:

• Shows different solutions to the selected exam question from the 2020 CNCEE;
• Proposes a new design framework concerning inequalities and zeros of functions with an unknown parameter;
• Designs two new simulated exam questions/samples;
• Introduces math exam questions of CNCEE to the world;
• Provides a new research direction for mathematics education in China.

Further, the results of this paper help students prepare mathematics for college entrance examinations, improve students’ core literacy and mathematics problem-solving ability and also help teachers better understand the guiding ideology of the standard of the curriculum, and the new college entrance examination evaluation system and obtain more efficient and high-quality high school mathematics teaching. Based on the scheme of the design framework, math teachers in senior high school can design math questions regarding always holding inequalities and zeros of functions with an unknown parameter.

5.2. Future Work

For further research, we would like to put forward the following unsolved problems:

Unsolved Problem. Establish the design framework of math exam questions for the CNCEE (or other college entrance examinations) concerning solid geometry, analytic geometry, trigonometric functions and other types of questions of function and derivatives, such as shifts of extreme point, hidden zeros, existence and inequalities and so on.

6. Conclusions

The paper analyzes the selected math exam question in the 2020 CNCEE mathematics and provides a creative design framework for math exam questions concerning always holding inequalities and zeros of functions with an unknown parameter. The design framework gives detailed steps for designing exam questions in derivatives. The two new simulated questions shown in Section 3.3 and Section 4.2 examine basic mathematical knowledge, such as elementary functions, monotonicity, maximum and minimum values, graphs of functions, derivatives and applications and the existence theorem of zero points. They also examine basic ideas and methods of mathematics, such as the combination of numbers and figures, the classification discussion and the idea of equations, and develop students’ mathematical skills such as mathematical operations, problem-solving, problem-posing, etc. Moreover, the expressions, questions and solutions of the two simulated questions are very similar to the selected question from the 2020 CNCEE mathematics. Therefore, the two new questions are closely consistent with CNCEE and Chinese high school mathematics teaching.

As we know, the standards for general senior high school math curriculum (2017 Edition) require students to learn the concept of function and properties (containing monotonicity, extreme value, parity), basic elementary function (containing power function, exponential function, logarithmic function, trigonometric function) and applications of functions in compulsory senior high school mathematics textbooks to learn the concept of derivative of one variable and limit and be able to calculate the derivatives of basic functions and use derivatives to investigate characteristics of simple compound functions and solve simple applied problems in selective compulsory textbooks [10].

Therefore, the two new simulated math exam questions focus on the basic, comprehensive and innovative characteristics and meet the basic aim and ability requirements of derivatives and their applications in the CNCEE. Accordingly, this study provides a new research direction for mathematics education in China.

The implications of the study for education are as follows: The study provides certain research paths and teaching ideas for innovative teaching of mathematics through an example of mathematical problem solving and problem posing about functions and derivatives. At the same time, the framework emphasizes the knowledge of functions and derivatives in high school and focuses on the basic and related mathematical knowledge and the universal mathematical methods, which is inspiring for the understanding and teaching of related content.

The research literature shows that the comprehensive difficulty and level of complex reasoning of the mathematics questions of the CNCEE are higher than that of the CSAT [2], A-level [4], ACT [5] and the college entrance examinations in France [3]. Since different countries have different secondary education policies, examination policies and admission policies, maths teaching plans and syllabus, our research has certain limitations. However, the CNCEE is very distinctive because it is for the vast majority of high school graduates in China, and there are nearly ten million candidates who take the college entrance examination every year. Therefore, the study of mathematics exam questions in the CNCEE mathematics has important academic value and reference value for teachers, students, parents and researchers in mathematics and mathematics education, and examination research experts. Applying the design framework for math exam questions concerning inequalities and zeros of functions with an unknown parameter in the CNCEE, the difficulty of the two simulated questions designed in this paper will be higher than that in the mentioned college entrance examinations. Therefore, this design framework can undoubtedly be referenced by math examination experts in China and some other countries.