Unified Convergence Analysis of Chebyshev–Halley Methods for Multiple Polynomial Zeros

Abstract

In this paper, we establish two local convergence theorems that provide initial conditions and error estimates to guarantee the Q-convergence of an extended version of Chebyshev–Halley family of iterative methods for multiple polynomial zeros due to Osada (J. Comput. Appl. Math. 2008, 216, 585–599). Our results unify and complement earlier local convergence results about Halley, Chebyshev and Super–Halley methods for multiple polynomial zeros. To the best of our knowledge, the results about the Osada’s method for multiple polynomial zeros are the first of their kind in the literature. Moreover, our unified approach allows us to compare the convergence domains and error estimates of the mentioned famous methods and several new randomly generated methods.

1. Introduction

Undoubtedly, the most popular iteration methods in the literature are the Newton’s method, the Halley’s method [1] and the Chebyshev’s method [2]. A vast historical survey of these illustrious iteration methods can be found in the papers of Ypma [3], Scavo and Thoo [4] and Ezquerro et al. [5]. It is well known that the Newton’s method is quadratically convergent while Halley and Chebyshev’s methods are cubically convergent to simple zeros. However, all these methods converge linearly if the zeros are multiple.

In 1870, Schröder [6] presented the following modification of Newton’s method:

$${\displaystyle x_{k+1}=x_k-m\frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)},}$$

(1)

which restores the quadratic convergence when the multiplicity $m\ge 1$ of the zero is known. Driven by the same reasons, in 1963 Obreshkov [7] developed the following modifications of Halley and Chebyshev’s methods:

$$x_{k+1}=x_k-{\left({\displaystyle \frac{m+1}{2m}\frac{f^{\prime }\left(x_k\right)}{f\left(x_k\right)}-\frac{1}{2}\frac{f^{″}\left(x_k\right)}{f^{\prime }\left(x_k\right)}}\right)}^{-1}$$

(2)

and

$${\displaystyle x_{k+1}=x_k-\frac{m^2}{2}\frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)}\left(\frac{3-m}{m}+\frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)}\frac{f^{″}\left(x_k\right)}{f^{\prime }\left(x_k\right)}\right).}$$

(3)

The methods (2) and (3) are known as Halley’s method for multiple zeros and Chebyshev’s method for multiple zeros, and their convergence order is known to be three if the multiplicity m of the zero is known.

In 1994, Osada [8] defined the following third order modification of the Newton’s method:

$${\displaystyle x_{k+1}=x_k-\frac{f\left(x_k\right)}{2f^{\prime }\left(x_k\right)}\left(m(m+1)-{(m-1)}^2\frac{f^{\prime }{\left(x_k\right)}^2}{f\left(x_k\right)f^{″}\left(x_k\right)}\right)}$$

(4)

known as Osada’s method for multiple zeros. In 2008, he [9] used an arbitrary real parameter to construct an iteration family for multiple zeros that includes as special cases the methods (1)–(4). Another member of the mentioned Osada’s iteration family is Super-Halley method for multiple zeros which can be defined by (see [10] and references therein):

$${\displaystyle x_{k+1}=x_k-\frac{f\left(x_k\right)}{2f^{\prime }\left(x_k\right)}\left(m+\frac{f^{\prime }{\left(x_k\right)}^2}{f^{\prime }{\left(x_k\right)}^2-f\left(x_k\right)f^{″}\left(x_k\right)}\right).}$$

(5)

Let $\alpha \in \mathbb{C}$ and $\delta =1-\alpha$. We define the following extension of the Osada’s iteration family:

$$x_{k+1}=T_{\alpha }\left(x_k\right),$$

(6)

where the iteration function $T_{\alpha }:\mathbb{C}\to \mathbb{C}$ is defined by:

$$T_{\alpha }\left(x\right)=\left\{\begin{array}{cc}{\displaystyle x-\frac{mF\left(x\right)}{2}\frac{3-m-2\alpha (1-m)+m(\delta -\alpha )L\left(x\right)}{1-\alpha (1-m)-m\alpha L\left(x\right)}}\hfill & \mathrm{if}{f}^{\prime }\left(x\right)\ne 0,\hfill \\ x\hfill & \mathrm{if}{f}^{\prime }\left(x\right)=0,\hfill \end{array}\right.$$

(7)

with $F\left(x\right)$ and $L\left(x\right)$ defined as follows:

$$F\left(x\right)=\frac{f\left(x\right)}{f^{\prime }\left(x\right)}\mathrm{and}L\left(x\right)=\frac{f\left(x\right)f^{″}\left(x\right)}{f^{\prime }{\left(x\right)}^2}=F\left(x\right)\frac{f^{″}\left(x\right)}{f^{\prime }\left(x\right)}.$$

(8)

Apparently, the domain of the iteration function (7) is the set:

$$D=\left\{x\in \mathbb{C}:f^{\prime }\left(x\right)\ne 0\Rightarrow 1-\alpha (1-m)-m\alpha L\left(x\right)\ne 0\right\}.$$

(9)

It is easy to see that the iteration (6) includes the Halley’s method (2) for $\alpha =1/2$, the Chebyshev’s method (3) for $\alpha =0$, Super–Halley method (5) for $\alpha =1$ and the Osada’s method (4) for $\alpha =1/(1-m)$ and $m>1$. Hereafter, the iteration (6) shall be called Chebyshev–Halley family for multiple zeros. Note that Chebyshev–Halley family for simple zeros ($m=1$) has been firstly introduced and studied in its explicit form by Hernández and Salanova [11].

In 2009, Proinov [12] established two types of local convergence theorems about the Newton’s method (1) (applied to polynomials) under two different types of initial conditions. In 2015 and 2016, Proinov and Ivanov [13] and Ivanov [14] used the same two types of initial conditions to establish local convergence theorems about the Halley’s method (2) and the Chebyshev’s method (3) for multiple polynomial zeros. Very recently, Ivanov [10] have proved two general theorems (Theorems 3 and 4) that provide sets of initial approximations to ensure the Q-convergence ([15] (Definition 2.1)) of Picard iteration $x_{k+1}=T\left(x_k\right)$ and have applied them to investigate the local convergence of Super–Halley method (5) for multiple polynomial zeros.

In this paper, we use the approach of [10] to investigate the Q-convergence of Chebyshev–Halley family (6). Thus, we obtain two kinds of local convergence theorems (Theorems 1 and 2) that supply the exact bounds of sets of initial approximations accompanied by a priori and a posteriori error estimates that guarantee the Q-convergence of the iteration (6). An assessment of the asymptotic error constant of the family (6) is also established. Our results unify and complement the results of Proinov and Ivanov [13] and Ivanov [10,14] about the methods (2), (3) and (5). On the other hand, the results about the Osada’s method (4) (Corollarys 4 and 5) are the first such results in the literature. At the end of our study, we use Theorem 1 to compare the convergence domains and error estimates of the methods (2)–(5) and several new randomly generated members of (6).

2. Main Results

From now on, $\mathbb{C}\left[x\right]$ shall denote the ring of univariate polynomials over $\mathbb{C}$. Let $f\in \mathbb{C}\left[x\right]$ be a polynomial of degree $n\ge 2$ and $\xi \in \mathbb{C}$ be a zero of f. We define the functions $E:\mathbb{C}\to {\mathbb{R}}_{+}$ and $\mathcal{E}:\mathcal{D}\subset \mathbb{C}\to {\mathbb{R}}_{+}$ by

$$E\left(x\right)=\frac{|x-\xi |}{d}\mathrm{and}\mathcal{E}\left(x\right)=\frac{|x-\xi |}{\rho \left(x\right)},$$

(10)

where d denotes the distance from $\xi$ to the nearest among the other zeros of f and $\rho \left(x\right)$ denotes the distance from x to the nearest zero of f not equal to $\xi$. Note that, if $\xi$ is an unique zero of f, then we set $E\left(x\right)\equiv 0$. Also, we note that the domain of $\mathcal{E}$ is the set,

$$\mathcal{D}=\{x\in \mathbb{C}:\rho (x)>0\}.$$

In this section, we present two local convergence theorems about Chebyshev–Halley family (7) under two different kinds of initial conditions regarding the functions of initial conditions defined by (10).

2.1. Local Convergence Theorem of the First Kind

Furthermore, for the integers n and m ($n\ge m\ge 1$) and the number $\alpha \in \mathbb{C}$, we define the real function ${\varphi }_{\alpha }$ by:

$${\varphi }_{\alpha }\left(t\right)=\frac{(n-m)t^2}{2(m-nt)}\frac{g_{\alpha }\left(t\right)}{h_{\alpha }\left(t\right),}$$

(11)

where the function $g_{\alpha }$ is defined by:

$$g_{\alpha }\left(t\right)=\left\{\begin{array}{cc}2(n-m)\left(\right(n-m\left)\right|\delta |+m|\alpha \left|\right)t+m\left(\right(n-m\left)\right|3\delta -\alpha |+m)(1-t)\hfill & \mathrm{if}\alpha \ne 1/2,\hfill \\ 2n(m-nt)\hfill & \mathrm{if}\alpha =1/2\hfill \end{array}\right.$$

(12)

and the function $h_{\alpha }$ is defined by:

$$h_{\alpha }\left(t\right)=\left\{\begin{array}{cc}m\left|\alpha \right|((2m-n)t^2-2mt+m)-\left|\delta \right|{(m+(n-2m)t)}^2\hfill & \mathrm{if}Re\left(\alpha \right)>1/2,\hfill \\ {\left|\delta \right|(m-nt)}^2-m\left|\alpha \right|(n{t}^2-2mt+m)\hfill & \mathrm{if}Re\left(\alpha \right)\le 1/2\mathrm{and}\alpha \ne 1/2,\hfill \\ 2m(1-t)(m-nt)-n(n-m)t^2\hfill & \mathrm{if}\alpha =1/2,\hfill \end{array}\right.$$

(13)

with $\delta =1-\alpha$. It is worth mentioning that $g_{\alpha }$ is positive and increasing while $h_{\alpha }$ is decreasing on the interval $(0,m/n)$.

The following is our first main theorem of this paper:

Theorem 1.

Let $f\in \mathbb{C}\left[z\right]$ be a polynomial of degree $n\ge 2$ and $\xi \in \mathbb{C}$ be a zero of f with known multiplicity $m\ge 1$. Suppose $x_0\in \mathbb{C}$ is an initial guess satisfying the conditions:

$$E\left(x_0\right)<m/nand{\mathsf{\Phi }}_{\alpha }\left(E\left(x_0\right)\right)>0,$$

(14)

where E is defined by (10) and the function ${\mathsf{\Phi }}_{\alpha }$ is defined by:

$${\mathsf{\Phi }}_{\alpha }\left(t\right)=h_{\alpha }\left(t\right)-\frac{(n-m)t^2}{2(m-nt)}{g}_{\alpha }\left(t\right),$$

with $h_{\alpha }$ and $g_{\alpha }$ defined by (13) and (12). Then the iteration (6) is well defined and convergent Q-cubically to ξ with error estimates for all $k\ge 0$:

$$|x_{k+1}-\xi |\le {\lambda }^{3^k}|x_k-\xi \left|and\right|x_k-\xi |\le {\lambda }^{(3^k-1)/2}|x_0-\xi |,$$

(15)

where $\lambda ={\varphi }_{\alpha }\left(E\left(x_0\right)\right)$ and the function ${\varphi }_{\alpha }$ is defined by (11). Besides, the following estimate of the asymptotic error constant holds:

$$\underset{k\to \infty }{lim\; sup}\frac{|x_{k+1}-\xi |}{|x_k{-\xi |}^3}\le \left\{\begin{array}{cc}{\displaystyle \frac{{(n-m)}^2|3\delta -\alpha |+m(n-m)}{2{\left(md\right)}^2\left|\left|\alpha \right|-\left|\delta \right|\right|}}\hfill & if\alpha \ne 1/2,\hfill \\ {\displaystyle \frac{n(n-m)}{2{\left(md\right)}^2}}\hfill & if\alpha =1/2.\hfill \end{array}\right.$$

In the cases $\alpha =0$, $\alpha =1/2$ and $\alpha =1$, we get the following consequences of Theorem 1 about Chebyshev, Halley and Super-Halley methods, which where proven in [10,13,14], but without the assessment of the asymptotic error constants:

Corollary 1

([14] (Theorem 2)). Let $f\in \mathbb{C}\left[x\right]$ be a polynomial of degree $n\ge 2$ and $\xi \in \mathbb{C}$ be a zero of f with multiplicity $m\ge 1$. Suppose $x_0\in \mathbb{C}$ satisfies the following initial conditions:

$$E\left(x_0\right)<m/nand{\varphi }_0\left(E\left(x_0\right)\right)<1,$$

(16)

where the function $E:\mathbb{C}\to {\mathbb{R}}_{+}$ is defined by (10) and the function ${\varphi }_0$ is defined by:

$${\varphi }_0\left(t\right)=\frac{2{(n-m)}^3{t}^3+m(n-m)(3n-2m)(1-t)t^2}{2{(m-nt)}^3}.$$

Then the Chebyshev’s iteration (3) is well defined and convergent Q-cubically to ξ with error estimates (15), where $\lambda ={\varphi }_0\left(E\left(x_0\right)\right)$, and with the following estimate of the asymptotic error constant:

$$\underset{k\to \infty }{lim\; sup}\frac{|x_{k+1}-\xi |}{|x_k{-\xi |}^3}\le \frac{(n-m)(3n-2m)}{2{\left(md\right)}^2}.$$

Corollary 2

([13] (Theorem 4.5)). Let $f\in \mathbb{C}\left[x\right]$ be a polynomial of degree $n\ge 2$ and $\xi \in \mathbb{C}$ be a zero of f with multiplicity $m\ge 1$. Suppose $x_0\in \mathbb{C}$ satisfies the following initial condition

$$E\left(x_0\right)<R=\frac{2m}{n+m+\sqrt{(n-m)(5n-m)}},$$

(17)

where $E:\mathbb{C}\to {\mathbb{R}}_{+}$ is defined by (10). Then the Halley’s iteration (2) is well defined and convergent Q-cubically to ξ with error estimates (15) where $\lambda ={\varphi }_{1/2}\left(E\left(x_0\right)\right)$ and the function ${\varphi }_{1/2}$ is defined by

$${\varphi }_{1/2}\left(t\right)=\frac{n(n-m)t^2}{2m(1-t)(m-nt)-n(n-m)t^2}.$$

Besides, the following estimate of the asymptotic error constant holds:

$$\underset{k\to \infty }{lim\; sup}\frac{|x_{k+1}-\xi |}{|x_k{-\xi |}^3}\le \frac{n(n-m)}{2{\left(md\right)}^2}.$$

(18)

Corollary 3

([10] (Theorem 3)). Let $f\in \mathbb{C}\left[x\right]$ be a polynomial of degree $n\ge 2$ and $\xi \in \mathbb{C}$ be a zero of f with multiplicity $m\ge 1$. Suppose $x_0\in \mathbb{C}$ satisfies the following initial condition

$$E\left(x_0\right)<\mathcal{R}=\frac{2m}{n+m+\sqrt{3(n-m)(n+m)}},$$

(19)

where $E:\mathbb{C}\to {\mathbb{R}}_{+}$ is defined by (10). Then Super-Halley iteration (5) is well defined and convergent Q-cubically to ξ with error estimates (15), where $\lambda ={\varphi }_1\left(E\left(x_0\right)\right)$ and the function ${\varphi }_1$ is defined by:

$${\varphi }_1\left(t\right)=\frac{(n-m)(n+(n-2m)t)t^2}{2(m-nt)((2m-n)t^2-2mt+m)}.$$

The estimate (18) of the asymptotic error constant holds.

In the case $\alpha =1/(1-m)$ and $m>1$, we get the following consequence of Theorem 1 about the Osada’s method (4):

Corollary 4.

Let $f\in \mathbb{C}\left[x\right]$ be a polynomial of degree $n\ge 2$ and $\xi \in \mathbb{C}$ be a zero of f with multiplicity $m>1$. Suppose $x_0\in \mathbb{C}$ satisfies the following initial conditions:

$$E\left(x_0\right)<\frac{m(m-1)}{m(n-1)+\sqrt{m(n-1)(n-m)}}and{\varphi }_{1/(1-m)}\left(E\left(x_0\right)\right)<1,$$

(20)

where $E:\mathbb{C}\to {\mathbb{R}}_{+}$ is defined by (10) and the function ${\varphi }_{1/(1-m)}$ is defined by:

$${\varphi }_{1/(1-m)}\left(t\right)=\frac{(n-m)t^2}{2(m-nt)}\frac{2(n-m)(n-m+1)t+\left(n\right(3m+1)-2m(m+1\left)\right)(1-t)}{n(n-1)t^2-2m(n-1)t+m(m-1)}.$$

Then the Osada’s iteration (4) is well defined and convergent Q-cubically to ξ with error estimates (15) where $\lambda ={\varphi }_{1/(1-m)}\left(E\left(x_0\right)\right)$. Besides, the following estimate of the asymptotic error constant holds:

$$\underset{k\to \infty }{lim\; sup}\frac{|x_{k+1}-\xi |}{|x_k{-\xi |}^3}\le \frac{(n-m)\left(\right(m+1\left)\right(n-2m)+2nm)}{2{\left(md\right)}^2(m-1)}.$$

2.2. Local Convergence Theorem of the Second Kind

Before stating our second main theorem, for the integers n and m ($n\ge m\ge 1$) and the number $\alpha \in \mathbb{C}$, we define the real function ${\beta }_{\alpha }$ by:

$${\beta }_{\alpha }\left(t\right)=\frac{(n-m)t^2}{2(m-(n-m\left)t\right)}\frac{v_{\alpha }\left(t\right)}{w_{\alpha }\left(t\right)}$$

(21)

where the function $v_{\alpha }$ is defined by:

$$v_{\alpha }\left(t\right)=\left\{\begin{array}{cc}2(n-m)\left((n-m)\right|\delta |+m|\alpha \left|\right)t+m(n-m)|3\delta -\alpha |+m^2\hfill & \mathrm{if}\alpha \ne 1/2,\hfill \\ 2n(m-(n-m\left)t\right)\hfill & \mathrm{if}\alpha =1/2\hfill \end{array}\right.$$

(22)

and the function $w_{\alpha }$ is defined by:

$$w_{\alpha }\left(t\right)=\left\{\begin{array}{cc}m\left|\alpha \right|(m-(n-m)t^2)-\left|\delta \right|{(m+(n-m)t)}^2\hfill & \mathrm{if}Re\left(\alpha \right)>1/2,\hfill \\ {\left|\delta \right|(m-(n-m)t)}^2-m\left|\alpha \right|(m+(n-m)t^2)\hfill & \mathrm{if}Re\left(\alpha \right)\le 1/2\mathrm{and}\alpha \ne 1/2,\hfill \\ 2m(m-(n-m)t)-n(n-m)t^2\hfill & \mathrm{if}\alpha =1/2,\hfill \end{array}\right.$$

(23)

with $\delta =1-\alpha$. Obviously, the function $v_{\alpha }$ is positive and increasing while the function $w_{\alpha }$ is decreasing on the interval $(0,m/(n-m\left)\right)$.

The next theorem is our second main result of this paper.

Theorem 2.

Let $f\in \mathbb{C}\left[z\right]$ be a polynomial of degree $n\ge 2$ and $\xi \in \mathbb{C}$ be a zero of f with known multiplicity $m\ge 1$. Suppose $x_0\in \mathbb{C}$ is an initial guess satisfying the conditions:

$$\mathcal{E}\left(x_0\right)<m/(n-m)and{\mathsf{\Psi }}_{\alpha }\left(\mathcal{E}\left(x_0\right)\right)\ge 0,$$

(24)

where the function $\mathcal{E}$ is defined by (10) and the function $\mathsf{\Psi }$ is defined by

$${\mathsf{\Psi }}_{\alpha }\left(t\right)=1-t-(1+t){\beta }_{\alpha }\left(t\right)$$

(25)

with ${\beta }_{\alpha }$ defined by (21). Then the iteration sequence (6) is well defined and convergent Q-cubically to ξ with error estimates for all $k\ge 0$:

$$|x_{k+1}-\xi |\le \theta {\lambda }^{3^k}|x_k-\xi \left|and\right|x_k-\xi |\le {\theta }^k{\lambda }^{(3^k-1)/2}|x_0-\xi |\mathrm{for}\mathrm{all}k\ge 0,$$

(26)

where $\theta ={\psi }_{\alpha }\left(\mathcal{E}\left(x_0\right)\right)$ and $\lambda ={\beta }_{\alpha }\left(\mathcal{E}\left(x_0\right)\right)/{\psi }_{\alpha }\left(\mathcal{E}\left(x_0\right)\right)$ with ${\psi }_{\alpha }={\mathsf{\Psi }}_{\alpha }+{\beta }_{\alpha }$.

In the cases $\alpha =0$, $\alpha =1/2$ and $\alpha =1$, from Theorem 2 we immediately get [14] (Theorem 3), [13] (Theorem 5.7) and [10] (Theorem 4) about Chebyshev, Halley and Super-Halley methods, respectively. In the case $\alpha =1/(1-m)$ and $m>1$, we get the following consequence of Theorem 2 about the Osada’s method.

Corollary 5.

Let $f\in \mathbb{C}\left[x\right]$ be a polynomial of degree $n\ge 2$ and $\xi \in \mathbb{C}$ be a zero of f with multiplicity $m>1$. Suppose $x_0\in \mathbb{C}$ satisfies the following initial conditions:

$$\mathcal{E}\left(x_0\right)<\frac{m(m-1)}{m(n-m)+\sqrt{m(n-1)(n-m)}}and{\phi }_{1/(1-m)}\left(\mathcal{E}\left(x_0\right)\right)\ge 0,$$

(27)

where $\mathcal{E}$ is defined by (10) and the function ${\phi }_{1/(1-m)}$ is defined by (25) with

$${\beta }_{1/(1-m)}\left(t\right)=\frac{(n-m)t^2}{2(m-(n-m\left)t\right)}\frac{2(n-m)(n-m+1)t+(n-m)(3m+1)+m(m-1)}{(n-m)(n-m-1)t^2-2m(n-m)t+m(m-1)}.$$

Then the Osada’s iteration (4) is well defined and convergent Q-cubically to ξ with error estimates (26).

3. Proof of the Main Results

As mentioned, in 2020 Ivanov [10] proved two general convergence theorems that give exact sets of initial approximations to guarantee the Q-convergence of Picard iteration

$$x_{k+1}=T{x}_k.$$

(28)

In this section, we use this general approach to prove our main results stated in the previous section.

3.1. Preliminaries

To make the paper self-contained, we recall some important results that will be applied in the proofs of the main theorems.

Lemma 1

([10] (Lemma 2)). Let $x,\xi \in \mathbb{C}$ and ${\xi }_1,\dots ,{\xi }_s\in \mathbb{C}$ be all zeros of f different from ξ, then for any $j=1,\dots ,s$ the following inequality holds:

$$|x-{\xi }_j|\ge (1-E\left(x\right))d,$$

(29)

where $E:\mathbb{C}\to {\mathbb{R}}_{+}$ is defined by (10).

Lemma 2

([10] (Lemma 1)). Let K be an arbitrary valued field and $f\in K\left[x\right]$ be a polynomial of degree $n\ge 2$ which splits over K. Let also ${\xi }_1,\dots ,{\xi }_s$ be all distinct zeros of f with multiplicities $m_1,\dots ,m_s$$\left({\sum }_{j=1}^s{m}_j=n\right)$.

(i)

If $x\in K$ is such that$f\left(x\right)\ne 0$, then for all$i=1,\dots ,s$we have

$$\frac{f^{\prime }\left(x\right)}{f\left(x\right)}=\frac{m_i+a_i}{x-{\xi }_i},where{a}_i=(x-{\xi }_i)\sum _{j\ne i}\frac{m_j}{x-{\xi }_j}.$$

(ii)

If$x\in K$is such that$f\left(x\right)\ne 0$and$f^{\prime }\left(x\right)\ne 0$, then for all$i=1,\dots ,s$we have$\frac{f^{\prime \prime }\left(x\right)}{f^{\prime }\left(x\right)}=\frac{{(m_i+a_i)}^2-(m_i+b_i)}{(x-{\xi }_i)(m_i+a_i)},where{a}_{i}isdefinedin\left(\mathrm{i}\right)and{b}_i={(x-{\xi }_i)}^2{\sum }_{j\ne i}\frac{m_j}{{(x-{\xi }_j)}^2}$.

For the proof of our first main result, we apply the next theorem that was proved in [10] without the estimate of the asymptotic error constant which, however, can be easily proven using the inequality in (30) and the concept of quasi-homogeneity of the exact degree of $\varphi$ (see [16] (Definition 8)). Such a proof is performed in [16] (Proposition 3).

Theorem 3

([10] (Theorem 1)). Let $T:D\subset \mathbb{C}\to \mathbb{C}$ be an iterative function, $\xi \in \mathbb{C}$ and $E:\mathbb{C}\to {\mathbb{R}}_{+}$ be defined by (10). Let $\varphi :J\to {\mathbb{R}}_{+}$ be a quasi-homogeneous function of exact degree $p\ge 0$ such that for each $x\in \mathbb{C}$ with $E\left(x\right)\in J$, we have

$$x\in Dand|Tx-\xi |\le \varphi \left(E\right(x\left)\right)|x-\xi |.$$

(30)

If $x_0\in \mathbb{C}$ is an initial approximation such that

$$E\left(x_0\right)\in Jand\varphi \left(E\left(x_0\right)\right)<1,$$

(31)

then Picard iteration (28) is well defined and convergent to ξ with Q-order $r=p+1$ and with error estimates, for all $k\ge 0$:

$$|x_{k+1}-\xi |\le {\lambda }^{r^k}|x_k-\xi \left|and\right|x_k-\xi |\le {\lambda }^{S_k\left(r\right)}|x_0-\xi |.$$

In addition, for all $k\ge 0$ the following error estimate holds:

$$|x_{k+1}{-\xi |\le \left(Rd\right)}^{1-r}{|x_k-\xi |}^r,$$

where R is the minimal solution of $\varphi \left(t\right)=1$ in the interval $J\backslash \left\{0\right\}$. Moreover, we have the following estimate of the asymptotic error constant:

$$\underset{k\to \infty }{lim\; sup}\frac{|x_{k+1}-\xi |}{|x_k{-\xi |}^r}\le \frac{1}{d^p}\underset{t\to 0^{+}}{lim}\frac{\varphi \left(t\right)}{t^p}.$$

The following theorem shall be applied for the proof of our second main result:

Theorem 4

([10] (Theorem 2)). Let $T:D\subset \mathbb{C}\to \mathbb{C}$ be an iterative function, $\xi \in \mathbb{C}$ and $\mathcal{E}:\mathcal{D}\subset \mathbb{C}\to {\mathbb{R}}_{+}$ be defined by (10). Let $\beta :J\to {\mathbb{R}}_{+}$ be a nonzero quasi-homogeneous function of exact degree $p\ge 0$ and for each $x\in \mathbb{C}$ with $\mathcal{E}\left(x\right)\in J$, we have $x\in D$ and $|Tx-\xi |\le \beta \left(\mathcal{E}\right(x\left)\right)|x-\xi |$. If $x_0\in \mathbb{C}$ is an initial guess satisfying

$$\mathcal{E}\left(x_0\right)\in Jand\beta \left(\mathcal{E}\left(x_0\right)\right)\le \psi \left(\mathcal{E}\left(x_0\right)\right),$$

(32)

where the function ψ is defined by

$$\psi \left(t\right)=1-t(1+\beta (t\left)\right),$$

(33)

then Picard iteration (28) is well defined and convergent to ξ with Q-order $r=p+1$ and with the following error estimates:

$$|x_{k+1}-\xi |\le \theta {\lambda }^{r^k}|x_k-\xi \left|and\right|x_k-\xi |\le {\theta }^k{\lambda }^{S_k\left(r\right)}|x_0-\xi |\mathrm{for}\mathrm{all}k\ge 0,$$

(34)

where $\lambda =\varphi \left(\mathcal{E}\left(x_0\right)\right)$ with $\varphi =\beta /\psi$ and $\theta =\psi \left(\mathcal{E}\left(x_0\right)\right)$. Moreover, the following estimate of the asymptotic error constant holds:

$$\underset{k\to \infty }{lim\; sup}\frac{|x_{k+1}-\xi |}{|x_k{-\xi |}^r}\le \frac{1}{d^p}\underset{t\to 0^{+}}{lim}\frac{\beta \left(t\right)}{t^p}.$$

3.2. Proof of Theorem 1

In the next lemma, we prove two inequalities that play a crucial role in the further proofs.

Lemma 3.

Let $f\in \mathbb{C}\left[x\right]$ be a polynomial of degree $n\ge 2$, $\alpha \in \mathbb{C}$ be a parameter and $\xi \in \mathbb{C}$ be a zero of f with known multiplicity $m\ge 1$. Suppose $x\in \mathbb{C}$ is such that:

$$E\left(x\right)<m/n,$$

(35)

where $E:\mathbb{C}\to {\mathbb{R}}_{+}$ is defined by (10). Then there exists a complex number $A_{\alpha }$ such that:

$$|A_{\alpha }|\ge \frac{m\left|\alpha \right|((2m-n)E{\left(x\right)}^2-2mE\left(x\right)+m)-\left|\delta \right|{(m-(2m-n)E\left(x\right))}^2}{{(1-E\left(x\right))}^2}$$

or

$$|A_{\alpha }|\ge \frac{{\left|\delta \right|(m-n)E\left(x\right)}^2-m\left|\alpha \right|(nE{\left(x\right)}^2-2mE\left(x\right)+m)}{{(1-E\left(x\right))}^2},$$

where $\delta =1-\alpha$.

Proof. 

Let $x\in \mathbb{C}$ satisfy (35) and let ${\xi }_1,\dots ,{\xi }_s$ be all distinct zeros of f with respective multiplicities $m_1,\dots ,m_s$. Then by $E\left(x\right)<m/n\le 1$ and Lemma 1, we infer that x is not a zero of f and so we can define the quantities $a_i$ and $b_i$ as in Lemma 2. Without loss of generality, for some $1\le i\le s$ we put $\xi ={\xi }_i,m=m_i,a=a_i$ and $b=b_i$.

Now, we shall prove that the number $A_{\alpha }\in \mathbb{C}$ defined by

$$A_{\alpha }=m\alpha (m+b)+\delta {(m+a)}^2,\mathrm{with}\delta =1-\alpha$$

(36)

satisfies the claims of the lemma.

Using some known technics (see e.g., [14] (Lemma 1) and [10] (Lemma 3)) we reach the following estimates:

$$\begin{array}{ccc}\hfill & & \left|a\right|\le \frac{(n-m)E\left(x\right)}{1-E\left(x\right)},\left|b\right|\le \frac{(n-m)E{\left(x\right)}^2}{{(1-E\left(x\right))}^2},\frac{m-nE\left(x\right)}{1-E\left(x\right)}\le |m+a|\le \frac{m+(n-2m)E\left(x\right)}{1-E\left(x\right)},\hfill \\ & & \frac{(2m-n)E{\left(x\right)}^2-2mE\left(x\right)+m}{{(1-E\left(x\right))}^2}\le |m+b|\le \frac{nE{\left(x\right)}^2-2mE\left(x\right)+m}{{(1-E\left(x\right))}^2}.\hfill \end{array}$$

(37)

If ${m\left|\alpha \right||m+b|>\left|\delta \right||m+a|}^2$, then using the reverse triangle inequality and (37) we obtain

$$|A_{\alpha }|\ge \left|{m\left|\alpha \right||m+b|-\left|\delta \right||m+a|}^2\right|\ge \frac{m\left|\alpha \right|((2m-n)E{\left(x\right)}^2-2mE\left(x\right)+m)}{{(1-E\left(x\right))}^2}-\frac{{\left|\delta \right|(m-(2m-n)E\left(x\right))}^2}{{(1-E\left(x\right))}^2}$$

which proves the first claim. Otherwise, we get

$$|A_{\alpha }|\ge \left|{\left|\delta \right||m+a|}^2-m\left|\alpha \right||m+b|\right|\ge \frac{{\left|\delta \right|(m-nE\left(x\right))}^2}{{(1-E\left(x\right))}^2}-\frac{m\left|\alpha \right|(nE{\left(x\right)}^2-2mE\left(x\right)+m)}{{(1-E\left(x\right))}^2}$$

which proves the second claim and completes the proof of the lemma. □

The following is our main lemma in this section. In its proof, we avoid the case $\alpha =1/2$ since in this case the lemma coincides with Lemma 4.4 of [13] concerning the Halley’s method.

Lemma 4.

Suppose $f\in \mathbb{C}\left[x\right]$ is a polynomial of degree $n\ge 2$, $\alpha \in \mathbb{C}$ is a parameter and $\xi \in \mathbb{C}$ is a zero of f with multiplicity $m\ge 1$. If $x\in \mathbb{C}$ is such that

$$E\left(x\right)<m/nand{h}_{\alpha }\left(E\left(x\right)\right)>0,$$

(38)

where $E:\mathbb{C}\to {\mathbb{R}}_{+}$ is defined by (10) and $h_{\alpha }$ is defined by (13), then

$$x\in Dand|T_{\alpha }\left(x\right)-\xi |\le {\varphi }_{\alpha }\left(E\left(x\right)\right)|x-\xi |,$$

(39)

where D is the set (9) and the real function ${\varphi }_{\alpha }$ is defined by (11).

Proof. 

Let $x\in \mathbb{C}$ satisfy (38). If either $m=n$ or $x=\xi$, then $T_{\alpha }\left(x\right)=\xi$ and so the assertions of the lemma hold. Suppose that $m<n$ and $x\ne \xi$. Let ${\xi }_1,\dots ,{\xi }_s$ be all distinct zeros of f with respective multiplicities $m_1,\dots ,m_s$ and the quantities $a_i$ and $b_i$ be defined as in Lemma 2. Without loss of generality for some $1\le i\le s$ we put $\xi ={\xi }_i,m=m_i,a=a_i$ and $b=b_i$.

First we shall prove that $x\in D$. According to (9) we need to prove that $f^{\prime }\left(x\right)\ne 0$ implies $1-\alpha (1-m)-m\alpha L\left(x\right)\ne 0$. To do this, we shall prove the inequality $|1-\alpha (1-m)-$$m\alpha L\left(x\right)|>0$ which in fact is equivalent to

$${|\delta (m+a)}^2+m\alpha (m+b)|>0.$$

(40)

Indeed, from Lemma 2 (i), (37) and the first condition of (38) we get $|m+a|>0$ which means that $f^{\prime }\left(x\right)\ne 0$ and so by Lemma 2 we have

$$F\left(x\right)=\frac{x-\xi }{m+a}\mathrm{and}L\left(x\right)=F\left(x\right)\frac{f^{″}\left(x\right)}{f^{\prime }\left(x\right)}=1-\frac{m+b}{{(m+a)}^2}$$

(41)

which in turn leads to

$$|1-\alpha (1-m)-m\alpha L\left(x\right)|=\left|\delta +m\alpha \frac{m+b}{{(m+a)}^2}\right|=\frac{{|\delta (m+a)}^2+m\alpha (m+b)|}{{|m+a|}^2}.$$

Now, let us define the number $A_{\alpha }$ by (36). If $Re\left(\alpha \right)>1/2$, then from the second condition of (38) and the estimates (37) we obtain ${m\left|\alpha \right||m+b|>\left|\delta \right||m+a|}^2$. Therefore, by Lemma 3 and the second condition of (38) we get

$${|\delta (m+a)}^2+m\alpha (m+b)|=|A_{\alpha }|\ge \frac{h_{\alpha }\left(E\left(x\right)\right)}{{(1-E\left(x\right))}^2}>0.$$

In the case $Re\left(\alpha \right)\le 1/2$, we get the same conclusion but regarding ${m\left|\alpha \right||m+b|<\left|\delta \right||m+a|}^2$. Consequently, (40) holds and therefore $x\in D$. Further, from (7) and (41) we obtain

$$Tx-\xi =x-\xi -\frac{m(x-\xi )}{2(m+a)}\frac{(3-m+(m-2)\alpha +m\delta ){(m+a)}^2-m(\delta -\alpha )(m+b)}{\delta {(m+a)}^2+m\alpha (m+b)}=\sigma (x-\xi ),$$

where

$${\sigma }_{\alpha }=\frac{[m(3\delta -\alpha )+2\delta a]a^2+m(m+2\alpha a)b}{2(m+a)[\delta {(m+a)}^2+m\alpha (m+b)]}$$

(42)

From this, the triangle inequality, the estimates (37) and the claims of Lemma 3, we obtain

$$|{\sigma }_{\alpha }|\le \frac{{\left(m\right|3\delta -\alpha |+2|\delta \left|\right|a\left|\right)\left|a\right|}^2+m(m+2|\alpha \left|\right|a\left|\right)\left|b\right|}{2|m+a||A_{\alpha }|}\le \frac{(n-m)E{\left(x\right)}^2}{2(m-nE(x\left)\right)}\frac{g_{\alpha }\left(E\left(x\right)\right)}{h_{\alpha }\left(E\left(x\right)\right)}={\varphi }_{\alpha }\left(E\left(x\right)\right),$$

which completes the proof of the lemma. □

Proof 

(Proof of Theorem 1). Let $T_{\alpha }:D\subset \mathbb{C}\to \mathbb{C}$ be Chebyshev–Halley iterative function defined by (7). If $m=n$, then $T_{\alpha }\left(x\right)=\xi$ for all $x\in \mathbb{C}$ and the conclusions of the theorem follow. Suppose $m<n$. From Lemma 4 and Theorem 3 it follows that the conclusions of Theorem 1 follow under the conditions

$$E\left(x_0\right)<m/n,h_{\alpha }\left(E\left(x_0\right)\right)>0\mathrm{and}{\varphi }_{\alpha }\left(E\left(x_0\right)\right)<1.$$

This completes the proof since $h_{\alpha }\left(t\right)>0$ with ${\varphi }_{\alpha }\left(t\right)<1$ is equivalent to ${\mathsf{\Phi }}_{\alpha }\left(t\right)>0$. □

3.3. Proof of Theorem 2

The proof of Theorem 2 is performed the same way as that of Theorem 1. One just have to use the estimate $|x-\xi |\ge \rho \left(x\right)$ instead of (29) to reach the estimates

$$\begin{array}{ccc}& & \left|a\right|\le (n-m)\mathcal{E}\left(x\right),\left|b\right|\le (n-m)\mathcal{E}{\left(x\right)}^2,m-(n-m)\mathcal{E}\left(x\right)\le |m+a|\le m+(n-m)\mathcal{E}\left(x\right),\hfill \\ & & m-(n-m)\mathcal{E}{\left(x\right)}^2\le |m+b|\le m+(n-m)\mathcal{E}{\left(x\right)}^2\hfill \end{array}$$

and then to apply Theorem 4 to Chebyshev–Halley iteration function (6) with ${\beta }_{\alpha }$ defined by (21).

4. Comparative Analysis

In this section, we use Theorem 1 to compare the convergence domains and the error estimates of several particular members of Chebyshev–Halley iteration family (6). Define the function ${\varphi }_{\alpha }$ by (11). It is easy to see that the initial condition (14) can be presented in the form $E\left(x_0\right)<R_{\alpha },$ where $R_{\alpha }$ is the unique solution of the equation ${\varphi }_{\alpha }\left(t\right)=1$ in the interval $(0,m/n)$ (see e.g., Corollarys 2 and 3). Observe that as bigger is $R_{\alpha }$ as larger is the convergence domain of the respective method and better are its error estimates. In order to compare the convergence domains of the Halley’s method (2), the Chebyshev’s method (3), Super-Haley method (5) and the Osada’s method (4) with each other and with some other members of the family (6), in the following figures we depict the functions ${\varphi }_{\alpha }$ obtained for the couples $n=5,m=3$ and $n=10,m=2$ with $\alpha =0$, $\alpha =1/2$, $\alpha =1$, $\alpha =1/(1-m)$ and with four complex numbers $\alpha$ randomly chosen from the rectangle

$$\{z\in \mathbb{C}:|Re\left(z\right)|\le 1.1\mathrm{and}|Im\left(z\right)|\le 0.1\}.$$

Note that these two couples $(n,m)$ have been chosen to highlight the cases $n\le 2m$ and $n>2m$ since we know that (see [10] (Remark 1)) in the second case Corollary 3 provides a larger convergence domain with better error estimates for Super–Halley method than Corollary 2 for the Halley’s method and vice versa in the first case.

One can see from the graphs (Figure 1, Figure 2, Figure 3 and Figure 4) that in all considered cases except the first one (Figure 1), the randomly chosen method has a larger convergence domain and better error estimates than the Osada’s method. In the second case (Figure 2), the random method is better than the Chebyshev’s method while in the last case (Figure 4) the random method is better even than the Halley’s method.

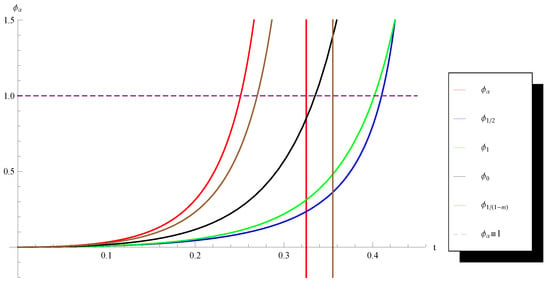
Figure 1. Graph of the functions ${\varphi }_0$, ${\varphi }_{1/2}$, ${\varphi }_1$, ${\varphi }_{1/(1-m)}$ and ${\varphi }_{\alpha }$ for $n=5$, $m=3$ and $\alpha =0.285+0.006i$.

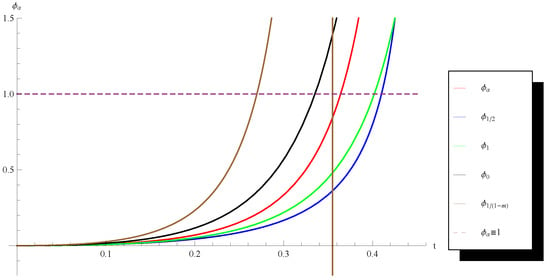
Figure 2. Graph of the functions ${\varphi }_0$, ${\varphi }_{1/2}$, ${\varphi }_1$, ${\varphi }_{1/(1-m)}$ and ${\varphi }_{\alpha }$ for $n=5$, $m=3$ and $\alpha =0.874-0.097i$.

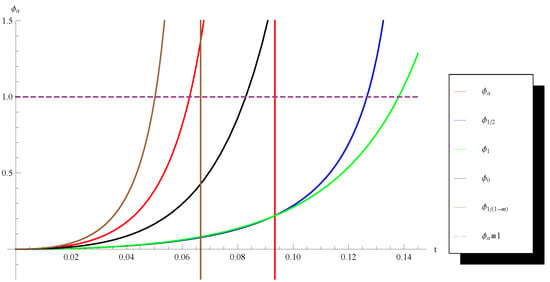
Figure 3. Graph of the functions ${\varphi }_0$, ${\varphi }_{1/2}$, ${\varphi }_1$, ${\varphi }_{1/(1-m)}$ and ${\varphi }_{\alpha }$ for $n=10$, $m=2$ and $\alpha =-0.487-0.083i$.

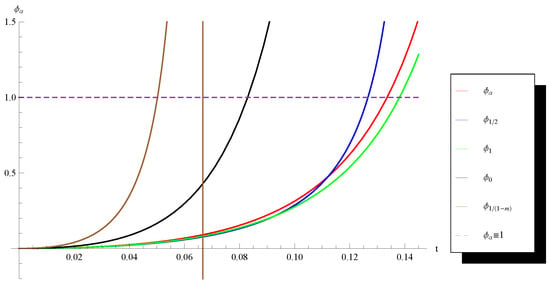
Figure 4. Graph of the functions ${\varphi }_0$, ${\varphi }_{1/2}$, ${\varphi }_1$, ${\varphi }_{1/(1-m)}$ and ${\varphi }_{\alpha }$ for $n=10$, $m=2$ and $\alpha =1.016+0.030i$.

5. Conclusions

Two kinds of convergence theorems (Theorems 1 and 2) that ensure exact sets of initial conditions, a priori and a posteriori error estimates right from the first step and assessments of the asymptotic error constant of Chebyshev–Halley iteration family (6) for multiple polynomial zeros have been proven in this paper. This results unify and complement the existing results about the known Halley, Chebyshev and Super-Haley methods for multiple polynomial zeros. The obtained theorems about Osada’s method (4) are new even in the case of simple zeros. Finally, this unifying study allowed us to compare the mentioned famous iteration methods with some new randomly generated ones. This comparison showed that our results assure larger convergence domains and better error estimates for Halley’s method (2) when $n\le 2m$ and for the Super-Haley method (5) when $n>2m$. However, in the second case, there exist many methods that are better than Halley’s method.