Abstract
This article focuses on the study of redial displacement, the carrier density, the conductive and thermodynamic temperatures and the stresses in a semiconductor medium with a spherical hole. This study deals with photo-thermoelastic interactions in a semiconductor material containing a spherical cavity. The new hyperbolic theory of two temperatures with one-time delay is used. The internal surface of the cavity is constrained and the density of carriers is photogenerated by a heat flux at the exponentially decreasing pulse boundaries. The analytical solutions by the eigenvalues approach under the Laplace transformation approaches are used to obtain the solution of the problem and the inversion of the Laplace transformations is performed numerically. Numerical results for semiconductor materials are presented graphically and discussed to show the variations of physical quantities under the present model.
1. Introduction
The thermoelastic theory, which is the most common engineered structural material, plays an important role in steel stresses analysis and applied mechanical sciences [1,2]. It can depict the solid mechanical behaviors of some popular elastic materials such as wood, concrete and coal. However, it cannot depict the mechanical behavior of many polymers and elastomer types of synthetic materials such as polyethylene. The temperature increment of the body is not only caused by internal and external heating source, but also by deformations of itself processed during the microinertia of the microelement.
In recent decades, thermoelastic theories have been developed by many authors. Biot [3] has studied the coupling thermoelasticity model (CD model) when Fourier’s law of thermal conduction suggested that it became convenient for modernistic engineering applications, especially in cases of high temperatures. Lord et al. [4] (LS) have presented a new model with one thermal relaxation time in the thermal conductivity relation (Fourier’s law of heating conductivity) to overcome these contradictions. The thermoelastic theories with the classic two temperatures are discussed by Williams and Gurtin [5] Chen and Gurtin [6] and Chen et al. [7] by using another depending on the classic two temperatures (the conductive temperature * and the thermodynamic temperature T*). Newly, Youssef et al. [8] have studied a new theory in generalized thermoelastic theories by the hyperbolic two-temperature model.
Taye et al. [9] have studied the hyperbolic two-temperature semiconductor thermoelastic wave caused by laser pulses. Saeed and Abbas [10] studied the hyperbolic two-temperature photothermal interaction in semiconducting mediums. Al-Lehaibi [11] studied the diagonalizations approach to hyperbolic two-temperature thermoelastic solid spheres under mechanical damage effects. Abbas et al. [12] discussed the hyperbolic two-temperature photothermal interactions in semiconducting materials with cylindrical holes. Ali et al. [13] have discussed the reflections of waves in a rotating semiconductor nano-structure material during torsion-free boundary conditions. Lotfy et al. [14] have investigated the response of Thomson and the magnetic impact of semiconductor material due to laser pulses under photo-thermoelastic theory. Hobiny and Abbas [15] have studied the photothermal interactions in a two-dimensional semiconductor plane under the GN model. Lotfy et al. [16] have discussed the variable thermal conductive effect of a semiconductor medium with cavities under the fractional-order magneto-photothermoelastic theory. Alzahrani and Abbas [17] have investigated the photothermal and elastic interactions in a semiconductor plane under Green and Naghdi type ii (GNii) dissipations. Lotfy et al. [18] have discussed the Thomson and electromagnetic effects under the photothermal model of rotator semiconductor materials. Yasein [19] has discussed the influences of variable heat conduction of semiconductor mediums under photothermal model. Abbas and Hobiny [20] have applied the finite difference scheme to investigate the photothermal interaction in a semiconductor medium. Youssef and El-Bary [21] have discussed the characterizations of the photothermal interaction of a semiconducting solid sphere caused by the fractional deformations, the thermal delay times and various references temperature under Lord and Shoulman’s theory. Lotfy et al. [22] have investigated the photothermal excitations process with the hyperbolic two-temperature model for magneto–thermoelastic semiconductor materials. Alshehri and Lotfy [23] studied the memory-dependent derivative (MDD) for magneto–thermo–plasma semiconductor mediums due to laser pulses with a hyperbolic two-temperature model. Kaur and Singh [24] investigated the plane waves in nonlocal semiconductor rotating mediums with hall effects and fractional three-phase lag. Hobiny and Abbas [25] have discussed the photothermal waves in unbounded semiconductor mediums containing cylindrical holes. Youssef and El-Bary [26] have studied the effects of the photothermal interactions under Lord-Shulman model on a visco-thermoelastic semiconducting solid cylinder caused by rotational movement. Saeed et al. have studied the thermoelastic with the photogenerated model of rotating micro stretch semiconductor material under the effect of initial stress. Mahdy et al. [27] have investigated the variable thermal conductivity during photo-thermoelastic models of semiconductor material under a hyperbolic two-temperature model induced by laser pulses. Many authors [28,29,30,31,32,33,34,35,36,37,38,39,40] used the numerical and analytical approaches to solve several problems of thermal and elastic waves.
This paper is devoted to an investigation of the analytical solution of photothermal interaction in semiconductor mediums with a spherical hole under the new hyperbolic of two-temperatures thermoelasticity. The effects of the two-temperature parameter on the redial displacement, the conductive and the thermodynamic temperatures, the stresses and the carrier density distributions have been depicted graphically. This work supposes a new consideration of the two types of temperature which depend on the acceleration of the conductor and the thermal temperature. Taking into account the photo-thermoelastic model coupled with the thermal and conductive temperatures is a significant phenomenon and has great effects on the distributions of the quantities of field.
2. Basic Equations
In this article, theoretical dissuasions during the heating transport process when the internal structures of the semiconductor are taken into consideration. The interactions between the elastic and thermal waves of the plasma are generated under two temperatures (both hyperbolic temperatures). The governing equations under the photothermal model with the hyperbolic two temperatures in semiconductor medium can be given by [8,41,42]:
The motion equations:
The coupling between thermoelastic and plasma wave are expressed by
The heat conduction equation
The new hyperbolic of two-temperature relation
The stress–strain relations can be given by
Let us consider a homogeneous and isotropic unbounded semiconducting medium containing a spherical hole, whose states are presented in terms of the time and the space variable which occupies the region as in Figure 1. Only the redial displacement is nonvanishing due to symmetry, hence the Equations (1)–(5) can be rewritten by:
with
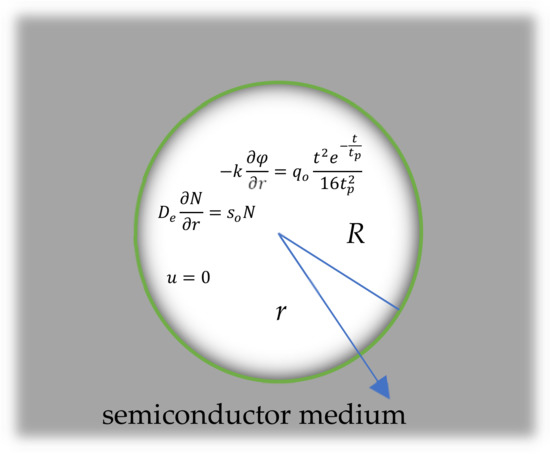
Figure 1.
The sketch of a semiconductor medium with a spherical cavity.
3. Initial and Boundary Conditions
The initial conditions are assumed to be homogeneous. The bounding internal surface of the cavity have the boundary conditions as
To obtain main fields in nondimensional forms, the nondimensional parameters are taken
where and .
Using the Equation (15) for the main basic formulations (neglecting the superscript ), yields:
where , , , , , , .
4. Laplace Transform
For function, the Laplace transforms can be defined as
Hence, the governing equations can be rewritten by
Differentiating Equations (24)–(26) with respect to and using Equation (27), yields:
where
Now, it is possible to obtain the solution of the Equations (31)–(33) by the eigenvalues approaches as in [43,44,45,46,47]. The vectors matrix of Equations (31)–(33) can be given by
where , and .
The characteristic formulation of matrix is defined by
The three roots of Equation (35) are the eigenvalue of matrix , which is presented by . Thus, the corresponding eigenvector is determined by:
The solutions of Equation (34) which are bounded as are expressed as
where is the modified of Bessel’s function of order and , and are constants that can be computed by using the boundary conditions of the problem. Thus, the variables solutions along and can be expressed by
Finally, Stehfest’s [48] numerical inversion approach was used as in [49] to obtain the numerical inversions of the physical quantities.
5. Numerical Result and Discussion
To theoretically study the results obtained, the physical constants and the physical properties of silicon as an elastic semiconductor material are used. The constants of silicon (Si) are used to perform the numerical simulations and discuss the calculation results; the constants of Si can be given by [50]:
Based on the above set of parameters, the calculations of physical quantities along the redial distance for the new hyperbolic two-temperature theory and the classical two-temperature theory are introduced in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7. The numerical computations are carried out when using the above set of constants of the field distributions as (thermal waves (thermodynamical temperature distributions), the redial displacement distribution (strain wave), the redial and hoop stress which depict the mechanical waves distributions and the carrier density distributions (plasma waves). Figure 2 explains the variations in carrier density along the radial distance . It is clear that it starts with its maximum values at the internal surface of cavity then it progressively decreases with the rise in until it reaches zero. Figure 3 shows the thermodynamic temperature variation along . It is seen that the thermodynamic temperature begins from the maximum values at the internal surface of cavity and reduces with the rise in the redial distance until it reaches zero value. Figure 4 displays the conductive temperature variation via the redial distance . It is noticed that it has ultimate values at the inner surface of the spherical hole ; after that it decreases gradually with the rise in to reach zero. Figure 5 displays the variation in radial displacement via the redial distance . It is seen that the radial displacement starts from zero values, which accept the boundary conditions, then the radial displacement progressively increases up to peak values and then decreases again to reach zero. Figure 6 shows the variation in radial stress with respect to the radial distance . The curves start from negative values and then the magnitude increases with the increase in redial distance up to peak values which near the cavity surface and then decrease again to reach zero. Figure 7 displays the variations in hoop stress along the redial distance . It is clear that the magnitudes of hoop stress begin from the maximum values at the inner surface of the spherical cavity decreases rapidly after that as rises to reach a value of zero. Finally, in comparisons between the results, one can conclude that the using new hyperbolic two-temperature photo-thermoelastic model has an important influence on the field quantities distributions. According to the numerical results, this new theory of photo-thermoelasticity offers finite speeds of propagation of photo-thermoelastic and mechanical waves.
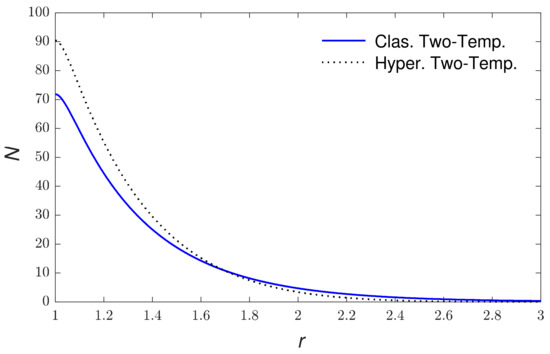
Figure 2.
The carrier density variations versus the redial distance.
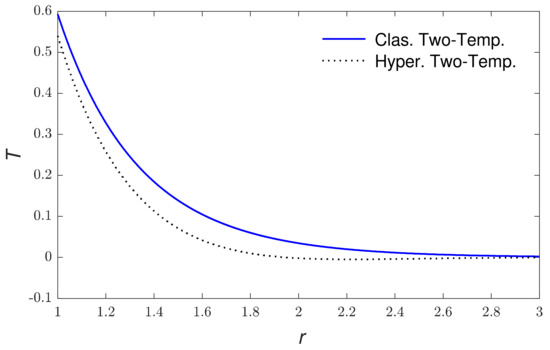
Figure 3.
The thermodynamic temperature variations along the redial distance.
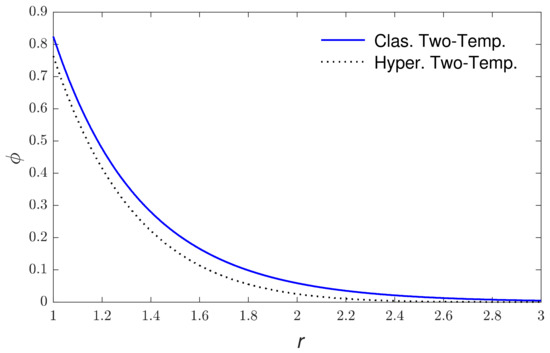
Figure 4.
The conductive temperature variations versus the redial distance.
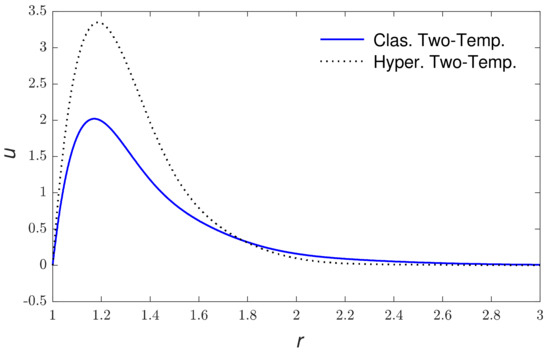
Figure 5.
The displacement variations versus the redial distance.
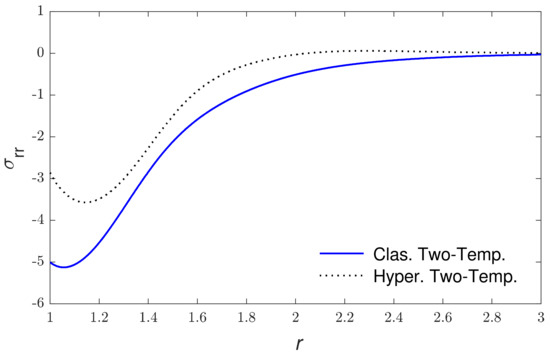
Figure 6.
The radial stress variations versus the redial distance.
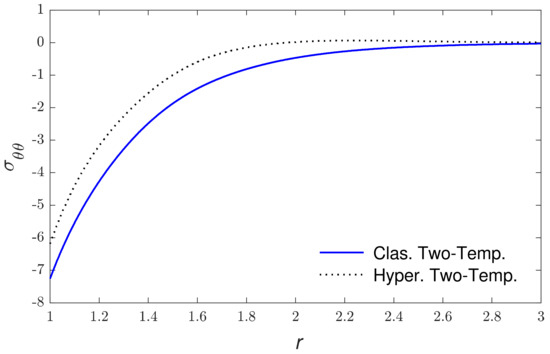
Figure 7.
The hoop stress variations versus the redial distance.
6. Conclusions
In this work, the coupling of the thermoelastic and plasma waves in semiconductor materials have been studied under hyperbolic two-temperature theory. The analytical expressions for the temperatures, the carrier density, the displacement and the stress in the materials are presented. By the study of the results and the comparison, one can conclude that considering the photothermal theory coupled with the thermal and conductive temperatures is an important phenomenon and has great effects on the distributions of the quantities of field. As stated by the numerical results, the new model of photothermoelasticity offers a finite velocity of propagation of photo-thermoelastic and mechanical waves.
Author Contributions
Conceptualization: A.H., I.A. and M.M.; methodology: I.A. and M.M.; validation: I.A. and M.M.; formal analysis: A.H., I.A. and M.M.; investigation: A.H. and I.A.; resources: I.A.; data curation: A.H., I.A. and M.M.; writing—original draft preparation: A.H., I.A. and M.M.; writing—review and editing: A.H.; visualization: I.A. and M.M.; supervision: A.H., I.A. and M.M.; project administration: I.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was founded by institutional Found Projects under grant no. (IFPIP: 502-130-1442). Therefore, authors gratefully acknowledge technical and financial support from the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This research work was founded by institutional Found Projects under grant no. (IFPIP: 502-130-1442). Therefore, authors gratefully acknowledge technical and financial support from the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| the time, | |
| the reference temperature, | |
| , | the temperature variation, |
| the displacement components, | |
| the material density, | |
| the coupling parameter of thermal activation, | |
| the specific heating at constant strain, | |
| , | the coefficient of electronic deformation, |
| the lifetime of photogenerated carrier, | |
| the linear thermal expansion coefficient, | |
| , | the carrier concentration at equilibrium, |
| the stress components, | |
| the thermal conductivity, | |
| the Lame’s constants, | |
| the coefficient of carrier diffusions, | |
| the thermal relaxation time, | |
| constant, | |
| the characteristic time of pulsing heat flux, | |
| the recombination speed on the surface, | |
| the internal redial of cavity, | |
| the parameter of two-temperature model, |
References
- Figueiredo, M.; Marseglia, G.; Moita, A.S.; Panão, M.R.; Ribeiro, A.P.; Medaglia, C.M.; Moreira, A.L. Thermofluid characterization of nanofluid spray cooling combining phase Doppler Interferometry with high-speed visualization and time-resolved IR thermography. Energies 2020, 13, 5864. [Google Scholar] [CrossRef]
- Sanches, M.; Marseglia, G.; Ribeiro, A.P.; Moreira, A.L.; Moita, A.S. Nanofluids Characterization for Spray Cooling Applications. Symmetry 2021, 13, 788. [Google Scholar] [CrossRef]
- Biot, M.A. Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Lord, H.W.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Williams, W.O. An axiomatic foundation for continuum thermodynamics. Arch. Ration. Mech. Anal. 1967, 26, 83–117. [Google Scholar] [CrossRef]
- Chen, P.J.; Gurtin, M.E. On a theory of heat conduction involving two temperatures. Z. Angew. Math. Phys. ZAMP 1968, 19, 614–627. [Google Scholar] [CrossRef]
- Chen, P.J.; Gurtin, M.E.; Williams, W.O. On the thermodynamics of non-simple elastic materials with two temperatures. Z. Angew. Math. Phys. ZAMP 1969, 20, 107–112. [Google Scholar] [CrossRef]
- Youssef, H.M.; El-Bary, A.A. Theory of hyperbolic two-temperature generalized thermoelasticity. Mater. Phys. Mech. 2018, 40, 158–171. [Google Scholar]
- Taye, I.M.; Lotfy, K.; El-Bary, A.; Alebraheem, J.; Asad, S. The hyperbolic two-temperature semiconducting thermoelastic waves by laser pulses. CMC-Comput. Mater. Contin. 2021, 67, 3601–3618. [Google Scholar] [CrossRef]
- Saeed, T.; Abbas, I. A hyperbolic two-temperature photo-thermal interactions in a semiconductor material. Indian J. Phys. 2020, 95, 2057–2062. [Google Scholar] [CrossRef]
- Al-Lehaibi, E.A. Diagonalization Method to Hyperbolic Two-Temperature Generalized Thermoelastic Solid Sphere under Mechanical Damage Effect. Crystals 2021, 11, 1014. [Google Scholar] [CrossRef]
- Abbas, I.; Saeed, T.; Alhothuali, M. Hyperbolic two-temperature photo-thermal interaction in a semiconductor medium with a cylindrical cavity. Silicon 2020, 13, 1871–1878. [Google Scholar] [CrossRef]
- Ali, H.; Jahangir, A.; Khan, A. Reflection of waves in a rotating semiconductor nanostructure medium through torsion-free boundary condition. Indian J. Phys. 2020, 94, 2051–2059. [Google Scholar] [CrossRef]
- Lotfy, K.; Hassan, W.; El-Bary, A.; Kadry, M.A. Response of electromagnetic and Thomson effect of semiconductor medium due to laser pulses and thermal memories during photothermal excitation. Results Phys. 2020, 16, 102877. [Google Scholar] [CrossRef]
- Hobiny, A.; Abbas, I. A GN model on photothermal interactions in a two-dimensions semiconductor half space. Results Phys. 2019, 15, 102588. [Google Scholar] [CrossRef]
- Lotfy, K.; El-Bary, A.; Tantawi, R. Effects of variable thermal conductivity of a small semiconductor cavity through the fractional order heat-magneto-photothermal theory. Eur. Phys. J. Plus 2019, 134, 280. [Google Scholar] [CrossRef]
- Alzahrani, F.S.; Abbas, I.A. Photo-thermo-elastic interactions without energy dissipation in a semiconductor half-space. Results Phys. 2019, 15, 102805. [Google Scholar] [CrossRef]
- Lotfy, K.; El-Bary, A.; Hassan, W.; Alharbi, A.; Almatrafi, M. Electromagnetic and Thomson effects during photothermal transport process of a rotator semiconductor medium under hydrostatic initial stress. Results Phys. 2020, 16, 102983. [Google Scholar] [CrossRef]
- Yasein, M.d.; Mabrouk, N.; Lotfy, K.; EL-Bary, A. The influence of variable thermal conductivity of semiconductor elastic medium during photothermal excitation subjected to thermal ramp type. Results Phys. 2019, 15, 102766. [Google Scholar] [CrossRef]
- Abbas, I.; Hobiny, A.D. Analytical-numerical solutions of photo-thermal interactions in semiconductor materials. Inf. Sci. Lett. 2021, 10, 189–196. [Google Scholar]
- Youssef, H.M.; El-Bary, A.A. Characterization of the Photothermal Interaction of a Semiconducting Solid Sphere Due to the Fractional Deformation, Relaxation Time, and Various Reference Temperature under L-S Theory. Silicon 2021, 13, 2103–2114. [Google Scholar] [CrossRef]
- Lotfy, K.; Elidy, E.S.; Tantawi, R.S. Photothermal Excitation Process during Hyperbolic Two-Temperature Theory for Magneto-Thermo-Elastic Semiconducting Medium. Silicon 2021, 13, 2275–2288. [Google Scholar] [CrossRef]
- Alshehri, H.M.; Lotfy, K. Memory-Dependent-Derivatives (MDD) for magneto-thermal-plasma semiconductor medium induced by laser pulses with hyperbolic two temperature theory. Alex. Eng. J. 2022, 61, 2396–2406. [Google Scholar] [CrossRef]
- Kaur, I.; Singh, K. Plane wave in non-local semiconducting rotating media with Hall effect and three-phase lag fractional order heat transfer. Int. J. Mech. Mater. Eng. 2021, 16, 1–16. [Google Scholar] [CrossRef]
- Hobiny, A.D.; Abbas, I.A. A study on photothermal waves in an unbounded semiconductor medium with cylindrical cavity. Mech. Time-Depend. Mater. 2017, 21, 61–72. [Google Scholar] [CrossRef]
- Youssef, H.M.; El-Bary, A.A. Influence of the Photothermal Interaction under Lord-Shulman Model on a Viscothermoelastic Semiconducting Solid Cylinder Due to Rotational Movement. Nov. Perspect. Eng. Res. 2021, 3, 119–140. [Google Scholar]
- Mahdy, A.; Lotfy, K.; El-Bary, A.; Roshdy, E.; Abd El-Raouf, M. Variable thermal conductivity during photo-thermoelasticy theory of semiconductor medium induced by laser pulses with hyperbolic two-temperature theory. Waves Random Complex. Media 2021, 1–23. [Google Scholar] [CrossRef]
- Bera, M.B.; Das, N.C.; Lahiri, A. Eigenvalue approach to two-temperature generalized thermoelastic interactions in an annular disk. J. Therm. Stresses 2015, 38, 1310–1324. [Google Scholar] [CrossRef]
- Santra, S.; Lahiri, A.; Das, N.C. Eigenvalue approach on thermoelastic interactions in an infinite elastic solid with voids. J. Therm. Stresses 2014, 37, 440–454. [Google Scholar] [CrossRef]
- Lata, P.; Kaur, I. Effect of hall current in Transversely Isotropic magneto thermoelastic rotating medium with fractional order heat transfer due to normal force. Adv. Mater. Res. 2018, 7, 203–220. [Google Scholar]
- Sarkar, N.; Mondal, S. Two-dimensional problem of two-temperature generalized thermoelasticity using memory-dependent heat transfer: An integral transform approach. Indian J. Phys. 2020, 94, 1965–1974. [Google Scholar] [CrossRef]
- Sur, A.; Mondal, S. The Caputo-Fabrizio heat transport law in vibration analysis of a microscale beam induced by laser. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. 2021, 101, e202000215. [Google Scholar] [CrossRef]
- Sarkar, N.; Mondal, S. Thermoelastic plane waves under the modified Green–Lindsay model with two-temperature formulation. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. 2020, 100, e201900267. [Google Scholar] [CrossRef]
- Bassiouny, E. Mathematical Model for Hyperbolic Two Temperature Fractional-Order Thermoelastic Materials Subjected to Thermal Loading. Appl. Math. Inf. Sci. 2021, 15, 23–29. [Google Scholar]
- Abbas, I.A.; Marin, M. Analytical Solutions of a Two-Dimensional Generalized Thermoelastic Diffusions Problem Due to Laser Pulse. Iran. J. Sci. Technol.-Trans. Mech. Eng. 2018, 42, 57–71. [Google Scholar] [CrossRef]
- Hobiny, A.; Alzahrani, F.; Abbas, I.; Marin, M. The effect of fractional time derivative of bioheat model in skin tissue induced to laser irradiation. Symmetry 2020, 12, 602. [Google Scholar] [CrossRef]
- Marin, M. Some estimates on vibrations in thermoelasticity of dipolar bodies. JVC/J. Vib. Control. 2010, 16, 33–47. [Google Scholar] [CrossRef]
- Marin, M. A domain of influence theorem for microstretch elastic materials. Nonlinear Anal. Real World Appl. 2010, 11, 3446–3452. [Google Scholar] [CrossRef]
- Marin, M. A temporally evolutionary equation in elasticity of micropolar bodies with voids. UPB Sci. Bull. Ser. A Appl. Math. Phys. 1998, 60, 3–12. [Google Scholar]
- Marin, M.; Othman, M.I.A.; Seadawy, A.R.; Carstea, C. A domain of influence in the Moore–Gibson–Thompson theory of dipolar bodies. J. Taibah Univ. Sci. 2020, 14, 653–660. [Google Scholar] [CrossRef]
- Song, Y.; Bai, J.; Ren, Z. Study on the reflection of photothermal waves in a semiconducting medium under generalized thermoelastic theory. Acta Mech. 2012, 223, 1545–1557. [Google Scholar] [CrossRef]
- Mandelis, A.; Nestoros, M.; Christofides, C. Thermoelectronic-wave coupling in laser photothermal theory of semiconductors at elevated temperatures. Opt. Eng. 1997, 36, 459–468. [Google Scholar] [CrossRef]
- Das, N.C.; Lahiri, A.; Giri, R.R. Eigenvalue approach to generalized thermoelasticity. Indian J. Pure Appl. Math. 1997, 28, 1573–1594. [Google Scholar]
- Abbas, I.A. Eigenvalue approach in a three-dimensional generalized thermoelastic interactions with temperature-dependent material properties. Comput. Math. Appl. 2014, 68, 2036–2056. [Google Scholar] [CrossRef]
- Abbas, I.A. Eigenvalue approach for an unbounded medium with a spherical cavity based upon two-temperature generalized thermoelastic theory. J. Mech. Sci. Technol. 2014, 28, 4193–4198. [Google Scholar] [CrossRef]
- Abbas, I.A. The effects of relaxation times and a moving heat source on a two-temperature generalized thermoelastic thin slim strip. Can. J. Phys. 2015, 93, 585–590. [Google Scholar] [CrossRef]
- Lahiri, A.; Das, B.; Sarkar, S. Eigenvalue approach to thermoelastic interactions in an unbounded body with a spherical cavity. In Proceedings of the World Congress on Engineering, London, UK, 30 June–2 July 2010. [Google Scholar]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms [D5]. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Alzahrani, F.S.; Abbas, I.A. Photo-thermal interactions in a semiconducting media with a spherical cavity under hyperbolic two-temperature model. Mathematics 2020, 8, 585. [Google Scholar] [CrossRef] [Green Version]
- Song, Y.; Todorovic, D.M.; Cretin, B.; Vairac, P.; Xu, J.; Bai, J. Bending of Semiconducting Cantilevers Under Photothermal Excitation. Int. J. Thermophys. 2014, 35, 305–319. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).