Knowledge Discovery in Databases of Proteomics by Systems Modeling in Translational Research on Pancreatic Cancer
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Processing
2.2. Bioinformatic Analysis
2.3. AI/ML
3. Results
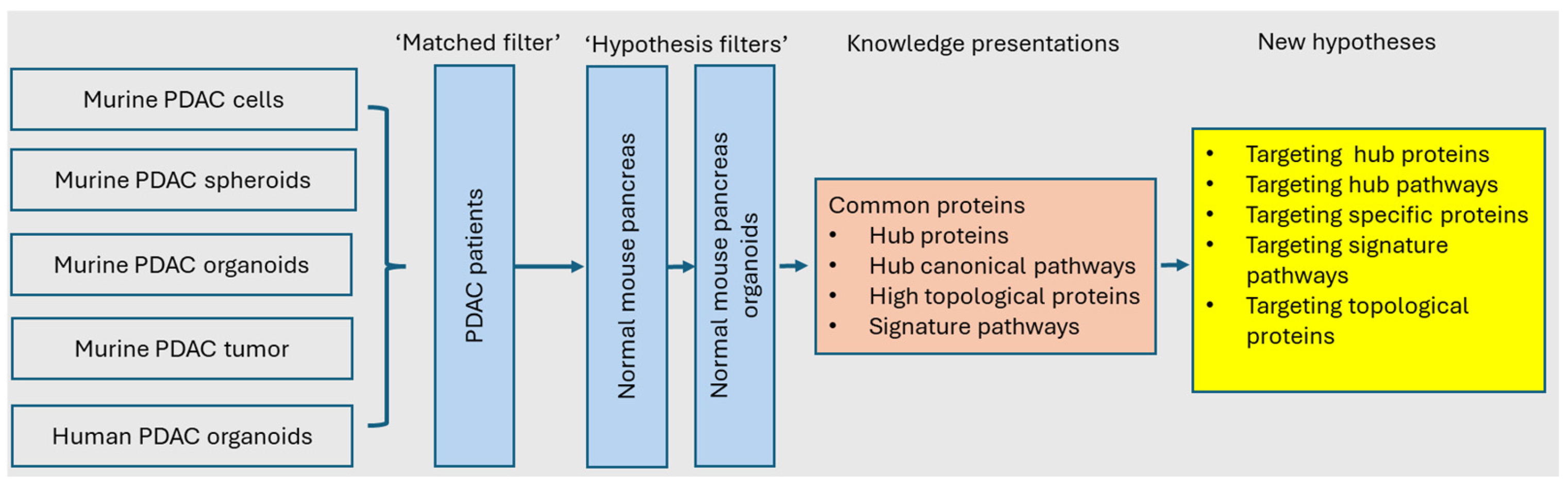
3.1. Workflow of Systems Modeling for KDD
3.2. Knowledge Presentation of Common Proteins Across Various Research Models and Human PDAC
3.3. Knowledge Presentation of Hub Proteins Across Various Research Models and Human PDAC
3.4. Knowledge Presentation of Hub Canonical Pathways
3.5. Knowledge Presentation of High Topological Proteins Across Various Research Models and Human PDAC
3.6. Knowledge Presentation of PDAC Signaling Network ‘Signature’
4. Discussion
4.1. Targeting Common Proteins, Particularly Hub Proteins
4.2. Targeting Hub Pathways
4.3. Targeting Specific Proteins
4.4. Targeting Specific Pathways
4.5. Targeting Topological Proteins
4.6. Notes on AI/ML
4.7. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mak, I.W.; Evaniew, N.; Ghert, M. Lost in translation: Animal models and clinical trials in cancer treatment. Am. J. Transl. Res. 2014, 6, 114. [Google Scholar] [PubMed]
- Sun, D.; Gao, W.; Hu, H.; Zhou, S. Why 90% of clinical drug development fails and how to improve it? Acta Pharm. Sin. B 2022, 12, 3049–3062. [Google Scholar] [CrossRef] [PubMed]
- Resell, M.; Rabben, H.-L.; Sharma, A.; Hagen, L.; Hoang, L.; Skogaker, N.T.; Aarvik, A.; Bjåstad, E.K.; Svensson, M.K.; Amrutkar, M. Proteomics profiling of research models for studying pancreatic ductal adenocarcinoma. Sci. Data 2025, 12, 266. [Google Scholar] [CrossRef]
- Advancing on pancreatic cancer. Nat. Rev. Gastroenterol. Hepatol. 2021, 18, 447. [CrossRef]
- Sarantis, P.; Koustas, E.; Papadimitropoulou, A.; Papavassiliou, A.G.; Karamouzis, M.V. Pancreatic ductal adenocarcinoma: Treatment hurdles, tumor microenvironment and immunotherapy. World J. Gastrointest. Oncol. 2020, 12, 173–181. [Google Scholar] [CrossRef]
- Partyka, O.; Pajewska, M.; Kwaśniewska, D.; Czerw, A.; Deptała, A.; Budzik, M.; Cipora, E.; Gąska, I.; Gazdowicz, L.; Mielnik, A. Overview of pancreatic cancer epidemiology in europe and recommendations for screening in high-risk populations. Cancers 2023, 15, 3634. [Google Scholar] [CrossRef]
- Oberstein, P.E.; Olive, K.P. Pancreatic cancer: Why is it so hard to treat? Ther. Adv. Gastroenterol. 2013, 6, 321–337. [Google Scholar] [CrossRef]
- Laface, C.; Memeo, R.; Maselli, F.M.; Santoro, A.N.; Iaia, M.L.; Ambrogio, F.; Laterza, M.; Cazzato, G.; Guarini, C.; De Santis, P.; et al. Immunotherapy and Pancreatic Cancer: A Lost Challenge? Life 2023, 13, 1482. [Google Scholar] [CrossRef]
- Farhangnia, P.; Khorramdelazad, H.; Nickho, H.; Delbandi, A.A. Current and future immunotherapeutic approaches in pancreatic cancer treatment. J. Hematol. Oncol. 2024, 17, 40. [Google Scholar]
- Hartupee, C.; Nagalo, B.M.; Chabu, C.Y.; Tesfay, M.Z.; Coleman-Barnett, J.; West, J.T.; Moaven, O. Pancreatic cancer tumor microenvironment is a major therapeutic barrier and target. Front. Immunol. 2024, 15, 1287459. [Google Scholar] [CrossRef]
- Rauth, S.; Malafa, M.; Ponnusamy, M.P.; Batra, S.K. Emerging Trends in Gastrointestinal Cancer Targeted Therapies: Harnessing Tumor Microenvironment, Immune Factors, and Metabolomics Insights. Gastroenterology 2024, 167, 867–884. [Google Scholar] [CrossRef] [PubMed]
- Conroy, T.; Pfeiffer, P.; Vilgrain, V.; Lamarca, A.; Seufferlein, T.; O’Reilly, E.M.; Hackert, T.; Golan, T.; Prager, G.; Haustermans, K.; et al. Pancreatic cancer: ESMO Clinical Practice Guideline for diagnosis, treatment and follow-up. Ann. Oncol. 2023, 34, 987–1002. [Google Scholar] [CrossRef] [PubMed]
- Strickler, J.H.; Satake, H.; George, T.J.; Yaeger, R.; Hollebecque, A.; Garrido-Laguna, I.; Schuler, M.; Burns, T.F.; Coveler, A.L.; Falchook, G.S.; et al. Sotorasib in KRAS p.G12C-Mutated Advanced Pancreatic Cancer. N. Engl. J. Med. 2023, 388, 33–43. [Google Scholar] [CrossRef]
- Olaoba, O.T.; Adelusi, T.I.; Yang, M.; Maidens, T.; Kimchi, E.T.; Staveley-O, K.F.; Li, G. Driver Mutations in Pancreatic Cancer and Opportunities for Targeted Therapy. Cancers 2024, 16, 1808. [Google Scholar] [CrossRef]
- Shannon, P.; Markiel, A.; Ozier, O.; Baliga, N.S.; Wang, J.T.; Ramage, D.; Amin, N.; Schwikowski, B.; Ideker, T. Cytoscape: A software environment for integrated models of biomolecular interaction networks. Genome Res. 2003, 13, 2498–2504. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Dorogush, A.V.; Ershov, V.; Gulin, A. CatBoost: Gradient Boosting with Categorical Features Support. arXiv 2018, arXiv:1810.11363. [Google Scholar]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- MacKay, D.J. Bayesian interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Kohavi, R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection; IJCAI: Montreal, QC, Canada, 1995; pp. 1137–1145. [Google Scholar]
- Nagelkerke, N.J. A note on a general definition of the coefficient of determination. Biometrika 1991, 78, 691–692. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- McKinney, W. Data structures for statistical computing in Python. SciPy 2010, 445, 51–56. [Google Scholar]
- Harris, C.R.; Millman, K.J.; Van Der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Ideker, T. Systems biology 101—What you need to know. Nat. Biotechnol. 2004, 22, 473–475. [Google Scholar] [CrossRef]
- Veenstra, T.D. Omics in systems biology: Current progress and future outlook. Proteomics 2021, 21, 2000235. [Google Scholar] [CrossRef] [PubMed]
- Chougoni, K.K.; Grossman, S.R. Extraction of high-quality RNA from mouse pancreatic tumors. MethodsX 2020, 7, 101163. [Google Scholar] [CrossRef] [PubMed]
- Augereau, C.; Lemaigre, F.P.; Jacquemin, P. Extraction of high-quality RNA from pancreatic tissues for gene expression studies. Anal. Biochem. 2016, 500, 60–62. [Google Scholar] [CrossRef]
- Monstein, H.; Nylander, A.; Chen, D. RNA extraction from gastrointestinal tract and pancreas by a modified Chomczynski and Sacchi method. Biotechniques 1995, 19, 340–344. [Google Scholar]
- Wang, D. Discrepancy between mRNA and protein abundance: Insight from information retrieval process in computers. Comput. Biol. Chem. 2008, 32, 462–468. [Google Scholar] [CrossRef]
- Danielsson, A.; Pontén, F.; Fagerberg, L.; Hallström, B.M.; Schwenk, J.M.; Uhlén, M.; Korsgren, O.; Lindskog, C. The human pancreas proteome defined by transcriptomics and antibody-based profiling. PLoS ONE 2014, 9, e115421. [Google Scholar] [CrossRef]
- Yu, H.; Kim, P.M.; Sprecher, E.; Trifonov, V.; Gerstein, M. The importance of bottlenecks in protein networks: Correlation with gene essentiality and expression dynamics. PLoS Comput. Biol. 2007, 3, e59. [Google Scholar] [CrossRef]
- Edkins, A.L.; Price, J.T.; Pockley, A.G.; Blatch, G.L. Heat shock proteins as modulators and therapeutic targets of chronic disease: An integrated perspective. Philos. Trans. R. Soc. B Biol. Sci. 2018, 373, 20160521. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Yu, C.; Li, F.; Zuo, Y.; Wang, Y.; Yao, L.; Wu, C.; Wang, C.; Ye, L. Wnt/β-catenin signaling in cancers and targeted therapies. Signal Transduct. Target. Ther. 2021, 6, 307. [Google Scholar] [CrossRef]
- Makena, M.R.; Gatla, H.; Verlekar, D.; Sukhavasi, S.; Pandey, M.K.; Pramanik, K.C. Wnt/β-catenin signaling: The culprit in pancreatic carcinogenesis and therapeutic resistance. Int. J. Mol. Sci. 2019, 20, 4242. [Google Scholar] [CrossRef]
- Ding, C.; Li, Y.; Xing, C.; Zhang, H.; Wang, S.; Dai, M. Research progress on slit/robo pathway in pancreatic cancer: Emerging and promising. J. Oncol. 2020, 2020, 2845906. [Google Scholar] [CrossRef] [PubMed]
- Gara, R.K.; Kumari, S.; Ganju, A.; Yallapu, M.M.; Jaggi, M.; Chauhan, S.C. Slit/Robo pathway: A promising therapeutic target for cancer. Drug Discov. Today 2015, 20, 156–164. [Google Scholar] [CrossRef] [PubMed]
- Thiel, V.; Renders, S.; Panten, J.; Dross, N.; Bauer, K.; Azorin, D.; Henriques, V.; Vogel, V.; Klein, C.; Leppä, A.-M. Characterization of single neurons reprogrammed by pancreatic cancer. Nature 2025, 640, 1042–1051. [Google Scholar] [CrossRef]
- O’Neill, R.E.; Talon, J.; Palese, P. The influenza virus NEP (NS2 protein) mediates the nuclear export of viral ribonucleoproteins. EMBO J. 1998, 17, 288–296. [Google Scholar] [CrossRef]
- Meric, F.; Hunt, K.K. Translation initiation in cancer: A novel target for therapy. Mol. Cancer Ther. 2002, 1, 971–979. [Google Scholar]
- Han, J.; Xiong, J.; Wang, D.; Fu, X.-D. Pre-mRNA splicing: Where and when in the nucleus. Trends Cell Biol. 2011, 21, 336–343. [Google Scholar] [CrossRef]
- Elvekrog, M.M.; Walter, P. Dynamics of co-translational protein targeting. Curr. Opin. Chem. Biol. 2015, 29, 79–86. [Google Scholar] [CrossRef]
- Chartron, J.W.; Hunt, K.C.; Frydman, J. Cotranslational signal-independent SRP preloading during membrane targeting. Nature 2016, 536, 224–228. [Google Scholar] [CrossRef]
- Alonso-Curbelo, D.; Ho, Y.-J.; Burdziak, C.; Maag, J.L.; Morris, J.P., IV; Chandwani, R.; Chen, H.-A.; Tsanov, K.M.; Barriga, F.M.; Luan, W. A gene–environment-induced epigenetic program initiates tumorigenesis. Nature 2021, 590, 642–648. [Google Scholar] [CrossRef]
- Jia, Y.; Polunovsky, V.; Bitterman, P.B.; Wagner, C.R. Cap-Dependent Translation Initiation Factor e IF4E: An Emerging Anticancer Drug Target. Med. Res. Rev. 2012, 32, 786–814. [Google Scholar] [CrossRef]
- Sriram, A.; Bohlen, J.; Teleman, A.A. Translation acrobatics: How cancer cells exploit alternate modes of translational initiation. EMBO Rep. 2018, 19, e45947. [Google Scholar] [CrossRef] [PubMed]
- Hao, P.; Yu, J.; Ward, R.; Liu, Y.; Hao, Q.; An, S.; Xu, T. Eukaryotic translation initiation factors as promising targets in cancer therapy. Cell Commun. Signal. 2020, 18, 175. [Google Scholar] [CrossRef] [PubMed]
- Golob-Schwarzl, N.; Puchas, P.; Gogg-Kamerer, M.; Weichert, W.; Göppert, B.; Haybaeck, J. New pancreatic cancer biomarkers eIF1, eIF2D, eIF3C and eIF6 play a major role in translational control in ductal adenocarcinoma. Anticancer. Res. 2020, 40, 3109–3118. [Google Scholar] [CrossRef]
- Blijlevens, M.; Li, J.; van Beusechem, V.W. Biology of the mRNA splicing machinery and its dysregulation in cancer providing therapeutic opportunities. Int. J. Mol. Sci. 2021, 22, 5110. [Google Scholar] [CrossRef]
- Braun, A.; Anders, H.-J.; Gudermann, T.; Mammadova-Bach, E. Platelet-cancer interplay: Molecular mechanisms and new therapeutic avenues. Front. Oncol. 2021, 11, 665534. [Google Scholar] [CrossRef]
- Li, S.; Sampson, C.; Liu, C.; Piao, H.-L.; Liu, H.-X. Integrin signaling in cancer: Bidirectional mechanisms and therapeutic opportunities. Cell Commun. Signal. 2023, 21, 266. [Google Scholar] [CrossRef]
- Brannon, A., III; Drouillard, D.; Steele, N.; Schoettle, S.; Abel, E.V.; Crawford, H.C.; di Magliano, M.P. Beta 1 integrin signaling mediates pancreatic ductal adenocarcinoma resistance to MEK inhibition. Sci. Rep. 2020, 10, 11133. [Google Scholar] [CrossRef]
- Lai, H.-C.; Ho, U.Y.; James, A.; De Souza, P.; Roberts, T.L. RNA metabolism and links to inflammatory regulation and disease. Cell. Mol. Life Sci. 2022, 79, 21. [Google Scholar] [CrossRef]
- Tsuruta, D.; Kobayashi, H.; Imanishi, H.; Sugawara, K.; Ishii, M.; Jones, J.C. Laminin-332-integrin interaction: A target for cancer therapy? Curr. Med. Chem. 2008, 15, 1968–1975. [Google Scholar] [CrossRef]
- Givant-Horwitz, V.; Davidson, B.; Reich, R. Laminin-induced signaling in tumor cells. Cancer Lett. 2005, 223, 1–10. [Google Scholar] [CrossRef]
- Fatima, I.; Singh, A.B.; Dhawan, P. MASTL: A novel therapeutic target for Cancer Malignancy. Cancer Med. 2020, 9, 6322–6329. [Google Scholar] [CrossRef] [PubMed]
- Pires-daSilva, A.; Sommer, R.J. The evolution of signalling pathways in animal development. Nat. Rev. Genet. 2003, 4, 39–49. [Google Scholar] [CrossRef] [PubMed]
- Qiu, F.; Yu, C.; Feng, Y.; Li, Y. Key node identification for a network topology using hierarchical comprehensive importance coefficients. Sci. Rep. 2024, 14, 12039. [Google Scholar] [CrossRef]

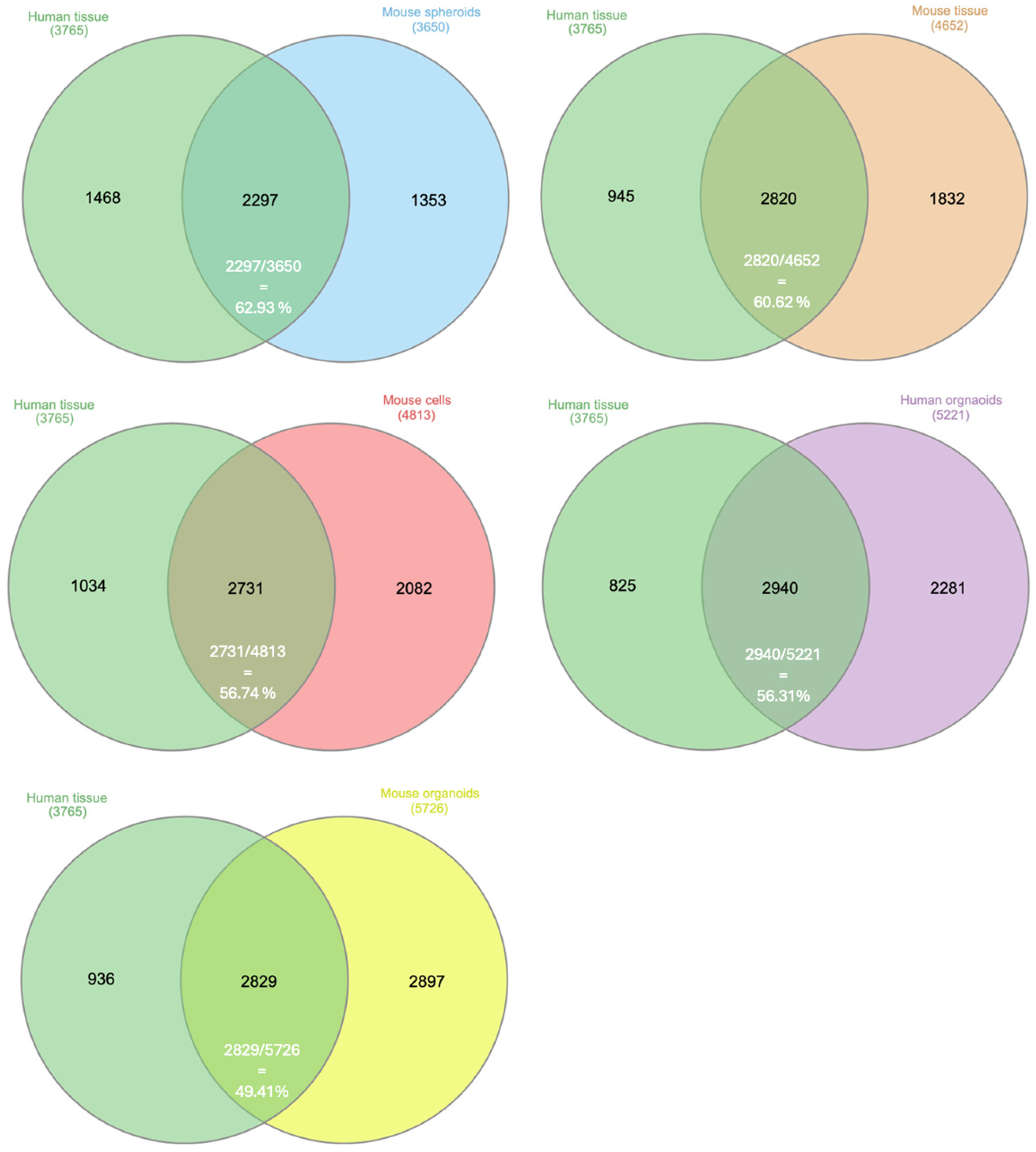
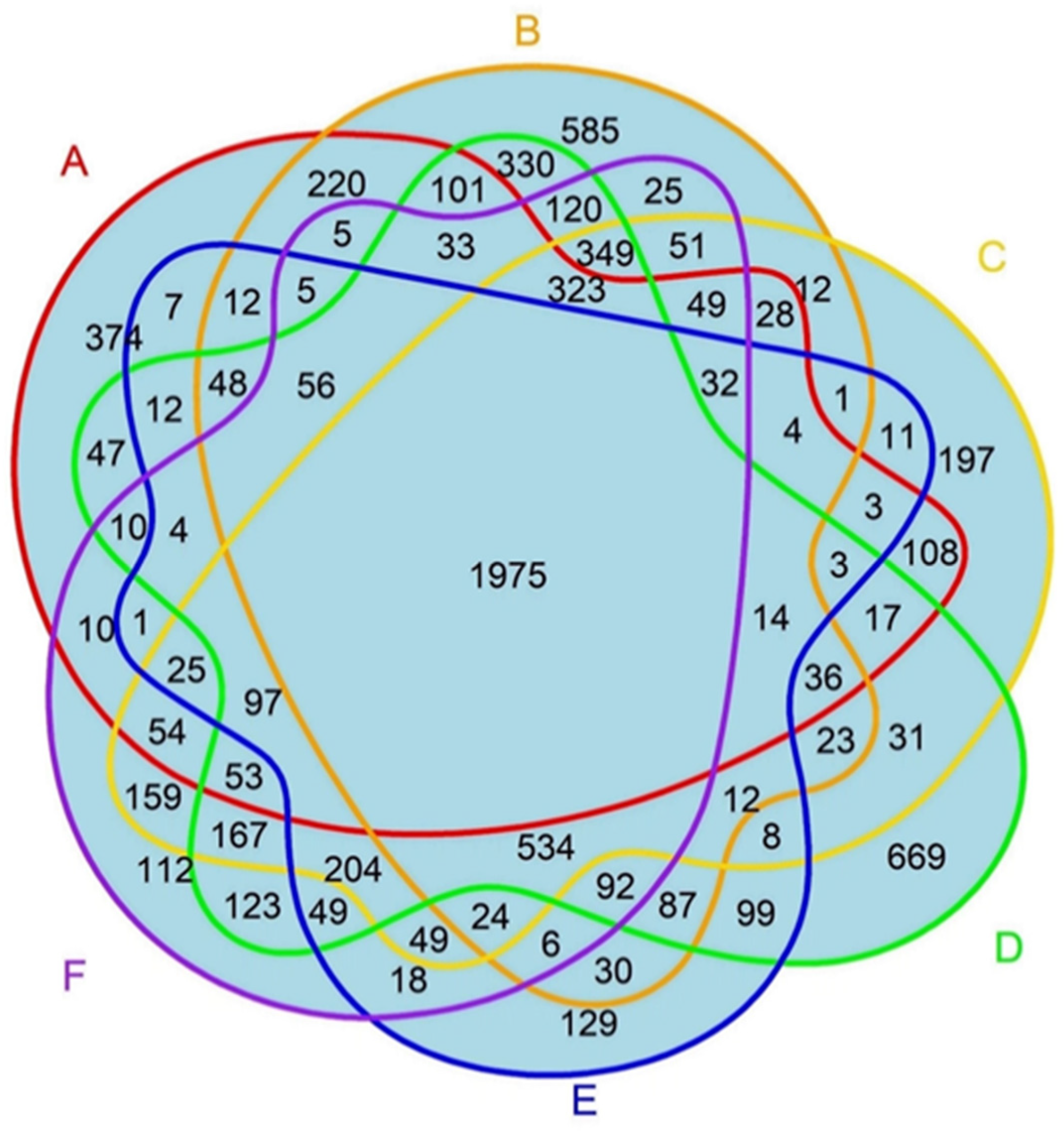


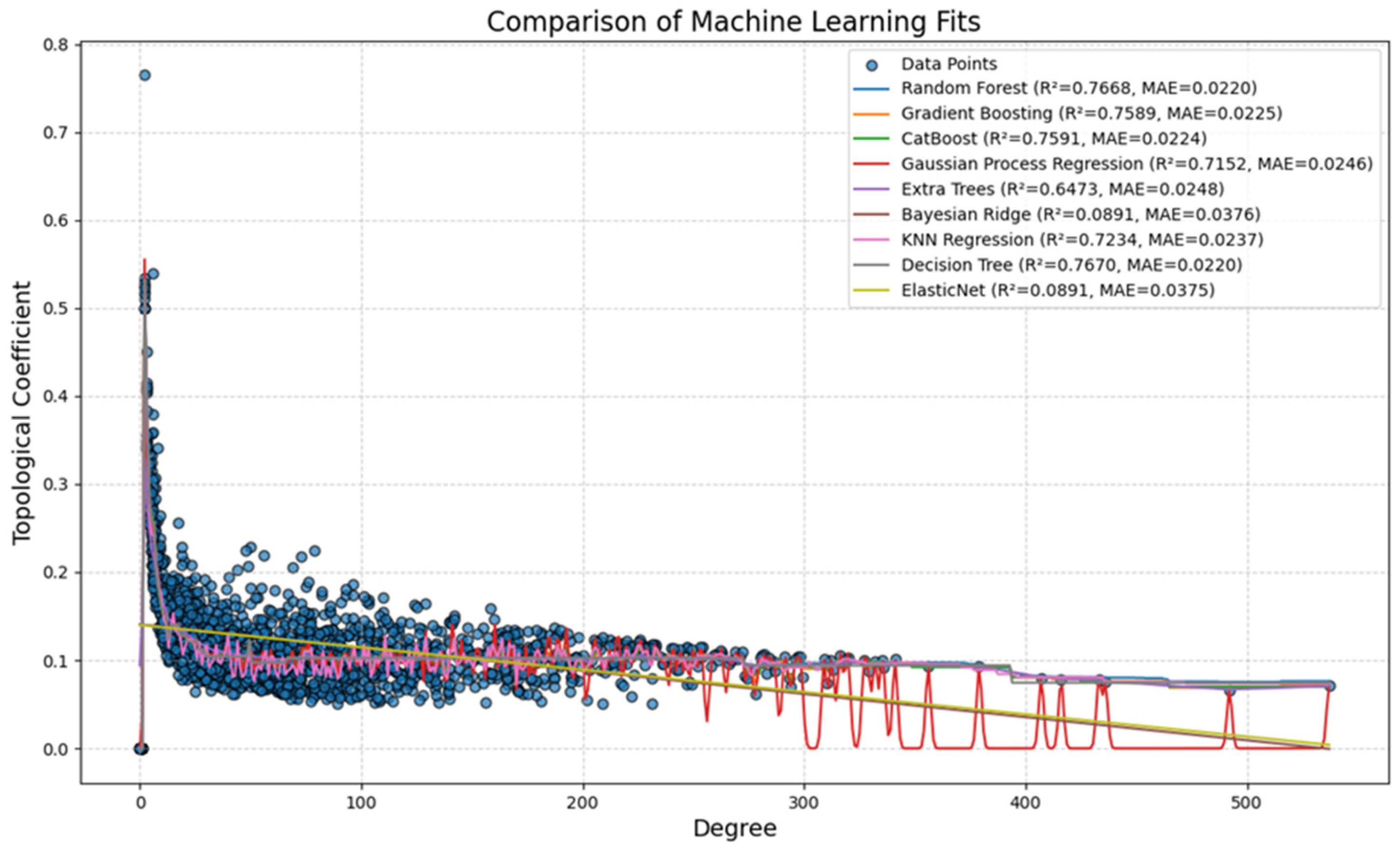
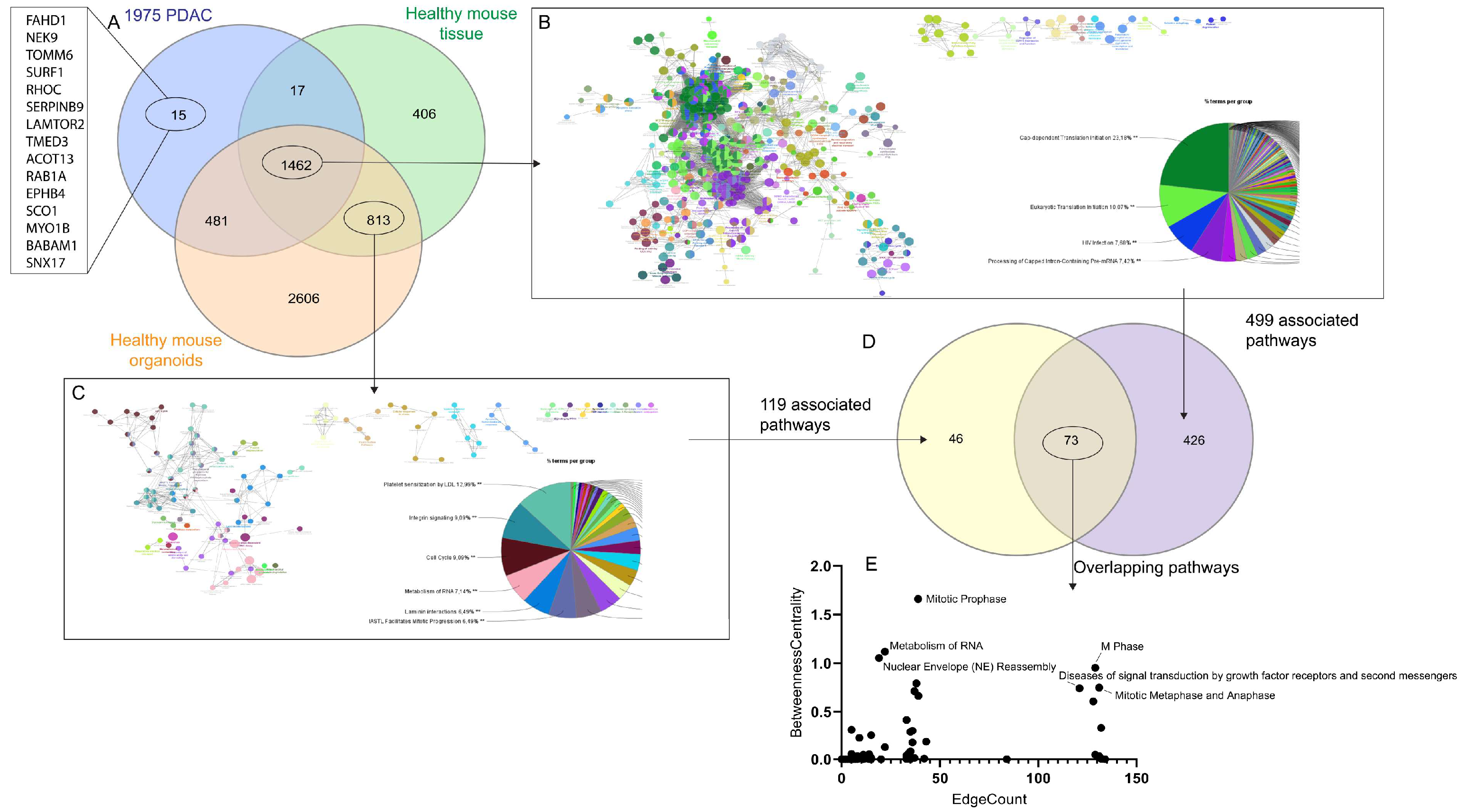
| Research Model | % of Common Proteins in Research Models |
|---|---|
| Murine PDAC cells | 1975/4813 = 41.0% |
| Murine PDAC tumor tissue | 1975/4652 = 42.5% |
| Murine PDAC spheroids | 1975/3650 = 54.1% |
| Murine PDAC organoids | 1975/5726 = 34.5% |
| Human PDAC organoids | 1975/5221 = 37.8% |
| Human PDAC tumor tissue | 1975/3765 = 52.5% |
| Gene Name | Degree | Betweenness Centrality | Description |
|---|---|---|---|
| HSP90AA1 | 436 | 0.01622 | Heat shock protein 90 alpha family class A member 1 |
| HSPA8 | 433 | 0.02005 | Heat shock protein family A (Hsp70) member 8 |
| HSP90AB1 | 416 | 0.01260 | Heat shock protein 90 alpha family class B member 1 |
| EEF2 | 379 | 0.00714 | Eukaryotic translation elongation factor 2 |
| VCP | 310 | 0.01041 | Valosin containing protein |
| RPL3 | 297 | 0.00179 | Ribosomal protein L3 |
| HSPA5 | 294 | 0.01109 | Heat shock protein family A (Hsp70) member 5 |
| HSPA9 | 293 | 0.00795 | Heat shock protein family A (Hsp70) member 9 |
| CTNNB1 | 278 | 0.01054 | Catenin beta 1 |
| PHB | 273 | 0.00736 | Prohibitin 1 |
| Term | Betweenness Centrality | Edge Count | Indegree | Outdegree |
|---|---|---|---|---|
| Regulation of expression of SLITs and ROBOs | 3.3599 | 122 | 15 | 107 |
| Signaling by ROBO receptors | 2.8086 | 99 | 65 | 34 |
| Disorders of transmembrane transporters | 2.7432 | 144 | 64 | 80 |
| Mitotic metaphase and anaphase | 1.6494 | 134 | 96 | 38 |
| Response of EIF2AK4 (GCN2) to amino acid deficiency | 1.3463 | 36 | 9 | 27 |
| Nuclear envelope (NE) reassembly | 1.2219 | 37 | 16 | 21 |
| RAF/MAP kinase cascade | 1.2031 | 128 | 58 | 70 |
| Nonsense-mediated decay (NMD) | 1.0862 | 38 | 10 | 28 |
| SARS-CoV-1-host interactions | 1.0032 | 25 | 8 | 17 |
| MAP2K and MAPK activation | 0.9931 | 12 | 8 | 4 |
| Post-translational protein modification (PTM) | 0.9517 | 9 | 3 | 6 |
| Metabolism of RNA | 0.9059 | 15 | 2 | 13 |
| Deubiquitination | 0.8379 | 125 | 52 | 73 |
| Signal transduction by growth factor receptors | 0.6253 | 66 | 31 | 35 |
| Defective TPR towards thyroid papillary carcinoma | 0.5965 | 51 | 14 | 37 |
| Energy-dependent regulation of mTOR by LKB1-AMPK | 0.5000 | 4 | 1 | 3 |
| Protein localization | 0.5000 | 3 | 1 | 2 |
| SARS-CoV-2-host interactions | 0.4988 | 19 | 4 | 15 |
| SARS-CoV-1 Infection | 0.4758 | 18 | 8 | 10 |
| Mitotic prophase | 0.4741 | 50 | 11 | 39 |
| tRNA processing | 0.4574 | 48 | 6 | 42 |
| Metabolism of amino acids and derivatives | 0.4316 | 35 | 16 | 19 |
| Infectious disease | 0.3851 | 14 | 7 | 7 |
| Axon guidance | 0.3843 | 36 | 20 | 16 |
| Fc epsilon receptor (FCERI) signaling | 0.3788 | 131 | 97 | 34 |
| Transport of small molecules | 0.3603 | 40 | 30 | 10 |
| Ingenuity Canonical Pathway | p-Value |
|---|---|
| Eukaryotic translation initiation | 5.01187 × 10−76 |
| Processing of capped intron-containing pre-mRNA | 5.01187 × 10−69 |
| SRP-dependent co-translational protein targeting to membrane | 1.58489 × 10−64 |
| EIF2 Signaling | 2.51189 × 10−61 |
| Eukaryotic translation elongation | 3.98107 × 10−57 |
| Nonsense-mediated decay (NMD) | 1.58489 × 10−56 |
| Eukaryotic translation termination | 3.16228 × 10−56 |
| Response of EIF2AK4 (GCN2) to amino acid deficiency | 1 × 10−51 |
| Selenoamino acid metabolism | 6.30957 × 10−50 |
| Major pathway of rRNA processing in the nucleolus and cytosol | 3.98107 × 10−44 |
| Sirtuin signaling pathway | 7.94328 × 10−40 |
| Mitochondrial dysfunction | 1 × 10−37 |
| BAG2 signaling pathway | 3.16228 × 10−35 |
| RHO GTPase cycle | 5.01187 × 10−35 |
| Huntington’s disease signaling | 1.99526 × 10−34 |
| Intra-Golgi and retrograde Golgi-to-ER traffic | 3.16228 × 10−33 |
| Regulation of eIF4 and p70S6K Signaling | 3.98107 × 10−33 |
| Mitotic metaphase and anaphase | 5.01187 × 10−33 |
| Protein sorting signaling pathway | 1.58489 × 10−32 |
| Microautophagy signaling pathway | 1.58489 × 10−30 |
| Protein ubiquitination pathway | 1.99526 × 10−28 |
| NIK-noncanonical NF-kB signaling | 3.16228 × 10−28 |
| Electron transport, ATP synthesis, and heat production by uncoupling proteins | 1.25893 × 10−27 |
| Regulation of apoptosis | 3.16228 × 10−27 |
| Granzyme A signaling | 7.94328 × 10−27 |
| FAT10 signaling pathway | 7.94328 × 10−27 |
| COPI-mediated anterograde transport | 1.25893 × 10−26 |
| Hedgehog ligand biogenesis | 2.51189 × 10−26 |
| mTOR signaling | 7.94328 × 10−26 |
| Estrogen Receptor Signaling | 3.16227 × 10−25 |
| Gene/Protein | Topological Coefficient | Degree |
|---|---|---|
| ANO10 | 0.765151515 | 2 |
| ZNRD2 | 0.539386401 | 6 |
| NADK2 | 0.534246575 | 2 |
| DDT | 0.528776978 | 2 |
| TINAGL1 | 0.525974026 | 2 |
| NIBAN2 | 0.52300885 | 2 |
| TM9SF3 | 0.518518519 | 2 |
| OXR1 | 0.516587678 | 2 |
| COBLL1 | 0.511111111 | 2 |
| ACP6 | 0.5 | 2 |
| CYP20A1 | 0.5 | 2 |
| DNPH1 | 0.5 | 2 |
| IKBIP | 0.5 | 2 |
| LRRC1 | 0.5 | 2 |
| MISP | 0.450084602 | 3 |
| HDGFL2 | 0.414609053 | 3 |
| DTD1 | 0.410480349 | 3 |
| LAD1 | 0.409883721 | 3 |
| IRF2BP1 | 0.406926407 | 3 |
| HERC4 | 0.403508772 | 3 |
| RPS16 | 0.105157843 | 316 |
| RPL4 | 0.102499291 | 320 |
| RPSA | 0.101460442 | 319 |
| RPS3 | 0.101350676 | 341 |
| RPL5 | 0.101052058 | 309 |
| RPLP0 | 0.100468112 | 327 |
| RPS20 | 0.100010894 | 335 |
| EEF1A1 | 0.099431337 | 312 |
| RPS9 | 0.098880581 | 319 |
| RPS2 | 0.098282586 | 332 |
| RACK1 | 0.098023878 | 317 |
| EEF2 | 0.093276023 | 379 |
| EFTUD2 | 0.092734482 | 356 |
| HNRNPA1 | 0.091633486 | 336 |
| EPRS1 | 0.089226511 | 313 |
| NPM1 | 0.087729822 | 329 |
| HSPA4 | 0.079882921 | 407 |
| HSPA8 | 0.078043369 | 433 |
| HSP90AB1 | 0.077569299 | 416 |
| HSP90AA1 | 0.074854808 | 436 |
| VCP | 0.074248602 | 310 |
| GAPDH | 0.07078761 | 537 |
| ACTB | 0.066307787 | 492 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Resell, M.; Graarud, E.P.; Rabben, H.-L.; Sharma, A.; Hagen, L.; Hoang, L.; Skogaker, N.T.; Aarvik, A.; Svensson, M.K.; Amrutkar, M.; et al. Knowledge Discovery in Databases of Proteomics by Systems Modeling in Translational Research on Pancreatic Cancer. Proteomes 2025, 13, 20. https://doi.org/10.3390/proteomes13020020
Resell M, Graarud EP, Rabben H-L, Sharma A, Hagen L, Hoang L, Skogaker NT, Aarvik A, Svensson MK, Amrutkar M, et al. Knowledge Discovery in Databases of Proteomics by Systems Modeling in Translational Research on Pancreatic Cancer. Proteomes. 2025; 13(2):20. https://doi.org/10.3390/proteomes13020020
Chicago/Turabian StyleResell, Mathilde, Elisabeth Pimpisa Graarud, Hanne-Line Rabben, Animesh Sharma, Lars Hagen, Linh Hoang, Nan T. Skogaker, Anne Aarvik, Magnus K. Svensson, Manoj Amrutkar, and et al. 2025. "Knowledge Discovery in Databases of Proteomics by Systems Modeling in Translational Research on Pancreatic Cancer" Proteomes 13, no. 2: 20. https://doi.org/10.3390/proteomes13020020
APA StyleResell, M., Graarud, E. P., Rabben, H.-L., Sharma, A., Hagen, L., Hoang, L., Skogaker, N. T., Aarvik, A., Svensson, M. K., Amrutkar, M., Verbeke, C. S., Batra, S. K., Qvigstad, G., Wang, T. C., Rustgi, A., Chen, D., & Zhao, C.-M. (2025). Knowledge Discovery in Databases of Proteomics by Systems Modeling in Translational Research on Pancreatic Cancer. Proteomes, 13(2), 20. https://doi.org/10.3390/proteomes13020020






