How Do Physics Teacher Candidates Substantiate Their Knowledge? An Analytical Framework for Examining the Epistemic Dimensions of Content Knowledge in Higher Education

Abstract

Supporting teacher candidates’ learning of coherent and well-ordered content knowledge is one of the most important educational aims in subject teacher education. To reach this aim, teacher educators need suitable tools to enhance the formation of such knowledge. In this article, we present an analytical framework to examine conceptual knowledge, meaning the ability to define the relevant concepts pertaining to a task; relational knowledge, i.e., the ability to consider interrelations between the concepts; and strategic knowledge, i.e., the ability to use the knowledge by providing (experimental or modeling) procedures, which build new knowledge. A sample analysis of 16 teacher candidates’ written reports is presented to illustrate how this framework can be used. The aim of the study was to reveal what kind of variation in teacher candidates’ content knowledge can be found. This study suggests that teacher candidates’ written reports can reveal remarkable differences in the epistemic dimensions of content knowledge. The framework shows the differences among the teacher candidates as well as produces information for teacher educators of the critical aspects, when and where to intervene, and where to focus using different teaching practices.

1. Introduction

The aim of subject teacher education is to support teacher candidates to form a coherent understanding of the teaching subject, enhance their pedagogical understanding of learning and teaching students as well as support them in learning to teach [1]. Subject teachers’ knowledge of how to teach the given subject is a combination of good understanding of didactical and pedagogical aspects of teaching and learning. This combination is referred to as teacher’s pedagogical content knowledge. To develop pedagogical content knowledge, a teacher should naturally have a good command over the content knowledge (e.g., [2,3,4]), as well as an understanding of the variety of pedagogies relevant and suitable for the discipline or subject in question [5]. Content knowledge consists of: (1) conceptual knowledge (i.e., declarative knowledge); (2) procedural knowledge; and (3) meta-knowledge about the nature of discipline [6]. The demand for coherent and well-ordered content knowledge is a self-evident aim, but it is still a viewpoint that needs to be emphasized [7]. Teachers’ expertise in content knowledge has been shown to be a prerequisite for its pedagogical use and, in addition, it can lead to students’ better learning outcomes (cf. [7,8]). Recent research has also highlighted that teachers’ ability to construct properly organized teaching plans in physics requires knowledge about how the concepts can be introduced and substantiated in a logically justified manner and in a way that it supports student learning [9,10]. In teaching physics, the mastery of the content can be recognized from some very basic features: clear introduction of new concepts, clear direction of progress, how new concepts to be learned are based on previously explained concepts, and clarity on how various concepts are related to each other [9,10].

Previous research has shown that students’ understanding of a subject domain is associated with a rich set of relations among relevant concepts and highly integrated frameworks of related concepts [11]. However, an open question remains as to what kind of teachers’ content understanding is relevant and useful for teaching (cf. [1,12]) and for promotion of pupils’ learning later in working life. In this article, we approach these questions by presenting an analytical framework to assess the physics teacher candidates’ understanding of physics knowledge and especially the epistemic dimensions of content knowledge in their written reports. This framework analyzes three epistemic dimensions: conceptual knowledge, relational knowledge and strategic knowledge. The framework can be used as a scoring system to evaluate written reports consistently. By analyzing the teacher candidates’ understanding of complex topics, it is possible to identify the critical aspects of content knowledge that teacher educators need enhance in order to improve teacher candidates understanding.

2. Theoretical Framework

2.1. Teachers’ Knowledge Base for Teaching

A relatively extensive body of theoretical and empirical research has focused on defining the characteristics and qualities of the knowledge base for teaching [13,14,15,16,17,18,19]. The research field is relatively diverse, and researchers have adopted multiple different ways to conceptualize and define teacher knowledge. Several researchers have agreed that teachers’ knowledge base should consist of pedagogical content knowledge, pedagogical knowledge and content knowledge [3,4,5,19,20].

In addition to general pedagogical knowledge and pedagogical content knowledge, the importance of specific content knowledge and its necessary role in teaching has been discussed. Similar notions have been made regardless of the subject [1,2,7,20,21]. For example, results regarding teaching and learning mathematics and physics are comparable in many cases. The few empirical studies that have been made show that teachers’ understanding of the specific contents of teaching defines the classroom activities that they organize for pupils [22,23]. Teachers’ orientations to their subjects have been shown to shape the ways in which they teach the subject to their students [24]. Teachers’ ability to analyze, understand, and direct classroom teaching and provide exact subject-specific feedback are also associated with their mastery of content knowledge [25,26]. Some studies have also supported the assumption that teachers’ content knowledge is positively related to pupils’ learning [8]. However, there is little empirical evidence for the significance of content knowledge for teachers’ classroom performance and pupil learning, partly due to the complexity of the phenomenon in its wholeness and challenges in measuring it in a controlled way. The evidence that exists is only limited to some subject areas [27], especially related to subjects representing exact disciplines such as mathematics (TEDS-M reported in [28], see also [7]) and physics [23]. From the viewpoint of teacher candidates’ learning and mastery of content knowledge, as well as from the viewpoint of teacher education, important questions to be explored are related to the required quantity and quality of content knowledge that effective teaching expects [20].

2.2. Physics Content Knowledge

Physics teacher candidates are studying to become experts on teaching physics. Physics instruction usually concentrates on learning well-established laws, models, and theories, which are regarded as facts with no need to question where they come from [29,30]. This might induce a shortage of strategic knowledge (i.e., know how to use the concepts in generating explanation or providing experiments and models, see more below), which are needed to connect the physics concepts together. In previous research, it has been pointed out that even after basic and intermediate physics studies, physics students (including physics teacher candidates) do possess relevant knowledge, but it consists of a collection of fragmented pieces [9]. Teacher candidates seem to lack a coherent view of the physics knowledge system, and, therefore, they need support in developing their overall understanding of physics content knowledge.

Physics is characterized by its empirical nature. Traditionally, physics knowledge is built through experiments and observations, starting from individual cases to more general laws, models, and theories. Therefore, besides experiments, models and modeling are essential in building physics knowledge. Formation of physics knowledge can be seen as a hypothetico-deductive process, where theory is usually a starting point for empirical testing of predictions and hypotheses. By testing a previous theory, we can either verify it or discover a demand for revising or even discarding it [31]. Quantitative experiments, data models and theoretical models are especially important in learning to build up students’ physics knowledge, by introducing or justifying new laws, and establishing new concepts [9,32,33]. Models and experiments mutually interact with each other: models are used to guide the planning of experiments, measurements, and interpretation of the results. Models give us predictions that can be tested experimentally and these results can be compared. Based on such experiments, we can revise previous models or even create new ones. Models are also used to describe and explain phenomena [34].

Physics content knowledge to be learned includes a collection of physics concepts (quantities), laws, general principles, models and experiments. It is of importance to understand how these different pieces are connected to each other and how they can be substantiated. Physics content knowledge can be approached by dividing it into three subcategories: (1) knowledge about relevant concepts; (2) knowledge about relations between concepts; and (3) knowledge about the epistemic strategies on how concepts and relations between concepts are formed. Besides these three aspects, it is important to understand the limitations and restrictions connected to conceptual, relational, and strategic knowledge in physics.

2.3. Various Frameworks for Analyzing Content Knowledge

Analysis on content knowledge has been discussed in many existing frameworks. Some frameworks analyzing students’ content knowledge focuses on students’ knowing and reasoning concepts and facts and their relations. For example, Sandoval and Millwood [35] introduced an analytical framework to analyze factual and conceptual knowledge. Similar notions were also presented by Kelly and Takao [36] and Kelly, Regev, and Prothero [37]. Krathwohl [38] provided a revision of Bloom’s taxonomy of educational objectives. The revised taxonomy contains, in addition to cognitive processes, four dimensions for knowledge: factual, conceptual, procedural and metacognitive knowledge. In this taxonomy, factual knowledge means basic elements of a discipline, conceptual knowledge refers to interrelationships between basic elements, procedural knowledge is defined as subject-specific skills and techniques and metacognitive knowledge refers to one’s awareness to one’s own cognition. In similar lines, De Jong and Ferguson-Hessler differentiated among situational knowledge, conceptual knowledge, procedural knowledge and strategic knowledge and their different qualities [39]. By strategic knowledge they referred to logical series of actions which form a strategy. One recent study has focused on analyzing the epistemic levels of the teacher candidates’ explanations by paying attention to the correct use of concepts and facts, and methodological aspects and the logical proceeding of the explanation [33]. That article concludes that teacher candidates were able to identify physics concepts and laws but had difficulties in explaining how physics laws are built, i.e., what processes are needed to produce such relations between concepts.

One general restriction for all these existing frameworks is that for analyzing content knowledge they seem to lack eliciting students’ strategic knowledge to knowing when and how to apply such conceptual and relational knowledge to form a logically coherent picture of a phenomenon. It has been noted that strategic knowledge can be assessed by a complex and novel task that entails “students’ interpreting the problem and selecting domain-specific strategies, an open item structure that supports the use of strategic knowledge, and a scoring that directly captures the differences in students’ use of strategic knowledge” ([39] p. 297).

Physics teacher education needs tools to help teacher candidates’ formation of more connected knowledge structures. In physics teacher education courses, much effort has been paid to emphasizing the epistemic aspects of physics knowledge. To this end, teacher candidates are asked to illustrate their understanding of the connectedness of physics concepts as a concept map, and to write down the detailed descriptions of the connections. Such written reports are found to be rich sources of information due to their proficiency in following the development of students’ understanding [33,40]. They provide several different forms of information, for example: how a student has recognized what concepts are relevant; how the concepts are linked to each other; what is the overall structure the concepts form; what kind of limitations and restrictions are connected to these concepts and their relations; and, finally, the ability to generate reasoned explanations. To complete the written reports, students need to apply different dimensions of domain-specific knowledge:

• Declarative knowledge to identify and evaluate what concepts are reasonable to apply. For example, relevant physics concepts, terms and quantities, such as electron, photon or frequency.
• Procedural knowledge to analyze the meanings and limitations of the concepts and to consider interrelations between the concepts. For example, physics relations and law, such as Compton relation or Einstein equation.
• Strategic knowledge to know when, where, and how these concepts in a specific context form a logically coherent picture of phenomenon, and to use the concepts in generating explanation or providing an experiment [39,41,42]. For example, explanation of Millikan’s experiment.

Therefore, we assume that such written reports can provide insight into what students know and how that knowledge is represented and used (see [40]).

In this article, we propose an analytic framework for examining and scoring teacher candidates’ written reports of content knowledge. The framework considers three different dimensions of knowledge and knowing. This analytical framework has similar notions concerning content knowledge and knowledge substantiation as previous research [7,39,41,42]. In this framework, teacher candidates’ written reports are evaluated and scored for conceptual, relational and strategic perspectives (for a more detail method description, see Section 5). It also allows the elaboration of these dimensions and their associations simultaneously.

3. Aim

The aim of the study was two-fold. First, we aimed to present an analytical framework to discern epistemic dimensions of teacher candidates’ knowledge. Second, we investigated physics teacher candidates’ substantiation of physics content knowledge and elaborate the epistemic dimensions of content knowledge that they explicate in their written reports in applying the framework. The specific research questions were:

• How do epistemic dimensions manifest themselves in teacher candidates’ written reports analyzed with the epistemic framework?
• What kind of variation of conceptual, relational, and strategic content knowledge can be found from the written reports?
• What kinds of combinations of conceptual, relational, and strategic knowledge can be detected in teacher candidates’ written reports?

The first research question sought to find how the framework elicits teacher candidates’ epistemic dimensions of content knowledge. The second and third research questions sought to describe the variation and combination of epistemic dimensions discerned by the framework.

4. Methods

4.1. Context

In Finland, physics teachers complete an academic, five-year Master’s level program (180 + 120 credits) at the university. The program includes orientation studies (25 credits), studies in physics (160 credits), studies in another teaching subject (often mathematics or chemistry or physics if not a major subject; 60 credits), optional physics studies (15 credits) and compulsory pedagogical studies (60 credits). The physics students who intend to become teachers need to apply to the pedagogical studies providing formal teacher qualification; usually, this takes place in the spring of the second year in major studies. This is required to gain a formal physics teacher qualification. Subject teachers teach physics for students aged between 13 and 19 years, in grades 7–9 in comprehensive school and in grades 10–12 in upper secondary school.

The studies for Finnish physics teachers are mostly organized at the Faculty of Science, and the pedagogical studies at the Faculty of Education. The major subject studies consist of lecture courses, mathematical exercises, small seminars, research studies related to the major subject, laboratory experiments, and demonstrations. In pedagogical studies, teacher candidates study general pedagogy and pedagogical content knowledge, do a pedagogical thesis related to teaching and learning physics as well as complete teaching practice periods in authentic school settings. Teacher candidates have the freedom to plan the progress of their major subject studies and to choose optional studies for the degree. The curriculum for pedagogical studies is relatively fixed, and thesis work and practicum periods allow students to make choices according to their preferences.

4.2. Participants

The participants of this study were teacher candidates who study to be qualified teaching physics in secondary and upper secondary schools (N = 16; male 12, female 4). The study was carried out at a large research-intensive university in Finland. The participants were in their third our fourth year of studies and most of them had mathematics as their major subject. The participants had not completed their pedagogical studies yet. The participants were at a teacher preparation course (obligatory intermediate physics teacher studies) and they had already passed the basic level physics courses. The mean age of the participants was 27 years (min–max: 21–35 years). All participants came from a homogeneous cultural background, and all shared the same first language (Finnish).

4.3. Data Collection

The data were collected as a part of an intermediate-level physics teacher preparation course (5 credits), which focused on organization of physics content knowledge, the specific context was quantum physics. The participation in the study was voluntary, but all teacher candidates volunteered to participate. The teacher candidates gave their informed consent to participate in the study and they were informed that the participation would not affect their subsequent grades in any way. The anonymity of the participants was ensured in all stages of the study. The teacher candidates were not given any incentives for participating in the study.

During the course, each physics teacher candidate generated four concept maps as course tasks. The topics of the tasks were the photoelectric effect, Compton effect, double slit experiment for single photons and double slit experiment for single electrons, respectively. The tasks were open and teacher candidates were free to address as many concepts and explain the connections between concepts in the length they felt necessary. The overall aim of the tasks was to represent a plan in which order the concepts would be introduced in teaching these topics. The concept maps represented the relational structure of physics concepts and they came with written reports describing the core content knowledge presented in the maps. In the concept maps, teacher candidates presented their views on how central concepts of a given topic were connected to each other with directed links. The concept map displayed how the relations between concepts were established and the written report reflects the teacher candidates’ understanding as to how the connections are justified [33]. The teacher candidates had worked with similar tasks during a previous course, which means that they were experienced in producing such representations.

This study concentrated only on these written reports because we want to examine the epistemic dimensions of the knowledge which were more easily detected from the written reports. (The maps themselves contain rich set of information of the connections between concepts. In the future, it would be interesting to combine epistemic analysis of written reports to detailed network analysis of concept maps to see how written explanations and network structure are connected [32,33].) The materials of this study consisted of written reports of the two tasks: teacher candidates’ written reports of the photoelectric effect and the Compton effect. We chose Tasks 1 and 2 (the photoelectric effect and Compton effect) since they concentrate on the simplest quantum phenomena to explain the original empirical results for quantization of energy and momentum and therefore form a natural starting point for teaching quantum physics. The sample of the study consisted of 16 written reports on the photoelectric effect and 16 reports on the Compton effect. The analysis framework and scoring are presented in the next sections.

The written reports consisted of N short descriptions of concept map nodes, where N is the number of nodes in the concept map. The number of nodes was not restricted and teacher candidates were free to introduce as many concepts they thought were needed to explain the phenomena. These data segments (description of the nodes) were used as units of analysis. Here below is one example of a unit of analysis, an explanation of qualitative notions about the photoelectric effect (translated from Finnish).

“In the photoelectric effect, light’s photon is absorbed into an atom and detaches an electron from it. The classical theory had problems also to explain this experimentally observed phenomenon. According to the classical theory, light’s frequency should not matter in detaching the electron–that is, if light’s intensity is sufficiently large. Neither could the classical theory explain the photo electron’s kinetic energy’s dependence on the radiation frequency instead of its intensity.”

5. Data Analysis Framework

The framework of analysis was developed to elicit the epistemic dimensions of content knowledge in teacher candidates’ written reports, namely conceptual, relational and strategic knowledge. The framework concentrated on the following dimensions: (1) conceptual knowledge (C); (2) relational knowledge (R); and (3) strategic knowledge (S). Each dimension had two subcategories: (1) identification and definition; and (2) conditions for usage, and all of them are scored using a scale of 0 to 2. Below, we present the detailed scoring system utilized in the analysis with the framework. If none of the mentioned criteria were met, the description of a node in question was given score 0. The scoring process is presented in more detail in Section 5.

Here, we also provide details that characterize the three dimensions. Similar discussions can be found in previous research on content knowledge and knowledge substantiation (see, e.g., [7,41,42]), which give theoretical support for this framework.

• Conceptual knowledge: Identification of concept(s) and their relevance to the task. The conceptual dimension (C) referred to the ability to identify and define relevant physics concepts and to reflect their applicability. Such a dimension entailed declarative knowledge about physics concepts and terms, such as “a photon” or “X-ray radiation” and about limitation(s) to the usability of the concept or term (cf. [6,7,41,42]). See detailed criteria in

  Table 1. The criteria for identifying conceptual knowledge, C1.

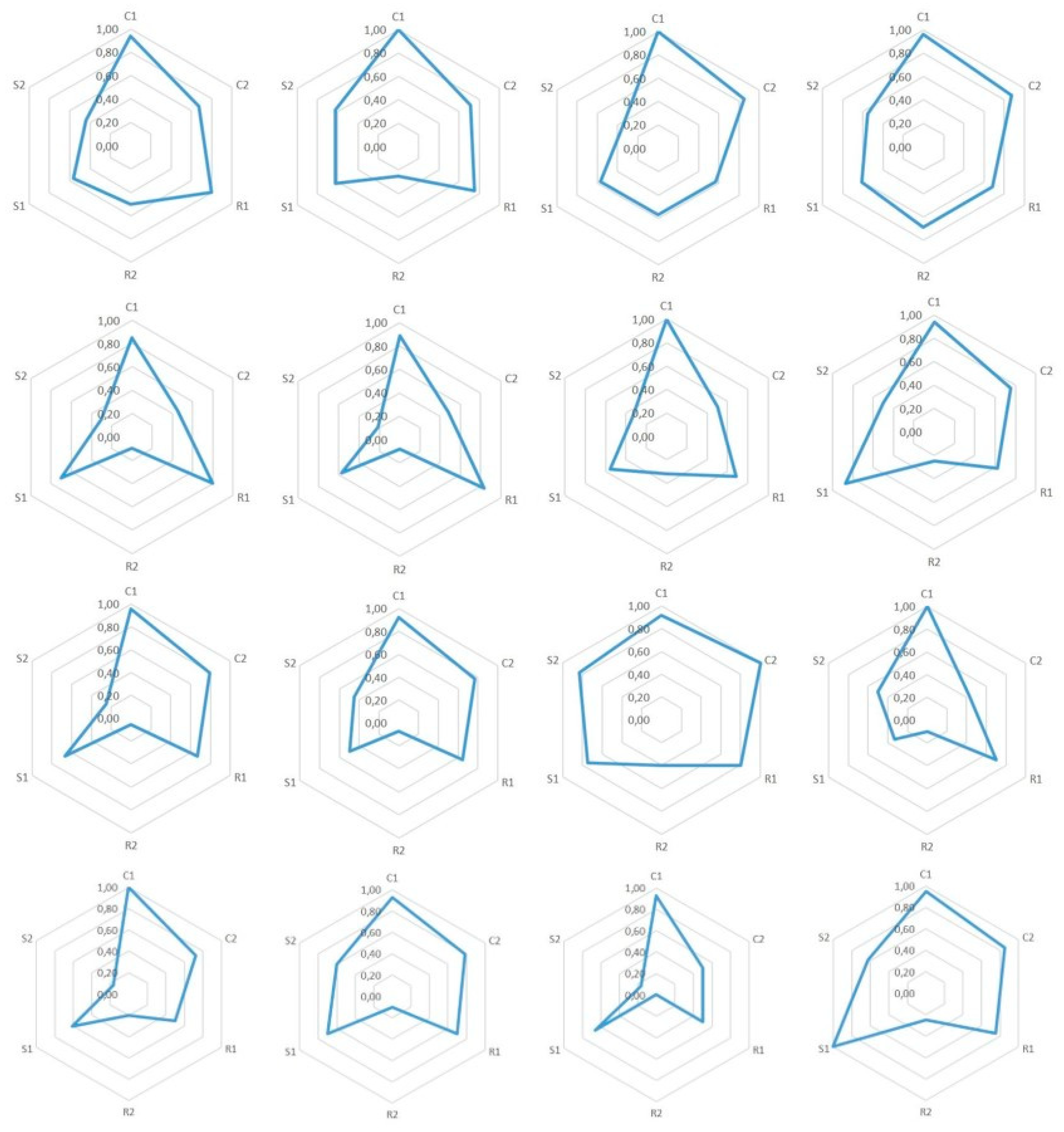
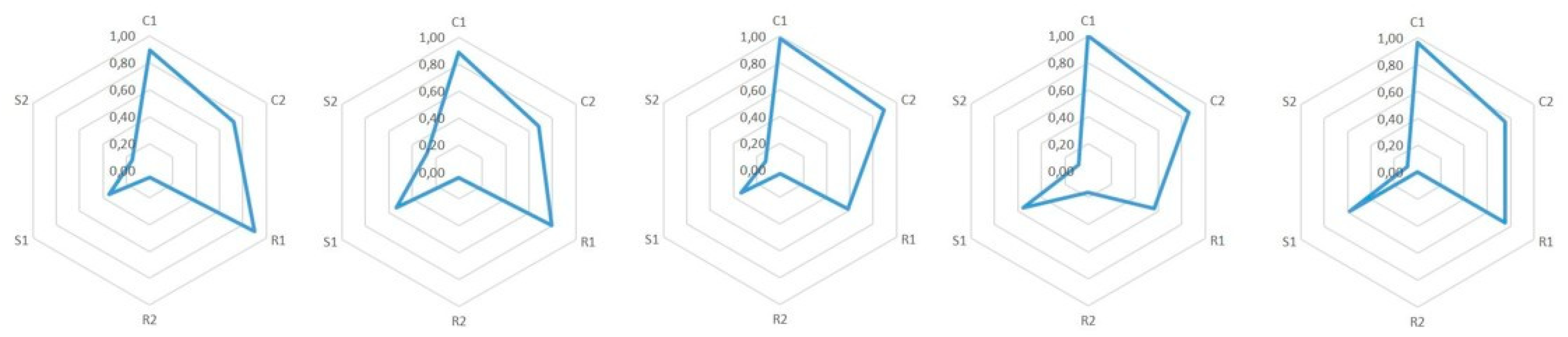
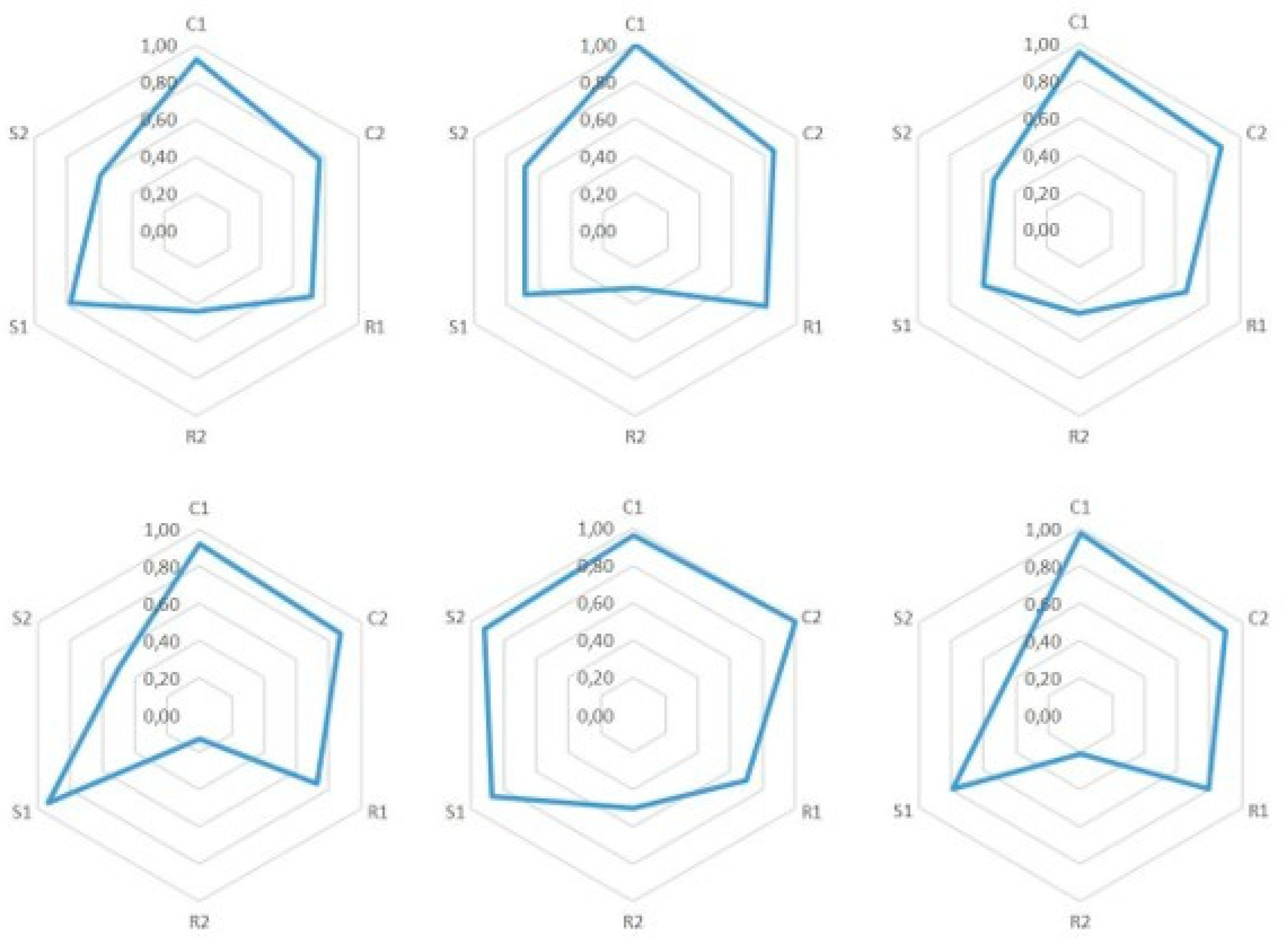
  C1: Identification and Definition of Concepts	Examples
  1 score = identifies and mentions at least one general concept which is relevant in the description	light, particle, energy, radiation, spectrum
  2 scores = identifies and mentions at least one special concept which is relevant in the description (cf. general concept)	ultraviolet light, monochromatic light, electron, photon, kinetic energy, maximum energy, x-ray radiation, electromagnetic radiation, discrete spectrum, spectrum of light, continuous spectrum
  or identifies an exact physical quantity	frequency, intensity, wavelength, electric current, voltage, temperature
  or presents a specification or limitation/requirement concerning mentioned general concept	for example, a particle having a property x
  or presents exact concepts	quantum, quantum hypothesis, Planck’s constant, black body radiation, threshold frequency, ultraviolet catastrophe, photoelectric effect

  and

  Table 2. The criteria to identify limitations and restrictions in conceptual knowledge, C2.

  C2: Conditions for Using the Concept(s)	Examples
  1 score = reflects on limitations of at least one concept, some inconsistency is allowed	“Owen Willans Richardson and Arthur Compton believed that the maximum energy of electrons would be constant. Millikan’s experiment pointed out that it was not the case. Maximum energy can be calculated by using the minimum energy to detach an electron, Ekin,max = hf-E0.” “Classical theory was not able to explain the black body radiation spectrum at all frequencies. Later this phenomenon was known as ‘ultraviolet catastrophe,’ and it was one of the first shortcomings of the classical theory.”
  or presents at least one relevant context to use the concept	“When a system returns from a state of excitation to its basic state, it releases extra energy as electromagnetic radiation, which consists of discrete spectrum lines. The reason for the appearance of exact frequencies on atom emission spectra was unclear before the development of quantum theory”.
  2 score = presents at least one consistent limitation to usability of the concept	“Einstein presented the idea that electromagnetic radiation is quantized. According to Einstein, light consisted of small ‘energy packages’, light quanta. We can see experimentally that electrons in metal can receive radiation energy only as packages of a certain size, quanta, the size of which was dependent only on the frequency of the radiation.” “With this experiment we can define a threshold energy, characteristic to each metal, f = E0/h (where E0 is the minimum energy required to detach electrons), which means the minimum frequency of electromagnetic radiation that can detach electrons from metal.”

  . Mathematical notations were not regarded as physics concepts unless they were clearly verbally explained, or if they had a well-known meaning in physics.
• Relational knowledge: Relations between concepts and their restrictions. Relational dimension (R) referred to the ability to identify how concepts are related to each other and what the forms and limitations are of such relations (cf. [7]). Relations and relational knowledge were essential for understanding analogies, explanations, learning concepts, proposing justifications, and problem solving [43]. See detailed criteria in

  Table 3. The criteria to identify relational knowledge R1.

  R1: Identification and Definition of a Relation between Concepts	Examples
  1 score = identifies at least one relation between relevant concepts (quantities), relation can be inconsistent	“We perceived that if the value for voltage is some integer times 4.9 volts, the current decreased considerably.” → there is a relation between current and voltage
  a physics law identified by name	“This law is later used to prove Stefan-Boltzmann’s law by integration.”
  2 scores = presents an exact mathematical relation between concepts (quantities)	“Light quantum has energy E = hf.”
  an explicit verbal relation	“By using stopping voltage we can calculate the electron’s maximum energy which is the difference between the electron’s energy and work function.”

  and

  Table 4. The criteria to identify limitations and restrictions in relational knowledge, R2.

  R2: Conditions for Using the Relation between Concepts	Examples
  1 score = reflects on the limitation of the relation, some inconsistency is allowed	“We perceived that if the value for voltage is some integer n times 4.9 volts, the current decreased considerably” → n is an integer “This experiment shows us in practice that, no matter how high the light intensity, if its frequency is not high enough, electrons are not detached from the plate.”
  2 scores = presents at least one consistent limitation to usability of the relation	“Planck was able to connect Wien’s and Rayleigh-Jeans’ radiation laws. The first one operates for short wavelengths and the second for longer ones. When merging these two laws together Planck had to assume that energy is transferred as quanta.” → quantization of energy transfer

  . This dimension entailed declarative knowledge, such as “Energy can have values E = nhf, where n is an integer, h is Planck’s constant and f is radiation frequency.”
• Strategic knowledge: Knowing when, where, and how to apply the other types of knowledge by providing experimental or a modeling procedure. The strategic dimension (S) in this context meant knowledge of either an experimental or a modeling procedure, and reflection on their restrictions or limitations. Strategic dimensions thus assessed whether or not a student knows when, where, and how to apply the other two types of knowledge by providing experimental or a modeling procedure (see, e.g., [9,33,42]). Such a dimension represented the integration of declarative and procedural (i.e., knowing how) aspects of knowledge and knowing see [39,41,42]. See detailed criteria for experiments in

  Table 5. The criteria for identifying strategic knowledge S1 for experiments.

  S1 for Experiments: Identification and Definition of an Experiment	Examples
  1 score = identifies (by name) a relevant experiment or proposes arrangements for an experiment. Some inconsistency is allowed.	“The phenomena works also the other way around as we can see in the Franck-Hertz experiment. An electron moving in a medium can release kinetic energy and this is perceived as x-ray emission.”
  2 scores = identifies a relevant experiment and proposes arrangements for this experiment. Description is clear and consistent.	“Wilhelm Hallwachs and Philipp Lenard were inspecting the photoelectric effect noted by Heinrich Hertz. In the experiment, a voltage is created between plate electrodes in a vacuum. A monochromatic light is aimed at the positive electrode. Light detaches electrons from the plate, which we can perceive by connecting an ampere meter to the circuit.”

  and

  Table 6. The criteria for identifying interpretation to strategic knowledge, S2 for experiments.

  S2: The Results and Meaning of the Experiment	Examples
  1 score = presents the result of the experiment OR explains the meaning or relevance of the experiment. Some inconsistency is allowed.	“The experiment showed us the meaning of light frequency to make the phenomenon happen.”
  2 scores = presents the result of the experiment AND explains the meaning or relevance of the experiment. Description is clear and consistent.	“James Franck and Gustaf Hertz developed an experiment which points out that electrons in an atom have quantized energy. The results of the experiment supported the atomic model created by Niels Bohr. In the experiment, there were three electrodes (cathode, anode and a third, netlike electrode in between them) in a tube containing low-pressure mercury gas. In addition, there was an ammeter in the tube to measure current between the electrodes. We perceived that if the value for voltage is some integer n times 4.9 volts, the current decreased considerably. According to quantum theory, atoms can absorb energy only in portions of a certain amount, and when electrons have enough kinetic energy, they excited mercury atoms by collations, which led to decreased electric current.”

  , and for models in

  Table 7. The criteria for identifying strategic knowledge S1 for models.

  S1 for Models: Identification and Definition of a Model	Examples
  1 score = identifies (by name) at least one relevant model	“Based on Planck’s hypothesis Niels Bohr created an atomic model, which explained why the spectrum is divided into lines. According to this atomic model, electrons circulate the nucleus along elliptical orbits, and the electrons’ energy is quantized. However, this model still had inconsistencies.”
  2 scores = explains the meaning of the model	“According to that hypothesis, light quantum’s energy was E = hf, and furthermore, photoelectron’s energy was Ekin = hf-W, where W is the work done to detach an electron” → consequences of the hypothesis

  and

  Table 8. The criteria for identifying relevance to strategic knowledge, S2 for models.

  S2: The Applicability and the Relevance of the Model	Examples
  1 score = presents limitations or assumptions that are needed in the model. Some inconsistency is allowed.	“Based on Planck’s hypothesis Niels Bohr created an atomic model, which explained why the spectrum is divided into lines. According to this atomic model, electrons circulate the nucleus along elliptical orbits, and the electrons’ energy is quantized. However, this model still had inconsistencies.” → quantization of energy
  2 scores = reflects on the relevance of the model, where the model leads.	“Albert Einstein took Planck’s ideas [Planck’s law] even further and created a hypothesis that electromagnetic radiation itself was quantized.” → Planck’s law is used to derive a new hypothesis

  .

6. Data Analysis and Scoring

The first author analyzed the data first. The analysis was based on the above-mentioned framework and detailed criteria using a scale of 0–2. After that, 30% of the data was double-scored by another expert on physics education to ensure the credibility of scoring. The inter-rater agreement between the scorers was 89.5% in Task 1 and 87.7 % in Task 2, indicating that researchers had a high degree of agreement, and the dimensions were scored similarly between the scorers. The disagreement between researchers were discussed through until an agreement was found.

The first part of the analysis was scoring the raw scores for each unit of analysis in the data. After scoring, averages and standard deviations of the scores were calculated. To address the second and third research questions, variation of scores and dimensions within and between the teacher candidates’ written reports was examined. In the last phase, teacher candidates were divided into three groups, based on their sum of normalized scores on both tasks (for a more detailed description of the created groups, see the Section 7), and different combinations of conceptual, relational, and strategic knowledge were analyzed. In addition, the qualitative variation in dimensions in the three groups was elaborated.

7. Results

7.1. Epistemic Dimensions Manifesting most in Teacher Candidates’ Written Reports

The results show that physics teacher candidates scored highest on the conceptual knowledge C1 (Task 1 M_C1 = 20.6, SD_C1 = 8.3 and Task 2 M_C1 = 15.4; SD_C1 = 4.3; see

Table 9. Raw scores for participants (N = 16) in Task 1. C1 and C2 stand for identification and restrictions of conceptual knowledge, respectively; R1 and R2 refer to relational knowledge, respectively; and S1 and S2 refer to strategic knowledge, respectively.

Task 1	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	M1	SD1
C1	32	14	20	23	17	39	34	15	23	24	11	14	18	13	13	19	20.6	8.3
C2	23	10	17	21	9	21	17	12	19	20	12	6	13	11	8	17	14.8	5.3
R1	8	6	8	11	8	10	15	5	12	9	8	7	5	7	4	6	8.1	2.9
R2	5	2	1	4	1	1	7	2	1	1	4	1	2	1	0	2	2.2	1.9
S1	5	2	1	4	1	1	7	2	1	1	4	1	2	1	0	2	2.2	1.9
S2	7	5	5	10	3	3	6	4	3	9	10	6	3	6	1	5	5.4	2.6

and

Table 10. Raw scores for participants (N = 16) in Task 2. C1 and C2 stand for identification and restrictions of conceptual knowledge, respectively; R1 and R2 refer to relational knowledge, respectively; and S1 and S2 refer to strategic knowledge, respectively.

Task 2	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	M2	SD2
C1	18	14	15	19	15	23	22	9	18	16	12	10	14	12	10	20	15.4	4.3
C2	17	14	17	18	16	23	19	10	18	16	12	10	14	12	10	19	15.3	3.8
R1	5	7	6	9	6	6	9	5	5	3	6	5	5	6	2	10	5.9	2.0
R2	3	3	0	3	0	0	0	0	0	1	6	0	1	1	0	2	1.3	1.7
S1	4	3	4	7	0	3	2	2	0	2	4	3	1	2	1	7	2.8	2.1
S2	3	3	1	6	0	2	5	1	0	1	4	2	0	0	0	3	1.9	1.9

). Relational knowledge scores on R1 were also relatively high (Task 1 M_R1 = 8.1 and Task 2 M_R1 = 5.9). However, scores on R2 were lower (M_R2 = 2.2 SD_R2 = 1.9 and M_R2 = 1.3, SD_R2 = 1.7 for Tasks 1 and 2, respectively) and teacher candidates scored lowest on the strategic knowledge. The standard deviations of strategic dimension compared to their means were high (Task 1 M_S1 = 2.2, SD_S1 = 1.9 and Task 2 M_S2 = 1.9; SD_S2 = 1.9).

At the general level, the scores were lower in Task 2. In Task 1, there was more variation between C1 and C2, whereas in Task 2 the scores for C1 and C2 were more similar. In addition, scores on S1 and S2 were lower in Task 2, compared to Task 1.

7.2. Variation of Conceptual, Relational, and Strategic Content Knowledge

The raw scores that teacher candidates received varied very much. To compare the scores, they were normalized. This was done for all teacher candidates according to the number of analysis units (see Appendix A and the previous Method Section) in their written reports. The analysis units were identified containing conceptual, relational or strategic knowledge. An example of a written report appears in Appendix A and has 17 conceptual analysis units, 10 relational units, and 10 strategic units. The same normalization constant was used for both subcategories in all dimensions. For example, C normalization constant was used to normalize C1 and C2 scores. The number of conceptual, relational and strategic analysis units form a personal maximum for these dimensions and these personal maximum scores could be used as normalization constants. The data normalization was then done according to these normalization constants so that all scores were normalized between values 0 and 1. The normalized scores for Task 1 is illustrated in Figure 1, and for Task 2 in Figure 2.

The average for normalized scores showed differences between teacher candidates in both Tasks 1 and 2. Average scores in Task 1 for conceptual knowledge were C1 = 0.95 and C2 = 0.70. Average scores for relational knowledge were R1 = 0.69 and R2 = 0.25. Average scores for strategic knowledge were S1 = 0.64 and S2 = 0.43.

Average scores in Task 2 for conceptual knowledge were C1 = 0.96 and C2 = 0.96. Average scores for relational knowledge were R1 = 0.74 and R2 = 0.13. Average scores for strategic knowledge were S1 = 0.62 and S2 = 0.37.

Data normalization gave us possibility to discern the prominence of different knowledge dimensions. The conceptual dimension was most prominent in both tasks. Moreover, the dimension R2 was lower in Task 2.

7.3. Combinations of Conceptual, Relational and Strategic Knowledge

There was variation between the dimensions of content knowledge among the participants, which allowed us to identify the teacher candidate groups. Teacher candidates were divided into three groups based on their total scores (i.e., the sum of normalized scores on both tasks). We used the mean (7.4) and standard deviation (1.1) of the total scores to create the groups (cf. [44]). Group 1 (n = 5) consisted of teacher candidates scoring half of the standard deviation above or below the average (7.4 ± 0.55). With this procedure, the lowest score for this group was 6.88 and the highest 7.98. Group 2 consisted of teacher candidates (n = 5) scoring below 6.88 and Group 3 consisted teacher candidates (n = 6) scoring above 7.98.

In Group 1, the teacher candidates identified and mentioned concepts, relations between concepts, and experiments and models. In addition, their scores demonstrated that these teacher candidates also presented the limitations to usability of concepts (see Figure 3). Compared to Group 2, these reports were longer and the explanations were more precise. Common to all the reports in this group was that there were also more descriptions on experiments and models. The following extract illustrates a typical report in this group. “Photoelectric effect was known already before Planck’s quantum hypothesis, but there was no proper explanation for it. It has been noted, however, that light can detach electrons from metal surface and give them kinetic energy, which is directly proportional to frequency of light.”

In Group 2, teacher candidates mainly identified concepts, relations between concepts, and experiments and models (see Figure 4). These five teacher candidates provided few or no conditions and limitations for using the concepts, or for using the relations between concepts. In addition, the teacher candidates in this group did not consider the applicability and the relevance of models or experiments. Their reports were quite short and consisted mainly on conceptual definitions, as the following extract demonstrates “Photoelectric effect takes place when electromagnetic radiation (light) causes electron detachment from metal surface.”

As Figure 5 illustrates, the different dimensions of conceptual, relational, and strategic knowledge were more evenly distributed in the cases showing in Group 3. These teacher candidates defined concepts, relations between concepts, and experiments and models as well as presented some conditions and limitation for usability of the concepts, and of experiments and models. In these reports the explanations were quite comprehensive in nature and, especially, compared to Groups 1 and 2, experiments and models were described in more detailed way. The following extract describes a typical report in this group. “Monochromatic light is pointed towards different metals and electrons are detached from metal surface. Metals are connected as part of electric circuit so that electron detaching causes electric current. This gives us an opportunity to calculate the kinetic energy for electrons. Then we seek a voltage which stops the current and we perceive that there is a direct proportionality between electrons’ kinetic energy and frequency of light. By varying the experimental conditions, we can verify that Einstein’s equation is correct, and that the phenomenon happens only when the work to detach electron is large enough. The energy of a photon is transferred to an electron as one portion, which is an indication of the particle nature of light.”

8. Discussion and Conclusions

8.1. Discussion of Benefits and Challenges Relating to the Framework Developed and Utilized in the Study

The study provides a basis for more systematic evaluation and understanding of epistemic characteristics of content knowledge, namely conceptual, relational, and strategic dimensions among physics teacher candidates. This epistemic framework provides possibilities for examining and scoring different epistemic dimensions separately and together. The analysis done by using the epistemic framework shows differences between teacher candidates’ knowledge even though the sample is small (N = 16). Previous frameworks allow focusing mainly on identification of concepts and facts (cf. [35]), and they do not yield to analyzing how and why the knowledge is formed. The importance of strategic knowledge was emphasized by Shavelson [42], while Nousiainen [33] discussed it from the viewpoint of physics knowledge formation. Understanding and commanding the strategic knowledge of physics can be regarded as one key item of physics teachers’ content knowledge [9,33].

The analysis shows us that for this sample (N = 16) conceptual knowledge is most prominent in teacher candidates’ written reports. Relational knowledge is presented less and strategic knowledge the least. This order is sensible because relational knowledge is dependent on conceptual knowledge, while strategic knowledge relying on both relational and conceptual knowledge is more complex and challenging to manage. However, we do not know what kind of combination of conceptual, relational, and strategic knowledge would be ideal for teacher candidates. The epistemic analysis shows that strategic knowledge is as important a dimension in physics content knowledge as conceptual knowledge and relational knowledge are. From physics knowledge point of view, all knowledge components are needed and therefore we need more understanding how physics teachers knowledge is formed (cf. [9,33]), and how it is related with general pedagogical knowledge (cf. [45]).

The assignments for the tasks were open, which means that teacher candidates were free to decide which concepts they chose in their concept maps to be explained in the written report. Therefore, the written reports (analyzed in this study) differed from each other, some having only few core components, but well explained (see, e.g., Tasks 1 and 2 from Teacher Candidate 11), and some expressing several concepts, but only at the level of identification (see, e.g., Task 1 from Teacher Candidate 6). One possible solution would be closing the assignment so that a list of core components (physics concepts, laws, models and experiments) would be handed out to teacher candidates and their task would be to link them together and explain the relations between the components. However, in that case, we would not be able to evaluate whether students are able to recognize the relevant and core components regarding the phenomenon. Thus, an obvious limitation of such a solution is that it changes the demands of the task and the aspects/dimensions that are supposed to be evaluated (cf. [40]).

Although concept maps together with written reports intend to provide information of students’ knowledge structure (i.e., what students know and how that knowledge used), it needs to be noted that one analysis framework alone does not capture different aspects of complex cognitive processes (see [41,46,47]). The key challenge in exploring students’ thinking, which involves mental processes, is that this kind of phenomenon is not directly observable. Therefore, interpretations of students’ understanding are always more or less indirect. Consequently, to explore students knowing thoroughly, varying methods for eliciting students’ performance regarding conceptual, relational, and strategic knowledge are needed (see [41]). A challenging question worth investigating is: How do the teacher candidates make use of their content knowledge in authentic classroom situations, and how is their knowledge realized in such situations?

8.2. Discussion of Findings Relating to the Framework Developed and Utilized in the Study

The results show that teacher candidates expressed very little strategic knowledge (S1) and even less reflection was presented about the conditions to use the strategic knowledge (S2). This may result from the way the teacher candidates are taught physics and therefore they do not pay attention in experiments and models (see, e.g., [3,29]). Physics teacher education should pay more attention in teaching strategic knowledge. Findings thus highlight dominance in conceptual knowledge and minority on strategic knowledge. This might be due to the way physics is taught at school, where not much effort is paid in questioning the well-established physics laws and models (cf. [30]).

The two tasks analyzed here (written reports about the photoelectric effect, Task 1, and Compton effect, Task 2) show the differences between the occurrence of the epistemic dimensions in the tasks. This means that epistemic dimensions are task-dependent. Therefore, the results discussed in this study can be used to exemplify the usability of the framework in discerning the epistemic dimensions. To make any further conclusions and before this framework can be used as an assessment tool in classrooms, more data and different tasks are needed to confirm the results and to provide reliability and validity information on the framework (see [40,41]).

This study has the several limitations: (1) a small sample of students in one discipline was involved; (2) only two tasks were analyzed; (3) one course was represented; and (4) only one university was involved. This may indicate the risk of potential bias in the results. Owing to these limitations, the results of this study should not be interpreted as an accurate prediction of the target population. However, the results of this study rather illustrate the nature of the phenomenon being studied. The results also indicate that the framework separated students in terms of their epistemic dimensions of content knowledge. The results has been utilized as a basis for further theoretical development as well as more extensive empirical studies.

There are still open questions for further research: (1) What is the desirable and relevant balance between the epistemic dimensions for physics teacher candidates during teacher education? (2) How do we ensure the suitable balance between the epistemic dimensions in teaching physics teacher candidates? (3) How is strategic knowledge in physics taught more efficiently to physics teacher candidates? We need longitudinal research where physics teacher candidates’ content knowledge and pedagogical knowledge development are investigated during the teacher preparation program and especially when entering to work as teachers. The framework introduced here would serve as one research tool in such studies. Such research would provide information on how strong content knowledge is integrated with the pedagogical knowledge and further translated into knowledge and skills necessary for teaching the subject in a classroom (see [12,20]).

The framework can be further used as a tool for facilitating and analyzing teacher candidates’ understanding of complex concepts as well as their ability to utilize these concepts. At the same time, this framework also produces information for teacher educators when and where to intervene and enhance teaching practices. Further development of university education needs high-quality teaching practices that meet appropriately the varied needs of a heterogeneous student population.