Educational Stakeholders’ Independent Evaluation of an Artificial Intelligence-Enabled Adaptive Learning System Using Bayesian Network Predictive Simulations
Abstract
1. Introduction
2. Research Problem
Potential Issues That Education Researchers Might Encounter
3. Methods
3.1. Rationale for Using the Bayesian Approach
3.2. The Bayesian Theorem
3.3. The Research Model
Section 4: “What has already happened?” Descriptive Analytics
Purpose: To use descriptive analytics to discover the pedagogical motif in the collected data.
For descriptive analytics, BN modeling (in Section 4.5, Section 4.6 and Section 4.7) utilizes the parameter estimation algorithm to automatically detect the data distribution of each column in the dataset. In Section 4.8, further descriptive statistical techniques are employed to understand more about the current baseline conditions of the students including quadrant analysis, curves analysis, and Pearson correlation analysis.
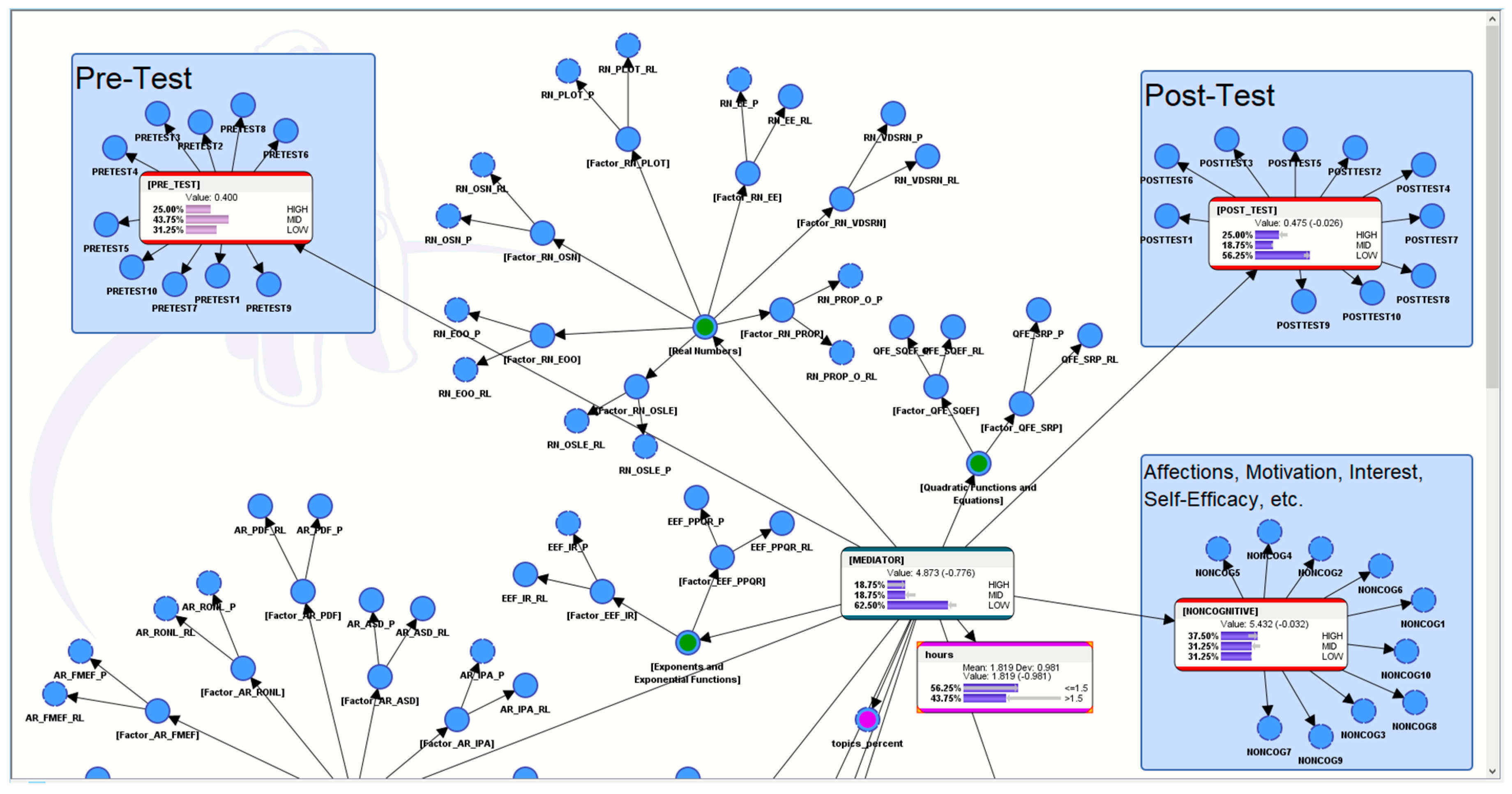
Section 5: “What If?” Predictive Analytics
Purpose: To use predictive analytics to perform in silico experiments with fully controllable parameters from the pre-test to the mediating intervention to the post-test to predict future outcomes. Beyond just simply measuring gains by subtracting the students’ post-test scores from the pre-test scores, this paper proffers a probabilistic Bayesian approach which could simulate various scenarios to better inform educators and policy-makers about the pedagogical characteristics of the AI-ALS that is being evaluated.
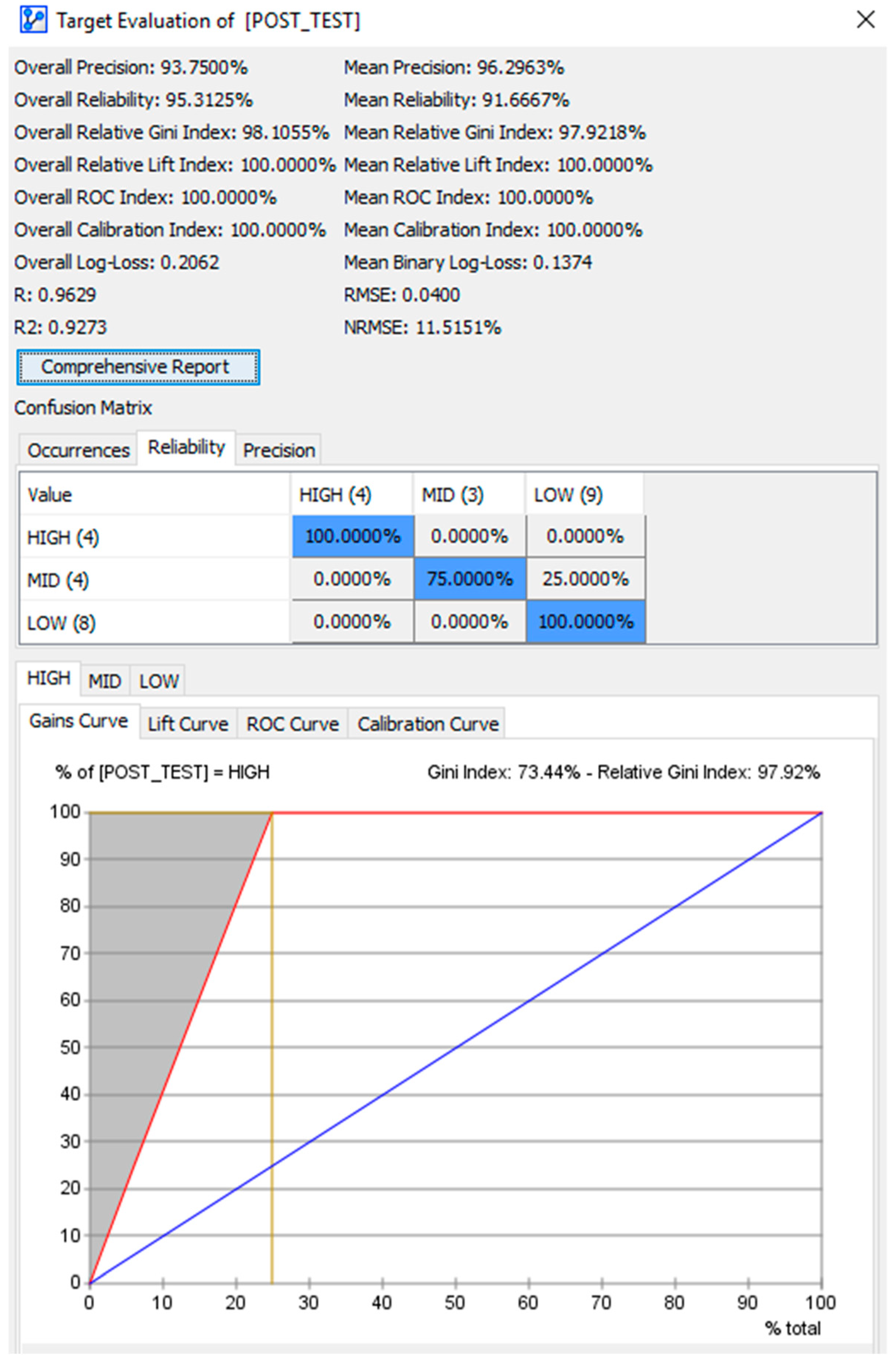
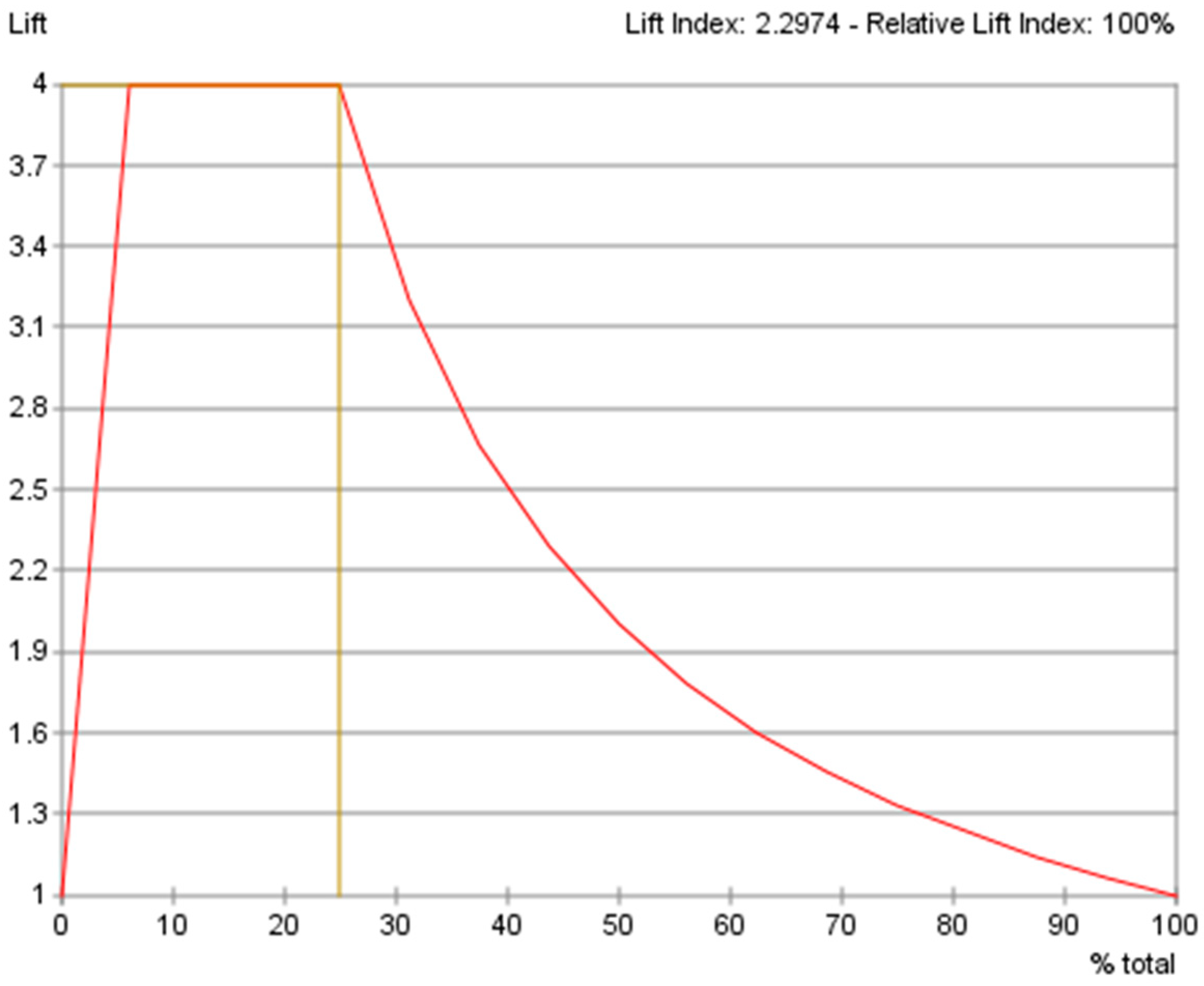
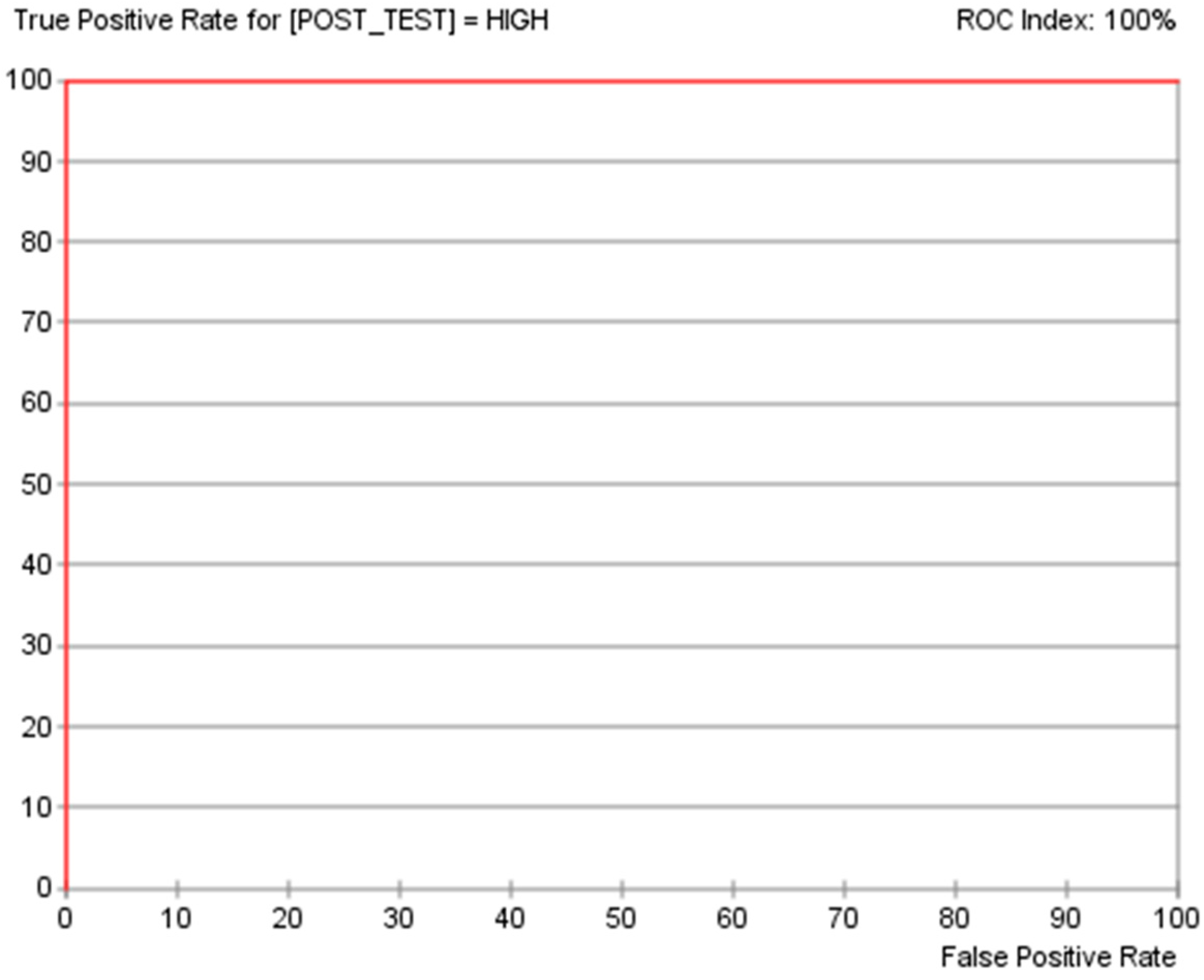
For predictive analytics, counterfactual simulations (in Section 5) will be employed to explore the pedagogical motif of the AI-ALS. In Section 6, the predictive performance of the BN model is evaluated using tools that include the gains curve, the lift curve, and the receiver operating characteristic curve, as well as by statistical bootstrapping of the data inside each column of the dataset (which is also the data distribution in each node of the BN model) 1000 times to generate a larger dataset to measure its precision, reliability, Gini index, lift index, calibration index, the binary log-loss, the correlation coefficient R, the coefficient of determination R2, root-mean-square error (RSME), and normalized root-mean-square error (NRSME).
4. Descriptive Analytics: “What Has Already Happened?”
4.1. The Dataset Procured from the Reports Generated by AI-ALS
4.2. Codebook of the Dataset
4.3. Software Used: Bayesialab
4.4. Pre-Processing: Checking for Missing Values or Errors in the Data
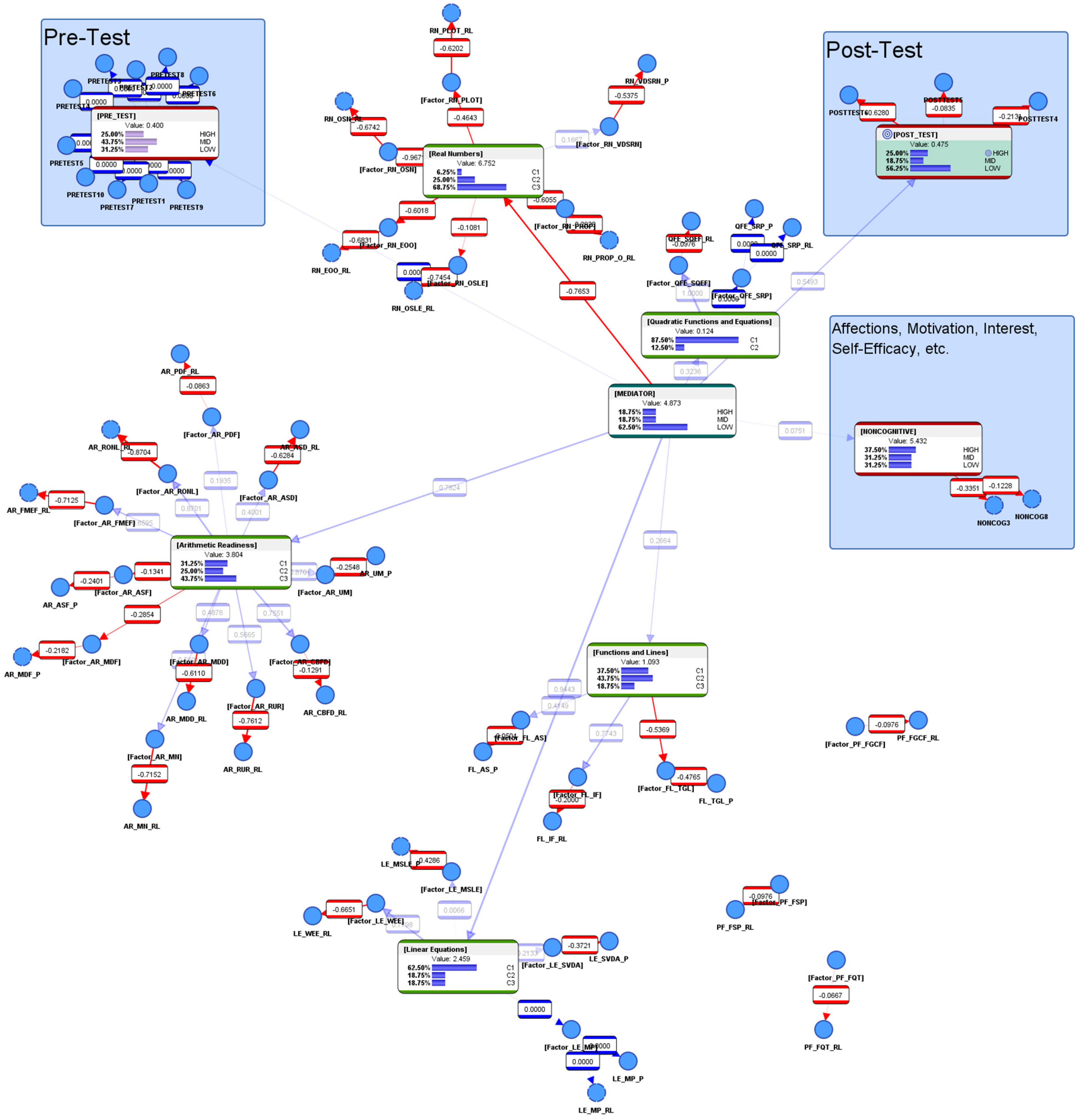
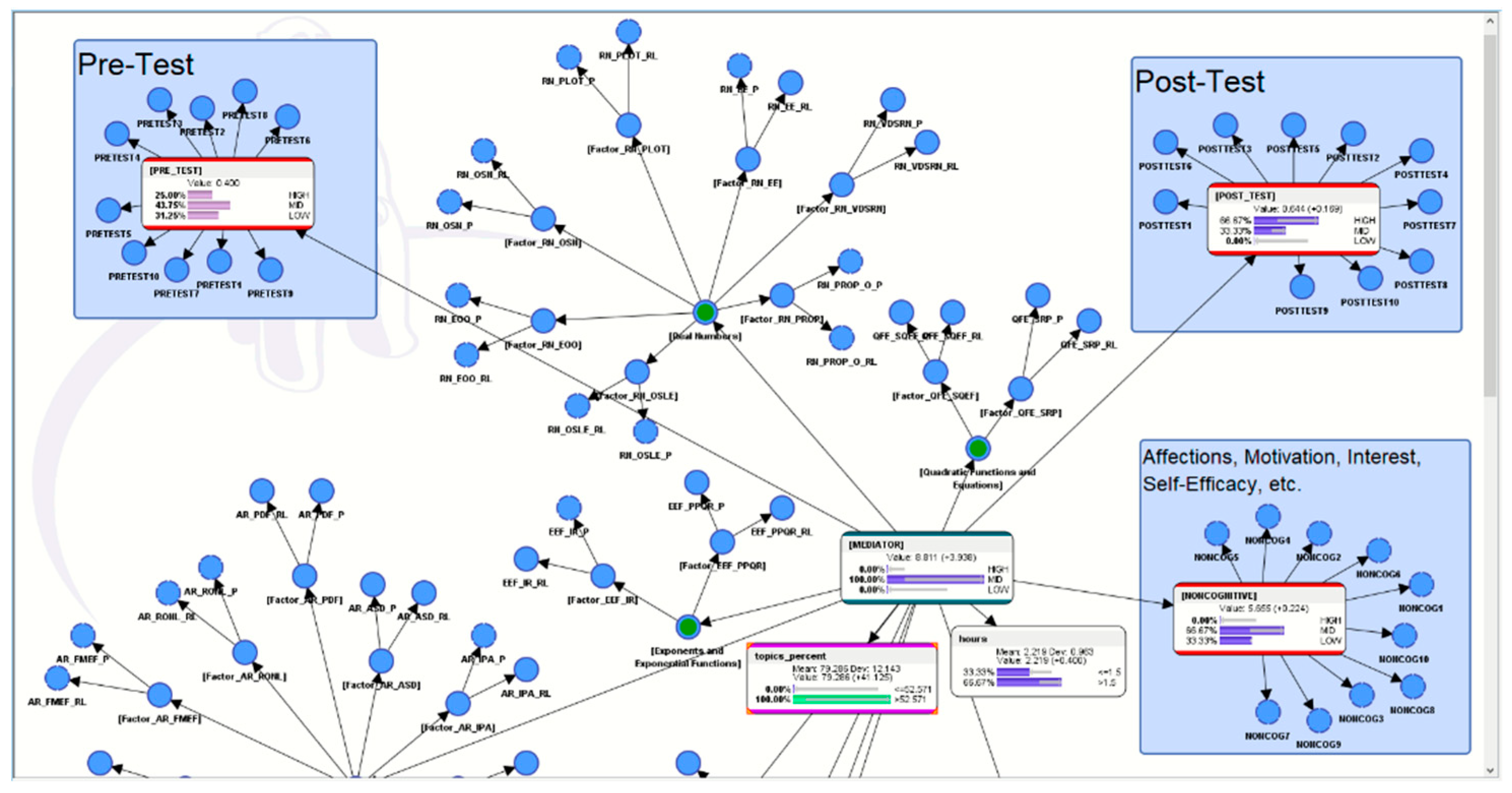
4.5. Overview of the BN Model
4.6. Initial Hypothetical Conjecture of the Researcher
4.7. Detailed Descriptions of the BN in the Current Paper
4.8. Descriptive Statistical Analysis of the Dataset
4.8.1. Descriptive Analytics: Quadrant Analysis
4.8.2. Descriptive Analytics: Curves Analysis
4.8.3. Descriptive Analytics: Pearson Correlation Analysis
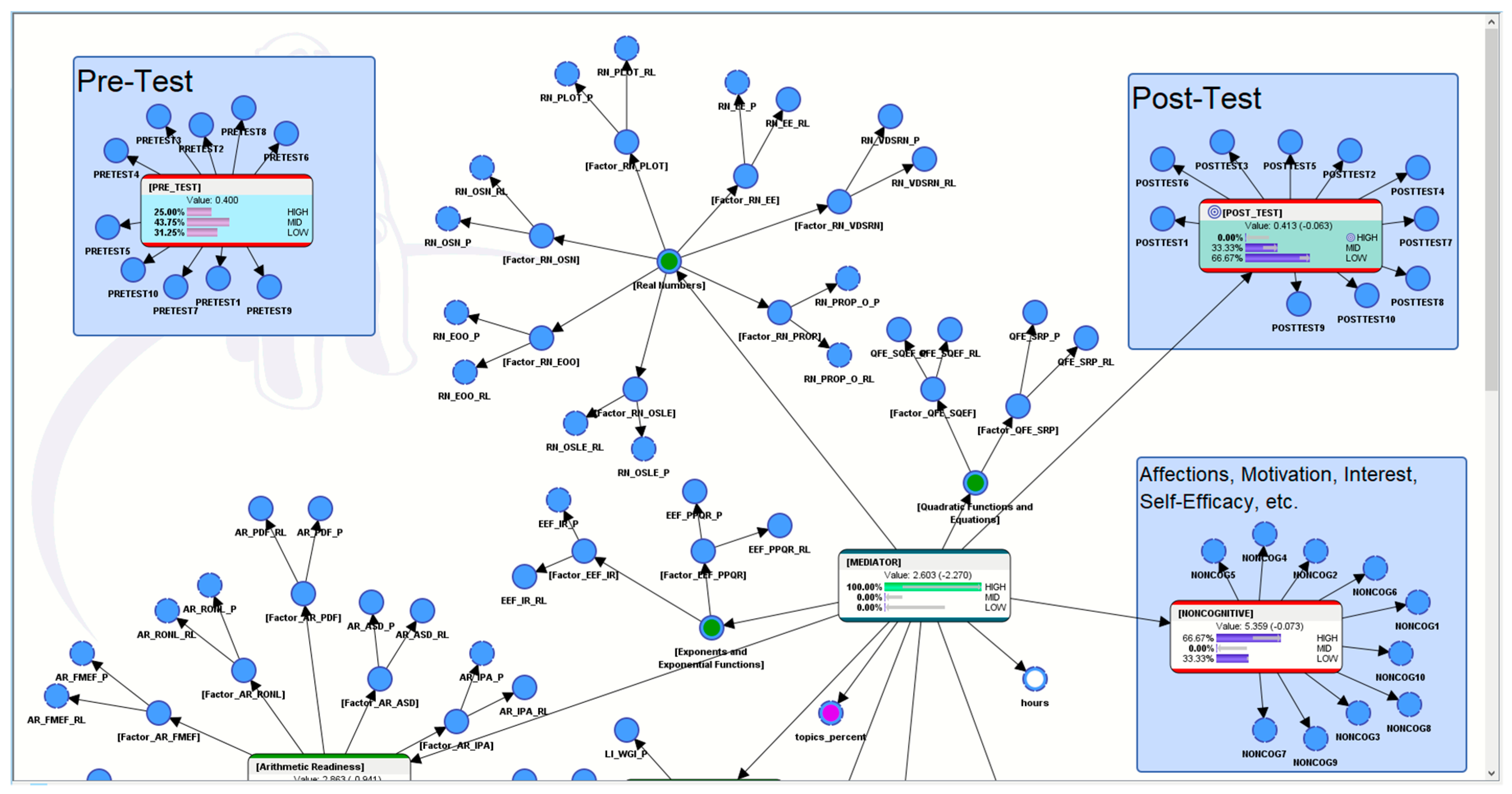
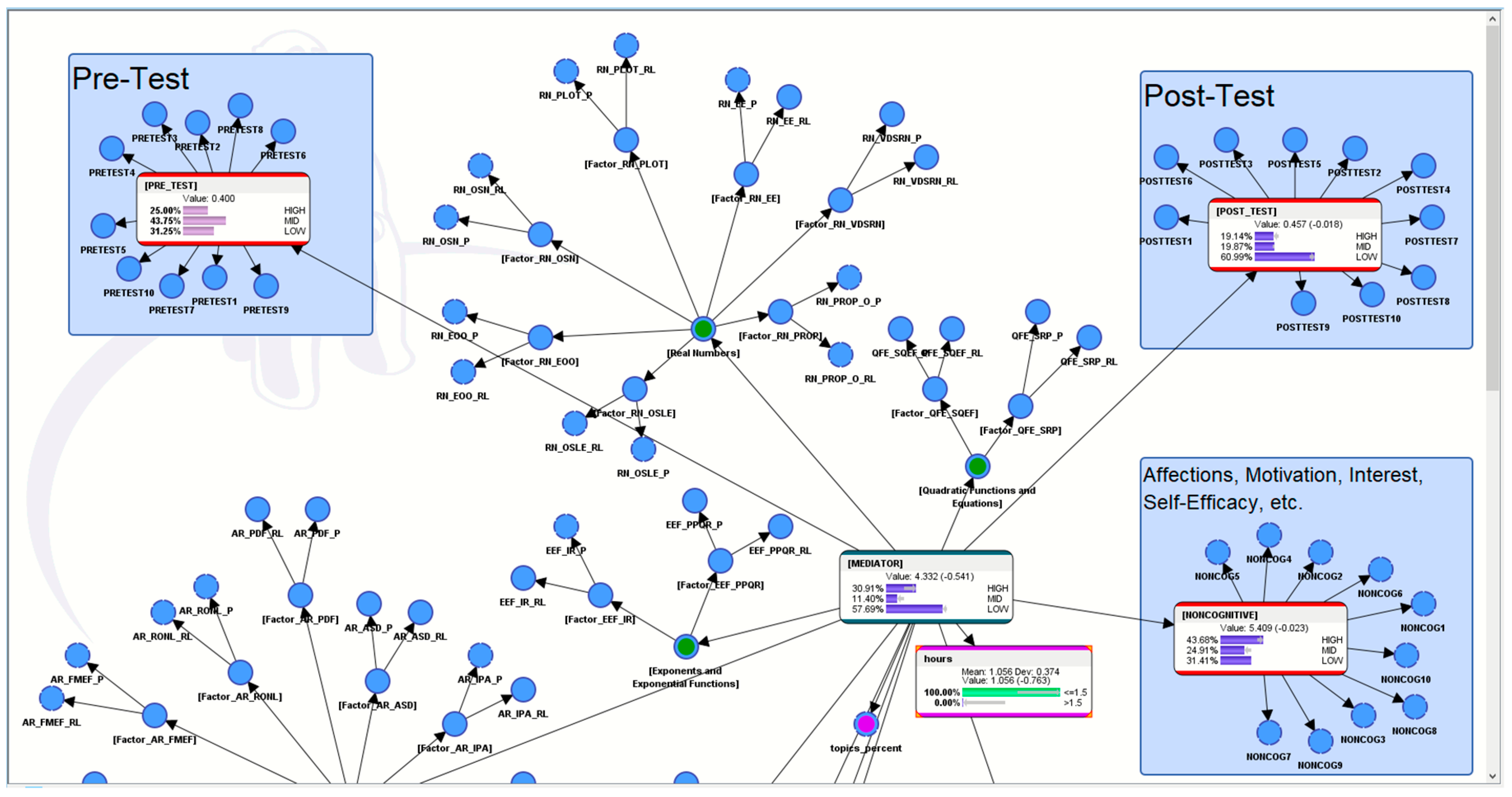
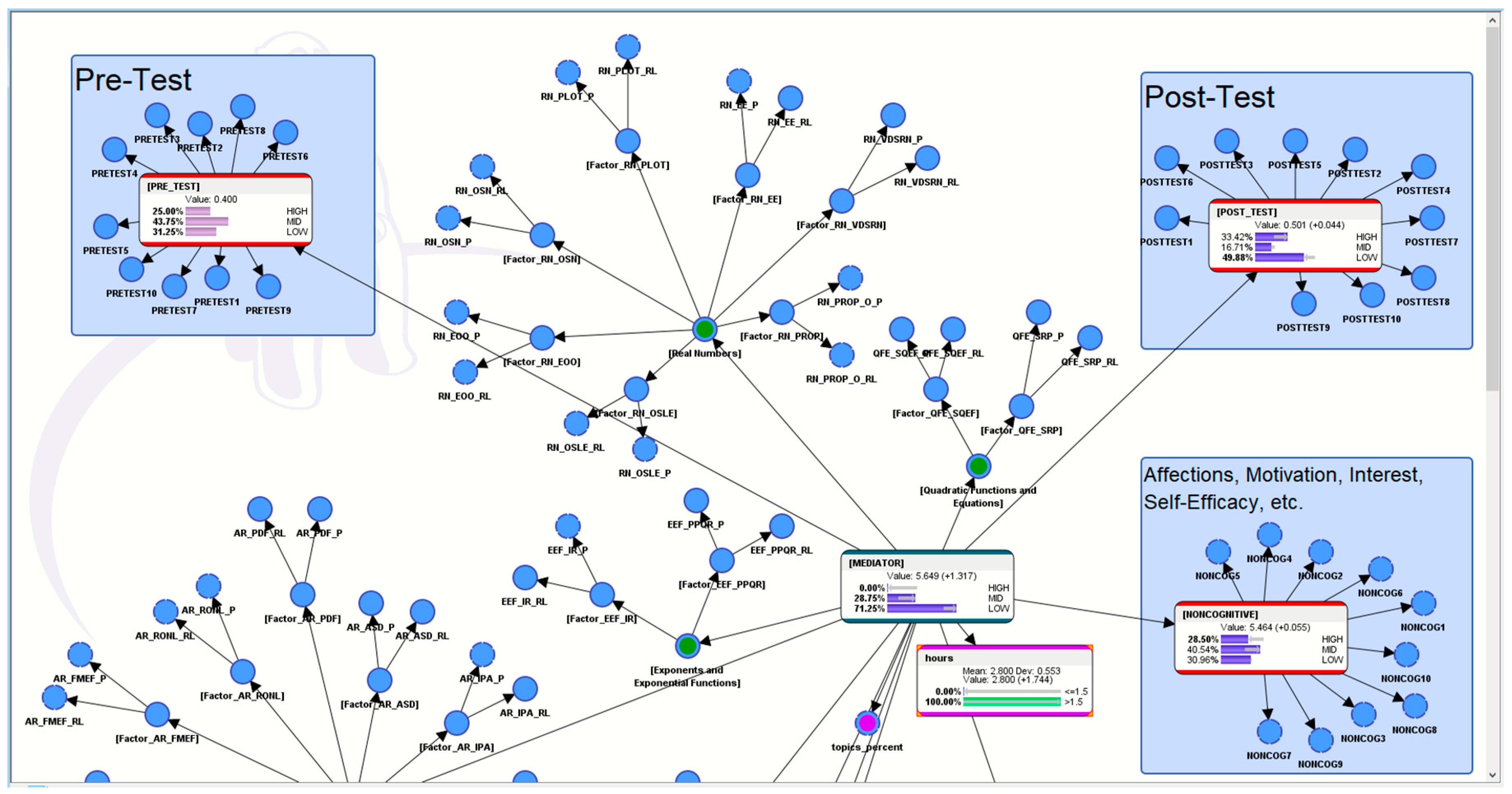
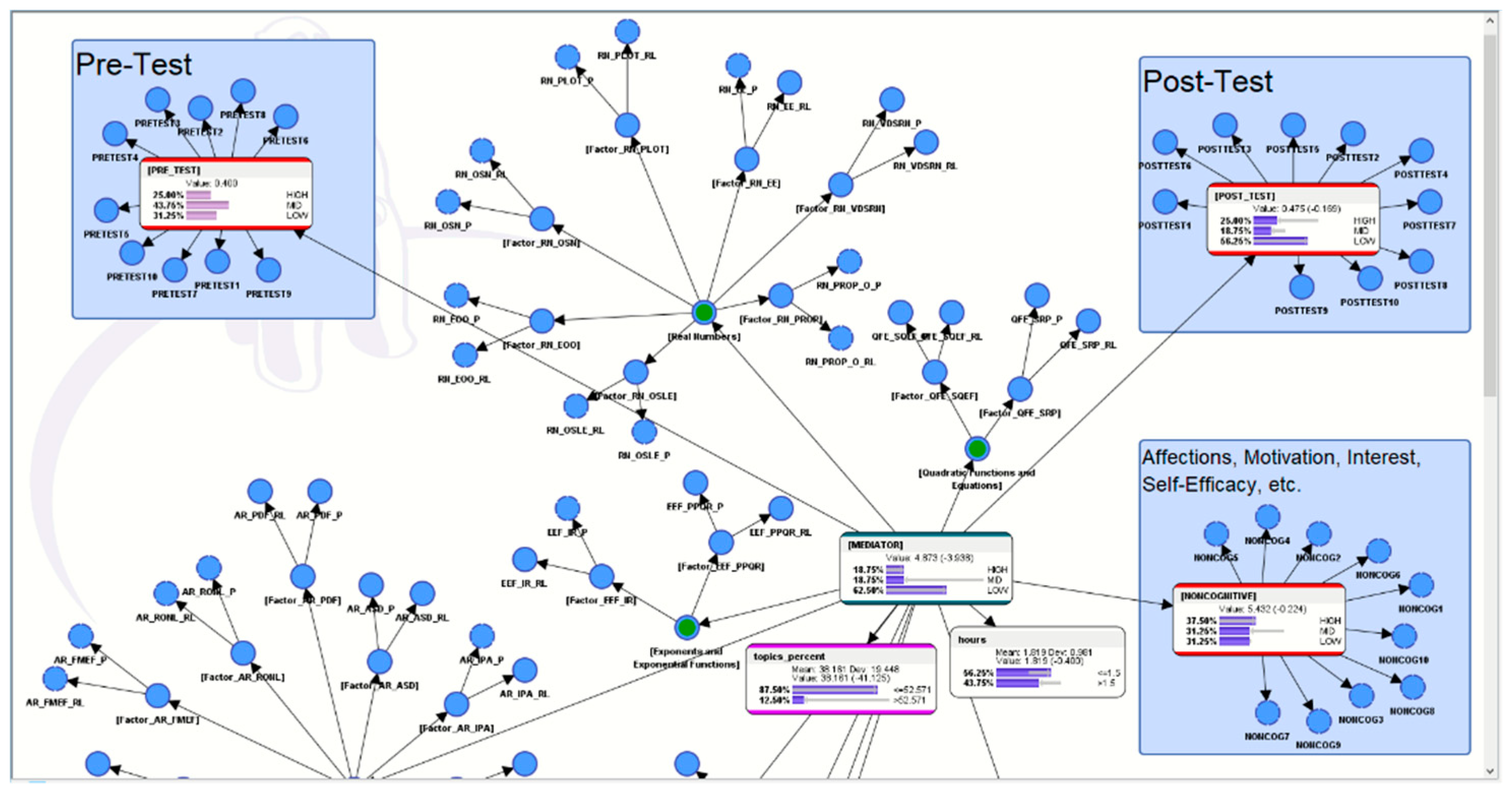
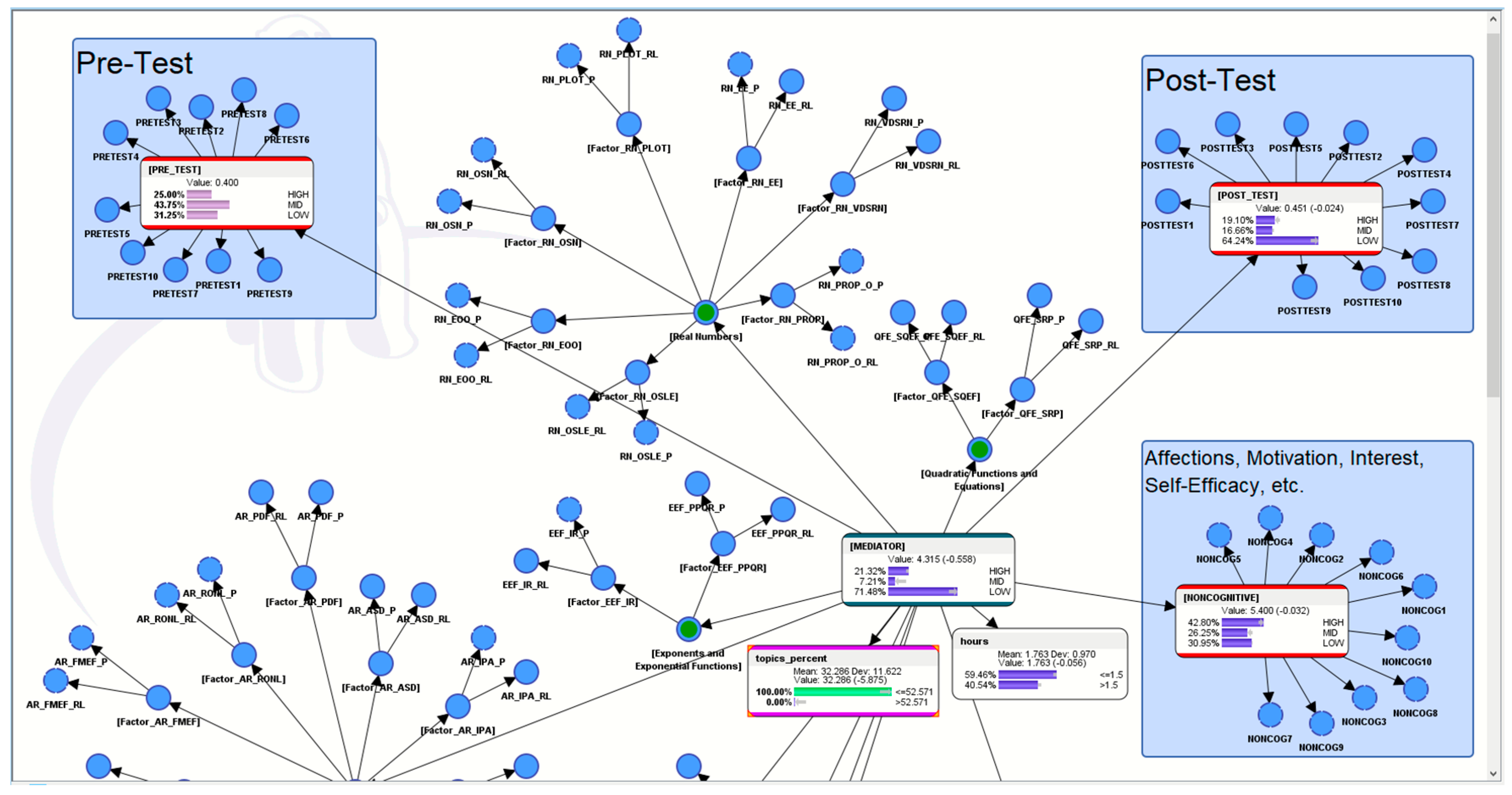
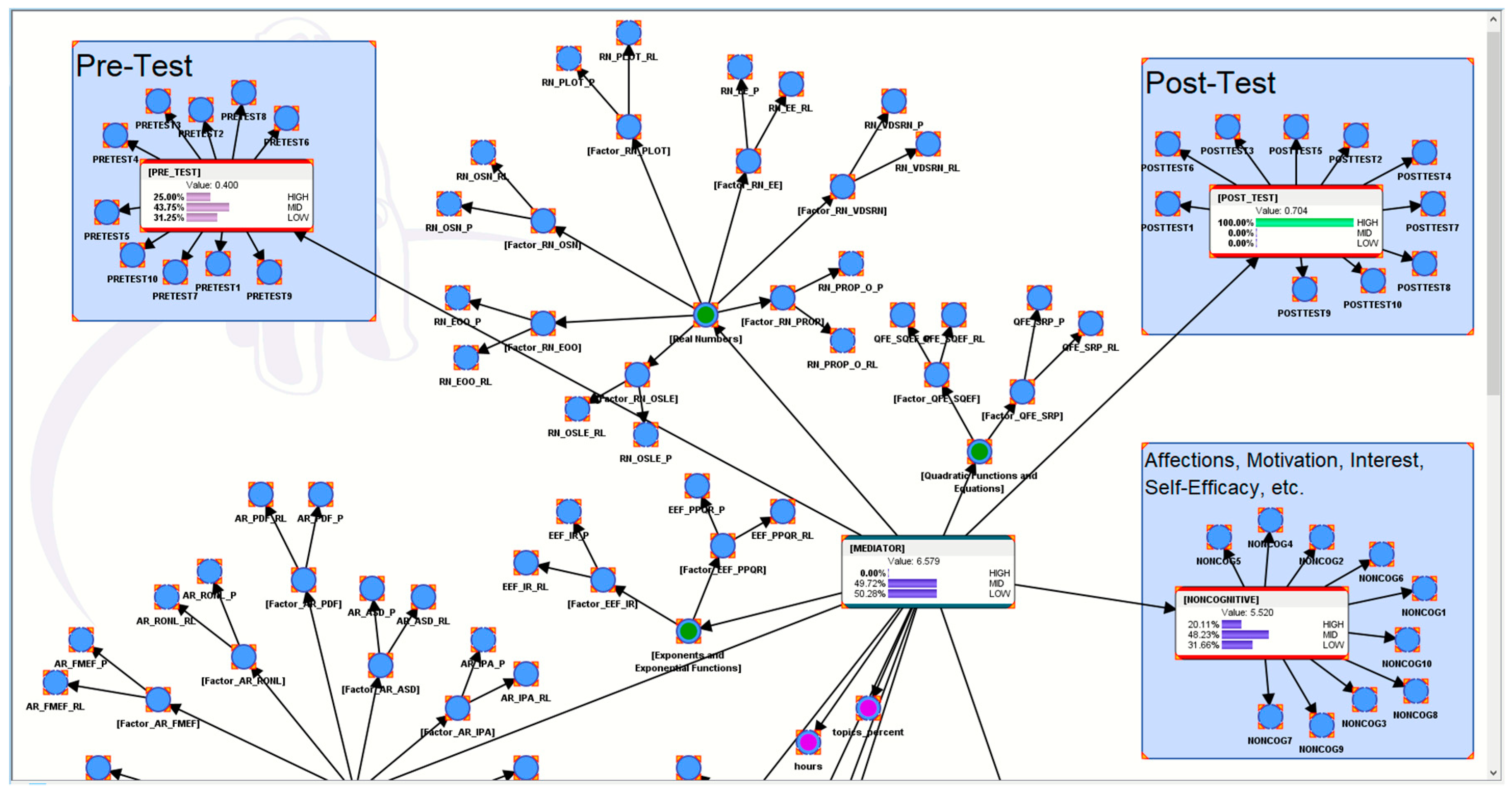
5. “What If?” Analytics to Understand More about the Pedagogical Motif of the AI-ALS
5.1. Hypothetical Scenario 1
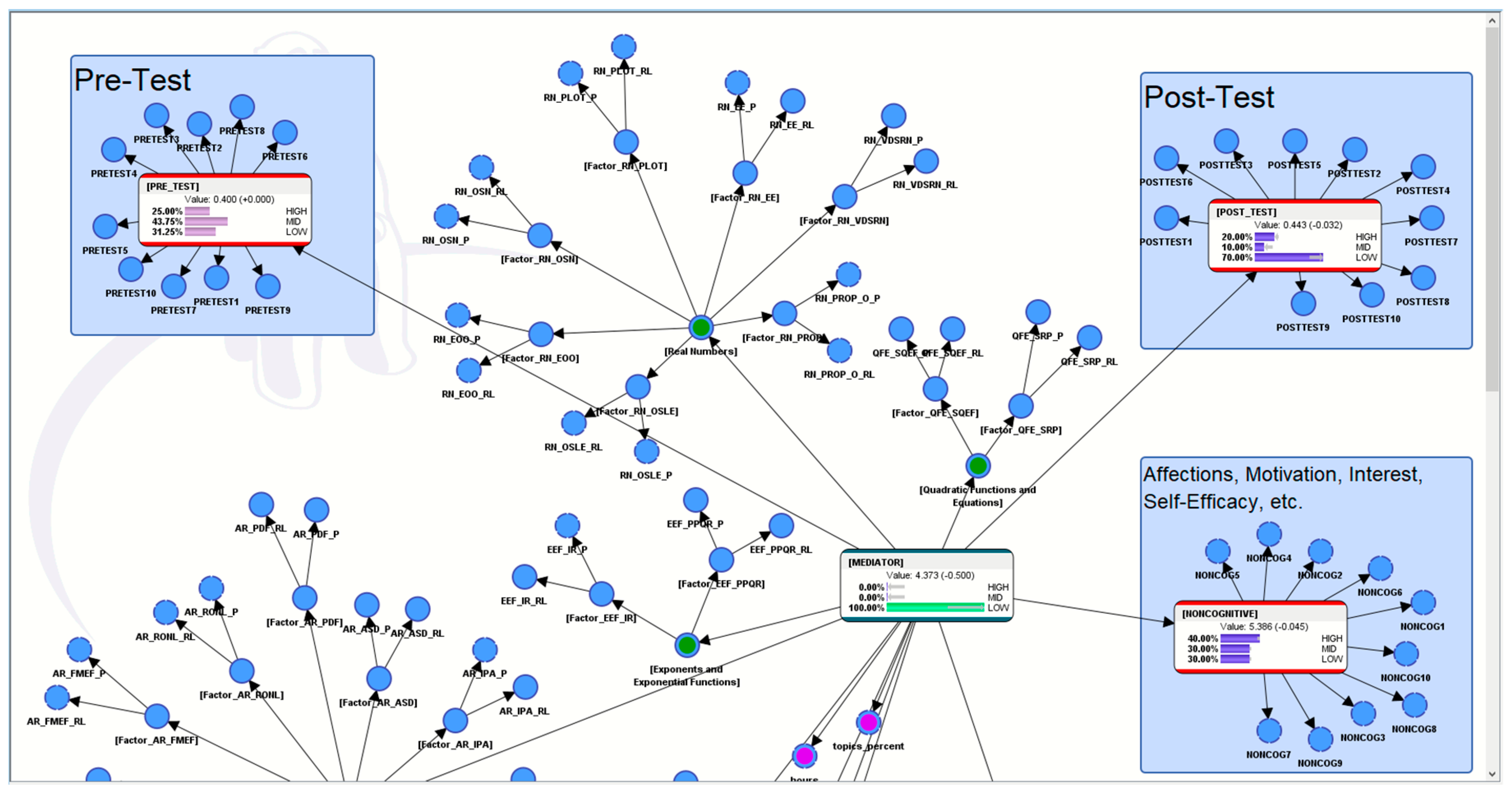
5.2. Hypothetical Scenario 2
5.3. Hypothetical Scenario 3
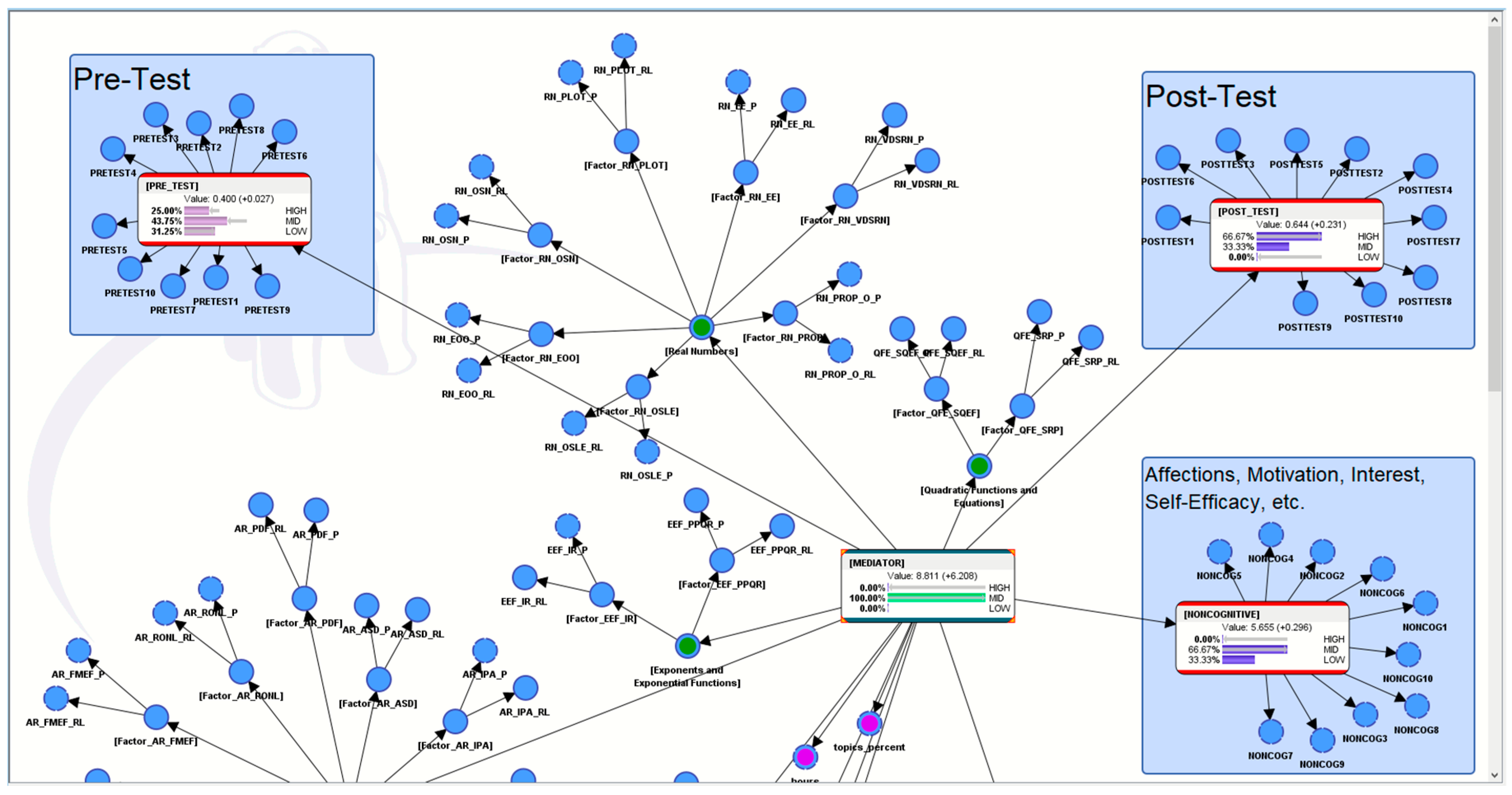
5.4. Hypothetical Scenario 4
5.5. Hypothetical Scenario 5
5.6. Hypothetical Scenario 6
5.7. Hypothetical Scenario 7
6. Evaluation of the Predictive Performance of the Bayesian Network Model
6.1. Gains Curve Analysis
6.2. Lift Curve Analysis
6.3. Receiver Operating Characteristic (ROC)
6.4. Statistical Bootstrapping
6.5. Limitations of the Study
7. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Ethical Considerations for Protection of the Identities of the Students and the AI-ALS Vendor
References
- Wilson, C.; Scott, B. Adaptive systems in education: A review and conceptual unification. Int. J. Inf. Learn. Technol. 2017, 34, 2–19. [Google Scholar] [CrossRef]
- Nkambou, R.; Mizoguchi, R.; Bourdeau, J. Introduction: What Are Intelligent Tutoring Systems, and Why This Book? In Advances in Intelligent Tutoring Systems; Nkambou, R., Mizoguchi, R., Bourdeau, J., Eds.; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2010; Volume 308, ISBN 978-3-642-14362-5. [Google Scholar]
- Garrido, A. AI and Mathematical Education. Educ. Sci. 2012, 2, 22–32. [Google Scholar] [CrossRef]
- VanLehn, K. The relative effectiveness of human tutoring, intelligent tutoring systems, and other tutoring systems. Educ. Psychol. 2011, 46, 197–221. [Google Scholar] [CrossRef]
- Cen, H.; Koedinger, K.R.; Junker, B. Is Over Practice Necessary?—Improving learning efficiency with the cognitive tutor through Educational Data Mining. Front. Artif. Intell. Appl. 2007, 158, 511. [Google Scholar]
- VanLehn, K. The behavior of tutoring systems. Int. J. Artif. Intell. Educ. 2006, 16, 227–265. [Google Scholar]
- Hawkins, W.J.; Heffernan, N.T.; Baker, R.S.J.D. Learning Bayesian Knowledge Tracing Parameters with a Knowledge Heuristic and Empirical Probabilities. In Intelligent Tutoring Systems; Trausan-Matu, S., Boyer, K.E., Crosby, M., Panourgia, K., Eds.; Springer International Publishing: Cham, Switzerland, 2014; Volume 8474, pp. 150–155. ISBN 978-3-319-07220-3. [Google Scholar]
- Magoulas, G.D.; Papanikolaou, Y.; Grigoriadou, M. Adaptive web-based learning: Accommodating individual differences through system’s adaptation. Br. J. Educ. Technol. 2003, 34, 511–527. [Google Scholar] [CrossRef]
- Brusilovsky, P.; Karagiannidis, C.; Sampson, D. Layered evaluation of adaptive learning systems. Int. J. Contin. Eng. Educ. Lifelong Learn. 2004, 14, 402. [Google Scholar] [CrossRef]
- Hox, J.; van de Schoot, R.; Matthijsse, S. How few countries will do? Comparative survey analysis from a Bayesian perspective. Surv. Res. Methods 2012, 6, 87–93. [Google Scholar]
- Bayes, T. A Letter from the Late Reverend Mr. Thomas Bayes, F.R.S. to John Canton, M.A. and F. R. S. R. Soc. Philos. Trans. 1763, 53, 269–271. [Google Scholar]
- van de Schoot, R.; Kaplan, D.; Denissen, J.; Asendorpf, J.B.; Neyer, F.J.; van Aken, M.A.G. A Gentle Introduction to Bayesian Analysis: Applications to Developmental Research. Child Dev. 2014, 85, 842–860. [Google Scholar] [CrossRef] [PubMed]
- Pearl, J. Causality: Models, Reasoning, and Inference, 2nd ed.; Cambridge University Press: Cambridge, UK, 2010; ISBN 978-0-521-89560-6. [Google Scholar]
- Pearl, J. Causes of Effects and Effects of Causes. Sociol. Methods Res. 2015, 44, 149–164. [Google Scholar] [CrossRef]
- Pearl, J. Fusion, propagation, and structuring in belief networks. Artif. Intell. 1986, 29, 241–288. [Google Scholar] [CrossRef]
- Lee, S.-Y.; Song, X.-Y. Evaluation of the Bayesian and maximum likelihood approaches in analyzing structural equation models with small sample sizes. Multivar. Behav. Res. 2004, 39, 653–686. [Google Scholar] [CrossRef]
- Button, K.S.; Ioannidis, J.P.; Mokrysz, C.; Nosek, B.A.; Flint, J.; Robinson, E.S.; Munafao, M.R. Power failure: Why small sample size undermines the reliability of neuroscience. Nat. Rev. Neurosci. 2013, 14, 365–376. [Google Scholar] [CrossRef]
- Kaplan, D.; Depaoli, S. Bayesian structural equation modeling. In Handbook of Structural Equation Modeling; Hoyle, R., Ed.; Guilford Press: New York, NY, USA, 2012; pp. 650–673. [Google Scholar]
- Walker, L.J.; Gustafson, P.; Frimer, J.A. The application of Bayesian analysis to issues in developmental research. Int. J. Behav. Dev. 2007, 31, 366–373. [Google Scholar] [CrossRef]
- Zhang, Z.; Hamagami, F.; Wang, L.; Grimm, K.J.; Nesselroade, J.R. Bayesian analysis of longitudinal data using growth curve models. Int. J. Behav. Dev. 2007, 31, 374–383. [Google Scholar] [CrossRef]
- Kaplan, D. Causal inference with large-scale assessments in education from a Bayesian perspective: A review and synthesis. Large-Scale Assess. Educ. 2016, 4, 7. [Google Scholar] [CrossRef]
- Levy, R. Advances in Bayesian Modeling in Educational Research. Educ. Psychol. 2016, 51, 368–380. [Google Scholar] [CrossRef]
- Mathys, C. A Bayesian foundation for individual learning under uncertainty. Front. Hum. Neurosci. 2011, 5, 39. [Google Scholar] [CrossRef]
- Muthén, B.; Asparouhov, T. Bayesian structural equation modeling: A more flexible representation of substantive theory. Psychol. Methods 2012, 17, 313–335. [Google Scholar] [CrossRef] [PubMed]
- Bekele, R.; McPherson, M. A Bayesian performance prediction model for mathematics education: A prototypical approach for effective group composition. Br. J. Educ. Technol. 2011, 42, 395–416. [Google Scholar] [CrossRef]
- Millán, E.; Agosta, J.M.; Cruz, J.L. Pérez de la Bayesian student modeling and the problem of parameter specification. Br. J. Educ. Technol. 2002, 32, 171–181. [Google Scholar]
- Shannon, C.E. The lattice theory of information. IRE Prof. Group Inf. Theory 1953, 1, 105–107. [Google Scholar] [CrossRef]
- Cowell, R.G.; Dawid, A.P.; Lauritzen, S.L.; Spieglehalter, D.J. Probabilistic Networks and Expert Systems: Exact Computational Methods for Bayesian Networks; Springer: New York, NY, USA, 1999; ISBN 978-0-387-98767-5. [Google Scholar]
- Jensen, F.V. An Introduction to Bayesian Networks; Springer: New York, NY, USA, 1999; ISBN 0-387-91502-8. [Google Scholar]
- Korb, K.B.; Nicholson, A.E. Bayesian Artificial Intelligence; Chapman & Hall/CRC: London, UK, 2010; ISBN 978-1-4398-1591-5. [Google Scholar]
- Tsamardinos, I.; Aliferis, C.F.; Statnikov, A. Time and sample efficient discovery of Markov blankets and direct causal relations. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining—KDD’03, Washington, DC, USA, 24–27 August 2003; p. 673. [Google Scholar]
- Guoyi, C.; Hu, S.; Yang, Y.; Chen, T. Response surface methodology with prediction uncertainty: A multi-objective optimisation approach. Chem. Eng. Res. Des. 2012, 90, 1235–1244. [Google Scholar]
- Fox, R.J.; Elgart, D.; Christopher Davis, S. Bayesian credible intervals for response surface optima. J. Stat. Plan. Inference 2009, 139, 2498–2501. [Google Scholar] [CrossRef]
- Miró-Quesada, G.; Del Castillo, E.; Peterson, J.J. A Bayesian approach for multiple response surface optimization in the presence of noise variables. J. Appl. Stat. 2004, 31, 251–270. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 3rd ed.; Wiley and Sons, Inc.: New Jersey, NJ, USA, 2009; ISBN 978-0-470-17446-3. [Google Scholar]
- Collins, J.A.; Greer, J.E.; Huang, S.H. Adaptive Assessment Using Granularity Hierarchies and Bayesian Nets; Springer: Berlin/Heidelberg, Germany, 1996; Volume 1086, pp. 569–577. [Google Scholar]
- Conati, C.; Gertner, A.; VanLehn, K.; Druzdzel, M. On-line student modelling for coached problem solving using Bayesian networks. In Proceedings of the UM’97, Sardinia, Italy, 2–5 June 1997; Springer: Berlin/Heidelberg, Germany, 1997; pp. 231–242. [Google Scholar]
- Jameson, A. Numerical uncertainty management in user and student modeling: An overview of systems and issues. User Modeling User-Adapt. Interact. 1996, 5, 193–251. [Google Scholar] [CrossRef]
- VanLehn, K.; Niu, Z.; Siler, S.; Gertner, A.S. Student Modeling from Conventional Test Data: A Bayesian Approach without Priors; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1452, pp. 434–443. [Google Scholar]
- Conrady, S.; Jouffe, L. Bayesian Networks & BayesiaLab: A Practical Introduction for Researchers; Bayesia: Franklin, TN, USA, 2015; ISBN 0-9965333-0-3. [Google Scholar]
- Lauritzen, S.L.; Spiegelhalter, D.J. Local computations with probabilities on graphical structures and their application to expert systems. J. R. Stat. Soc. 1988, 50, 157–224. [Google Scholar] [CrossRef]
- Kschischang, F.; Frey, B.; Loeliger, H. Factor graphs and the sum product algorithm. IEEE Trans. Inf. Theory 2001, 47, 498–519. [Google Scholar] [CrossRef]
- Pezzulo, G.; Cartoni, E.; Rigoli, F.; Pio-Lopez, L.; Friston, K. Active inference, epistemic value, and vicarious trial and error. Learn. Mem. 2016, 23, 322–338. [Google Scholar] [CrossRef] [PubMed]
- Al-Mutawah, M.A.; Fateel, M.J. Students’ Achievement in Math and Science: How Grit and Attitudes Influence? Int. Educ. Stud. 2018, 11, 97. [Google Scholar] [CrossRef]
- Chamberlin, S.A.; Moore, A.D.; Parks, K. Using confirmatory factor analysis to validate the Chamberlin affective instrument for mathematical problem solving with academically advanced students. Br. J. Educ. Psychol. 2017, 87, 422–437. [Google Scholar] [CrossRef] [PubMed]
- Egalite, A.J.; Mills, J.N.; Greene, J.P. The softer side of learning: Measuring students’ non-cognitive skills. Improv. Sch. 2016, 19, 27–40. [Google Scholar] [CrossRef]
- Lipnevich, A.A.; MacCann, C.; Roberts, R.D. Assessing Non-Cognitive Constructs in Education: A Review of Traditional and Innovative Approaches. In The Oxford Handbook of Child Psychological Assessment; Oxford University Press: New York, NY, USA, 2013. [Google Scholar]
- Mantzicopoulos, P.; Patrick, H.; Strati, A.; Watson, J.S. Predicting Kindergarteners’ Achievement and Motivation from Observational Measures of Teaching Effectiveness. J. Exp. Educ. 2018, 86, 214–232. [Google Scholar] [CrossRef]
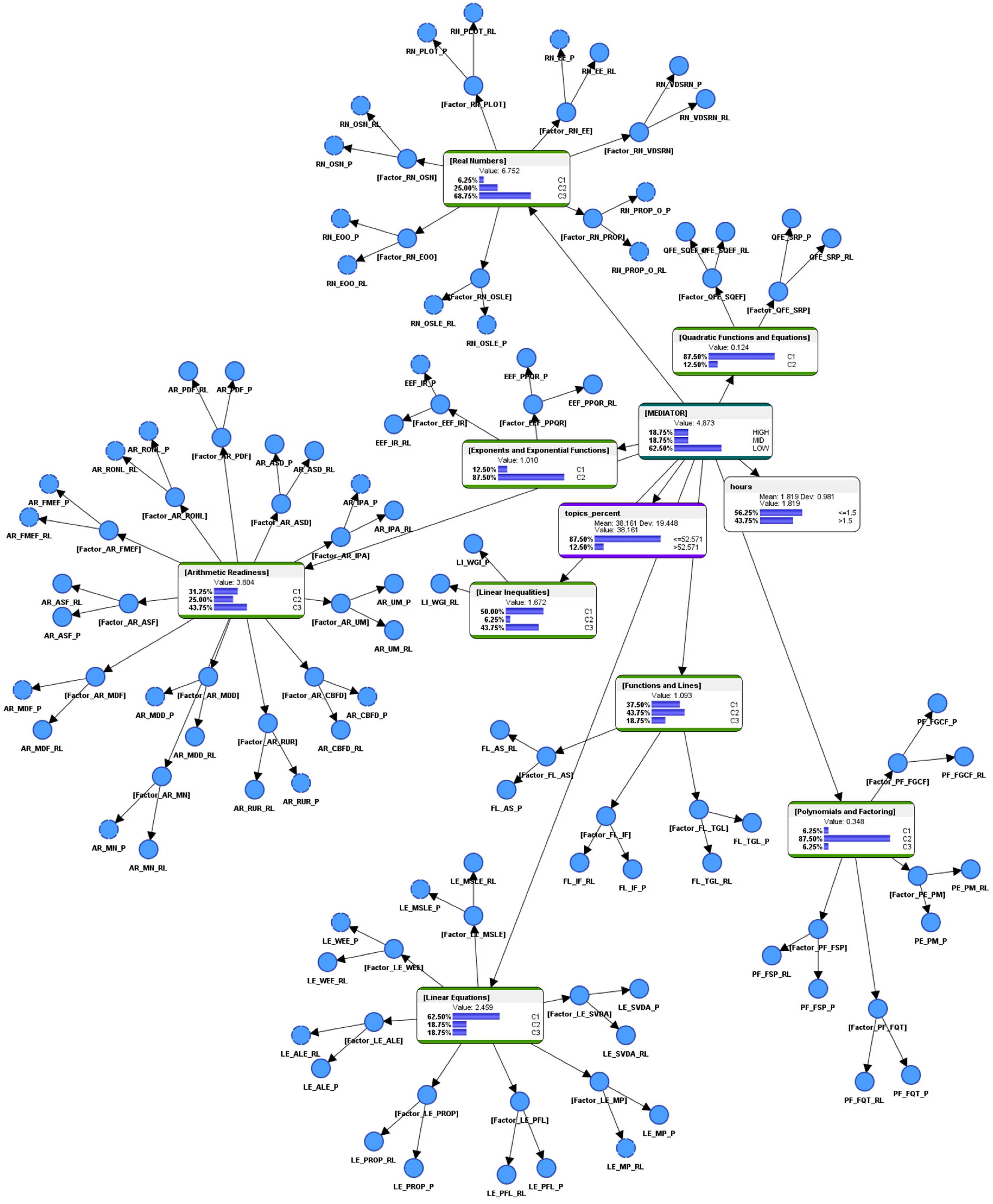
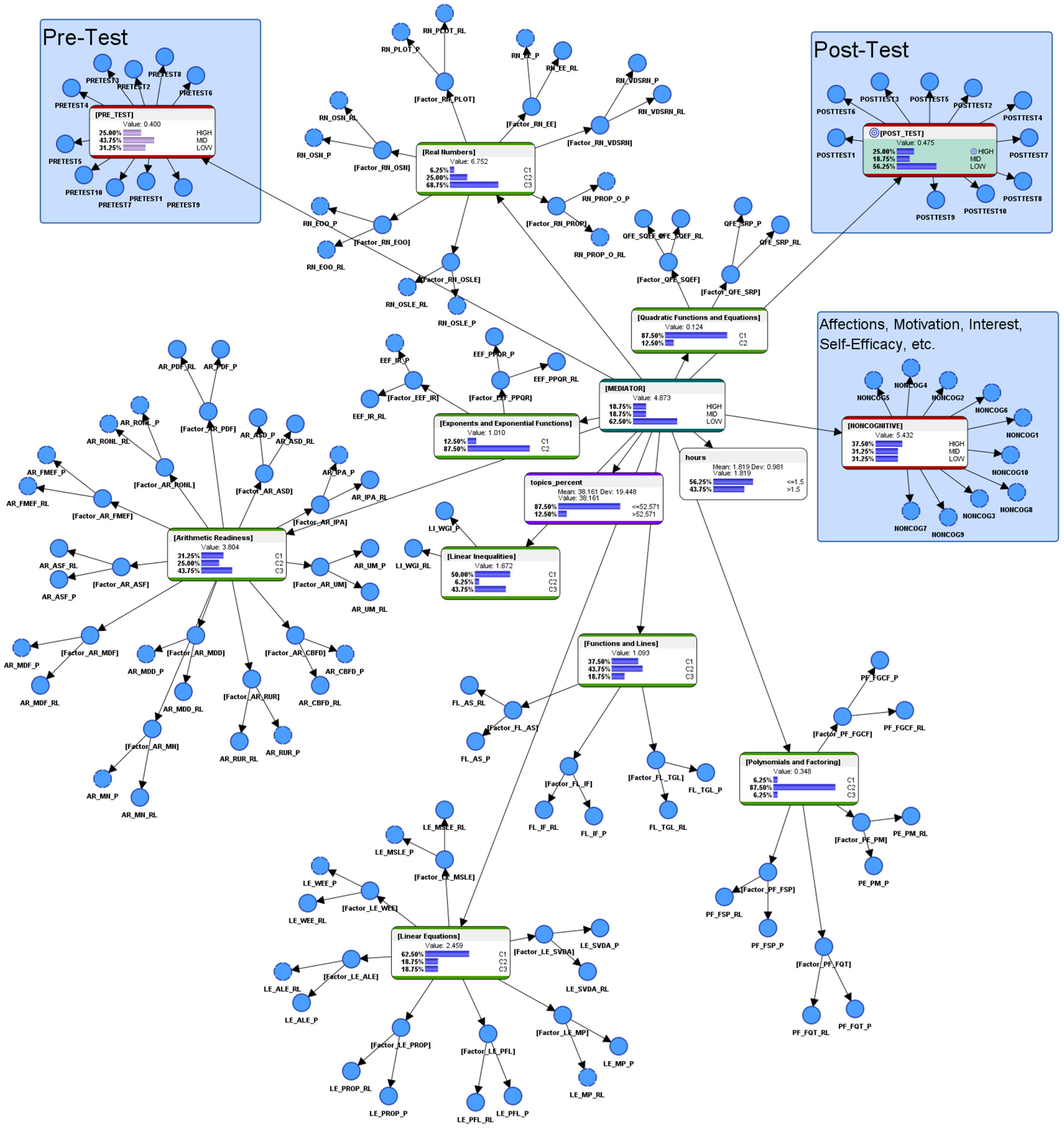


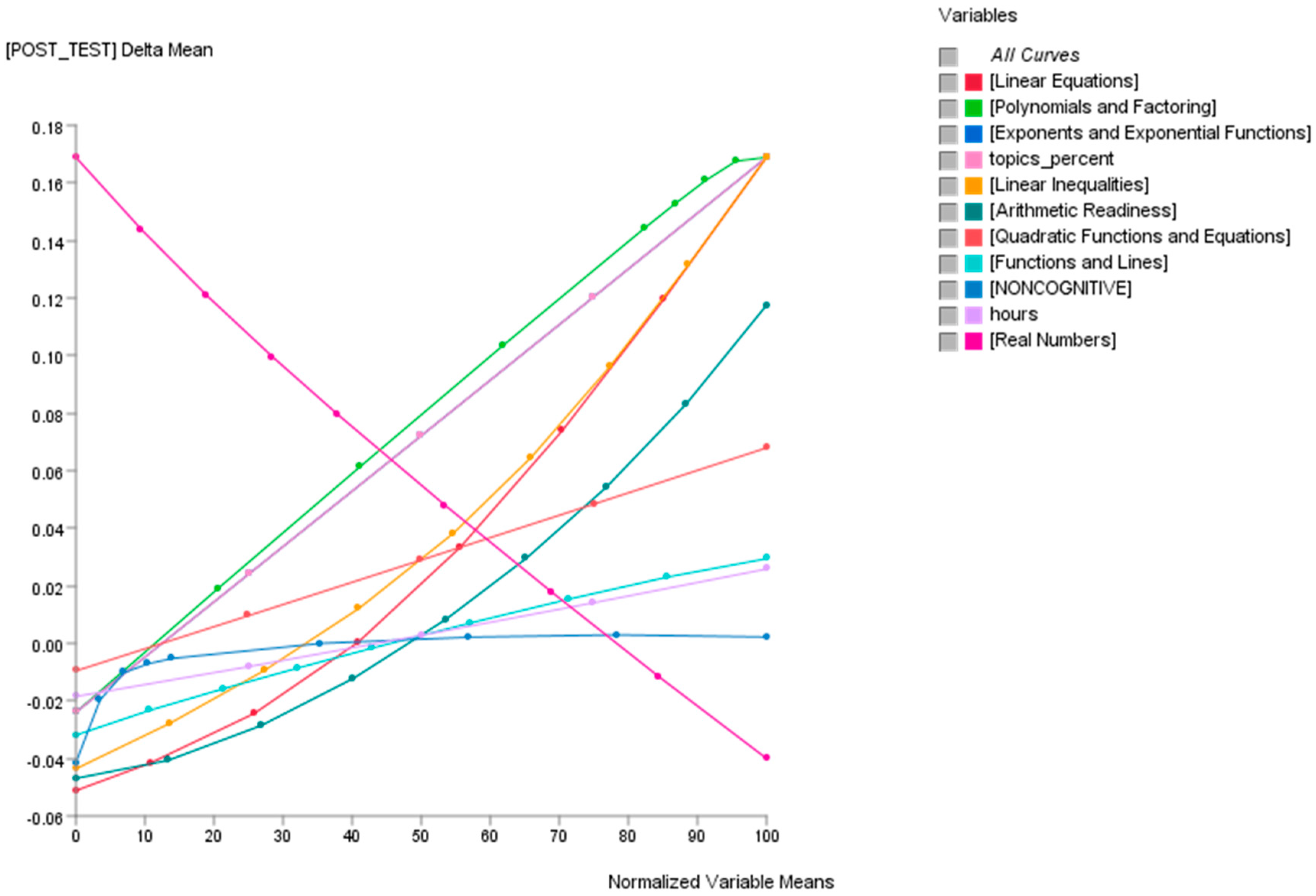
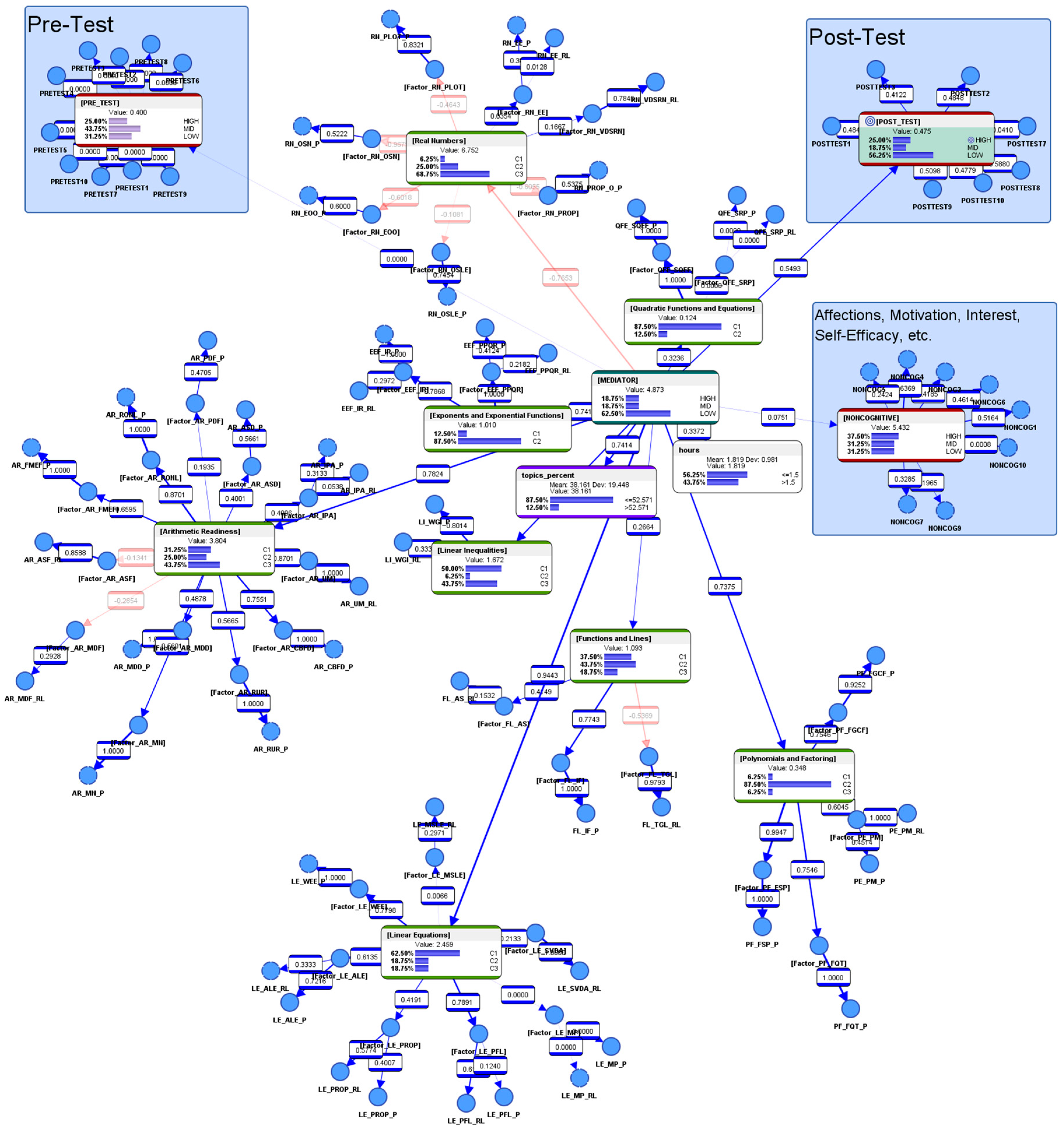

| Node Name | Description |
|---|---|
| student_id | Student identifier (ID) |
| hours | Number of hours spent by student using the AI-ALS |
| topics_350 | Number of topics out of a total of 350 completed by the student in the AI-ALS |
| topics_percent | Percentage of topics out of a total of 350 completed by the student in the AI-ALS |
| Arithmetic readiness (AR) | |
| AR_FMEF_P | AR_Factors_Multiples_Equivalent_Fractions_Passed |
| AR_FMEF_RL | AR_Factors_Multiples_Equivalent_Fractions_Ready_For_Learning |
| AR_ASF_P | AR_Addition_Subtraction_with_Fractions_Passed |
| AR_ASF_RL | AR_Addition_Subtraction_with_Fractions_Ready_for_Learning |
| AR_MD_P | AR_Multiplication_Division_with_Decimals_Passed |
| AR_MD_RL | AR_Multiplication_Division_with_Decimals_Ready_for_Learning |
| AR_MN_P | AR_Mixed_Numbers_Passed |
| AR_MN_RL | AR_Mixed_Numbers_Ready_for_Learning |
| AR_RONL_P | AR_Rounding_Number Line_Passed |
| AR_RONL_RL | AR_Rounding_Number Line_Ready_for_Learning |
| AR_ASD_P | AR_Addition_Subtraction_with_Decimals_Passed |
| AR_ASD_RL | AR_Addition_Subtraction_with_Decimals_Ready_for_Learning |
| AR_MDD_P | AR_Multiplication_Division_with_Decimals_Passed |
| AR_MDD_RL | AR_Multiplication_Division_with_Decimals_Ready_for_Learning |
| AR_CBFD_P | AR_Converting_Between_Fractions_Decimals_Passed |
| AR_CBFD_RL | AR_Converting_Between_Fractions_Decimals_Ready_for_Learning |
| AR_RUR_P | AR_Ratios_Unit_Rates_Passed |
| AR_RUR_RL | AR_Ratios_Unit_Rates_Ready_for_Learning |
| AR_PDF_P | AR_Percents_Decimals_Fractions_Passed |
| AR_PDF_RL | AR_Percents_Decimals_Fractions_Ready_for_Learning |
| AR_IPA_P | AR_Intro_Percent_Applications_Passed |
| AR_IPA_RL | AR_Intro_Percent_Applications_Ready_for_Learning |
| AR_UM_P | AR_Units_Measurement_Passed |
| AR_UM_RL | AR_Units_Measurement_Ready_for_Learning |
| Real numbers (RN) | |
| RN_PLOT_P | RN_Plotting_Ordering_Passed |
| RN_PLOT_RL | RN_Plotting_Ordering_Ready_for_Learning |
| RN_OSN_P | RN_Operations_Signed_Numbers_Passed |
| RN_OSN_RL | RN_Operations_Signed_Numbers_Ready_for_Learning |
| RN_EOO_P | RN_Exponents_Order_Operations_Passed |
| RN_EOO_RL | RN_Exponents_Order_Operations_Ready_for_Learning |
| RN_EE_P | RN_Evaluation_Expressions_Operations_Passed |
| RN_EE_RL | RN_Evaluation_Expressions_Ready_for_Learning |
| RN_VDSRN_P | RN_Venn_Diagrams_Sets_Real_Num_Passed |
| RN_VDSRN_RL | RN_Venn_Diagrams_Sets_Real_Num_Ready_for_Learning |
| RN_PROP_O_P | RN_Properties_Operations_Passed |
| RN_PROP_O_RL | RN_Properties_Operations_Ready_for_Learning |
| RN_OSLE_P | RN_One_Step_Linear_Equations_Passed |
| RN_OSLE_RL | RN_One_Step_Linear_Equations_Ready_for_Learning |
| Linear equations (LE) | |
| LE_MSLE_P | LE_Multi_Step_Linear_Equations_Passed |
| LE_MSLE_RL | LE_Multi_Step_Linear_Equations_Ready_for_Learning |
| LE_WEE_P | LE_Writing_Expressions_Equations_Passed |
| LE_WEE_RL | LE_Writing_Expressions_Equations_Ready_for_Learning |
| LE_ALE_P | LE_Applications_Linear_Equations_Passed |
| LE_ALE_RL | LE_Applications_Linear_Equations_Ready_for_Learning |
| LE_SVDA_P | LE_Solving_Variable_Dimensional_Analysis_Passed |
| LE_SVDA_RL | LE_Solving_Variable_Dimensional_Analysis_Ready_for_Learning |
| LE_PROP_P | LE_Proportions_Passed |
| LE_PROP_RL | LE_Proportions_Ready_for_Learning |
| LE_MP_P | LE_More_Percents_Passed |
| LE_MP_RL | LE_More_Percents_Ready_for_Learning |
| LE_PFL_P | LE_Personal_Financial_Literacy_Passed |
| LE_PFL_RL | LE_Personal_Financial_Literacy_Ready_for_Learning |
| Linear inequalities (LI) | |
| LI_WGI_P | LI_Writing_Graphing_Inequalities_Passed |
| LI_WGI_RL | LI_Writing_Graphing_Inequalities_Ready_for_Learning |
| Functions and lines (FL) | |
| FL_TGL_P | FL_Tables_Graphs_Lines_Passed |
| FL_TGL_RL | FL_Tables_Graphs_Lines_Ready_for_Learning |
| FL_IF_P | FL_Introduction_Functions_Passed |
| FL_IF_RL | FL_Introduction_Functions_Ready_for_Learning |
| FL_AS_P | FL_Arithmetic_Sequences_Passed |
| FL_AS_RL | FL_Arithmetic_Sequences_Ready_for_Learning |
| Exponents and exponential functions (EEF) | |
| EEF_PPQR_P | EEF_Product_Power_Quotient_Rules_Passed |
| EEF_PPQR_RL | EEF_Product_Power_Quotient_Rules_Ready_for_Learning |
| EEF_IR_P | EEF_Intro_Radicals_Passed |
| EEF_IR_RL | EEF_Intro_Radicals_Ready_for_Learning |
| Polynomials and factoring (PE) | |
| PE_PM_P | PE_Polynomial_Multiplication_Passed |
| PE_PM_RL | PE_Polynomial_Multiplication_Ready_for_Learning |
| PF_FGCF_P | PE_Factoring_Greatest_Common_Factor_Passed |
| PF_FGCF_RL | PE_Factoring_Greatest_Common_Factor_Ready_for_Learning |
| PF_FQT_P | PE_Factoring_Quadratic_Trinomials_Passed |
| PF_FQT_RL | PE_Factoring_Quadratic_Trinomials_Ready_for_Learning |
| PF_FSP_P | PE_Factoring_Special_Products_Passed |
| PF_FSP_RL | PE_Factoring_Special_Products_Ready_for_Learning |
| Quadratic functions and equations (QFE) | |
| QFE_SQEF_P | QFE_Solving_Quadratic_Equations_Factoring_Passed |
| QFE_SQEF_RL | QFE_Solving_Quadratic_Equations_Factoring_Ready_for_Learning |
| QFE_SRP_P | QFE_Square_Root_Property_Passed |
| QFE_SRP_RL | QFE_Square_Root_Property_Ready_for_Learning |
| Pre-test (PRETEST) | Synthetic data for pre-test questions 1–10 |
| Post-test (POSTTEST) | Synthetic data for post-test questions 1–10 |
| Noncognitive (NONCOG) | Synthetic data for noncognitive survey questions 1–10 |
| Parent | Child | Overall Contribution | GKL Test | df | p-Value | Pearson’s Correlation |
|---|---|---|---|---|---|---|
| [Factor_FL_TGL] | FL_TGL_RL | 2.2709% | 34.2954 | 4 | 0.0001% | 0.9793 |
| [MEDIATOR] | [Linear Equations] | 1.9526% | 29.4878 | 4 | 0.0006% | 0.9443 |
| [Linear Inequalities] | LI_WGI_RL | 1.8679% | 28.2090 | 4 | 0.0011% | 0.3331 |
| [Functions and Lines] | [Factor_FL_TGL] | 1.7651% | 26.6572 | 4 | 0.0023% | −0.5369 |
| [Factor_AR_ASF] | AR_ASF_RL | 1.7598% | 26.5768 | 6 | 0.0174% | 0.8588 |
| [Factor_AR_CBFD] | AR_CBFD_P | 1.4687% | 22.1807 | 1 | 0.0002% | 1.0000 |
| [Factor_LE_MSLE] | LE_MSLE_RL | 1.4521% | 21.9301 | 3 | 0.0067% | 0.2971 |
| [Factor_AR_IPA] | AR_IPA_RL | 1.4018% | 21.1700 | 3 | 0.0097% | 0.0538 |
| [Factor_FL_IF] | FL_IF_P | 1.4018% | 21.1700 | 1 | 0.0004% | 1.0000 |
| [Factor_AR_MN] | AR_MN_P | 1.4018% | 21.1700 | 1 | 0.0004% | 1.0000 |
| [Factor_FL_AS] | FL_AS_P | 1.4018% | 21.1700 | 2 | 0.0025% | −0.0504 |
| [Factor_LE_SVDA] | LE_SVDA_RL | 1.4018% | 21.1700 | 1 | 0.0004% | 1.0000 |
| [Factor_FL_TGL] | FL_TGL_P | 1.3849% | 20.9156 | 6 | 0.1900% | −0.4765 |
| [Factor_AR_ASF] | AR_ASF_P | 1.3233% | 19.9851 | 8 | 1.0393% | −0.2401 |
| [Real Numbers] | [Factor_RN_OSN] | 1.3160% | 19.8748 | 2 | 0.0048% | −0.9671 |
| [Factor_AR_UM] | AR_UM_RL | 1.3160% | 19.8748 | 1 | 0.0008% | 1.0000 |
| [Factor_AR_RUR] | AR_RUR_P | 1.3160% | 19.8748 | 1 | 0.0008% | 1.0000 |
| [Factor_AR_RONL] | AR_RONL_P | 1.3160% | 19.8748 | 1 | 0.0008% | 1.0000 |
| [Arithmetic Readiness] | [Factor_AR_UM] | 1.3160% | 19.8748 | 2 | 0.0048% | 0.8701 |
| [Arithmetic Readiness] | [Factor_AR_RONL] | 1.3160% | 19.8748 | 2 | 0.0048% | 0.8701 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
HOW, M.-L.; HUNG, W.L.D. Educational Stakeholders’ Independent Evaluation of an Artificial Intelligence-Enabled Adaptive Learning System Using Bayesian Network Predictive Simulations. Educ. Sci. 2019, 9, 110. https://doi.org/10.3390/educsci9020110
HOW M-L, HUNG WLD. Educational Stakeholders’ Independent Evaluation of an Artificial Intelligence-Enabled Adaptive Learning System Using Bayesian Network Predictive Simulations. Education Sciences. 2019; 9(2):110. https://doi.org/10.3390/educsci9020110
Chicago/Turabian StyleHOW, Meng-Leong, and Wei Loong David HUNG. 2019. "Educational Stakeholders’ Independent Evaluation of an Artificial Intelligence-Enabled Adaptive Learning System Using Bayesian Network Predictive Simulations" Education Sciences 9, no. 2: 110. https://doi.org/10.3390/educsci9020110
APA StyleHOW, M.-L., & HUNG, W. L. D. (2019). Educational Stakeholders’ Independent Evaluation of an Artificial Intelligence-Enabled Adaptive Learning System Using Bayesian Network Predictive Simulations. Education Sciences, 9(2), 110. https://doi.org/10.3390/educsci9020110






