Achieving Elusive Teacher Change through Challenging Myths about Learning: A Blended Approach
Abstract
1. Introduction
1.1. A Mathematical Mindset Approach
1.2. Teacher Learning through Professional Development
2. Materials and Methods
2.1. The Blended Mathematical Mindset Professional Development Approach
2.2. Research Methods
- (1)
- What shifts were evident in the teacher’s beliefs and attitudes about math and math teaching as a result of completing the online teacher course? (Data sources: online course responses, surveys, interviews.)
- (2)
- What shifts were evident in the teacher’s practice as a result of completing the online course? (Data source: coaches conducted classroom observations using a Mathematical Mindset observation tool)
- (3)
- For students of teachers participating in the online teacher course, what shifts were evident in student’s beliefs about mindset and the nature of mathematics? (Data source: Student Mindset survey)
- (4)
- On a standardized assessment of learning, were there any differences in learning outcomes from students with teachers who participated in the online course compared with similar students with teachers who did not participate? (Data source: Student-level results from Smarter Balanced Assessment for California)
- (1)
- Teacher Fosters Culture where all Students can Learn to High Levels
- (2)
- Teacher Provides and Facilitates Open Mathematics
- (3)
- Teacher Maintains High Challenge and Cognitive Demand
- (4)
- Mistakes are seen as Valuable, Risk Taking is Encouraged
- (5)
- Teacher Maximizes Student–Student Interactions.
2.3. Data Analysis
3. Results
3.1. Teacher Change
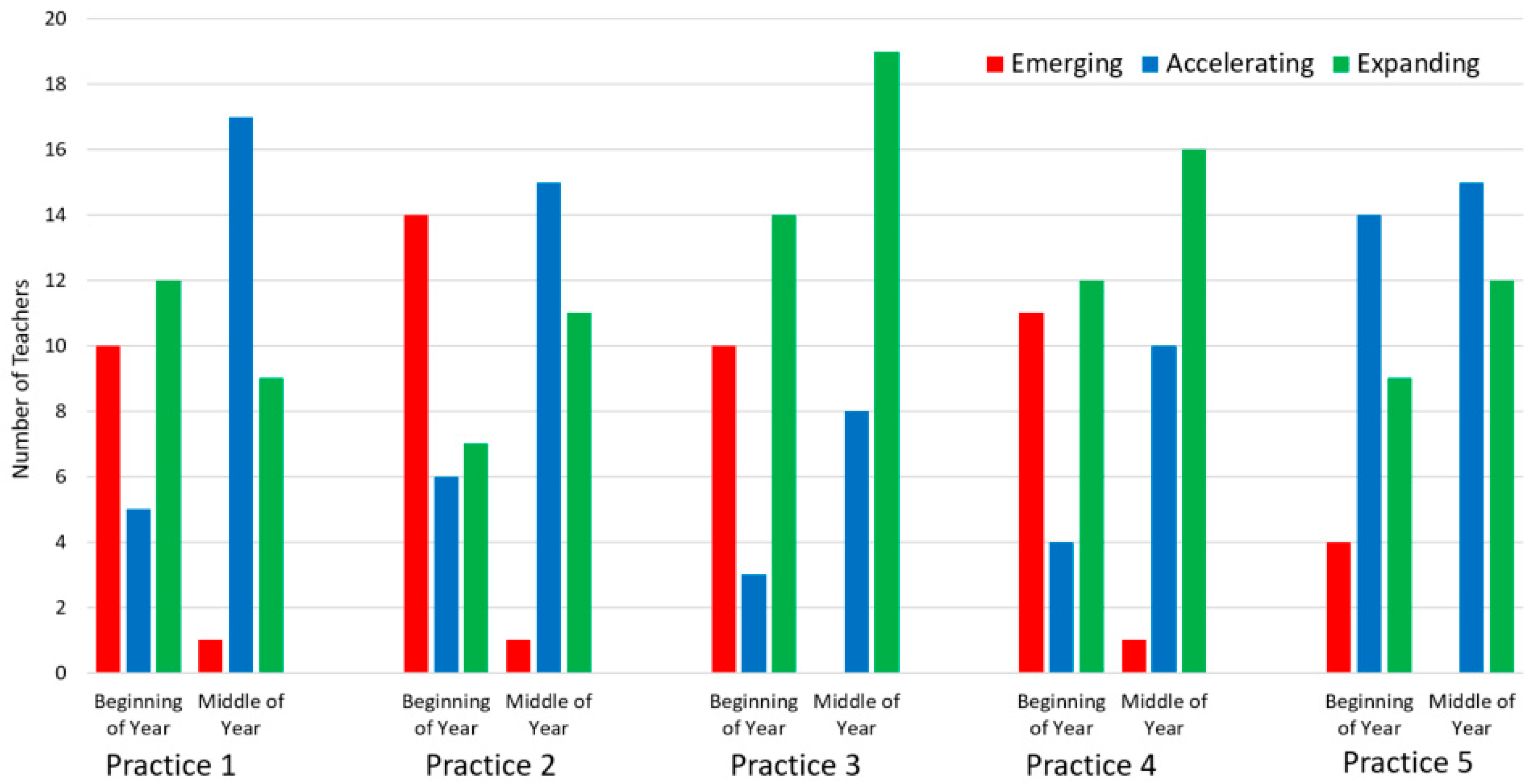
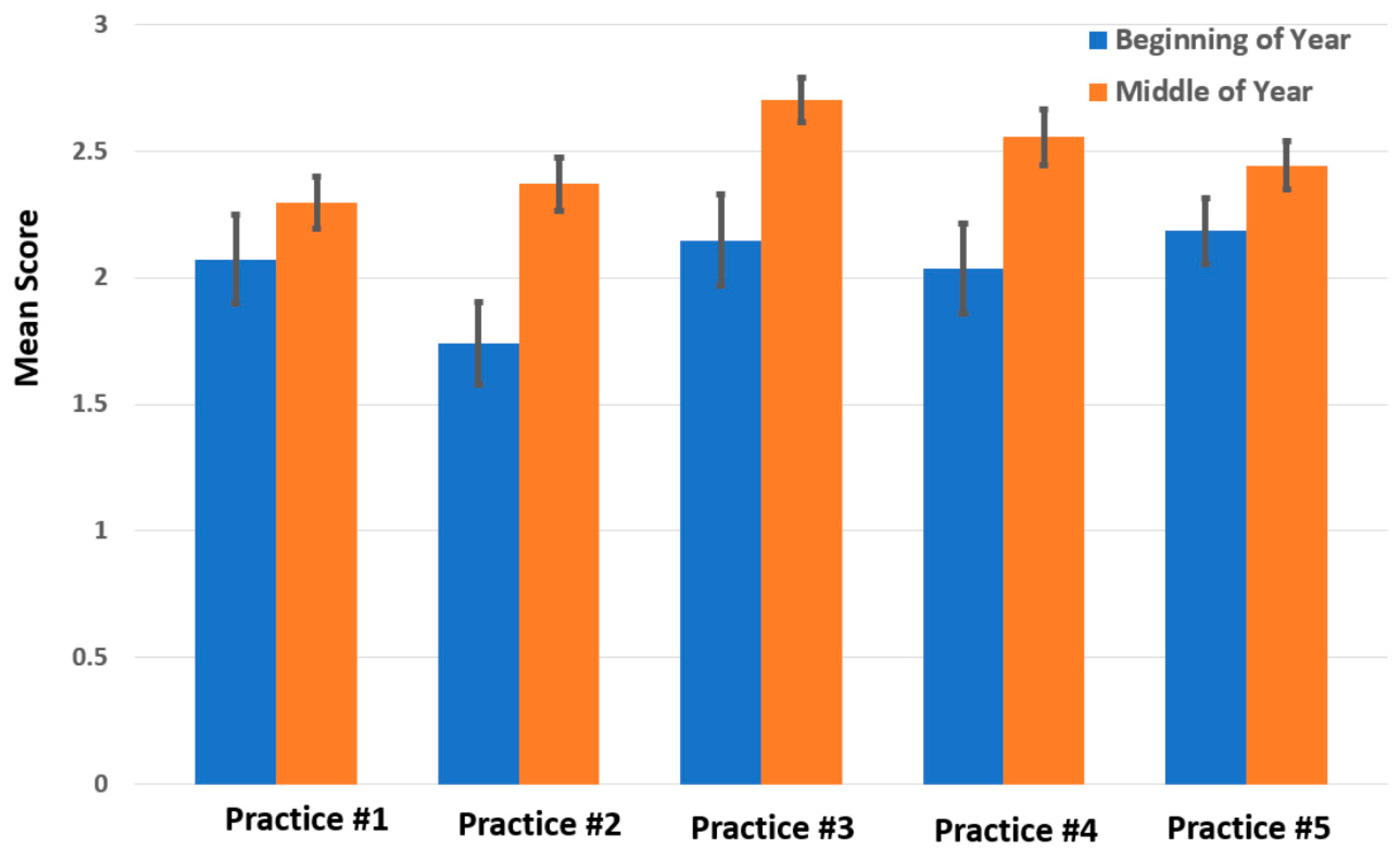
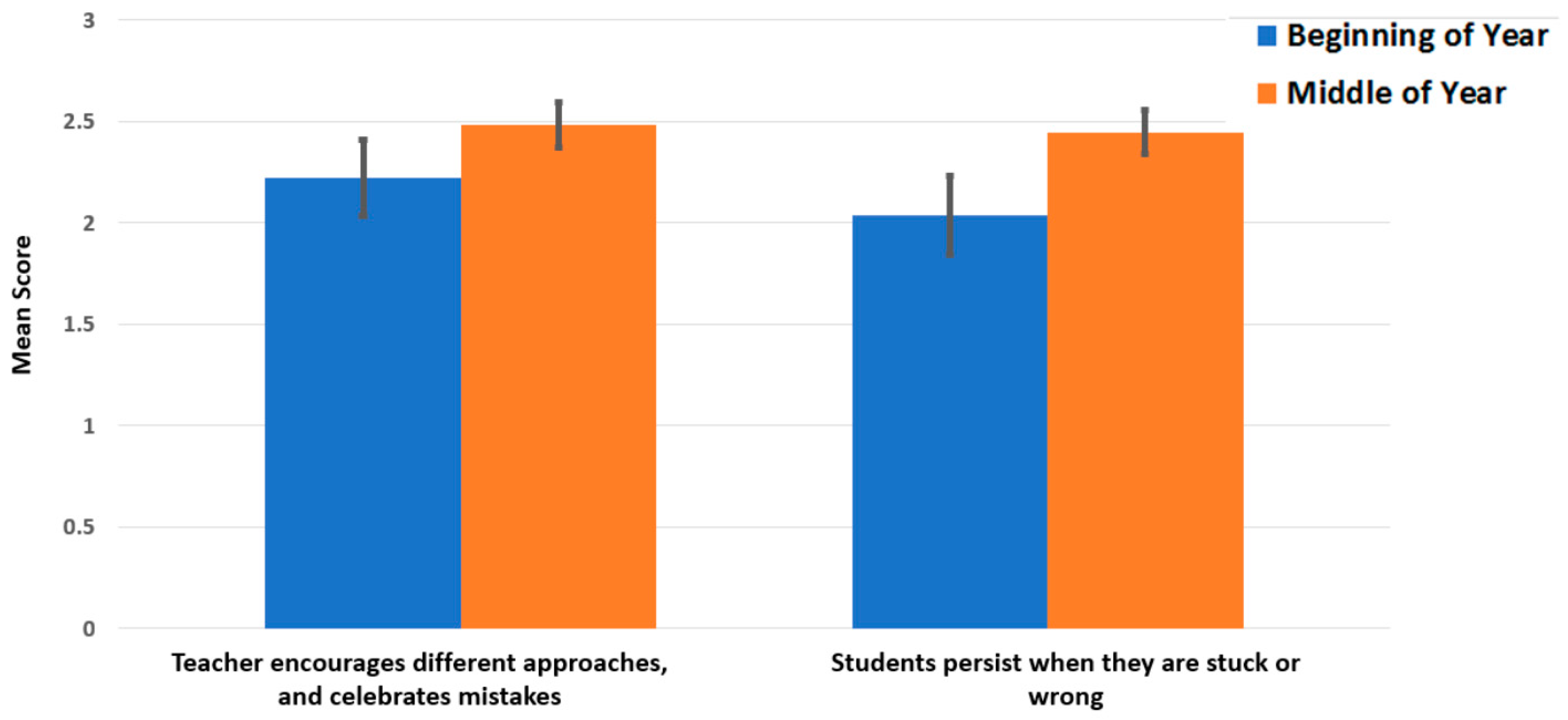
3.1.1. Observation of Lessons
3.1.2. Teacher Reflections (Online Course Responses and Surveys)
As a first year teacher, I never.... It was like every time we did math was like, “Open up a book.” And it was just this negative connotation to it.—Maurice V (Online Course Reflection)
What I feel has made the most difference in my teaching is, quite simply, the change of mindset. I used to think that direct instruction was the only way. I felt I had to always be in control in order for learning to occur.—Jolie (Online Course Reflection)
Because for years it was I teach, we practice, you practice alone. That type of directed instruction, and now it’s given me the confidence as a teacher to just sit back and watch them explore, and it’s okay. Even though they’re making mistakes as they work through it it’s okay, because now they’re learning the conversation that they need to have with each other as groups, as partners.—Anonymous 5th Grade Teacher (Survey)
I’ve gone from direct instruction (DII) with little exploration of tasks to a complete shift of teacher role and I’ve become a facilitator. I anticipate their answers to math tasks, but they share their thinking and ask each other questions. They clear up their own misunderstandings most of the time with little direction from me. My students are thoroughly enjoying math.—Anonymous 5th Grade Teacher (Survey)
3.1.3. Interviews
I will definitely change my way of thinking about all of my student abilities. All of the data given to me regarding my students will not be looked at the same way as it had been in previous years. I will now see the student first rather than see a test score and then a student. My Students will be viewed as individuals who no matter what level of math skills should be attended to as a student with mindset that needs some TLC.—Maria
I’ve really seen an impact on my students and how they view themselves, and it’s changed their level of perseverance in the classroom. And everything, really. And even during art, one kid was saying, “I can’t. I can’t do this,” and another kid said, “That’s a fixed mindset.” And I’m getting positive feedback from parents about this. Their children that really didn’t believe that they could do math, or really just saw themselves as deficient in some way, that their attitudes are changing.—Holly
From the get go we talked about and continue to talk about the Fixed and Growth mindset. I continue to remind my class that we must change our old ways of thinking about math to a new way, which is to always approach math with the attitude of “yes, if I try and keep on trying, I can” explaining that this is the Growth Mindset!! The information on the brain and how its plasticity is affected by the learning or lack of learning/struggle. In my class we always refer to our brain synapses firing which is a good thing especially when we are challenged.—Maria
The week of imaths was incredible for kids, I’ve never seen a classroom more fired up for math in my life.—Maria
I think it’s because it doesn’t look like math, a typical practice sheet with 50 problems on it. … So, they’re more excited, because it’s more like an activity. It’s more like they get to discover on their own and do something that is different than what they’ve done before. So, I think that’s why they’re enthused about it.—Fred
The whole week was wonderful. At first we pulled different youcubed problems so we didn’t have to do GoMath on Fridays, now we come up with our own open ended questions. We just create. The other day on the board I wrote: The answer is 17 how many different ways can you get me to the answer? I thought they might just say 1 plus 16 but they were doing orders of operations and they got really fancy and I was really impressed with them.—Janice
What we’ll do is we’ll plan an enrichment task. We’ll kind of go through the process of how we think the kids are gonna solve it, maybe how we think what we’re gonna see. … So that’s been our biggest goal, kind of setting up a rich task…—Jeremy
Think back to some time when you were learning maths and you made a mistake. How did that make you feel?
The kids were thrilled, going “Oh my gosh, he’s doing it like that? It’s OK that we struggle? It’s OK we think differently?”—Janice
I liked watching them struggle, and I know if the teacher says that it always sounds kind of odd, but it was a really good struggle because it really got them to think much differently about what math was, and that math is not just going to come out of a textbook, I am not just gonna sit there and look at you and go, “You’re gonna do this many problems.” We don’t do that, and the kids have now accepted that going, “Okay, so things are definitely gonna be different.” And they all have math notebooks and keeping ideas of their journals, and what they need to do.—Janice
I just want you to know this [the online course] has meant a lot. Seeing how positive the kids are about their learning now has made a world of difference. The confidence they have is unlike anything I have ever seen.—Fred
But now it’s easier for me to accept the wrong answer from a student. Usually it’s, “Come on, you guys can do this.” Now it’s, “Okay. Let’s do it this way. Let’s see what else we can come up. Talk to your partner.” So it’s more engagement for me, and it’s a lot easier for me. It’s a lot more relaxing.—Fred
But I still had a lot of kids that were incredibly frustrated, “This isn’t gonna work.” The next day we talked about those norms again, and those mindsets that in this class you’re going to be expected to think, and it’s okay, you’re gonna be challenged, and you are gonna struggle. And struggle is not a bad thing. And then all the sudden, you could almost see kind of like this wave of kids, and the whole reaction started to change, so their mindset totally completely began to change. And then they got more of them pulled in.—Janice
Oh, the visuals.... They love that too, cause with their ideas of how it would form, and how they would build. I do it periodically. Just throw up a visual with different things and say, “Okay, what do you see? What don’t you see? What might you see? What could be the next thing?”—Leila
Well, the big take-aways for me are the connections they make. We were doing a paper-folding activity where we were using it for fractions, but the paper-folding activity, they started folding the paper with triangles from a square. And they on their own discovered that there was an exponential relationship, so when they folded it once they had two pieces. And then when they folded it twice, they had four. And they started seeing the exponents of two with every fold. And they made that connection all by themselves, cause we’ve been doing base 10, and powers of 10. So I see those connections happening during these iMath lessons, and that’s huge for me.—Fred
Last year I probably would’ve been more of the one to help jump in a little bit more and give them more scaffolding. This year, I’ve been working really hard at not jumping in and scaffolding quite so much, but the kids are helping each other, so it’s not relying on me. It’s where the kids, when we’ve been doing these different tasks from the five practices, where it’s me kind of stepping back and letting them, and doing maybe more of the question asking.—Janice
And even individually, I can tell that they sit and they think about it when it’s time to think. Before, they just tried to work through it and be done, and that’s a lot of what happened last year, was just the race to be done. And so I’m trying to expel that, I just wanna do away with the whole race. There’s no value in that.—Kayla
I’ve kinda slowed things way down, and focusing more on the concept for the day.—Fred
So, I have noticed, I have a couple of students that really have taken on that it’s okay to take their time to do their work. I have a girl who just raised her hand and shared this with the rest of the class which I thought was “Wow.” She always thought that she wasn’t good at math because it takes her a long time to do the work.—Julie
Okay, why are these kids so much better at focusing? Is it because they’ve had a couple more years of Common Core and they understand it better? They’re used to the routine? They’re used to the collaboration? Or is it because they have a different mindset now? And that’s what I’m leaning more towards, because last year it was like if they can’t finish it in five minutes they don’t wanna do it. And this year they’re okay with taking time on it, and I’m okay on taking time. In fact, I mentioned to our superintendent this morning, she was here with us and I said, “I don’t know that I’m gonna be completely prepared for our benchmark in a couple of weeks.” And she goes, “Don’t worry about it. Just let the kids explore, it’s more important that they think about what they’re doing. That they grow this mindset, because it’ll work out for them better in the end.” And so that’s the major difference I see.—Kayla
The biggest freedom that we’ve had is our administrator has empowered us to not look at “This is the lesson I have to get done,” it’s “How can I take elements and resources?”, covering the standard… So I think hearing that as a teacher, it’s like you have a blank canvas. It’s your freedom to... You have the freedom to add to what you want with the structure of common core and standards. But hearing that, as a teacher, there’s no complaining. It’s taking from here, taking from there, and then blending it together.”—Maurice
When it said on the week that I might have to teach this, like, “No, no, no, no, no that’s too much for fifth graders.” But they thought it was really cool.And the very first day we did it, oh my gosh, the struggle and the upset and, “Oh my gosh, I’m gonna have to do this, this is hard.” The second day, they got more into it, they got more experience. And then I had two girls the following week come in on their own, and figured out the missing ones, and they thought that was the coolest thing, and they were just like, “It’s totally filled out!”—Janice
The most powerful is the mindset, and that’s not only for my students but more for me because I didn’t think I was a math person. I’ve never enjoyed math, I’ve never felt that I was good at math… before when it was just that one right answer then that left a lot out. I like the mindset and the kids have really picked up on that and they’re really applying that. In class, we’ll say, we don’t say that something is hard, we say it’s challenging. I am the one that usually says about something being hard and then they’ll all tell me, “No, it’s not hard, it’s challenging.” So they’re doing really well with the growth mindset.—Heather
I am making more of an effort to help my students develop a math mindset of success. One example I have took place about two weeks ago during our Go Math lesson. A new student had arrived in our classroom, and he came with an IEP(Individualized Education Plan). We were doing a problem together whole group, and I noticed he was not writing down the problem. I asked him why, and he said “I am not good at math; it is hard.” Before I could respond, the entire class looked directly at him and said “don’t say that, everyone can be good at math.” We then gave him our class cheer which is “I can, you can, and we can.” It was totally spontaneous, and I am seeing more effort from him.—Joel
The information has made me reflect on my fear in my English and literature courses. I have always loved my literature courses but I was always scared of failing and the subject not being for me as a Mexican-American and English learner. Applying it to math I had a similar thing going on where I liked math and even considered being a math major but decided against it because of the fear of failing.—Miguel (Online Course Reflection)
I thought it was going to be great for the kids, I never expected it to change me, that’s been my greatest revelation in all of it.—Kayla
I have to defend math a lot and why I teach math the way I do because it goes against what parents have learned. It goes against what I have learned. I’ve never done it this way. I tell parents I go home now and I study and I practice and I figure it out. If I’d learned math this way I wouldn’t have cried every night in math going through school.—Janice
3.2. Student Change
3.2.1. Changes in Student Beliefs
3.2.2. Changes in Student Achievement
4. Discussion
I thought it was going to be great for the kids, I never expected it to change me, that’s been my greatest revelation in all of it.—Kayla
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A. Mathematical Mindset Classroom Observational Tool)
| Mathematical Mindset Practice 1: Teacher fosters culture where all students can learn to high levels | |||
| Emerging | Accelerating | Expanding | |
| Mindset Messages | ● Teacher communicates higher and lower expectations to different students ● Teacher communicates that some are “math people” and some are not | ● Teacher attempts to give belief messages but too broad, too generic, mechanical, disconnected | ● Teacher gives belief messages in a meaningful way: “I know you can do this”, “I believe in you” |
| Praising Effort | ● Teacher does not acknowledge student effort or progress in thinking (may focus only on answer) | ● Teacher praises effort at times, but may focus on praising individuals at other times | ● Teacher praises effort, ideas and specific strategies |
| Student’s Mindset | ● Students communicate lack of confidence in their ability to do math, and those messages go unchallenged by the teacher | ● Students convey a mix of confidence and doubt in themselves | ● Most students vocalize/show self-belief and confidence |
| Mathematical Mindset Practice 2: Teacher provides and facilitates open mathematics | |||
| Emerging | Accelerating | Expanding | |
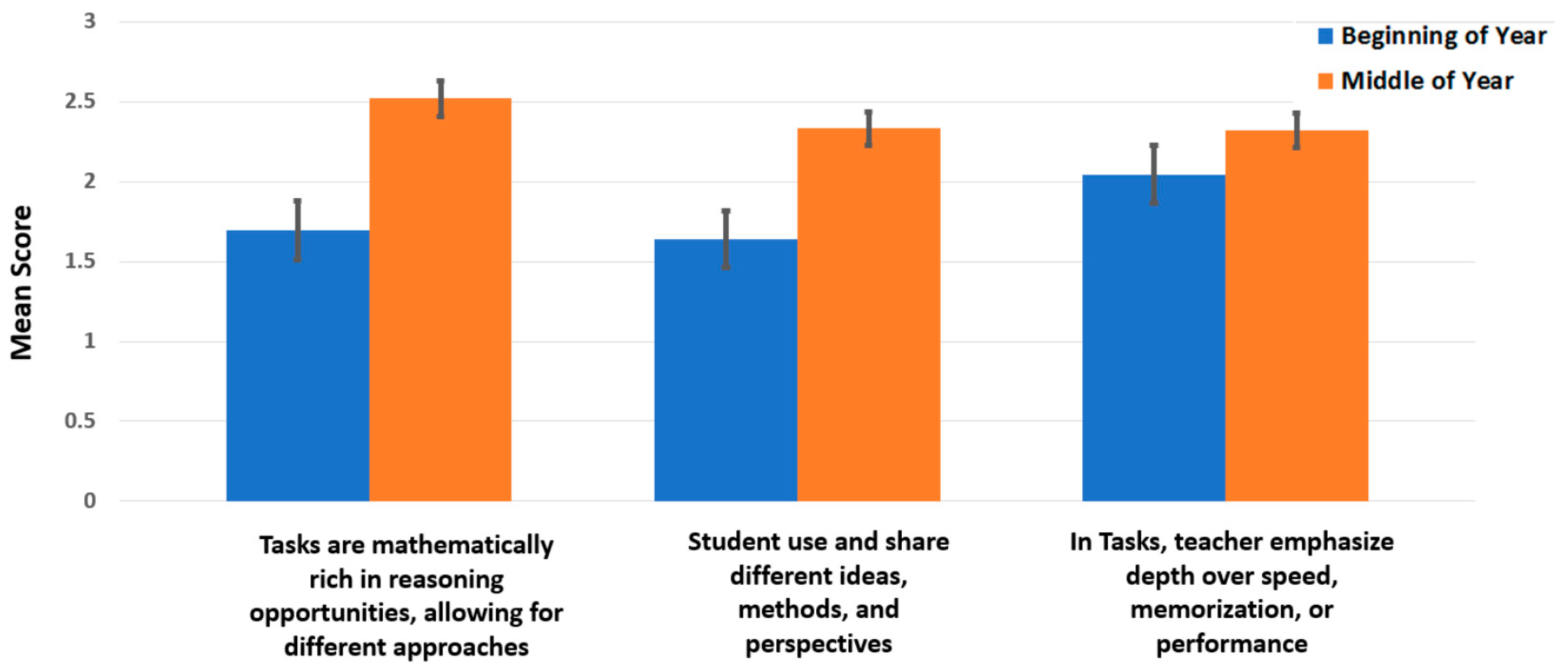
| Open Tasks | ● Tasks are relatively closed, emphasizing routine procedures with little reasoning | ● Tasks are mathematically rich in reasoning opportunities but not fully mined | ● Tasks are mathematically rich in reasoning opportunities, allowing for different approaches ● Students’ creative work in math is displayed in the room |
| Reasoning and multiple perspectives | ● All or most of the student work looks the same ● The teacher does not point out variability in student thinking | ● Only one or two methods are elicited or explored ● The teacher asks for students to think of their own ideas but different ideas are not shared | ● Students use ownership words–“my method”, “my idea” ● Students are invited to see math in a different, more expansive way ● Students use and share different ideas, methods, and perspectives |
| Depth over speed | ● Strong emphasis on speed, memorization or performance | ● Teacher occasionally emphasizes speed, memorization or performance | ● In tasks, teacher emphasizes depth over speed, memorization or performance |
| Mathematical Mindset Practice 3: Teacher maintains high challenge & cognitive demand | |||
| Emerging | Accelerating | Expanding | |
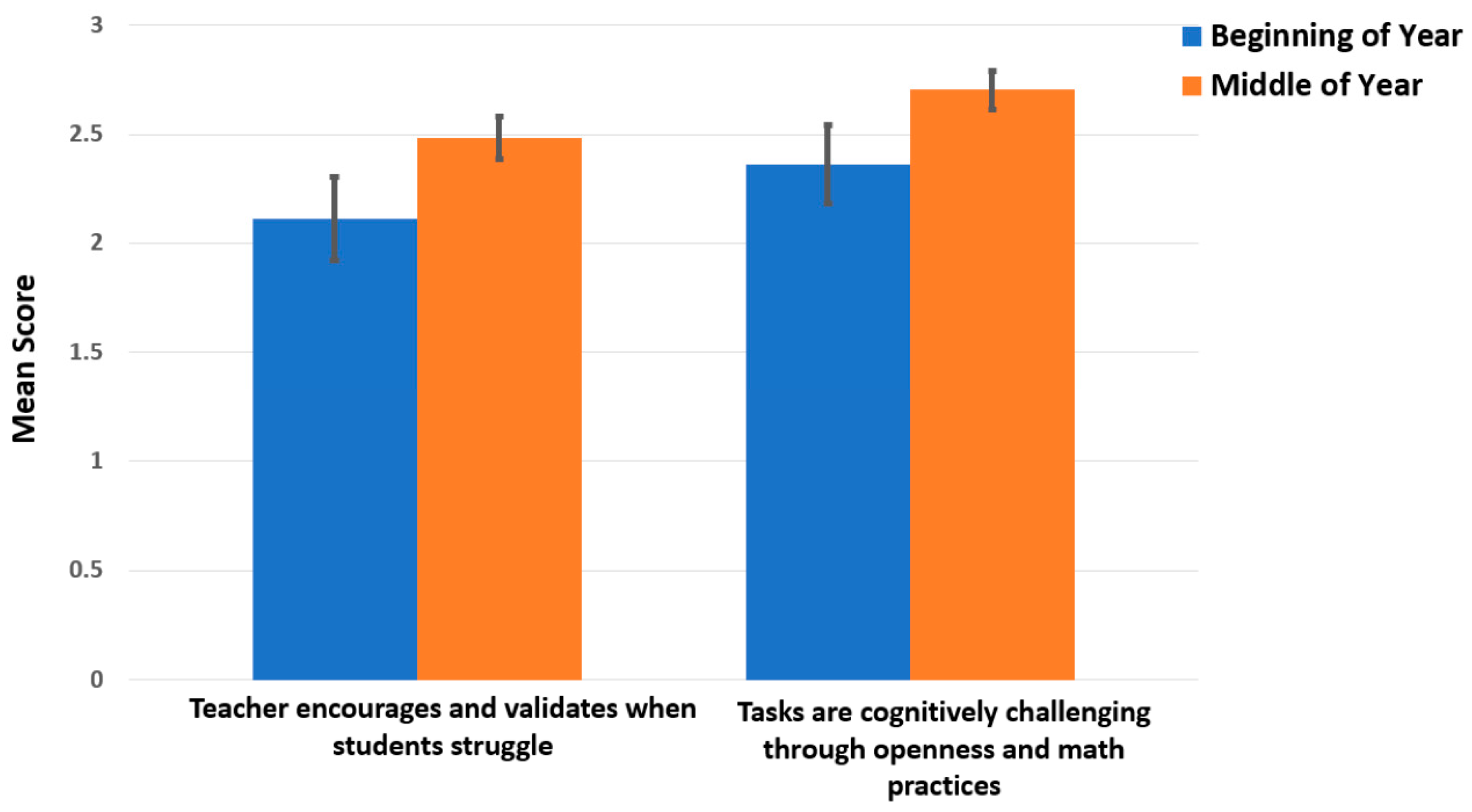
| Struggle | ● Teacher does the thinking for students or helps the students too much when they are finding work difficult | ● In development | ● Teacher encourages and validates when students struggle ● Teachers provides sufficient wait time ● Teacher connects struggle to brain growth, synapse-firing from brain research ● Teacher listens closely to how students approach the task on their own before deciding on forms of assistance |
| Tasks | ● Teacher offers no opportunity to explore the task ● Teacher has low-challenge or closed questions ● Teacher reduces cognitive demand in interaction with students or with task | ● Teacher scaffolds tasks into discrete parts by giving hints too early | ● Tasks are cognitively challenging through content ● Tasks are cognitively challenging through openness of the problem and encouragement of math practices |
| Questioning | ● Teacher tells instead of asking questions to encourage students to think deeply | ● Teacher attempts to question but structures too much, or questions are too leading | ● Teacher asks open, conceptual questions celebrating multiple methods, ways of seeing, ways of thinking |
| Mathematical Mindset Practice 4: Mistakes are seen as valuable, risk-taking is encouraged | |||
| Emerging | Accelerating | Expanding | |
| Sharing mistakes | ● Teacher emphasizes complete and correct work ● Mistakes are dealt with negatively ● Mistakes are marked on a paper with no or limited feedback (if applicable) | ● Teacher ends eliciting ideas upon hearing the correct answer ● Students share mostly correct answers ● Students don’t share when they are unsure or incorrect ● Mistakes are acknowledged but not explored by class | ● Teacher encourages different approaches; doesn’t stop with the correct answer ● Students share ideas, both correct and incorrect ● Teacher celebrates when learning occurs from mistakes ● Students disagree with each other’s reasoning and with the teacher |
| Persistence | ● Students give up when they are stuck or wrong | ● Students ask teacher for help, but the teacher rescues rather than encouraging persistence | ● Students persist when they are stuck or wrong ● Teachers and students work together when they are stuck |
| Mathematical Mindset Practice 5: Teacher maximizes student-student interactions | |||
| Emerging | Accelerating | Expanding | |
| Groupings | ● Arrangement of desks does not allow for collaboration ● No group work or collaboration is available to students ● Working together on class assignments may be viewed as cheating | ● student’s desks are in groups, but no collaboration is observed ● Some students choose to collaborate but the teacher doesn’t prompt or encourage all to do so. | ● Students work in groups to solve problems, sharing ideas and visuals |
| Student Discussions | ● Students direct questions or present ideas to teachers, rather than to peers ● Same few students contribute ideas, teacher does not actively elicit ideas from others | ● Some students present ideas to peers but only when prompted by the teacher ● Teacher encourage sharing from different students but students are reluctant. | ● Students ask questions to each other to understand peer’s ideas ● In class discussions, peers interact directly with peers ● Students build off of each other’s ideas |
| Teacher Facilitation | ● Teacher dominates classroom talk, discussion or IRE (initiate, respond, evaluate) | ● Teacher interacts with individual students, rather than students interacting with each other, students contribute ideas but teachers finish their sentences, or insert their ideas | ● Teacher facilitates student-student interaction: “Does anyone want to respond to X’s idea?” ● Students talk with each other in class discussion without going through the teacher |
Appendix B. Teacher Interview Protocols
| Strongly disagree | Disagree | Somewhat disagree | Somewhat agree | Agree | Strongly agree | |
| 1. I enjoy being challenged in math. | ||||||
| 2. In math, answers are either right or wrong. | ||||||
| 3. Math is boring. | ||||||
| 4. People who really understand math will get an answer quickly. | ||||||
| 5. I can tell if my answers in math make sense. | ||||||
| 6. When I get a bad grade in math, I think that I am not very smart in math. | ||||||
| 7. I believe that I can do well in math. | ||||||
| 8. When I make a mistake in math, I feel bad. | ||||||
| 9. It is important in math to be fast. | ||||||
| 10. There are limits to how much people can improve their basic math ability. | ||||||
| 11. If I put in enough effort I can succeed in mathematics. | ||||||
| 12. You have a certain amount of math intelligence, and you can’t really do much to change it. | ||||||
| 13. Math is a subject with lots of connections between ideas. | ||||||
| 14. It is really helpful to talk about math with others. | ||||||
| 15. There is usually only one way to solve a math problem. | ||||||
| 16. I like to solve complex math problems. |
Appendix C. Mathematical Mindset Student Survey
- How much of the online course have you completed? (less than half?)
- Did you complete the modules in teacher groups? On your own? Did you discuss?
- When do you expect to complete the course?
- Do you still use your district adopted curriculum? [If so how?
- ○
- Are you supplementing the curriculum? [Ask if they did not describe above]
- ▪
- Where are you finding supplemental material?
- In general, are you bringing more rich tasks into your classroom? How often?
- How has your perception of student struggle changed this year?
- When reflecting on your current teaching practice, is speed a factor in your classroom?
- Have you as a math learner changed since taking the online course?
- Have you as a math teacher changed since taking the online course?
- How do you think the students would describe you last year as a teacher versus how they would describe you this year?
References
- Cohen, D.K. A revolution in one classroom: The case of Mrs. Oublier. Educ. Eval. Policy Anal. 1990, 12, 311–329. [Google Scholar] [CrossRef]
- Santagata, R.; Kersting, N.; Givvin, K.B.; Stigler, J.W. Problem implementation as a lever for change: An Experimental study of the effects of a professional development program on students’ mathematics learning. J. Res. Educ. Eff. 2011, 4, 1–24. [Google Scholar] [CrossRef]
- Geijsel, F.; Meijers, F. Identity learning: The core process of educational change. Educ. Stud. 2005, 31, 419–430. [Google Scholar] [CrossRef]
- Maguire, E.A.; Woollett, K.; Spiers, H.J. London taxi drivers and bus drivers: A structural MRI and neuropsychological analysis. Hippocampus 2006, 16, 1091–1101. [Google Scholar] [CrossRef] [PubMed]
- Woollett, K.; Maguire, E.A. Acquiring “the Knowledge” of London’s layout drives structural brain changes. Curr. Biol. 2011, 21, 2109–2114. [Google Scholar] [CrossRef] [PubMed]
- Luculano, T.; Rosenberg-Lee, M.; Richardson, J.; Tenison, C.; Fuchs, L.; Supekar, K.; Menon, V. Cognitive tutoring induces widespread neuroplasticity and remediates brain function in children with mathematical learning disabilities. Nat. Commun. 2015, 6, 8453. [Google Scholar] [CrossRef] [PubMed]
- Leslie, S.; Cimpian, A.; Meyer, M.; Freeland, E. Expectations of brilliance underlie gender distributions across academic disciplines. Science 2015, 347, 262–265. [Google Scholar] [CrossRef] [PubMed]
- Chestnut, E.; Lei, L.S.; Cimpian, A.; Chestnut, E.K.; Lei, R.F.; Leslie, S.J.; Cimpian, A. The Myth that only brilliant people are good at math and its implications for diversity. Educ. Sci. 2018, 8, 65. [Google Scholar] [CrossRef]
- Boaler, J. Mathematical Mindsets; Jossey-Bass: San Francisco, CA, USA, 2016. [Google Scholar]
- Menon, V. Arithmetic in child and adult brain. In Handbook of Mathematical Cognition; Cohen, K.R., Dowker, A., Eds.; Oxford University Press: London, UK, 2014. [Google Scholar]
- Beilock, S.L. Grounding cognition in action: Expertise, comprehension, and judgment. Prog. Brain Res. 2009, 174, 3–11. [Google Scholar] [PubMed]
- Bussey, K.; Bandura, A. Influence of gender constancy and social power on sex-linked modeling. J. Pers. Soc. Psychol. 1984, 47, 1292–1302. [Google Scholar] [CrossRef] [PubMed]
- Gunderson, E.A.; Ramirez, G.; Levine, S.C.; Beilock, S.L. The role of parents and teachers in the development of gender-related math attitudes. Sex Roles 2012, 66, 153–166. [Google Scholar] [CrossRef]
- Borko, H. Professional development and teacher learning: Mapping the terrain. Educ. Res. 2004, 33, 3–15. [Google Scholar] [CrossRef]
- Opfer, V.D.; Pedder, D. Conceptualizing teacher professional learning. Rev. Edu. Res. 2011, 81, 376–407. [Google Scholar] [CrossRef]
- Dweck, C.S. Mindset: The New Psychology of Success; Random House Incorporated: New York, NY, USA, 2006. [Google Scholar]
- Blackwell, L.S.; Trzesniewski, K.H.; Dweck, C.S. Implicit theories of intelligence predict achievement across an adolescent transition: A longitudinal study and an intervention. Child Dev. 2007, 78, 246–263. [Google Scholar] [CrossRef] [PubMed]
- Aronson, J.; Fried, C.B.; Good, C. Reducing the effects of stereotype threat on African American college students by shaping theories of intelligence. J. Exp. Soc. Psychol. 2002, 38, 113–125. [Google Scholar] [CrossRef]
- Steele, C.M. A threat in the air: How stereotypes shape intellectual identity and performance. Am. Psychol. 1997, 52, 613–629. [Google Scholar] [CrossRef] [PubMed]
- Jonsson, A.C.; Beach, D.; Korp, H.; Erlandson, P. Teachers’ implicit theories of intelligence: Influences from different disciplines and scientific theories. Eur. J. Teach. Educ. 2012, 35, 387–400. [Google Scholar] [CrossRef]
- Stipek, D.; Givven, K.; Salmon, J.; MacGyvers, V. Teachers’ beliefs and practices related to mathematics instruction. Teach. Teach. Educ. 2001, 17, 213–226. [Google Scholar] [CrossRef]
- Horn, I. Fast kids, slow kids, lazy kids: Framing the mismatch problem in mathematics teachers’ conversation. J. Learn. Sci. 2007, 16, 37–79. [Google Scholar]
- The “Mindset” Mindset: What We Miss by Focusing on Kids’ Attitudes: Essay by Alfie Kohn. Available online: https://www.alfiekohn.org/article/mindset/ (accessed on 10 January 2018).
- Sun, K.L. There’s no Limit: Mathematics Teaching for a Growth Mindset. Ph.D. Thesis, Stanford University, Palo Alto, CA, USA, 2015. [Google Scholar]
- Suh, J.M.; Graham, S.; Ferranone, T.; Kopeinig, G.; Bertholet, B. Developing persistent and flexible problem solvers with a growth mindset. In Motivation and Disposition: Pathways to Learning Mathematics, NCTM 2011 Yearbook; Brahier, D.J., Ed.; National Council of Teachers of Mathematics: Reston, VA, USA, 2011; pp. 169–184. [Google Scholar]
- Boaler, J.; Chen, L.; Williams, C.; Cordero, M. Seeing as understanding: The importance of visual mathematics for our brain and learning. J. Appl. Computat. Math. 2016, 5, 325. [Google Scholar] [CrossRef]
- Mayer, R.E. The promise of multimedia learning: Using the same instructional design methods across different media. Learn Instr. 2003, 13, 125–139. [Google Scholar] [CrossRef]
- Desimone, L. Improving impact studies of teachers’ professional development: Toward better conceptualizations and measures. Educ. Res. 2009, 38, 181–199. [Google Scholar] [CrossRef]
- Borko, H.; Jacobs, J.; Koellner, K. Contemporary approaches to teacher professional development. Int. Encycl. Educ. 2010, 7, 548–556. [Google Scholar]
- Sherin, M.G.; van Es, A.E. Effects of video club participation on teachers’ professional vision. Educ. J. Teach. Educ. 2009, 60, 20–37. [Google Scholar] [CrossRef]
- Ball, D.L.; Cohen, D.K. Developing practice, developing practitioners. In Teaching as the Learning Profession: Handbook of Policy and Practice; Darling-Hammond, L., Sykes, G., Eds.; Jossey-Bass: San Francisco, CA, USA, 1999; pp. 3–22. [Google Scholar]
- Jacobs, V.R.; Lamb, L.L.C.; Philipp, R.A. Professional noticing of children’s mathematical thinking. J. Res. Math. Educ. 2010, 41, 169–202. [Google Scholar]
- Bastable, V.; Schifter, D. Classroom stories: Examples of elementary students engaged in early algebra. In Algebra in the Early Grades; Kaput, J., Carraher, D., Blanton, M., Eds.; Erlbaum: Mahwah, NJ, USA, 2008; pp. 165–184. [Google Scholar]
- Festinger, L. A Theory of Cognitive Dissonance; Stanford University Press: Stanford, CA, USA, 1957. [Google Scholar]
- Initial Achievement Level Descriptors and College Content-Readiness Policy: Smarter Balanced Assessment Consortium. Available online: https://portal.smarterbalanced.org/library/en/mathematics-alds-and-college-content-readiness-policy.pdf (accessed on 10 January 2018).
- Strauss, A.; Corbin, J.M. Basics of Qualitative Research: Grounded Theory Procedures and Techniques; Sage Publications: Thousand Oaks, CA, USA, 1990. [Google Scholar]
- Eisenhart, K. Building theories from case study research. In The Qualitative Researcher’s Companion; Huberman, A.M., Miles, M., Eds.; Sage Publications: Thousand Oaks, CA, USA, 2002; pp. 3–36. [Google Scholar]
- Glesne, C.; Peshkin, A. Becoming Qualitative Researchers; Longman: White Plains, NY, USA, 1992. [Google Scholar]
- Costello, A.B.; Osborne, J.W. Best practices in exploratory factor analysis: Four recommendations for getting the most from your analysis. Pract. Assess. Res. Eval. 2005, 10, 1–9. [Google Scholar]
- Gates, B.; Gates, M. Teachers Know Best: Teachers’ Views on Professional Development; Bill and Melinda Gates Foundation: Seatle, WA, USA, 2015; pp. 1–20. [Google Scholar]
- Cuban, L. Inside the Black Box of Classroom Practice: Change without Reform in American Education; Harvard Education Press: Cambridge, MA, USA, 2013. [Google Scholar]
| Regional Schools | Student N | Percent Latino | Percent English Learner | Percent Low SES | Percent Proficient (All Students) on CA 5th Grade, Test * (2016) |
|---|---|---|---|---|---|
| School 1 | 572 | 72% | 28% | 83% | 8% |
| School 2 | 410 | 68% | 35% | 86% | 17% |
| School 3 | 712 | 98% | 64% | 97% | 7% |
| School 4 | 624 | 95% | 63% | 96% | 8% |
| School 5 | 445 | 28% | 42% | 21% | 5% |
| School 6 | 487 | 19% | 68% | 19% | 3% |
| School 7 | 687 | 11% | 58% | 11% | 4% |
| Data Source | Date of Collection | Complete Responses |
|---|---|---|
| Mathematical Mindset Observation Tool—Teacher Observations | October 2016 (1st Observation) February 2017 (2nd Observation) | 27 |
| Online Course Responses | September 2016–June 2017 | 34 |
| Teacher Surveys | September 2016, October 2016, February 2017 | 93 |
| Teacher Interviews | October 2016, February 2017 | 12 |
| Student Mindset Survey | September 2016 (1st Observation) February 2017 (2nd Observation) | 383 |
| Student Achievement Data | April 2017 | 1068 |
| Code Name | Description | Number of Respondents |
|---|---|---|
| Student Voice | Students sharing their ideas. | 15 |
| Space | Students explore, make sense, discuss, and play with ideas. Allowing for time. | 14 |
| Mistakes | Valuing mistakes and struggle. | 14 |
| Valuing Strategies | Pedagogical choice to allow students to share ideas and methods to help others learn. | 11 |
| Ownership | Student ownership of ideas, students being empowered through their ideas. | 8 |
| Release | Turning over teacher lead activities to students. Release power and control. Giving up control allowing students to do things on their own. | 6 |
| Talks | Number talks, Number sense talks. | 2 |
| 5 Mathematical Mindset Teaching Practices | Themes from Teacher Online Reflections and Surveys | Themes from Teacher Interviews |
|---|---|---|
| 1 Teacher Fosters Culture where all Students can Learn to High Levels | Mindset, Students’ role in change | |
| 2 Teacher Provides and Facilitates Open Mathematics | Valuing strategies, Ownership of ideas, Number talks, Making space | Using open tasks and questions, Celebrating multiple ways of seeing and doing math, Valuing slower thinking |
| 3 Teacher Maintains High Challenge and Cognitive Demand | Encouraging struggle, Reducing scaffolding | |
| 4 Mistakes are seen as Valuable, Risk Taking is Encouraged | Mistakes | Teacher’s own relationship with mathematics, Encouraging struggle, Reducing scaffolding |
| 5 Teacher Maximizes Student—Student Interactions. | Releasing control, Student voice | Celebrating multiple ways of seeing and doing math |
| Student Survey Items for A Growth Mathematical Mindset | ||
|---|---|---|
| Survey Item | Loading Weights | |
| 1. | I believe that I can do well in math | 0.699 |
| 2. | When I get a bad grade in math, I think that I am not very smart (reverse-coded) | 0.698 |
| 3. | I like to solve complex math problems | 0.697 |
| 4. | When I make a mistake in math, I feel bad (reverse-coded) | 0.665 |
| 5. | I enjoy being challenged in math | 0.652 |
| 6. | Math is boring (reverse-coded) | 0.577 |
| 7. | I can tell if my answers in math make sense | 0.484 |
| 8. | If I put enough effort, I can succeed in mathematics | 0.430 |
| District | Teachers | Schools | Students | ||
|---|---|---|---|---|---|
| Treatment | Control | Total | |||
| 1 | 8 | 3 | 225 | 116 | 341 |
| 2 | 11 | 3 | 165 | 142 | 307 |
| 3 | 17 | 6 | 100 | 438 | 538 |
| 4 | 9 | 2 | 209 | 13 | 222 |
| 5 | 3 | 1 | 27 | 15 | 42 |
| 6 | 24 | 12 | 342 | 1804 | 2146 |
| Total | 72 | 27 | 1068 | 2528 | 3596 |
| Variable | Obs. | Mean | Std. Dev. | Min | Max |
|---|---|---|---|---|---|
| Mathematics scale score | 3584 | 2455.0 | 83.1 | 2219.0 | 2700.0 |
| Mathematics achievement level | 3584 | 1.759 | 0.945 | 1 | 4 |
| Concepts procedures | 3243 | 1.496 | 0.705 | 1 | 3 |
| Problem solving & modeling data analysis | 3243 | 1.543 | 0.644 | 1 | 3 |
| Communicating reasoning | 1103 | 1.641 | 0.665 | 1 | 3 |
| Baseline Traits | |||||
| Treatment | 3596 | 0.297 | 0.457 | 0 | 1 |
| Female | 3596 | 0.517 | 0.500 | 0 | 1 |
| English Learner status | 3596 | 0.266 | 0.442 | 0 | 1 |
| Economic disadvantage status | 3596 | 0.796 | 0.403 | 0 | 1 |
| Migrant status | 3596 | 0.018 | 0.133 | 0 | 1 |
| Disability status | 3596 | 0.083 | 0.276 | 0 | 1 |
| White | 3244 | 0.116 | 0.320 | 0 | 1 |
| African-American | 3244 | 0.021 | 0.142 | 0 | 1 |
| American-Indian | 3244 | 0.002 | 0.046 | 0 | 1 |
| Asian | 3244 | 0.011 | 0.103 | 0 | 1 |
| Filipino | 3244 | 0.005 | 0.068 | 0 | 1 |
| Hawaiian or Pacific Islander | 3244 | 0.156 | 0.363 | 0 | 1 |
| Hispanic | 3244 | 0.609 | 0.488 | 0 | 1 |
| Other race | 3244 | 0.081 | 0.273 | 0 | 1 |
| Baseline Trait | Observations | Percentage |
|---|---|---|
| Female | 1736 | 48.3 |
| Male | 1860 | 51.7 |
| Total | 3596 | |
| White | 375 | 11.6 |
| African-American | 67 | 2.1 |
| American-Indian | 7 | 0.2 |
| Asian | 35 | 1.1 |
| Filipino | 15 | 0.5 |
| Hawaiian or Pacific Islander | 506 | 15.6 |
| Hispanic | 1976 | 60.9 |
| Other race | 263 | 8.1 |
| Total | 3244 | |
| English Learner status | 957 | 26.6 |
| Total | 3596 | |
| Economic disadvantage status | 2864 | 79.6 |
| Total | 3596 | |
| Migrant status | 65 | 1.8 |
| Total | 3596 | |
| Disability status | 299 | 8.3 |
| Total | 3596 |
| SBAC Math | |||||
|---|---|---|---|---|---|
| OLS | Overall Scale Score | Overall Proficiency Levels | Concepts & Procedures | Data Analysis & Modeling | Communicating Reasoning |
| Treatment status | 7.952 ** | 0.053 | 0.063 ** | 0.055 ** | 0.097 ** |
| (3.340) | (0.039) | (0.029) | (0.026) | (0.044) | |
| Observations | 3232 | 3232 | 3232 | 3232 | 1092 |
| R-squared | 0.211 | 0.155 | 0.129 | 0.135 | 0.121 |
| Variable | Obs | Mean | Std. Dev. | SBAC Point Gains | SD Gains | Academic Months Gains | Percentile Gain |
|---|---|---|---|---|---|---|---|
| Math Overall Scale Score | 3584 | 2455.0 | 83.1 | 7.952 | 0.096 | 3.4 | 0.54 |
| Overall Proficiency Levels | 3584 | 1.759 | 0.945 | ||||
| Concepts & Procedures | 3243 | 1.496 | 0.705 | 0.063 | 0.089 | 3.2 | 0.54 |
| Data Analysis & Modeling | 3243 | 1.543 | 0.644 | 0.055 | 0.085 | 3.1 | 0.53 |
| Communicating Reasoning | 1103 | 1.641 | 0.665 | 0.097 | 0.146 | 5.2 | 0.56 |
| Dependent Variable | Estimate |
|---|---|
| Female | −0.019 |
| (0.022) | |
| Limited English proficiency status | 0.045 ** |
| (0.019) | |
| Economic disadvantage status | 0.039 ** |
| (0.016) | |
| Migrant status | 0.003 |
| (0.005) | |
| Disability status | −0.029 *** |
| (0.011) | |
| White | −0.002 |
| (0.003) | |
| African-American | −0.001 |
| (0.003) | |
| Asian | −0.001 |
| (0.002) | |
| Hawaiian or Pacific Islander | −0.000 |
| (0.003) | |
| Hispanic | 0.001 |
| (0.003) |
| Dependent Variable | |||||
|---|---|---|---|---|---|
| SBAC Math | |||||
| Subgroup | Overall Scale Score | Overall Proficiency Levels | Concepts & Procedures | Data Analysis & Modeling | Communicating Reasoning |
| All Students | 7.952 ** | 0.053 | 0.063 ** | 0.055 ** | 0.097 ** |
| (3.340) | (0.039) | (0.029) | (0.026) | (0.044) | |
| N | 3232 | 3232 | 3232 | 3232 | 1092 |
| Female | 13.950 *** | 0.080 | 0.052 | 0.098 *** | 0.119 * |
| (4.483) | (0.054) | (0.041) | (0.037) | (0.066) | |
| N | 1680 | 1680 | 1680 | 1680 | 542 |
| Male | 0.134 | 0.006 | 0.068 | −0.003 | 0.068 |
| (5.001) | (0.056) | (0.042) | (0.037) | (0.059) | |
| N | 1552 | 1552 | 1552 | 1552 | 550 |
| Limited English proficiency status | 20.214 *** | 0.214 *** | 0.129 *** | 0.135 *** | 0.165 ** |
| (5.931) | (0.058) | (0.045) | (0.040) | (0.064) | |
| N | 822 | 822 | 822 | 822 | 396 |
| Economic disadvantage status | 10.592 *** | 0.077 * | 0.075 ** | 0.072 *** | 0.109 ** |
| (3.611) | (0.041) | (0.031) | (0.028) | (0.048) | |
| N | 2594 | 2594 | 2594 | 2594 | 866 |
| Disability status | 6.475 | −0.067 | −0.040 | −0.083 | 0.147 |
| (10.728) | (0.057) | (0.045) | (0.054) | (0.102) | |
| N | 258 | 258 | 258 | 258 | 64 |
| White | 5.313 | −0.002 | 0.049 | 0.086 | 0.124 |
| (12.243) | (0.155) | (0.116) | (0.107) | (0.304) | |
| N | 375 | 375 | 375 | 375 | 13 |
| Hawaiian or Pacific Islander | 15.933 | 0.163 | 0.072 | 0.112 | 0.054 |
| (9.673) | (0.118) | (0.087) | (0.073) | (0.071) | |
| N | 505 | 505 | 505 | 505 | 503 |
| Hispanic | 5.098 | 0.016 | 0.057 * | 0.008 | 0.142 ** |
| (3.993) | (0.045) | (0.034) | (0.031) | (0.070) | |
| N | 1969 | 1969 | 1969 | 1969 | 299 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anderson, R.K.; Boaler, J.; Dieckmann, J.A. Achieving Elusive Teacher Change through Challenging Myths about Learning: A Blended Approach. Educ. Sci. 2018, 8, 98. https://doi.org/10.3390/educsci8030098
Anderson RK, Boaler J, Dieckmann JA. Achieving Elusive Teacher Change through Challenging Myths about Learning: A Blended Approach. Education Sciences. 2018; 8(3):98. https://doi.org/10.3390/educsci8030098
Chicago/Turabian StyleAnderson, Robin Keturah, Jo Boaler, and Jack A. Dieckmann. 2018. "Achieving Elusive Teacher Change through Challenging Myths about Learning: A Blended Approach" Education Sciences 8, no. 3: 98. https://doi.org/10.3390/educsci8030098
APA StyleAnderson, R. K., Boaler, J., & Dieckmann, J. A. (2018). Achieving Elusive Teacher Change through Challenging Myths about Learning: A Blended Approach. Education Sciences, 8(3), 98. https://doi.org/10.3390/educsci8030098




