Abstract
The idea that success in mathematics is only available to those born as “mathematics people” has been challenged in recent years by neuroscience, showing that mathematics pathways develop in the brain through learning and practice. This paper reports on a blended professional learning model of online and in-person meetings during which 40 teachers in 8 school districts in the US learned about the new brain science, challenging the “math person” myth, as well as effective mathematics teaching methods. We refer to the combination as a Mathematical Mindset Approach. Using mixed methods, we conducted a one-year study to investigate teacher and student learning in a Mathematical Mindset network. We collected data on teacher and student beliefs, teacher instructional practice, and student learning gains on state achievement tests. The results from our quantitative analyses found statistically significant positive improvements in student beliefs, teacher’s instructional practice, and on students’ math test scores. The mindset approach particularly raised the achievement of girls, English learners, and economically disadvantaged students. Based on our qualitative analysis, we propose that the success of the intervention rests upon two central factors: (1) The different forms of PD served to eradicate the learning myths that had held up teachers and learners; and that (2) Teachers had space for identity work as mathematical learners.
1. Introduction
Teacher change is hard; over the last several decades, researchers and teacher leaders have attempted to improve the teaching of mathematics with different forms of professional development, but ineffective procedural mathematics teaching has endured [1,2]. Geijse & Meijers [3] propose that teacher learning opportunities are often ineffective because they do not pay attention to the sense making nature of teaching, and the need to give teachers opportunities to change their own identities as learners. In the study that is the focus of this paper, we will report upon an unusual teacher learning opportunity that focused upon eradicating the myth that only some students can learn mathematics to a high level, through an online course supported by face-to-face meetings. The success of the teacher learning initiative centered upon the opportunities teachers received to change ideas about their own potential as learners that differed from those they had received as learners of mathematics. As teachers reconsidered their own potential as learners, they became open to new relationships with students and new forms of teaching.
The idea that some of us are “math people” and some are not is a myth that pervades Western society. This damaging idea has been challenged in recent years by neuroscience showing that mathematics is a subject, like all others, that is learned through hard work and practice. A range of studies have demonstrated the neuroplasticity of the brain and the potential of all students to grow brain pathways that enable mathematics learning [4,5,6]. Studies also show the damage of fixed ability thinking and its potential to deter students from mathematics pathways. Leslie, Cimpian, Meyer & Freeland [7] interviewed University professors to determine how much they believed that students needed a “gift” in order to be successful in their field. Their results were stunning; they found that the more any academic field believed in the idea of a gift, the fewer women and African American students were in the field. This held across all 30 subjects they considered (see also [8] this volume). Mathematics professors held the most fixed views of any STEM field. Boaler [9] has proposed that the idea that only some people can be successful in mathematics is at the root of the widespread mathematics anxiety that pervades the US and elsewhere. Mathematics anxiety has been shown to reduce performance [10], and to be passed on from teachers and parents to students. Beilock et al. [11] conducted a study of female elementary teachers and their levels of mathematics anxiety, finding that the greater the math anxiety among teachers, the lower the achievement of their female students. The negative impact of teachers’ anxiety transferred to the female, but not the male students. Bussey and Bandura [12] found that children emulate the actions of same-sex adults, and even during experiments where an opposite-sex individual expressed social power, girls still emulated adult females when they had muted social power. Gunderson et al. [13] found that the levels of mathematics anxiety held by parents, but not the extent of mathematics knowledge, predicted their children’s achievement in the school year. These different studies highlight the role of people’s beliefs about mathematics in students’ learning and achievement. But messages do not only come from parents and teachers; the idea that people are or are not “math people” is transmitted throughout our culture, and has been found to be evident on clothing (https://goo.gl/ZTfrxD), television shows, and movies (https://goo.gl/hnLoH6). Traditionally, professional development focuses on different ways of teaching mathematics, but recent evidence from neuroscience, psychology, and education, all points to a need to change teachers’ and students’ ideas about who can achieve in mathematics, and a need to directly challenge the myth of the math person.
Studies of professional development and teacher change initiatives often rely on single forms of data: teacher interviews recalling change or test scores to show impact, categorized as phase 1 studies in Borko’s review of the field [14]. This study contributes to the field in different ways, as it is a mixed method study that draws from a wide range of data. The study was not designed to isolate variables, as would be appropriate in an experiment, but to consider a wide range of variables and the ways they interacted with each other. In designing the study, we paid attention to Opfer and Pedder’s [15] call to the field to conceptualize the complex work of teacher learning in a more dynamic way than has typically been the case. In the study that follows, a combination of teacher interview data, teacher observations, teacher and student surveys, and student achievement results will be considered together, in order to understand the change that occurred across 8 school districts.
This paper reports upon a professional learning opportunity during which 40 teachers were invited to learn about the new brain science, challenging the “math person” myth, as well as effective mathematics teaching methods. As the paper will report, the teachers became open to different teaching methods only when they changed their views about learning potential—of themselves, as well as their students. We refer to the combination of research about neuroscience and potential and effective teaching methods as a Mathematical Mindset Approach that was at the center of the initiative we studied.
1.1. A Mathematical Mindset Approach
Carol Dweck has pioneered a field of research showing that students with a “fixed mindset”, i.e., who believe that their ability is fixed, do not learn as well as those with a “growth mindset”, i.e., who believe their intelligence can grow and change [16]. Research has repeatedly shown that growth mindset interventions can shift students’ mindsets, and in so doing, counter negative outcomes [17]. In one study [18], students who were encouraged to see intelligence as malleable rather than fixed were less vulnerable to “stereotype threat” [19]—an often unconscious response to a negative stereotype that can impede academic engagement and performance. The students who received a growth mindset intervention earned higher grade point averages, and reported greater academic enjoyment and engagement. Despite the wealth of evidence showing the value of growth mindsets, most interventions have been conducted with students, rather than teachers who can amplify or undermine ideas about mindset. Mindset work with mathematics teachers seems particularly important as it is the subject where more teachers are likely to ascribe to fixed mindset beliefs [20]. Different studies have shown that mathematics teachers commonly hold fixed ideas about their own ability and about their students’ mathematics learning [7,21,22].
In the last decade mindset ideas have pervaded education, and many teachers have talked to students about the importance of having a growth mindset, and the importance of trying hard, without changing the nature of their teaching [16,23]. Dweck has pointed out that this can be damaging—as teachers encouraging students to try hard but giving students no resources or ideas for ways of doing so is frustrating for students. Boaler [9] has highlighted the importance of changing mathematics questions so they can be consistent with growth mindset ideas. When questions are narrow and closed, i.e., with one correct answer, students are likely to become frustrated if they do not know how to succeed. Over time, they come to see mathematics as a fixed and closed subject. When questions are opened to become low floor and high ceiling, with many entry points and where many different ways of working are valued, students are more likely to experience success and to see mathematics as an open and growth subject. While the field is developing awareness that changing student mindsets happens through teaching practices as much as it does through changing verbal messages [9,24,25], no study has yet examined the impact of professional development focused on the intersection of mathematics teaching, brain science, and mindset.
In addition to ideas about neuroplasticity and the openness of mathematics, our mathematical mindset approach includes other research from brain science and education about effective learning. For example, recent brain science has shown that when people work on mathematics, five different pathways in the brain are involved, and two of them are visual pathways [10,26]. The mathematical mindset approach teaches about the value of different representations in mathematics, with students creating ideas in visual, numerical, verbal, and other forms, encouraging connections between pathways in the brain. Mayer [27] studied the impact of a “multimedia” approach to learning, and found that teaching through different representations, including visuals, deepened understanding for students. Our approach also shares the importance of struggle and of making mistakes for brain growth. At its core, the mathematical mindset approach to teaching focuses on providing all students with access to complex and rich mathematical work that encourages brain connections through multiple representations of ideas [9].
1.2. Teacher Learning through Professional Development
Professional development is intended to provide teachers time and space to grow as educators. Many experts agree on four core principles of professional development: being content focused, engaging teachers in active learning and inquiry, having coherence with state standards, and building a community of learners [28,29]. Research has also shown that effective professional development provides on-going support to teachers as they seek to implement new ideas in their classrooms [29]. Additionally, research on high quality professional development emphasizes involving teachers in studying records of practice, including videos of instruction [30], and examples of student work [31] and student thinking, such as those developed within the Cognitively Guided Instruction Program [28,32,33].
Geijse & Meijers [3] propose that professional development often falls short because leaders do not acknowledge that for teachers to change their approach to learning, they need to change their identities as people. Such identity work is complex, and, as Geijse & Meijers point out, requires teachers to receive emotional support as they surface deeply held beliefs. Geijse & Meijers also highlight the fact that teacher learning is often expected to be reproductive instead of creative, with teachers creating new ideas for their classrooms. As part of the process of identity learning, Geijse and Meijers highlight the need for teachers to encounter a “boundary experience”, which provides them an opportunity to reflect on their previously held beliefs [3] (p. 424). During a boundary experience, teachers encounter cognitive dissonance, defined by social psychologist Leon Festinger [34] as the uncomfortable feeling that occurs when new knowledge does not match old knowledge. The resolution of dissonance is not as easy as replacing one’s prior knowledge with new knowledge. As active participants in their sense making, teachers must participate in a deep analysis of current beliefs and proposed practices. Geijse and Meijers describe this reflective process as critical for new knowledge and practices to be retained within a teacher’s practice. As the professional development of the Mathematical Mindset approach unfolded, as will be described now, it became clear that teachers were engaging in boundary experiences and identity learning, adding support to Geijse and Meijers’ proposals.
2. Materials and Methods
2.1. The Blended Mathematical Mindset Professional Development Approach
The professional development that is the focus of this paper was taught through a blended online and face-to-face approach. The PD was organized by leaders from a County Office of Education in California, themselves experienced teachers of mathematics. The County Leaders invited 5th grade teachers from 8 school districts to take part in a 3 year-long network, the focus of which was an online class taught by Professor Boaler, entitled How to Learn Mathematics (see Supplementary Material for course weblink). Fifth grade was chosen as it was the grade level with the lowest state test scores. Districts were asked to nominate teachers who would be willing to learn; teachers then had the option to join the network or not. Forty teachers joined the network. The course was supplemented by face-to-face network meetings and in-school coaching, as set out below.
The Online Course: The first component of the PD model was the online professional development course for teachers entitled “How to Learn Math”, offered through Stanford’s OpenEdX platform. The course translates research on mathematics education, mindset, and neuroscience into practical teaching ideas, directly targeting inequities in mathematics education. The course consists of eight modules, and takes approximately 30–40 h to complete. Unlike most online courses, the pedagogy of the course is built around a principle of active engagement: participants do not watch videos for more than 5 min without being asked to engage in a task or question. Through watching videos, designing tasks, working on mathematics problems, engaging with each other, and constructing interventions for their own classrooms, the online teacher course invites teachers to create new knowledge, beliefs, and practices. The course challenges the myth of the math person and the idea that only some students can learn mathematics to high levels, and it teaches new ways of teaching mathematics based upon research in neuroscience and education. Within the online course, the neuroscience about brain plasticity and growth serves as a boundary experience, causing many teachers to rethink their previously held beliefs about themselves as mathematics learners and about the teaching and learning of mathematics. Participants are provided time to reflect on the lessons through reflection and journal questions, lesson planning exercises, and interactions on discussion boards.
Outside of this study, approximately 70,000 people have taken the online course. In the end-of-course survey, 95% of teachers say they will change their teaching as a result of the course, and 96% say that they are more excited about teaching mathematics. Participants also significantly change their mindsets from fixed to growth, their beliefs about student potential, and their beliefs about mathematics [9]. Further information on the online course can be found at https://www.youcubed.org/online-teacher-courses/.
In-Person Network: The second component of the PD was in-person meetings. Mathematics leaders at the county office invited teachers to join a 3-year-long network. The teachers were told they would be taking the online course over many weeks, with half of the lessons being taken at school sites in teacher groups and half at the network meetings, all during the first year of the network.
In addition to the online course, the county leaders held seven network meetings to bring all teachers, coaches, and administrators together to discuss the content of the online course and make action plans for the integration of any ideas they wished to absorb into their practice. The in-person meetings were structured so that school sites sat together and worked on context-specific topics for their school sites, while participating in group interactions. Teachers were invited to work on mathematics together, which is an important part of constructing a different relationship with mathematics. This study was carried out in accordance with the recommendations of Stanford University Research Compliance Office. The protocol was approved by the Stanford Graduate School of Education Institutional Review Board. All subjects gave written informed consent, in accordance with Stanford’s Institutional Review Board (IRB).
During the meetings, the teachers were given multiple opportunities to compare teaching practices that were proposed within the online course with their current teaching practices. This comparison time is important if teachers are expected to implement a new teaching idea into their current practice. Teachers were given plenty of time to reflect on their learning during the in-person network meetings with supportive colleagues, coaches, and county office leaders.
The leaders introduced the teachers to the Week of Inspirational Math lessons on Stanford’s youcubed site (https://www.youcubed.org/week-inspirational-math/), and all teachers used the lessons with their students.
On-Site Coaching. In a third important component of the network, the county office coaches observed and coached teachers in their schools. The county office coaches visited the teachers in their school every month. Coaching meetings ranged from lesson planning sessions and shared analysis of student work to coaches enacting sample lessons.
Administrator Training. Site and district administrators attended the network meetings and took part in the online course. They engaged as learners and reflected upon their experiences in teaching and learning mathematics. The County Office Coaches included administrators in their site visit supports, offering guidance on how to spread the mathematical mindset message throughout their campus.
The County that is the focus of this work is situated in an agricultural region of California, with high numbers of English learners, and a majority of students designated as low socio-economic status. Mathematics achievement across the county is low, as shown in Table 1, making this an ideal context for professional learning.

Table 1.
Demographic of regional district schools and math proficiency levels for Grade 5 Math.
2.2. Research Methods
The mixed-method, one-year study that is the focus of this paper investigated teacher learning in the Mathematical Mindset network and student change in beliefs and achievement. The study considered the extent to which the PD approach changed teachers’ ideas about mathematics learners, about mindset, and about mathematics teaching and learning, and investigated changes in student achievement and beliefs. The data from the study were collected during year one of implementation, and the subsequent year when student-level achievement was made available.
A mixed-methods approach is ideally suited for studying teaching and teacher change, as it can take account of the complex and contextualized nature of teacher learning, considering multiple perspectives and events. Drawing on the strengths of both qualitative and quantitative research methods, researchers can develop robust interpretive frameworks that lead to deeper understandings than could be possible with either method alone. With a mixed-method approach, both narrative and numerical data are integrated to generate more complete knowledge about the inter-relationship of beliefs, participation in mathematical practices, and learning outcomes in school mathematics.
Given the complexity of the study designed to capture teacher learning, changes in teachers’ practices and student learning, we gathered a wide array of data, both qualitative and quantitative. We have presented the data sources in our results section to help the reader navigate our analyses. We begin with teaching shifts using quantitative measures to capture key instructional shifts. To understand teachers’ shifts in beliefs associated with the instructional shifts, we provide a corpus of data from teachers’ online reflections, survey responses, and semi-structured interviews. We then present data sources from students which include pre/post mindset survey responses, and finally, student-level state math achievement data.
Our study was guided by the following questions:
- (1)
- What shifts were evident in the teacher’s beliefs and attitudes about math and math teaching as a result of completing the online teacher course? (Data sources: online course responses, surveys, interviews.)
- (2)
- What shifts were evident in the teacher’s practice as a result of completing the online course? (Data source: coaches conducted classroom observations using a Mathematical Mindset observation tool)
- (3)
- For students of teachers participating in the online teacher course, what shifts were evident in student’s beliefs about mindset and the nature of mathematics? (Data source: Student Mindset survey)
- (4)
- On a standardized assessment of learning, were there any differences in learning outcomes from students with teachers who participated in the online course compared with similar students with teachers who did not participate? (Data source: Student-level results from Smarter Balanced Assessment for California)
Mathematical Mindset Observation Tool: An observation tool was created in partnership between the research team and county office mathematics leadership. This observation tool was used both as a discussion guide for coaching sessions and as a formative assessment tool by coaches in the classroom. The evolution, refinement, and implementation of the observation tool will be reported in detail in a future paper. The tool is included in the Appendix A. It had 4 levels for rating: Not observed, Emerging, Accelerating, Expanding.
The tool collected information on five mathematical mindset teaching practices:
- (1)
- Teacher Fosters Culture where all Students can Learn to High Levels
- (2)
- Teacher Provides and Facilitates Open Mathematics
- (3)
- Teacher Maintains High Challenge and Cognitive Demand
- (4)
- Mistakes are seen as Valuable, Risk Taking is Encouraged
- (5)
- Teacher Maximizes Student–Student Interactions.
As this protocol emerged from our partnership and in a direct response to the county leaders’ request to have a formative tool to guide instruction, we do not yet have validation studies or reliability estimates. However, we did iterate this instrument in close communication with network leaders and teachers who gave substantive feedback about each of the indicators. We conducted a formal, half-day, in-person session where all participants reviewed a version of the protocol and gave written feedback. The teaching practices were tightly aligned with the online course, the Mathematical Mindset book [9], and the substance of their monthly meetings, which supported the research team’s and network leaders’ shared understanding of the meaning of each of the 5 teaching practices in the protocol.
Coaches conducted teaching observations. The observation protocol was used by district coaches at two different time points. The coaches rated the teachers’ methods before the PD and then observed and rated them again mid-way through the first network year. Data is included for 27 of the teachers for whom we had a pre and post scores. Several of the network teachers were not observed, as their smaller districts did not provide instructional coaches.
Coaching sessions for the network varied across the involved schools districts in terms of focus and duration. The research team did not direct coaching activities. To support a mathematical mindset teaching approach, the network leaders asked instructional coaches to make at least two observations, with some providing more than two. The duration of the classroom observations ranged from 30 min to 1 h, depending on the time apportioned to mathematics at each school. Coaches connected by email prior to the lesson to agree on a particular focus. Teachers could choose among the wide range of topics within the mathematical mindset approach, such as giving growth mindset messages, using rich and open tasks, valuing mistakes, and collaborating with peers in groups. The coaches took notes during the observation and then held a loosely-structured post-lesson conference to discuss the lesson.
Online Course Responses: Throughout the online course, teachers were asked forty-three times to either reflect on a lesson or idea, share their ideas, work on a mathematics problem, or plan lesson ideas based on the modules. Prompts ranged from personal reflections (What were the main ideas you learned that you plan to make use of in your work/parenting?) to hypothetical teaching scenarios (If you had an hour a week to spend with a low-achieving 3rd grader, over say, six weeks, what would you focus on with them?). All responses to these questions were collected for all network participating teachers. For this analysis, responses were analyzed that reflected change in teaching practice and shifts in teacher identity. Remaining responses will be analyzed and reported in future papers.
Teacher Surveys: During the course of the school year, teachers were asked to reflect on their learning through both online and in-person surveys. The surveys were used to capture any ways in which the online course was influencing teacher beliefs and practices. The surveys provided information to the research team and opportunities for the teachers to participate in the emotional work necessary to reconcile the boundary experiences they were experiencing in the course. The surveys were representative of the teachers, and ranged from 35–40 respondents on each.
Teacher Interviews: To create an in-depth picture of teacher growth and identity work through this professional development, twelve teachers were interviewed. The interviews investigated any changes in teachers’ ideas, beliefs, and teaching practices. During the interviews, teachers were also asked about the ways students, parents, and administration were reacting to changes that they wanted to make or were currently making in their classrooms. The teachers were also asked to reflect on themselves as learners, and ways in which they had been challenged to think differently about the myths of mathematics.
Of the 12 teachers we interviewed, 7 volunteered to be interviewed in early fall, after completing half of the online course. The interview was semi-structured and focused on how the course was affecting their practice. They represent four schools in four different districts in the network. The remaining 5 teachers were a purposive sample, selected as case study teachers, and were interviewed in the spring. These 5 teachers were nominated by coaches based on high levels of implementation of mathematical mindset practices. Semi-structured interviews of case study teachers focused on how the course was affecting their teaching, and also how it has affected their personal relationship with mathematics. The interview protocols are found in Appendix B.
Student Mindset Surveys: 383 Students were given a teaching and mindset survey at the beginning of the year and in the middle of the spring semester. The items assessed students’ beliefs about mathematics, about their own potential, and the teaching environment. Shifts in student beliefs are at the heart of the intervention, guided by the view that mathematics teaching shapes how students experience and form deep beliefs about the nature of mathematics, and what it means to be a successful learner [9]. The results of the student survey give an indication of changes in teaching and the success of the professional development approach. The survey items are provided in Appendix C.
Student Achievement Data: To assess learning gains on state tests, we collected the Smarter Balanced Assessment Consortium (SBAC) Summative Assessment for California [35] at the 5th grade level for individual students who were taught by teachers participating in the study. The SBAC assessments determine students’ progress toward college and career readiness in English language, arts/literacy, and mathematics. These are given at the end of the school year and consist of two parts: a computer adaptive test and a performance task. For mathematics, results are reported in overall scale scores, overall proficiency levels, and the sub-scores in the areas of (a) concept and procedures, (b) data analysis and modeling, and (c) communicating reasoning.
A summary of the data sources is given in Table 2.

Table 2.
Summary of Data Sources.
2.3. Data Analysis
Teacher shifts in beliefs were captured through open-ended surveys, as well as Likert-based surveys within and outside of the online course. Interviews were transcribed and coded by pairs of the research team to identify themes. These interviews gave us initial insights into shifts in teacher beliefs and teaching practices. We also examined artifacts from the monthly network meetings such as exit slips and open-ended reflection prompts.
Instructional shifts were captured not only through teacher self-reporting, but also through the data from structured observations by instructional coaches directly working with participants. Coaches provided two time points of assessments (beginning and middle of year) using a formative observational tool designed to capture math mindset teaching practices. This provided confirmatory evidence for the teacher-reported data on instructional practices.
Across this repository of data sources, open coding [36] was used to analyze data. All of the interviews were coded, and the 25 resultant codes were reduced to eight bigger themes. The interviews, and other forms of data, were then analyzed using these themes which were regularly revisited during meetings of the research team. The iterative process of data analysis and the multiple forms of data collected increases our confidence in the validity of our analyses and findings [37]. In the last month of the intervention, the research team conducted a videotaped extended interview with county education program leaders and instructional coaches to confirm and elaborate upon instructional shifts that they captured in their structured observations of teachers. Furthermore, we shared our analyses with key instructional leaders as a form of member checking [38], which further supports the validity of the findings.
The observation tool was used by district coaches at two different time points. To measure statistical significance, a matched-pair t-test was conducted for each of the 5 measures using average scores on the indicators within the measure.
The student survey was analyzed using a Principal Components Analysis (PCA) for factor analyses [39]. The items assessed students’ beliefs about mathematics, about their own potential, and about the teaching environment. A matched t-test, was used to determine whether students’ views of themselves, of mathematics, and of the teaching environment changed after teachers had engaged in the professional development program, as indication of changes in teaching and success of the professional development approach.
Using state data for student achievement in 5th grade mathematics, we provide descriptive statistics for the baseline traits of the students in the sample. A control group of students in the same school districts and academic year but whose teachers had not participated in the professional development was constructed. We then applied Ordinary Least Squares (OLS) regression analysis, controlling for baseline differences (gender, race, free and reduced lunch status, English language learner (ELL) status among other covariates available), testing for the effects of the professional development intervention. We investigated the effects of the intervention on Smarter Balanced scores in math overall, as well as the Mathematics Claims sub-scores in concept and procedures, data analysis and modeling, and communicating reasoning. To increase validity within our design, we included statistical checks that students’ baseline traits were statistically similar for both treated and control students. Finally, we measured the achievement effect of the professional development intervention on specific subpopulations of students defined by gender, race, free and reduced lunch status, and English learner status.
3. Results
3.1. Teacher Change
In order to consider whether the Mathematical Mindset approach changed teachers’ ideas about mathematics learners, about mindset, and about mathematics teaching and learning, we gathered a range of data sources that have been used to triangulate findings. The different sources of data give a consistent picture of teacher change.
3.1.1. Observation of Lessons
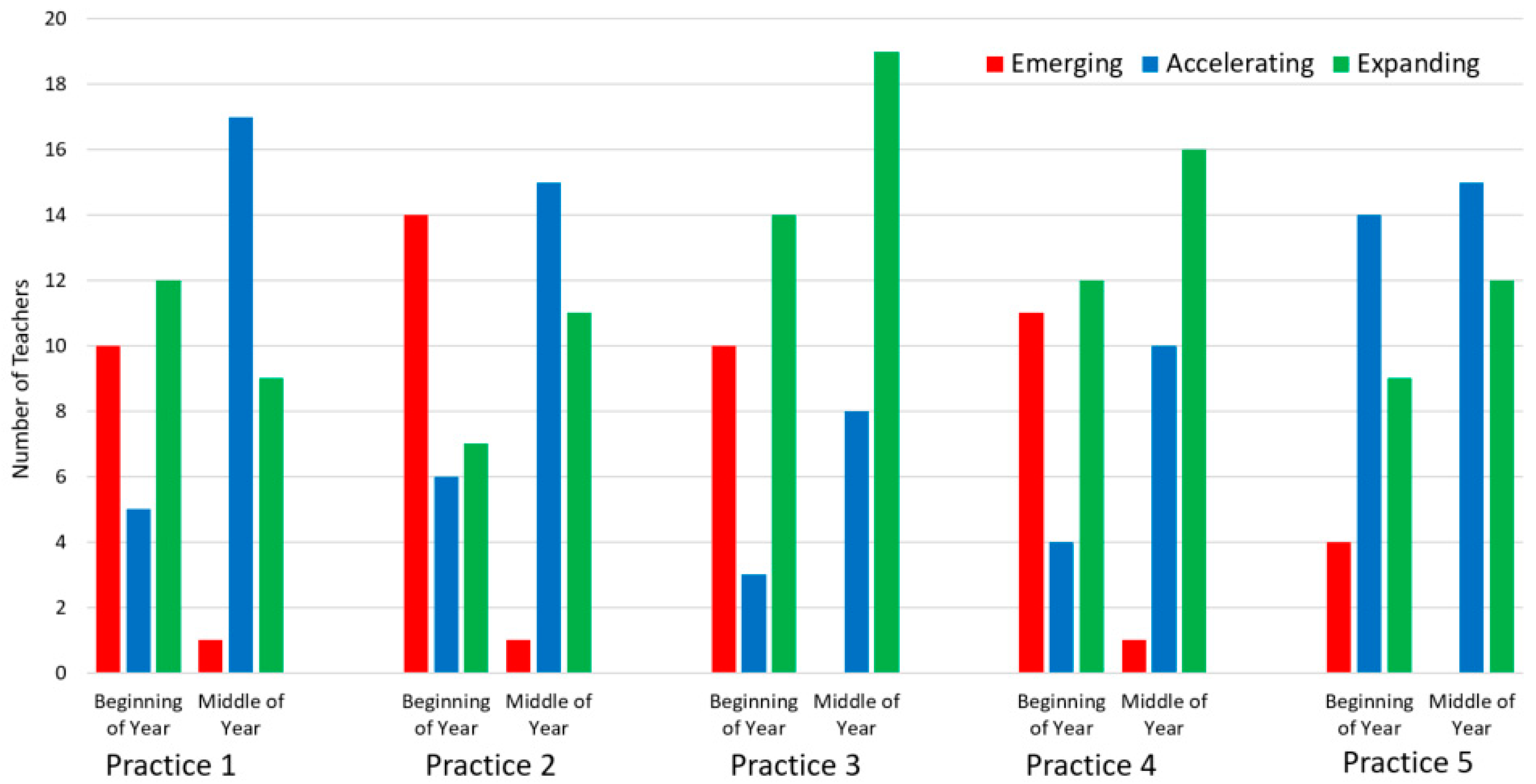
On the 5 measures in the mathematical mindset observation tool, the teachers improved in every area, with three of the areas reaching statistical significance. To perform an analysis of the observation tool scores, the three scores (Emerging, Accelerating, and Expanding) were converted into numerical scores (1, 2, and 3). We did not assign numerical values for Not Observed rating. For example, under Mathematical Mindset Practice 1 (Teachers fosters a positive culture), there are 3 sub-categories: mindset messages, praising effort, and students’ mindset. Thus, three sub-scores were generated for this practice and summed to construct a total score for that practice. Averages of scores were taken for each practice across the 27 teachers for whom we had complete observation records. The 5 areas of growth are shown in Figure 1.
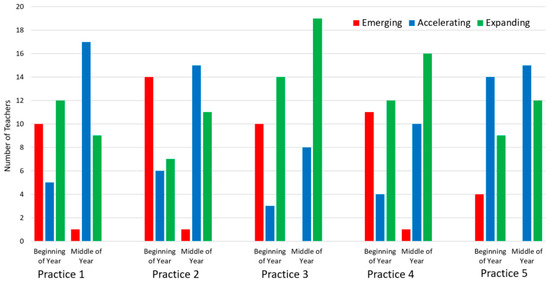
Figure 1.
Total counts from each sub-indicator of classroom observational tool for two time points for observed teachers.
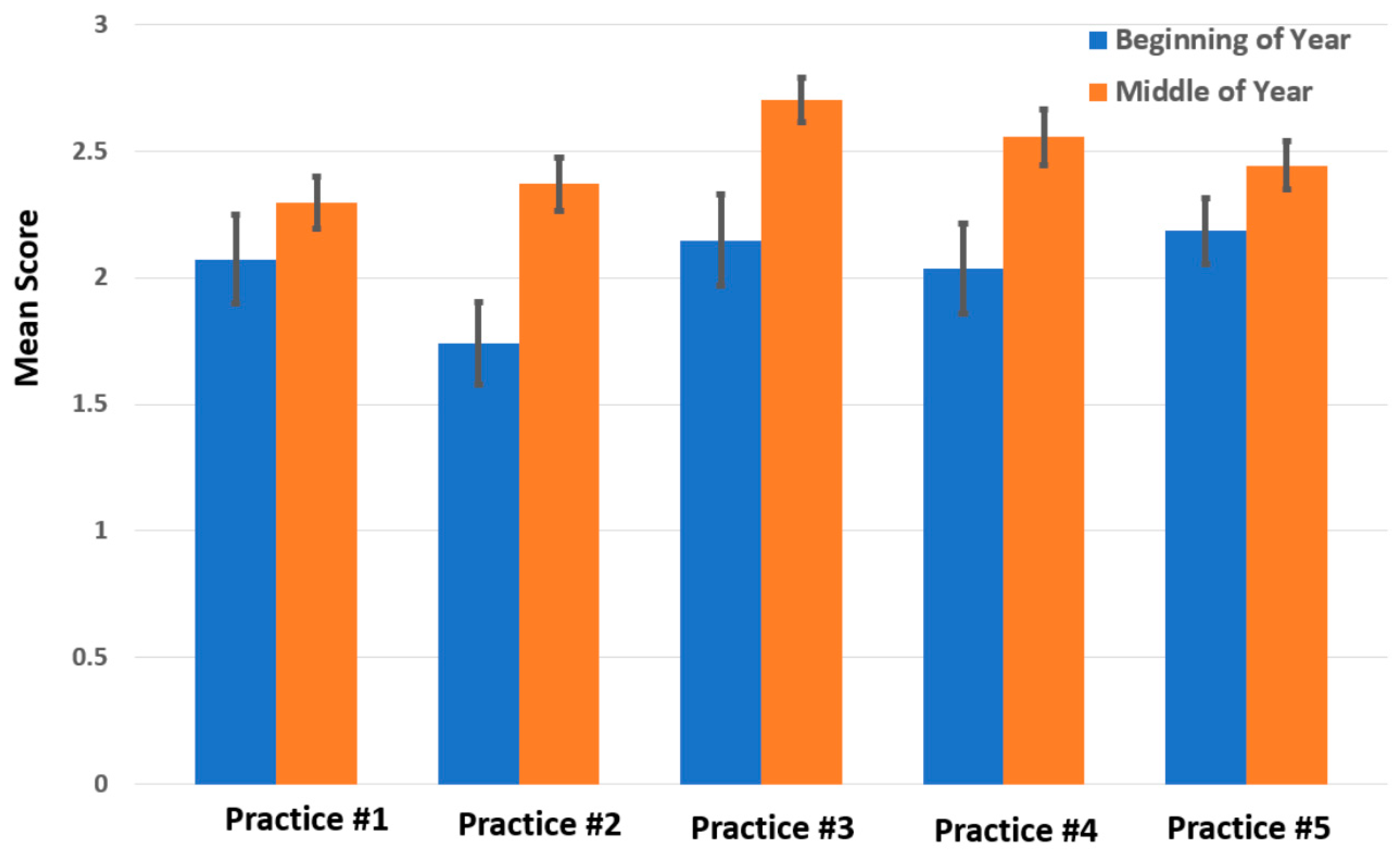
Figure 1 shows the instructional shifts in terms of subcategories and total counts, while Figure 2 shows the mean scores of the 5 teaching practices.
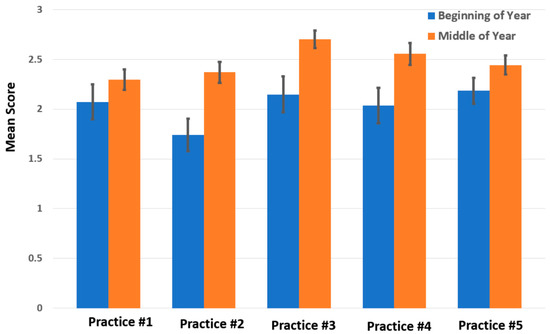
Figure 2.
Means scores aggregated for each of the 5 practices of classroom observational tool for two time points for observed teachers. (Standard errors included).
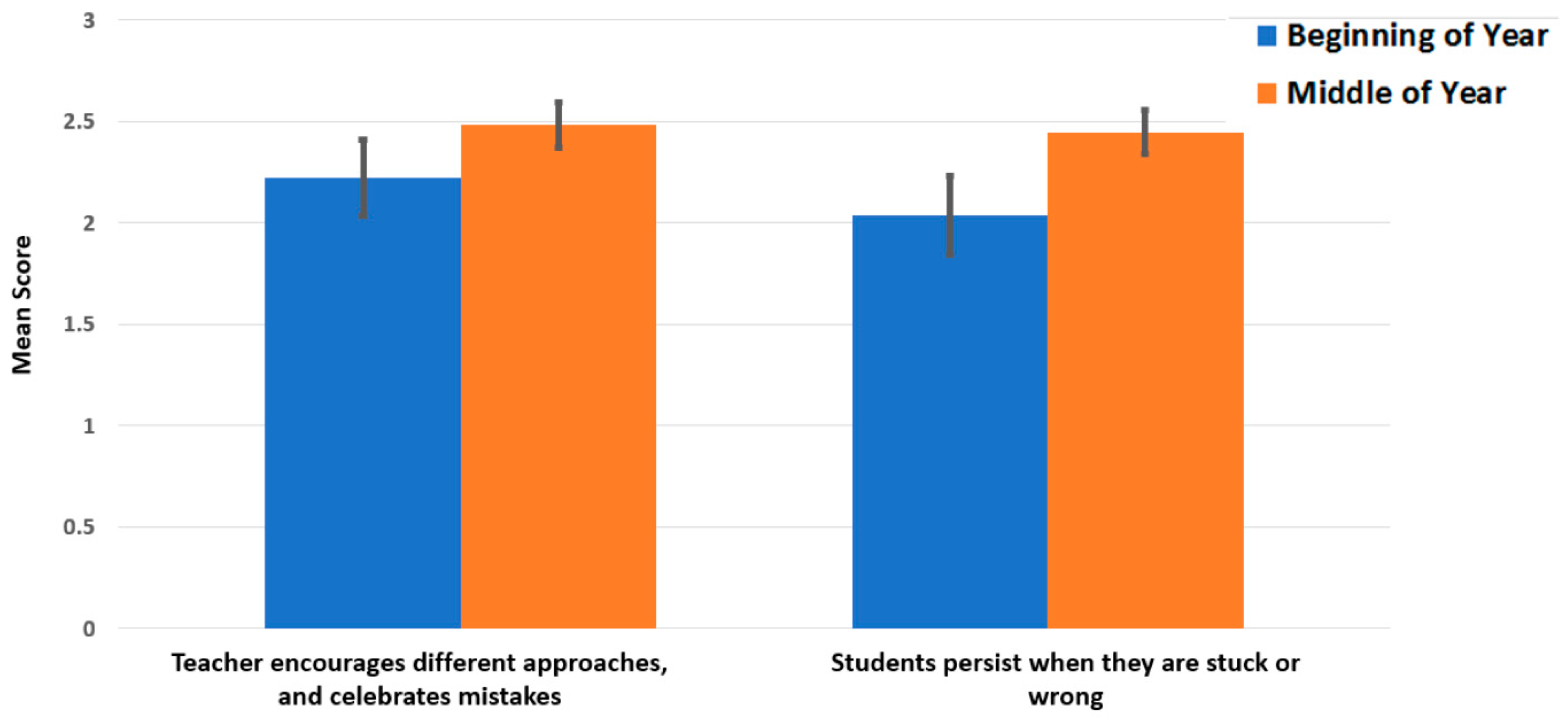
To measure statistical significance, a matched-pair t-test was conducted for each of the 5 measures using mean score on the indicators within the measure (due to a county office error, only 2 indicators were used for practice 3, instead of the 3 on the observation tool). Practice 2 had a statistically significant difference from beginning to middle of the year, indicated by a t-statistic = 3.03 and p-value = 0.005 with a Cohen’s d effect size of 0.883. Practice 3 had a statistically significant difference from beginning to middle of the year, indicated by a t-statistic = 2.75 and p-value = 0.012 with a Cohen’s d effect size of 0.758. Practice 4 had a statistically significant difference from the beginning to the middle of the year, indicated by a t-statistic = 2.40 and p-value = 0.024 with a Cohen’s d effect size of 0.678. The 3 areas that showed significant growth (Practices 2, 3, and 4) included a number of sub-areas that are shown in Figure 3, Figure 4 and Figure 5. Sub-areas are reported to help illuminate, with standard error bars, where the significant changes in observable practices occurred in each practice.
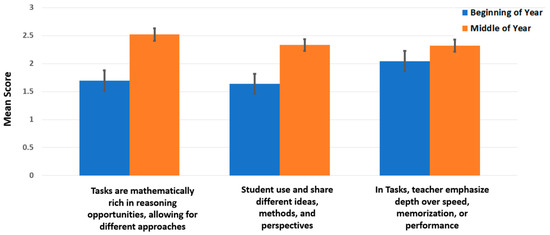
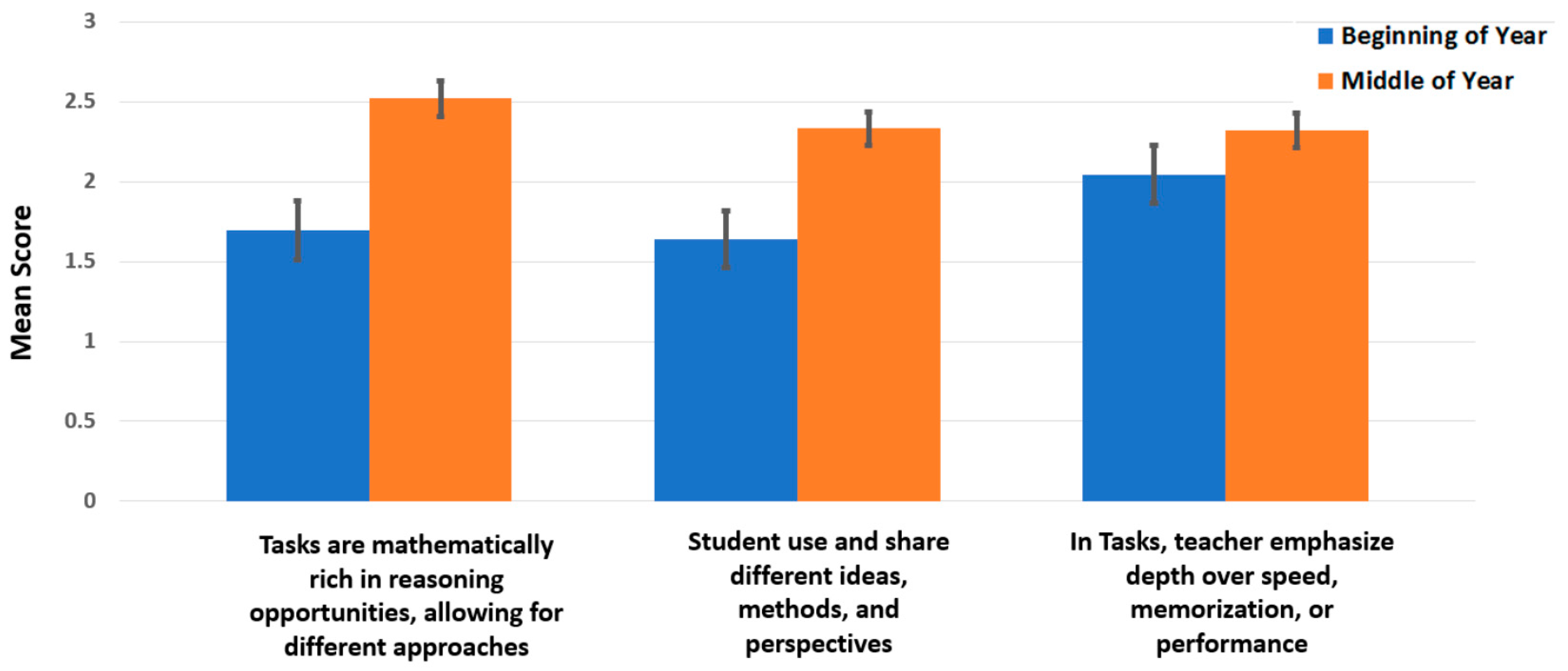
Figure 3.
Means scores for Practice 2 (Teacher Provides and Facilitates Open Mathematics) for observed teachers. (Standard errors included).
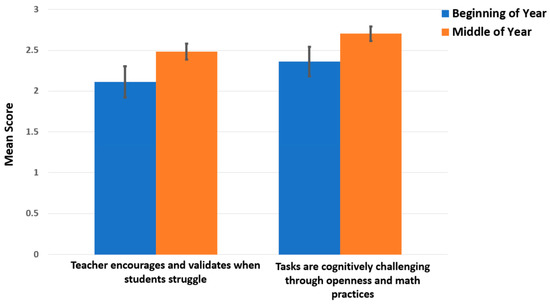
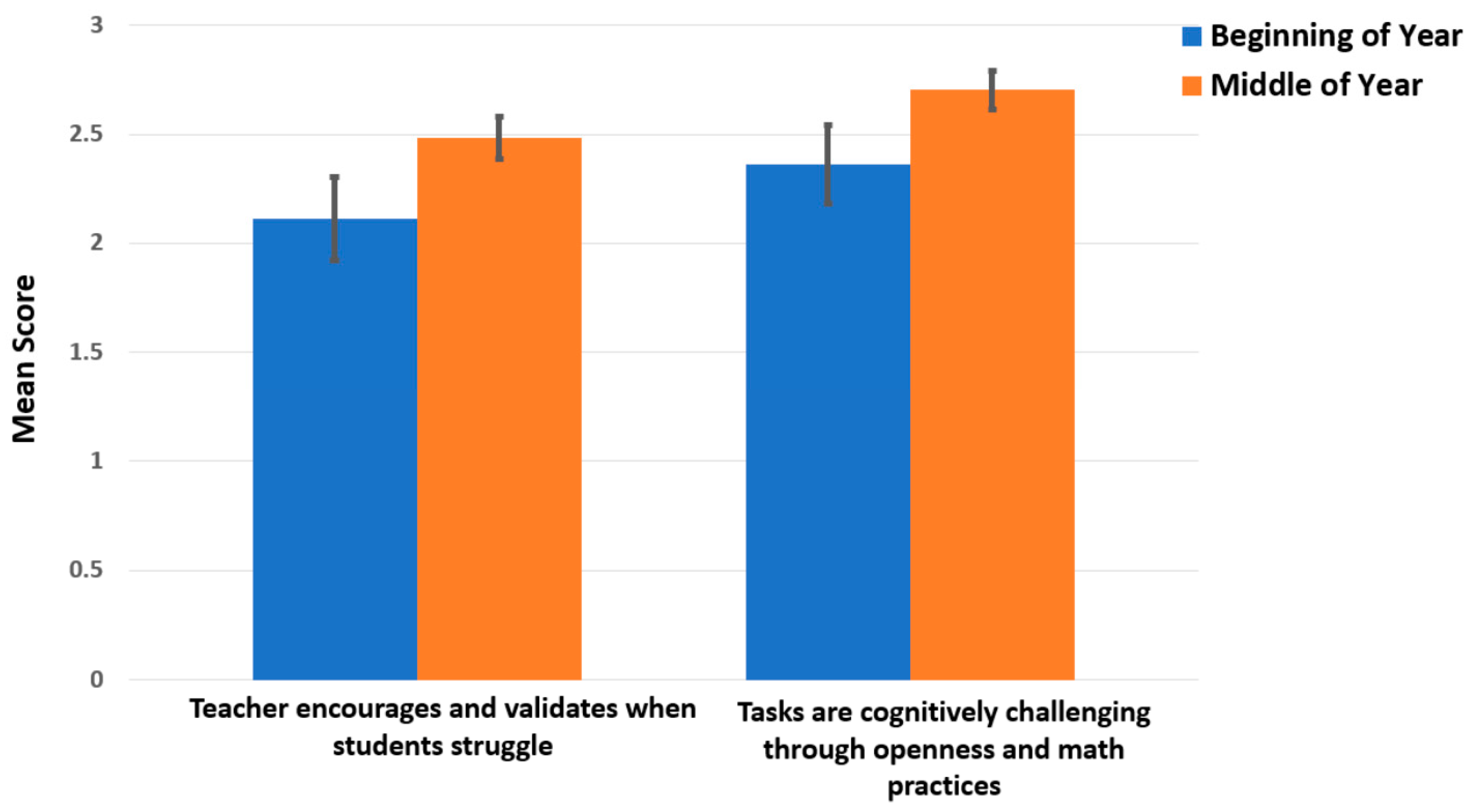
Figure 4.
Means scores for Practice 3 (Teacher Maintains High Challenge and Cognitive Demand) for observed teachers. (Standard errors included).
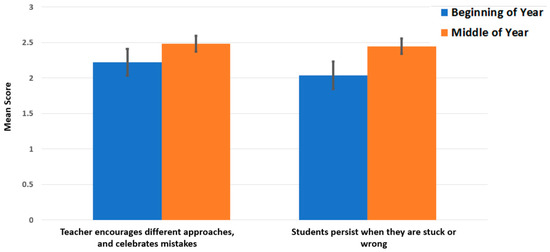
Figure 5.
Means scores for Practice 4 (Mistakes are Seen as Valuable, Risk-Taking is Encouraged) for observed teachers. (Standard errors included).
The areas reflected in practices 2, 3, and 4, i.e., using more open tasks that encourage reasoning, depth, and multiple perspectives, maintaining high challenge and cognitive demand, and encouraging risk-taking and valuing mistakes, respectively, are critically important teacher practices. It could be argued that the 2 areas that improved but did not reach significant levels are more difficult to achieve, particularly in the first year of change. Practice 1 is focused upon providing a teaching environment in which all students can be successful, and Practice 5 is focused on the facilitation of productive student to student interactions. These two areas reflect high-level teaching practices.
3.1.2. Teacher Reflections (Online Course Responses and Surveys)
Online course reflection prompts and teacher surveys that asked teachers which of the ideas in the course were more salient to them and would be the basis for change, produced findings consistent with the observation tool. Teachers were asked, through an anonymous survey, to share how their teaching practice had changed from the previous year due to the professional development they had received. The following shows the coded responses to the question: “In what ways has your teaching of math changed this year?” Table 3 provides a sample of how surveys were coded. For all responses, we provide pseudonyms for all teachers we quote, as per our consent agreement.

Table 3.
Sample Coded Teacher Survey.
Before the Mathematical Mindset PD Approach, the teachers talked about both themselves and the students “dreading” math time, and the time being taken up with strict teacher control and students working through textbook questions.
As a first year teacher, I never.... It was like every time we did math was like, “Open up a book.” And it was just this negative connotation to it.—Maurice V (Online Course Reflection)
When reflecting on their previous practice, teachers shared that they relied heavily on direct instruction. When it became time for mathematics, teachers felt that they needed to control the environment in the classroom by being the sole provider of knowledge.
What I feel has made the most difference in my teaching is, quite simply, the change of mindset. I used to think that direct instruction was the only way. I felt I had to always be in control in order for learning to occur.—Jolie (Online Course Reflection)
Because for years it was I teach, we practice, you practice alone. That type of directed instruction, and now it’s given me the confidence as a teacher to just sit back and watch them explore, and it’s okay. Even though they’re making mistakes as they work through it it’s okay, because now they’re learning the conversation that they need to have with each other as groups, as partners.—Anonymous 5th Grade Teacher (Survey)
The survey responses indicate that teachers had moved far from direct instruction, instead valuing student ideas and strategies. As Table 3 shows, the 2 most commonly cited changes the teachers reported making were asking students to share their ideas, and students having the space to explore mathematical ideas. Teachers also talked about valuing different student strategies, and students owning their ideas. There was a clear contrast between the teacher-led environment the teachers describe as dominating their practice before the Mathematical Mindset PD, i.e., working through textbooks and pacing guides, to an environment they describe in which students explored and played with ideas and then discussed them with each other. The teacher online responses and surveys give teachers’ self-reports of their changes, which are consistent with the observations of the coaches who saw the teachers using more open tasks that encouraged student reasoning. One of the teachers wrote in an anonymous survey about the “complete shift” s/he had gone through:
I’ve gone from direct instruction (DII) with little exploration of tasks to a complete shift of teacher role and I’ve become a facilitator. I anticipate their answers to math tasks, but they share their thinking and ask each other questions. They clear up their own misunderstandings most of the time with little direction from me. My students are thoroughly enjoying math.—Anonymous 5th Grade Teacher (Survey)
The vast shift in teaching practices that emerged from the coaches’ observations and the teacher survey are further elucidated by the teacher interviews.
3.1.3. Interviews
The coaches’ observations, teacher online course response, and surveys reveal considerable teacher change. Interviews with 12 of the teachers who volunteered to share their perspectives add depth and nuance to the other data. The coding of the interviews produced 8 different themes that were important to the teachers and reflected their biggest areas of change: Mindset, Using Open Tasks and Questions, Encouraging Struggle, Celebrating Multiple Ways of Seeing and Doing Math, Scaffolding Less, Valuing Slower Thinking, Student Role in Change, and Own Relationship with Mathematics. Each of these themes will be discussed below.
Mindset. In the online class, teachers were introduced to research showing that brains grow and change, and that self-belief—having a growth mindset—is important for learning. When asked in their second teacher survey about the ideas they were implementing from the course, over half, 25 of the 40 teachers, chose to write about mindset, which was the single biggest idea chosen. In the interviews, teachers expanded on the ways they had integrated mindset ideas into their teaching:
I will definitely change my way of thinking about all of my student abilities. All of the data given to me regarding my students will not be looked at the same way as it had been in previous years. I will now see the student first rather than see a test score and then a student. My Students will be viewed as individuals who no matter what level of math skills should be attended to as a student with mindset that needs some TLC.—Maria
During the interviews, teachers also shared the ways in which they had integrated mindset messages into their classrooms. They also reported that students were not only internalizing the messages, but also taking the initiative to set the tone of the classroom, and encouraging each other to have growth mindsets.
I’ve really seen an impact on my students and how they view themselves, and it’s changed their level of perseverance in the classroom. And everything, really. And even during art, one kid was saying, “I can’t. I can’t do this,” and another kid said, “That’s a fixed mindset.” And I’m getting positive feedback from parents about this. Their children that really didn’t believe that they could do math, or really just saw themselves as deficient in some way, that their attitudes are changing.—Holly
Teachers also shared that they brought the research they learned in the online course back to their classroom to share with the students. The teachers talked with the students about brain growth, neuroplasticity and synapses firing in the brain, which became part of the classroom conversations:
From the get go we talked about and continue to talk about the Fixed and Growth mindset. I continue to remind my class that we must change our old ways of thinking about math to a new way, which is to always approach math with the attitude of “yes, if I try and keep on trying, I can” explaining that this is the Growth Mindset!! The information on the brain and how its plasticity is affected by the learning or lack of learning/struggle. In my class we always refer to our brain synapses firing which is a good thing especially when we are challenged.—Maria
It seems noteworthy that the teachers were sufficiently excited about the research they learned that they returned immediately to share it with their students, who in turn used it to encourage each other.
Using Open Tasks and Questions. As mentioned in the introduction to this paper, encouraging a growth mindset means more than teachers using different words with students. Narrow textbook questions, with one method and one solution, often give students the idea that mathematics is a fixed subject. Considerable portions of the online course and the network meetings were devoted to mathematics, and the value of more open tasks that encourage different student ideas to be shared and discussed. Additionally, all of the teachers in the network used the “Week of Inspirational Math” tasks from youcubed: a pre-planned week of low floor, high ceiling mathematics lessons, and accompanying lesson plans encouraging student discussion of the ideas. The teachers spoke about the impact of the youcubed lessons (that they referred to as imaths), which were very different from their previously used textbook questions:
The week of imaths was incredible for kids, I’ve never seen a classroom more fired up for math in my life.—Maria
One of the teachers reflected that the mathematics that students learned through open tasks did not “look” like math to the students, as they were so used to narrow closed questions:
I think it’s because it doesn’t look like math, a typical practice sheet with 50 problems on it. … So, they’re more excited, because it’s more like an activity. It’s more like they get to discover on their own and do something that is different than what they’ve done before. So, I think that’s why they’re enthused about it.—Fred
The results from the coaches’ observations tool suggest that teachers continued with open tasks throughout the year, and in interviews the teachers talked about the ways they managed to do this: finding tasks on line and creating their own:
The whole week was wonderful. At first we pulled different youcubed problems so we didn’t have to do GoMath on Fridays, now we come up with our own open ended questions. We just create. The other day on the board I wrote: The answer is 17 how many different ways can you get me to the answer? I thought they might just say 1 plus 16 but they were doing orders of operations and they got really fancy and I was really impressed with them.—Janice
Janice’s reflection reveals a high degree of teacher agency, as she describes first looking for new tasks online, then creating her own, using the principles she had learned through the network. One teacher shared that teacher collaboration time had changed since taking the course, and that he and his colleagues now work to develop rich tasks together:
What we’ll do is we’ll plan an enrichment task. We’ll kind of go through the process of how we think the kids are gonna solve it, maybe how we think what we’re gonna see. … So that’s been our biggest goal, kind of setting up a rich task…—Jeremy
As the teachers describe their creation and use of different tasks, they suggest a different relationship with mathematics, which is more enjoyable and playful, and leads to deeper learning of their own.
Encouraging Struggle: A key message of the online course concerned the value of mistakes and struggle for brain growth. Many mathematics learners come to feel ashamed if they make mistakes and do not realize that times of making mistakes and struggle are very important for brain growth. In the online class, participants were asked this question:
Think back to some time when you were learning maths and you made a mistake. How did that make you feel?
58% of respondents answered “I’m not good at this”, while 42% answered “Slightly irritated—I need to do the problem again”. Teachers talked in interviews about the ways they integrated their new knowledge of the benefits of struggle and mistakes into their classrooms, creating, as one teacher said “safe, risk-free environments” where students were “more willing to share openly without worrying about right/wrong because they know as we work on they will have (the) opportunity to modify their answer/thinking without any stigma being attached.”
The teachers shared that the creation of mistakes-friendly environments had deeply impacted their students:
The kids were thrilled, going “Oh my gosh, he’s doing it like that? It’s OK that we struggle? It’s OK we think differently?”—Janice
When a student asks if “It’s OK that we think differently?”, it suggests that they had held damaging ideas about mathematics learning, including the idea that they should all think in the same way. The teachers were quick to notice how powerful the new ideas were for the students, particularly around the permission to struggle:
I liked watching them struggle, and I know if the teacher says that it always sounds kind of odd, but it was a really good struggle because it really got them to think much differently about what math was, and that math is not just going to come out of a textbook, I am not just gonna sit there and look at you and go, “You’re gonna do this many problems.” We don’t do that, and the kids have now accepted that going, “Okay, so things are definitely gonna be different.” And they all have math notebooks and keeping ideas of their journals, and what they need to do.—Janice
Allowing and acknowledging the value of struggle helped teachers redefine what mathematics was for their students. Instead of a finished product that is laid out in a textbook, the teachers helped students see mathematics as the product of student thinking and purposeful struggle. The teachers were grateful for the changes they saw in their students:
I just want you to know this [the online course] has meant a lot. Seeing how positive the kids are about their learning now has made a world of difference. The confidence they have is unlike anything I have ever seen.—Fred
Through their new-found appreciation of struggle, the teachers became more relaxed when teaching mathematics, and were less tense when students made mistakes:
But now it’s easier for me to accept the wrong answer from a student. Usually it’s, “Come on, you guys can do this.” Now it’s, “Okay. Let’s do it this way. Let’s see what else we can come up. Talk to your partner.” So it’s more engagement for me, and it’s a lot easier for me. It’s a lot more relaxing.—Fred
One of the teachers described the frustration students could fall back into when they struggled, but when she reminded them of the importance of struggle, she saw a “wave” of change with students developing growth mindsets and appreciating mathematics more:
But I still had a lot of kids that were incredibly frustrated, “This isn’t gonna work.” The next day we talked about those norms again, and those mindsets that in this class you’re going to be expected to think, and it’s okay, you’re gonna be challenged, and you are gonna struggle. And struggle is not a bad thing. And then all the sudden, you could almost see kind of like this wave of kids, and the whole reaction started to change, so their mindset totally completely began to change. And then they got more of them pulled in.—Janice
Celebrating Multiple ways of Seeing and Doing Math. An important area of change that was discussed in the online course and the teachers’ network meetings concerns the need to make mathematics more multi-dimensional, encouraging students to see mathematics visually and to make connections between areas. Many of the teachers discussed the change in the way they and students saw mathematics:
Oh, the visuals.... They love that too, cause with their ideas of how it would form, and how they would build. I do it periodically. Just throw up a visual with different things and say, “Okay, what do you see? What don’t you see? What might you see? What could be the next thing?”—Leila
Well, the big take-aways for me are the connections they make. We were doing a paper-folding activity where we were using it for fractions, but the paper-folding activity, they started folding the paper with triangles from a square. And they on their own discovered that there was an exponential relationship, so when they folded it once they had two pieces. And then when they folded it twice, they had four. And they started seeing the exponents of two with every fold. And they made that connection all by themselves, cause we’ve been doing base 10, and powers of 10. So I see those connections happening during these iMath lessons, and that’s huge for me.—Fred
Reducing Scaffolding: Another key message of the online course is the importance of allowing students to struggle and the need to step back on scaffolding and rescuing students. The reduction in scaffolding was one of the themes that emerged from the interview:
Last year I probably would’ve been more of the one to help jump in a little bit more and give them more scaffolding. This year, I’ve been working really hard at not jumping in and scaffolding quite so much, but the kids are helping each other, so it’s not relying on me. It’s where the kids, when we’ve been doing these different tasks from the five practices, where it’s me kind of stepping back and letting them, and doing maybe more of the question asking.—Janice
As the teachers developed an appreciation of struggle they became more comfortable leaving the students to engage in productive struggle and to use each other as resources.
Valuing Slower Thinking: One of the online course lessons focused on the value of depth in mathematics, and the need to counter the damaging idea that to be good at mathematics, students need to be fast with numbers. Many of the teachers talked about the ways they had slowed down to allow students to go into more depth and think more conceptually about math:
And even individually, I can tell that they sit and they think about it when it’s time to think. Before, they just tried to work through it and be done, and that’s a lot of what happened last year, was just the race to be done. And so I’m trying to expel that, I just wanna do away with the whole race. There’s no value in that.—Kayla
When teachers stopped valuing speed, it allowed them to focus more on mathematical concepts:
I’ve kinda slowed things way down, and focusing more on the concept for the day.—Fred
Teachers talked about the students who, previous to the Mathematical Mindset PD, had decided they were not “math people” because they were not fast, and how they had been able to feel included as competent mathematics students:
So, I have noticed, I have a couple of students that really have taken on that it’s okay to take their time to do their work. I have a girl who just raised her hand and shared this with the rest of the class which I thought was “Wow.” She always thought that she wasn’t good at math because it takes her a long time to do the work.—Julie
Many teachers do not feel that they are able to slow down in their teaching, even if that means moving quickly over important concepts, because of pacing guides from districts. The teachers in the network were greatly helped in bringing about change as the County leaders had worked with administrators to make sure that they were supportive of the change teachers were making. This next comment highlights the importance of administrator support, in letting the teachers embrace the important research they were learning without being hampered by the need to meet district pacing guides and benchmark tests:
Okay, why are these kids so much better at focusing? Is it because they’ve had a couple more years of Common Core and they understand it better? They’re used to the routine? They’re used to the collaboration? Or is it because they have a different mindset now? And that’s what I’m leaning more towards, because last year it was like if they can’t finish it in five minutes they don’t wanna do it. And this year they’re okay with taking time on it, and I’m okay on taking time. In fact, I mentioned to our superintendent this morning, she was here with us and I said, “I don’t know that I’m gonna be completely prepared for our benchmark in a couple of weeks.” And she goes, “Don’t worry about it. Just let the kids explore, it’s more important that they think about what they’re doing. That they grow this mindset, because it’ll work out for them better in the end.” And so that’s the major difference I see.—Kayla
The different teachers appreciated the administrator support that is often lacking in teacher reform efforts and one of the reasons teachers are fearful of making changes.
The biggest freedom that we’ve had is our administrator has empowered us to not look at “This is the lesson I have to get done,” it’s “How can I take elements and resources?”, covering the standard… So I think hearing that as a teacher, it’s like you have a blank canvas. It’s your freedom to... You have the freedom to add to what you want with the structure of common core and standards. But hearing that, as a teacher, there’s no complaining. It’s taking from here, taking from there, and then blending it together.”—Maurice
Student Role in Change: One of the most encouraging and unexpected themes to emerge from the teacher interviews was the role of students in encouraging teachers to make changes. Many of the teachers talked about being afraid of some of the more open tasks, or not thinking that students would be able to cope with them, and then being surprised when the students did well. In one instance, a teacher did not want to use one of the recommended tasks and then was surprised when students took ownership of it. The task is called: Four 4’s, and students are invited to find every number between 1 and 20 using exactly four 4’s and any operation:
When it said on the week that I might have to teach this, like, “No, no, no, no, no that’s too much for fifth graders.” But they thought it was really cool.And the very first day we did it, oh my gosh, the struggle and the upset and, “Oh my gosh, I’m gonna have to do this, this is hard.” The second day, they got more into it, they got more experience. And then I had two girls the following week come in on their own, and figured out the missing ones, and they thought that was the coolest thing, and they were just like, “It’s totally filled out!”—Janice
Others talked about how the students took the messages they had learned and used them to encourage the teachers to have a better mathematical relationship, in a reversal of the expected role of teachers encouraging students in their mathematical relationships:
The most powerful is the mindset, and that’s not only for my students but more for me because I didn’t think I was a math person. I’ve never enjoyed math, I’ve never felt that I was good at math… before when it was just that one right answer then that left a lot out. I like the mindset and the kids have really picked up on that and they’re really applying that. In class, we’ll say, we don’t say that something is hard, we say it’s challenging. I am the one that usually says about something being hard and then they’ll all tell me, “No, it’s not hard, it’s challenging.” So they’re doing really well with the growth mindset.—Heather
The students also took it upon themselves to use the mindset messages they had learned to encourage each other:
I am making more of an effort to help my students develop a math mindset of success. One example I have took place about two weeks ago during our Go Math lesson. A new student had arrived in our classroom, and he came with an IEP(Individualized Education Plan). We were doing a problem together whole group, and I noticed he was not writing down the problem. I asked him why, and he said “I am not good at math; it is hard.” Before I could respond, the entire class looked directly at him and said “don’t say that, everyone can be good at math.” We then gave him our class cheer which is “I can, you can, and we can.” It was totally spontaneous, and I am seeing more effort from him.—Joel
Eight of the teachers who took the teacher survey chose to talk about the ways students felt empowered by the new knowledge the teachers were sharing, which certainly seemed evident in the reflections of the teachers in the interviews.
Own Relationship with Math. The seven themes reviewed speak to important changes in teaching, confirming the observational data and the survey data. The considerable teacher change that resulted from the Mathematical Mindset observation is noteworthy, particularly when considered against a backdrop of a general lack of interest in professional development by teachers [40]. One of the codes that emerged from the interviews was different in nature from the other seven, although related to the teaching that was described in the seven codes; it concerned the teachers’ own relationships with mathematics and learning. As the teachers learned in the course that they could, themselves, learn mathematics well and there were no limits to their learning, they began to rethink their past experiences in school and as learners. The teachers, like many learners of the past, had believed the myth that they were not a “math person” and could not learn math well. They had internalized this idea and it had shaped their experiences, not only as a student but later as a teacher. While this theme emerged in the coding of the interviews, teachers also shared how they had been affected by the myth of the “math person” in their online responses and surveys.
In one of the reflection prompts inside the class, one of the teachers shared how his fear of failure had shaped his own personal experiences in education, in both English and mathematics.
The information has made me reflect on my fear in my English and literature courses. I have always loved my literature courses but I was always scared of failing and the subject not being for me as a Mexican-American and English learner. Applying it to math I had a similar thing going on where I liked math and even considered being a math major but decided against it because of the fear of failing.—Miguel (Online Course Reflection)
This extract speaks both to the ways Miguel had been held up in his learning by myths around failure and the effectiveness of the spaces in the online class to reflect. The online reflection spaces seemed important for teachers to do the emotional work necessary to engage in personal sense-making of the information provided.
Many of the teachers in their interviews described feelings of being incapable of learning or teaching math well prior to the intervention, and were surprised by the impact the course had on their own relationship with mathematics:
I thought it was going to be great for the kids, I never expected it to change me, that’s been my greatest revelation in all of it.—Kayla
The teachers talked about taking problems home and working on them in the evenings:
I have to defend math a lot and why I teach math the way I do because it goes against what parents have learned. It goes against what I have learned. I’ve never done it this way. I tell parents I go home now and I study and I practice and I figure it out. If I’d learned math this way I wouldn’t have cried every night in math going through school.—Janice
Another teacher shared that she had been in a network meeting working on a challenging problem when another teacher had looked up the answer on his phone. Rather than look at the answer she chose to keep working on the problem, not only in the meeting but through the next day and into the next week, until she solved it. The teachers started challenging themselves to look at mathematics visually and approach it differently, and struggle through hard problems until they had a solution.
The new relationship with mathematics that many of the teachers seemed to develop, based upon the knowledge they had learned about brain growth, seemed instrumental in their willingness to embrace new teaching approaches. They started to see mathematics and themselves differently, which allowed them to see learners differently.
Table 4 shows the relationship between the themes we found across the teacher surveys and interviews, as they map onto the five key mathematical mindset practices of our observation protocol. Such a mapping provides information to researchers and network leaders about areas that appeared more salient to teachers. This mapping could also indicate practices that might need more emphasis or support. By mapping themes to key instructional practices, both researchers who design follow-up interventions and network leaders can maintain programmatic coherence.

Table 4.
Map of Themes from Teacher Data onto Mathematical Mindset Practices.
3.2. Student Change
3.2.1. Changes in Student Beliefs
Prior to the teachers engaging in the network, students of the 40 teachers were given a survey to measure their ideas about mathematics learning and mindset. The survey was then given to students again after the professional development intervention. The shift in students’ beliefs about themselves and mathematics adds weight to the other forms of evidence of teaching change. Our conceptual link between teaching practice and students’ beliefs is rooted in the design of the online course which explicitly demonstrates how methods of teaching mathematics carry powerful messages to students. For example, if speed is given priority over depth of understanding by the teacher, then students come to believe that speed is an important part of learning mathematics. Although the teacher may not intend this message, it is nevertheless communicated implicitly and consistently.
Complete data, with pre and post student surveys, was available for 18 of the 40 teachers. The survey was coordinated by district and county staff. The survey was given online, making it accessible to some classrooms, but not to others who did not have computers for every student (hence the returns from only 18 of the 40 teachers). On the pre-survey we received 467 responses, and 485 on the post-survey, with 383 students with both pre/post responses. With a treatment sample of 1068, our response rate was 35%. We excluded surveys where only one or two questions of the 16 questions were answered. In some cases, we found students did not include their school or teacher. From the two time points, we suspect that some students may have transferred or been absent on the day the surveys were administered.
The survey consisted of 16 items for which students were asked to respond with one of Strongly disagree, Disagree, Somewhat disagree, Somewhat agree, Agree, or Strongly agree, with assigned values of 1–6, respectively. Using the 16 items administered, we applied a Principal Components Analysis (PCA) with 4 components detected, explaining the 51% variance in survey responses. (Kaiser-Meyer-Olkin (KMO) statistics of 0.84 and Bartlett’s Test of Sphericity, p < 0.001). From the Varimax rotated components matrix, we found the first component of 8 items that loaded strongest, accounting for 24% of the variability in survey responses. The research team inspected these items to ensure that the items formed a coherent construct. The other 3 components were not used because of low loading estimates, at or below 0.4, or they consisted of one or two items, or they did not appear to have a unifying theme. The 8 items listed in Table 5 indicate a Growth Mathematical Mindset.

Table 5.
Items loading for Growth Mathematical Mindset in Principal Components Analysis.
As a group, this cluster of items had an alpha reliability of 0.72. The students who scored highly on this scale have a highly positive set of ideas about themselves as mathematics leaners, which can be thought of as a growth mathematical mindset. A matched pair t-test was used to investigate changes in the average score of students on this mindset scale before and after the Professional Development intervention. It was found that students had a statistically significant increase in their average score on the above questions, with a t-statistic of −8.69 at a p < 0.001 level. The effect size in pre/post was 1.48 (using Cohen’s d).
3.2.2. Changes in Student Achievement
In addition to looking for shifts in students’ beliefs, we also analyzed student state mathematics scores for the tests given at the end of the year of the intervention. A control group was constructed to consider impact, with the teachers who did not take part in the network but taught 5th grade in the same districts. We could not collect information about the instructional practices in the control group due to resource constraints, as teachers were spread across a large geographic region and worked in different school districts; nonetheless, the control teachers were in the same school and same grade level as the teachers in the network. Comparing state test scores for the network group and the control group, we found robust evidence indicating that students of the network teachers had significantly higher SBAC mathematics scores. Overall, their mathematics achievement was 7.95 points higher (0.1SD), their concepts and procedures subscore was 0.06 points (0.09SD) higher, data analysis and modeling subscore was 0.06 points (0.09SD) higher, and communicating reasoning subscore was 0.09 points (0.15SD) higher.
Further detail of the samples and the achievement study are given in Table 6, which lists the number of teachers, schools, and students in treatment or control condition by school district. Two of the eight schools were excluded from the student achievement analysis because of incomplete data–the schools did not identify which students had treatment and control status. Students from the two missing schools consist of 143 individuals, only 3.8% of our sample size.

Table 6.
Observations used in the study.
Table 7 presents descriptive statistics on students’ SBAC scores and baseline covariate traits. The baseline covariate traits are gender, English Learner status, economic disadvantage status, migrant status, disability status, and race. Our analysis does not include prior achievement data which could not be reliably collected from the districts. While we acknowledge that this is a restriction, all our robustness checks indicate that the treatment and control samples are statistically not different in terms of baseline covariates. Our robustness checks are discussed in this section. The proportion of females in the sample is 52%, English learners 27%, economic disadvantage students 80%, migrant students 2%, disable students 8%, White students 12%, and Hispanic students 61%. The theoretical sub-scores range from 1 to 4, and the mathematics scale score ranges from a minimum score of 2219 to a maximum score of 2700.

Table 7.
Summary student-level statistics on SBAC and baseline covariate traits.
Table 8 presents the number of observations used in the analysis by each of the student baseline traits.

Table 8.
Baseline traits categories.
Table 9 presents Ordinary Least Squares (OLS) regression results examining the effects of the intervention on the SBAC academic performance of students in 5th grade. The dependent variables used in the estimates are SBAC math scores and subscores. Regression specifications control not only for the “treatment” variable (participating in the Mathematical Mindset network), but also for student controls (gender, English learner status, economic disadvantage status, migrant status, and race-ethnicity). Additional detail on regression estimates is available in Supplementary Materials, Table S1.

Table 9.
Regression estimates, Mathematical Mindset network effect on SBAC math scores.
To better interpret the effect sizes of mathematics achievement gains, we convert regression coefficients into gains of academic months and percentile gains in Table 9. The academic month gains are calculated based on the average gain of 0.33SD by academic year earned in middle school. In other words, 1SD test score gain is equivalent to 3 years (36 months) of middle school instruction, on average, in the U.S. For example, in the last row of Table 10, for an effect-size of 0.097 in SBAC communicating reasoning subscore, the average student in the experimental group would score higher than 56% of the control group that was initially equivalent, and gain learned equivalent to 5.2 additional months.

Table 10.
Interpreting Gains on SBAC Math scores.
The most crucial internal validity concern when estimating causal effects is the assumption that students’ assignment to treatment and control conditions is random. Under this assumption, the estimates are valid if baseline traits are statistically similar for treated and control students. Table 11 validates this assumption by examining whether students’ traits vary with treatment/control condition. (See Supplementary Table S2 for additional information on balance analysis). Each point estimate is from a separate regression where each baseline student’s covariate (i.e., gender, English learner status, economic disadvantage status, migrant status, and race-ethnicity) is the dependent variable. The estimated effect of treatment status on these covariates is small and statistically insignificant, suggesting that students’ baseline traits are statistically similar for both treated and control students. However, this internal validity check also shows that students whose teachers participated in the study are statistically more likely to be English learners and economically disadvantaged. This finding suggests that teachers who decided to participate in the study were teaching higher-need students in their schools.

Table 11.
Auxiliary regressions of baseline covariate balance.
The impact of having a teacher who participated in the professional development (“treatment”) could vary for students with different demographic and baseline traits. Table 11 shows estimates in samples defined by these students’ demographic and baseline traits (i.e., gender, English learner status, economic disadvantage status, and race-ethnicity categories) in order to explore these achievement differences associated to the treatment. Table 9 point estimates show that there are consistently positive academic effects for all students regardless of their baseline traits. This important finding supports the argument of the equitable nature of the intervention. Furthermore, the treatment is particularly more effective in terms of SBAC scores on female students, English learners, and economically disadvantaged students, as depicted in Table 12.

Table 12.
Regression Estimates, effect on SBAC Math.
Table 12 explores a form of treatment heterogeneity based on student’s traits. Each row of Table 12 presents the effect of treatment on SBAC scores for subsamples of the population of interest. The first row provides point estimates for the entire sample, the second shows point estimates only for females, the third only for males, the fourth only for limited English status students, etc. By restricting the sample by student’s traits, we can assess heterogeneity effects of the treatment effect.
Table 12 shows that the impact of having a teacher who participated in the study (“treatment”) varies for students with different demographic and baseline traits. Table 12 point estimates show that there are consistently positive academic effects for all students regardless of their baseline traits. However, the treatment is particularly more effective in terms of SBAC scores on female students, limited English proficient students, and economically disadvantaged students.
4. Discussion
Educational reforms have been difficult to implement in schools. Even when teachers learn about new teaching methods through professional development, many remain committed to previous teaching approaches, and minimal change happens [41]. The teachers who took part in the Mathematical Mindset professional development approach, through a supported teacher network, went against this trend, making changes in their relationships with mathematics which caused changes in their classrooms, resulting in corresponding student changes in beliefs and increases in achievement. Although it was the 40 teachers who attended the network, it would be inaccurate to represent the changes as a one directional process of teachers impacting students. The students took it upon themselves to be change agents and create different environments for the teachers and other students. It seemed that both teachers and students, as well as county and district coaches, were excited about the new knowledge they learned that went against the pervasive myth of the “math person” and limits to mathematics learning.
We propose that the success of the Mathematical Mindset Intervention, while drawing from a multitude of effective practices that were both embedded in the online course and enacted by the County office leaders, rests upon the two central factors that we discuss below:
1 The different forms of the Mathematical Mindset PD worked to eradicate the learning myths that had held up the teachers and the learners.
The vast majority of the mathematics teacher professional development of the last century has focused upon sharing different teaching ideas with teachers. Teachers have been introduced to problem-solving teaching, project-based teaching, assessment for learning, Cognitively Guided Instruction (CGI), and other ideas [32]. While these different initiatives are all worthwhile, they have not worked to change teachers’ ideas about their own and their students’ mathematics potential through sharing neuroscience, partly because the new evidence of mathematics learning and the brain has only recently been discovered. The various forms of data collected in this study suggest that teachers radically changed their teaching, and the changes came about when they changed their ideas about themselves–particularly about the potential of brains to grow and change, the importance of mindset, the power of struggle and the rejection of the need to be fast. When teachers let go of myths that had held back their own learning, they became open to change, and willingly embraced the teaching ideas shared that encourage a growth mindset for students. It is noteworthy that the main source of new information for the teachers was an online course, making this study the first of its kind to show the impact of online learning on teacher change.
The second critical factor in the teacher change was the space teachers were given to change their identities as learners.
2 Teachers had space for identity work and boundary experiences
Within the professional development provided by the online course and the network meetings, teachers were given multiple opportunities to struggle with and reflect on their deeply held beliefs about themselves and about mathematics. During these times of struggle, the teachers met “boundary experiences” [3], often in the form of neuroscience, and they had the space to take part the critical emotional work that is necessary to change how one feels about oneself as a learner and teacher of mathematics. The teachers were enabled to make changes in their self-perceptions and their teaching because all aspects of the Professional Development gave space for the teachers to think and talk. Even the online class included reflection times for teachers to think and write about their own emotional journeys. The professional development both inside the online course and in the network meetings was based upon respect for the learners. Nothing was forced upon teachers; rather, they were given time and space to reflect and process. The network meetings were organized for teachers to work out what they wanted to do. As such, change in their classrooms was a creative, rather than a reproductive, process. It seemed clear that the teachers were involved in the identity work that Geijse and Meijers [3] talk about, and that the spaces they had been provided to work through emotional issues, with support and respect, had been critical.
Mathematics achievement across the US and in many other countries in the world is low, and is plagued by inequalities [9]. Professional development has largely proven to be ineffective at changing the procedural nature of mathematics teaching, with teachers demonstrating methods that students passively follow. Based on our contextual analysis conversations with county office leaders at the beginning of the study, and interviews with the teachers, we knew that the 40 teachers in the studied network were not different, and classrooms prior to the professional development program were largely dominated by direct instruction. After a year-long network in which teachers learned about neuroscience, mindset, and active student engagement, teachers made profound changes in their self-beliefs, beliefs about mathematics, and expectations of their students. Teachers became excited to share new information with students, who also became excited both to help their teachers think differently about mathematics and to serve as change agents for other students. The study reported here provides hope for mathematics change. It also highlights the important role of a supportive and reflective network of teachers who come together to learn with colleagues and knowledgeable coaches. Teachers in this study changed their identities as mathematics learners and became excited to approach mathematics differently, with a new mindset. This study highlights the importance of careful identity work in teacher learning that starts with teachers being able to examine their own selves as learners—free from damaging myths. Kyla’s reflection captures this idea:
I thought it was going to be great for the kids, I never expected it to change me, that’s been my greatest revelation in all of it.—Kayla
As we move forward in the 21st century, equipped with important neuroscience about learning, we may need to recognize the important process Kyla alludes to—the process of teacher change, and of allowing teachers to rethink who they are and who they can be as learners of mathematics.
The program design and findings of this research can provide a roadmap to other school systems in bringing to scale professional learning opportunities around mathematical mindset. Yet, in scaling up, there is a tendency for districts to want to standardize and control learning, often assuming that all teachers will grow in lock-step and a predictable fashion. This is antithetical to the central message of the mathematical mindset, to the space and freedom teachers need to disentangle themselves from the damaging and fixed views that have been instilled in many, and to the creation of a new narrative for themselves as powerful mathematics learners.
5. Conclusions
The study reported in this paper is an unusual one; it was enacted with practitioners in the field and it draws from multiple sources of data, both qualitative and quantitative. It lacks the clinical and seemingly objective veneer of studies that focus on one variable, yet it seems important for the field to move on from such studies and recognize that when teachers change their teaching, many dimensions of change need to be considered, and different forms of data need to be collected and analyzed. In the current educational and funding climate, there is little space for such complex work, and single variable studies dominate publications and funding initiatives. Yet, a reliance on experimental or single method data that is easy to analyze and publish will not allow important educational interventions that draw from multiple inputs to be well understood. We hope that this study provides an example of what is possible when researchers work with practitioners and study multiple forms of data and change. Previous research on professional development has recommended that PD be face to face, long term, and focused on content standards. This study gives a different result, showing the impact of an online class which is focused less upon standards and more upon personal growth, mindset, and belief in the potential of all learners. Importantly, the course was offered to teachers as part of a supportive network; just as the online course taught teachers that learning should sometimes be slow, and should always include room for struggle, exploration, and growth, the coaches enacted these principles in their network approach. The results of the Mathematical Mindset approach are noteworthy with the students most at need of support—girls, language learners and economically disadvantaged students—changing their ideas and their achievement most significantly. At the heart of the student and the teacher change was a change in mindset, in beliefs about learning, and the eradication of learning myths that have held back generations of mathematics learners. The network studied produced a cohort of teachers who now think differently, who believe in the potential of all of their students, as well as themselves as learners and teachers—some of the most important shifts that any teacher or learner, can take. The data from this study adds weight to a growing realization that changing the myth that people are born as “math people” or not is one of the most important responsibilities for educators, now and in the future.
Supplementary Materials
Description of Online Course: How to Learn Mathematics for Teachers can be found at http://www.mdpi.com/2227-7102/8/3/98/s1, Table S1. Regression Estimates, Achievement effect on SBAC Math (additional information); Table S2. Auxiliary regressions of baseline covariate balance (additional information).
Author Contributions
All three authors have contributed equally to this article.
Funding
This study was sponsored by the Technology of Equity in Learning Opportunities at Stanford University (TELOS) faculty grant to Jo Boaler, 2016-17.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Appendix A. Mathematical Mindset Classroom Observational Tool)
| Mathematical Mindset Practice 1: Teacher fosters culture where all students can learn to high levels | |||
| Emerging | Accelerating | Expanding | |
| Mindset Messages | ● Teacher communicates higher and lower expectations to different students ● Teacher communicates that some are “math people” and some are not | ● Teacher attempts to give belief messages but too broad, too generic, mechanical, disconnected | ● Teacher gives belief messages in a meaningful way: “I know you can do this”, “I believe in you” |
| Praising Effort | ● Teacher does not acknowledge student effort or progress in thinking (may focus only on answer) | ● Teacher praises effort at times, but may focus on praising individuals at other times | ● Teacher praises effort, ideas and specific strategies |
| Student’s Mindset | ● Students communicate lack of confidence in their ability to do math, and those messages go unchallenged by the teacher | ● Students convey a mix of confidence and doubt in themselves | ● Most students vocalize/show self-belief and confidence |
| Mathematical Mindset Practice 2: Teacher provides and facilitates open mathematics | |||
| Emerging | Accelerating | Expanding | |
| Open Tasks | ● Tasks are relatively closed, emphasizing routine procedures with little reasoning | ● Tasks are mathematically rich in reasoning opportunities but not fully mined | ● Tasks are mathematically rich in reasoning opportunities, allowing for different approaches ● Students’ creative work in math is displayed in the room |
| Reasoning and multiple perspectives | ● All or most of the student work looks the same ● The teacher does not point out variability in student thinking | ● Only one or two methods are elicited or explored ● The teacher asks for students to think of their own ideas but different ideas are not shared | ● Students use ownership words–“my method”, “my idea” ● Students are invited to see math in a different, more expansive way ● Students use and share different ideas, methods, and perspectives |
| Depth over speed | ● Strong emphasis on speed, memorization or performance | ● Teacher occasionally emphasizes speed, memorization or performance | ● In tasks, teacher emphasizes depth over speed, memorization or performance |
| Mathematical Mindset Practice 3: Teacher maintains high challenge & cognitive demand | |||
| Emerging | Accelerating | Expanding | |
| Struggle | ● Teacher does the thinking for students or helps the students too much when they are finding work difficult | ● In development | ● Teacher encourages and validates when students struggle ● Teachers provides sufficient wait time ● Teacher connects struggle to brain growth, synapse-firing from brain research ● Teacher listens closely to how students approach the task on their own before deciding on forms of assistance |
| Tasks | ● Teacher offers no opportunity to explore the task ● Teacher has low-challenge or closed questions ● Teacher reduces cognitive demand in interaction with students or with task | ● Teacher scaffolds tasks into discrete parts by giving hints too early | ● Tasks are cognitively challenging through content ● Tasks are cognitively challenging through openness of the problem and encouragement of math practices |
| Questioning | ● Teacher tells instead of asking questions to encourage students to think deeply | ● Teacher attempts to question but structures too much, or questions are too leading | ● Teacher asks open, conceptual questions celebrating multiple methods, ways of seeing, ways of thinking |
| Mathematical Mindset Practice 4: Mistakes are seen as valuable, risk-taking is encouraged | |||
| Emerging | Accelerating | Expanding | |
| Sharing mistakes | ● Teacher emphasizes complete and correct work ● Mistakes are dealt with negatively ● Mistakes are marked on a paper with no or limited feedback (if applicable) | ● Teacher ends eliciting ideas upon hearing the correct answer ● Students share mostly correct answers ● Students don’t share when they are unsure or incorrect ● Mistakes are acknowledged but not explored by class | ● Teacher encourages different approaches; doesn’t stop with the correct answer ● Students share ideas, both correct and incorrect ● Teacher celebrates when learning occurs from mistakes ● Students disagree with each other’s reasoning and with the teacher |
| Persistence | ● Students give up when they are stuck or wrong | ● Students ask teacher for help, but the teacher rescues rather than encouraging persistence | ● Students persist when they are stuck or wrong ● Teachers and students work together when they are stuck |
| Mathematical Mindset Practice 5: Teacher maximizes student-student interactions | |||
| Emerging | Accelerating | Expanding | |
| Groupings | ● Arrangement of desks does not allow for collaboration ● No group work or collaboration is available to students ● Working together on class assignments may be viewed as cheating | ● student’s desks are in groups, but no collaboration is observed ● Some students choose to collaborate but the teacher doesn’t prompt or encourage all to do so. | ● Students work in groups to solve problems, sharing ideas and visuals |
| Student Discussions | ● Students direct questions or present ideas to teachers, rather than to peers ● Same few students contribute ideas, teacher does not actively elicit ideas from others | ● Some students present ideas to peers but only when prompted by the teacher ● Teacher encourage sharing from different students but students are reluctant. | ● Students ask questions to each other to understand peer’s ideas ● In class discussions, peers interact directly with peers ● Students build off of each other’s ideas |
| Teacher Facilitation | ● Teacher dominates classroom talk, discussion or IRE (initiate, respond, evaluate) | ● Teacher interacts with individual students, rather than students interacting with each other, students contribute ideas but teachers finish their sentences, or insert their ideas | ● Teacher facilitates student-student interaction: “Does anyone want to respond to X’s idea?” ● Students talk with each other in class discussion without going through the teacher |
Appendix B. Teacher Interview Protocols
Please answer the extent to which you agree or disagree with each statement.
| Strongly disagree | Disagree | Somewhat disagree | Somewhat agree | Agree | Strongly agree | |
| 1. I enjoy being challenged in math. | ||||||
| 2. In math, answers are either right or wrong. | ||||||
| 3. Math is boring. | ||||||
| 4. People who really understand math will get an answer quickly. | ||||||
| 5. I can tell if my answers in math make sense. | ||||||
| 6. When I get a bad grade in math, I think that I am not very smart in math. | ||||||
| 7. I believe that I can do well in math. | ||||||
| 8. When I make a mistake in math, I feel bad. | ||||||
| 9. It is important in math to be fast. | ||||||
| 10. There are limits to how much people can improve their basic math ability. | ||||||
| 11. If I put in enough effort I can succeed in mathematics. | ||||||
| 12. You have a certain amount of math intelligence, and you can’t really do much to change it. | ||||||
| 13. Math is a subject with lots of connections between ideas. | ||||||
| 14. It is really helpful to talk about math with others. | ||||||
| 15. There is usually only one way to solve a math problem. | ||||||
| 16. I like to solve complex math problems. |
Appendix C. Mathematical Mindset Student Survey
Teacher Mid-year Interview Protocol
TEACHING CONTEXT: Can you tell me about your teaching? (grade level, campus, district, math curriculum).
PROGRESS IN COURSE: Tell me about your experience with the online course:
- How much of the online course have you completed? (less than half?)
- Did you complete the modules in teacher groups? On your own? Did you discuss?
- When do you expect to complete the course?
POWEFUL IDEAS: What ideas from the course have been the most powerful for you? Explain.
PUTTING INTO PRACTICE: Have you been able to put any ideas of the course into practice yet? If so, in what ways?
RESPONSES FROM STUDENTS: What responses/reactions have seen from students as you put these ideas into practice?
BARRIERS: there any barrier you perceive that keep you from putting any of the ideas of the course into practice?
CONCERNS: Are there any ideas from the online course for which you still have questions/concerns?
ADDITIONAL SUPPORT: Are there any additional support that would help you implement the ideas of the course?
Case study Teacher Interview Protocol
TEACHING CONTEXT: Please tell me about your teaching context? (grade level, campus, district, math curriculum).
POWERFUL IDEAS: What ideas from the course have been the most powerful for you? Explain.
PUTTING INTO PRACTICE:
Have you been able to put any ideas of the course into practice? If so, in what ways?
- Do you still use your district adopted curriculum? [If so how?
- ○
- Are you supplementing the curriculum? [Ask if they did not describe above]
- ▪
- Where are you finding supplemental material?
- In general, are you bringing more rich tasks into your classroom? How often?
- How has your perception of student struggle changed this year?
- When reflecting on your current teaching practice, is speed a factor in your classroom?
RESPONSES FROM STUDENTS: What responses/reactions have seen from students as you put these ideas into practice?
IDENTITY OF TEACHER:
- Have you as a math learner changed since taking the online course?
- Have you as a math teacher changed since taking the online course?
- How do you think the students would describe you last year as a teacher versus how they would describe you this year?
BARRIERS: Are there any barriers you perceive that keep you from putting any of the ideas of the course into practice?
References
- Cohen, D.K. A revolution in one classroom: The case of Mrs. Oublier. Educ. Eval. Policy Anal. 1990, 12, 311–329. [Google Scholar] [CrossRef]
- Santagata, R.; Kersting, N.; Givvin, K.B.; Stigler, J.W. Problem implementation as a lever for change: An Experimental study of the effects of a professional development program on students’ mathematics learning. J. Res. Educ. Eff. 2011, 4, 1–24. [Google Scholar] [CrossRef]
- Geijsel, F.; Meijers, F. Identity learning: The core process of educational change. Educ. Stud. 2005, 31, 419–430. [Google Scholar] [CrossRef]
- Maguire, E.A.; Woollett, K.; Spiers, H.J. London taxi drivers and bus drivers: A structural MRI and neuropsychological analysis. Hippocampus 2006, 16, 1091–1101. [Google Scholar] [CrossRef] [PubMed]
- Woollett, K.; Maguire, E.A. Acquiring “the Knowledge” of London’s layout drives structural brain changes. Curr. Biol. 2011, 21, 2109–2114. [Google Scholar] [CrossRef] [PubMed]
- Luculano, T.; Rosenberg-Lee, M.; Richardson, J.; Tenison, C.; Fuchs, L.; Supekar, K.; Menon, V. Cognitive tutoring induces widespread neuroplasticity and remediates brain function in children with mathematical learning disabilities. Nat. Commun. 2015, 6, 8453. [Google Scholar] [CrossRef] [PubMed]
- Leslie, S.; Cimpian, A.; Meyer, M.; Freeland, E. Expectations of brilliance underlie gender distributions across academic disciplines. Science 2015, 347, 262–265. [Google Scholar] [CrossRef] [PubMed]
- Chestnut, E.; Lei, L.S.; Cimpian, A.; Chestnut, E.K.; Lei, R.F.; Leslie, S.J.; Cimpian, A. The Myth that only brilliant people are good at math and its implications for diversity. Educ. Sci. 2018, 8, 65. [Google Scholar] [CrossRef]
- Boaler, J. Mathematical Mindsets; Jossey-Bass: San Francisco, CA, USA, 2016. [Google Scholar]
- Menon, V. Arithmetic in child and adult brain. In Handbook of Mathematical Cognition; Cohen, K.R., Dowker, A., Eds.; Oxford University Press: London, UK, 2014. [Google Scholar]
- Beilock, S.L. Grounding cognition in action: Expertise, comprehension, and judgment. Prog. Brain Res. 2009, 174, 3–11. [Google Scholar] [PubMed]
- Bussey, K.; Bandura, A. Influence of gender constancy and social power on sex-linked modeling. J. Pers. Soc. Psychol. 1984, 47, 1292–1302. [Google Scholar] [CrossRef] [PubMed]
- Gunderson, E.A.; Ramirez, G.; Levine, S.C.; Beilock, S.L. The role of parents and teachers in the development of gender-related math attitudes. Sex Roles 2012, 66, 153–166. [Google Scholar] [CrossRef]
- Borko, H. Professional development and teacher learning: Mapping the terrain. Educ. Res. 2004, 33, 3–15. [Google Scholar] [CrossRef]
- Opfer, V.D.; Pedder, D. Conceptualizing teacher professional learning. Rev. Edu. Res. 2011, 81, 376–407. [Google Scholar] [CrossRef]
- Dweck, C.S. Mindset: The New Psychology of Success; Random House Incorporated: New York, NY, USA, 2006. [Google Scholar]
- Blackwell, L.S.; Trzesniewski, K.H.; Dweck, C.S. Implicit theories of intelligence predict achievement across an adolescent transition: A longitudinal study and an intervention. Child Dev. 2007, 78, 246–263. [Google Scholar] [CrossRef] [PubMed]
- Aronson, J.; Fried, C.B.; Good, C. Reducing the effects of stereotype threat on African American college students by shaping theories of intelligence. J. Exp. Soc. Psychol. 2002, 38, 113–125. [Google Scholar] [CrossRef]
- Steele, C.M. A threat in the air: How stereotypes shape intellectual identity and performance. Am. Psychol. 1997, 52, 613–629. [Google Scholar] [CrossRef] [PubMed]
- Jonsson, A.C.; Beach, D.; Korp, H.; Erlandson, P. Teachers’ implicit theories of intelligence: Influences from different disciplines and scientific theories. Eur. J. Teach. Educ. 2012, 35, 387–400. [Google Scholar] [CrossRef]
- Stipek, D.; Givven, K.; Salmon, J.; MacGyvers, V. Teachers’ beliefs and practices related to mathematics instruction. Teach. Teach. Educ. 2001, 17, 213–226. [Google Scholar] [CrossRef]
- Horn, I. Fast kids, slow kids, lazy kids: Framing the mismatch problem in mathematics teachers’ conversation. J. Learn. Sci. 2007, 16, 37–79. [Google Scholar]
- The “Mindset” Mindset: What We Miss by Focusing on Kids’ Attitudes: Essay by Alfie Kohn. Available online: https://www.alfiekohn.org/article/mindset/ (accessed on 10 January 2018).
- Sun, K.L. There’s no Limit: Mathematics Teaching for a Growth Mindset. Ph.D. Thesis, Stanford University, Palo Alto, CA, USA, 2015. [Google Scholar]
- Suh, J.M.; Graham, S.; Ferranone, T.; Kopeinig, G.; Bertholet, B. Developing persistent and flexible problem solvers with a growth mindset. In Motivation and Disposition: Pathways to Learning Mathematics, NCTM 2011 Yearbook; Brahier, D.J., Ed.; National Council of Teachers of Mathematics: Reston, VA, USA, 2011; pp. 169–184. [Google Scholar]
- Boaler, J.; Chen, L.; Williams, C.; Cordero, M. Seeing as understanding: The importance of visual mathematics for our brain and learning. J. Appl. Computat. Math. 2016, 5, 325. [Google Scholar] [CrossRef]
- Mayer, R.E. The promise of multimedia learning: Using the same instructional design methods across different media. Learn Instr. 2003, 13, 125–139. [Google Scholar] [CrossRef]
- Desimone, L. Improving impact studies of teachers’ professional development: Toward better conceptualizations and measures. Educ. Res. 2009, 38, 181–199. [Google Scholar] [CrossRef]
- Borko, H.; Jacobs, J.; Koellner, K. Contemporary approaches to teacher professional development. Int. Encycl. Educ. 2010, 7, 548–556. [Google Scholar]
- Sherin, M.G.; van Es, A.E. Effects of video club participation on teachers’ professional vision. Educ. J. Teach. Educ. 2009, 60, 20–37. [Google Scholar] [CrossRef]
- Ball, D.L.; Cohen, D.K. Developing practice, developing practitioners. In Teaching as the Learning Profession: Handbook of Policy and Practice; Darling-Hammond, L., Sykes, G., Eds.; Jossey-Bass: San Francisco, CA, USA, 1999; pp. 3–22. [Google Scholar]
- Jacobs, V.R.; Lamb, L.L.C.; Philipp, R.A. Professional noticing of children’s mathematical thinking. J. Res. Math. Educ. 2010, 41, 169–202. [Google Scholar]
- Bastable, V.; Schifter, D. Classroom stories: Examples of elementary students engaged in early algebra. In Algebra in the Early Grades; Kaput, J., Carraher, D., Blanton, M., Eds.; Erlbaum: Mahwah, NJ, USA, 2008; pp. 165–184. [Google Scholar]
- Festinger, L. A Theory of Cognitive Dissonance; Stanford University Press: Stanford, CA, USA, 1957. [Google Scholar]
- Initial Achievement Level Descriptors and College Content-Readiness Policy: Smarter Balanced Assessment Consortium. Available online: https://portal.smarterbalanced.org/library/en/mathematics-alds-and-college-content-readiness-policy.pdf (accessed on 10 January 2018).
- Strauss, A.; Corbin, J.M. Basics of Qualitative Research: Grounded Theory Procedures and Techniques; Sage Publications: Thousand Oaks, CA, USA, 1990. [Google Scholar]
- Eisenhart, K. Building theories from case study research. In The Qualitative Researcher’s Companion; Huberman, A.M., Miles, M., Eds.; Sage Publications: Thousand Oaks, CA, USA, 2002; pp. 3–36. [Google Scholar]
- Glesne, C.; Peshkin, A. Becoming Qualitative Researchers; Longman: White Plains, NY, USA, 1992. [Google Scholar]
- Costello, A.B.; Osborne, J.W. Best practices in exploratory factor analysis: Four recommendations for getting the most from your analysis. Pract. Assess. Res. Eval. 2005, 10, 1–9. [Google Scholar]
- Gates, B.; Gates, M. Teachers Know Best: Teachers’ Views on Professional Development; Bill and Melinda Gates Foundation: Seatle, WA, USA, 2015; pp. 1–20. [Google Scholar]
- Cuban, L. Inside the Black Box of Classroom Practice: Change without Reform in American Education; Harvard Education Press: Cambridge, MA, USA, 2013. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).