Instructional Support for Intuitive Knowledge Acquisition When Learning with an Ecological Computer Simulation
Abstract
1. Introduction
2. Theoretical Background
2.1. Intuitive Knowledge
- Intuitive knowledge can only be acquired by using already existing previous knowledge in perceptually rich dynamic situations. It is assumed that when applying previous knowledge in situations containing a huge amount of information, implicitly induced learning processes lead to intuitive knowledge acquisition.
- Intuitive knowledge is hard to verbalize. This means that intuitive knowledge differs from conceptual knowledge, which is regarded as a network of concepts and their relationships to a functional structure generated through reflective learning that can be articulated (cf. [38]). However, according to Lindström, Marton and Ottoson [22], intuitive and conceptual understanding should not be considered as separate knowledge types. They believe intuitive and conceptual understanding to be intertwined aspects of a learner’s awareness. Hence, intuitive knowledge can be seen as a quality of conceptual knowledge [39].
- Perception is crucial when referring to intuitive knowledge. The illustration of situations plays an essential role in the acquisition of intuitive knowledge. In this regard, Fischbein [26] emphasized the importance of visualization through external representation.
- Another characteristic referring to intuitive knowledge is the importance of anticipation. Anticipation refers to the presumption of occurrences, developments, or actions. Intuitions anticipate what will or will not happen, and intuitive evaluation anticipates the possible outcomes of a situation without the ability to explicitly explain them [7,29,40,41]. Here, intuitive knowledge can be ascribed as ‘know without knowing’ [10] (p. 4), so that ‘the input to this process is mostly provided by knowledge stored in the long-term memory that has been primarily acquired via associative learning. The input is processed automatically and without conscious awareness. The output is a feeling that can serve as a basis for judgments and decisions’ [10] (p. 4).
- It is assumed that the access to intuitive knowledge in the memory is different to the access to declarative knowledge as factual and conceptual knowledge. The difficulty of verbalizing intuitive knowledge might be one reason for this differential access. Swaak and de Jong [8] mention that ‘the action-driven and perception-driven elements in learning ‘tune’ the knowledge and give it an intuitive quality’ (p. 287).
2.2. Learning with Computer Simulations
2.3. Supporting Learning from Computer Simulations
- (1)
- Interpretative support enables learners to access and use prior knowledge and develop appropriate hypotheses;
- (2)
- Experimental support enhances learners’ ability to design verifiable experiments, to predict and to observe simulation results, and to adequately draw conclusions;
- (3)
- Reflective support increases the learners’ ability to raise self-awareness of the learning processes and helps support the combining of abstract and reflective integration of their discoveries.
2.4. Assessing Outcomes from Learning with Computer Simulations
2.5. Research Aims and Hypotheses
3. Materials and Methods
3.1. Participants
3.2. Materials
3.2.1. Content and the Computer Program ‘SimBioSee’
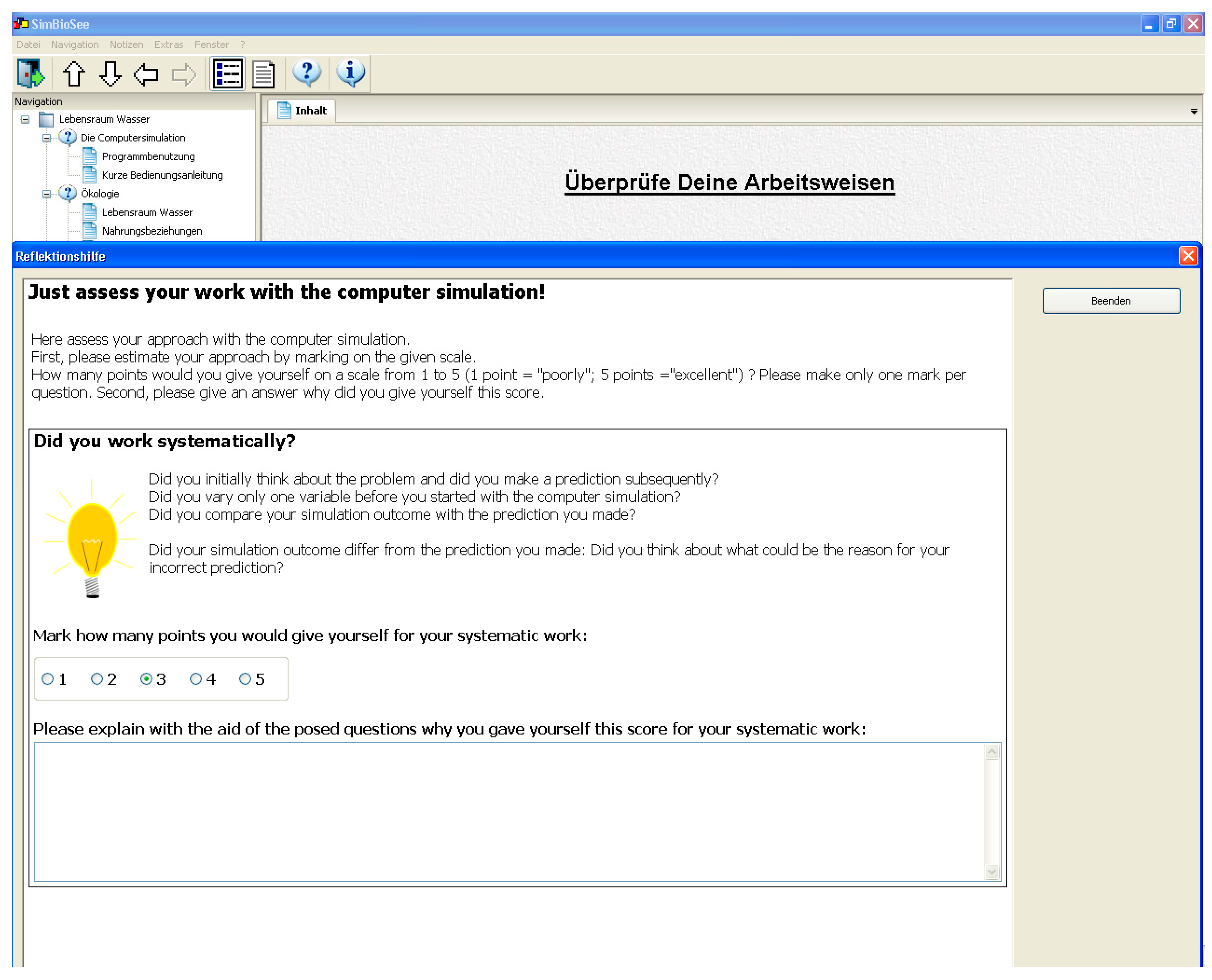
3.2.2. Instructional Support
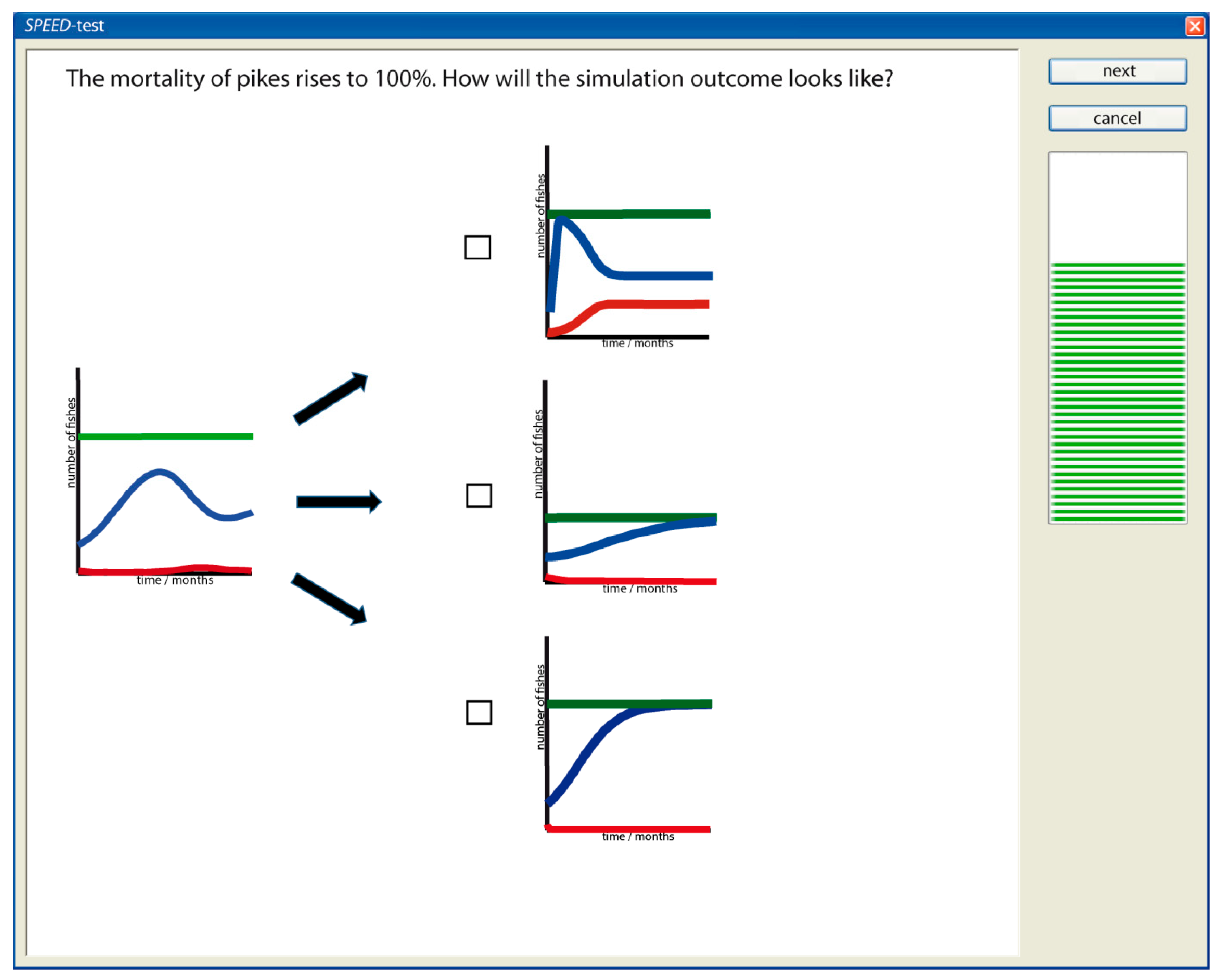
3.2.3. Intuitive Knowledge Test: ‘SPEED-test’
3.3. Procedure
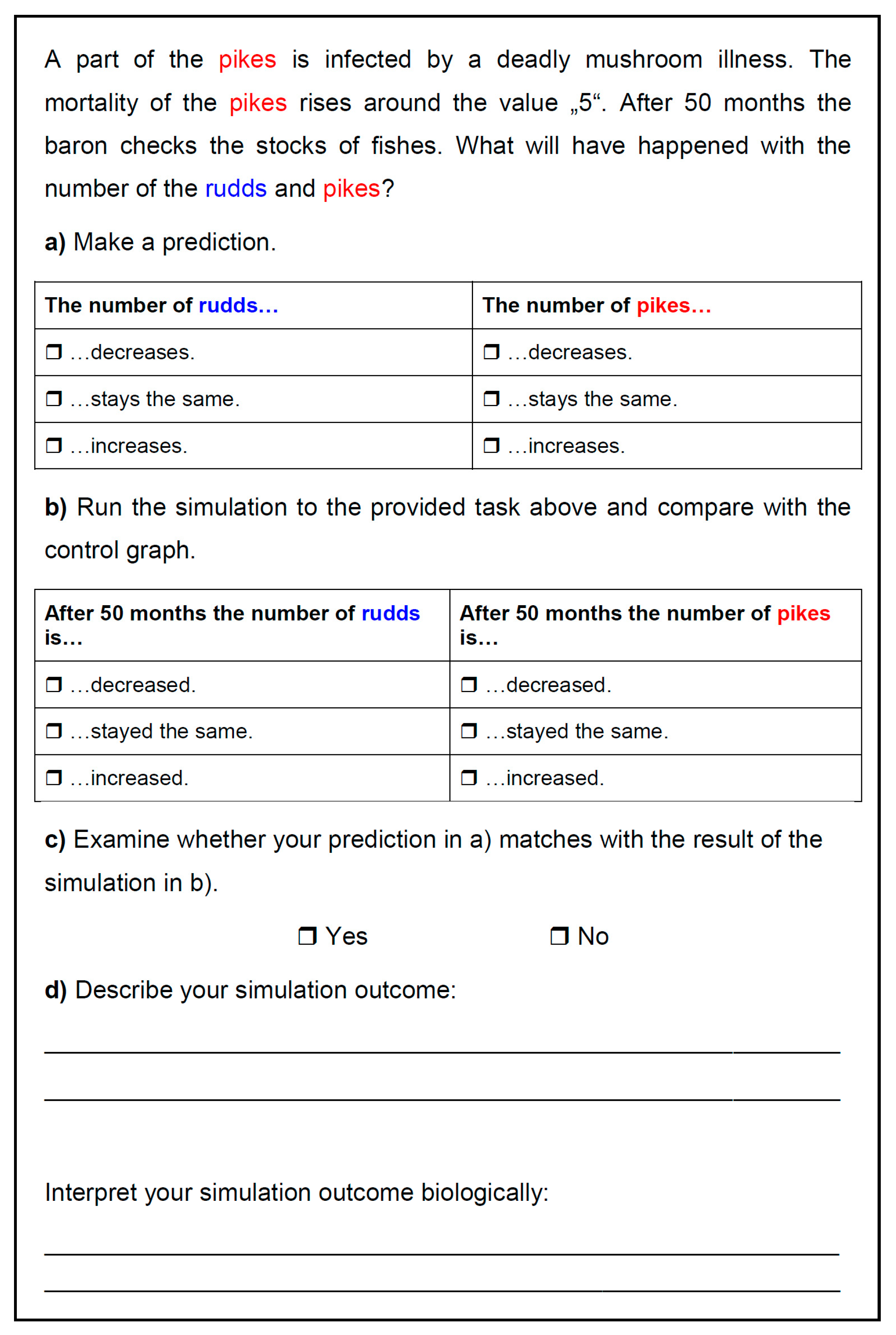
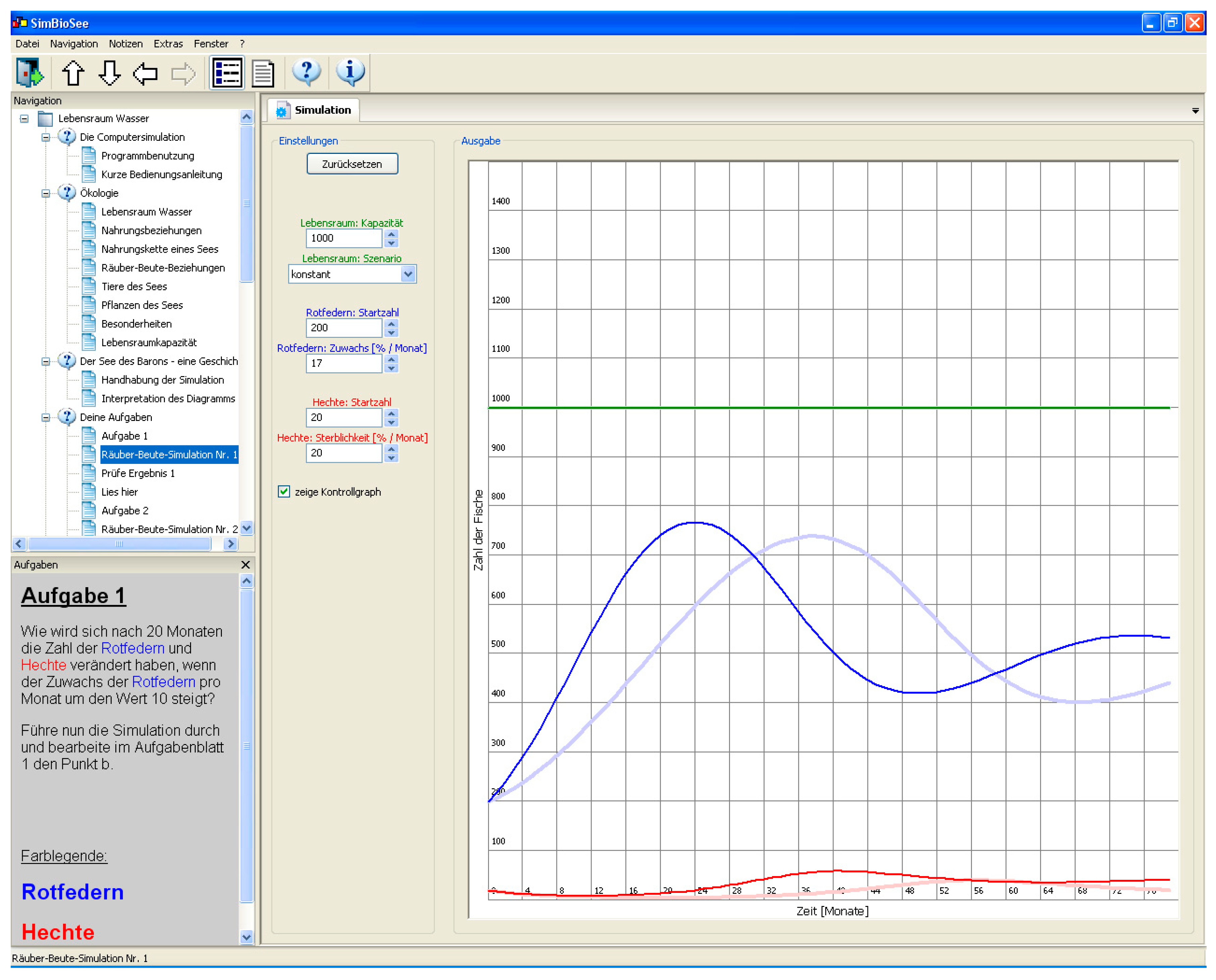
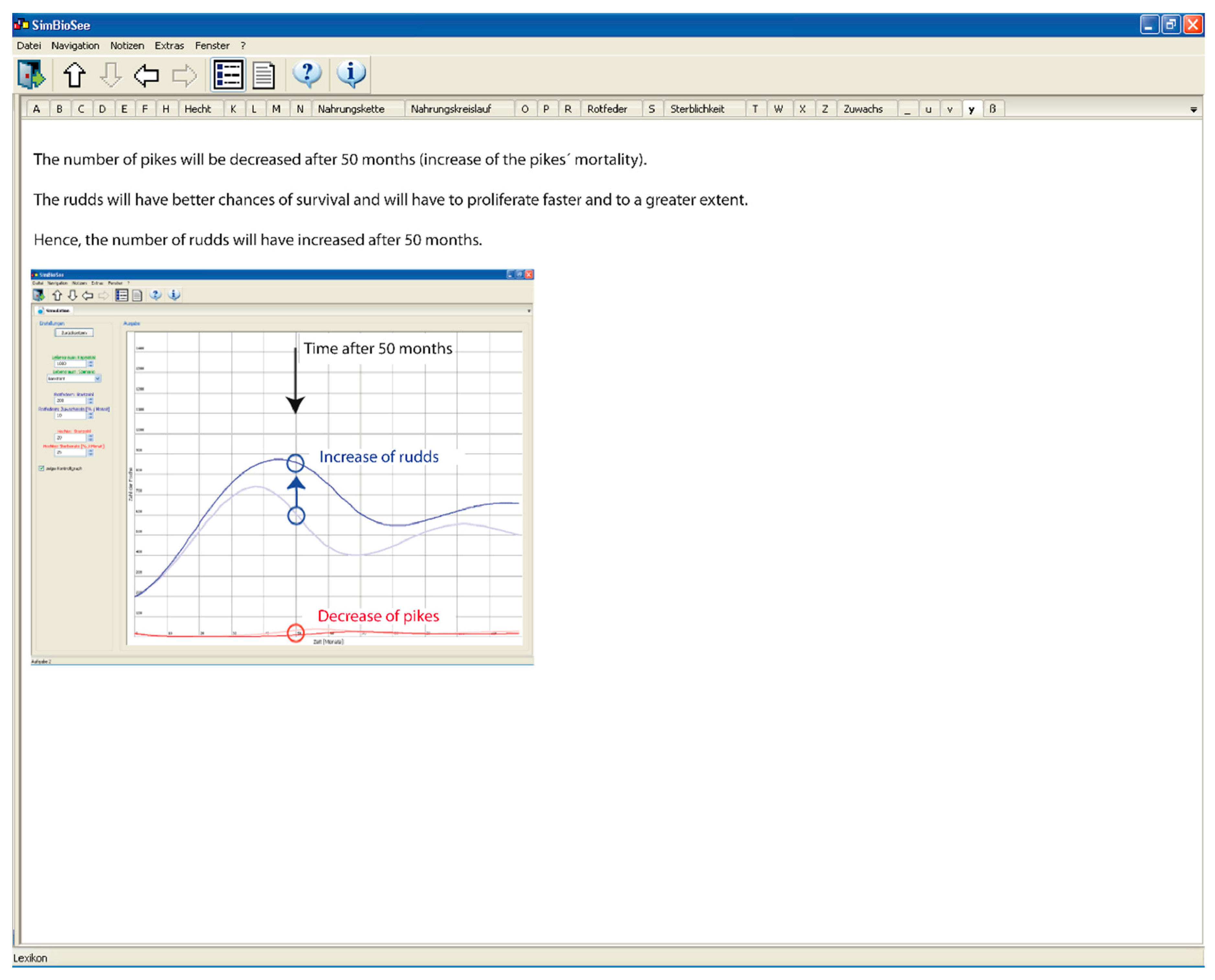
3.3.1. Assignments
3.3.2. Design
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Bruner, J.S. The act of discovery. Harv. Educ. Rev. 1961, 31, 21–32. [Google Scholar]
- De Jong, T.; van Joolingen, W.R. Scientific discovery learning with computer simulations of conceptual domains. Rev. Educ. Res. 1998, 68, 179–202. [Google Scholar] [CrossRef]
- Kistner, S.; Vollmeyer, R.; Burns, B.D.; Kortenkamp, U. Model development in scientific discovery learning with a computerbased physics task. Comput. Hum. Behav. 2016, 59, 446–455. [Google Scholar] [CrossRef]
- Klahr, D.; Dunbar, K. Dual space search during scientific reasoning. Cogn. Sci. 1988, 12, 1–48. [Google Scholar] [CrossRef]
- Künsting, J.; Kempf, J.; Wirth, J. Enhancing scientific discovery learning through metacognitive support. Contemp. Educ. Psychol. 2013, 38, 349–360. [Google Scholar] [CrossRef]
- De Jong, T.; van Joolingen, W.; Scott, D.; de Hoog, R.; Lapied, L.; Valent, R. SMISLE: System for multimedia integrated simulation learning environments. In Design and Production of Multimedia and Simulation-Based Learning Material; de Jong, T., Sarti, L., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1994; pp. 133–165. [Google Scholar]
- Swaak, J.; de Jong, T. Measuring intuitive knowledge in science: The development of the what-if test. Stud. Educ. Eval. 1996, 22, 341–362. [Google Scholar] [CrossRef]
- Swaak, J.; de Jong, T. Discovery simulations and the assessment of intuitive knowledge. J. Comput. Assist. Learn. 2001, 17, 284–294. [Google Scholar] [CrossRef]
- Rosenblatt, A.D.; Thickstun, J.T. Intuition and Consciousness. Psychoanal. Q. 1994, 63, 696–714. [Google Scholar] [PubMed]
- Betsch, T. The nature of intuition and its neglect in research on judgment and decision making. In Intuition in Judgment and Decision Making; Plessner, H., Betsch, C., Betsch, T., Eds.; Lawrence Erlbaum Associates: New York, NY, USA, 2008; pp. 3–22. ISBN 978-0805857412. [Google Scholar]
- Sadler-Smith, E.; Shefy, E. The intuitive executive: Understanding and applying ‘gut feel’ in decision-making. Acad. Manag. Rev. 2004, 18, 76–91. [Google Scholar] [CrossRef]
- Sherin, B. Common sense clarified: The role of intuitive knowledge in physics problem solving. J. Res. Sci. Teach. 2006, 43, 535–555. [Google Scholar] [CrossRef]
- De Jong, T.; van Joolingen, W.R.; Swaak, J.; Veermans, K.; Limbach, R.; King, S.; Gureghian, D. Self-directed learning in simulation-based discovery environments. J. Comput. Assist. Learn. 1998, 14, 235–246. [Google Scholar] [CrossRef]
- Kirschner, P.A.; Sweller, J.; Clark, R.E. Why minimal guidance during instruction does not work: An analysis of the failure of constructivist, discovery, problem-based, experiential, and inquiry-based teaching. Educ. Psychol. 2006, 41, 75–86. [Google Scholar] [CrossRef]
- Manlove, S.; Lazonder, A.W.; de Jong, T. Regulative support for collaborative scientific inquiry learning. J. Comput. Assist. Learn. 2006, 22, 87–98. [Google Scholar] [CrossRef]
- Rey, G.D. Instructional advice, time advice and learning questions in computer simulations. Australas. J. Educ. Technol. 2010, 26, 675–689. [Google Scholar] [CrossRef]
- Yaman, M.; Nerdel, C.; Bayrhuber, H. The effects of instructional support and learner interests when learning using computer simulations. Comput. Educ. 2008, 51, 1784–1794. [Google Scholar] [CrossRef]
- Strack, F.; Deutsch, R. Reflective and impulsive determinants of social behavior. Personal. Soc. Psychol. Rev. 2004, 8, 220–247. [Google Scholar] [CrossRef] [PubMed]
- Kahneman, D. Maps of Bounded Rationality: Psychology for Behavioral Economics. Am. Econ. Rev. 2003, 93, 1449–1475. [Google Scholar] [CrossRef]
- Dane, E.; Pratt, M.G. Exploring intuition and its role in managerial decision making. Acad. Manag. Rev. 2007, 32, 33–54. [Google Scholar] [CrossRef]
- Fensham, P.J.; Marton, F. What has happened to intuition in science education? Res. Sci. Educ. 1991, 22, 114–122. [Google Scholar] [CrossRef]
- Lindström, B.; Marton, F.; Ottoson, T. Computer simulation as a tool for developing intuitive and conceptual understanding in mechanics. Comput. Hum. Behav. 1993, 9, 263–281. [Google Scholar] [CrossRef]
- Blume, B.D.; Covin, J.G. Attributions to intuitions in the venture founding process: Do entrepreneurs actually use intuition or just say that they do? J. Bus. Ventur. 2011, 26, 137–151. [Google Scholar] [CrossRef]
- Cheng, M.-F.; Brown, D.E. Conceptual resources in self-developed explanatory models: The importance of integrating conscious and intuitive knowledge. Int. J. Sci. Educ. 2010, 32, 2367–2392. [Google Scholar] [CrossRef]
- Chudnoff, E. Intuitive knowledge. Philos. Stud. 2013, 162, 359–378. [Google Scholar] [CrossRef]
- Fischbein, E. Intuition in Science and Mathematics: An Educational Approach; Reidel: Dordrecht, The Netherlands, 1987. [Google Scholar]
- Holzinger, A.; Kickmeier-Rust, M.D.; Wassertheurer, S.; Hessinger, M. Learning performance with interactive simulations in medical education: Lessons learned from results of learning complex physiological models with the haemodynamics simulator. Comput. Educ. 2009, 52, 292–301. [Google Scholar] [CrossRef]
- Reber, R.; Ruch-Monachon, M.A.; Perrig, W.A. Decomposing intuitive components in a conceptual problem solving task. Conscious. Cognit. 2007, 16, 294–309. [Google Scholar] [CrossRef] [PubMed]
- Brock, R. Intuition and insight: Two concepts that illuminate the tacit in science education. Stud. Sci. Educ. 2015, 51, 127–167. [Google Scholar] [CrossRef]
- Policastro, E. Intuition. In Encyclopedia of Creativity; Runco, M.A., Pritzker, S.R., Eds.; Academic Press: San Diego, CA, USA, 1999; pp. 89–93. ISBN 9780080548500. [Google Scholar]
- Broadbent, D.E.; Fitzgerald, P.; Broadbent, M.H.P. Implicit and explicit knowledge in the control of complex systems. Br. J. Psychol. 1986, 77, 33–50. [Google Scholar] [CrossRef]
- Sinclair, M.; Ashkanasy, N.M. Intuition: Myth of a decision-making tool? Manag. Learn. 2005, 36, 353–370. [Google Scholar] [CrossRef]
- Holzinger, A.; Softic, S.; Stickel, C.; Ebner, M.; Debevc, M. Intuitive e-teaching by using combined hci devices: Experiences with wiimote applications. In Universal Access in Human-Computer Interaction. Applications and Services, Lecture Notes in Computer Science; Stephanidis, C., Ed.; Springer: Berlin, Germany, 2009; pp. 44–52. ISBN 3-642-02712-1. [Google Scholar]
- Hodgkinson, G.P.; Langan-Fox, J.; Sadler-Smith, E. Intuition: A fundamental bridging construct in the behavioural sciences. Br. J. Psychol. 2008, 99, 1–27. [Google Scholar] [CrossRef] [PubMed]
- Westcott, M.R. Toward a Contemporary Psychology of Intuition; Holt, Rinehart & Winston: New York, NY, USA, 1968; ISBN 978-0030677304. [Google Scholar]
- Sweller, J.; van Merrienboër, J.J.G.; Paas, F.G.W.C. Cognitive Architecture and Instructional Design. Educ. Psychol. Rev. 1998, 10, 251–296. [Google Scholar] [CrossRef]
- Rümmele, A. Intuitives Wissen. [Intuitive knowledge]. In Kognitive Entwicklungspsychologie: Aktuelle Forschungsergebnisse; [Cognitive Developmental Psychology: Current research Results]; Rümmele, A., Pauen, S., Schwarzer, G., Eds.; Pabst Science Publishers: Lengerich, Germany, 1997; pp. 89–92. [Google Scholar]
- Krathwohl, D.R. A Revision of Bloom´s Taxonomy: An Overview. Theory Pract. 2002, 41, 212–218. [Google Scholar] [CrossRef]
- Kolloffel, B.; Eysink, T.H.S.; de Jong, T. Comparing the effects of representational tools in collaborative and individual inquiry learning. Comput.-Support. Collab. Learn. 2011, 6, 223–251. [Google Scholar] [CrossRef]
- De Jong, T.; Wilhelm, P.; Anjewierden, A. Inquiry and assessment: Future developments from a technological perspective. In Technology-Based Assessments for 21th Century Skills: Theoretical and Practical Implications from Modern Research; Mayrath, M.C., Clarke-Midura, J., Robinson, D.H., Schraw, G., Eds.; Information Age Publishing Inc.: Charlotte, NC, USA, 2012; pp. 249–266. ISBN 978-I-61735-632-2. [Google Scholar]
- Duma, G.M.; Mento, G.; Manari, T.; Martinelli, M.; Tressoldi, P. Driving with intuition: A preregistered study about the EEG anticipation of simulated random car accidents. PLoS ONE 2017, 12, e0170370. [Google Scholar] [CrossRef] [PubMed]
- Swaak, J.; van Joolingen, W.R.; de Jong, T. Supporting simulation-based learning: The effects of model progression and assignments on definitional and intuitive knowledge. Learn. Instr. 1998, 8, 235–253. [Google Scholar] [CrossRef]
- Thomas, R.; Hooper, E. Simulations: An opportunity we are missing. J. Res. Comput. Educ. 1991, 23, 497–513. [Google Scholar] [CrossRef]
- Swaak, J.; de Jong, T.; van Joolingen, W.R. The effects of discovery learning and expository instruction on the acquisition of definitional and intuitive knowledge. J. Comput. Assist. Learn. 2004, 20, 225–234. [Google Scholar] [CrossRef]
- Blake, C.; Scanlon, E. Reconsidering simulations in science education at a distance: Features of effective use. J. Comput. Assist. Learn. 2007, 23, 491–502. [Google Scholar] [CrossRef]
- D’Angelo, C.; Rutstein, D.; Harris, C.; Bernard, R.; Borokhovski, E.; Haertel, G. Simulations for STEM Learning: Systematic Review and Meta-Analysis; SRI International: Menlo Park, CA, USA, 2014. [Google Scholar]
- Lindgren, R.; Tscholl, M.; Wang, S.; Johnson, E. Enhancing learning and engagement through embodied interaction within a mixed reality simulation. Comput. Educ. 2016, 95, 174–187. [Google Scholar] [CrossRef]
- De Jong, T. Computer simulations: Technological advances in inquiry learning. Science 2006, 312, 532–533. [Google Scholar] [CrossRef] [PubMed]
- Ryoo, K.L.; Linn, M.C. Can dynamic visualizations improve middle school students’ understanding of energy in photosynthesis? J. Res. Sci. Teach. 2012, 49, 218–243. [Google Scholar] [CrossRef]
- Urhahne, D.; Prenzel, M.; von Davier, M.; Senkbeil, M.; Bleschke, M. Computereinsatz im naturwissenschaftlichen Unterricht—Ein Überblick über die pädagogisch-psychologischen Grundlagen und ihre Anwendung [Computer use in science education—An overview of the psychological and educational foundations and its applications]. Zeitschrift für Didaktik der Naturwissenschaften 2000, 6, 157–186. [Google Scholar]
- Swaak, J.; de Jong, T. Learner vs. system control in using online support for simulation-based discovery learning. Learn. Environ. Res. 2001, 4, 217–241. [Google Scholar] [CrossRef]
- Van Joolingen, W.R.; de Jong, T.; Lazonder, A.W.; Savelsbergh, E.R.; Manlove, S. Co-Lab: Research and development of an online learning environment for collaborative scientific discovery learning. Comput. Hum. Behav. 2005, 21, 671–688. [Google Scholar] [CrossRef]
- Leutner, D. Guided discovery learning with computer-based simulation games: Effects of adaptive and non-adaptive instructional support. Learn. Instr. 1993, 3, 113–132. [Google Scholar] [CrossRef]
- Mayer, R.E. Should there be a three-strikes rule against pure discovery learning? The case for guided methods of instruction. Am. Psychol. 2004, 59, 14–19. [Google Scholar] [CrossRef] [PubMed]
- Urhahne, D.; Harms, U. Instruktionale Unterstützung beim Lernen mit Computersimulationen [Instructional support for learning with computer simulations]. Unterrichtswissenschaft 2006, 34, 358–377. [Google Scholar]
- Van Joolingen, W.R.; de Jong, T.; Dimitrakopoulout, A. Issues in computer supported inquiry learning in science. J. Comput. Assist. Learn. 2007, 23, 111–119. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, Q.; Sun, Y.; Reid, D.J. Triple scheme of learning support design for scientific discovery learning based on computer simulation: Experimental research. J. Comput. Assist. Learn. 2004, 20, 269–282. [Google Scholar] [CrossRef]
- Reid, D.J.; Zhang, J.; Chen, Q. Supporting scientific discovery learning in a simulation environment. J. Comput. Assist. Learn. 2003, 19, 9–20. [Google Scholar] [CrossRef]
- Elshout, J.J.; Veenman, M.V.J. Relation between intellectual ability and working method as predictors of learning. J. Educ. Res. 1992, 85, 134–143. [Google Scholar] [CrossRef]
- Vreman-de Olde, C.; de Jong, T. Scaffolding learners in designing investigation assignments for a computer simulation. J. Comput. Assist. Learn. 2006, 22, 63–73. [Google Scholar] [CrossRef]
- White, R.T.; Gunstone, R.F. Probing Understanding; Falmer Press: London, UK, 1992; ISBN 978-0750700481. [Google Scholar]
- Atkinson, R.K.; Derry, S.J.; Renkl, A.; Wortham, D. Learning from examples: Instructional principles from the worked examples research. Rev. Educ. Res. 2000, 70, 181–214. [Google Scholar] [CrossRef]
- Nerdel, C.; Prechtl, H. Learning complex systems with simulations in science education. In Instructional Design for Effective and Enjoyable Computer—Supported Learning: Proceedings of the First Joint Meeting of the EARLI SIGs Instructional Design and Learning and Instruction with Computers; Gerjets, P., Kirschner, P.A., Elen, J., Joiner, R., Eds.; Knowledge Media Research Center: Tuebingen, Germany, 2004; pp. 160–171. Available online: http://www.iwm-kmrc.de/workshops/SIM2004/pdf_files/Nerdel_et_al.pdf (accessed on 15 February 2018).
- Neubrand, C.; Borzikowsky, C.; Harms, U. Adaptive prompts for learning Evolution with worked examples—Highlighting the students between the “novices” and the “experts” in a classroom. Int. J. Environ. Sci. Educ. 2016, 11, 6774–6795. [Google Scholar]
- Neubrand, C.; Harms, U. Tackling the difficulties in learning evolution: Effects of adaptive self-explanation prompts. J. Biol. Educ. 2017, 51, 336–348. [Google Scholar] [CrossRef]
- Renkl, A. The worked-out examples principle in multimedia learning. In The Cambridge Handbook of Multimedia Learning; Mayer, R., Ed.; Cambridge University Press: Cambridge, UK, 2005; pp. 229–246. ISBN 978-1107610316. [Google Scholar]
- Renkl, A.; Atkinson, R.K. Learning from examples: Fostering self-explanations in computer-based learning environments. Interact. Learn. Environ. 2002, 10, 105–119. [Google Scholar] [CrossRef]
- Mulder, Y.; Lazonder, A.W.; de Jong, T. Simulation-based inquiry learning and computer modelling: Pitfalls and potentials. Simul. Gaming 2015, 46, 322–347. [Google Scholar] [CrossRef]
- Biesinger, K.; Crippen, K. The effects of feedback protocol on self-regulated learning in a web-based worked example learning environment. Comput. Educ. 2010, 55, 1470–1482. [Google Scholar] [CrossRef]
- Kalyuga, S.; Chandler, P.; Tuovinen, J.; Sweller, J. When problem solving is superior to studying worked examples. J. Educ. Psychol. 2001, 93, 579–588. [Google Scholar] [CrossRef]
- Pedaste, M.; Mäeots, M.; Siiman, L.A.; de Jong, T.; van Riesen, S.A.N.; Kamp, E.T.; Manoli, C.C.; Zacharias, C.Z.; Tsourlidaki, E. Phases of inquiry-based learning: Definitions and the inquiry cycle. Educ. Res. Rev. 2015, 14, 47–61. [Google Scholar] [CrossRef]
- White, B. Computer microworlds and scientific inquiry: An alternative approach to science education. In International Handbook of Science Education; Fraser, B., Tobin, K., Eds.; Kluwer: Dordrecht, The Netherlands, 1998; pp. 295–314. ISBN 978-0-7923-3531-3. [Google Scholar]
- Lewis, E.L.; Stern, J.L.; Linn, M.C. The effect of computer simulations on introductory thermodynamics understanding. Educ. Technol. 1993, 33, 45–58. [Google Scholar]
- Moreno, R.; Mayer, R.E. Role of guidance, reflection and interactivity in an agent-based multimedia game. J. Educ. Psychol. 2005, 97, 117–128. [Google Scholar] [CrossRef]
- White, B.; Frederiksen, J.R. Inquiry, modeling, and metacognition: Making science accessible to all students. Cognit. Instr. 1998, 16, 3–118. [Google Scholar] [CrossRef]
- White, B.; Shimoda, T.A.; Frederiksen, J.R. Enabling students to construct theories of collaborative inquiry and reflective learning: Computer support for metacognitive development. Int. J. Artif. Intell. Educ. 1999, 10, 151–182. [Google Scholar]
- Moreno, R. Decreasing cognitive load for novice students: Effects of explanatory versus corrective feedback in discovery-based multimedia. Instr. Sci. 2004, 32, 99–113. [Google Scholar] [CrossRef]
- Lin, X.; Lehmann, J.D. Supporting learning of variable control in a computer-based biology environment: Effects of prompting college students to reflect on their thinking. J. Res. Sci. Teach. 1999, 36, 837–858. [Google Scholar] [CrossRef]
- Zimmermann, B.J.; Bonner, S.; Kovach, R. Developing Self-Regulated Learners: Beyond Achievement to Self-Efficacy; American Psychological Association: Washington, DC, USA, 1996; ISBN 978-1-55798-392-3. [Google Scholar]
- Zimmermann, B.J.; Tsikalas, K.E. Can computer-based learning environments (CBLEs) be used as self-regulatory tools to enhance learning? Educ. Psychol. 2005, 40, 267–271. [Google Scholar] [CrossRef]
- Wichmann, A.; Timpe, S. Can dynamic visualizations with variable control enhance the acquisition of intuitive knowledge? J. Sci. Educ. Technol. 2015, 24, 709–720. [Google Scholar] [CrossRef]
- NGSS Lead States. Next Generation Science Standards: For states, by States; The National Academies Press: Washington, DC, USA, 2013; ISBN 978-0-309-27227-8. [Google Scholar]
- Finley, F.N.; Steward, J.; Yarroch, N.L. Teachers’ perceptions of important difficult science content. Sci. Educ. 1982, 66, 531–538. [Google Scholar] [CrossRef]
- Eckhardt, M.; Urhahne, D.; Conrad, O.; Harms, U. How effective is instructional support for learning with computer simulations? Instr. Sci. 2013, 41, 105–124. [Google Scholar] [CrossRef]
- Webb, N.M. Peer interaction and learning in small groups. Int. J. Educ. Res. 1989, 13, 21–39. [Google Scholar] [CrossRef]
- Chi, M.T.H.; Bassok, M. Learning from examples via self-explanations. In Knowing, Learning and Instruction: Essays in Honor of Robert Glaser; Resnick, L.B., Ed.; Lawrence Erlbaum Associates Inc.: Hillsdale, MI, USA, 1989; pp. 251–282. [Google Scholar]
- Chi, M.T.H.; de Leeuw, N.; Chiu, M.H.; La Vancher, C. Eliciting self-explanations improves understanding. Cognit. Sci. 1994, 18, 439–477. [Google Scholar] [CrossRef]
- Wong, R.M.F.; Lawson, M.J.; Keeves, J. The effects of self-explanation training on students’ problem solving in high-school mathematics. Learn. Instr. 2002, 12, 233–262. [Google Scholar] [CrossRef]
- Tajika, H.; Nakatsu, N.; Nozaki, H.; Ewald, N.; Shunichi, M. Effects of self-explanation as a metacognitive strategy for solving mathematical word problems. Jpn. Psychol. Res. 2007, 49, 222–233. [Google Scholar] [CrossRef]
- Van den Boom, G.; Paas, F.; van Merriënboer, J.; van Gog, Y. Reflection prompts and tutor feedback in a web-based learning environment: Effects on students’ self-regulated learning competence. Comput. Hum. Behav. 2004, 20, 551–567. [Google Scholar] [CrossRef]
- Mayer, R.E. Multimedia Learning; Cambridge University Press: Cambridge, UK, 2001; ISBN 978-0521787499. [Google Scholar]
- Eysink, T.H.; de Jong, T. Does instructional approach matter? How elaboration plays a crucial role in multimedia learning. J. Learn. Sci. 2012, 21, 583–625. [Google Scholar] [CrossRef]
- Holzinger, A.; Dehmer, M.; Jurisica, I. Knowledge discovery and interactive data mining in bioinformatics—state-of-the-art, future challenges and research directions. BMC Bioinform. 2014, 15 (Suppl. 6), I1. [Google Scholar] [CrossRef] [PubMed]
- Holzinger, A.; Biemann, C.; Pattichis, C.S.; Kell, D.B. What do we need to build explainable ai systems for the medical domain? arXiv, 2017; arXiv:1712.09923. [Google Scholar]
- Holzinger, A.; Plass, M.; Holzinger, K.; Crisan, G.C.; Pintea, C.-M.; Palade, V. A glass-box interactive machine learning approach for solving np-hard problems with the human-in-the-loop. arXiv, 2017; arXiv:1708.01104. [Google Scholar]
| Self-Regulation | Data Interpretation | ||
|---|---|---|---|
| (NS) | (GiS) | (GeS) | |
| (NR) | n = 19 | n = 15 | n = 20 |
| (R) | n = 17 | n = 23 | n = 23 |
| Condition | Pre-Test | Post-Test | ||||||
|---|---|---|---|---|---|---|---|---|
| M | SD | M | SD | df | F | Part. η2 | p | |
| No solution/no reflective support (NS/NR, control) | 0.49 | 0.13 | 0.52 | 0.16 | 1.18 | 0.60 | 0.03 | 0.450 |
| No solution/reflective support (NS/R) | 0.58 | 0.20 | 0.61 | 0.23 | 1.16 | 0.18 | 0.01 | 0.680 |
| Given solution/no reflective support (GiS/NR) | 0.47 | 0.11 | 0.53 | 0.17 | 1.14 | 0.16 | 0.11 | 0.221 |
| Given solution/reflective support (GiS/R) | 0.48 | 0.15 | 0.64 | 0.19 | 1.22 | 120.11 | 0.36 | 0.002 |
| Generated solution/no reflective support (GeS/NR) | 0.50 | 0.16 | 0.65 | 0.16 | 1.19 | 120.24 | 0.39 | 0.002 |
| Generated solution/reflective support (GeS/R) | 0.43 | 0.10 | 0.45 | 0.17 | 1.22 | 0.21 | 0.01 | 0.652 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eckhardt, M.; Urhahne, D.; Harms, U. Instructional Support for Intuitive Knowledge Acquisition When Learning with an Ecological Computer Simulation. Educ. Sci. 2018, 8, 94. https://doi.org/10.3390/educsci8030094
Eckhardt M, Urhahne D, Harms U. Instructional Support for Intuitive Knowledge Acquisition When Learning with an Ecological Computer Simulation. Education Sciences. 2018; 8(3):94. https://doi.org/10.3390/educsci8030094
Chicago/Turabian StyleEckhardt, Marc, Detlef Urhahne, and Ute Harms. 2018. "Instructional Support for Intuitive Knowledge Acquisition When Learning with an Ecological Computer Simulation" Education Sciences 8, no. 3: 94. https://doi.org/10.3390/educsci8030094
APA StyleEckhardt, M., Urhahne, D., & Harms, U. (2018). Instructional Support for Intuitive Knowledge Acquisition When Learning with an Ecological Computer Simulation. Education Sciences, 8(3), 94. https://doi.org/10.3390/educsci8030094




