“Can I Use My Leg Too?” Dancing with Uncertainty: Exploring Probabilistic Thinking Through Embodied Learning in a Jerusalem Art High School Classroom

Abstract

Despite increased interest in embodied learning, the role of sensorimotor activity in shaping students’ probabilistic reasoning remains underexplored. This design-based study examines how high school students develop key probabilistic concepts, including sample space, certainty, and event probability, through whole-body movement activities situated in an authentic classroom setting. Grounded in embodied cognition theory, we introduce a two-axis interpretive framework. One axis spans sensorimotor exploration and formal reasoning, drawing from established continuums in the literature. The second axis, derived inductively from our analysis, contrasts engagement with distraction, foregrounding the affective and attentional dimensions of embodied participation. Students engaged in structured yet open-ended movement sequences that elicited intuitive insights. This approach, epitomized by one student’s spontaneous question, “Can I use my leg too?”, captures the agentive and improvisational character of the embodied learning environment. Through five analyzed classroom episodes, we trace how students shifted between bodily exploration and formalization, often through nonlinear trajectories shaped by play, uncertainty, and emotionally driven reflection. While moments of insight emerged organically, they were also fragile, as they were affected by ambiguity and the difficulty in translating physical actions into mathematical language. Our findings underscore the pedagogical potential of embodied design for probabilistic learning while also highlighting the need for responsive teaching that balances structure with improvisation and supports affective integration throughout the learning process.

1. Introduction

Embodied learning has emerged as a promising approach in mathematics education, grounded in theories of embodied cognition that emphasize the role of bodily action and sensorimotor experience in shaping thought (Varela et al., 2017; Lakoff & Núñez, 2000). In contrast to traditional instruction, which frames mathematics as purely abstract, embodied approaches suggest that conceptual understanding can develop through movement, gesture, and spatial interaction (Abrahamson & Lindgren, 2014; Nathan, 2021; Nemirovsky & Ferrara, 2009).

Research in mathematics education has increasingly demonstrated the value of embodied approaches across multiple domains. Gestures have been shown to scaffold mathematical reasoning and support transitions from perceptual to abstract representation (Goldin-Meadow, 2014; Alibali & Nathan, 2012). Spatial movement and embodied modeling play a central role in geometry and proportional reasoning (Abrahamson, 2012; Nemirovsky & Ferrara, 2009; Bakker et al., 2019), and embodied design has been proposed as a methodological framework for structuring tasks that guide students from intuitive sensorimotor exploration to formal concepts (Abrahamson & Lindgren, 2014; Abrahamson et al., 2020; Palatnik et al., 2023). More recently, scholars have begun to theorize the relationship between embodiment, affect, and engagement in authentic classrooms, emphasizing that learning is always situated in emotional and social contexts (Castro-Alonso et al., 2024; Farsani, 2025).

Despite these advances, probability has received comparatively limited attention within embodied mathematics education. Students’ well-documented difficulties with probabilistic concepts, such as distinguishing between certainty and impossibility, enumerating sample spaces, and reasoning about likelihood (Jones et al., 1997; Batanero & Diaz, 2012; Kazak & Pratt, 2017; Gal, 2005; Batanero & Álvarez-Arroyo, 2024), make it a particularly important area for innovation. Prior work has explored embodied approaches to probability. Abrahamson’s (2012) “marble scooping” task in controlled one-on-one settings demonstrated how sensorimotor interaction can ground formal probabilistic reasoning. Similarly, Soto-Andrade and colleagues developed “random walks” as enactive metaphors for chance processes, highlighting how bodily enactment can model stochastic structures (Soto-Andrade et al., 2018). While these studies illustrate the potential of embodied designs, they were conducted in experimental or semi-structured contexts. Recent classroom-based research has begun to address this gap: movement-based lessons have been shown to support students in grasping probability concepts such as randomness, certainty, and sample space through collective enactment and discussion (Efron et al., 2023). Building on this trajectory, the present study investigates embodied probability learning in an authentic high school classroom, where unpredictability, affect, and social negotiation shape how students construct probabilistic concepts, where unpredictability, social interaction, and affective dynamics are central (Skulmowski & Rey, 2018).

As Trninic (2018) points out, embodied learning in authentic classrooms introduces additional layers of complexity, where unpredictability, emotional engagement, and the negotiation of shared meaning become integral to the learning process. Similarly, Palatnik et al. (2023) emphasize that embodied actions are dynamically shaped by evolving social interactions, emotional responses, and spatial configurations, underscoring the need for research that captures how embodied learning develops in real classroom environments. Recent scholarship has also highlighted the role of attentional processes in embodied mathematics learning (Marco & Shvarts, 2025; Benally et al., 2022), suggesting that engagement itself must be theorized alongside reasoning.

This study examines how high school students engaged with core probabilistic concepts—including sample space (Ω), certain and impossible events, and event probability—through a sequence of embodied, movement-based lessons. Our analysis was guided by the axis from sensorimotor exploration to formal reasoning, which has been widely established as a theoretical foundation in embodied learning research (Nemirovsky & Ferrara, 2009; Abrahamson & Sánchez-García, 2016; Way & Ginns, 2024). In addition, we identified a second, emergent axis—distraction to engagement—that proved valuable for interpreting students’ activity. This dimension captured fluctuations in attention, participation, group dynamics, and affect, which were essential to understanding how learning unfolded within the socially and emotionally rich context of the classroom. Although prior research has addressed aspects of this engagement dimension (Fredricks et al., 2004; Hidi & Renninger, 2006; D’Mello & Graesser, 2012; Ainley et al., 2006), it has rarely been explicitly situated within an embodied learning framework. Together, these dual axes offer a situated account of embodied probability learning that foregrounds both its conceptual affordances and its contingent, dynamic nature in classroom settings (Palatnik et al., 2023). Building on these insights, this study investigates how students’ embodied trajectories across the sensorimotor–formal reasoning and engagement–distraction dimensions contribute to their reconstruction of key probabilistic concepts.

2. Theoretical Framework and Rationale

This study draws on embodied cognition as a foundational perspective on learning, emphasizing that knowledge is not only constructed through mental processes but also through bodily activity, sensory engagement, and spatial interaction. According to Varela et al. (2017) and Shapiro (2019), cognition emerges from dynamic interactions between the body, environment, and perception, challenging traditional models that separate mind and body. In mathematics education, this view is supported by research showing that gestures and movements play a key role in developing conceptual understanding (Goldin-Meadow, 2003; Roth, 2001). These embodied actions are not supplementary to thought but integral to the reasoning process, particularly in early phases of learning.

Building on this perspective, the field of embodied learning in STEM education has developed pedagogical approaches that deliberately structure bodily activity to support conceptual learning. Abrahamson and Lindgren (2014) define embodied learning design as the intentional arrangement of learning environments that elicit sensorimotor interactions, which can be recruited to construct formal mathematical ideas. A well-known example is the ‘Mathematical Imagery Trainer for Proportion’ (MIT-P) (Abrahamson, 2012), in which students move their hands through continuous space, such as maintaining one hand twice as high as the other, to discover proportional relationships. Only later are symbolic grids and numerical representations introduced. This task exemplifies how embodied design can bridge intuitive physical experience with formal representations. The effectiveness of this coordination is enhanced through design elements such as attentional anchors: motor-perceptual patterns that help learners map bodily actions onto mathematical structures (Abrahamson & Sánchez-García, 2016). Similar approaches have been applied in physics education, where choreographed movement has been shown to deepen understanding of motion phenomena (Zohar et al., 2018). Additional studies emphasize how the manipulation of materials or navigation through space can align embodied experience with mathematical reasoning (Shvarts et al., 2021; Palatnik, 2022).

In the domain of probability, abstract concepts such as randomness, sample space, and event likelihood are particularly resistant to instruction via static representations (Batanero & Diaz, 2012; Gal, 2005). Embodied approaches offer a means to ground these concepts in physical experience. Prior work has demonstrated that physical tasks, such as marble draws or chance simulations, can support the transition from intuitive to ratio-based reasoning (Abrahamson, 2012). More recently, researchers, such as Soto-Andrade et al. (2018), Valdés-Zorrilla et al. (2023), and Efron et al. (2023), have explored how dance and movement can serve as metaphors and enactments for stochastic processes, suggesting that probabilistic thinking can be developed through multimodal, sensorimotor engagement.

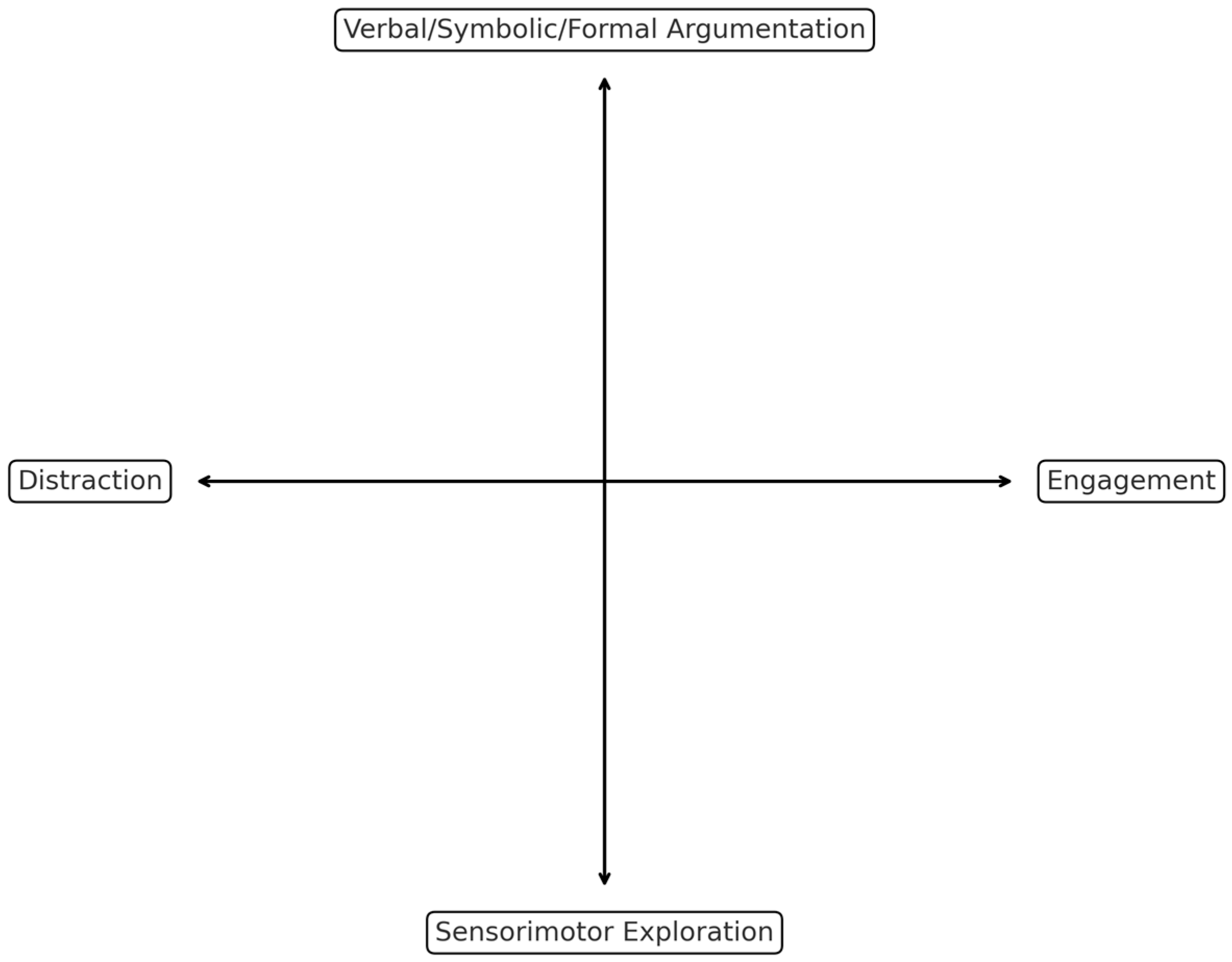
This study builds on these foundations by introducing a dual-axis interpretive framework for analyzing embodied learning (Figure 1). The first axis spans a continuum from sensorimotor exploration to verbal, symbolic, and formal reasoning, reflecting well-documented transitions in multimodal learning, where gesture and movement often precede or accompany abstraction (Radford, 2003; Hall & Nemirovsky, 2012). Nemirovsky and Ferrara’s (2009) notion of perceptuo–motor–imaginary activity deepens this continuum by emphasizing how meaning emerges through the interplay of action, perception, and mental imagery. Trninic (2018) similarly positions repeated embodied practice as a historically grounded pathway for cultivating mathematical understanding.

The second axis, developed inductively from classroom observations during iterative cycles of coding, contrasts distraction with engagement, capturing affective and attentional fluctuations characteristic of open-ended, movement-based environments. While the vertical axis is grounded in established scholarship on embodied learning (Nemirovsky & Ferrara, 2009; Abrahamson & Sánchez-García, 2016), the horizontal axis reflects recurring patterns we identified in students’ shifting attention, affect, and participation. Taken together, the two dimensions provide a lens for tracing how students construct probabilistic understanding through physical action, social interaction, and reflective dialogue in a naturalistic classroom setting.

Figure 1 illustrates the dual-axis framework that guided our analysis of classroom activity.

Building on Kazak and Pratt’s (2017) view of learning as an emergent, iterative process shaped by embodied interaction, this study explores how students construct probabilistic meaning through their physical, spatial, and verbal engagement in a movement-based learning environment. Specifically, the research asks the following: how do students’ embodied trajectories across the dual axes of sensorimotor–formal reasoning and distraction-distraction contribute to their reconstruction of key probabilistic concepts such as sample space, certain and impossible events, and event probability? This framing allows us to interpret students’ meaning-making not as a linear progression but as dynamic shifts across a multidimensional learning space, where physical action, affective involvement, and formal articulation intersect.

3. Materials and Methods

3.1. Research Design

This qualitative study draws on Wilmes and Siry’s (2021) multimodal interaction analysis to explore how students engage in embodied probability learning within authentic classroom environments. Rather than testing a predefined hypothesis, this approach enables the iterative development and refinement of both theory and practice through close analysis of students’ lived, moment-to-moment experiences. Multimodal interaction analysis facilitated a detailed examination of how students coordinate gesture, language, and material interaction in real time. Together, the analytical and design frameworks supported this study’s goal of investigating emergent meaning-making and improving pedagogical approaches to embodied mathematics learning.

3.2. Participants and Setting

This study was conducted at a government-funded mainstream secondary school in Israel with a dual emphasis on academic and arts-based education. Participants were 9th-grade students (aged 14–15 years) enrolled in a low-level mathematics track, several of whom had recognized special educational needs. Participation was voluntary.

Sessions were conducted during students’ regular mathematics class time in a flexible classroom setting, where furniture was removed to create an open space conducive to movement-based activities. Group sizes ranged from five to seven students, with some continuity and some variation across the four lessons, reflecting the enrichment-based structure of the program. The lessons were facilitated by the researcher, with the students’ regular mathematics teacher present throughout to provide continuity with the class context.

This study was conducted as part of a master’s degree research seminar paper; therefore, it did not require formal approval from an Institutional Review Board. Nevertheless, full ethical procedures were observed. Written consent was obtained from the students, their parents, and the school headmaster, and the students provided assent for the use of classroom images in academic publications. All identifying details have been anonymized, and the images are presented exclusively for scholarly purposes.

3.3. Embodied Task Design

The lessons were designed by the authors and facilitated by the first author, whose background integrates mathematics education with over four decades of professional practice in dance and movement. Task design drew on embodied pedagogy and embodied design principles, partially on the concepts of attentional anchoring (Abrahamson & Sánchez-García, 2016), which emphasizes the coordination of perception and action toward mathematically relevant features, and task integration (Skulmowski & Rey, 2018), which stresses coherence between bodily activity and abstract reasoning. Abrahamson’s (2012) framework for probabilistic thinking further inspired the design, highlighting perceptual reasoning and embodied interaction as central to conceptual development.

Activities were structured to elicit sensorimotor engagement with key probabilistic concepts: sample space, event occurrence, certainty, and impossibility through full-body movement, gesture, spatial positioning, and peer collaboration. The four lessons followed a cumulative and iterative trajectory, with each session revisiting and extending prior activity through variation and guided reflection. This structure was intended to scaffold students’ transitions from embodied exploration to verbal articulation and symbolic reasoning, progressively refining their understanding across multiple representational modes.

The sequence of lessons unfolded as follows:

Lesson 1: Defining sample space through discrete gestures. Students generated three distinct hand movements to represent outcomes in a simple probability space. Ambiguities such as returning to a neutral pose prompted group negotiation of event boundaries.

Lesson 2: Exploring certainty and impossibility. Students worked within constrained sample spaces (e.g., “only hand gestures allowed”) and reasoned about excluded possibilities, such as using a leg movement. These embodied constraints supported discussion of p = 1 and p = 0.

Lesson 3: Expanding sample space. Students enlarged the set of gestures (e.g., adding head or leg movements) and constructed six-event sample spaces. Improvised overlaps gradually gave way to more clearly enumerated events through facilitator prompts.

Lesson 4: Cumulative and representational probability. Students created extended gesture sequences (up to twelve events) and recalibrated probabilities when subsets were removed. In a culminating task, they embodied a marble-draw scenario using different movement qualities (e.g., “relaxed movements” for green marbles), translating probabilistic ratios into physical enactments.

3.4. Study Design and Rationale

As outlined above, the four lessons were designed as part of a cumulative sequence that gradually increased in complexity while revisiting core probabilistic ideas. This study adopts a qualitative, classroom-based, design-based research approach (Cobb et al., 2003). The aim was not to conduct controlled experiments with replicates or statistical comparisons but to explore how students engage with probabilistic concepts through embodied tasks in an authentic classroom environment. The focus was on generating rich descriptions of students’ reasoning and participation, capturing the dynamic interplay of action, affect, and discourse.

Given the small group size and exploratory nature of the project, statistical methods were not applicable. Instead, analysis concentrated on multimodal documentation (video recordings, field notes, classroom artifacts) and interpretive coding of episodes. This approach enabled us to foreground the situated, contingent nature of embodied learning processes, which would not be adequately reflected through aggregate measures of frequency or significance.

The sequence of lessons was intentionally cumulative. Each session introduced a new variation that extended prior activity: beginning with discrete gestures to represent simple probability spaces, progressing to constrained spaces to highlight certainty and impossibility, expanding event sets to encourage systematic enumeration, and culminating in embodied modeling of ratios through a marble-draw scenario. This design embodied the principle of variation and scaffolding, enabling students to iteratively revisit and refine their understanding as they transitioned from intuitive movement to verbal and symbolic reasoning.

3.5. Data Collection

Data sources included the following:

• Video recordings capturing movement, gesture, and student interaction.
• Field notes documenting affective responses, engagement levels, and facilitator interventions.
• Student reflections, written or verbal, offering insight into students’ interpretations and evolving understandings.

3.6. Data Analysis

The analysis followed a multimodal interpretive framework, drawing on Nemirovsky and Ferrara (2009), to investigate how students constructed mathematical meaning through coordinated use of gesture, gaze, posture, spatial configuration, and speech. These communicative modes were treated as interdependent resources that jointly shaped students’ reasoning and participation in embodied probability tasks.

Video data were subjected to iterative viewing cycles following Powell et al.’s (2003) guidelines for multimodal video analysis. Critical episodes were identified based on observable shifts in reasoning modality and engagement and analyzed comparatively across sessions. Coding was both thematic and temporal, capturing evolving patterns such as movement constraints, spatial negotiation, transitions between bodily and verbal reasoning, and the emergence of structured sample spaces.

The interpretive process emphasized alignment with the study’s dual-axis framework, i.e., engagement vs. distraction and sensorimotor vs. formal reasoning. Through collaborative coding and repeated viewings, the research team reached interpretive consensus regarding each episode’s positioning and advancement along these axes. This enabled a dynamic mapping of students’ learning trajectories.

To ensure analytic trustworthiness, findings were triangulated across multiple sources, including video recordings, researcher field notes, and student reflections. Rather than quantifying learning gains, the analysis foregrounded the emergent and processual nature of conceptual development as it unfolded through embodied interaction and collaborative exploration.

4. Results

This section presents five classroom episodes that illustrate how students engaged with foundational probabilistic concepts, sample space (Ω), certainty (p = 1), impossibility (p = 0), and event probability (0 < p < 1), through embodied learning tasks involving movement, spatial negotiation, and collaborative improvisation.

The analysis draws on the conceptual model, which maps student activity along two intersecting interpretive axes: from sensorimotor exploration to formal reasoning and from distraction to engagement. Each episode traces student transitions across these dimensions, highlighting how bodily interaction, peer dialogue, and facilitator guidance co-construct moments of conceptual emergence, ambiguity, and clarification.

While the episodes exhibit discernible shifts across the dual axes, they do not represent fixed or linear progressions. Instead, they highlight the situated and often recursive nature of embodied learning, where understanding emerges through cycles of exploration, reflection, and re-engagement. The analysis underscores how structured tasks and responsive facilitation support students’ movement from intuitive physical engagement toward increasingly formal mathematical articulation.

4.1. Episode 1: Defining Sample Space: From Physical Ambiguity to Conceptual Clarity

In an introductory task to define a three-element sample space using hand gestures, students were invited to use full-body movement to represent discrete probabilistic outcomes. Initial attempts revealed high physical engagement but also conceptual ambiguity: many students included the return to a neutral pose as part of the gesture itself, leading to miscounts, overlapping representations, and confusion. As shown in Figure 2a–d, Student Y performs one gesture but integrates the return motion, treating it as a new event. Similarly, as shown in Figure 2e, another student misidentifies a three-event sequence as two, indicating uncertainty in identifying discrete outcomes.

These early moments reflect an intuitive, sensorimotor approach to the task, physically grounded but lacking formal delineation of event boundaries. The students were not disengaged, but their focus was diffuse, leading to conceptual slippage between continuous movement and discrete probabilistic outcomes.

Through facilitator intervention and group discussion, students began to articulate and negotiate the criteria for distinguishing one outcome from another. The process included revisiting the movement sequences, testing them collectively, and collaboratively agreeing on when an event “begins” and “ends.” This led to a shared understanding of event segmentation and more precise mappings between gesture and outcome.

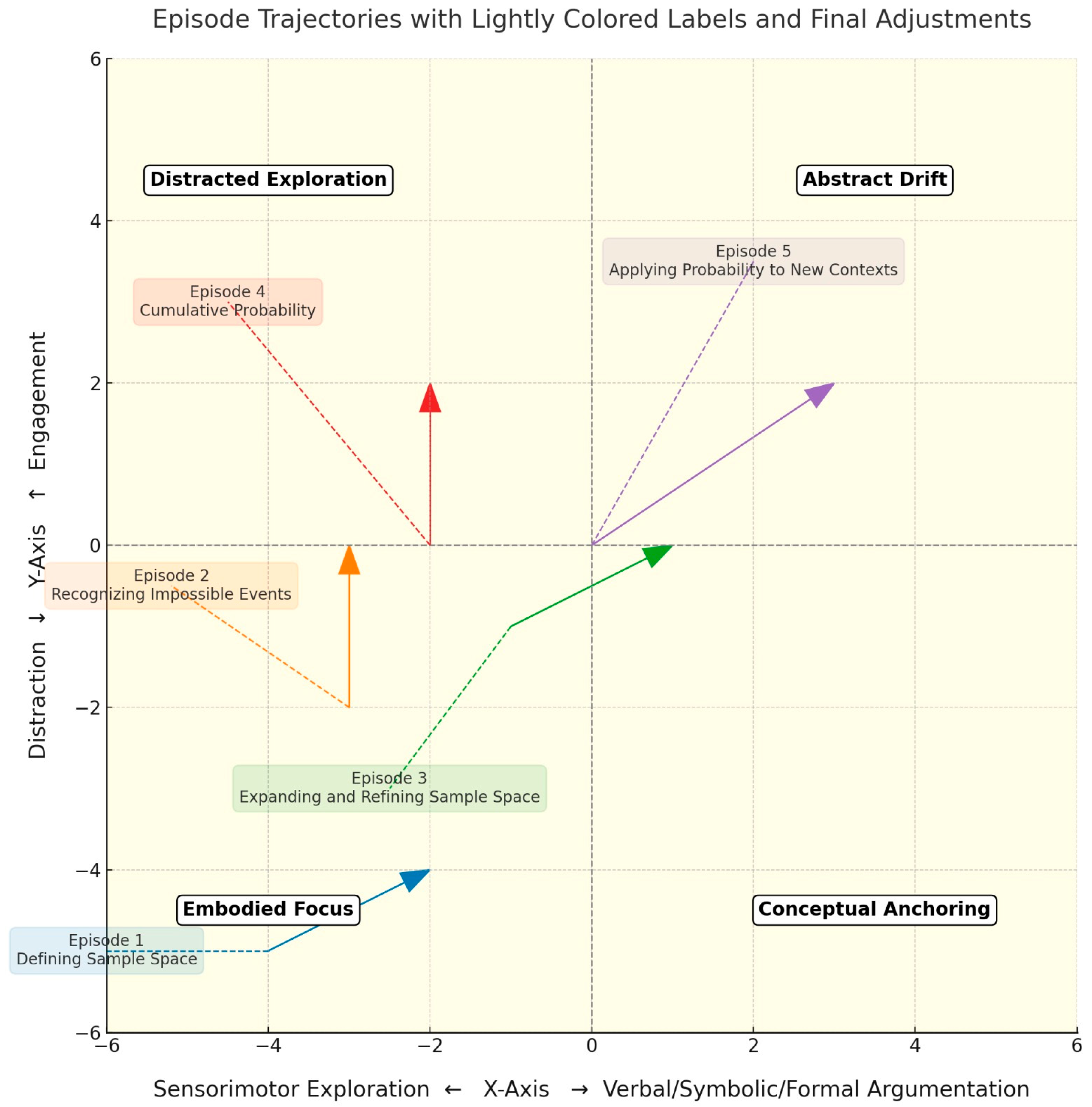
Trajectory of episode 1 on the Double Axes (see Section 5.1, blue line): This episode begins in the lower-left quadrant (sensorimotor exploration with partial distraction) due to ambiguity around event boundaries. As facilitation and discussion unfold, students shift to the right and upward toward greater engagement and formal reasoning. The episode illustrates how embodied confusion, when guided, can become a catalyst for conceptual clarity.

4.2. Episode 2: Recognizing Impossible Events: Bridging Physical and Verbal Reasoning

During a task restricted to hand gestures, a student was asked about the probability of performing a leg movement. As shown in Figure 3, without hesitation, she clenched her fists and declared “zero,” using a physical gesture to express the concept of impossibility (p = 0). This spontaneous moment demonstrated how embodied constraints can elicit precise conceptual reasoning, bridging physical exclusion and formal abstraction (Figure 3).

The student’s response reflects an intuitive understanding of probability grounded in task structure. Her verbal articulation, anchored in an embodied refusal, illustrates how constraint can support conceptual clarity, not limit it.

Trajectory of episode 2 on the Double Axes (see Section 5.1, orange line): This episode begins in the left-center region, with exploratory movement and informal reasoning. The student’s immediate, embodied response marks a clear vertical shift upward toward formal articulation and high engagement while remaining near the midline of the sensorimotor–formal axis. In Figure 7, this is represented as a compact but steep trajectory, highlighting the productive role of constraint in prompting conceptual insight.

4.3. Episode 3: Expanding and Refining Sample Space: From Improvisation to Structured Enumeration

This episode unfolded in two phases. As shown in Figure 4a,b, first, students suggested a new head movement to an existing three-gesture set, prompting a shift in the probability structure from 1 in 3 to 1 in 4. In the second phase, students were asked to construct a six-event sample space using hand and leg gestures. As shown in Figure 4c–f, initially, they improvised by overlapping movements, which led to ambiguity around discrete outcomes. Facilitator guidance prompted a shift from blended gestures to clearly defined, countable events, encouraging the group to articulate and refine their evolving understanding of sample space.

Trajectory of episode 3 on the Double Axes (see Section 5.1, green line): This episode begins in the lower-left quadrant, marked by playful sensorimotor exploration and intermittent distraction. Across both phases, students move diagonally toward the center of the model, reflecting increased engagement and a transition toward formal reasoning. The trajectory in Figure 7 captures this rising coordination between embodied creativity and emerging conceptual clarity.

4.4. Episode 4: Cumulative Probability: From Repetition to Abstract Reasoning

In a group task, as shown in Figure 5, students built a cumulative sequence of gestures, eventually creating a sample space of twelve movements. When prompted to reduce the set and recalculate probabilities, the group discussed proportional reasoning. A previously quiet student confidently identified a 2-out-of-8 likelihood, demonstrating a shift from peripheral participation to accurate, ratio-based reasoning. This marked a turning point: collaborative embodiment gave way to focused articulation of probabilistic ideas.

Trajectory of episode 4 on the Double Axes (see Section 5.1, p. 11, red line): This episode begins near the center-left, grounded in embodied engagement with fluctuating attention. As the group co-constructs structure and meaning, the trajectory shifts sharply upward, signaling a vertical move from shared physical play to formal reasoning. It represents a pivotal moment where conceptual understanding begins to solidify through collective focus.

4.5. Episode 5: Applying Probability to New Contexts: From Improvised Movement to Representational Precision

In the final activity, students were asked to represent a marble-draw probability scenario through movement. Initial attempts were improvised and inconsistent, reflecting a conceptual struggle to align gestures with abstract quantities. As shown in Figure 6, A turning point occurred when one student suggested using “relaxed movements” to represent green marbles. This embodied analogy anchored the group’s gesture-to-event mapping and catalyzed a shift toward precise verbal reasoning.

Trajectory of episode 5 on the Double Axes (see Section 5.1, purple line): The episode begins with conceptual ambiguity and diffuse interpretations, situating it near the center-left of the model. As the analogy took hold, students moved sharply upward and rightward, toward focused engagement and formal representation. This episode reflects a steep diagonal trajectory, illustrating how embodied exploration, when supported by peer insight, can lead to symbolic clarity.

5. Discussion: Navigating Complexity in Embodied Probability Learning

This study was designed as a qualitative, design-based investigation situated in an authentic classroom rather than a controlled experiment. The small group size and open-ended nature of embodied tasks precluded statistical methods or replicates. Instead, the research prioritized capturing rich, situated accounts of students’ reasoning as they unfolded in practice. This interpretive stance aimed at generating conceptual and pedagogical insights rather than statistical generalizations.

Within this framework, our analysis traced how students engaged with core probabilistic concepts through a sequence of movement-based lessons. Using the dual-axis model, we mapped shifts between sensorimotor exploration and formal articulation alongside fluctuations in engagement and distraction. The findings highlight the potential of embodied probability learning in authentic classrooms, where meaning emerges from bodily action, interaction, and affect as much as from abstract structures.

5.1. From Movement to Meaning: Mapping Embodied Learning Trajectories

Figure 7 visualizes how five episodes unfolded across the dual-axis framework, showing trajectories along two intersecting dimensions: sensorimotor to formal reasoning (horizontal) and distraction to engagement (vertical). While Figure 1 outlined the framework, Figure 7 illustrates its application.

Most episodes begin in the lower-left quadrant, marked by exploratory movement and improvisation. Over time, trajectories typically rise toward greater engagement and shift toward formal reasoning. Episode 3 shows a smooth progression toward abstraction, Episode 4 highlights deepening engagement without major conceptual shift, while Episode 5 demonstrates a sharper move into formal reasoning. These trajectories, however, were not linear: moments of detachment, re-engagement, or improvisation punctuated the pathways. Such fluctuations underscore that embodied learning is emotionally textured, recursive, and pedagogically rich, where detours may generate insight rather than distraction.

5.2. Embodied Learning as a Site of Complexity

Engaging with probabilistic concepts through movement required students to interpret spatial relations, negotiate task constraints, and connect physical action to abstract reasoning. This process was often nonlinear, marked by uncertainty and improvisation, echoing perspectives that see embodied learning as involving both embodied and disembodied affordances (Farsani, 2025). Ambiguity and play created conditions for assimilation, negotiation, and conceptual breakthrough.

Our findings suggest that movement-based learning can deepen engagement and support conceptual breakthroughs, but it also introduces significant challenges. The embodied learning environment, rich with multisensory stimuli and open-ended tasks, demands continuous negotiation between structure and freedom. Students must navigate ambiguity, sustain focus, and translate lived experience into formal mathematical representations. These tensions, while sometimes challenging, are not obstacles to learning; instead, they are productive spaces where meaning is constructed.

5.3. Embodied Learning and Managing Unpredictability

Probability’s abstract and counterintuitive nature poses well-known instructional challenges. Here, embodied learning provided tangible ways to enact probabilistic ideas, yet openness also introduced ambiguity. Episode 1, where students struggled to define discrete events in a sample space, exemplifies both the potential and limits of bodily representation. These tensions resonate with Soto-Andrade et al.’s (2018) claim that bodily action can reveal and obscure structure and with Trninic’s (2018) emphasis on discovery through exploratory repetition. Reflection and facilitation proved essential in stabilizing insights (Abrahamson & Lindgren, 2014).

5.4. Transitioning from Physical to Verbal/Formal Reasoning

Episodes 3–5 exemplified students’ movement from physical enactment to symbolic reasoning. A critical example occurred when “relaxed movements” were introduced to represent green marbles in Episode 5. This attentional anchor (Abrahamson & Sánchez-García, 2016) coordinated group reasoning, transforming improvisation into structured probability talk. Such moments reflect Skulmowski and Rey’s (2018) principle of task-concept integration: embodied learning supports abstraction when physical engagement is coherently tied to conceptual aims.

5.5. Balancing Engagement and Distraction in Open Learning Spaces

Open classroom spaces fostered creativity but also playful detours. As Soto-Andrade et al. (2018) and Marco and Shvarts (2025) note, shifts in bodily focus can signify emergent possibilities rather than mere distraction. Managing engagement in embodied contexts requires facilitation that balances openness and constraint while attending to affective and spatial rhythms (Fredricks et al., 2004; Hidi & Renninger, 2006; Ainley et al., 2006). The spontaneous question ‘can I use my leg too?’ epitomizes how apparent digressions may open conceptual ground.

5.6. Iterative Learning Through Repetition and Variation

Repetition and variation, especially in Episodes 3 and 4, proved crucial for refining understanding. Students used repeated enactments not as rote rehearsal but as opportunities to test and revise ideas, echoing Trninic’s (2018) account of embodied iteration and Palatnik et al.’s (2023) emphasis on variation as a stabilizing force. These cycles transformed rhythm and movement into abstract regularities, supporting confidence and conceptual clarity. These cycles of embodied experimentation and discursive reflection reflect the developmental arc described by Abrahamson (2012), in which learners move from intuitive enactment toward symbolic formalization through structured variation and repeated engagement.

5.7. Social Dynamics and Collaborative Problem-Solving

Embodied learning unfolded as a collective process. Students interpreted, negotiated, and refined gestures together, creating semiotic bundles of speech, movement, and symbolism (Roth, 2001; Arzarello et al., 2009). Collaboration fostered engagement but also introduced tensions over gesture meaning or leadership. These dynamics often produced movements along both axes: affective shifts from distraction to deepened focus and cognitive shifts from improvisation to abstraction. Our findings extend Benally et al.’s (2022) account of collective sensorimotor reasoning, showing how peer negotiation serves as a mechanism for conceptual growth.

5.8. Supporting Conceptual Breakthroughs Through Structured Facilitation

Across all episodes, facilitation was central to stabilizing insights and guiding transitions from embodied exploration to symbolic reasoning. Structured prompts, reflective dialogue, and affective support transformed improvisation into coherent probabilistic reasoning. The Episode 5 marble-draw task illustrates this: facilitator guidance supported the emergence of meaningful analogies bridging embodiment and formalism. This aligns with Abrahamson and Lindgren’s (2014) model of embodied design and with recent calls for integrating facilitation into embodied pedagogy (Way & Ginns, 2024).

6. Conclusions

This study illustrates both the transformative potential and inherent complexity of embodied learning in mathematics education. By engaging students in movement-based tasks that explored probabilistic concepts such as sample space, certainty, and event probability, we observed how understanding emerged through a dynamic interplay of physical action, emotional assimilation, social negotiation, and facilitator support.

To interpret these processes, we developed a dual-axis conceptual framework. The first axis, sensorimotor exploration to formal reasoning, was informed by theory; the second, engagement to distraction, emerged from classroom observations. Through five episodes, we traced students’ nonlinear learning trajectories, marked by ambiguity, detours, insight, and affective intensity. Rather than obstructing learning, moments of distraction and playfulness often acted as generative thresholds for conceptual breakthroughs, particularly when supported by attuned facilitation.

A seemingly offhand question, “Can I use my leg too?”, captured a central tension of embodied learning: the impulse to expand participation, test boundaries, and co-author the learning space. When nurtured, such impulses can lead to abstraction and formalization, revealing how embodied agency fuels mathematical insight.

Our findings have implications for pedagogy and theory. Tasks should invite revisitable movement sequences that support conceptual refinement through variation and reflection. Facilitation must remain responsive, helping students navigate ambiguity and link intuition to abstraction. The dual-axis framework, grounded in classroom practice, offers both an analytical lens and a design tool for future work.

In practical terms, although this study was initially carried out as exploratory research, it shows that movement-based activities can be integrated into everyday classroom practice without requiring special resources. Teachers can adapt simple embodied tasks such as gesture, spatial positioning, or coordinated group movement to help students reason through probabilistic concepts. The dual-axis framework also provides educators with a tool for interpreting classroom dynamics: recognizing when distraction may signal the need for variation or redirection and when sustained engagement offers an opportunity to formalize ideas. In this way, the framework serves not only as an analytical model but also as a guide for pedagogical decision-making in probability education.

Further research should investigate how embodied experiences affect retention and transfer over time, how facilitation style shapes student engagement, and how technologies such as eye-tracking or motion capture might support finer-grained analysis. Extending this approach to domains like geometry or proof may clarify the broader potential and limits of embodied mathematics education.

Ultimately, embodied learning is not merely a method, it is a relational and exploratory mode of knowing, one that thrives on vulnerability, variation, and surprise. When classrooms embrace the full range of students’ expressive capacities, cognitive, physical, and emotional, new forms of inquiry and understanding become possible.