Preparing Prospective Mathematics Teacher Educators to Teach Mathematics Through Problem Solving

Abstract

Mathematics teacher educators (MTEs) play a significant role in supporting prospective teachers (PTs) to develop the mathematical content and pedagogical knowledge they need for teaching. We examined how four novice prospective MTEs learn within a Community of Practice (CoP) and develop Mathematical Knowledge for Teaching Teachers (MKTT) and MTE identities when they are serving as interns in a mathematics content course for PTs taught through problem solving. We collected data through weekly reflections written by the novice prospective MTEs, researcher memos, and interviews with each participant at three points in the semester. We found that within the CoP, the novice prospective MTEs exhibited their growth predominately through learning as experience and learning as doing. We found that they indicated their development of MKTT most notably by noting new insights into pedagogical practices and enacting new pedagogical practices. We contribute (a) a model of how prospective MTEs can experience and learn how to teach PTs mathematics through problem solving, and (b) evidence of how this learning occurred and how their MTE identities developed through this experience.

1. Introduction

Mathematics teacher educators (MTEs) play a significant role in supporting prospective teachers (PTs) to develop the mathematical content and pedagogical knowledge they need for teaching. Research has shown, however, that most of the MTEs in the United States have little experience teaching students at the level of mathematics that they are preparing PTs to teach (e.g., elementary school), and that they receive little to no training or support either in their graduate programs or in their jobs (Masingila & Olanoff, 2022; Masingila et al., 2012).

Mathematics professional organizations (e.g., Conference Board of the Mathematics Sciences (CBMS) in the USA, Association of Mathematics Teacher Educators (2017) in the USA) have recommended that PTs develop deep and connected understandings of foundational mathematical ideas and be engaged in doing mathematics that “allows time to engage in reasoning, explaining, and making sense of the mathematics that prospective teachers will teach” (CBMS, 2012, p. 17) and “develop the habits of mind of a mathematical thinker and problem-solving” (p. 19). Researchers have proposed that one way to support deep mathematical knowledge development in PTs is to engage them in learning mathematics via problem solving (Escudero-Ávila et al., 2021; Masingila et al., 2018). Since prospective MTEs have often experienced traditional mathematics teaching and learning in their academic and teaching experiences, we argue that for MTEs to be prepared to support PTs in learning via problem solving, they need to experience, reflect on, discuss with others, and learn from teaching and learning through problem solving. In particular, we found that our participants had not experienced learning via problem solving, but rather traditional mathematics teaching, as noted by several of our participants “the teacher gives the example, gives the procedure to solve the example, then allows students to solve different examples” (Cameron, Beginning Interview) and that their experience “focused on passing the exams rather than understanding the concepts” (John, Beginning Interview).

For this research concerning teaching and learning via problem solving, we view problem solving using Lesh and Zawojewski’s (2007) definition:

A task, or goal-directed activity, becomes a problem (or problematic) when the “problem solver” (which may be a collaborating group of specialists) needs to develop a more productive way of thinking about the given situation.

(p. 782)

Based on this definition, we note that mathematical exercises are not problems since students complete exercises using procedures that they have learned. We engaged PTs in problem solving by providing them with problematic tasks for which they did not have known procedures to use to solve them. Additionally, supporting these PTs in learning via problem solving was a problem-solving task for novice prospective MTEs as they had not previously learned pedagogical strategies for teaching through problem solving.

In this paper, our goal is to contribute to the mathematics education community’s understanding of how novice MTEs develop Mathematical Knowledge for Teaching Teachers (MKTT) as part of a Community of Practice (CoP) while interning in a mathematics content course where PTs are learning mathematics through problem solving. Our research question was:

RQ: How do novice prospective MTEs develop MKTT and learn about teaching and learning mathematics through problem solving, as well as how do their MTE identities develop, when they are part of a CoP comprised of instructors and interns (novice prospective MTEs) working together to support PTs’ learning in developing mathematical understandings through problem solving?

We refer to MTEs as people who have been prepared through a doctoral program as a mathematics teacher educator and are working in preparing prospective mathematics teachers. We refer to prospective MTEs as students who are in a graduate program in mathematics education and are learning about preparing prospective mathematics teachers. We distinguish between prospective MTEs and novice prospective MTEs in that the novice prospective MTEs are at the very beginning of their graduate mathematics education program. In our program, an internship is a semester (or more) where a graduate student works under the supervision of an MTE in mathematics or mathematics education course focused on preparing PTs. The goal for the intern is to grow in their development of Mathematical Knowledge for Teaching Teachers.

Our model consisted of engaging prospective MTEs in an internship with particular design features situated within a Community of Practice (CoP) and the context of a mathematics content course for PTs taught through problem solving. The mathematics content of the course included the concepts of numeration, operations, number theory, and probability and statistics. The course met for 80 min twice a week with the 22–28 PTs working collaboratively on problem-solving tasks that the instructor introduced. For example, during a unit on number theory ideas, which came after PTs had engaged in problem solving with numeration tasks involving bases other than base ten, the instructor gave the PTs two tasks (see Figure 1 and Figure 2) involving determining divisibility tests, first in base ten and then in other bases.

The instructor engaged the PTs in a discussion of what divisibility means and what it means for a number to be divisible by another number. The instructor used base ten blocks with a document camera to pose the question of what a rule (divisibility test) would be for determining if a number is divisible by 5. After a whole class discussion about this, the PTs began working on the remaining part of the task shown in Figure 1. The instructor and the interns walked among the groups observing their work, listening to their discussions, and sometimes posing questions to prompt their thinking. When the PTs finished the task, the instructor led a whole-class discussion asking groups to present their divisibility rules and verifications for why these are valid. The instructor then engaged the PTs with applying their understandings of divisibility in base ten to extend this to divisibility concepts in bases other than ten through the task shown in Figure 2. The instructor and interns used the same pedagogical strategies as they did for the first task with the second task and the instructor led the PTs in a wrap-up discussion bringing out the mathematical ideas from the tasks. There is emphasis on conjecturing, testing, justifying and communicating mathematically throughout the course. For more information on this course and a second course with content including the concepts of geometry, measurement and rational numbers see Masingila et al. (2018).

2. Theoretical Framing

The bodies of literature that guided our work involve (a) Communities of Practice, (b) Mathematical Knowledge for Teaching and Mathematical Knowledge for Teaching Teachers, and (c) Learning and Teaching through Problem Solving.

2.1. Communities of Practice

Wenger et al. (2002) defined CoPs as “groups of people who share a concern, a set of problems, or a passion about a topic, and who deepen their knowledge and expertise in this area by interacting on an ongoing basis” (p. 7). Through a CoP, members develop and articulate new knowledge in response to questions and problems they have about their practice. A CoP offers a way for its members to engage in negotiating shared understandings, learning, meaning making, and identity.

Wenger (1998) defined learning within a CoP in four broad dimensions: learning as doing, learning as belonging, learning as becoming, and learning as experience as shown in Figure 3.

According to Wenger (1998), learning as doing in a CoP involves the practice that members of the community engage in. In the CoP we report on in this paper, our practice was teaching preservice elementary teachers mathematics content through a problem solving approach. Learning as belonging refers to one’s relation to a community characterized by a specific practice. Members in our CoP had different social configurations, for example, some were brand new to the community and others had developed a strong sense of belonging to the CoP over many years of participation. Learning as becoming refers to the changing identities of the members of a CoP as defined by indication of growth that is negotiated within the community. As Lave and Wenger (1991) stated, “learning thus implies becoming a different person with respect to the possibilities enabled by these systems of relations [i.e., communities of practice]. To ignore this aspect of learning is to overlook the fact that learning involves the construction of identities” (p. 53). In our paper, we observe novice MTEs’ changing self-reported identities in the context of our CoP. Finally, learning as experience is the development of meaning in a CoP related to growth of individuals in the community and the collective members of the community as a whole. In our CoP, learning as experience involved the ongoing growth of members through engaging in the practice of teaching preservice teachers through problem solving and making sense of this growth through discussion and reflection.

2.2. Mathematical Knowledge for Teaching and Mathematical Knowledge for Teaching Teachers

Based on Shulman’s (1986) work, Ball and colleagues (Ball & Bass, 2002; Ball et al., 2008) introduced the term mathematical knowledge for teaching (MKT) and developed a framework for MKT that expanded on Shulman’s descriptions of content knowledge and pedagogical content knowledge to include sub-categories of the mathematical knowledge that teachers need to know. More recently, researchers have examined the mathematical knowledge needed by MTEs to support PTs in developing MKT (Castro Superfine & Li, 2014; Castro Superfine et al., 2024; Muir et al., 2021; Olanoff et al., 2018; Zopf, 2010)—mathematical knowledge for teaching teachers (MKTT). Zopf defined MKTT as, “the mathematical knowledge used by mathematics teacher educators in the work of teaching mathematics to teachers” (p. 11), and claimed that, “the major purpose of the work of [mathematics] teacher education is beginning with people who already know some mathematics and developing that knowledge into mathematical knowledge for teaching” (p. 165).

Drawing on the work of a number of mathematics teacher educator researchers, we propose four dimensions of how the development of MKTT may be identified in prospective MTEs: noting new insights into pedagogical practices (Escudero-Ávila et al., 2021), noting new insights into mathematical content (Escudero-Ávila et al., 2021), understanding the rationale for pedagogical practices (Muir et al., 2021), and enacting new pedagogical practices (Castro Superfine et al., 2024; Muir et al., 2021). As Castro Superfine et al. (2024) noted in their review of research on MTE knowledge, numerous studies that have examined how MTEs learn to support PT learning have found that MTEs develop new knowledge, practices and perspectives through working with PTs and reflecting on that work.

Our prospective MTEs have already been prepared, and have experience, as mathematics teachers and thus have developed some MKT. We view learning through the internship as an opportunity for them to build on their MKT and develop that knowledge into MKTT so they will be ready to support PTs in developing MKT. In this way, prospective MTEs’ learning is also related to their becoming MTEs and so, we consider this an aspect of their MTE identity. Our CoP supported us in developing our collective and individual MKTT and afforded us the opportunity to observe the growth of the novice interns’ MKTT.

2.3. Learning and Teaching Through Problem Solving

Problem solving as a concept and a practice has been around for as long as humans have tried to overcome challenges. Mathematics educators and professional associations have long advocated for engaging students in learning mathematics through problem solving. The CBMS (2001) argued that PTs can develop deep understandings of mathematical ideas “with classroom experiences in which their ideas for solving problems are elicited and taken seriously, their sound reasoning affirmed, and their missteps challenged in ways that help them make sense of their errors” (p. 17). The CBMS (2012) continued arguing for engaging PTs in problem solving with its recommendation that courses for mathematics teachers should “develop the habits of mind of a mathematical thinker and problem-solver, such as reasoning and explaining, modeling, seeing structure, and generalizing” (p. 19). Teaching through problem solving, however, is quite challenging with the need for the teacher to select and facilitate high-level tasks, scaffold student learning as appropriate, and orchestrate discussions about the mathematics arising from the students’ problem-solving work. Masingila et al. (2016a) argued that the teacher’s responsibility is to “establish a mathematical community in the classroom where everyone’s thinking is respected and in which reasoning and discussing mathematical ideas and meanings is the norm” (p. 14). We were interested to see how novice prospective MTEs make sense of the teaching and learning in a mathematics course taught through problem solving.

3. Materials and Methods

Our aim in this study was to investigate how novice prospective MTEs learn about teaching and learning through problem solving and how their MTE identities develop when serving as interns in a mathematics content course for prospective elementary teachers taught through problem solving. Our research design was a descriptive case study. Merriam (1988) noted that there are four characteristics that “are essential properties of a qualitative case study: particularistic, descriptive, heuristic, and inductive” (p. 11). Qualitative case studies are (a) particularistic in focusing on a “particular situation, event, program, or phenomenon” (p. 11), (b) descriptive of what is being studied, (c) heuristic in that case studies “illuminate the reader’s understanding” (p. 11) of what is being studied, and (d) are inductive in the reasoning researchers use to analyze the data. Our case study presents, with rich descriptions, data we analyzed deductively how each participant learned about teaching and learning through problem solving and how their MTE identities developed. We argue that the case is heuristic in that they assist the reader in understanding how the participants learned through our CoP and developed MKTT.

3.1. Participants

Our participants in this research study were four novice prospective MTEs who were each beginning their studies in a graduate mathematics education program. They were each serving as interns in a mathematics content course taught through problem solving. Our sample was an opportunity sample as these were the novice prospective MTEs who were available at the time of this study. However, we anticipate that the findings will be relevant beyond this study and these participants.

Alex was an American student who had just completed a secondary mathematics teacher preparation program in which they did their student teaching across two semesters. They were very interested in being an intern in the mathematics content course for PTs because they wanted to experience teaching and learning through problem solving.

Cameron was an international student who completed a secondary mathematics teacher preparation program in his home country and taught for about four years. He was interested in being an intern in the mathematics content course for PTs because he had not experienced teaching or learning through problem solving and wanted to see it in action.

John was an international student who completed a secondary mathematics and physics teacher preparation program in his home country and taught for about three years. He was interested in being an intern in the mathematics content course for PTs because he was interested in learning how to teach students mathematics through problems.

Michael was an international student who completed a secondary mathematics and physics teacher preparation program in his home country and taught for 10 years. He was interested in being an intern in the mathematics content course for PTs as he was curious how the tasks for the students would be chosen and how the instructors would facilitate the students’ learning.

3.2. Context

As noted previously, the course content focused on whole numbers and operations, number theory, probability, and statistics. This course was taught with an emphasis on PTs learning mathematics through collaborative problem solving. PTs worked together in small groups to solve problems with the goal of developing deeper understandings of the mathematics taught in elementary school and their own MKT. The role of the instructors of the course was to facilitate the PTs’ problem solving and knowledge development and the role of the interns was to support the instructor and the students in their problem solving.

Mathematics Education faculty members in our program expect and plan for graduate students to have a variety of experiences during their graduate studies. One of the experiences that faculty members encourage prospective MTEs to complete is an internship in at least one of the two mathematics content courses for PTs taught through problem solving. This internship is taken for course credit. The internship for novice prospective MTEs was created with these design features: (a) the CoP met twice each week, on Monday before the two lessons for the week and on Thursday after the two lessons; (b) there was an expectation that all members of the CoP come to the Monday meeting having worked through and thought carefully about the lessons for the week ahead; (c) the course supervisor would ask interns and instructors questions about the goals of the tasks, where they thought the PTs would have challenges, and what were the mathematical ideas that were important to bring out of the PTs’ work on the tasks; (d) interns were paired with an instructor and assisted with facilitating the two lessons each week; (e) there were structures for accountability that included an assigned professional reading each week (e.g., selected chapters from Hiebert, 1986; selected chapters from Lester & Charles, 2003; Schroeder & Lester, 1989) and writing and submitting a weekly reflection based on the reading, their observations of PT learning, and their own learning as a teacher; (f) the course supervisor responded in writing to the interns’ reflections and gave specific writing prompts midway and at the end of the semester asking the interns to reflect on the PTs’ learning and their learning cumulatively from the beginning of the semester; (g) interns, along with instructors, held weekly office hours to support PT learning; and (h) the CoP had a repository of materials within the university’s learning management system with information such as the weekly readings, other materials for instructors and interns, past quizzes and exams, and project information.

These design features were guided by our theoretical framework of learning, MKTT, and learning through problem solving. Design features (a), (c), (d) and (f) align with the conceptualization of learning as belonging, design features (b), (d) and (g) align with learning as doing, design features (c) and (e) align with learning as becoming, and design features (a), (d) and (g) align with learning as experience. Design features (c), (e) and (f) support the novice prospective MTEs’ development of MKTT through new insights about pedagogical practices, design features (b), (c) and (e) support the interns in new insights about mathematical content, design feature (d) supports the interns in enacting new pedagogical practices, and design features (a), (c), (e) and (f) support the interns understanding the rationale for new pedagogical practices. Additionally, all of the design features were intended to support the novice prospective MTEs’ learning of teaching via problem solving.

Table 1. Theoretical Frameworks Aligned with Design Features.

Theoretical Framing	Code	Design Features
		CoP Meetings	Expected Preparation for CoP Meetings	Supervisor Questions	Interns Paired with Instructor and Assisted in Facilitating Lessons	Accountability Structures (Professional Reading, Reflection)	Supervisor Responds to Intern Reflections	Interns Have Weekly Office Hours	CoP Repository of Materials
Learning within a CoP	Learning as Experience	X			X			X
	Learning as Becoming			X		X
	Learning as Belonging	X		X	X		X
	Learning as Doing		X		X			X
Learning through developing MKTT	Noting New Insights into Mathematical Content		X	X		X
	Noting New Insights into Pedagogical Practices			X		X	X
	Understanding Rationale for Pedagogical Practices	X		X		X	X
	Enacting New Pedagogical Practices				X

shows the alignment of our theoretical framings with our design features.

3.3. Data Collection

The participants for this study were four new graduate students serving as interns. The participants were all in a master’s program consisting of mathematics and mathematics education courses and each had a graduate assistantship where they taught undergraduate mathematics courses or recitations. The data collected were (a) weekly reflections written by each novice intern as part of their intern work, (b) weekly or bi-weekly memos from the researchers who were working with the interns in teaching, and (c) interviews with each intern individually at the beginning, middle and end of the semester. Researchers also took notes informally at CoP meetings and included them in researcher memos.

In the interviews that took place at the end of the semester, we asked participants to place themselves on a diagram showing a progression from being a mathematics student to being an MTE. This prompt is displayed in Figure 4. Participants were then asked to explain their placement on the diagram to better understand their MTE identity at the end of the internship.

For the weekly reflections, the interns were given a published article or book chapter related to teaching and learning through problem solving to read each week. They were asked to reflect on what insights they gained from the article and what insights they gained about both student learning and their own learning through their experience in the two lessons that week. Given the challenge of teaching through problem solving, instructors first serve as interns to experience teaching and learning through problem solving so the instructors had read and reflected on the readings when they were interns. The course supervisor and instructor of record for the internship course (the first author) read and responded to the interns’ reflections individually via email. Additionally, she would often mention points raised by the interns in their reflections and bring it to the CoP for discussion during the twice weekly meetings. In this way, the readings were shared texts for the CoP members and situated the discussions of teaching and learning problem solving within the mathematics education literature.

The researcher memos were written individually by three of the authors, each of whom was working as an instructor or experienced intern in one of the course sections, with their observations of the novice interns in the course. The interviews were conducted by the second author who was not an instructor or intern at the time of this study but had previously been an intern in the course. The purpose of the interviews was to understand each participants’ experiences prior to, during, and after the internship.

3.4. Data Analysis

We analyzed our data using a deductive, theory-driven approach (Boyatzis, 1998). Our methodology included preparing the data, reading and coding it, generating themes, and interpreting the significance of these themes across the dataset. Using deductive coding, we identified themes and patterns that helped us understand how the interns learned through their participation in a Community of Practice (CoP) and how they developed their Mathematical Knowledge for Teaching Teachers (MKTT) in the process.

To explore the interns’ learning within a CoP, we focused on themes within four categories of codes based on Wenger’s (1998) framework: (a) learning as doing, (b) learning as experience, (c) learning as belonging, and (d) learning as becoming. To explore the interns’ development of MKTT, we sought themes and patterns reflecting this development based on researchers’ framings of MKTT (Castro Superfine et al., 2024; Escudero-Ávila et al., 2021; Muir et al., 2021) within four code categories: (a) interns noting new insights into mathematical content, (b) interns noting new insights in pedagogical practices for supporting PT learning, (c) interns indicating understanding of the rationale behind specific pedagogical practices for PT learning, and (d) interns enacting new pedagogical practices for PT learning.

Our analysis was both ongoing and retrospective. The ongoing analysis took place during the semester, informing the development of midway and end-of-semester interview questions and allowing us to test emerging hypotheses. The retrospective analysis involved a comprehensive review of the data corpus—interns’ weekly reflections, researcher memos, and interview transcripts. We organized and analyzed all data using MAXQDA 2024 (VERBI Software, 2024) in two rounds.

Our first phase of analysis began with the interns’ weekly reflections. After establishing definitions for the Learning within a CoP codes, we each reviewed one intern’s 14 weekly reflections to identify themes aligned with our CoP codes that would help answer our research questions. We then met to discuss the four codes, identifying patterns among researchers. Once we reached consensus on the initial codes, we proceeded to code the reflections for the remaining interns, followed by researcher memos and interview transcripts to get evidence on how the interns learned through our CoP.

In the second coding round, we reread the data artifacts in sequence—starting with reflections, followed by memos, and then interview transcripts—to gather evidence of the interns’ MKTT development. After completing the coding rounds, we extracted codebooks from MAXQDA into a Word document to review and confirm that our coding reflected clear evidence of the interns’ learning as a CoP and their MKTT development. One challenge we encountered in the second round of coding is that most evidence on how the interns developed their MKTT also supported our theory on how the interns learned within the CoP, a relationship we will present in our results. After realizing this relationship—that the learning within a CoP codes and the interns developing MKTT codes were related—we developed a matrix of frequencies showing the relationship between each of our eight codes, and a larger matrix showing actual evidence from the data artifacts that was coded in more than one code.

Table 2. Codes with Definitions and Examples.

Codes		Definition	Examples
Learning within a CoP	Learning as Experience	Intern notes or researcher observes intern expressing ongoing growth through engaging in the practice of teaching preservice teachers through problem solving and making sense of this growth through discussion and reflection. This code is closely related to “learning and doing, but then this code entails the broader meaning-making based on “doing.”	“As I have helped facilitate students’ engagement with the math tasks in the course, I have grown in my ability to effectively prompt students. I have become better at asking members of a group to share their thinking with each other when they seem to be working independently.” (Alex, Week 6 Reflection)
	Learning as Doing	Intern reports or researcher observes intern’s practice in teaching preservice elementary teachers’ mathematics content through a problem-solving approach. This code is different from learning as experience because here, the participants articulate something they are doing/did in the teaching process.	“I hear them [John and Cameron] asking students to explain what they have done so far, how they can explain their solution, etc. The students have responded well to them and appear to view the three of us as a team.” (Researcher J, Week 2 Memo)
	Learning as Becoming	Intern gives evidence or researcher observes intern expressing changing identities [becoming a different person with respect to the possibilities enabled by the communities of practice] or showing evidence of how learning changes who they [interns] are.	“I think I have progressed from a math student. Maybe from the beginning, I will say I was a math student, but now I can also, I know what it takes to teach mathematics. Okay, so I see myself as a math teacher, but then I also see myself that I haven’t gotten to the level of math and teacher education. So, like, I will stick with being a math teacher for now.” (Cameron, Post Interview)
	Learning as Belonging	Intern shows evidence of the different social configurations in the CoP, including evidence of one’s position in the CoP for example, some were brand new to the community [interns] and others had developed a strong sense of belonging to the CoP over many years of participation [researchers].	[We found no examples of this code in our data.]
Learning through developing MKTT	Noting new insights into mathematical content	Intern states or researcher observes intern noting new mathematical insights	“I cannot count how many times I’ve had to use the ideas developed in [this course] when doing my [Graph Theory & Combinatorics] course, especially when it came to the probability section. I borrowed ideas such as the Fibonacci sequence, counting techniques, and probability. Most importantly, the Fibonacci sequence I did in Graph Theory & Combinatorics, was not introduced in the form of rabbits.” (John, Week 14 Reflection)
	Noting new insights into pedagogical practices	Intern states or researcher observes intern noting new pedagogical insights	“This perhaps shows my role as a teacher in teaching mathematics via problem solving, by not giving answers and solving problems for learners, but rather asking them questions that prompt their thinking towards achieving a desired solution.” (John, Week 1 Reflection)
	Understanding rationale for pedagogical practices	Intern states or researcher observes intern indicating understanding of rationale for new pedagogical practices	“When students are able to come to mathematical concepts for themselves, they gain deeper conceptual understanding which allows for flexibility of the associated procedures. This connects to the key idea of allowing students to struggle with math rather than trying to make everything as easy as possible.” (Alex, Week 7 Reflection 7)
	Enacting new pedagogical practices	Intern states or researcher observes intern enacting new pedagogical practices	“I have observed that Alex does not just settle with the solution given by the groups, but they try to question them using sentence stems such as “What strategy did you use?” and “How did you get this value”” (Researcher F, Weeks 8 & 9 Memo)

shows the codes we used, how we defined them, and examples of evidence from our data artifacts for each code.

Our theoretical framings of Communities of Practice (CoP), Mathematical Knowledge for Teaching (MKT) and Mathematical Knowledge for Teaching Teachers (MKTT) and Learning and Teaching through Problem Solving influenced how we designed this study, what data we collected, and how we analyzed the data. These framings influenced us to examine how the four participants (a) learned within the context of a CoP, (b) made sense of the MKT needed by PTs and their own developing MKTT, and (c) learned about teaching and learning mathematics through problem solving. The framings influenced us to collect data that (a) drew on conversations in the CoP meetings and in the classrooms among the instructors and interns that were reflected in researcher memos and participants’ weekly reflections, (b) prompted the participants to reflect on and write about the PTs’ learnings and their own learning through their weekly reflections, and (c) asked the participants to respond to questions about how and what they were learning, along with how they saw their mathematical identity, through the interviews. The framings also influenced our analysis in that we drew on Wenger’s (1998) construct of learning within a CoP to develop four codes on how our interns learned within a CoP, and several researchers’ development of MKTT (Castro Superfine et al., 2024; Escudero-Ávila et al., 2021; Muir et al., 2021) to develop codes on how the interns developed MKTT. These codes influenced us to look for evidence of how the CoP impacted the prospective MTEs’ learning, what the participants noted about MKT and MKTT, and how they learned about teaching and learning through problem solving.

4. Results

Below we share our findings of how prospective MTEs learned about teaching and learning through problem solving (a) within a CoP, and (b) through developing MKTT. As described above, we analyzed our data using codes related to learning within a CoP and the development of MKTT.

Table 3. Frequency Table of Coded Data.

Theoretical Framing	Code	Alex	Cameron	John *	Michael	Totals
Learning within a CoP	Learning as Experience	6	4	26	7	43
	Learning as Becoming	2	1	9	4	16
	Learning as Belonging	0	0	0	0	0
	Learning as Doing	7	6	24	3	40
Learning through developing MKTT	Noting New Insights into Mathematical Content	0	5	6	4	15
	Noting New Insights into Pedagogical Practices	13	9	30	13	65
	Understanding Rationale for Pedagogical Practices	4	0	9	2	15
	Enacting New Pedagogical Practices	10	7	17	2	36
Totals		42	32	121	35	230

* Note that we found John to be highly motivated and quite reflective and produced longer reflections and interview responses. Thus, we found that he had higher frequencies in all categories as compared to the other participants.

shows the frequency of coded excerpts for each of our codes for each of our participants. Note that all names used are pseudonyms.

We next present evidence for our participants’ learning within a CoP (presented in the order of how frequently the codes occurred) and then evidence of our participants developing MKTT (presented in the order of how frequently the codes occurred).

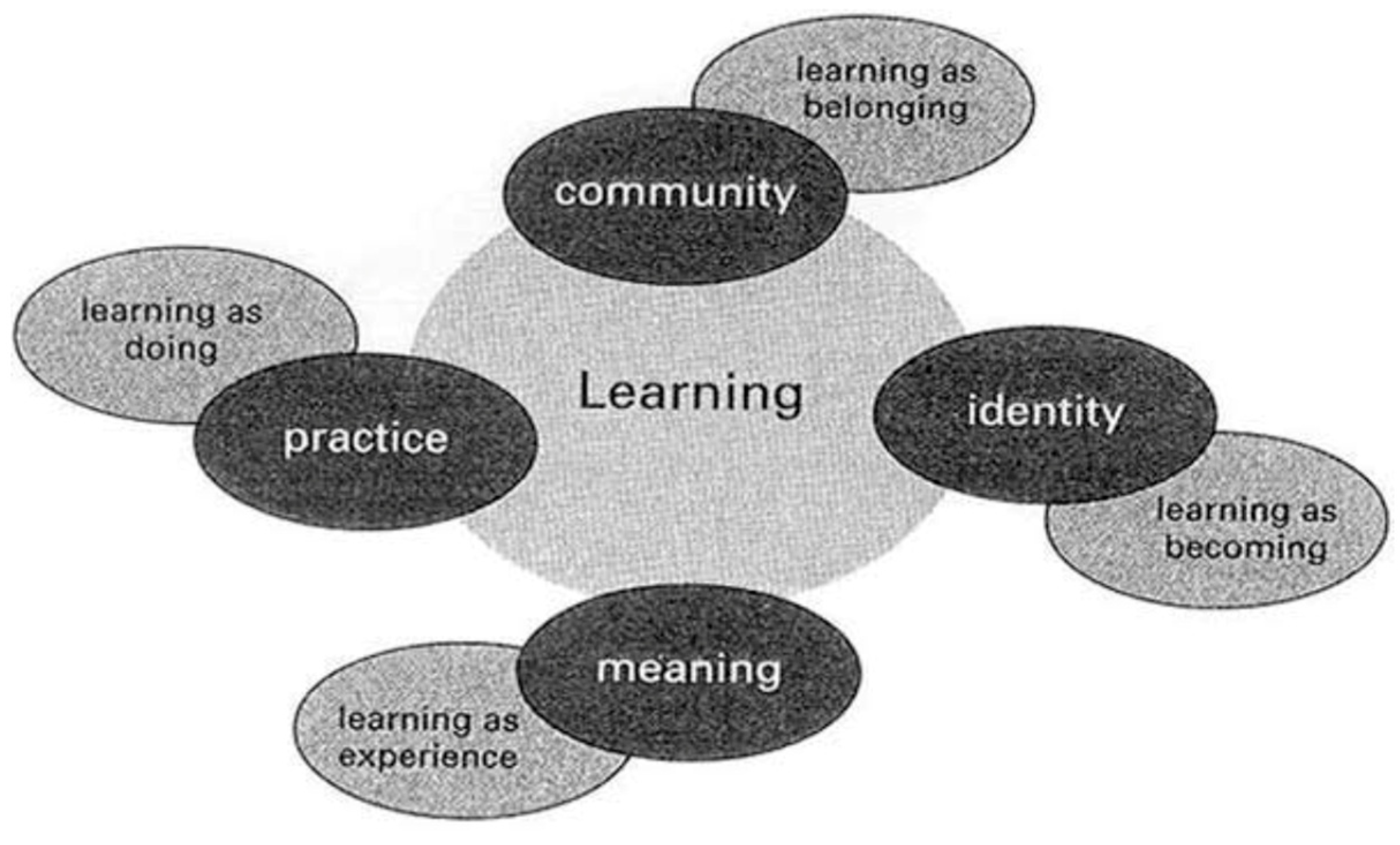
4.1. Learning Within a CoP: Learning as Experience

We coded data as learning as experience when an intern noted, or a researcher observed an intern expressing, ongoing growth through engaging in the practice of teaching PTs through problem solving and making sense of this growth through discussion and reflection. As can be seen in Table 3, this code occurred the most frequently among our codes for learning within a CoP.

Two instances of Alex commenting on their learning as experience occurred in their Week 6 and Week 14 reflections. In the first excerpt, Alex noted their growth in asking questions to prompt students’ thinking.

As I have helped facilitate students’ engagement with the math tasks in the course, I have grown in my ability to effectively prompt students. … At first, I stayed away from giving too much prompting, as I didn’t want to just give students an answer or process without them contributing their thoughts. More recently, I am realizing I can give effective prompts by asking students the right questions to get their thinking started.

(Week 6 Reflection)

In the second excerpt, Alex described that they learned to allow students to engage in productive struggle and how to best support them.

Now, as the course comes to a close, I have learned more about how we can let math be problematic for students in a thoughtful way. Allowing for struggle is necessary so students will grow, but as an educator I need to provide supports so my students do not struggle fruitlessly or become disengaged because of their frustration. Proper questioning and prompting comes from understanding how my students understand mathematics and helping them recognize the strategies and supports that help them engage in productive struggle without my help.

(Week 14 Reflection)

Michael also wrote about learning to support students to persist in their problem solving: “I have also realized that students need to be encouraged when they are struggling such that they do not give up. In our classes, I am learning how crucial the teacher’s presence and monitoring can be” (Week 11 Reflection). He also commented on how he learned how to create a learning environment that supports student contributions: “I have learned how to organize a class in small groups … grouping students to create a conducive learning environment so that students can share ideas freely” (Week 14 Reflection).

Cameron noted that he learned about how to better understand PTs’ learning and how they learned:

I learned that reflecting on students’ work at the lesson can be very helpful in gaining an understanding of where the class is as well as concepts that individual students may have understood or may be struggling with. … As a teacher, my goal is to help students understand mathematics, but understanding is not something that one can teach directly. It takes place in the students’ minds as they connect new information with previously developed ideas.

(Week 14 Reflection)

Some instances of John’s learning as experience demonstrate his growth through the semester. About midway through the course, John stated, “I think I’m still trying to make a clear connection between how long I should wait for them to get stuck. How much time I should give them before I come in and say, ‘So, how about doing it this way?’ … I’m not sure how much time I should give them, but I think that’s something I’ll keep working on through the course” (Midsemester Interview). John was trying to make sense of how best to support PTs’ problem solving work, including when seem stuck.

In an excerpt from near the end of the semester, John reflected on his learning through this internship to respond to PTs’ incorrect responses:

I, honestly, am one person who growing up did not have the best responses from teachers whenever I gave wrong answers …. I have seen how students take [the instructor’s] responses with positivity and how they are always ready to answer questions whether or not they’re wrong, and I hope one day I can teach that way. At the start of the semester, I couldn’t find better words to use in correcting students when I thought they were doing something incorrectly, but nowadays I’m getting the perspective of that.

(Week 12 Reflection)

John summed up his learning as experience this way: “Through interning in [this course], I have redefined my approach to teaching, from showing students how to do math to allowing students to do the math” (Week 14 Reflection).

We found that our four participants learned within the CoP through learning as experience. Their full participation in the CoP discussions about the upcoming lessons, PTs’ learning and debrief on the lessons, as well as serving as interns in supporting the PT learning during the lessons, our participants grew in their knowledge and understanding of preparing PTs to teach children mathematics through developing MKT.

4.2. Learning Within a CoP: Learning as Doing

We coded data as learning as doing when an intern discussed their, or a researcher observed an intern’s, practice in teaching PTs. As can be seen in Table 3, this was the second most frequently occurring code among our codes for learning within a CoP.

In their weekly reflections, the interns often wrote about their actions in practice. For example, Alex wrote after the third week about pedagogical actions they were using to support student problem solving and how a student found a particular representation helpful to them:

One student expressed how ‘the tables just work for me’, referring to how information presented in a table makes patterns and processes clearer to her. I acknowledged and expressed my appreciation for this statement when I heard her say this, and also prompted the group to think about how they can represent their knowledge in multiple ways so the whole group can understand.

(Week 3 Reflection)

In another example, at the end of the semester, John reflected on how his practice changed through the internship experience:

While in class, my role changes to understand the methods students have used, and how they might differ from the methods I used. This has helped me to appreciate the input students make in their learning, and while in the past I always thought the teacher was at the center of learning, it now blows my mind that the students’ input and thinking through problem solving is key to learning.

(Week 14 Reflection)

Researcher memos also noted instances of interns’ pedagogical practice that supported PTs’ problem solving work. One researcher’s memo recorded observations of Cameron and John’s practice in the first few weeks of the semester: “I heard [Cameron and John] asking groups to explain conjectures and to explain what they had done thus far” (Researcher J, Week 1 Memo); “They are continuing to improve in listening to students, trying to understand their work, and then pose questions that will prompt students to think about their work” (Researcher J, Week 3 Memo).

Another researcher commented on Michael’s practice in demonstrating “a proactive approach by encouraging students to draw upon their prior knowledge from previous lessons to tackle a range of problems. He consistently initiated conversations with student groups, prompting them to carefully consider their approaches” (Researcher C, Week 3 Memo). A third researcher noted that “Alex asked students deep reflection questions on this activity, and this helped reveal students’ understanding of the problem” (Researcher F, Weeks 5 and 6 Memo).

We found that our participants learned within the CoP through learning as doing. Their active participation in the classroom as interns afforded them the opportunity to practice new pedagogical skills to support the PTs in developing MKT.

4.3. Learning Within a CoP: Learning as Becoming

We coded data as learning as becoming when an intern provided evidence, or a researcher observed an intern expressing, of changing identities (e.g., from mathematics learning to mathematics teacher to mathematics teacher educator, or by changing their view of teaching). As can be seen in Table 3, this was the third most frequently occurring code among our codes for learning within a CoP.

Six weeks into the semester, Michael noted that he has learned new practices as a mathematics teacher:

I have learned to ask prompting questions to students. … I used to ask questions like, ‘What is the answer? What formula have you used? What has failed to get the answer?’ The language … in [this class] should be prompting; for example, ‘How have you solved the task? Why do you think this strategy works? Can you justify your answer?’ I realized that these questions give more insight to students and help them have meaningful learning and sharing of different approaches amongst the groups.

(Week 6 Reflection)

In the end-of-semester interview, Michael talked about how he had changed as a mathematics teacher in thinking “about creating a classroom environment … choosing prompts or questions … encouraging students in their work” to support students’ problem solving and mathematical communication; “this is showing that I’m growing as a mathematics educator” (Post Interview). Michael shared that he had changed as a teacher, however, Michael also shared that he viewed himself only as being a math teacher rather than having become an MTE at the end of the semester.

Cameron talked about his changing identity from mathematics learner to mathematics teacher and not quite yet as mathematics teacher educator in the end-of-semester interview:

Maybe from the beginning, I will say I was a math student, but now I … know what it takes to teach mathematics. … So, I see myself as a math teacher, but then I also see myself that I haven’t gotten to the level of mathematics teacher educator.

(Post Interview)

Like Michael, Cameron described change in his identity but focused on change in his mathematics teacher identity rather than a shift to identifying as an MTE. When asked to explain their response to the MTE identity prompt, Alex shared:

But yeah, I see myself mostly as a teacher of mathematics right now. I think that’s like, where I’m at, and you know, we are teaching future educators. But I wouldn’t say we’re teaching math education theory, necessarily. So, I think I have a foot in that mindset of, you know, I am teaching about how to teach math. But it’s sort of, it’s sort of the more underlying theme. Whereas the overtones are mostly like, getting them used to like learning through problem solving.

(Post Interview)

Alex described a similar change in becoming to Michael and Cameron in that change was focused primarily on their mathematics teacher identity. However, Alex did note that there was some identification with the role of being an MTE.

John also noted that he began the internship as a mathematics student, but John differed from the other three participants in the way that he described his identity evolving. John said:

So, as a math student, then from here onwards through all the other weeks, I have developed as a math teacher educator, so that’s like the overall because then I get … to encourage my students to think in terms of being a math teacher in future. So here, growing students’ thinking through asking critical questions, so I ask them questions so that they can explain their answers and when they are explaining, this is important because they are going to explain it to their students.

(Post Interview)

We found that our participants learned within the CoP by learning as becoming. They viewed themselves as evolving in their mathematics teacher identities and, for some in their MTE identities, as they grew in their understanding of how to support PTs’ in developing MKT and grew in their pedagogical skills to facilitate learning through problem solving.

4.4. Learning Within a CoP: Learning as Belonging

We coded data as learning as belonging when an intern provided evidence of the different social configurations in the CoP. As can be seen in Table 3, we did not find any instances of this during our coding for learning within a CoP. However, there was an instance of this that was reported through informal conversation among CoP members. The interns had made the decision at the beginning of the semester to meet on each weekend prior to the CoP’s Monday meeting to work through and discuss the mathematical tasks for the coming week. It was during one of these meetings that the interns reached out to a more senior graduate student who had previously been an intern and an instructor in this course to ask about a particular task that they were struggling with that involved base four blocks and regrouping. Using pedagogical problem-solving strategies he learned and employed in the course, the more senior graduate student supported the interns in engaging with the task and coming to understand the mathematical goals involved. We anticipate that if we had designed questions for the interviews that would prompt interns to think about the social configurations in the CoP, the interns may have commented on this.

4.5. Learning Through Developing MKTT: Noting New Insights into Pedagogical Practices

We coded data as noting new insights into pedagogical practices when an intern noted, or a researcher observed an intern expressing, new pedagogical insights. As can be seen in Table 3, this code occurred the most frequently among our codes for learning through developing MKTT.

Alex wrote in their reflection after the first week the challenge they noticed in engaging students in problem-solving tasks without overwhelming them:

We will need to properly scaffold our students’ learning so that while they will be challenged, they won’t become discouraged by the higher cognitive load required when engaging with conceptual knowledge.

(Week 1 Reflection)

Alex had observed that the PTs were challenged by the problems—looking for patterns, making conjectures, justifying their solutions, convincing themselves and others that their solutions were correct. Six weeks into the semester, Alex shared their insights into some newly gained pedagogical practices they had acquired that enabled them to support PTs’ problem solving: “I have grown in my ability to effectively prompt students. I have become better at asking members of a group to share their thinking with each other when they seem to be working independently” (Week 6 Reflection).

Michael noted his insights into creating an environment that supports student problem solving:

I have learned how to organize a class in small groups to create a conducive learning environment such that students [are engaged in] active learning. … The instructor keeps attending to the different groups; however, some groups may need more support than others. … I have learned to ask prompting questions. … how have you solved the task? Why do you think this strategy works? Can you justify your answer? I realized that these questions give more insight to students and help them have meaningful learning and sharing of different approaches amongst the groups.

(Week 6 Reflection)

Michael also wrote about insights he gained into how decisions made by the MTE affect the problem-solving activity:

I learned how a classroom climate can be shaped by the teachers’ decision about lesson components; for example, amount of time devoted for investigation, the value placed on discussion, the treatment of incorrect answers and errors in reasoning. … the way the teacher reacts to the students’ responses and questions affects students willingness to respond to questions, share their solutions and methods, suggest generalizations, participation in doing mathematics, and mistakes should be recognized as [a] means to learn.

(Week 12 Reflection)

Cameron shared insights he gained about reflecting on PTs’ work: “I learned that reflecting on students’ work after the lesson can be very helpful in gaining an understanding of where the class is, as well as concepts that individual students may have understood or may be struggling with” (Week 14 Reflection).

John wrote about his insight into a change in his teaching focus:

my perspectives … have now changed and are focused on helping my learners understand why procedures work and the use of procedures as a means of learning rather than a means to achieving other end goals; that is, learning via problem solving rather than for problem solving.

(Week 7 Reflection)

John also stated that he realized the benefits pedagogically of reflecting on many aspects of teaching and learning, a change from his prior perspective:

I always thought we only reflect on exams, mainly after giving students exams, and you revisit and check where they went wrong and … revise with them. But I’m getting to see that even the [usual] lessons, as a teacher, just getting to reflect and see what went well and what did not go well, and I’ve … grown through [these] teaching methods.

(Post Interview)

We found that our participants learned through developing MKTT by noting new insights into pedagogical practices. Through their internships they became aware of different ways to support PT learning and gained different perspectives on what they wanted the focus of learning to be.

4.6. Learning Through Developing MKTT: Enacting New Pedagogical Practices

We coded data as enacting new pedagogical practices when an intern noted, or a researcher observed an intern, enacting new pedagogical practices. As can be seen in Table 3, this was the second most frequently occurring code among our codes for learning through developing MKTT.

Alex wrote about their experience enacting new pedagogical practices involving group problem solving and questioning in their reflection six weeks into the semester:

I have … been prompting students to support each other and ensure everyone has understood and completed a particular task before the group moves on. I am also finding ways to ask students questions that prompt their thinking.

(Week 6 Reflection)

A researcher observing Alex noted the enactment of pedagogical practices to support PTs in making connections in a memo in writing that Alex “guided the students to understand the problem by guiding them to link their understanding from the previous activity to the current one” (Researcher F, Weeks 5 and 6 Memo).

Michael talked about being prepared for PT questions that may arise during their problem solving:

I … imagine myself … being a student. … I must ask myself very many questions. There are very many questions that, of course, you might think you as a teacher, if you’re preparing, you have to think ahead and say that maybe the student might ask me this question. … So … I come to the class prepared for such questions.

(Pre Interview)

A researcher observing Cameron and John noted that by the second week they were “asking students to explain what they have done so far, how they can explain their solution, etc.” (Researcher J, Week 2 Memo). In the next week’s memo, the same researcher wrote that Cameron and John “are continuing to improve in listening to students, trying to understand their work, and then pose questions that will prompt students to think about their work” (Researcher J, Week 3 Memo).

Six weeks into the semester, John noted his pedagogical practice for dealing with PT questions about how to solve a problem: “when I … walk around groups and get students asking me to solve a problem for them, I … always try to prompt them into thinking more about the problem so as to solve it by themselves” (Week 6 Reflection).

Near the end of the semester, John wrote about his adopted pedagogical practice to best support PTs in their problem solving:

One thing I always plan on … before the lesson is the possible methods of solving problems, and the possible methods and thinking strategies students may use. Outlining the possible approaches enables me to develop … thought-provoking questions I may use to guide students towards understanding the tasks and solving them.

(Week 12 Reflection)

We found that our participants learned through developing MKTT by enacting new pedagogical practices. Through their internships they had the opportunity to observe in action, understand and then enact pedagogical practices that were new to them and supported the PTs in collaborative problem solving and mathematical communication.

4.7. Learning Through Developing MKTT: Understanding Rationale for Pedagogical Practices

We coded data as understanding rationale for pedagogical practices when an intern noted, or a researcher observed an intern indicating, understanding the rationale for new pedagogical practices. As can be seen in Table 3, this code was the third most frequently occurring among our codes for learning through developing MKTT.

Through our data analysis, we found instances of our participants indicating their understanding of the rationale for some of the new pedagogical practices they were experiencing during their internships. Alex wrote in a reflection about the rationale for engaging students in solving problems, which may be quite challenging for them:

When students are able to come to [understand] mathematical concepts for themselves, they gain deeper conceptual understanding, which allows for flexibility of the associated procedures. This connects to the key idea of allowing students to struggle with math rather than trying to make everything as easy as possible.

(Week 7 Reflection)

Michael wrote about coming to understand the rationale for the type of questions used in teaching through problem solving:

The language used to ask questions in [this class] should be promoting [problem solving]; for example, how have you solved the task? Why do you think this strategy works? Can you justify your answer? I realized that these questions give more insight to students and help them have meaningful learning and sharing of different approaches amongst the groups they are assigned.

(Week 6 Reflection)

Toward the end of the semester, Michael wrote about coming to value group projects to assess student understanding:

I learned that group projects are a powerful form of assessment that I have never used. It promotes collaboration and teamwork since the students had to choose with whom they wanted to work. These forms of assessment drive students to do extra work outside the classroom.

(Week 13 Reflection)

John noted his insights into the rationale for preparing PTs to develop mathematical understandings and be prepared to support their future students in developing mathematical understandings:

One thing I’m sure about to this point, which I never thought about in the past, is that when preparing math educators, we’re not only helping them to understand the concepts at a personal level, but rather to understand the concepts with their future students in mind.

(Week 6 Reflection)

John extended this in a reflection near the end of the semester to note the rationale for mathematical knowledge for teachers and teacher educators:

The teacher needs to first act as a learner by understanding the material, as a teacher by scaffolding students’ thinking, and in our case for [this course], as a teacher educator by supporting student teachers in their career preparation.

(Week 13 Reflection)

We found that our participants learned through developing MKTT by understanding the rationale for pedagogical practices used in the course. The internship readings, experience in the classroom engaged in supporting PTs’ problem solving, their weekly reflections, and the discussions within the Community of Practice prompted our participants to think about the rationale underlying the pedagogical practices used to support the PTs mathematical development.

4.8. Learning Through Developing MKTT: Noting New Insights into Mathematical Content

We coded data as noting new insights into mathematical content when an intern noted, or a researcher observed an intern expressing, new mathematical insights. As can be seen in Table 3, this code occurred the least frequently among our codes for learning through developing MKTT.

While the mathematical ideas in this course align with grades 1–8 mathematics, we found that our participants (graduate students who have experience teaching secondary and perhaps undergraduate mathematics) gained some new insights into mathematical ideas.

One of Michael’s insights concerned being able to identify the number of factors a number has based on the prime factorization of the number. During a conversation with one of our researchers, Michael talked about his mathematical insights and the researcher included these in his memo.

Michael recognized that students could formulate conjectures simply by observing the behavior of a given set of numbers. A significant revelation for him was the understanding that a prime number raised to the power of x yields a total of (x + 1) factors, two prime numbers with exponents x and y, respectively have a total of (x + 1)(y + 1) factors, etc.—an insight that marked a notable milestone in his learning journey.

(Researcher C, Week 9 Memo)

Another researcher noted that the PTs’ learning to illustrate why a negative integer multiplied by a negative integer equals a positive integer was a new insight for Cameron and John and wrote about it in a memo: “The multiplication and division patterns to show a negative integer multiplied by (or divided by) a negative integer is equal to a positive integer seemed new to the students as well as John and Cameron” (Researcher J, Weeks 5 and 6 Memo).

John noted some mathematical insights in his end-of-the semester reflection:

“I cannot count how many times I’ve had to use the ideas developed in [this course] when doing my [Graph Theory & Combinatorics] course, especially when it came to the probability section. I borrowed ideas such as the Fibonacci sequence, counting techniques, and probability. Most importantly, the Fibonacci sequence I did in … Graph Theory & Combinatorics, was not introduced in the form of rabbits [as it was in the problem solving course for PTs]. So, for me to encounter the sequence in [Graph Theory & Combinatorics] in the form of counting rabbits boosted my understanding of the concept.

(Week 14 Reflection)

We found that our participants learned through developing MKTT by gaining some new insights into the mathematical ideas explored in the course. These new insights were often discussed within our Community of Practice weekly meetings and participants sometimes chose to write about them in their weekly reflections. The focus throughout the course on the mathematical ideas and justification for the relationships we explored engaged our participants in making sense of the mathematics in ways they had not done previously, and they gained some new insights through that engagement.

5. Discussion

Researchers have argued that one way to support PTs to deep mathematical knowledge is to engage them in learning mathematics through problem solving (Masingila et al., 2016a; Schroeder & Lester, 1989). We have proposed that engaging prospective MTEs in supporting PTs to develop this mathematical knowledge through problem solving is also a problem-solving activity for the MTEs. The prospective MTEs are engaged in problem solving as they learn to support PTs’ mathematical development in learning what type of questions to ask, how to support PTs in productive struggle, how to facilitate a class discussion to bring out mathematical ideas that arise through the PTs’ problem solving, etc. Thus, the MTEs are also learning through problem solving and their learning is about supporting PTs’ mathematical and MKT development while the MTEs themselves develop MKTT. We found that within the CoP the novice prospective MTEs exhibited their growth predominately through learning as experience and learning as doing (Wenger, 1998). We found that they indicated their development of MKTT most notably by noting new insights into pedagogical practices and enacting new pedagogical practices.

Some researchers have examined how to prepare prospective MTEs to support PTs’ development (e.g., Sztajn et al., 2006; Van Zoest et al., 2006; Van Zoest & Levin, 2021). Sztajn et al. (2006) designed a summer institute for MTEs that was anchored in a shared experience of observing PTs to provide a “common frame of reference for discussions and debate” (p. 156). In the same way, we have designed our work with prospective MTEs to involve an internship where members of the CoP have a shared experience of observing and working with PTs in a mathematics content course taught through problem solving.

Van Zoest and Levin (2021), in analyzing research studies of MTE development, found a theme in these studies of “the value of collegial reflections on artifacts” (p. 168). These artifacts included (a) personal narratives (e.g., Lovin et al., 2012), (b) artifacts of practice such as mathematical tasks (e.g., Zaslavsky & Leikin, 2004), (c) shared instructional products that are revised as needed based on conversations among the MTEs of the learning outcome data (Morris & Hiebert, 2011), and (d) discussions of differences between MTE practice and mathematics teacher practice (e.g., Van Zoest et al., 2006). Our analysis also brought out the value of collegial reflections on artifacts. We found that our participants drew on CoP discussions of observations of PT work, mathematical tasks and instructor notes used in the course, as well as the readings, in what they wrote in their reflections, said in the interviews, and discussed with CoP members.

Van Zoest et al. (2006), in their study with prospective MTEs in mentored clinical experiences, found that the novice MTEs learned the most through “observing, analyzing, and discussing classroom interactions” (p. 143). Our analysis aligned with this claim as we found our participants mentioned notable instances of individual PT or group learning that provided new insights for the intern about what the PTs were learning, their process of learning, their dispositions toward the problem solving work, and/or connections that the PTs were making among mathematical ideas. Our participants wrote about their observations of the PTs’ learning in their weekly reflections, they talked with other members of the CoP about their observations and mentioned these in the interviews. Their observations were often brought up, analyzed and discussed during the CoP’s twice weekly meetings. We found that the interns’ opportunities to observe and reflect on the PTs’ learning in the context of a mathematics course taught through problem solving was key to their learning as experience and doing.

Van Zoest et al. (2006) recommended having key readings for the prospective MTEs to support their learning. We found that the weekly readings connected the interns to literature on developing mathematical understandings and teaching and learning through problem solving. The readings provided a grounding from which the interns could situate their observations of student learning and the pedagogical strategies they observed and were trying to enact themselves. Since the readings were shared texts in the CoP, ideas from the readings became part of the shared language used by members of the CoP to discuss challenges and developments in students’ understandings. This also prompted the prospective MTEs to make connections with the readings and their new insights into pedagogical practices.

While some researchers have studied the preparation of prospective MTEs, few have investigated preparing prospective MTEs to support PTs in learning mathematics through problem solving (e.g., Masingila et al., 2018; Olanoff et al., 2021). Our study contributes to this area of research by providing evidence of how four novice prospective MTEs experienced, made sense of, and learned how to teach through problem solving in supporting PTs’ mathematical development. In the same way that “prospective teachers need mathematics courses that develop a deep understanding of the mathematics they will teach” (CBMS, 2001, p. 7), MTEs need opportunities that will enable them to develop a deep understanding of the mathematics that they will teach to PTs and support them in understanding mathematical ideas deeply. We argue that one site for prospective MTEs to gain this knowledge and pedagogical skills is through a CoP with experienced and novice MTEs working with PTs in which the novice MTEs have an active role in supporting the PTs. The prospective MTEs develop their MKTT in collaboration with the CoP as the PTs develop their MKT. The prospective MTEs learn how to facilitate (a) student thinking with prompting questions, (b) collaboration as a means of active engagement, (c) PTs’ problem-solving efforts, and to value multiple approaches to solving problems. While it is possible for prospective MTEs to reflect on their teaching alone by observing student learning and examining their own practice, without a CoP and being an active member in the mathematics content course taught through problem solving, there would have been no opportunity to reflect on the actions of others, to receive feedback on their observations and reflections and teaching, or to see other ways of approaching a teaching or learning challenge.

A major contribution of our research is providing a model of how prospective MTEs can develop through a CoP while serving as interns. This CoP, in fact, serves as a pedagogical content methods course for prospective MTEs. We have illustrated how prospective MTEs can be mentored and gain experience in working to support PTs’ mathematical learning through problem solving in a CoP. Further research in this area could examine ways to support prospective MTEs’ developing MTE identities. We note that only one of the four participants in this study self-reported that they viewed themself as an MTE. Escudero-Ávila et al. (2021) wrote that “MTEs’ knowledge should encompass both awareness of how the different skills of the mathematical work of teaching are related and the relationship of these skills with different elements of knowledge or professional identity which are mobilized in putting them into practice” (p. 30). Identity development is complex and multifaceted. Osborn et al. (2021), in their examination of collective identity formation found that the MTEs in their study “formed productive collective identities in layers and in overlapping ways” (p. 260). We envision our future research including a clearer design feature of identity with explicit discussions connecting MTEs’ new knowledge with their developing identity as an MTE. Finally, future research might also explore ways that may specifically support prospective MTEs who are international graduate students and may have mathematics learner experiences that differ from prospective MTEs who are American graduate students.