Digital Resources in Support of Students with Mathematical Modelling in a Challenge-Based Environment
Abstract
1. Introduction
a growing approach in higher education and has been promoted as a means for students to align the acquisition of disciplinary knowledge with the development of transversal competencies while working on authentic and socio-technical societal problems. (…) This flexible approach frames learning with challenges using multidisciplinary actors, technology enhanced learning, multi-stakeholder collaboration and an authentic, real-world focus.(p. 1135)
2. Theoretical Framework
2.1. Challenge-Based Education (CBE)
2.2. Use of Resources and Instrumental Approach
Instrumentalization process can go through different stages: a stage of discovery and selection of the relevant functions, a stage of personalization (one fits the artifact to one’s hand) and a stage of transformation of the artifact, sometimes in directions un-planned by the designer: modification of the task bar, creation of keyboard shortcuts, storage of game programs, automatic execution of some tasks.
2.3. Modelling and Digital Technology
- How can digital resources support students in the early stages of mathematical modelling in a CBE environment?
3. Methodology
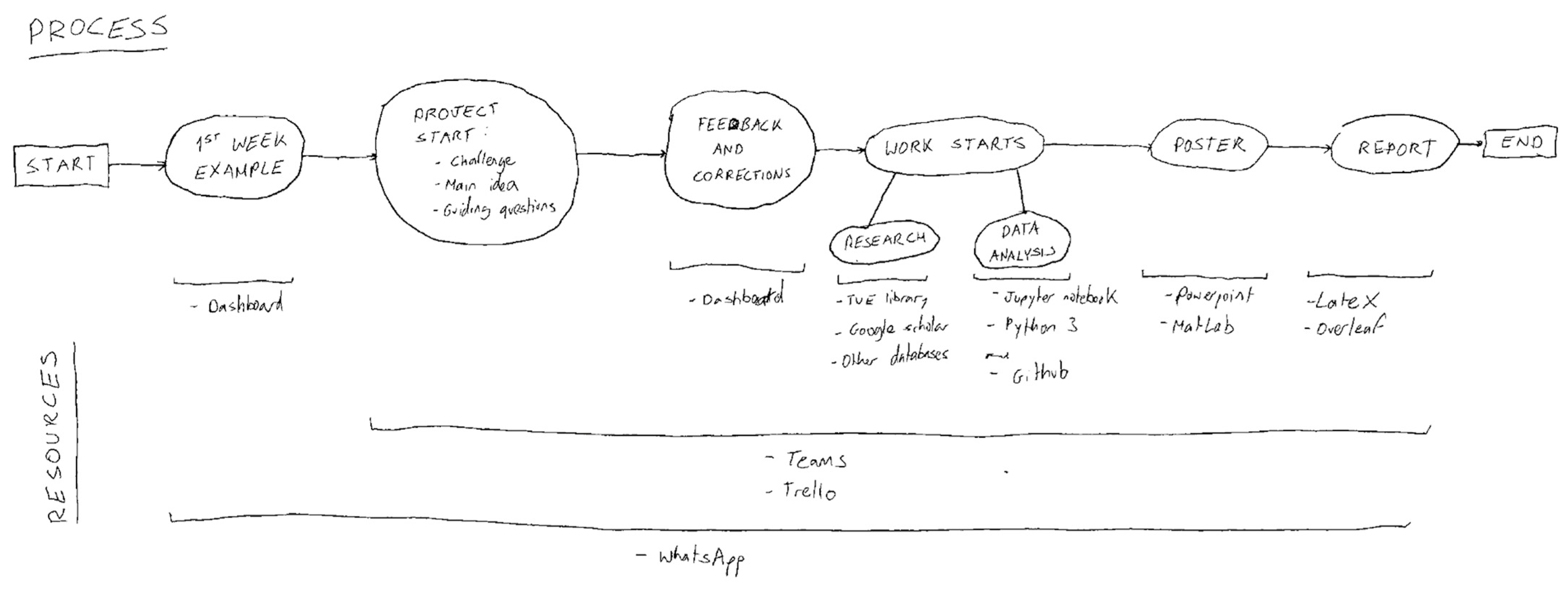
3.1. Context
3.2. Description of the Challenge/Task and the Dashboard
3.3. Data Collection and Data Analysis Strategies
4. Results and Findings
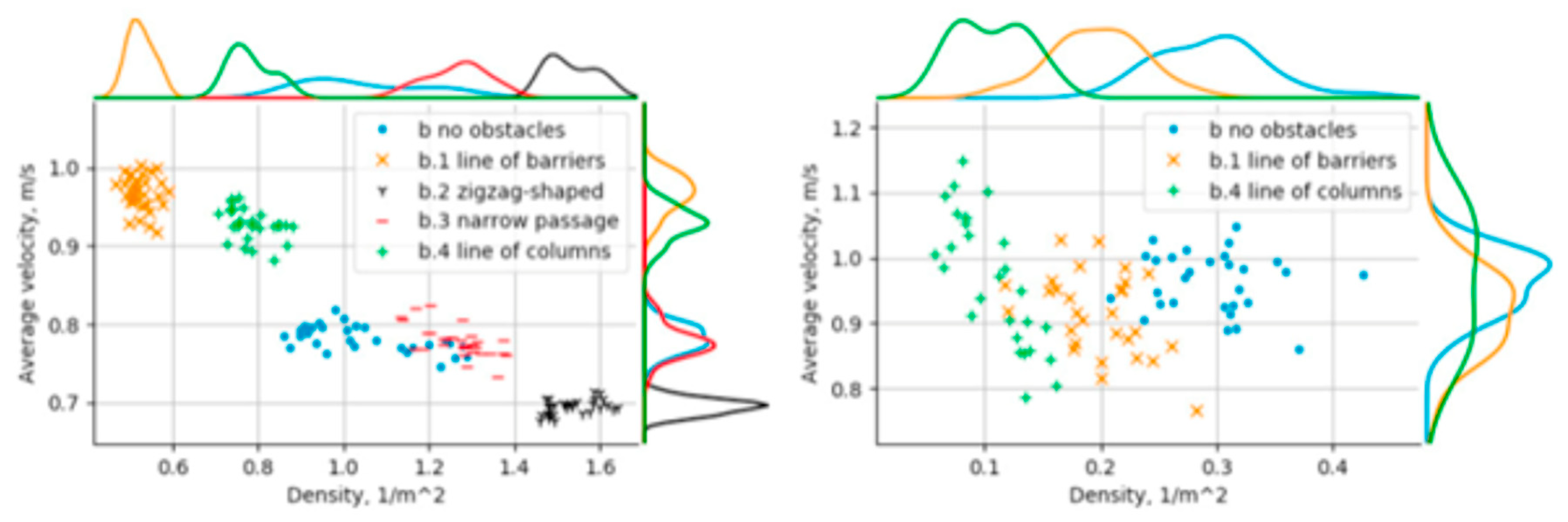
4.1. Team 1
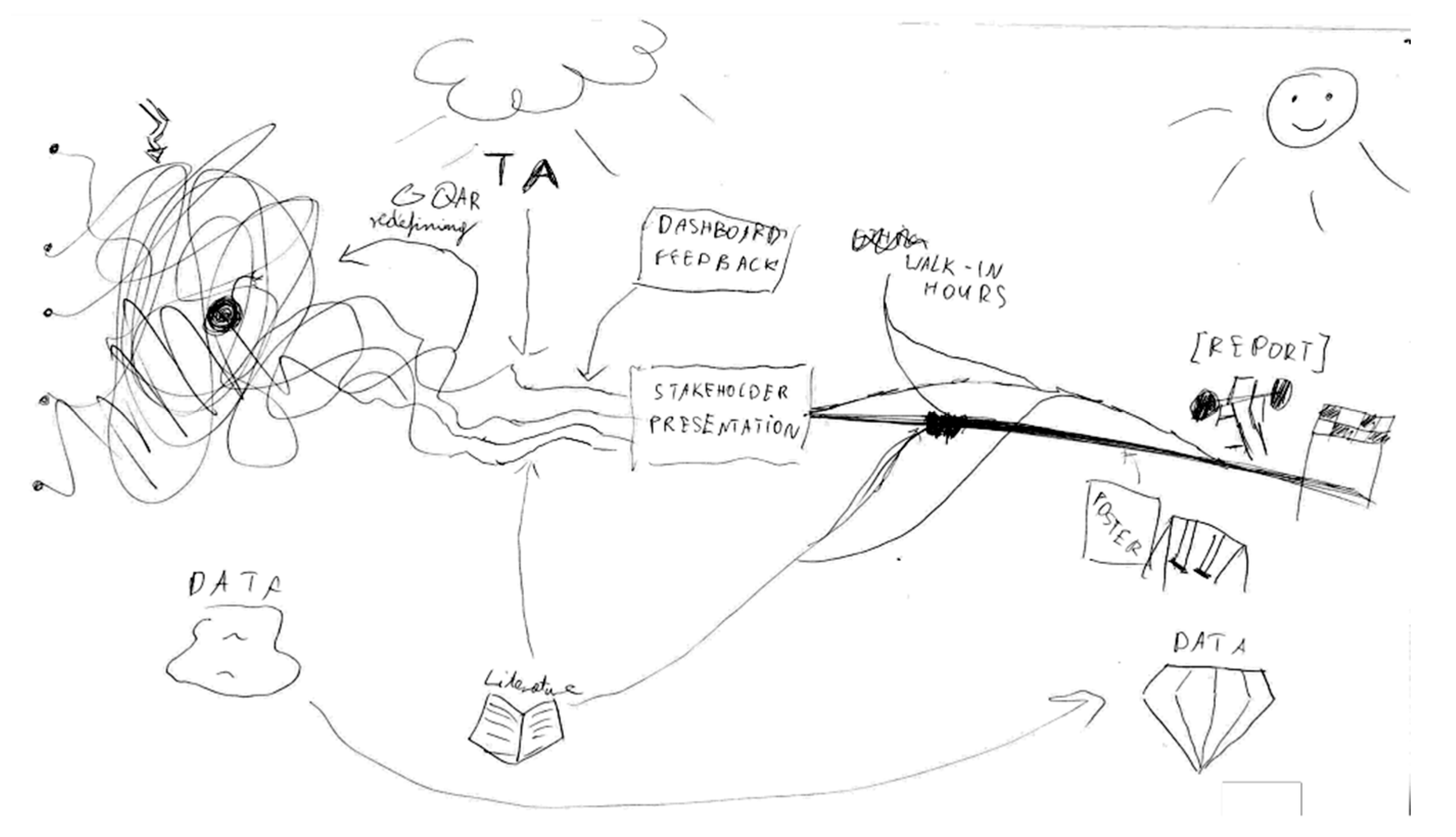
4.1.1. Instrumentation Process Related to the Use of Digital and Other Resources
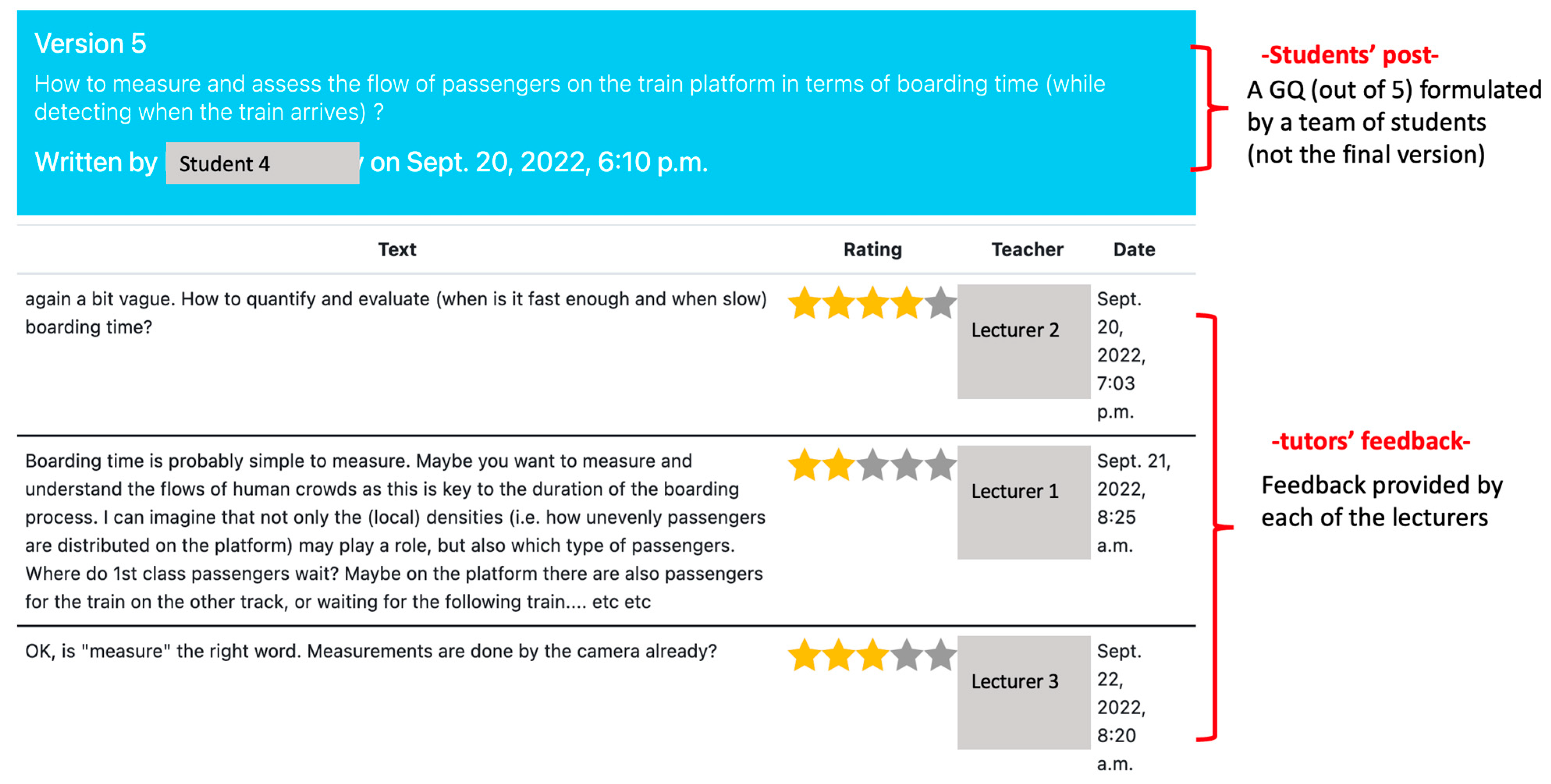
4.1.2. Dashboard-Related Instrumentalization Process
- (1)
- How do we quantitatively define efficiency?
- (2)
- To what extent do present spatial factors (such as columns, fences, etc.) influence the way crowds choose their routes?
- (3)
- What processes are currently a bottleneck to the efficiency at platform 2.1?
- (4)
- What are the trends for pedestrians’ path on platform 2.1 and what are the reasons behind it?
- (5)
- What are improvements in efficiency that can be made?
4.2. Team 2
4.2.1. Instrumentation Process Related to the Use of Digital and Other Resources
4.2.2. Dashboard-Related Instrumentalization Process
- (1)
- How do we find the correlation between dwell time and distribution, and how does this change with the number of people on the platform?
- (2)
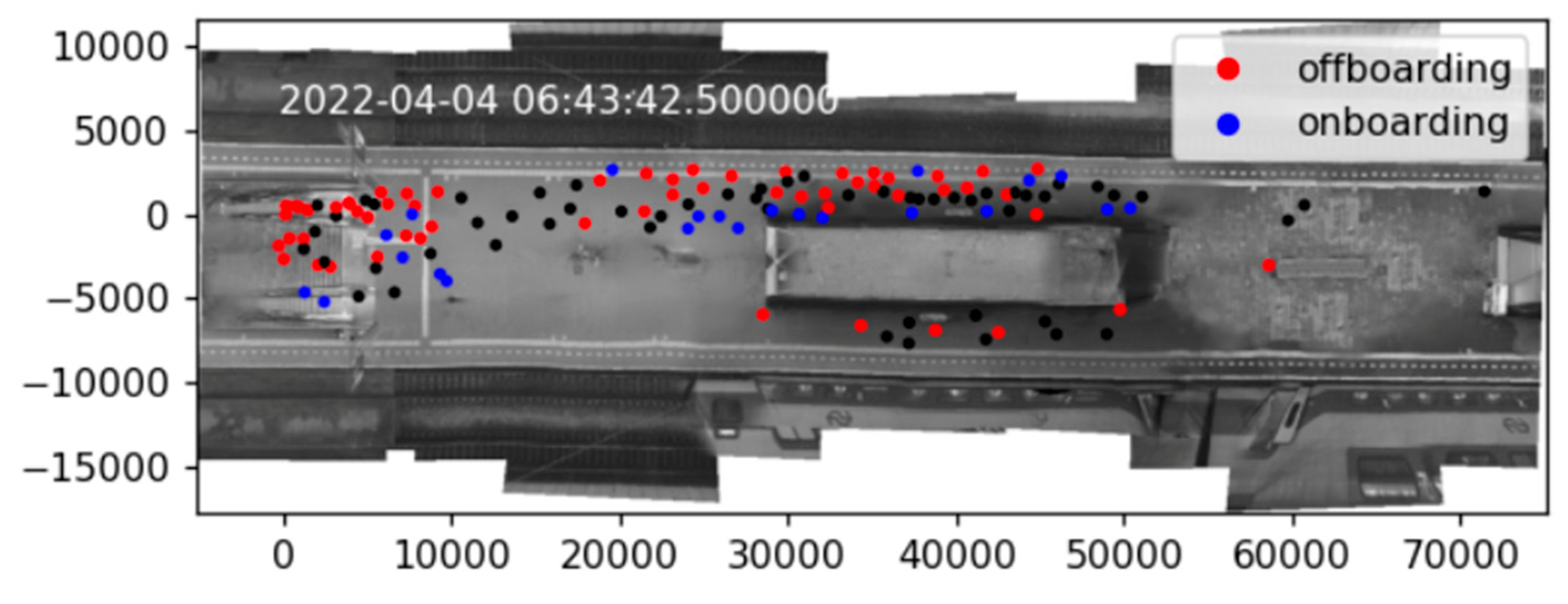
- How to define and measure the flow of (off-)boarding passengers on the train platform, by using the data containing their position in time?
- (3)
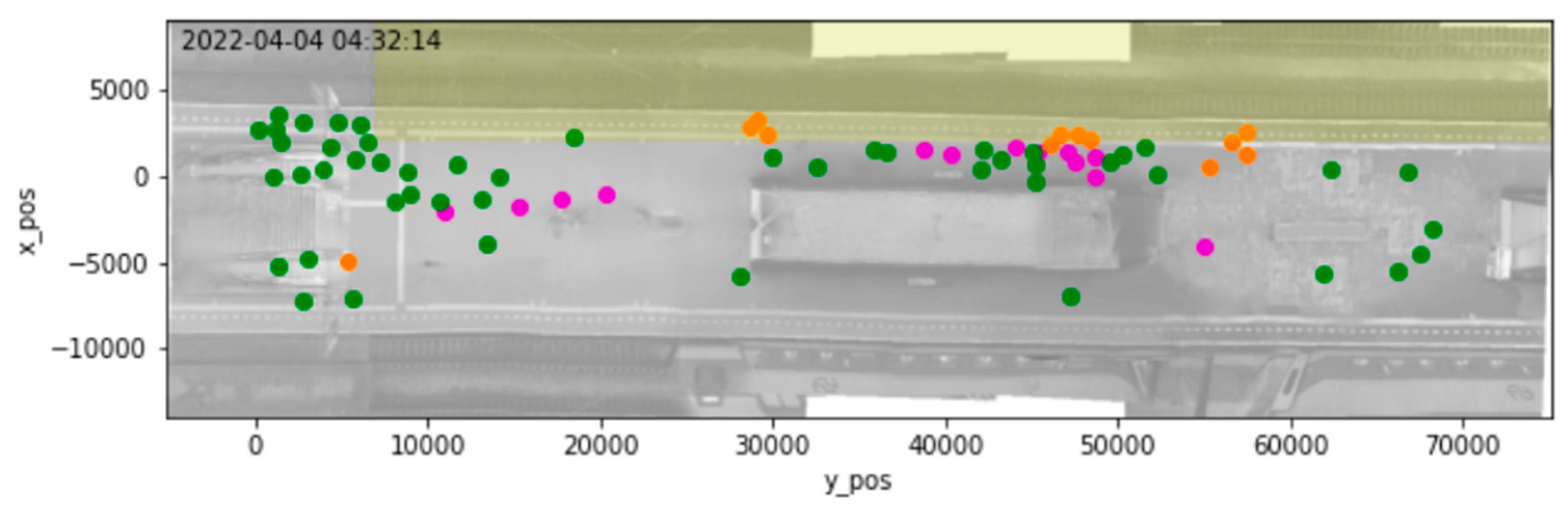
- How to identify the factors that influence passengers’ decision on avoiding/approaching different parts of the station, e.g., benches or trash bins, and how do these factors affect the passenger’s distribution on the platform?
- (4)
- What are the ethical constrains and concepts we have to keep in mind while analyzing the data?
- (5)
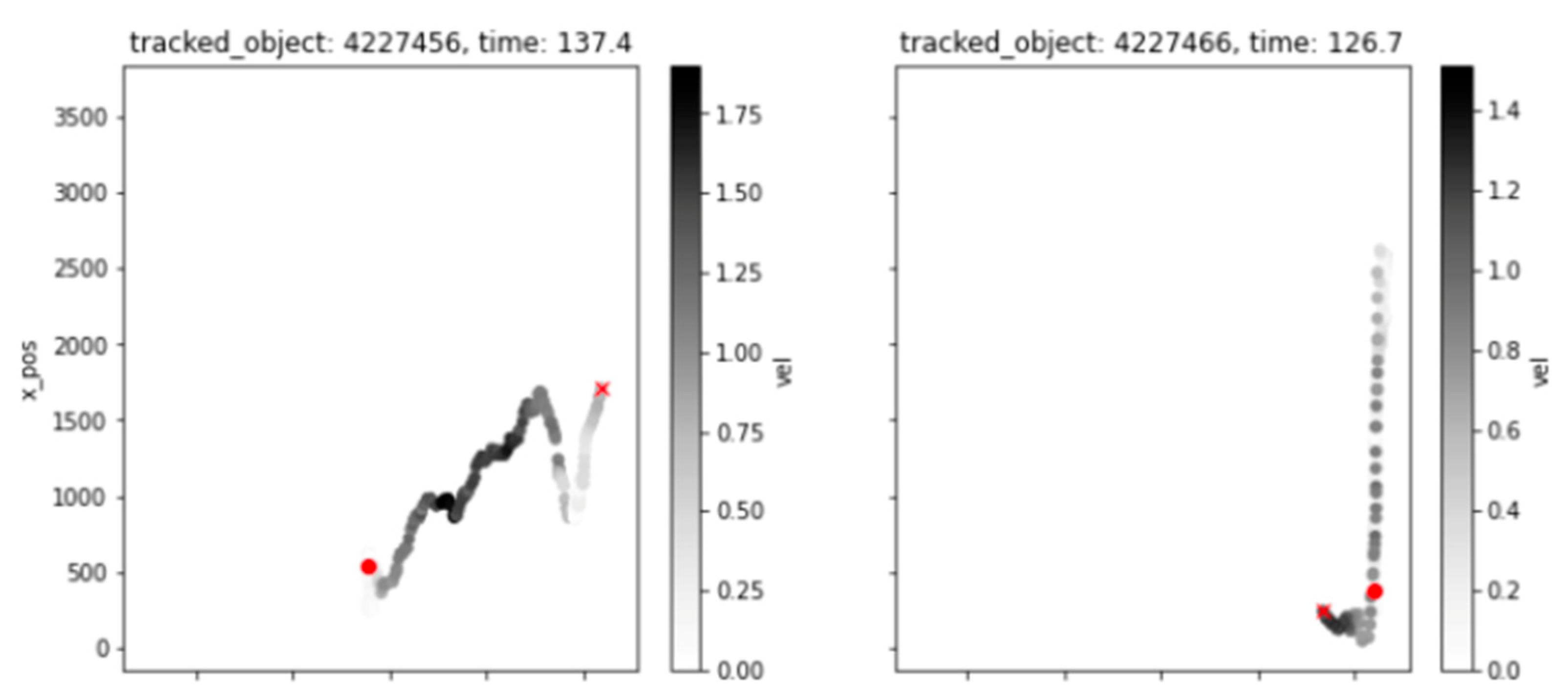
- How do we recognize moments in the data when a train arrives and leaves, to visualize and measure the boarding process?
4.3. The Use of the Dashboard in a CBE Environment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CBE | Challenge-Based Education |
| SRRS | Schematic Representation of Resource System |
| TA | teaching assistant |
| DCR | digital curriculum resource |
References
- Abassian, A., Safi, F., Bush, S., & Bostic, J. (2019). Five different perspectives on mathematical modeling in mathematics education. Investigations in Mathematics Learning, 12(1), 53–65. [Google Scholar] [CrossRef]
- Artigue, M. (2002). Learning mathematics in a CAS environment: The genesis of a reflection about Instrumentation and the dialectics between technical and conceptual work. International Journal of Computers for Mathematical Learning 7, 245–274. [Google Scholar] [CrossRef]
- Blum, W., & Borromeo Ferri, R. (2009). Mathematical modelling: Can it be taught and learnt? Journal of Mathematical Modelling and Application, 1(1), 45–58. Available online: https://eclass.uoa.gr/modules/document/file.php/MATH601/3rd%20%26%204rth%20unit/3rd%20unit_Modelling%20cycle.pdf (accessed on 26 August 2025).
- Blum, W., & Leiss, D. (2007). How do students and teachers deal with modelling problems? In C. Haines, P. Galbraith, W. Blum, & S. Khan (Eds.), Mathematical modelling: Education, engineering and economics-ICTMA 12 (pp. 222–231). Chichester. [Google Scholar]
- Borba, M. de C., & Villarreal, M. E. (2005). Humans-with-media and the reorganization of mathematical thinking. Springer. [Google Scholar] [CrossRef]
- Conde, M. Á., García-Peñalvo, F. J., Fidalgo-Blanco, Á., & Sein-Echaluce, M. L. (2017). Can we apply learning analytics tools in challenge based learning contexts? In Learning and collaboration technologies. Technology in education: 4th international conference, LCT 2017, held as part of HCI international 2017, Vancouver, BC, Canada, July 9–14, 2017, Proceedings, Part II 4 (pp. 242–256). Springer International Publishing. [Google Scholar]
- Dahl, B. (2018). What is the problem in problem-based learning in higher education mathematics. European Journal of Engineering Education, 43(1), 112–125. [Google Scholar] [CrossRef]
- Deemer, P., Benefield, G., Larman, C., & Vodde, B. (2013). The SCRUM primer. [PDF]. Available online: http://www.brianidavidson.com/agile/docs/scrumprimer121.pdf (accessed on 23 June 2023).
- Doulougeri, K., Bombaerts, G., Martin, D., Watkins, A., Bots, M., & Vermunt, J. D. (2022, March 28–31). Exploring the factors influencing students’ experience with challenge-based learning: A case study. 2022 IEEE Global Engineering Education Conference (EDUCON) (pp. 981–988), Tunisia, North Africa. [Google Scholar] [CrossRef]
- Elicer, R., & Tamborg, A. L. (2022). Nature of the relations between programing and computational thinking and mathematics in Danish teaching resources. In U. T. Jankvist, R. Elicer, A. Clark-Wilson, H.-G. Weigand, & M. Thomsen (Eds.), Proceedings of the 15th international conference on technology in mathematics teaching (ICTMT 15) (pp. 45–52). Aarhus University. [Google Scholar]
- Gallagher, S. E., & Savage, T. (2020). Challenge-based learning in higher education: An exploratory literature review. Teaching in Higher Education, 28(6), 1135–1157. [Google Scholar] [CrossRef]
- Gaskins, W. B., Johnson, J., Maltbie, C., & Kukreti, A. R. (2015). Changing the Learning environment in the college of engineering and applied science using challenge based learning. International Journal of Engineering Pedagogy, 5(1), 33–41. [Google Scholar] [CrossRef]
- Gueudet, G., & Pepin, B. (2018). Didactic Contract at the Beginning of University: A Focus on Resources and their Use. International Journal of Research in Undergraduate Mathematics Education, 4, 56–73. [Google Scholar] [CrossRef]
- Järvelä, S., Kirschner, P. A., Panadero, E., Malmberg, J., Phielix, C., Jaspers, J., Koivuniemi, M., & Järvenoja, H. (2015). Enhancing socially shared regulation in collaborative learning groups: Designing for CSCL regulation tools. Educational Technology Research and Development, 63, 125–142. [Google Scholar] [CrossRef]
- Kynigos, C. (2022). Embedding mathemathics in socio-scientific games: The case of the mathematical in grappling with wicked problems. In U. T. Jankvist, R. Elicer, A. Clark-Wilson, H.-G. Weigand, & M. Thomsen (Eds.), Proceedings of the 15th international conference on technology in mathematics teaching (ICTMT 15) (pp. 11–28). Aarhus University. [Google Scholar]
- Leijon, M., Gudmundsson, P., Staaf, P., & Christersson, C. (2021). Challenge based learning in higher education—A systematic literature review. Innovations in Education and Teaching International, 59(5), 609–618. [Google Scholar] [CrossRef]
- Malmqvist, J., Rådberg, K. K., & Lundqvist, U. (2015). Comparative analysis of challenge-based learning experiences. In CDIO (Ed.), Proceedings of the 11th international CDIO conference (Vol. 8, pp. 87–94). Chengdu University of Information Technology. [Google Scholar]
- Mayring, P. (2015). Qualitative content analysis: Theoretical background and procedures. In A. Bikner-Ahsbahs, C. Knipping, & N. Presmeg (Eds.), Approaches to qualitative research in mathematics education: Examples of methodology and methods (pp. 365–380). Springer. [Google Scholar] [CrossRef]
- Membrillo-Hernández, J., J. Ramírez-Cadena, M., Martínez-Acosta, M., Cruz-Gómez, E., Muñoz-Díaz, E., & Elizalde, H. (2019). Challenge based learning: The importance of world-leading companies as training partners. International Journal on Interactive Design and Manufacturing (IJIDeM), 13(3), 1103–1113. [Google Scholar] [CrossRef]
- Misfeldt, M., Jankvist, U. T., Geraniou, E., & Bråting, K. (2020). Relations between mathematics and programming in school: Juxtaposing three different cases. In A. Donevska-Todorova, E. Faggiano, J. Trgalova, Z. Lavicza, R. Weinhandl, A. Clark-Wilson, & H.-G. Weigand (Eds.), Proceedings of the 10th ERME topic conference on mathematics education in the digital era, MEDA 2020 (pp. 255–262). Johannes Kepler University. [Google Scholar]
- Molina-Toro, J. F., Rendón-Mesa, P. A., & Villa-Ochoa, J. (2019). Research trends in digital technologies and modeling in mathematics education. EURASIA Journal of Mathematics, Science and Technology Education, 15(8), em1736. [Google Scholar] [CrossRef] [PubMed]
- Niss, M., & Blum, W. (2020). The learning and teaching of mathematical modelling. Routledge. [Google Scholar]
- Niss, M., & Højgaard, T. (2019). Mathematical competencies revisited. Educational Studies in Mathematics, 102(1), 9–28. [Google Scholar] [CrossRef]
- Pepin, B., Biehler, R., & Gueudet, G. (2021). Mathematics in Engineering Education: A Review of the Recent Literature with a View towards Innovative Practices. International Journal of Research in Undergraduate Mathematics Education, 7(2), 163–188. [Google Scholar] [CrossRef]
- Pepin, B., Choppin, J., Ruthven, K., & Sinclair, N. (2017a). Digital curriculum resources in mathematics education: Foundations for change. ZDM Mathematics Education, 49(5), 645–661. [Google Scholar] [CrossRef]
- Pepin, B., & Kock, Z. (2021). Students’ Use of Resources in a Challenge-Based Learning Context Involving Mathematics. International Journal of Research in Undergraduate Mathematics Education, 7(2), 306–327. [Google Scholar] [CrossRef]
- Pepin, B., Xu, B., Trouche, L., & Wang, C. (2017b). Developing a deeper understanding of mathematics teaching expertise: Chinese mathematics teachers’ resource systems as windows into their work and expertise. Educational studies in Mathematics, 94(3), 257–274. [Google Scholar] [CrossRef]
- Rabardel, P., & Bourmaud, G. (2003). From computer to instrument system: A developmental perspective. Interacting with Computers, 15(5), 665–691. [Google Scholar] [CrossRef]
- Smith, R. C., Bossen, C., Dindler, C., & Sejer Iversen, O. (2020, June 15–20). When participatory design becomes policy: Technology comprehension in Danish education. 16th Participatory Design Conference 2020—Participation(s) Otherwise (Vol. 1, pp. 148–158), Manizales, Colombia. [Google Scholar] [CrossRef]
- Soares, D. d. S., & Borba, M. d. C. (2014). The role of software Modellus in a teaching approach based on model analysis. ZDM Mathematics Education, 46(4), 575–587. [Google Scholar] [CrossRef]
- Stake, R. E. (1995). The art of case study research. SAGE Publications. [Google Scholar]
- Toschi, F., Gabbana, A., Lazendic-Galloway, J., Boonacker-Dekker, A., & Vervuurt, Y. (2023). Designing a learning dashboard to facilitate project development and teamwork in a CBL physics course. In A. Guerra, J. Chen, R. Lavi, L. Bertel, & E. Lindsay (Eds.), Transforming Engineering Education (pp. 178–182). Aalborg Universitetsforlag. [Google Scholar]
- Trouche, L. (2004). Managing the complexity of human/machine interactions in computerized learning environments. International Journal of Computers for Mathematical Learning, 9(3), 281–307. [Google Scholar] [CrossRef]
- van den Beemt, A., van de Watering, G., & Bots, M. (2022). Conceptualising variety in challenge-based learning in higher education: The CBL-compass. European Journal of Engineering Education, 48(1), 24–41. [Google Scholar] [CrossRef]
- van Uum, M. S. J., & Pepin, B. (2022). Students’ self-reported learning gains in higher engineering education. European Journal of Engineering Education, 1–17. [Google Scholar] [CrossRef]
- Vergnaud, G. (1998). Toward a cognitive theory of practice. In A. Sierpinska, & J. Kilpatrick (Eds.), Mathematics education as a research domain: A search for identity (pp. 227–240). Kluwer. [Google Scholar] [CrossRef]
- Vérillon, P., & Rabardel, P. (1995). Artefact and cognition: A contribution to the study of thought in relation to instrumented activity. European Journal of Psychology in Education, 10(1), 77–101. [Google Scholar] [CrossRef]
- Villa-Ochoa, J. A., González-Gómez, D., & Carmona-Mesa, J. A. (2018). Modelling and technology in the study of the instantaneous rate of change in mathematics [Modelación y tecnología en el estudio de la tasa de variación instantánea en matemáticas]. Formación Universitaria, 11(2), 25–34. [Google Scholar] [CrossRef]
- Vreman-de Olde, C., Van Der Meer, F., Van Der Voort, M., Torenvlied, R., Kwakman, R., Goudsblom, T., Zeeman, M. J., & Damoiseaux, P. (2021). Challenge based learning @ UT: Why, what, how (pp. 1–9). University of Twente. Available online: https://www.utwente.nl/en/cbl/documents/seg-innovation-of-education-challenge-based-learning.pdf (accessed on 26 August 2025).
- Yazan, B. (2015). Three approaches to case study methods in education: Yin, merriam, and stake. The Qualitative Report, 20(2), 134–152. [Google Scholar] [CrossRef]
- Yin, R. K. (2002). Case study research: Design and methods. SAGE Publications. [Google Scholar]
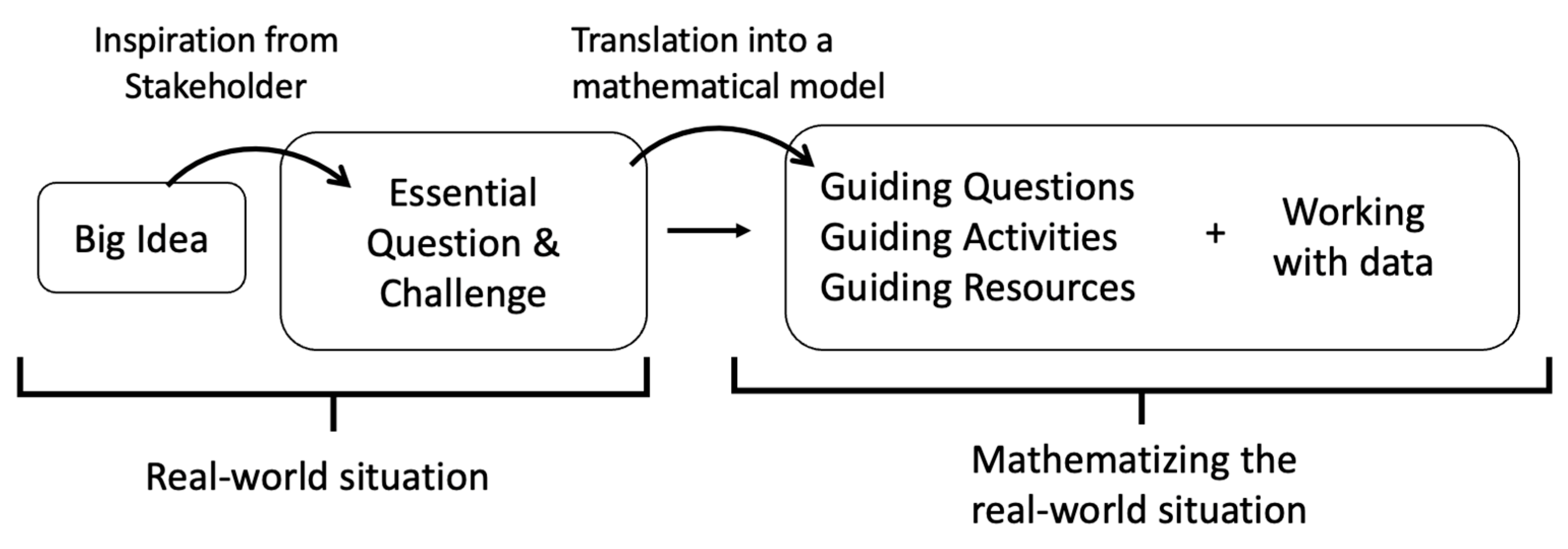

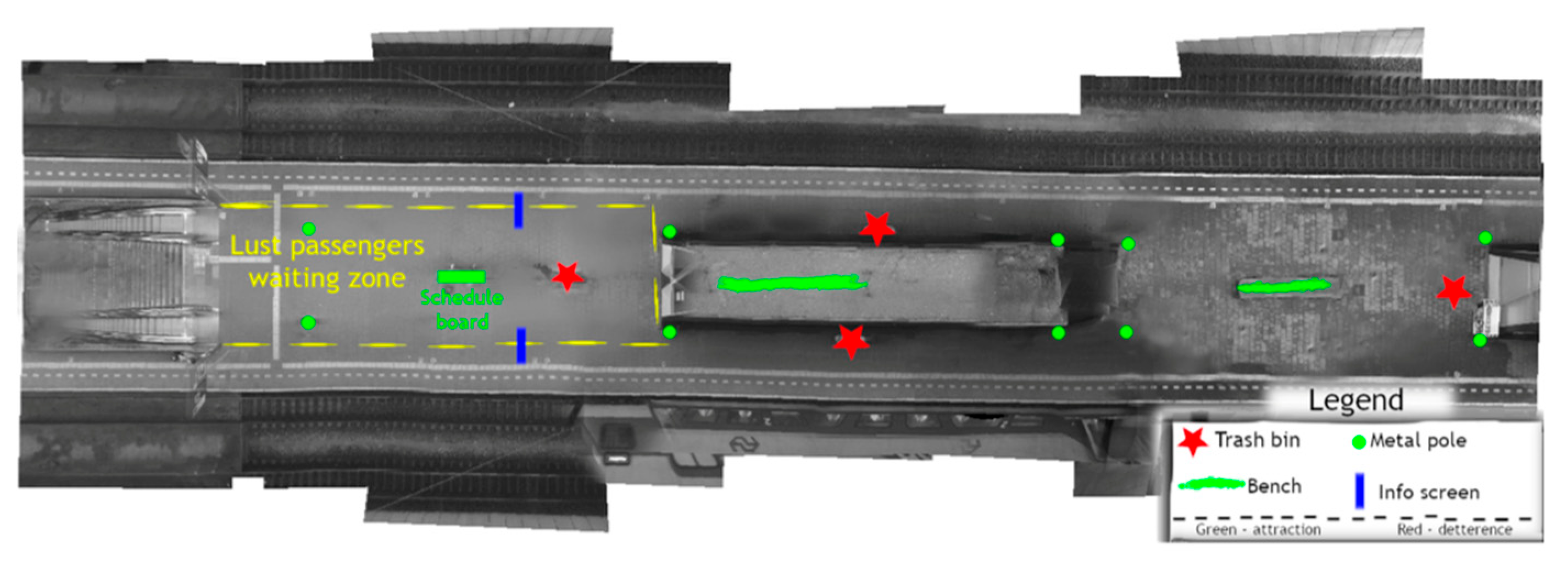
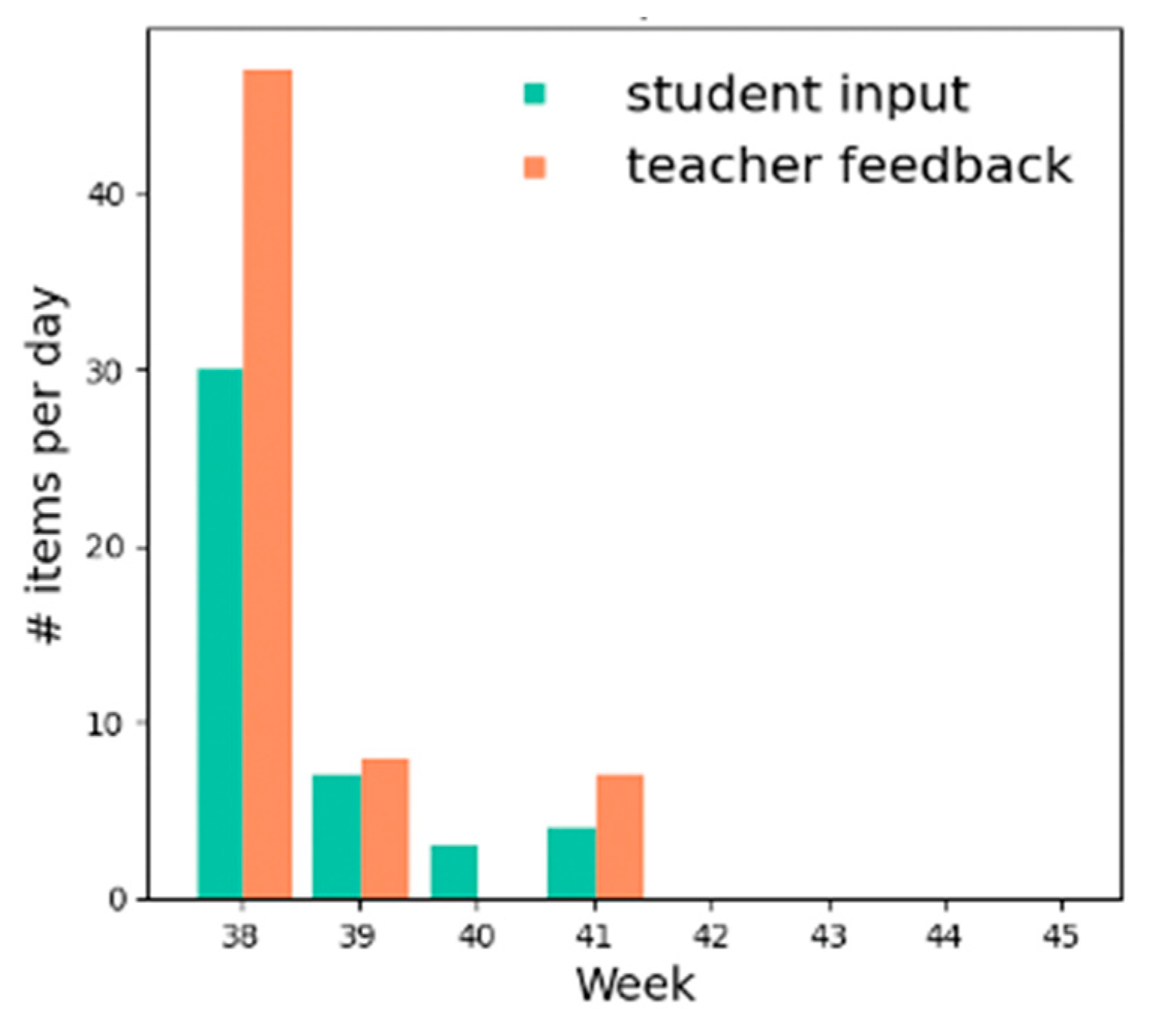
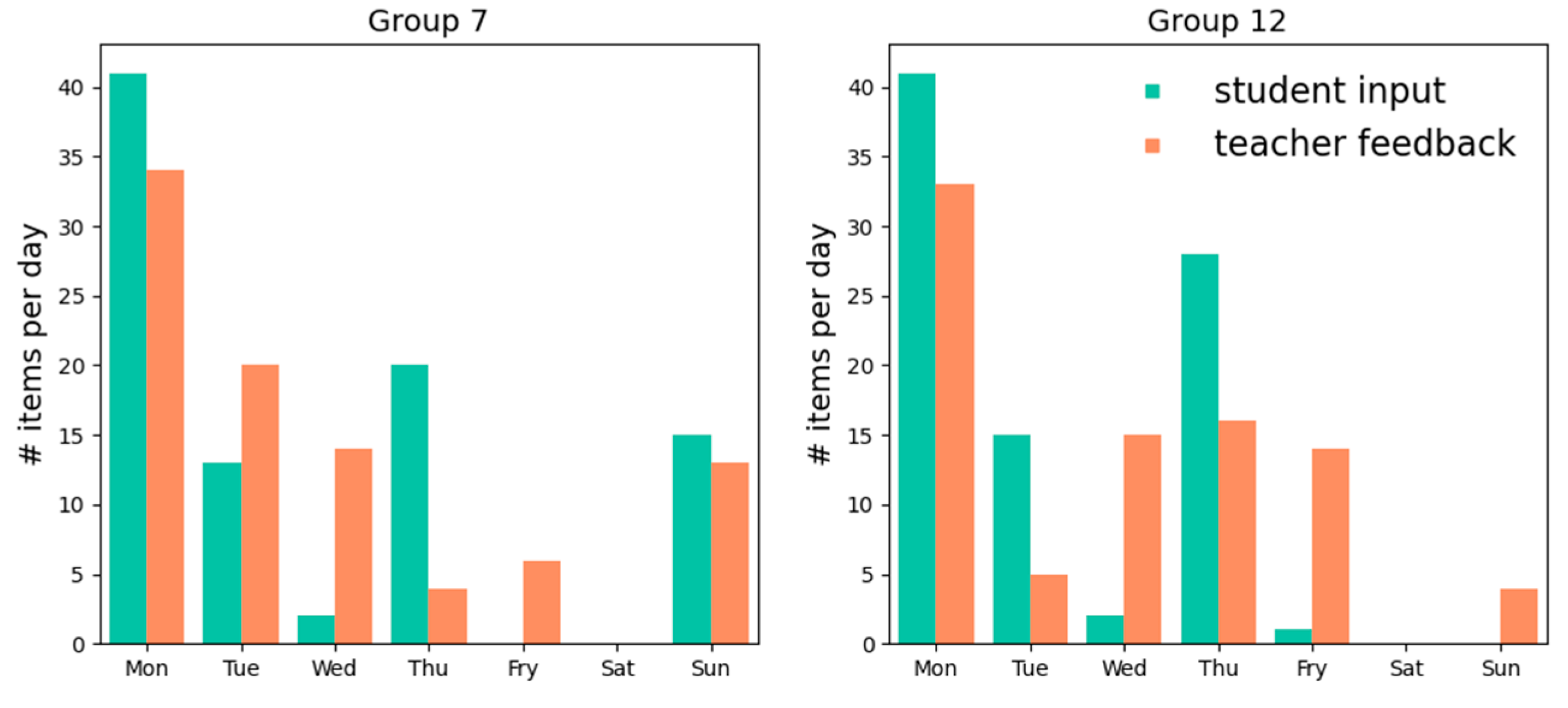
| Team 1 | Team 2 | |
|---|---|---|
| Big Idea | Efficiency | The flow of human crowds—efficiency |
| Essential Question | How can efficiency on the platforms be improved by influencing pedestrians’ routing decisions (choice of route from A to B and choice of B)? | How to improve the efficiency of the boarding process? |
| Challenge | Improve efficiency on the platforms by influencing pedestrians’ routing decisions. | Design methods to optimally (not necessarily homogeneously) distribute passengers on a train platform to improve the boarding time. |
| Data Sources | Data Collection Methods |
|---|---|
| Students: 2 teams of 5 students each | Observations, group interviews, Schematic Representation of Resource Systems (drawings), student products (presentations, poster, and final report) |
| Tutors: 3 lectures and 2 TAs (one per team) | Observation, interviews |
| Dashboard | Student posts, tutor feedback |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salinas-Hernández, U.; Kock, Z.-j.; Pepin, B.; Gabbana, A.; Toschi, F.; Lazendic-Galloway, J. Digital Resources in Support of Students with Mathematical Modelling in a Challenge-Based Environment. Educ. Sci. 2025, 15, 1123. https://doi.org/10.3390/educsci15091123
Salinas-Hernández U, Kock Z-j, Pepin B, Gabbana A, Toschi F, Lazendic-Galloway J. Digital Resources in Support of Students with Mathematical Modelling in a Challenge-Based Environment. Education Sciences. 2025; 15(9):1123. https://doi.org/10.3390/educsci15091123
Chicago/Turabian StyleSalinas-Hernández, Ulises, Zeger-jan Kock, Birgit Pepin, Alessandro Gabbana, Federico Toschi, and Jasmina Lazendic-Galloway. 2025. "Digital Resources in Support of Students with Mathematical Modelling in a Challenge-Based Environment" Education Sciences 15, no. 9: 1123. https://doi.org/10.3390/educsci15091123
APA StyleSalinas-Hernández, U., Kock, Z.-j., Pepin, B., Gabbana, A., Toschi, F., & Lazendic-Galloway, J. (2025). Digital Resources in Support of Students with Mathematical Modelling in a Challenge-Based Environment. Education Sciences, 15(9), 1123. https://doi.org/10.3390/educsci15091123








