Abstract
Extraneous details in visual representations can prompt children to use well-rehearsed, yet inappropriate, strategies that can hinder mathematics learning. Prior domain knowledge can reduce the negative effects of extraneous details in instructional materials. The present study tested whether prior knowledge of fractions and instruction on measurement division (MD) could overcome children’s inappropriate counting strategies when solving fraction division problems with images of LEGO® bricks. Fourth and fifth graders (N = 39) were randomly assigned to two instructional conditions: one that demonstrated how to solve fraction division problems using LEGO bricks that included explanations on MD concepts, and the other with the same demonstrations but without explanations. All participants then completed a task that measured whether the studs on the bricks prompted inappropriate counting when solving the problems. Almost one-third of the sample counted the studs to some degree. Greater prior knowledge of fractions concepts and knowledge of how to represent fractions with LEGO bricks were related to fewer inappropriate counting strategies, but contrary to expectations, fraction magnitude was not related. The two conditions did not differ on participants’ counting strategies. Extraneous details on LEGO bricks are related to the application of well-practiced counting strategies for children with lower domain knowledge.
1. Introduction
Visual representations are commonly used in the teaching of mathematics (Bolden et al., 2015; Schraw et al., 2013) because they can help students assign meaning to the concepts being taught (Rau, 2017b; Schoenherr & Schukajlow, 2024). Various factors influence the impact of visual representations on learning, including the extent to which their perceptual features are relevant to the target concept (Belenky & Schalk, 2014; Glenberg et al., 2013; Goldstone & Son, 2005; Kaminski et al., 2009) and the amount of prior domain knowledge the learner possesses (Cook, 2006; Cooper et al., 2018). Our research aims to investigate the impact of visual representations of LEGO® bricks on children’s learning of fraction division. LEGO bricks can be used to capture children’s interest in mathematics (Lenzner et al., 2013; Moyer, 2001), but they possess perceptual features, such as the studs (i.e., the cylindrical bumps that attach the bricks together), that may not be relevant to the target concepts. Tellos and Osana (2025) found that the studs on images of LEGO bricks prompted fifth and sixth graders to use inappropriate strategies on fraction division problems. In particular, some students inappropriately used the studs instead of the bricks as units to solve the problems, which, in some cases, negatively impacted their problem-solving performance.
Despite recent research on the effects of perceptual features in visual representations on learning (Kaminski & Sloutsky, 2013, 2020; Menendez et al., 2020), questions about how prior domain knowledge influences the effects of perceptual features on LEGO bricks, which have become increasingly popular for mathematics instruction within the educational community (Kidspot, 2016; TheDadLab, 2019, 2020; We Are Teachers, 2018), remain unanswered. Therefore, the first objective of the present study was to extend the research conducted by Tellos and Osana (2025) on the extent to which the studs in visual representations of LEGO bricks prompt inappropriate strategies in the context of fraction division. The second objective was to contribute to current understandings of how prior domain knowledge impacts children’s response to materials that contain irrelevant perceptual features. Specifically, in this study, we aimed to investigate the role of prior knowledge in children’s strategies when solving fraction division problems with LEGO bricks.
1.1. Visual Representations in Fraction Division
A meaningful explanation of fraction division involves measurement division concepts, specifically, determining how many times the divisor fits into the dividend (Barnett-Clarke et al., 2011; Gregg & Gregg, 2007). In the context of measurement division, the divisor is conceptualized as a unit of measure to determine the size of the dividend (Zembat, 2017). In elementary mathematics instruction, however, fraction division is frequently taught using the “flip and multiply” algorithm, often without presenting associated concepts that explain why the algorithm works (Olanoff et al., 2014). To address this typical shortcoming in the teaching of fraction division, teacher educators have recommended the use of visual representations (e.g., bar diagrams) to enhance students’ understanding of measurement division concepts when learning fraction division (Barnett-Clarke et al., 2011; Reys et al., 2015). Both physical LEGO bricks and images of bricks can serve as useful visual tools in this context (e.g., Tellos & Osana, 2025; TheDadLab, 2019). LEGO bricks can depict the whole, the dividend fraction, and the divisor fraction, facilitating the process of determining how many times a divisor brick can be stacked onto a dividend brick to reach a solution. In an exploratory study, Tellos and Osana (2025) provided instruction to fifth- and sixth-grade students on how to use images of LEGO bricks to solve fraction division problems (e.g., 1/4 ÷ 1/16 =). An error analysis suggested that 18% of the sample inappropriately counted the studs on the bricks rather than the bricks themselves, which may have been one of the reasons they had difficulty applying concepts of measurement division on a transfer task administered after the instruction.
1.2. Extraneous Details in Visual Representations
Visual representations used to teach mathematics often include perceptual details that are not directly related to the to-be-learned concept (Belenky & Schalk, 2014; Kaminski & Sloutsky, 2013). Such perceptual details have been referred to as “extraneous” (Kaminski & Sloutsky, 2013). In teaching fractions to children, teachers have a strong preference for using images of real-world items, such as pizzas and cookies (Kaminski & Sloutsky, 2020). Many such representations include irrelevant perceptual information, such as pepperonis and chocolate chips that have been shown to impede learning and transfer (Kaminski & Sloutsky, 2013; Macevicius & Osana, 2024). Consistent with the cognitive load theory, extraneous information can overwhelm learners, leaving fewer cognitive resources to attend to the task (Sweller et al., 2011). Further, extraneous details in visual representations can prompt learners to activate inappropriate schemas that are then used to erroneously interpret the information in representations (Harp & Mayer, 1998). Interpretations based on the extraneous information can, in turn, disrupt learning and transfer (Mayer, 2019; Rey, 2012; Son & Goldstone, 2009).
Researchers have observed young children using inappropriate counting schemas when presented with instructional materials that contain extraneous details that are presented in the form of discrete elements. Shipley and Shepperson (1990) presented children aged 3 to 7 years with arrays of identical images of forks that were either intact or spatially detached (e.g., prongs and handle). When asked how many forks there were, children often inappropriately counted the separated parts as distinct, countable objects. In other words, children tended to treat spatially separated elements as individual units, suggesting that perceptual cues, such as spacing, may reinforce object-by-object enumeration as a default strategy. In another study, Wege et al. (2023) asked 4- and 5-year-old children to sort animal toys (i.e., discrete objects) by color (e.g., brown, pink) and kind (e.g., horses, pigs), and to count the number of sets they created. The results revealed that some children struggled to count the grouped sets of animals as units and instead counted the individual animals within each set.
With school-aged children, Kaminski and Sloutsky (2013) provided instruction to kindergartners, first graders, and second graders on how to use the y-axis to read quantities in bar graphs. They found that when the bars in the graphs contained extraneous images of shoes and flowers, children inappropriately counted the images in the bars instead of using the y-axis to read the quantities represented. In the context of fractions more specifically, Kaminski and Sloutsky (2020) asked first graders to write a fraction symbol that corresponded to shaded portions of circular area models, some of which were generic grey circles and others were images of pizzas with extraneous details (e.g., pepperonis, mushrooms). Children who used the representations of pizzas with extraneous details tended to focus only on the number of slices present (i.e., the numerator), suggesting that they emphasized counting the slices rather than thinking relationally about fractional quantities. Together, these findings suggest that children’s inclination to count individual elements may be a perceptually-driven response to the discrete nature of the items and that spatial separation encourages children to perceive elements—such as studs on LEGO bricks—as countable, even when appropriate group-based strategies may be more accurate or efficient.
Children’s early numeracy experiences in the home and in educational contexts frequently involve object-by-object counting (Clements & Sarama, 2007). For this reason, the tendency for children to count discrete elements in representations may be traced back to their early educational experiences. Children’s initial encounters with numbers are shaped by mathematical tasks that center around individual object counting, which establishes a strong association between numerical value and physical items in their environment (Alibali & DiRusso, 1999; Graham, 1999). Early instruction typically emphasizes one-to-one correspondences between each individual item and a number word in the counting sequence (Mix, 2008), which then creates a well-rehearsed routine on which children repeatedly rely when faced with counting tasks (Mix, 2008; Sophian, 2008). Thus, when teachers use concrete and visual representations to teach mathematical concepts, children can default to counting perceptual details, even when the details are extraneous to the learning objective.
The impulse to attend to discrete elements in instructional materials appears to persist in later elementary years when children are introduced to multiplicative concepts in the mathematics curriculum (Fitzpatrick & Hallett, 2019). In one study, Tellos and Osana (2024) presented children with multiplication expressions (e.g., 2 × 5) and asked the children to rate the extent to which visual displays of LEGO bricks represented the expressions. The authors found that 8-year-olds attended to the studs in their ratings more so than 10-year-olds, who more often used entire bricks when rating the visual displays. In another study, Jeong et al. (2007) compared the influence of discrete and continuous visual representations of quantities on the proportional reasoning of children aged 6 to 10 years. Participants were shown circular spinners with red and blue regions representing different proportions. In one condition, both regions were presented as undivided areas, whereas in the other condition, the regions were divided into equal partitions that could be individually counted but would result in the incorrect solution. The results demonstrated that the children used more appropriate strategies when reasoning with the undivided regions than the divided ones. Similar findings were reported by Boyer et al. (2008), who found that children between kindergarten and the fourth grade counted discrete partitions in images of juice mixtures instead of correctly identifying and applying the underlying ratios in the mixtures. Collectively, these studies highlight that the tendency to count discrete elements in visual representations—while rooted in early mathematical experience—can persist into later childhood, and that extraneous details in the form of discrete quantities may continue to prompt inappropriate counting strategies, possibly hindering children’s ability to grasp more advanced mathematical concepts.
In sum, discrete extraneous details in visual representations can prompt children to fall back on familiar, yet inappropriate, counting strategies that can deflect attention away from the underlying mathematical structure. An example of an inappropriate counting strategy would be using the studs on the LEGO bricks as units to solve certain measurement division problems. The tendency to count objects highlights how easily children’s attention can be drawn to extraneous details, even in mathematical tasks where counting individual items is not relevant. In the context of fraction division with LEGO bricks, for instance, learners’ attention may be drawn to perceptual details on the bricks, such as the individual studs, that in some cases may be irrelevant to the solution.
1.3. Prior Domain Knowledge
Factors beyond the perceptual characteristics of visual representations themselves can explain children’s learning from visual displays (e.g., Cooper et al., 2018), such as age and prior domain knowledge. We use Simonsmeier et al.’s (2022) definition of domain knowledge as “specialized knowledge of a topic” (p. 31). We define prior domain knowledge, therefore, as information related to a topic that is stored in long-term memory. Theoretical accounts highlight the critical role of prior knowledge in shaping how learners interpret and process incoming information (e.g., Kalyuga, 2007). When individuals receive visual and verbal inputs, as is often the case in mathematics, they must select information relevant to the task and integrate it with what they already know (Bransford & Johnson, 1972; Brod et al., 2013; Mayer, 2008). With respect to visual representations specifically, prior domain knowledge can help learners direct their attention toward the most relevant features in visual representations (Chi et al., 1981; Cook, 2006; Kalyuga, 2013), leading to the accurate encoding and interpretation of new information (Brod et al., 2013; van Kesteren et al., 2014). Prior knowledge not only guides attention but also supports the organization of new material into meaningful chunks (i.e., bundles of information), which facilitates retrieval and application during problem solving (Gobet, 2005; Gobet et al., 2001). Glaser (1990) further argued that these knowledge-driven chunks enable learners to perceive the underlying structure of a task, which is essential for successful learning and performance (Richland et al., 2012; Verschaffel et al., 2020). Therefore, prior knowledge not only aids in filtering out extraneous information, but also enables learners to accurately apply appropriate strategies, leading to more effective problem solving and a deeper understanding of associated concepts.
The role of prior knowledge as directing learners’ attention to the relevant information in representations has received empirical support. For example, Magner et al. (2014) investigated how secondary students’ understanding of angles influenced learning after a geometry lesson. Some students received instructional materials containing extraneous details, such as an illustration of a person riding a bicycle, while others did not. In the extraneous details condition, students with high prior knowledge outperformed those with low prior knowledge on a near transfer task. Similarly, Cooper et al. (2018) examined the effect of students’ mathematics ability, as measured by standardized test scores, on their accuracy on trigonometry problems. Half of the problems contained diagrams that presented problem-relevant information, and the other half included no diagrams. Half of the diagrams were accompanied by an illustration that highlighted the real-world context described in the problem text but was not required for the solution. The remaining diagrams were not accompanied by an illustration. The results indicated that students with low prior knowledge had more difficulty when illustrations contained additional, yet extraneous, information than students with high prior knowledge. These studies demonstrated that prior knowledge not only helps learners filter out extraneous details but also enables them to focus on the essential mathematics concepts.
The previous research has examined how prior knowledge influences learners’ responses to the presence of visual representations that are irrelevant to the target concepts (e.g., an image of the Statue of Liberty; Cooper et al., 2018). Less is known, however, about how learners respond to individual, discrete details within such representations. Nonetheless, studies reporting developmental trends in children’s counting strategies highlight the potential role of prior knowledge in attention to such individual details. Kaminski and Sloutsky (2013), for example, found that younger children were more likely to count individual elements, such as images of flowers and shoes, in their graph reading task, whereas older children more frequently attended to the relational structure of the task, suggesting a developmental shift possibly influenced by prior knowledge. Similarly, both Jeong et al. (2007) and Boyer et al. (2008) found that younger children inappropriately counted the discrete segments in visual representations more frequently than older children. The younger children in Tellos and Osana (2024) also relied on the individual studs on LEGO bricks to a greater extent than the older children when rating multiplicative structures. Finally, Barmby et al. (2009) found that the 8-to-9-year-olds in their sample attended more to the lower-level units in visual representations of dot arrays than the 10-to-11-year-olds, who used strategies that demonstrated greater attention to the multiplicative structures in the arrays. Thus, to the extent that age effects can be explained by an accumulation of domain-specific knowledge as children progress through school, we hypothesized that prior knowledge influences the way children respond to discrete perceptual details that are irrelevant to the target concept. As children gain more conceptual knowledge, they become better equipped to recognize which aspects of a visual representation are structurally meaningful and which are not (Cook, 2006). Building on this literature, we hypothesized that prior knowledge plays a critical role in children’s ability to focus on the visual elements in LEGO bricks that are conceptually aligned with measurement division when solving fraction division problems.
1.4. Present Study
Little is known about the role of prior domain knowledge when learners interact with visual representations that contain extraneous details. The aim of the present study, therefore, was to investigate the extent to which children’s prior domain knowledge would play a role in their attention to extraneous details in visual representations of LEGO bricks when solving fraction division problems. Specifically, we hypothesized that various types of prior knowledge would influence children’s application of the inappropriate strategy of counting the individual studs on LEGO bricks, namely, knowledge of the following: (a) fractions concepts, (b) fraction magnitude, (c) fraction representation with LEGO bricks, and (d) measurement division concepts. This was assessed experimentally by assigning participants to two different instructional conditions: demonstrations only and demonstrations plus explanations. These categories of domain knowledge differ in terms of the extent to which they are specific to the task of solving fraction division with LEGO bricks (Brod, 2021). More specifically, general knowledge of fractions concepts and fraction magnitude are ostensibly broader constructs than those more directly related to fraction division with LEGO bricks. In contrast, knowing how to represent fractions with images of LEGO bricks may be more directly related to the task at hand. Finally, instruction in the meaning of measurement division may have a direct impact on counting the correct representations of the divisors in fraction division problems.
We used a fractions test and a number line estimation task to assess participants’ knowledge of fractions concepts and fraction magnitude, respectively. Further, we designed a task to measure knowledge of fraction representation with LEGO bricks, and we manipulated the delivery of explanations of measurement division using an instructional intervention. All participants received instruction on how to use visual representations of LEGO bricks to solve fraction division problems. In one condition, the instruction also included explanations of measurement division concepts, whereas in the other condition, no explanations were provided.
The outcome measure was a fraction division task that we used to assess the use of measurement division concepts when solving fraction division problems, operationalized as the extent to which the participants counted the studs or the bricks when solving the problems (Harp & Mayer, 1998; Kaminski & Sloutsky, 2013; Menendez et al., 2020; Tellos & Osana, 2025). The two research questions were as follows:
- To what extent do children use inappropriate counting strategies (i.e., counting studs) on images of LEGO bricks when solving fraction division problems (RQ1)?
- Does knowledge of fractions concepts, fraction magnitude, fraction representation with LEGO bricks, along with the children’s instructional condition, predict the extent to which the children use inappropriate counting strategies when solving fraction division problems with LEGO bricks (RQ2)?
In terms of RQ1, we expected that some of the participants would count the studs instead of the bricks when solving fraction division problems in a measurement division context. With respect to RQ2, we predicted that each type of fractions knowledge and the children’s instructional condition would contribute uniquely to the children’s counting strategies when solving fraction division problems with LEGO bricks. Higher prior knowledge of fractions concepts would facilitate learners’ attention to the relevant features in the visual representations, namely the bricks as the unit of measure, which would lead to correctly encoding them as the divisor quantity in a measurement division context. The abstraction of the measurement division context would in turn support the grouping of the studs on the bricks as units and then counting how many times the divisor brick fits onto the dividend brick. In contrast, those with lower prior knowledge would be more likely to attend to irrelevant features in the visual representations, which would then mask the underlying measurement division context. Without an accurate problem structure, children would then fall back on well-practiced strategies of counting discrete elements in visual representations.
2. Materials and Methods
2.1. Participants
The participants were 39 fourth- (n = 23) and fifth- (n = 16) grade students (14 girls and 9 boys in Grade 4; age: M = 10.04, SD = 0.33, and 5 girls and 11 boys in Grade 5; age: M = 11.14 years, SD = 0.28) from two fourth-grade classrooms and two fifth-grade classrooms in one French-speaking, private suburban school in eastern Canada. A majority of the sample (81.5% of 27 participants who responded) reported a family income of over 100,000 CAD. No participant was excluded from the study.
2.2. Design
In sum, the design of the study included both correlational and experimental elements. We assessed the influence of three continuous predictor variables, namely knowledge of fractions concepts, fraction magnitude, and fraction representation with LEGO bricks, on the outcome measure, which was the extent to which the participants counted the studs instead of entire divisor bricks to solve fraction division problems. We also tested the effect of an experimentally manipulated variable—the presence or absence of explanations providing the meaning of measurement division (MD) in a fraction division context—on the participants’ counting strategies. As has already been noted, participants were randomly assigned to two instructional conditions, one in which the procedure for solving fraction division problems with LEGO bricks was demonstrated, accompanied by explanations of the meaning of MD; and the other in which no explanations of MD were provided beyond demonstrations of the fraction division procedure.
2.3. Instructional Intervention
The instructional intervention consisted of three phases, namely Phase 1 (introduction to fractions lesson), Phase 2 (fraction division lesson), and Phase 3 (procedure consolidation). All instruction was delivered in French in online individual sessions with participants. The lessons in Phases 1 and 2 were delivered using a pre-recorded video with narration and animation. In Phase 1, the video lesson demonstrated how to represent nine target fractions (1/2, 1/4, 1/8, 2/4, 3/4, 1/2, 1/3, 1/12, 2/3) using bricks of different colors to represent the target fraction and the whole. In Phase 2, the video lesson consisted of demonstrations of how to use LEGO bricks to solve three fraction division problems using measurement division (1/4 ÷ 1/16 =, 5/6 ÷ 1/12 =, and 3/4 ÷ 1/8 =). Figure 1 presents screenshots from the lesson for the problem 1/4 ÷ 1/16 =. Different colored bricks were used to represent the whole, the dividend, and the divisor (see Figure 1a). The divisors were always unit fractions represented by a LEGO brick with one stud in all three problems.
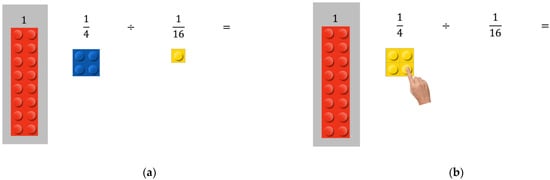
Figure 1.
Screenshots of the problem 1/4 ÷ 1/16 = in the Fraction Division lesson: (a) LEGO bricks representing the whole, the dividend, and the divisor; (b) four divisor bricks covering the dividend brick.
The procedure was shown through an animation that showed the yellow divisor brick sliding onto the blue dividend brick until no other divisor bricks could fit. Once the dividend brick was fully covered by divisor bricks, an image of a hand appeared that pointed to each divisor brick one at a time (see Figure 1b). Then, the solution (e.g., “4”) appeared to the right of the equal sign.
The objective of Phase 3 was to consolidate the procedure of solving fraction division problems as demonstrated in Phase 2. The researcher presented three problems (2/3 ÷ 1/12 =, 1/2 ÷ 1/16 = and 3/4 ÷ 1/16 = 1) to the participants, all of which again required the use of a one-stud divisor brick for the solution. Each problem was presented with the symbolic representation of the fraction division problem placed at the top of the screen (e.g., 1/2 ÷ 1/16 =), the correct bricks placed underneath the dividend (e.g., 1/2) and divisor (e.g., 1/16), and a selection of bricks of various sizes at the bottom of the screen (see sample item in Figure 2). Because the intervention was delivered online, the participants directed the researcher to select specific bricks from among those at the bottom of the screen and asked her to move them around in ways that would lead to a solution. The researcher provided corrective feedback by repeating the condition-specific instructions in the fraction division lesson, if required. Phase 3 was terminated when the last problem was solved correctly regardless of performance on the other two problems, a criterion reached by all participants. To avoid a potential confound of color, the colors of the bricks were identical to the ones used in the instructional intervention and were the same across all items used in the study (e.g., the whole bricks were always red).
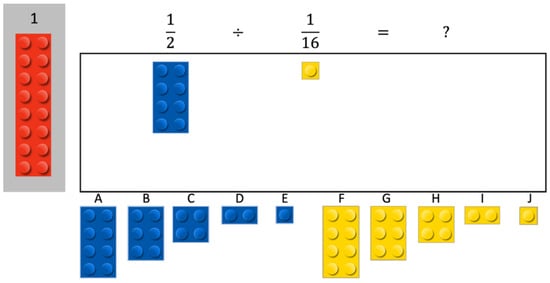
Figure 2.
Sample problem in Phase 3 of the intervention.
Experimental Conditions
Within each grade, the participants were randomly assigned to one of two conditions: (a) MD explanation (n = 19; 11 in Grade 4 and 8 in Grade 5) and (b) no-MD explanation (n = 20; 12 in Grade 4 and 8 in Grade 5). Assignment to conditions resulted in approximately even distributions in each classroom: in classroom 4A, there were 12 participants, with 7 in the MD explanation condition. In classroom 4B, there were 11 participants, with 4 in the MD explanation condition. In classroom 5A, there were 7 participants with 3 in the MD explanation condition, and in classroom 5B, there were 9 participants with 5 in the MD explanation condition.
Participants in both conditions received the same instructional intervention described earlier, except that in the MD explanation condition, additional verbal explanations about the meaning of measurement division were given. The additional explanations were delivered during the demonstrations in the fraction division lesson in Phase 2. In two of the explanations, the narrator said, “I have to find how many [divisors] are in [dividend]” (e.g., “I have to find how many one-sixteenths are in one-fourth.”). In the animation, when the hand began pointing at the divisor bricks on the dividend brick, the narrator then said, “So I am going to count the [divisors]” (e.g., “So I am going to count the one-sixteenths.”). The same explanations were provided for all problems at the same points in the lesson.
In the no-MD explanation condition, participants viewed the identical video lesson used in the MD explanation condition, with one key difference: The verbal explanations about the meaning of measurement division were omitted from the narration. Specifically, the explanations of measurement division during each demonstration problem (e.g., “I have to find how many one-sixteenths are in one-fourth”) were removed. As a result, participants in the no-MD explanation condition did not hear any verbal explanation about the meaning of measurement division during those segments, but the visual content remained unchanged.
2.4. Measures
All to-be-described measures were administered in French.
2.4.1. Fractions Concepts
The Fractions test is a paper-and-pencil test based on Saxe et al.’s (2001) work that assesses participants’ conceptual and procedural knowledge of fractions. Only the conceptual subscale was used in the present study. The test consists of nine items: (a) three items that require writing a fraction that corresponds to a shaded amount in an area model; (b) two estimation items that require circling a fraction from a choice of three that best represents the unpartitioned shaded region in a circle; (c) three fair-sharing items, each of which requires partitioning area models evenly among a given number of people; and (d) one item that requires the participants to use drawings to compute 2/5 + 3/5. The fractions score is the proportion of correct responses. The internal reliability of the fractions concepts measure was 0.68.
2.4.2. Fraction Magnitude
The Number Line Estimation (NLE) task (Hansen et al., 2017) assesses participants’ fraction magnitude. We administered the pencil-and-paper version of the task. The participants placed a hash mark on a number line where they thought a target fraction was located. Participants completed nine items on a 0–1 number line (i.e., 1/5, 13/14, 2/13, 3/7, 5/8, 1/3, 1/2, 1/19, 5/6) and 10 items on a 0–2 number line (i.e., 1/3, 7/4, 5/6, 7/6, 1, 3/8, 1 5/8, 1 1/5, 7/9, 4/3). The Percent Absolute Error (PAE) was computed for each item using the formula PAE = (|child answer − correct answer|)/numerical range. Two separate NLE scores were computed by averaging the PAE across relevant trials: (a) magnitude 0–1 score for the 0–1 number line items, and (b) magnitude 0–2 score for the 0–2 number line items. Each score ranged from 0 to 1, with lower scores indicating greater accuracy. The internal reliability of the number line estimation measure was 0.87 for the magnitude 0–1 score and 0.78 for the magnitude 0–2 score.
2.4.3. Representation Task
The Representation task assessed participants’ knowledge of how to represent fractions with LEGO bricks immediately after the introduction to fractions lesson. Knowledge of how to represent fractions with LEGO bricks was operationalized by the rate at which the studs were used in their responses on six multiple-choice items. Participants chose the fraction among three that correctly represented a quantity shown with LEGO bricks. On each item, one of the distractors was 1 over the number of studs found on the whole (i.e., 1/16 in the sample item in Figure 3) and the other was the number of studs on the target brick (i.e., 8 in the sample item in Figure 3). The representation score was the proportion of correct responses. The internal reliability of the representation measure was 0.75.
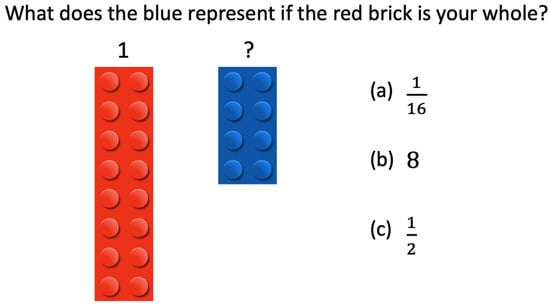
Figure 3.
Sample item on the Representation task.
2.4.4. Extraneous Details Task
The Extraneous Details task was used to assess the participants’ understanding of measurement division concepts, operationalized by the extent to which participants counted the studs instead of the bricks when solving fraction division problems. The task consisted of 10 problems: 1/2 ÷ 1/6 =, 1/6 ÷ 1/12 =, 2/3 ÷ 1/6 =, 1/2 ÷ 1/8 =, 4/6 ÷ 1/3 =, 1/4 ÷ 1/12 =, 1/4 ÷ 1/8 =, 1/2 ÷ 1/4 =, 1/3 ÷ 1/6 =, and 1/3 ÷ 1/12 = 2. On each item, the participants directed the researcher to select specific bricks from among those at the bottom of the screen and to move them around in ways that would lead to a solution. No reminders or corrective feedback was provided.
The items on the Extraneous Details task were presented in the same way as those in the procedure consolidation phase of the intervention with two exceptions. First, the brick used to represent the divisor contained more than one stud (see sample item in Figure 4). Because the fraction division lesson in Phase 2 of the intervention always involved one-stud divisors, using divisors with more than one stud on the Extraneous Details task served to evaluate whether the participants counted studs, which would suggest attention to individual discrete elements on the images, or the bricks. That in turn would indicate a conceptual misunderstanding of the unit required to solve the problem. Of the 10 items, seven items involved a divisor brick with two studs, two items used a four-stud divisor brick, and one item used an eight-stud divisor brick. Second, the bricks at the bottom of the screen did not offer the choice of a one-stud brick to solve the problem. The counting strategy score was the proportion of items on which the studs were counted.
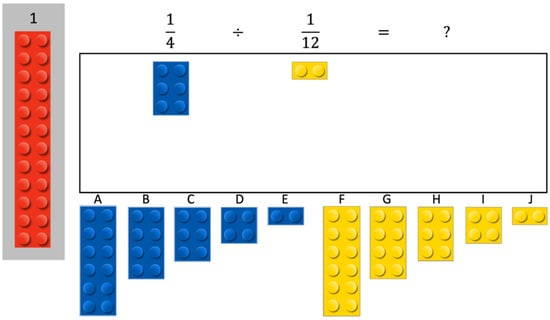
Figure 4.
Sample item on the Extraneous Details task. Figure shows the problem to be solved; corresponding LEGO brick representations for the whole, dividend, and divisor; and brick options A to J for students to use for the solution.
2.5. Procedure
The Fractions test and the NLE task, in that order, were administered in person at the participants’ school. Five participants at a time were removed from the classroom for individual testing in the school cafeteria. After the in-person testing, the researcher contacted the participating families to schedule individual online sessions for the instruction and remaining testing. The online session was delivered on average 17 days after the in-person testing. There were no instructional condition differences in the number of days between the in-person testing and the day on which the online session took place, t(37) = 0.63, p = 0.53.
The researcher’s camera and microphone remained on during the online sessions and all sessions were recorded using the software’s recording feature. Participants shared their video and audio. The researcher shared a slide deck to deliver the instructional intervention and to administer the Representation task and the Extraneous Details task. The researcher scored the latter two tasks using a scoring sheet during administration and all scoring was confirmed by reviewing the recordings.
2.6. Analytic Plan
To address the first research question, we first computed the proportion of all items on the Extraneous Details task that were solved by inappropriately counting the studs. To address the second research question, we conducted a multiple-regression analysis with the counting strategy score as the criterion measure and the fractions knowledge measures and instructional condition as predictors in the model.
3. Results
3.1. Research Question 1: Frequencies of Inappropriate Counting Strategies
With items as the units of analysis, participants across both conditions counted the studs on over one-quarter of all items (106 of the 390 items or 27%) on the Extraneous Details task. We next switched to an analysis with participants as the units of analysis. Figure 5 presents the frequency distribution of the participants who counted the studs on the task. Almost one-third of the sample (12 participants, 31%) counted the studs on at least one item, whereas eight (21%) counted the studs on all 10 items. These data suggest a bimodal pattern where 35 participants (90% of the sample) either counted the studs on all (23% of the 35 participants) or none (77% of the 35 participants) of the items.
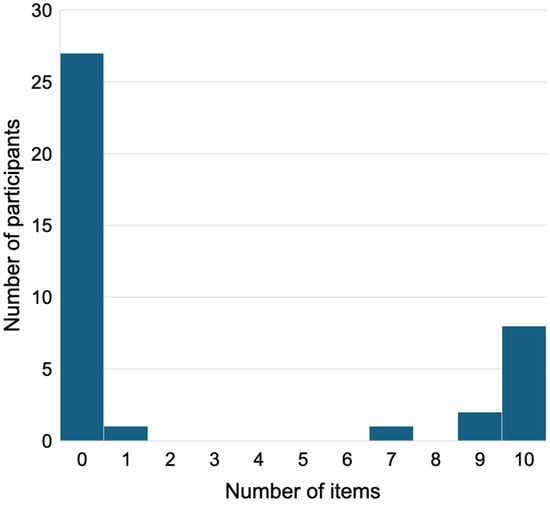
Figure 5.
Distribution of participants who counted studs by item.
3.2. Research Question 2: The Role of Prior Domain Knowledge
Table 1 presents the means and the standard deviations for the fractions scores, magnitude 0–1 and 0–2 scores, representation scores, and counting strategy scores by condition. All inferential statistical tests were based on a Type I error probability (α) of 0.05. The counting strategy scores on the Extraneous Details task were not statistically correlated with grade, t(37) = 0.48, r = −0.08, p = 0.64; age, r = −0.07, p = 0.70; family income, t(25) = 1.77, r = 0.33, p = 0.09; or gender, t(37) = 1.13, r = 0.18, p = 0.27.

Table 1.
Means and standard deviations for fractions scores, magnitude scores, representation scores, and counting strategy scores by instructional condition.
The mean proportion of correct responses on the Representation task across the sample was 0.79, meaning that on average, the participants chose responses that were based on counting the studs 21% of the time. Similarly, the mean proportion of participants choosing the brick as the unit of measure on the Extraneous Details task was 0.73, suggesting that on average, they inappropriately counted the studs at approximately the same rate as on the Representation task (i.e., 27%). The MD explanation and no-MD explanation conditions did not differ statistically on any of the predictor variables nor on the Extraneous Details task, all ps > 0.055.
Table 2 presents the zero-order correlations among all four predictors.

Table 2.
Zero-order correlations for fractions scores, magnitude scores, representation scores, and counting strategy scores (N = 39).
All measures except the two fraction magnitude measures were statistically correlated with the counting strategy scores, based on an α of 0.05. We conducted a simultaneous multiple-regression analysis with counting strategy score as the dependent measure and the Fractions test, NLE 0–2 task, and Representation task as the predictors. Correct performance on the NLE 0–2 task would require greater attention to the units than the NLE 0–1 task in much the same way as correct performance on the Extraneous Details task, which required the counting of two or more studs as if they were one. For this reason, the NLE 0–2 task was the only fraction magnitude measure entered into the regression model. Given that instructional condition produced no observable impact on the dependent measure, it was also excluded from the regression model. The top portion of Table 3 presents the results of the multiple-regression analysis with the Extraneous Details task as the dependent variable.

Table 3.
Simultaneous multiple-regression analysis of extraneous details and representation scores on knowledge predictors (N = 39).
Knowledge of fractions concepts was a statistically significant predictor of the extent to which the participants counted the studs on the division problems, showing that the greater their knowledge, the less frequently they applied incorrect counting strategies, β = −0.35, t(35) = −2.47, p = 0.02. The NLE 0–2 fraction magnitude measure was not a statistically significant predictor, p = 0.76. Finally, the extent to which participants counted the studs on the Extraneous Details task varied as a function of representation score, β = −0.48, t(35) = −3.44, p = 0.002, indicating that the greater the children’s performance on the Representation task, the less likely they were to use inappropriate counting strategies. The complete multiple-regression model accounted for a substantial 51% of the variance in the counting strategy score, F(3, 35) = 11.99, p < 0.001.
The Representation task also assessed the extent to which the participants attended to the studs when choosing the fraction that matched the target LEGO representation. We thus explored whether knowledge of fractions concepts and fraction magnitude predicted performance on the Representation task. The results of the multiple-regression model are presented in the bottom portion of Table 3. Results similar to the first analysis were found, namely, that the extent to which the participants inappropriately counted the studs varied as a function of their performance on the Representation task, β = 0.50, t(36) = 3.30, p = 0.002. Specifically, the greater the children’s knowledge of fractions concepts, the less likely they were to attend to the studs in the LEGO representations on the task. The NLE 0–2 fraction magnitude measure was again not predictive of inappropriate counting strategies, p > 0.05. The complete multiple-regression model accounted for a statistically significant 26% of the variance in children’s attending to the studs in their responses on the Representation task, F(2, 36) = 6.30, p = 0.004.
4. Discussion
Visual representations are widely used in mathematics instruction, yet relatively little is known about how individual differences, such as prior knowledge, influence children’s attention to the perceptual details in the representations. The objective of the present study was to examine the impact of perceptual features in visual representations that contain extraneous information about the target concepts. We examined children’s mathematical problem solving and the role of prior domain knowledge in reducing any negative effects of extraneous features. We provided instruction to fourth- and fifth-grade students on how to use images of LEGO bricks to solve fraction division problems. After instruction, the participants were assessed on the extent to which they counted the individual studs on the divisor bricks in a task where such a strategy would lead to the incorrect solution.
Extraneous details in visual representations can have a negative impact on mathematics performance, particularly when those details are in the form of discrete elements within representations (e.g., Kaminski & Sloutsky, 2013, 2020; Tellos & Osana, 2025). We hypothesized that images of LEGO bricks would hamper children’s fraction division performance by their considering the studs rather than the bricks themselves as the units of measure. The results revealed that almost one-third of our sampled children inappropriately counted the studs on at least some fraction division problems. Researchers have documented children’s tendency to count discrete elements in visual representations of multiplicative structures (e.g., Barmby et al., 2009; Bolden et al., 2015; Boyer et al., 2008), and that such counting can negatively impact performance (Jeong et al., 2007; Kaminski & Sloutsky, 2013). One-to-one counting, including that which we observed in our study, may be a result of the participants’ early experiences with numbers and extensive practice counting individual objects in school (Mix, 2008; Sophian, 2008).
Next, we explored the extent to which prior domain knowledge accounted for the variance in the participants’ strategies. In line with theoretical accounts (e.g., Bransford & Johnson, 1972; Mayer, 2008; Simonsmeier et al., 2022), we expected that students with more fractions knowledge would be better equipped to interpret visual representations meaningfully, attend to structurally relevant details (i.e., the bricks as units), and filter out extraneous or misleading features (i.e., the studs). The data partially supported our predictions. First, knowledge of fractions concepts, such as estimating fractional quantities and fair sharing as assessed on the Fractions test, accounted for a significant proportion of the variance in participants’ counting strategies. One interpretation of this finding is that participants with more fractions knowledge may have been better able to identify which features in the LEGO representations were relevant to the new information about measurement division concepts delivered in the instruction. Greater attention to the correct fractional units (i.e., the bricks) with which to measure the dividend during instruction (Brod, 2021; Sidney & Thompson, 2019) were then successfully applied to solve the fraction division problems. Participants with less fractions knowledge, on the other hand, may not have known which aspects of the visual representation were relevant. As such, their proclivity to count the discrete elements in the images may have drawn their attention to the studs and masked the underlying measurement division structure used in the instruction to demonstrate fraction division (Sidney & Alibali, 2015).
In addition, because of its operationalization, the Representation task served as an additional indicator of the extent to which the participants used either bricks or individual studs in their responses. A secondary regression analysis allowed us to draw similar conclusions about their strategies, namely that prior knowledge of fractions concepts accounts for a substantial proportion of the variance in their attention to the studs when representing fractions with LEGO bricks. More specifically, students with greater fraction knowledge were more likely to ignore extraneous features, thereby demonstrating the filtering function of prior knowledge, as explained by Kalyuga (2007).
The data also supported our hypothesis that students’ representational knowledge would predict their counting strategies. The participants’ knowledge of how to represent fractional quantities may have helped them recognize which bricks in the visual representations correctly corresponded to the divisors that were presented symbolically (e.g., 1/16) in the instruction and in the problems they solved after instruction. Accurate encoding of the divisor bricks was critical to counting the number of bricks, rather than studs, that fit on the dividend.
Contrary to our predictions, knowledge of fraction magnitude as assessed by number line estimation was unrelated to the participants’ strategies. This finding was unexpected, particularly because performance on the number line task was correlated with the participants’ knowledge of fractions concepts and also because of existing evidence that number line estimation predicts fractions arithmetic performance (Bailey et al., 2017; Schneider et al., 2018). Brod’s (2021) framework outlining the effects of prior knowledge on learning emphasized that domain knowledge must be relevant to the specific task at hand. Although Schneider et al. (2018) found in their meta-analysis that number line estimation correlates with mathematical tasks that typically involve symbolic representations, such as counting, mental and written arithmetic, as well as standardized tests of mathematical achievement, we propose that number line estimation may not be useful for learning about the conceptual underpinnings of fraction division. The instruction and the fraction division problems administered in our study were presented using visual representations, which were not within the scope of Schneider et al.’s (2018) meta-analysis. It is thus possible that even if knowledge of fraction magnitude was activated during instruction, it might not be congruent with the conceptual demands of fraction division using visual representations (Brod, 2021). Thus, our findings are in line with Brod’s (2021) account that not all types of prior domain knowledge are equally accessible or functionally relevant in a given learning context.
Finally, we predicted that instruction that included explanations of measurement division concepts would be a stronger predictor of children’s counting strategies than instruction on the fraction division procedure alone. The conceptual emphasis on measurement division was expected to facilitate the children’s problem-solving performance. This hypothesis was not supported by the data, however. The instructional manipulation did not yield the anticipated benefits on the dependent measure, nor did it result in differences on any of the other measures used in the study. There are several possible explanations for this finding. First, the differences between the instructional conditions may have been too subtle to produce measurable effects. Second, we did not administer a direct measure of participants’ understanding of measurement division, nor did we include a pretest in the study design. As a result, we cannot determine whether the instructional condition that included explanations of measurement division in fact enhanced participants’ conceptual understanding relative to the condition that did not include explanations. Consequently, our data do not allow for conclusions about the extent to which participants’ solutions to the fraction division problems with LEGO bricks were facilitated by instruction in measurement division.
Despite our results, it remains unclear whether prior knowledge has a direct positive influence on how children manage extraneous perceptual features, such as the studs on LEGO bricks. Research on executive functioning has shown that inhibition—the ability to suppress irrelevant or misleading information—is a key predictor of early numeracy and mathematics achievement (e.g., Fuhs & McNeil, 2013; Gilmore et al., 2015; Merkley et al., 2016). Moreover, some evidence suggests that children with greater mathematics knowledge may demonstrate more inhibitory control (Ashkenazi & Blum-Cahana, 2023; Gilmore & Cragg, 2018). Thus, it is possible that prior domain knowledge not only supports problem-solving but also enhances children’s ability to inhibit perceptual features that are not directly related to the to-be-learned concept. Future studies should further examine the relationship between prior knowledge of mathematics and inhibitory control to better understand how children learn to extract relevant information from visual representations that possess perceptual details.
4.1. Contributions to the Literature
The present study is one of the first to investigate how images of LEGO bricks used as visual representations of mathematical concepts are related to children’s problem-solving performance. Prior research has examined other educational uses of LEGO bricks, such as the relation between construction in a play context and spatial reasoning (e.g., McDougal et al., 2023; McDougal et al., 2024), but none to our knowledge has tested the use of bricks as mathematical tools for teaching concepts in the elementary curriculum. In particular, we explored how children respond to perceptual features in visual representations of LEGO bricks when learning about fraction division. An important contribution is that children attended to different aspects of the perceptual features in the LEGO images, which was associated with varying levels of performance. In some cases, children attended to the bricks as the units and appropriately counted them to solve fraction division problems. In other cases, the children were drawn to extraneous details on the images of the LEGO bricks, namely the studs, when solving the problems. The results contribute to a small but growing body of research (e.g., Boyer et al., 2008; Jeong et al., 2007; Kaminski & Sloutsky, 2013, 2020; Tellos & Osana, 2024, 2025; Wege et al., 2023) demonstrating that under certain conditions, the presence of discrete perceptual elements in visual representations can prompt children as old as 12 years of age to count them.
These findings are noteworthy first because children’s attention to discrete elements in visual representations can derail learning in mathematical domains other than multiplication and proportional reasoning (e.g., Boyer et al., 2008), namely, fraction division. Second, we showed that undue attention to discrete features can also occur when representations of LEGO bricks are used in the teaching and learning of mathematics. Investigating what other perceptual features of LEGO bricks, such as color, shape, and spatial configurations (Tellos & Osana, 2023), capture students’ attention in instructional contexts is a consideration for future research.
Prior research on the effects of extraneous details in visual representations have predominantly used stimuli that have arguably stronger real-world referents than studs on LEGO bricks, such as pepperonis and mushrooms on pizzas (Kaminski & Sloutsky, 2020) and images of beetles and ladybugs (Menendez et al., 2022). Researchers have explained that children’s attention can shift away from the targeted mathematical concept when familiar and interesting details are inserted into visual representations (e.g., Cooper et al., 2018; Kaminski & Sloutsky, 2020), particularly when they are irrelevant to the task (Kaminski & Sloutsky, 2013; Magner et al., 2014; Menendez et al., 2022). In contrast, one would be hard-pressed to consider a stud on a LEGO brick, a relatively generic feature, as possessing inherently “seductive” (see Harp & Mayer, 1998; Mayer, 2019; Rey, 2012) or visually distracting qualities. Nonetheless, we found that studs prompted the children to use inappropriate strategies when solving fraction division problems. This finding is important because there are few studies that have examined how children respond to details in instructional materials in mathematics that are not perceptually rich or “realistic” (e.g., Carbonneau & Marley, 2015; Petersen & McNeil, 2013). In sum, our findings show that even perceptual features that do not have real-world referents can also interfere with learning and performance in mathematics.
Finally, our data suggest that different types of prior knowledge play an important role in how children interpret and apply visual representations. This finding is noteworthy, first because it suggests an explanation based on individual differences in children’s tendency to count discrete extraneous details beyond a purely developmental one (e.g., Barmby et al., 2009; Jeong et al., 2007; Wege et al., 2023). Nevertheless, more research is needed to identify more precisely the cognitive and task-related factors that impact learners’ interpretations of visual information. Second, the finding that more than one dimension of prior knowledge contributes to children’s responses to extraneous details extends previous research, which has focused primarily on a single type of prior knowledge (e.g., mathematics achievement, Bolden et al., 2015; Cooper et al., 2018; principles related to angles, Magner et al., 2014). Our results suggest that at least two domain-specific knowledge structures–knowledge of general fractions concepts and representation knowledge–form key elements of the conceptual landscape of fraction division. We speculate that these forms of prior knowledge provided the children with efficient searches of the problem space that guided their attention to the relevant information in the representations, thereby facilitating appropriate counting strategies (Kalyuga, 2007).
4.2. Strengths and Weaknesses
A strength of the present study is the way in which participants’ counting of the studs on LEGO bricks was operationalized. We designed a task that provided more direct evidence of inappropriate counting strategies than measures of performance accuracy used in previous studies (e.g., Kaminski & Sloutsky, 2020; Magner et al., 2014). More specifically, our measure involved solving fraction division problems using divisor bricks with more than one stud, which provided a clearer indication of whether studs or bricks were counted. Confirmation with observational data (e.g., verbal counting, pointing, or tagging behaviors), however, would provide a direct verification of the participants’ counting strategies. Another strength of the study is the use of a video-based intervention, which ensured that all participants received identical instruction. This type of delivery strengthened the implementation fidelity by eliminating potential differences in how the content was presented to the participants.
We note that although our outcome measure produced a more valid indicator of the extent to which the participants used inappropriate counting strategies than what has been used in prior research, it did not directly indicate a conceptual understanding of fraction division. The act of counting the bricks only indicated that the participants knew to count something other than the individual studs, but not the reasons for doing so. On the one hand, they may have counted the bricks because of their grasp of measurement division, which directed them to use the appropriate units to solve the problems. On the other hand, they may have simply used the brick as a strategy or “trick” to best represent the divisor fraction without relying on an understanding of measurement division. A task that directly assesses measurement division concepts likely would provide insight into these speculations. Along the same lines, the participants who counted the individual studs may have done so for reasons other than an impulse to count discrete elements in the images of LEGO bricks. A plausible alternate explanation may be that they learned to count the studs because it was demonstrated in the instruction. Thus, measures that could better reveal the cognitive mechanisms underlying participants’ behaviors, such as additional qualitative data based on think-aloud protocols (Ericsson & Simon, 1980), could provide a deeper understanding of how children engage with perceptual features of instructional materials.
Another potential methodological weakness pertains to the design of the study, which could be argued did not yield sufficient statistical power to detect the expected effects. As the argument goes, conducting the multiple-regression analyses with a larger sample would have increased our ability to detect relations between prior knowledge and children’s responses to extraneous details in visual representations if such effects were actually to exist in the population. Given the small sample, the likelihood of Type II errors was increased, reducing the credibility of our conclusions. That said, we remind the reader that the present design and analyses proved capable of detecting a number of omnibus test and statistically controlled pairwise relationships that addressed our primary research questions.
An additional weakness of the present study was that it was conducted in a private school, which restricts the study’s external validity. Our findings were based on a sample from a relatively high socioeconomic level with mathematical competencies that may not have reflected those of children in the same grades in public schools. Further, a sample drawn from a population with wider variability in prior mathematical knowledge might have produced differences between the experimental conditions. Replicating the current study in more diverse settings would allow for more generalizable findings.
We also note several limitations because of the online procedures that were required because of COVID restrictions. First, because the delivery of the instruction and the administration of the measures were carried out online in students’ home environments, any data on the extent to which the students paid attention to the video lessons—such as documenting their gaze during the instruction—might not have adequately captured their engagement levels. Furthermore, we could not ensure that the students completed the prior knowledge assessments and the fraction division tasks independently. Second, the online format limited the conclusions to visual representations of LEGO bricks. Given that learning opportunities provided by mathematical tools depend heavily on the types of actions they support (Donovan & Alibali, 2022; Manches et al., 2010), the extent to which our findings can be generalized to physical LEGO bricks is limited. Physical objects enable sensorimotor engagement: students can touch, move, or arrange bricks, which can help ground abstract concepts in concrete experiences (Abrahamson et al., 2020; Martin, 2009; Pouw et al., 2014). In contrast, when learners use digital manipulatives, like those used in the current study, they tend to rely more on visual and pattern-based reasoning (Pouw et al., 2014). The difficulty in transferring our conclusions to physical LEGO bricks also constrains the practical implications of the research because teachers might be more likely to use physical bricks in the mathematics classroom than their digital images. Third, and as an aside, even a mathematically sophisticated adult who was unfamiliar with the present study experienced difficulty in examining the visually depicted LEGO bricks and performing the requested division task.
4.3. Educational Implications
The results of the present study highlight the importance of identifying not just whether learners possess prior knowledge, but whether they have access to the specific knowledge that is most relevant and readily activated to support problem solving. Simply having prior knowledge is not always sufficient insofar as educators must consider how instructional contexts and representations can cue the use of that knowledge in productive ways. Further, educators interested in using LEGO bricks in fractions instruction may wish to establish students’ knowledge of related concepts and how to represent fractional quantities with the bricks. Without this foundation, students might not possess the conceptual tools necessary to accurately identify the visual elements that will assist in abstracting the relevant conceptual structure.
Beyond these points, our findings raise additional considerations for instructional practice. First, teachers may need to explicitly draw students’ attention to the elements of visual representations that are mathematically meaningful and those that are not. In the context of fraction division, this could involve guiding students to focus on the conceptual units (e.g., bricks) and helping them filter out perceptual details that may be irrelevant or misleading for the task at hand (e.g., studs). Second, the knowledge that perceptual information in visual representations can impact the ways in which children interpret them is an important component of teachers’ mathematical knowledge for teaching (Ball et al., 2008). Therefore, teachers are advised to select or adapt instructional materials with the foresight that reducing extraneous perceptual details—particularly for children with less prior knowledge—can facilitate more appropriate teaching and learning strategies. When teachers use images of LEGO bricks in particular, they might benefit from observing which perceptual features are capturing their students’ attention and if necessary, modify the representations accordingly.
Furthermore, we recommend that teachers be cautious when generalizing our findings, which were based on visual representations, to classroom practice with concrete LEGO materials. The ways in which students engage with visual materials might be different from the ways they interact with concrete manipulatives, such as LEGO bricks. Pouw et al. (2014) suggested that manipulatives offer experiences that can support motor-based strategies and embodied understanding (see also Glenberg, 2008), whereas virtual ones emphasize visual cues and patterns. It is worth noting that we do not discourage the use of physical LEGO materials in the classroom; however, more research is needed to examine whether the same results based on images of LEGO bricks can be extended to concrete instantiations of those images.
Finally, the findings support the notion that students’ representational competence–that is, their ability to select, interpret, and use visual representations to reason through mathematical ideas, solve problems, and communicate thinking (Rau, 2017a)—is a consideration for effective mathematics instruction. Explicit teaching of why, for instance, a specific LEGO brick represents one-sixteenth or why a 2 × 2 brick should be counted instead of its individual studs can facilitate the development of representational competence, allowing learners to shift the external images of LEGO bricks into visualizations that can be used to enhance problem-solving performance (see Daniel et al., 2018). Such scaffolding is likely to support successful problem solving in fraction division but may also promote more flexible representational thinking that will equip students to work with a wide range of mathematical representations more effectively (Rau, 2017c).
5. Conclusions
The present study examined how extraneous details on images of LEGO bricks, particularly the bricks’ studs, influenced children’s strategies when solving fraction division problems. Nearly one-third of the participants inappropriately counted the studs instead of the bricks to solve the problems, likely because they resorted to well-rehearsed counting routines. Prior conceptual understanding of fraction concepts and knowledge of how to represent fractions with LEGO bricks accounted for a statistically significant proportion of variance in the children’s problem-solving strategies. Specifically, children with more prior knowledge were better able to identify the bricks—rather than the studs—as the correct units in their solutions. These findings highlight the role of prior knowledge in directing children’s attention toward structurally meaningful features in visual representations. Accordingly, educators can benefit from observing how their students interpret specific perceptual features in visual representations when teaching new mathematical concepts and procedures.
Author Contributions
Conceptualization, A.T., H.P.O. and J.R.L.; methodology, A.T., H.P.O. and J.R.L.; validation, A.T., H.P.O. and J.R.L.; formal analysis, H.P.O. and J.R.L.; investigation, A.T.; resources, A.T.; data curation, A.T.; writing—original draft preparation, A.T.; writing—review and editing, H.P.O. and J.R.L.; visualization, A.T.; supervision, H.P.O.; project administration, A.T.; funding acquisition, H.P.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Social Sciences and Humanities Research Council (SSHRC) of Canada, grant number 435-2015-2002.
Institutional Review Board Statement
The study was conducted in accordance with the relevant ethical principles and standards and has been approved by the Human Research Ethics Committee of Concordia University (protocol code 30014807, issued on 12 August 2021).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The authors did not obtain permission from participants or the relevant ethics committee to share the data publicly.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| MD | Measurement division |
| NLE | Number line estimation |
| PAE | Percent absolute error |
Notes
| 1 | Expected answers are: 2/3 ÷ 1/12 = 8; 1/2 ÷ 1/16 = 8; 3/4 ÷ 1/16 = 12. |
| 2 | Expected answers are: 1/2 ÷ 1/6 = 3; 1/6 ÷ 1/12 = 2; 2/3 ÷ 1/6 = 4; 1/2 ÷ 1/8 = 4; 4/6 ÷ 1/3 = 2; 1/4 ÷ 1/12 = 3; 1/4 ÷ 1/8 = 2; 1/2 ÷ 1/4 = 2; 1/3 ÷ 1/6 = 2; 1/3 ÷ 1/12 = 4. |
References
- Abrahamson, D., Nathan, M. J., Williams-Pierce, C., Walkington, C., Ottmar, E. R., Soto, H., & Alibali, M. W. (2020). The future of embodied design for mathematics teaching and learning. Frontiers in Education, 5(147), 147. [Google Scholar] [CrossRef]
- Alibali, M. W., & DiRusso, A. A. (1999). The function of gesture in learning to count: More than keeping track. Cognitive Development, 14(1), 37–56. [Google Scholar] [CrossRef]
- Ashkenazi, S., & Blum-Cahana, I. Y. (2023). The role of inhibition and speed of processing in mathematics. Applied Cognitive Psychology, 37(1), 111–124. [Google Scholar] [CrossRef]
- Bailey, D. H., Hansen, N., & Jordan, N. C. (2017). The codevelopment of children’s fraction arithmetic skill and fraction magnitude understanding. Journal of Educational Psychology, 109(4), 509–519. [Google Scholar] [CrossRef]
- Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5), 389–407. [Google Scholar] [CrossRef]
- Barmby, P., Harries, T., Higgins, S., & Suggate, J. (2009). The array representation and primary children’s understanding and reasoning in multiplication. Educational Studies in Mathematics, 70(3), 217–241. [Google Scholar] [CrossRef]
- Barnett-Clarke, C., Fisher, W., Marks, R., & Ross, S. (2011). Developing essential understanding of rational numbers for teaching mathematics in grade 3–5. National Council of Teachers of Mathematics. [Google Scholar]
- Belenky, D. M., & Schalk, L. (2014). The effects of idealized and grounded materials on learning, transfer, and interest: An organizing framework for categorizing external knowledge representations. Educational Psychology Review, 26(1), 27–50. [Google Scholar] [CrossRef]
- Bolden, D., Barmby, P., Raine, S., & Gardner, M. (2015). How young children view mathematical representations: A study using eye-tracking technology. Educational Research, 57(1), 59–79. [Google Scholar] [CrossRef]
- Boyer, T. W., Levine, S. C., & Huttenlocher, J. (2008). Development of proportional reasoning: Where young children go wrong. Developmental Psychology, 44(5), 1478–1490. [Google Scholar] [CrossRef] [PubMed]
- Bransford, J. D., & Johnson, M. K. (1972). Contextual prerequisites for understanding: Some investigations of comprehension and recall. Journal of Verbal Learning & Verbal Behavior, 11(6), 717–726. [Google Scholar] [CrossRef]
- Brod, G. (2021). Toward an understanding of when prior knowledge helps or hinders learning. Npj Science of Learning, 6(1), 24. [Google Scholar] [CrossRef] [PubMed]
- Brod, G., Werkle-Bergner, M., & Shing, Y. L. (2013). The influence of prior knowledge on memory: A developmental cognitive neuroscience perspective. Frontiers in Behavioral Neuroscience, 7(139), 139. [Google Scholar] [CrossRef] [PubMed]
- Carbonneau, K. J., & Marley, S. C. (2015). Instructional guidance and realism of manipulatives influence preschool children’s mathematics learning. Journal of Experimental Education, 83(4), 495–513. [Google Scholar] [CrossRef]
- Chi, M. T. H., Feltovich, P. J., & Glaser, R. (1981). Categorization and representation of physics problems by experts and novices. Cognitive Science, 5(2), 121–152. [Google Scholar] [CrossRef]
- Clements, D. H., & Sarama, J. (2007). Early childhood mathematics learning. In F. K. Lester Jr. (Ed.), Second handbook of research on mathematics teaching and learning (pp. 461–555). Information Age Publishing. [Google Scholar]
- Cook, M. P. (2006). Visual representations in science education: The influence of prior knowledge and cognitive load theory on instructional design principles. Science Education, 90(6), 1073–1091. [Google Scholar] [CrossRef]
- Cooper, J. L., Sidney, P. G., & Alibali, M. W. (2018). Who benefits from diagrams and illustrations in math problems? Ability and attitudes matter: Diagrams and illustrations. Applied Cognitive Psychology, 32(1), 24–38. [Google Scholar] [CrossRef]
- Daniel, K. L., Bucklin, C. J., Austin Leone, E., & Idema, J. (2018). Towards a definition of representational competence. In K. L. Daniel (Ed.), Towards a framework for representational competence in science education: Models and modeling in science education (pp. 3–11). Springer. [Google Scholar] [CrossRef]
- Donovan, A. M., & Alibali, M. W. (2022). Manipulatives and mathematics learning: The roles of perceptual and interactive features. In S. L. Macrine, & J. M. B. Fugate (Eds.), Movement matters: How embodied cognition informs teaching and learning (pp. 147–161). The MIT Press. [Google Scholar] [CrossRef]
- Ericsson, K. A., & Simon, H. A. (1980). Verbal reports as data. Psychological Review, 87(3), 215–251. [Google Scholar] [CrossRef]
- Fitzpatrick, C. L., & Hallett, D. (2019). Early understanding of fractions via early understanding of proportion and division. In K. M. Robinson, H. P. Osana, & D. Kotsopoulos (Eds.), Mathematical learning and cognition in early childhood (pp. 249–271). Springer. [Google Scholar]
- Fuhs, M. W., & McNeil, N. M. (2013). ANS acuity and mathematics ability in preschoolers from low-income homes: Contributions of inhibitory control. Developmental Science, 16(1), 136–148. [Google Scholar] [CrossRef] [PubMed]
- Gilmore, C., & Cragg, L. (2018). The role of executive function skills in the development of children’s mathematical competencies. In A. Henik, & W. Fias (Eds.), Heterogeneity of function in numerical cognition (pp. 263–286). Elsevier Science & Technology. [Google Scholar] [CrossRef]
- Gilmore, C., Keeble, S., Richardson, S., & Cragg, L. (2015). The role of cognitive inhibition in different components of arithmetic. ZDM, 47(5), 771–782. [Google Scholar] [CrossRef]
- Glaser, R. (1990). The reemergence of learning theory within instructional research. American Psychologist, 45(1), 29–39. [Google Scholar] [CrossRef]
- Glenberg, A. M. (2008). Embodiment for education. In P. Calvo, & A. Gomila (Eds.), Handbook of cognitive science: An embodied approach (pp. 355–372). Elsevier. [Google Scholar]
- Glenberg, A. M., Witt, J. K., & Metcalfe, J. (2013). From the revolution to embodiment: 25 years of cognitive psychology. Perspectives on Psychological Science, 8(5), 573–585. [Google Scholar] [CrossRef] [PubMed]
- Gobet, F. (2005). Chunking models of expertise: Implications for education. Applied Cognitive Psychology, 19(2), 183–204. [Google Scholar] [CrossRef]
- Gobet, F., Lane, P. C. R., Croker, S., Cheng, P. C.-H., Jones, G., Oliver, I., & Pine, J. M. (2001). Chunking mechanisms in human learning. Trends in Cognitive Sciences, 5(6), 236–243. [Google Scholar] [CrossRef] [PubMed]
- Goldstone, R. L., & Son, J. Y. (2005). The transfer of scientific principles using concrete and idealized simulations. Journal of the Learning Sciences, 14(1), 69–110. [Google Scholar] [CrossRef]
- Graham, T. A. (1999). The role of gesture in children’s learning to count. Journal of Experimental Child Psychology, 74(4), 333–355. [Google Scholar] [CrossRef] [PubMed]
- Gregg, J., & Gregg, D. U. (2007). Measurement and fair-sharing models for dividing fractions. Mathematics Teaching in the Middle School, 12(9), 490–496. [Google Scholar] [CrossRef]
- Hansen, N., Rinne, L., Jordan, N. C., Ye, A., Resnick, I., & Rodrigues, J. (2017). Co-development of fraction magnitude knowledge and mathematics achievement from fourth through sixth grade. Learning and Individual Differences, 60, 18–32. [Google Scholar] [CrossRef]
- Harp, S. F., & Mayer, R. E. (1998). How seductive details do their damage: A theory of cognitive interest in science learning. Journal of Educational Psychology, 90(3), 414–434. [Google Scholar] [CrossRef]
- Jeong, Y., Levine, S. C., & Huttenlocher, J. (2007). The development of proportional reasoning: Effect of continuous versus discrete quantities. Journal of Cognition and Development, 8(2), 237–256. [Google Scholar] [CrossRef]
- Kalyuga, S. (2007). Expertise reversal effect and its implications for learner-tailored instruction. Educational Psychology Review, 19, 509–539. [Google Scholar] [CrossRef]
- Kalyuga, S. (2013). Knowledge and working memory effects on learning from visual displays. In G. Schraw, M. T. McCrudden, & D. Robinson (Eds.), Learning through visual displays (pp. 75–96). Information Age. [Google Scholar]
- Kaminski, J. A., & Sloutsky, V. M. (2013). Extraneous perceptual information interferes with children’s acquisition of mathematical knowledge. Journal of Educational Psychology, 105(2), 351–363. [Google Scholar] [CrossRef]
- Kaminski, J. A., & Sloutsky, V. M. (2020). The use and effectiveness of colorful, contextualized, student-made material for elementary mathematics instruction. International Journal of STEM Education, 7(6), 6. [Google Scholar] [CrossRef]
- Kaminski, J. A., Sloutsky, V. M., & Heckler, A. (2009). Transfer of mathematical knowledge: The portability of generic instantiations. Child Development Perspectives, 3(3), 151–155. [Google Scholar] [CrossRef]
- Kidspot. (2016, January 16). Maths activity: How to teach fractions using lego [Video]. YouTube. Available online: https://www.youtube.com/watch?v=JONriZyiYpM (accessed on 20 July 2025).
- Lenzner, A., Schnotz, W., & Müller, A. (2013). The role of decorative pictures in learning. Instructional Science, 41(5), 811–831. [Google Scholar] [CrossRef]
- Macevicius, C., & Osana, H. P. (2024, June 26–28). Does sharing distract you? Effects of perceptual features on third-graders’ partitioning strategies [Poster presentation]. Mathematical Cognition and Learning Society 7th Annual Conference, Washington, DC, USA. [Google Scholar]
- Magner, U. I. E., Schwonke, R., Aleven, V., Popescu, O., & Renkl, A. (2014). Triggering situational interest by decorative illustrations both fosters and hinders learning in computer-based learning environments. Learning and Instruction, 29, 141–152. [Google Scholar] [CrossRef]
- Manches, A., O’Malley, C., & Benford, S. (2010). The role of physical representations in solving number problems: A comparison of young children’s use of physical and virtual materials. Computers & Education, 54(3), 622–640. [Google Scholar] [CrossRef]
- Martin, T. (2009). A theory of physically distributed learning: How external environments and internal states interact in mathematics learning. Child Development Perspectives, 3(3), 140–144. [Google Scholar] [CrossRef]
- Mayer, R. E. (2008). Applying the science of learning: Evidence-based principles for the design of multimedia instruction. American Psychologist, 63(8), 760–769. [Google Scholar] [CrossRef] [PubMed]
- Mayer, R. E. (2019). Taking a new look at seductive details. Applied Cognitive Psychology, 33(1), 139–141. [Google Scholar] [CrossRef]
- McDougal, E., Silverstein, P., Treleaven, O., Jerrom, L., Gilligan-Lee, K., Gilmore, C., & Farran, E. K. (2023). Associations and indirect effects between LEGO® construction and mathematics performance. Child Development, 94(5), 1381–1397. [Google Scholar] [CrossRef] [PubMed]
- McDougal, E., Silverstein, P., Treleaven, O., Jerrom, L., Gilligan-Lee, K., Gilmore, C., & Farran, E. K. (2024). Assessing the impact of LEGO® construction training on spatial and mathematical skills. Developmental Science, 27(2), e13432. [Google Scholar] [CrossRef] [PubMed]
- Menendez, D., Rosengren, K. S., & Alibali, M. W. (2020). Do details bug you? Effects of perceptual richness in learning about biological change. Applied Cognitive Psychology, 34(5), 1101–1117. [Google Scholar] [CrossRef]
- Menendez, D., Rosengren, K. S., & Alibali, M. W. (2022). Detailed bugs or bugging details? The influence of perceptual richness across elementary school years. Journal of Experimental Child Psychology, 213, 105269. [Google Scholar] [CrossRef] [PubMed]
- Merkley, R., Thompson, J., & Scerif, G. (2016). Of huge mice and tiny elephants: Exploring the relationship between inhibitory processes and preschool math skills. Frontiers in Psychology, 6, 1903. [Google Scholar] [CrossRef] [PubMed]
- Mix, K. S. (2008). Surface similarity and label knowledge impact early comparisons. British Journal of Developmental Psychology, 26(1), 13–32. [Google Scholar] [CrossRef]
- Moyer, P. S. (2001). Are we having fun yet? How teachers use manipulatives to teach mathematics. Educational Studies in Mathematics, 47(2), 175–197. [Google Scholar] [CrossRef]
- Olanoff, D., Lo, J. J., & Tobias, J. (2014). Mathematical content knowledge for teaching elementary mathematics: A focus on fractions. The Mathematics Enthusiast, 11(2), 5. [Google Scholar] [CrossRef]
- Petersen, L. A., & McNeil, N. A. (2013). Effects of perceptually rich manipulatives on preschoolers’ counting performance: Established knowledge counts. Child Development, 84(3), 1020–1033. [Google Scholar] [CrossRef] [PubMed]
- Pouw, W. T. J. L., van Gog, T., & Paas, F. (2014). An embedded and embodied cognition review of instructional manipulatives. Educational Psychology Review, 26, 51–72. [Google Scholar] [CrossRef]
- Rau, M. A. (2017a). A framework for educational technologies that support representational competencies. IEEE Transactions on Learning Technologies, 10(3), 290–305. [Google Scholar] [CrossRef]
- Rau, M. A. (2017b). Conditions for the effectiveness of multiple visual representations in enhancing STEM learning. Educational Psychology Review, 29, 717–761. [Google Scholar] [CrossRef]
- Rau, M. A. (2017c). Do knowledge-component models need to incorporate representational competencies? International Journal of Artificial Intelligence in Education, 27, 298–319. [Google Scholar] [CrossRef]
- Rey, G. D. (2012). A review of research and a meta-analysis of the seductive detail effect. Educational Research Review, 7(3), 216–2371. [Google Scholar] [CrossRef]
- Reys, R., Lindquist, M., Lambdin, D. V., & Smith, N. L. (2015). Helping children learn mathematics (11th ed.). Wiley. [Google Scholar]
- Richland, L. E., Stilger, J. W., & Holyoak, K. J. (2012). Teaching the conceptual structure of mathematics. Educational Psychologist, 47(3), 189–203. [Google Scholar] [CrossRef]
- Saxe, G. B., Gearhart, M., & Nasir, N. S. (2001). Enhancing students’ understanding of mathematics: A study of three contrasting approaches to professional support. Journal of Mathematics Teacher Education, 4(1), 55–79. [Google Scholar] [CrossRef]
- Schneider, M., Merz, S., Stricker, J., De Smedt, B., Torbeyns, J., Verschaffel, L., & Luwel, K. (2018). Associations of number line estimation with mathematical competence: A meta-analysis. Child Development, 89(5), 1467–1484. [Google Scholar] [CrossRef] [PubMed]
- Schoenherr, J., & Schukajlow, S. (2024). Characterizing external visualization in mathematics education research: A scoping review. Mathematics Education, 56, 73–85. [Google Scholar] [CrossRef]
- Schraw, G., McCrudden, M. T., & Robinson, D. (2013). Learning through visual displays. Information Age. [Google Scholar]
- Shipley, E. F., & Shepperson, B. (1990). Countable entities: Developmental changes. Cognition, 34(2), 109–136. [Google Scholar] [CrossRef] [PubMed]
- Sidney, P. G., & Alibali, M. W. (2015). Making connections in math: Activating a prior knowledge analogue matters for learning. Journal of Cognition and Development, 16(1), 160–185. [Google Scholar] [CrossRef]
- Sidney, P. G., & Thompson, C. A. (2019). Implicit analogies in learning: Supporting transfer by warming up. Current Directions in Psychological Science, 28(6), 619–625. [Google Scholar] [CrossRef]
- Simonsmeier, B. A., Flaig, M., Deiglmayr, A., Schalk, L., & Schneider, M. (2022). Domain-specific prior knowledge and learning: A meta-analysis. Educational Psychologist, 57(1), 31–54. [Google Scholar] [CrossRef]
- Son, J. Y., & Goldstone, R. L. (2009). Fostering general transfer with specific simulations. Pragmatics and Cognition, 17(1), 1–42. [Google Scholar] [CrossRef]
- Sophian, C. (2008). The origins of mathematical knowledge in childhood. Routledge. [Google Scholar] [CrossRef]
- Sweller, J., Ayres, P., & Kalyuga, S. (2011). Cognitive load theory. Springer. [Google Scholar] [CrossRef]
- Tellos, A., & Osana, H. P. (2023, June 5–8). What makes an array? How perceptual features of LEGO bricks influence children’s interpretations of multiplicative structures [Conference presentation]. Mathematical Cognition and Learning Society 6th Annual Conference, Loughborough, UK. [Google Scholar]
- Tellos, A., & Osana, H. P. (2024, June 26–28). The role of form and perceptual features in visual representations on children’s interpretations of multiplicative structure in the third and fifth grades [Conference presentation]. Mathematical Cognition and Learning Society 7th Annual Conference, Washington, DC, USA. [Google Scholar]
- Tellos, A., & Osana, H. P. (2025). Watch those studs! How prior domain knowledge and extraneous details on LEGO bricks influence children’s fraction division. Journal of Research in Science, Mathematics and Technology Education, 8(SI), 241–262. [Google Scholar] [CrossRef]
- TheDadLab. (2019, October 29). How to teach fractions with LEGO bricks [Video]. YouTube. Available online: https://www.youtube.com/watch?v=UCkS0afSjm0&t=1s (accessed on 20 July 2025).
- TheDadLab. (2020, January 29). How to teach multiplication with LEGO bricks [Video]. YouTube. Available online: https://www.youtube.com/watch?v=GW4DDBdh3MA (accessed on 20 July 2025).
- van Kesteren, M. T. R., Rijpkema, M., Ruiter, D. J., Morris, R. G. M., & Fernández, G. (2014). Building on prior knowledge: Schema-dependent encoding processes relate to academic performance. Journal of Cognitive Neuroscience, 26(10), 2250–2261. [Google Scholar] [CrossRef] [PubMed]
- Verschaffel, L., Schukajlow, S., Star, J., & Van Dooren, W. (2020). Word problems in mathematics education: A survey. ZDM, 52(1), 1–16. [Google Scholar] [CrossRef]
- We Are Teachers. (2018, November 12). Teaching fractions with LEGO bricks [Video]. YouTube. Available online: https://www.youtube.com/shorts/pbmLnP7Qh_4 (accessed on 20 July 2025).
- Wege, E. T., Smedt, B. D., Gilmore, C., & Inglis, M. (2023). Counting many as one: Young children can understand sets as units except when counting. Journal of Experimental Child Psychology, 225, 105533. [Google Scholar] [CrossRef] [PubMed]
- Zembat, I. O. (2017). Fostering remainder understanding in fraction division. Australian Mathematics Teacher, 73(3), 19–26. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).