Next Article in Journal
Youth Data Visualization Practices: Rhetoric, Art, and Design
Previous Article in Journal
A Scoping Review of STEAM Policies in Europe
Previous Article in Special Issue
A Meta-Analysis of Technology-Based Word-Problem Interventions for Students with Disabilities
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Education Sciences
Volume 15
Issue 6
10.3390/educsci15060780
education-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Exploring the Effects of a Problem-Posing Intervention with Students at Risk for Mathematics and Writing Difficulties

by
Jing Wang
1,*,
Pamela Shanahan Bazis
1 and
Qingli Lei
2
1
Department of Special Education and Communication Disorders, University of Nebraska-Lincoln, Lincoln, NE 68503, USA
2
Department of Special Education, University of Illinois Chicago, Chicago, IL 60607, USA
*
Author to whom correspondence should be addressed.
Educ. Sci. 2025, 15(6), 780; https://doi.org/10.3390/educsci15060780
Submission received: 26 January 2025 / Revised: 29 May 2025 / Accepted: 16 June 2025 / Published: 19 June 2025
(This article belongs to the Special Issue Conceptual Understanding in Mathematics: Focusing on Students with Learning Disabilities or Difficulties)
Browse Figures
Review Reports Versions Notes

Abstract

:
Word problem posing is a critical component of student mathematics learning. This study examined the effects of a problem-posing intervention designed to improve mathematics performance and sentence-writing conventions. Using a multiple baseline across participants design, three third-grade students with mathematics and writing difficulties received one-on-one intervention delivered after school at a university reading center. Data were collected from baseline, intervention, and maintenance phases. Visual analysis and Tau-U statistical analysis indicated that all three students showed improvements in problem solving, problem posing, total words written, words spelled correctly, and correct writing sequence. Post-intervention data suggested that students maintained the improvement over baseline. Discussion and implications for future practice and research were provided.

1. Introduction

According to the National Assessment of Educational Progress (National Center for Educational Statistics, 2022), 64% of fourth-grade students and 74% of eighth-grade students performed below the proficient level in mathematics. Although students’ challenges with learning mathematics might be caused by various issues, such as memory problems, anxiety, and low confidence (Fuchs et al., 2020; Namkung et al., 2024), and may manifest across multiple mathematical domains (e.g., fractions, four operations; Fuchs et al., 2017b; Zhang et al., 2014), word problems remain an especially challenging area for many students (Rojo et al., 2024). One key factor contributing to this challenge is the limited emphasis on problem-posing instruction in many classrooms (Arsenault et al., 2024), despite evidence that writing word problems can deepen conceptual understanding and improve problem-solving skills. As the Common Core Mathematics State Standards (CCMSS; 2010) has highlighted the importance of incorporating writing tasks (e.g., problem posing) to develop and assess students’ understanding of mathematical concepts (Casa et al., 2016), the question remains as to how to best teach mathematics and writing in tandem. Exploring ways to incorporate writing tasks into mathematics instruction may hold value to improve overall mathematics and writing outcomes.
Writing instruction focusing on content areas, such as mathematics, has been found to improve students’ understanding of the content and enhance overall comprehension (Graham & Hebert, 2011; Swanson et al., 2013). When writing and mathematics instruction are integrated, students are more likely to better apply mathematics skills (Bicer et al., 2013). Effective writing requires focused instruction in foundational writing skills and conventions such as forming complete sentences, using subject–verb agreement, and applying correct capitalization and punctuation (Datchuk & Kubina, 2013; Graham et al., 2012a). However, explicit instruction in foundational writing skills is often inadequate or even absent from writing instruction, which can hinder writing quality, especially for students with writing difficulties and disabilities (Berninger et al., 2010). Research has shown that writing interventions that incorporate writing processes (i.e., planning, drafting, revising, editing), alongside targeted strategies and instruction in transcription skills, had positive impacts on overall writing quality (Graham et al., 2012b).

2. Conceptual-Model-Based Problem-Solving Approach

Conceptual-Model-Based Problem Solving (COMPS), developed by Xin (2008, 2012), is an evidence-based instructional approach designed to enhance the mathematical problem-solving abilities of students, particularly those with learning disabilities in mathematics or those at risk for mathematics difficulties. COMPS emphasizes understanding mathematical relationships within additive and multiplicative word problems by guiding students to represent these relationships through generalized mathematical equations. The cohesive problem-solving model “unit rate × number of units = product” provides visual scaffolding and serves as a graphic organizer that helps students map word problems into model equations for reasoning and problem solving. For example, when students encounter a word problem story where all quantities are given (e.g., “Emily owns 8 bags of marbles. Each bag has 3 marbles. She has a total of 24 marbles.”), COMPS enables them to align the information into a balanced equation without solving for unknowns. This approach helps students recognize the mathematical relationships among the three quantities that make up the model equation (Xin et al., 2020). Additionally, COMPS incorporates linguistic scaffolding through Word Problem Story Grammar, which consists of a series of prompting questions (e.g., who, what, where) that assist students in extracting key information from the problem (Xin et al., 2020). The explicit reasoning behind mathematical operations in COMPS allows students to approach various problem types systematically.
Previous research on the COMPS approach has demonstrated its effectiveness in improving word problem-solving performance among elementary students with or who are at risk for mathematics difficulties. A number of studies consistently show that COMPS results in significant gains in both additive and multiplicative problem-solving skills among students with mathematics disabilities or difficulties across various instructional settings (e.g., Bruno et al., 2024; Ma & Xin, 2024). For instance, Griffin et al. (2018) conducted a group experimental study in a rural elementary classroom in the U.S. with fourth- and fifth-grade students with and without disabilities. Their findings indicated that students in the COMPS group outperformed their peers in the business-as-usual group, with a large effect size of 0.25, suggesting substantially important outcomes. Additionally, a single-subject design study by Xin et al. (2020) indicated that COMPS significantly enhances additive word problem-solving abilities in English learners with mathematics difficulties, yielding a strong Tau-U effect size of 0.96 and demonstrating improvements in generalization measures. Collectively, these findings validate that COMPS effectively addresses both mathematical and linguistic challenges and improves problem-solving outcomes.

3. Problem Posing

Problem posing is a major component of mathematics writing, often described as a form of mathematically creative writing (Arsenault et al., 2024). In problem posing, students write their own word problems or mathematical story problems (Casa et al., 2016). Prior research has categorized problem posing into three types: (a) free problem posing, in which students create a problem from an open-ended prompt; (b) semi-structured problem posing, in which students apply previously acquired knowledge to formulate a problem using the partial information they are given (e.g., a picture, a diagram); and (c) structured problem posing, in which students modify the numbers, context, or the question of an existing problem to formulate a new one (Stoyanova & Ellerton, 1996; see also Yang & Xin, 2022). Research shows that engagement in problem-posing activities leads to improved reasoning and problem-solving abilities (Cai, 2003; Cai & Hwang, 2002). These gains stem from opportunities to reflect on prior knowledge, construct new knowledge, and establish meaningful connections among mathematical ideas (Arsenault et al., 2024; Cai et al., 2013).
Although several intervention studies have examined different forms of mathematics writing to enhance word problem learning outcomes, including exploratory (e.g., Swanson et al., 2014), informative (e.g., Hughes et al., 2019), and argumentative writing (e.g., Hacker et al., 2019), unfortunately, only one investigation to date has focused on creative writing (i.e., problem posing; Yang & Xin, 2022) for students with mathematics learning disabilities. Yang and Xin (2022) conducted an intervention study involving three seventh-grade students with identified learning disabilities. The study utilized a multiple baseline design across students, with students engaging in problem-posing instruction that incorporated the COMPS strategy for approximately 50 min per day, five days a week. In these sessions, students learned how to (a) represent and map the three elements of multiplicative comparison problems in the COMPS diagram equation to solve for an unknown quantity and (b) apply “What-if-Not” strategies to create new multiplicative comparison types of word problems. Results showed that the intervention effectively improved both students’ problem-solving and problem-posing skills. Given these documented benefits for students at the middle-school level, it is important to understand the extent to which problem-posing instruction affects elementary students with mathematics difficulties or disabilities, as these students may encounter increasingly significant challenges in mathematics in later grades when presented with more complex word problems (Lei & Xin, 2023; Wang et al., 2023).

4. Writing Theory and the Role of Working Memory

Effective writing requires the interplay of foundational skills and cognitive processes (Berninger & Winn, 2006; Graham & Harris, 2000; McCutchen, 2000). The Not So Simple View of Writing cognitive model emphasizes that successful composition relies on both transcription skills (e.g., handwriting, spelling) and higher-order cognitive functions (e.g., organization, self-monitoring; Berninger & Amtmann, 2003; Berninger et al., 2002). However, these skills are limited by an individual’s working memory capacity, meaning that difficulties in either area can place excessive demands on working memory, ultimately hindering the ability to produce coherent written work.
Furthermore, effective writing is reliant on the individual’s ability to transcribe individual letters and combine them into meaningful words (Graham & Perin, 2007). Therefore, a critical factor in improving written composition is developing automaticity in transcription skills, which refers to achieving a level of forming letters and spelling words that requires minimal-to-no conscious effort (Graham & Harris, 2000; Ritchey et al., 2016). Thus, as writers move beyond the word level, the ability to construct cohesive and meaningful sentences becomes critical. Research suggests that strengthening sentence-level writing skills reduces cognitive demands during composition, freeing up mental resources for higher-level tasks, such as organizing and revising text (Berninger et al., 2002; Datchuk & Kubina, 2013; Datchuk & Rodgers, 2019). This reduction in cognitive load allows writers to focus more on idea generation and content improvement rather than being constrained by the mechanics of transcription.

5. Scaffolded Writing Support

To further reduce cognitive load and support students in writing tasks, scaffolded writing support, such as graphic organizers, sentence models, and word banks, have been found to enhance writing quality (Graham & Harris, 2000, 2003; Graham & Perin, 2007; Hebert et al., 2023). For example, sentence models that demonstrate proper sentence structure and punctuation help students improve writing coherence and allow them to focus on one aspect of writing at a time. Similarly, providing students with access to a personal dictionary or word bank has been shown to improve vocabulary use and spelling accuracy, further enhancing overall writing quality (Harris et al., 2017; Donnelly & Roe, 2010). Checklists, another effective scaffold, can be used at any stage in the writing process to guide students’ work and ensure that the key components of writing are addressed (Jagaiah et al., 2019; Troia, 2009). Overall, these scaffolded writing supports reduce the cognitive demands associated with word retrieval, sentence structure, and organization, allowing students to focus on higher-level tasks such as content development and revision.

6. Purpose of the Study

Researchers have documented the efficacy of the COMPS approach in improving word problem-solving and problem-posing skills, as well as the positive impact of sentence-writing conventions in improving overall writing quality. While previous research has reported positive outcomes, few studies have explored integrating instruction in writing conventions to support word problem learning. The purpose of this single-case design study is to provide scaffolded support to elementary students with word problem and sentence-writing convention difficulties, examining the effects of a problem-posing intervention incorporating writing instructions on multiplication word problem solving, problem posing, and sentence-writing conventions. More specifically, this study seeks to answer the following research questions:
  • What is the relationship between the problem-posing intervention and the word problem performance (i.e., problem solving and problem posing)?
  • What is the relationship between the problem-posing intervention and the sentence-writing conventions in the problem-posing response performance (i.e., total words written, words spelled correctly, and correct writing sequence)?

7. Method

7.1. Participants

Participants were recruited from the university reading center after receiving approval from the institutional review board. Participants were recruited based on the following inclusion criteria: (a) enrolled in grades 3 through 6, (b) experiencing mathematical difficulties in the area of word problems as reported by parents, (c) scored below the 40th percentile on the Test of Mathematical Abilities-3rd edition (TOMA-3) (Jitendra et al., 2013), (d) experiencing difficulties in sentence writing as reported by parents, and (e) scored below the 40th percentile on the Weschler Individual Achievement Test-4th edition (WIAT-4) sentence-building subtest. Three participants met the inclusion criteria and were all attending the reading center tutoring program at the time of the study. Participant demographic information is displayed in Table 1 (all names are pseudonyms).

7.2. Setting and Interventionists

This study took place at a university reading center’s after-school reading tutoring program. The reading center is affiliated with University A in a midwestern state in the U.S. and serves students in grades K-12 from different parts of the region. Students who enrolled in the tutoring program were experiencing difficulties in school, and their reading performances were between one and three years below grade level, as verified by reading center staff. Once enrolled at the reading center, students receive one-semester-long supervised one-on-one tutoring in reading-related skills from university students majoring in education as part of their coursework. This study was conducted immediately after the participants’ 60-min reading center tutoring session. All intervention sessions were held in a semi-private instructional area that contained tables and chairs, or a designated office assigned by the reading center director, depending on the space availability of that day’s tutoring schedule. The first authors served as the interventionists for this study and both of them are special education faculty members of University A. The former interventionist holds a special education teaching license and has more than eight years of experience in research and teaching focused on mathematics interventions for students experiencing mathematics disabilities and difficulties across varied settings. The latter interventionist holds a K-8 general education teaching license and certification as an academic language therapist for students with specific learning disabilities. They worked with the participants one-on-one twice a week for a total of 11 weeks, and each session lasted approximately 20–30 min.

7.3. Materials

Interventionists collaboratively designed materials for the study. The materials included problem-posing intervention worksheets (i.e., mathematics-writing mats) and test worksheets. In addition, to understand students’ perceptions of the intervention, interventionists designed a five-point Likert-scale social validity questionnaire. Interventionists used the mathematics-writing mats during instruction while using the test worksheets across the intervention sessions. The second author, a university faculty member with intensive mathematics teaching and research experience, reviewed all mathematics problems to ensure content validity. Also, a non-author (a university faculty member with expertise in writing instruction for students with learning difficulties) reviewed all the writing tasks for appropriateness and rigor.
Mathematics-writing mat. Sixteen mathematics-writing mats were created by the interventionists. Each intervention session used two mathematics-writing mats to teach word problem posing and problem solving (one for modeling and one for guided practice). Each mathematics-writing mat included seven sections (each section is marked using a capital letter, see Figure 1): (1) A—a three-box table with unique name tags (i.e., total #, # of groups, and # of items in each group) to represent the known and unknown quantities, as well as pictures to visualize the problem scenario, (2) B—a structured working space with writing lines for problem posing, (3) C—a six-element sentence-writing convention checklist (e.g., a capital letter at the beginning), (4) D—the standardized problem-solving conceptual model “number of groups × number of items in each group = total number” (Xin, 2008), (5) E—suggested vocabulary specific to problem posing (e.g., painting, students), (6) F—sample sentence example with components labeled (e.g., “We see 3 dogs.”; “see-is doing or did”), and (7) G—empty working space for students to solve the problem. Researchers created a total of eight mathematics-writing mats and used one unique mat during each intervention session.
Word problem worksheets. Nineteen word problem test worksheets were created by the interventionists, each consisting of two parts. Part 1 included three one-step equal-group word problems: one problem with the “number of groups” as the unknown, one with the “number of items in each group” as the unknown, and one with the “total” as the unknown. All problems were one-step equal-group word problems, and these problems closely mirrored those used in daily instruction, with the order of the three problem types randomized within each worksheet. Part 2 included three mathematical expressions (e.g., 3 × 4 = y). Each expression represented the three elements of the equal-group problem structure, containing two known quantities and one unknown quantity. The unknown quantity, “y”, appeared in different positions (i.e., at the beginning, middle, or end) of the expression. The order of the three expressions with the letter “y” was also randomized. No word problems or mathematical expressions were repeated across the worksheets.

7.4. Design and Procedures

A multiple baseline design across participants (Ledford & Gast, 2024) was used to evaluate the effects of the intervention. A single-case research design fits the purpose of the study because it allows researchers to examine the functional relationship between the intervention and the dependent measures (Kratochwill et al., 2010). This study included three phases: baseline, intervention, and maintenance. All students began baseline simultaneously. As suggested by Kratochwill et al. (2010), at least five baseline data points were collected from each student during the baseline condition. After baseline data were collected, a student who demonstrated a stable baseline data pattern started receiving intervention, while the other two students remained in the baseline phase. In total, the first, second, and third students received baseline measures for five, seven, and nine sessions, respectively. All students entered the maintenance phase after receiving eight intervention sessions.

7.5. Baseline

During the baseline condition, students were asked to complete the worksheet independently. No instruction or corrective feedback was given. However, interventionists provided praise (e.g., “Good job!”, “Thank you for your hard work!”) or prompts (e.g., “Can you please continue working on this?”) when necessary. Each baseline session took approximately 10–12 min.

7.6. Intervention

During the intervention phase, the lessons were structured to address specific types of unknowns in the word problems. Lessons 1–4 focused on “total number” unknown problems, Lessons 5–6 targeted “number of items in each group” unknown problems, and Lessons 7–8 covered “number of groups” unknown problems. Each session followed the same instructional procedures: modeling one problem, guided practice with one problem, and independent practice with five problems. The interventionists delivered the instruction using a script, though they did not read it verbatim, to ensure adherence to lesson plans and consistency in the instructional sequence between the two interventionists. The script is available upon request. Each session lasted approximately 25–30 min.
Modeling. Each session began with a statement of the lesson objectives of the day. The first instructional step involved the interventionists providing explicit instructions on constructing sentences corresponding to each element of the equal-group word problem and the associated pictures (see section A in Figure 1). Given the limited session time, sample sentences for direct modeling were created and printed on the mat before each session. To facilitate the problem-posing process, the interventionists reviewed the suggested vocabulary with the students (see section E in Figure 1). Next, the interventionists demonstrated how to map the information onto the conceptual problem-solving model (see section D in Figure 1). Using think-aloud techniques, they modeled how to interpret information from the pictures and labels in each box and populate the diagram labeled with names. By reading aloud the sample sentences and pointing to the pictures and name tags on the diagram, the interventionists aimed to guide students in accurately matching the information and reviewing the problem they posed. Then, the interventionists demonstrated the problem based on the mathematical expression established in the previous step. Finally, the interventionists modeled a self-assessment of the problem-posing response using a sentence-writing convention checklist and the sample sentence as a guide (see sections C and F in Figure 1). The demonstration moved across each sentence from left to right, beginning at the top of the checklist (i.e., a capital letter at the beginning), then moving through grammar- and syntax-related steps (e.g., who or what, object related to who/what), and ending with a check for appropriate punctuation at the end of the sentence.
Guided Practice. Using another new mathematics-writing mat with a different problem scenario, the interventionists provided students with an opportunity for guided practice. The interventionist brainstormed with students about the problem scenario using the suggested vocabulary and then prompted them to create sentences in the structured working space (see sample student’s work in section B in Figure 1). Throughout the problem-posing and problem-solving process, the interventionist provided corrective feedback when needed. For example, if a student struggled with spelling or writing sentences, the interventionists modeled the correct spelling or sentence construction to provide support. Students were also guided to self-assess their sentence-writing conventions in the problem-posing response using the checklist. The interventionist offered additional support for revision and edits to ensure that the sentences were accurate and included all the required elements outlined in the checklist. Finally, students were guided to map the information onto the cohesive problem-solving diagram and then proceeded to solve the problem (see sections D and G in Figure 1).
Independent Practice. Independent problem-solving and problem-posing assessment was administered to each student immediately after guided practice. Each independent practice worksheet consisted of six problems in total (i.e., three equal-group word problems for problem solving and three equations for problem posing). All the problems were similar to those used during modeling and guided practice.

7.7. Maintenance

The maintenance condition was implemented one week after each student completed their intervention and followed the same procedures as the baseline phase. The interventionist did not provide prompts or feedback. However, praise and encouragement were provided to keep students motivated and engaged.

7.8. Dependent Measures

Two sets of dependent measures were assessed. The first set was word problem performance, which included problem-solving accuracy and problem-posing performance. For problem-solving accuracy, each problem on the worksheet was scored based on two components: the problem expression worth 1 point and the answer worth another 1 point. The maximum value for problem-solving performance was 6. Zero points were awarded for incorrect answers with no problem expression, incorrect problem expression and answer, or leaving no response to the problem. Additionally, problem-posing performance was assessed by scoring the sentences written to describe each component of the mathematical expression, each containing two known numbers and an unknown quantity, “y”. The total maximum score was 18 points. Table 2 provides details on the scoring method for problem posing. The dependent variables for word problem performance were the percentage of correct responses out of three problems in each set.
Additionally, to evaluate sentence-writing conventions in the problem-posing response performance, the second set of dependent measures included (a) words written (TWW), a common proxy for examining writing fluency; (b) words spelled correctly (WSC), assessing the ability to apply orthographic knowledge; and (c) correct writing sequence (CWS), evaluating the ability to construct grammatically correct sentences. These measures are standard components of writing-curriculum-based measures (CBM; e.g., Allen et al., 2020; Deno, 2003). Written responses were scored using the following methods. First, for TWW, any letter or group of letters representing a word was awarded one point, with spaces between letters or groups of letters considered in the scoring decision. Second, for WSC, words were awarded one point if spelled correctly. This included words with inconsistent capitalization or words spelled correctly but not grammatically correct in the context of the sentence (e.g., plural forms). Also, words with letter reversals were scored as incorrect if the reversed letter forms a different letter (e.g., “dag” for “bag”). Third, for CWS, scoring adjustments were made to better reflect mathematics writing (Hebert et al., 2019). Specifically, any word pair, including numerals or symbols, was considered a correct writing sequence if it adhered to proper capitalization, spelling, and syntax.

8. Data Analysis

To investigate the presence of a functional relationship between the problem-posing intervention and the dependent measures, student performances were graphically represented across baseline, intervention, and maintenance phases. Visual analysis was the main method of data analysis. In addition, level, trend, variability, immediacy, overlap, and consistency were analyzed (Kratochwill et al., 2010). Further, as a supplementary visual analysis, we computed Tau-U scores via an online tool (http://www.singlecaseresearch.org/calculators/tau-u (accessed on 16 June 2024). Following Parker et al.’s (2011) guidelines, a Tau-U score in the range of 0–0.65 indicates weak effect sizes, 0.66–0.92 represents a moderate effect size, and 0.93–1 indicates a strong effect size.

8.1. Implementation Procedure Fidelity

A doctoral student (non-author) in a special education program observed at least 33% of sessions in person for each student during each intervention phase (i.e., baseline, intervention, and maintenance). The first authors trained the doctoral student on observation before collecting implementation fidelity data. An implementation fidelity checklist was created to assess the interventionists’ adherence to the intervention plan. The fidelity checklist included the intervention components and relative examples of interventionist behaviors that might be observed during intervention delivery. The fidelity of implementation was calculated as a percentage of intervention components as present for each observed session × 100%. The fidelity scores were collected during baseline (M = 100%), intervention (M = 93.3%, range = 84.4–100%), and maintenance (M = 100%).

8.2. Inter-Rater Agreement

Prior to scoring the independent worksheets, the two interventionists underwent mutual training. After achieving at least 80% agreement on the practice worksheet, they began independently scoring all the worksheets. A minimum of 33% of all worksheets across conditions for each student were assessed between the two interventionists. Inter-rater Agreement (IOA) data were calculated by the total number of agreements divided by the total number of agreements plus the total number of disagreements and multiplied by 100 (Kennedy, 2005). IOA was 100% for the baseline phase on both word problem and sentence-writing convention measures. During the intervention phase, IOA for mathematics measures across the students was 96.7%, 97.1%, and 97.4%, and IOA for sentence-writing convention measures across the students was 91.1%, 86.3%, and 94.7%. During the maintenance phase, IOA for mathematics measures across the students was 100%, and IOA for sentence-writing conventions in the problem-posing response measures across the students was 93.8%, 88.6%, and 96.1%.

8.3. Social Validity

Students were asked to orally respond to an interventionist-developed social validity questionnaire at the end of the session during the last maintenance session. The questionnaire included five statements: (1) I enjoyed this word problem and sentence-writing conventions class; (2) The pictures helped me with creating word problems; (3) The writing checklist helped me to write complete sentences; (4) I can solve word problems more easily in school; and (5) I like learning mathematics and writing at the same time. Questions were rated via a five-point Likert-type scale, ranging from 1 (Strongly Disagree) to 5 (Strongly Agree). A higher rating indicates a higher social validity.

9. Results

Results are reported for word problem and sentence-writing conventions in problem-posing response performance, as well as social validity data. Figure 2 displays the effects of the problem-posing intervention on word problem performance for each of the three students, and Figure 3 shows the effects of the problem-posing intervention on sentence-writing conventions in problem-posing response performance. Overall, the visual analysis of the data revealed a functional relationship between the intervention and performances in both word problem and sentence-writing conventions across the three students.

9.1. Word Problem Performance

Derek. During the baseline phase, Derek did not demonstrate any problem-solving accuracy (M = 0%, range 0–0%). After the intervention was introduced, his problem-solving performance improved sharply. In the first three intervention sessions, his accuracy increased to 33.3%. By the fourth intervention session, he exhibited a marked improvement, achieving 66.7% accuracy. However, in subsequent sessions, his performance stabilized at 33.3%. During the maintenance phase, Derek maintained a stable level of problem-solving accuracy (M = 33.3%, range 33.3–33.3%). The Tau-U was 1, p < 0.01, 90% confidence interval [CI: 0.44, 1]. Similarly, Derek’s problem-posing performance was initially low during the baseline phase (M = 0%, range 0–0%). After the intervention was introduced, his performance increased steadily. In the first two intervention sessions, he achieved 16.7% and 38.9%, respectively. Over the next three sessions, his problem-posing performance declined slightly, ranging from 11.1% and 16.7%. In the sixth session, he reached his highest problem-posing performance at 44.4%. Unfortunately, his performance declined again during the final two sessions. In the maintenance phase, Derek maintained problem-posing performance at a medium level (M = 22.2%, range 11.1–33.3%). The Tau-U for problem posing was 1, p < 0.01, 90% confidence interval [CI: 0.44, 1].
Ian. During the baseline phase, Ian demonstrated a medium level of problem-solving performance (M = 35.7%, range 16.7–50%). Upon the introduction of the intervention, his problem-solving performance exhibited an upward trend, reaching 100% accuracy from the fourth to the eighth intervention sessions. During the intervention phase, Ian’s mean problem-solving accuracy was 77.1% (range 33.3–100%). In the maintenance phase, Ian maintained his improved performance levels, maintaining 100% accuracy in problem solving (M = 100%, range 100–100%). The Tau-U for problem solving was 0.68, p > 0.01, 90% confidence interval [CI: 0.17, 1]. Regarding problem-posing performance, Ian also demonstrated a medium level of performance during the baseline phase (M = 27.8%, range 11.1–38.9%). After the intervention began, his problem-posing performance showed an immediate improvement, with a steady upward trend. The mean problem-posing performance during the intervention was 59.5% (range 44.4–72.2%). In the maintenance phase, Ian’s problem-posing performance was 77.8% (M = 77.8%, range 77.8–77.8%). The Tau-U for problem posing was 1, p < 0.01, 90% confidence interval [CI: 0.48, 1].
Roy. Across the baseline sessions, Roy’s problem-solving performance was 0 (M = 0%, range 0–0%). Following the introduction of the intervention phase, there was an immediate increase in his problem-solving performance. His accuracy increased from 0% in the last baseline session to 16.7% in the first intervention session. Roy maintained this accuracy during the first three intervention sessions, followed by a slight upward trend, reaching 33.3% in the fourth intervention session. Although his accuracy decreased to 16.7% during the fifth and sixth sessions, he reached 50% accuracy in the seventh session. Roy’s average problem-solving accuracy was 25.0% (range 16.7–50%) during the intervention. After the completion of the intervention, Roy maintained his improvement in problem solving (M = 58.3%, range 33.3–83.3%). The Tau-U for problem solving was 1, p < 0.01, 90% confidence interval [CI: 0.53, 1]. Regarding problem-posing performance, Roy also showed a low level of performance during baseline (M = 0%, range 0–0%). After the intervention began, his problem-posing performance remained static initially due to his refusal to complete the entire worksheet. Across the three worksheets he completed during the intervention phase, Roy’s performance improved compared to baseline (M = 16.7%, range 11.1–27.8%). During the maintenance, Roy’s problem-posing performance was maintained (M = 30.6%, range 16.7–44.4%). The Tau-U for problem posing was 1, p > 0.01, 90% confidence interval [CI: 0.34, 1].
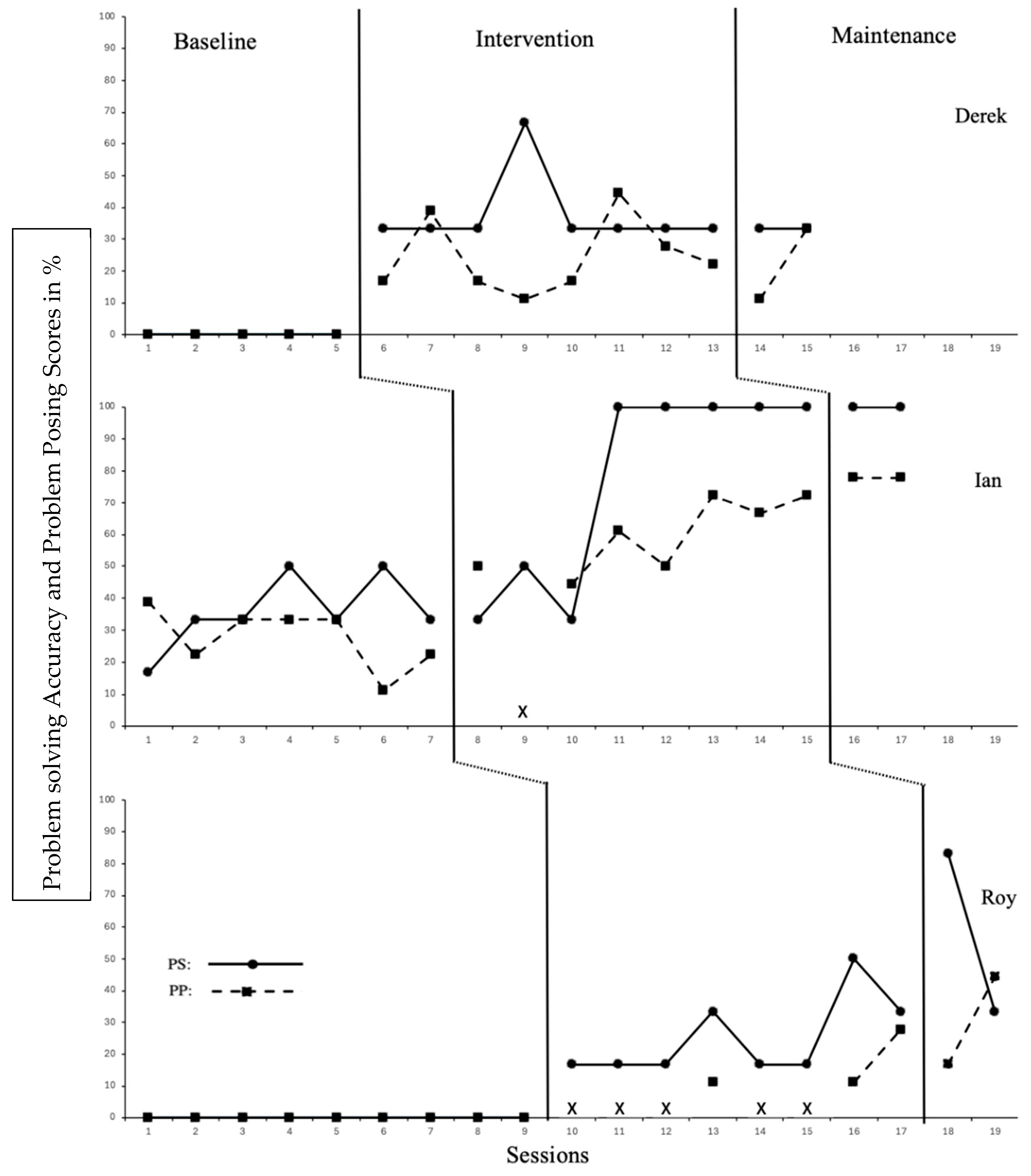
Education 15 00780 g002
Figure 2. Word problem performance. Note. PS = problem solving, PP = problem posing, x indicates missing data.
Figure 2. Word problem performance. Note. PS = problem solving, PP = problem posing, x indicates missing data.
Education 15 00780 g002

9.2. Sentence-Writing Conventions in Problem-Posing Response Performance

Derek. The mean of Derek’s performance in baseline was 0% across all three measures. Upon intervention, there was an immediacy of effect and an accelerating trend with moderate variability across all measures. For TWW, the intervention mean score was 25.5 (range = 12–44). For WSC, the intervention mean score was 17.5 (range = 7–33). For CWS, the intervention mean score was 9.5 (range = 4–16). During maintenance, Derek demonstrated low-to-medium performance levels across the three measures. For TWW, the maintenance mean score was 21 (range = 12–30) and the Tau-U was 1, p < 0.01, 90% confidence interval [CI: 0.44, 1]. For WSC, the maintenance mean score was 16 (range = 10–22) and the Tau-U was 1, p < 0.01, 90% confidence interval [CI: 0.44, 1]. For CWS, the maintenance mean score was 7 (range = 4–10) and the Tau-U was 1, p < 0.01, 90% confidence interval [CI: 0.44, 1].
Ian. Ian’s performance showed low-to-medium levels during the baseline, with a mean score of 26.1 (range = 11–35) on TWW, 24.4 (range = 11–32) on WSC, and 10.1 (range = 4–16) on CWS. During the intervention, Ian demonstrated a gradual accelerating trend across the three measures. However, during the second intervention session, he was unable to complete the worksheet due to time constraints. Across the intervention phase, Ian achieved a mean score of 44.6 (range = 12–57) for TWW, 40.2 (range = 11–54) for WSC, and 23.5 (range = 7–35) for CWS. After the implementation of the intervention, Ian maintained high levels of sentence-writing conventions in the problem-posing response performance. His mean score was 53.5 (range = 51–56) for TWW, 47.5 (range = 46–49) for WSC, and 25.5 (range = 24–27) for CWS. The Tau-U was 0.79 for TWW, p < 0.01, 90% confidence interval [CI: 0.28, 0.1]; 0.75 for WSC, p < 0.01, 90% confidence interval [CI: 0.24, 0.1]; and 0.80 for CWS, p < 0.01, 90% confidence interval [CI: 0.30, 0.1].
Roy. Roy’s sentence-writing conventions in the problem-posing response performance was low during the baseline, with a mean score of 0 across all three measures. Upon entering the intervention phase, Roy’s performance in the first three intervention sessions showed no improvement from baseline, as he refused to engage in problem-posing tasks. He began attempting problem posing in the fourth intervention session but expressed reluctance again to posing problems during the fifth and sixth sessions. With encouragement, Roy completed the worksheets in the final two intervention sessions. Despite completing only three worksheets, his performance showed improvement compared to the baseline. During the intervention phase, Roy’s mean scores were 4.6 (range = 0–22) for TWW, 3.5 (range = 0–18) for WSC, and 2.1 (range = 0–12) for CWS. In the maintenance phase, Roy maintained similar performance levels to the intervention phase. His maintenance mean score was 22.5 (range = 19–26) for TWW, 14.5 (range = 11–18) for WSC, and 12.5 (range = 7–18) for CWS. The Tau-U values were 1 across the measures (p > 0.01) with a 90% confidence interval [CI: 0.34, 1].
Education 15 00780 g003
Figure 3. Sentence-writing conventions in the problem-posing response performance. Note. CWS = correct writing sequence, TWW = total words written, WSC = words spelled correctly, x indicates missing data.
Figure 3. Sentence-writing conventions in the problem-posing response performance. Note. CWS = correct writing sequence, TWW = total words written, WSC = words spelled correctly, x indicates missing data.
Education 15 00780 g003

9.3. Social Validity Results

Two students completed the post-intervention questionnaire. The third student’s parent picked him up right after the session, so he could not complete the questionnaire. The average score was 3.8 out of 5. A higher score indicates a higher level of acceptance and satisfaction of the intervention procedures and outcomes. Overall, students expressed enjoying the intervention sessions and appreciated using the mathematics-writing mat to create word problems and write complete sentences. Both students stated that they found it easier to solve word problems in school. In particular, Roy expressed a preference for learning word problem and sentence-writing conventions simultaneously.

10. Discussion

Posing word problems is a critical component of mathematics instruction across the K-12 curriculum. However, attending to sentence-writing conventions is essential for constructing clear and meaningful word problems. The current study was the first known study to examine an intervention simultaneously targeting both word problem and sentence-writing convention outcomes for students who experience difficulties in these two areas. The findings revealed that the students demonstrated improvements in both word problem performance and sentence-writing conventions in the problem-posing response after receiving the intervention. Visual analysis of the data suggested a functional relationship between the intervention and the two sets of dependent measures. In addition, all three students maintained their improved performance in word problem and sentence-writing conventions in the problem-posing response, with no overlap in data compared to baseline. Overall, the results indicated that integrating sentence-writing convention instruction into a word problem intervention can enhance outcomes in both word problem and sentence-writing conventions.
Regarding the word problem performance, the results aligned with prior research of Yang and Xin (2022), demonstrating that problem-posing intervention can enhance student learning. Specifically, students who engaged in problem posing and problem solving using the COMPS approach showed improved problem-solving accuracy and an increased ability to create equal-group word problems. This improvement may be attributed to students constructing sentences that describe each element of the COMPS model, thereby reinforcing their grasp of the linguistic structures (i.e., story grammar; Xin, 2008) emphasized in equal-group word problems and deepening their understanding of the problem-solving process embedded in these tasks. For example, during baseline, students primarily relied on addition or subtraction to solve all problems. Following the intervention, they became more proficient in mapping problem information onto diagrams, leading to greater accuracy in their solutions. One student (Derek) explicitly stated: “We need to get rid of ‘y’ when solving this (equation).”, reflecting an awareness of the unknown value to be determined. This finding supports a growing body of research suggesting that the early development of algebraic reasoning, beginning as early as third grade, can facilitate success in setting up equations and solving for the unknown quantities (e.g., Powell et al., 2020).
In addition, during the baseline phase, two of the three students (Derek and Roy) did not pose any problems, while one student (Ian) made only a minimal attempt. The interventionists explicitly modeled and guided students in posing problems based on semi-structured problem scenarios (i.e., pictures with nametags; # of groups). These scenarios were particularly beneficial given that the students in this study were performing below grade level in reading, mathematics, and writing. The pictures with nametags representing key elements within the COMPS model allowed students to engage with the problem context, interact with abstract mathematics concepts (Yang & Xin, 2022), and transfer their understanding from visual representations of key problem elements to the construction of complete mathematically correct problems (Bevan & Capraro, 2021). As a result, the intervention may have supported students in developing a conceptual understanding of the mathematical relationships among the different quantities, as well as improving their problem-posing ability.
When examining the writing conventions of the problem-posing responses, students displayed varying performance patterns before and after receiving the intervention (samples shown as Figure 4). Ian demonstrated the most consistent and sustained growth, whereas Derek and Roy’s progress was more variable. One potential factor contributing to this variability was handwriting proficiency. An analysis of the students’ written responses revealed persistent difficulties with letter formation and letter case usage, such as capital letters appearing in the middle of words (shown in Figure 4). In addition, a close examination of student worksheets revealed that most spelling errors occurred in high-frequency words (e.g., “thar/ther” for “there”, “frad” for “friend”), rather than in the vocabulary specific to the word problem. It is worth noting that the intervention did not include explicit instructions in high-frequency-word spelling or handwriting, nor did it provide supports such as letter formation models or alphabet strips, which may have limited students’ ability to create clear and meaningful word problems. However, the observed improvements in students’ problem-posing performance suggest that an intervention integrating word problem and sentence-writing conventions may be effective in supporting students identified with mathematics and writing difficulties.
The novel aspect of the current study was using a writing mat containing multiple elements (e.g., word bank, writing checklist) to support learning. Prior research has shown that the processes involved in mathematical problem solving and problem posing place considerable demands on working memory, which can be particularly challenging for students with mathematics and writing difficulties (Alloway & Alloway, 2010; Swanson & Beebe-Frankenberger, 2004). To address these challenges, the intervention incorporated scaffolded support designed to reduce extraneous cognitive load and help students focus on content learning (Berninger & Amtmann, 2003). For example, interventionists observed that students frequently referred to the word bank embedded in the writing mat, which appeared to reduce the cognitive demands associated with spelling problem-specific vocabulary. Also, interventionists observed that students often used the sentence model as a visual guide for checking sentence-writing conventions. The use of the writing checklist appeared to promote self-monitoring, enabling students to independently identify and correct errors, likely contributing to gains on the CWS measure. This suggested that the combined use of sentence model and checklist supported students in attending to problem-posing tasks and improving the precision of their responses (e.g., Graham & Harris, 2000; Graham & Perin, 2007). Taken together, these findings highlighted the importance of targeted scaffolds in supporting students’ engagement with problem-posing tasks and their attention to sentence-level writing conventions.

11. Limitations

This study had several limitations. First, the number of sessions was constrained by the university reading center’s schedule, which included planned days off for conferences and spring break. This limitation may have restricted the intervention’s duration and, consequently, the potential to maximize intervention effectiveness. Second, the timing of the intervention and data collection, which occurred immediately after the students’ reading center sessions, may have negatively impacted student engagement. Sessions were conducted close to dinner time and after a full day of school, which likely contributed to student fatigue and restlessness. Interventionists observed signs of decreased motivation and perseverance, such as inattentiveness and reluctance to complete tasks. Third, the current study focused only on the one-step equal-group type of word problems with three third-grade students, and the recruitment was limited to students already participating in the tutoring at the university reading center. Fourth, the interventionists did not collect information about whether students were receiving additional mathematics or writing support at school, nor were they permitted to contact teachers for this information due to University A’s IRB requirements. As such, a potential carryover effect from school-based instruction may have influenced the outcomes observed in this study. Therefore, the findings may not be generalized to other types of word problems or broader populations of students experiencing word problem and sentence-writing convention difficulties.

Implications for Practice and Research

One implication of this study is the demonstrated value of the COMPS approach in supporting students with mathematics difficulties in solving and posing one-step word problems. This study aligns with prior research (e.g., Yang & Xin, 2022; Xin et al., 2017, 2023), which further demonstrated the effectiveness of the cohesive problem-solving model in supporting word problem learning in students with learning disabilities in mathematics. As such, the COMPS approach is recommended to be incorporated as a useful instructional approach in teaching word problems, particularly for students experiencing challenges in mathematics. Additionally, this study implies the need to refine instructional tools to enhance student motivation and engagement. For example, practitioners may consider incorporating manipulatives and visually engaging features to facilitate student interest and participation, such as color-coded representations on the mathematics-writing mat. While the study revealed positive findings, students could benefit from more intensive interventions. This could include extending the duration of the intervention, either by increasing the number of sessions or the length of each session (Fuchs et al., 2017a), as well as implementing incentives to encourage on-task behaviors. Such practices may further enhance the effectiveness of the intervention.
As noted above, the students in this study were experiencing reading difficulties, a compounding factor that needs further investigation to better understand its impact on their word problem and sentence-writing conventions in their problem-posing response performance. Additionally, because the students received reading tutoring immediately before the problem-posing intervention on the same days, the observed outcomes may have been influenced by the preceding reading instruction. Future research could scale up the current study and include a control group to distinguish the effects of the problem-posing intervention from other instructions or support students received. Interventionists also noted that students encountered significant challenges in posing problems during guided and independent practice opportunities. Future research could explore whether providing additional scaffolded support would enhance intervention effectiveness, such as incorporating fill-in-the-blank prompts and sentence starters. Exploring the effectiveness of these supports could inform researchers about how to better address the needs of students with word problem and sentence-writing convention difficulties.

Author Contributions

Conceptualization, J.W. and P.S.B.; methodology, J.W. and P.S.B.; software: J.W.; validation, Q.L.; formal analysis, J.W.; investigation, J.W. and P.S.B.; resources, J.W. and P.S.B.; data curation, J.W. and P.S.B.; writing-original draft preparation, J.W., P.S.B. and Q.L.; writing-review and editing, J.W., P.S.B. and Q.L.; visualization: J.W. and P.S.B.; supervision, J.W. and P.S.B.; project administration, J.W. and P.S.B.; funding acquisition, N/A. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by the Office of The Responsible Conduct of Research (RCR) at the University of Nebraska-Lincoln (Protocol Code: UNL-00061766; Date of Approval: 22 January 2024).

Informed Consent Statement

Informed consent was obtained from all subjects involved in this study.

Data Availability Statement

The data that support the fundings of this study are available upon request from the corresponding author. The data are not publicly available due to confidentiality and research ethics.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Allen, A. A., Jung, P. G., Poch, A. L., Brandes, D., Shin, J., Lembke, E. S., & McMaster, K. L. (2020). Technical adequacy of curriculum-based measures in writing in grades 1–3. Reading & Writing Quarterly, 36(6), 563–587. [Google Scholar] [CrossRef]
  2. Alloway, T. P., & Alloway, R. G. (2010). Investigating the predictive roles of working memory and IQ in academic attainment. Journal of Experimental Child Psychology, 106(1), 20–29. [Google Scholar] [CrossRef] [PubMed]
  3. Arsenault, T. L., Powell, S. R., & King, S. G. (2024). Mathematics-writing synthesis: Kindergarten through Grade 12 mathematics-writing outcomes and instructional methods. In Reading and writing (pp. 1–43). Springer. [Google Scholar] [CrossRef]
  4. Berninger, V. W., Abbott, R. D., Nagy, W., & Carlisle, J. (2010). Growth in phonological, orthographic, and morphological awareness in grades 1 to 6. Journal of Psycholinguistic Research, 39(2), 141–163. [Google Scholar] [CrossRef] [PubMed]
  5. Berninger, V. W., & Amtmann, D. (2003). Preventing written expression disabilities through early and continuing assessment and intervention for handwriting and/or spelling problems: Research into practice. In H. L. Swanson, K. Harris, & S. Graham (Eds.), Handbook of research on learning disabilities (pp. 345–363). Guilford Press. [Google Scholar]
  6. Berninger, V. W., Vaughan, K., Abbott, R. D., Begay, K., Coleman, K. B., Curtin, G., Hawkins, J. M., & Graham, S. (2002). Teaching spelling and composition alone and together: Implications for the simple view of writing. Journal of Educational Psychology, 94(2), 291–304. [Google Scholar] [CrossRef]
  7. Berninger, V. W., & Winn, W. (2006). Implications of advancements in brain research and technology for writing development, writing instruction, and educational evolution. In C. Mac Arthur, S. Graham, & J. Fitzgerald (Eds.), Handbook of writing research (pp. 96–114). Guilford. [Google Scholar]
  8. Bevan, D., & Capraro, M. M. (2021). Posing creative problems: A study of elementary students’ mathematics understanding. International Electronic Journal of Mathematics Education, 16(3), em0654. [Google Scholar] [CrossRef]
  9. Bicer, A., Capraro, R. M., & Capraro, M. M. (2013). Integrating writing into mathematics classroom to increase students’ problem solving skills. International Online Journal of Educational Sciences, 5(2), 361–369. [Google Scholar]
  10. Bruno, A., Polo-Blanco, I., Van Vaerenbergh, S., Fernández-Cobos, R., & González-López, M. J. (2024). Strategies for solving multiplicative problems using a conceptual model-based problem-solving approach. A case study with a student with autism spectrum disorder. ZDM–Mathematics Education, 56(6), 1239–1256. [Google Scholar] [CrossRef]
  11. Cai, J. (2003). Singaporean students’ mathematical thinking in problem solving and problem posing: An exploratory study. International Journal of Mathematical Education in Science and Technology, 34(5), 719–737. [Google Scholar] [CrossRef]
  12. Cai, J., & Hwang, S. (2002). Generalized and generative thinking in U.S. and Chinese students’ mathematical problem solving and problem posing. Journal of Mathematical Behavior, 21(4), 401–421. [Google Scholar] [CrossRef]
  13. Cai, J., Moyer, J. C., Wang, N., Hwang, S., Nie, B., & Garber, T. (2013). Mathematical problem posing as a measure of curricular effect on students’ learning. Educational Studies in Mathematics, 83(1), 57–69. [Google Scholar] [CrossRef]
  14. Casa, T. M., Firmender, J. M., Cahill, J., Cardetti, F., Choppin, J. M., Cohen, J., Cole, S., Colonnese, M. W., Copley, J., DiCicco, M., Dieckmann, J., Dorl, J., Gavin, M. K., Hebert, M. A., Karp, K. S., LaBella, E., Moschkovich, J. N., Moylan, K., Olinghouse, N. G., … Zawodniak, R. (2016). Types of and purposes for elementary mathematical writing: Task force recommendations. Available online: https://mathwriting.education.uconn.edu/wp-content/uploads/sites/1454/2016/04/Types_of_and_Purposes_for_Elementary_Mathematical_Writing_for_Web-2.pdf (accessed on 1 March 2024).
  15. Datchuk, S. M., & Kubina, R. M. (2013). A review of teaching sentence-level writing skills to students with writing difficulties and learning disabilities. Remedial and Special Education, 34(3), 180–192. [Google Scholar] [CrossRef]
  16. Datchuk, S. M., & Rodgers, D. B. (2019). Text writing within simple sentences: A writing fluency intervention for students with high–incidence disabilities. Learning Disabilities Research & Practice, 34(1), 23–34. [Google Scholar] [CrossRef]
  17. Deno, S. L. (2003). Curriculum-based measures: Development and perspectives. Assessment for Effective Intervention, 28(3–4), 3–12. [Google Scholar] [CrossRef]
  18. Donnelly, W. B., & Roe, C. J. (2010). Using sentence frames to develop academic vocabulary for English learners. The Reading Teacher, 64(2), 131–136. [Google Scholar] [CrossRef]
  19. Fuchs, L. S., Fuchs, D., & Malone, A. S. (2017a). The taxonomy of intervention intensity. Teaching Exceptional Children, 50(1), 35–43. [Google Scholar] [CrossRef]
  20. Fuchs, L. S., Fuchs, D., Seethaler, P. M., & Barnes, M. A. (2020). Addressing the role of working memory in mathematical word-problem solving when designing intervention for struggling learners. ZDM, 52, 87–96. [Google Scholar] [CrossRef]
  21. Fuchs, L. S., Malone, A. S., Schumacher, R. F., Namkung, J., & Wang, A. (2017b). Fraction intervention for students with mathematics difficulties: Lessons learned from five randomized controlled trials. Journal of Learning Disabilities, 50(6), 631–639. [Google Scholar] [CrossRef]
  22. Graham, S., Bollinger, A., Booth Olson, C., D’Aoust, C., MacArthur, C., McCutchen, D., & Olinghouse, N. (2012a). Teaching elementary school students to be effective writers: A practice guide (NCEE 2012-4058). What Works Clearinghouse. National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education. Available online: https://ies.ed.gov/ncee/wwc/practiceguide/17 (accessed on 1 May 2025).
  23. Graham, S., & Harris, K. R. (2000). The role of self-regulation and transcription skills in writing and writing development. Educational Psychologist, 35(1), 3–12. [Google Scholar] [CrossRef]
  24. Graham, S., & Harris, K. R. (2003). Students with learning disabilities and the process of writing: A meta-analysis of SRSD studies. In H. L. Swanson, K. R. Harris, & S. Graham (Eds.), Handbook of learning disabilities (pp. 323–344). The Guilford Press. [Google Scholar]
  25. Graham, S., & Hebert, M. (2011). Writing to read: A meta-analysis of the impact of writing and writing instruction on reading. Harvard Educational Review, 81(4), 710–744. [Google Scholar] [CrossRef]
  26. Graham, S., McKeown, D., Kiuhara, S., & Harris, K. R. (2012b). A meta-analysis of writing instruction for students in the elementary grades. Journal of Educational Psychology, 104(4), 879. [Google Scholar] [CrossRef]
  27. Graham, S., & Perin, D. (2007). A meta-analysis of writing instruction for adolescent students. Journal of Educational Psychology, 99, 445–476. [Google Scholar] [CrossRef]
  28. Griffin, C. C., Gagnon, J. C., Jossi, M. H., Ulrich, T. G., & Myers, J. A. (2018). Priming mathematics word problem structures in a rural elementary classroom. Rural Special Education Quarterly, 37(3), 150–163. [Google Scholar] [CrossRef]
  29. Hacker, D. J., Kiuhara, S. A., & Levin, J. R. (2019). A metacognitive intervention for teaching fractions to students with or at-risk for learning disabilities in mathematics. ZDM Mathematics Education, 51(4), 601–612. [Google Scholar] [CrossRef]
  30. Harris, K. R., Graham, S., Aitken, A. A., Barkel, A., Houston, J., & Ray, A. (2017). Teaching spelling, writing, and reading for writing: Powerful evidence-based practices. Teaching Exceptional Children, 49(4), 262–272. [Google Scholar] [CrossRef]
  31. Hebert, M. A., Powell, S. R., Bohaty, J., & Roehling, J. (2019). Piloting a mathematics–writing intervention with late elementary students at–risk for learning difficulties. Learning Disabilities Research & Practice, 34(3), 144–157. [Google Scholar] [CrossRef]
  32. Hebert, M. A., Shanahan Bazis, P., & Santangelo, T. (2023). Addressing the needs of students who struggle with literacy. In Z. A. Philippakos, & S. Graham (Eds.), Writing and reading connections: Building research and practice (pp. 289–310). The Guilford Press. [Google Scholar]
  33. Hughes, E. M., Lee, J. Y., Cook, M. J., & Riccomini, P. J. (2019). Exploratory study of a self-regulation mathematical writing strategy: Proof-of-concept. Learning Disabilities: A Contemporary Journal, 17(2), 185–203. [Google Scholar]
  34. Jagaiah, T., Howard, D., & Olinghouse, N. (2019). Writer’s checklist: A procedural support for struggling writers. The Reading Teacher, 73(1), 103–110. [Google Scholar] [CrossRef]
  35. Jitendra, A. K., Rodriguez, M., Kanive, R., Huang, J. P., Church, C., Corroy, K. A., & Zaslofsky, A. (2013). Impact of small-group tutoring interventions on the mathematical problem solving and achievement of third-grade students with mathematics difficulties. Learning Disability Quarterly, 36(1), 21–35. [Google Scholar] [CrossRef]
  36. Kennedy, C. H. (2005). Single-case designs for educational research. Allyn & Bacon. [Google Scholar]
  37. Kratochwill, T. R., Hitchcock, J., Horner, R. H., Levin, J. R., Odom, S. L., Rindskopf, D. M., & Shadish, W. R. (2010). Single-case designs technical documentation. What Works Clearinghouse. Available online: https://ies.ed.gov/ncee/wwc/Docs/ReferenceResources/wwc_scd.pdf (accessed on 5 July 2024).
  38. Ledford, J. R., & Gast, D. L. (2024). Single case research methodology: Applications in special education and behavioral sciences (4th ed.). Routledge. [Google Scholar]
  39. Lei, Q., & Xin, Y. P. (2023). A synthesis of mathematical word problem-solving instructions for English learners with learning disabilities in mathematics. Review of Education, 11(2), e3396. [Google Scholar] [CrossRef]
  40. Ma, X., & Xin, Y. P. (2024). Teaching mathematics word problem solving to students with autism spectrum disorder. The Journal of Special Education, 58(1), 47–58. [Google Scholar] [CrossRef]
  41. McCutchen, D. (2000). Knowledge, processing, and working memory: Implications for a theory of writing. Educational Psychologist, 35(1), 13–23. [Google Scholar] [CrossRef]
  42. Namkung, J. M., Peng, P., & Goodrich, M. J. (2024). The relation between mathematics anxiety and mathematics competence for students with versus without mathematics learning difficulties. Learning Disability Quarterly, 48(2), 143–153. [Google Scholar] [CrossRef]
  43. Parker, R. I., Vannest, K. J., Davis, J. L., & Sauber, S. B. (2011). Combining nonoverlap and trend for single-case research: Tau-U. Behavior Therapy, 42, 284–299. [Google Scholar] [CrossRef] [PubMed]
  44. Powell, S. R., Berry, K. A., & Barnes, M. A. (2020). The role of pre-algebraic reasoning within a word-problem intervention for third-grade students with mathematics difficulty. ZDM, 52(1), 151–163. [Google Scholar] [CrossRef]
  45. Ritchey, K. D., McMaster, K. L., Al Otaiba, S., Puranik, C. S., Kim, Y.-S. G., Parker, D. C., & Ortiz, M. (2016). Indicators of fluent writing in beginning writers. In K. D. Cummings, & Y. Petscher (Eds.), The fluency construct: Curriculum-based measurement concepts and applications (pp. 21–66). Springer Science + Business Media. [Google Scholar] [CrossRef]
  46. Rojo, M., Gersib, J., Powell, S. R., Shen, Z., King, S. G., Akther, S. S., Arsenault, T. L., Bos, S. E., Lariviere, D. O., & Lin, X. (2024). A meta-analysis of mathematics interventions: Examining the impacts of intervention characteristics. Educational Psychology Review, 36(1), 9. [Google Scholar] [CrossRef]
  47. Stoyanova, E., & Ellerton, N. F. (1996). A framework for research into students’ problem posing in school mathematics. In P. C. Clarkson (Ed.), Technology in mathematics education (pp. 518–525). Mathematics Education Research Group of Australasia. [Google Scholar]
  48. Swanson, H. L., & Beebe-Frankenberger, M. (2004). The relationship between working memory and mathematical problem solving in children at risk and not at risk for serious math difficulties. Journal of Educational Psychology, 96(3), 471. [Google Scholar] [CrossRef]
  49. Swanson, H. L., Harris, K. R., & Graham, S. (2013). Handbook of learning disabilities (2nd ed.). Guilford. [Google Scholar]
  50. Swanson, H. L., Moran, A., Lussier, C., & Fung, W. (2014). The effect of explicit and direct generative strategy training and working memory on word problem-solving accuracy in children at risk for math difficulties. Learning Disability Quarterly, 37(2), 111–123. [Google Scholar] [CrossRef]
  51. Troia, G. A. (2009). Self-regulation and the writing process: Enhancing the performance of students with language and learning difficulties. Perspectives on Language Learning and Education, 16(1), 28–36. [Google Scholar] [CrossRef]
  52. Wang, J., Lopez-Reyna, N., & Kim, S. (2023). Word problem solving interventions for English learners at elementary grade levels: A review of the literature. Learning Disabilities: A Contemporary Journal, 21(2), 111–131. [Google Scholar]
  53. Xin, Y. P. (2008). The effect of schema-based instruction in solving mathematics word problems: An emphasis on prealgebraic conceptualization of multiplicative relations. Journal for Research in Mathematics Education, 39(5), 526–551. [Google Scholar] [CrossRef]
  54. Xin, Y. P. (2012). Conceptual model-based problem solving: Teach students with learning difficulties to solve math problems. Sense Publishers. [Google Scholar]
  55. Xin, Y. P., Kim, S. J., Lei, Q., Liu, B. Y., Wei, S., Kastberg, S. E., & Chen, Y. V. (2023). The effect of model-based problem solving on the performance of students who are struggling in mathematics. The Journal of Special Education, 57(3), 181–192. [Google Scholar] [CrossRef]
  56. Xin, Y. P., Kim, S. J., Lei, Q., Wei, S., Liu, B., Wang, W., Kastberg, S. E., Chen, Y., Xuan, Y., & Richardson, S. E. (2020). The effect of computer-assisted conceptual model-based intervention program on mathematics problem-solving performance of at-risk English learners. Reading & Writing Quarterly, 36(2), 104–123. [Google Scholar]
  57. Xin, Y. P., Tzur, R., Hord, C., Liu, J., Park, J. Y., & Si, L. (2017). An intelligent tutor-assisted mathematics intervention program for students with learning difficulties. Learning Disability Quarterly, 40(1), 4–16. [Google Scholar] [CrossRef]
  58. Yang, X., & Xin, Y. P. (2022). Teaching problem posing to students with learning disabilities. Learning Disability Quarterly, 45(4), 280–293. [Google Scholar] [CrossRef]
  59. Zhang, D., Xin, Y. P., Harris, K., & Ding, Y. (2014). Improving multiplication strategic development in children with math difficulties. Learning Disability Quarterly, 37(1), 15–30. [Google Scholar] [CrossRef]
Education 15 00780 g001
Figure 1. Sample of mathematics-writing mat used in guided practice. Note. A = a three-box table, B = a structured working space, C = a six-element sentence-writing convention checklist, D = the standardized problem-solving conceptual, E = suggested vocabulary, F = sample sentence example, and G = empty working space.
Figure 1. Sample of mathematics-writing mat used in guided practice. Note. A = a three-box table, B = a structured working space, C = a six-element sentence-writing convention checklist, D = the standardized problem-solving conceptual, E = suggested vocabulary, F = sample sentence example, and G = empty working space.
Education 15 00780 g001
Education 15 00780 g004
Figure 4. Student work samples collected during baseline and intervention.
Figure 4. Student work samples collected during baseline and intervention.
Education 15 00780 g004
Table 1. Characteristics of participants.
Table 1. Characteristics of participants.
ParticipantGenderEthnicityAgeGradeDisability DiagnosisTOMA %ile RankWIAT %ile Rank
MSCOMLWPSB
IanMWhite8 years 11 months3rdat risk for MWD16759516
RoyMWhite10 years 5 months3rdat risk for MWD<1<11<12
DerekMAfrican American9 years 6 months3rdat risk for MWD5343<1
Note. CO = computation, MWD = mathematics and writing difficulties, ML = mathematics in everyday life, MS = mathematical symbols and concepts, SB = sentence building, TOMA = Test of Mathematical Abilities, WIAT = Weschler Individual Achievement Test, WP = word problems.
Table 2. Scoring method for mathematics word problem posing.
Table 2. Scoring method for mathematics word problem posing.
Mathematical expression “2 × 3 = y”
For the first quantity “2”
2 pointsStudents explicitly included the concept of “number of groups” in the problem and constructed a complete sentence. Example: “There are 2 bags of apples”, where “2 bags of apples” represents the “number of groups.”
1 pointStudents included the number and/or a word indicating groups but did not include a complete description of the group objects. Example: “There are 2.” or “There are 2 bags.”
0 pointNo response is provided.
For the second quantity “3”
2 pointsStudents explicitly included the “number of items in each group” in the problem and constructed a complete sentence. Example: “Each bag has 3 apples”, where “each” indicates the concept of “unit” and “3 apples” specifies the “number of items” in each group.
1 pointStudents included a number and/or a term indicating grouping but omitted the word “each” or description of items. Examples: “Each bag has 3.” or “There are 3 apples.”
0 pointNo response is provided.
For the last quantity “y”
2 pointsStudents formulated a complete and relevant question that includes the term “How many” and indicates the concept of “total”. Example: “How many apples are there in total?” or “How many apples do I have?”
1 pointStudents formulated a question but lacked full clarity or completeness. Examples: “How many are there?” or “How many do I have?”
0 pointNo response is provided.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wang, J.; Shanahan Bazis, P.; Lei, Q. Exploring the Effects of a Problem-Posing Intervention with Students at Risk for Mathematics and Writing Difficulties. Educ. Sci. 2025, 15, 780. https://doi.org/10.3390/educsci15060780

AMA Style

Wang J, Shanahan Bazis P, Lei Q. Exploring the Effects of a Problem-Posing Intervention with Students at Risk for Mathematics and Writing Difficulties. Education Sciences. 2025; 15(6):780. https://doi.org/10.3390/educsci15060780

Chicago/Turabian Style

Wang, Jing, Pamela Shanahan Bazis, and Qingli Lei. 2025. "Exploring the Effects of a Problem-Posing Intervention with Students at Risk for Mathematics and Writing Difficulties" Education Sciences 15, no. 6: 780. https://doi.org/10.3390/educsci15060780

APA Style

Wang, J., Shanahan Bazis, P., & Lei, Q. (2025). Exploring the Effects of a Problem-Posing Intervention with Students at Risk for Mathematics and Writing Difficulties. Education Sciences, 15(6), 780. https://doi.org/10.3390/educsci15060780

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Article metric data becomes available approximately 24 hours after publication online.
Back to TopTop