Capturing the Complex: An Intraindividual Temporal Network Analysis of Learning Resource Regulation
Abstract
1. Introduction
1.1. Systemic Framework and the Theory of Educational and Learning Capitals
1.2. New Approaches to Capture Systemic Interplay
1.3. Study Aims
2. Materials and Methods
2.1. Study Design
2.2. Participant and Procedure
2.3. Measures
2.4. Data Analyses
2.4.1. Data Preprocessing
2.4.2. Network Estimation Using Graphical Vector Autoregression (graphicalVAR)
3. Results
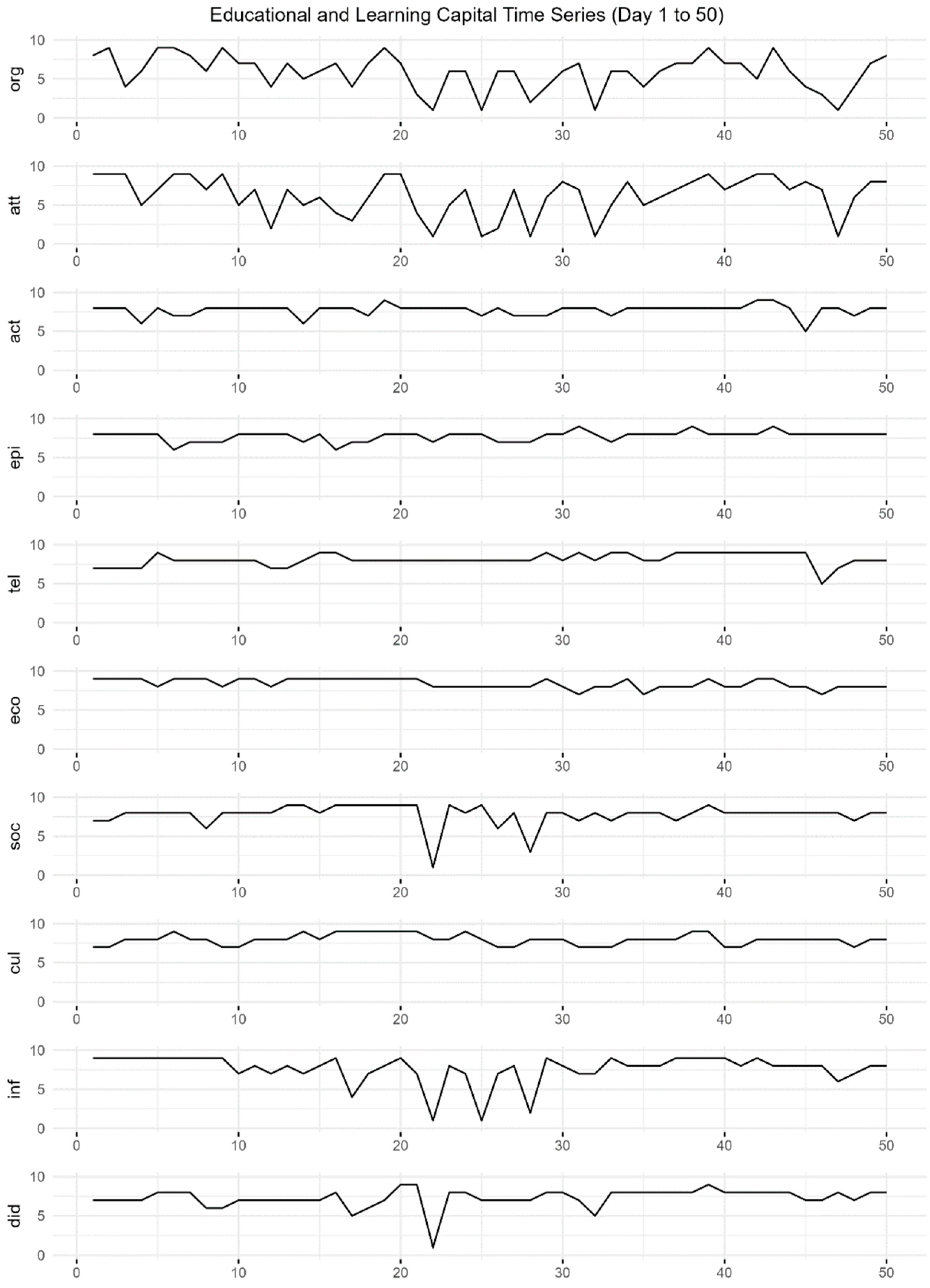
3.1. Description of System Dynamics
3.1.1. Learning Capital
3.1.2. Educational Capital
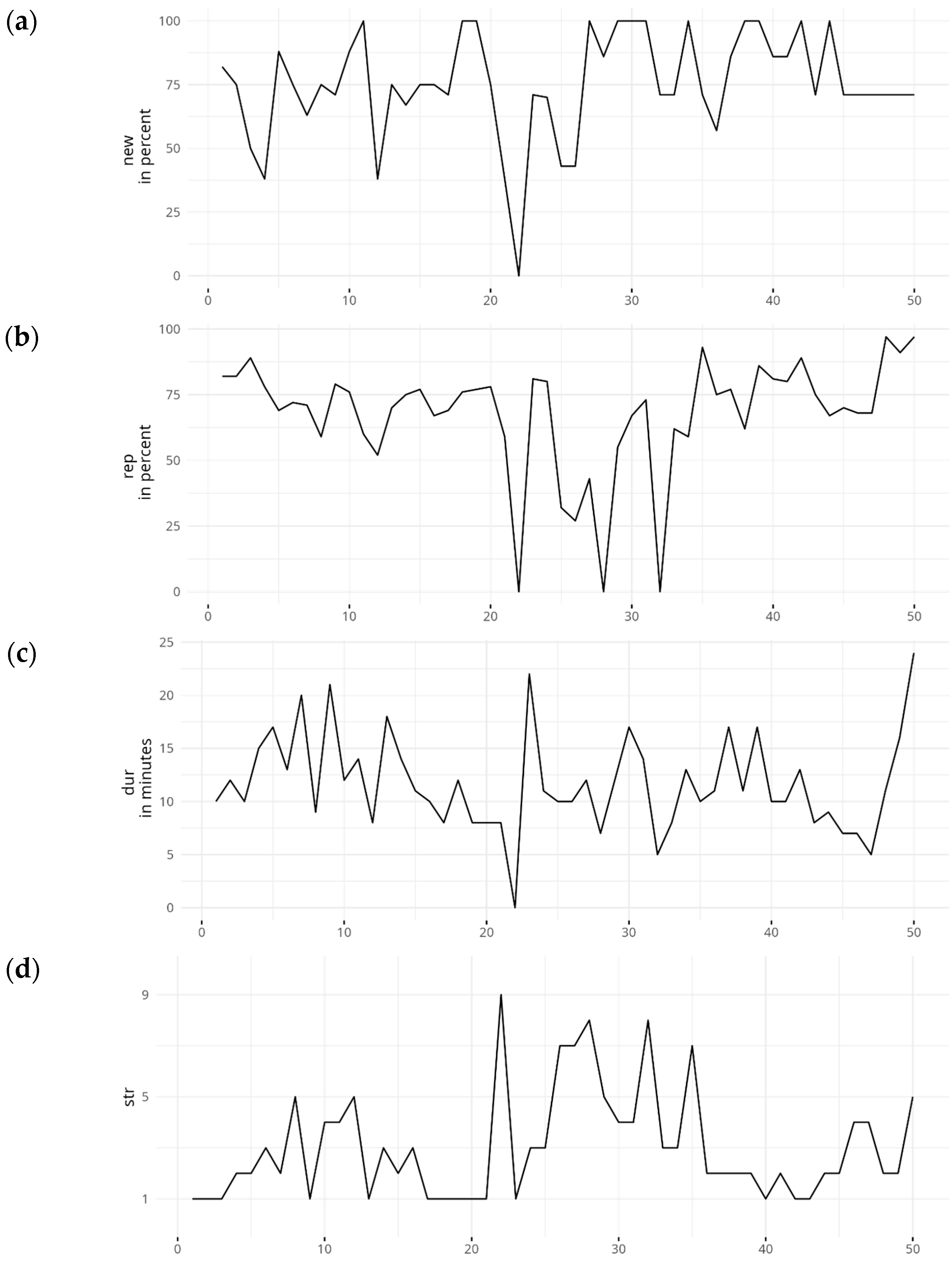
3.1.3. Performance, Duration, and Stress Level
3.2. Network Analyses
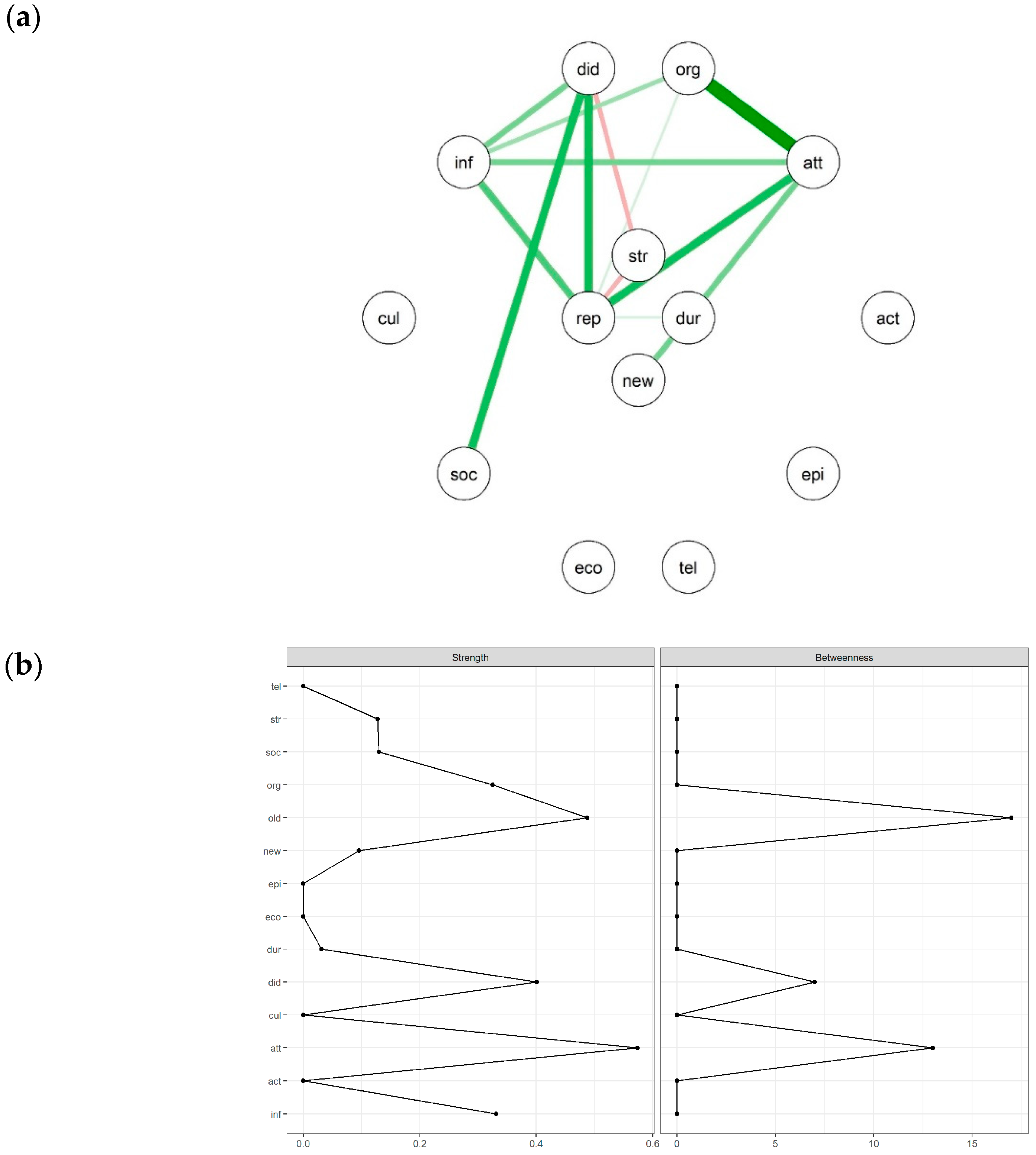
3.2.1. Regulation Within Learning Episodes—Contemporaneous Network
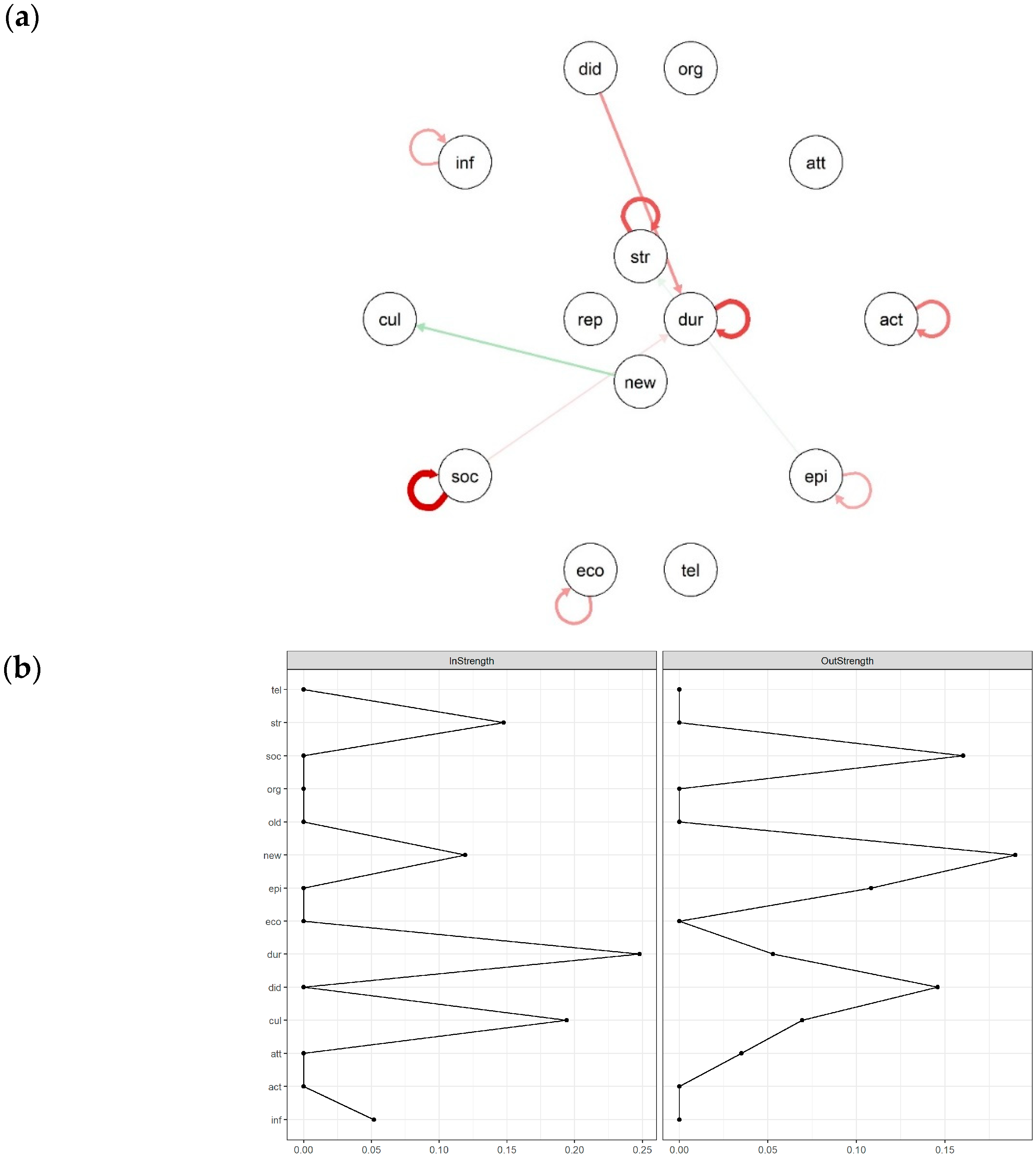
3.2.2. Temporal Dynamics—Directed Temporal Network
3.2.3. Summary of Network Findings
4. Discussion
4.1. Insights into the Regulation of the Learning Process
4.1.1. Contemporaneous Regulation
4.1.2. Day-to-Day Dynamics
4.2. Implications for Learning Diagnostics and Targeted Interventions
4.3. Limitations and Future Directions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arlinghaus, K. R., & Johnston, C. A. (2019). The importance of creating habits and routine. American Journal of Lifestyle Medicine, 13(2), 142–144. [Google Scholar] [CrossRef] [PubMed]
- Bargh, J. A., & Chartrand, T. L. (1999). The unbearable automaticity of being. American Psychologist, 54(7), 462–479. [Google Scholar] [CrossRef]
- Bellhäuser, H., Mattes, B., & Liborius, P. (2019). Daily fluctuations in motivation. Zeitschrift für Entwicklungspsychologie und Pädagogische Psychologie, 51(4), 228–242. [Google Scholar] [CrossRef]
- Blasiman, R. N., Dunlosky, J., & Rawson, K. A. (2017). The what, how much, and when of study strategies: Comparing intended versus actual study behaviour. Memory, 25(6), 784–792. [Google Scholar] [CrossRef]
- Boekaerts, M. (2011). Emotions, emotion regulation, and self-regulation of learning: Center for the study of learning and instruction, Leiden University, The Netherlands, and KU Leuven. In Handbook of self-regulation of learning and performance (pp. 422–439). Routledge. [Google Scholar]
- Borsboom, D. (2017). A network theory of mental disorders. World Psychiatry, 16(1), 5–13. [Google Scholar] [CrossRef]
- Borsboom, D., & Cramer, A. O. J. (2013). Network analysis: An integrative approach to the structure of psychopathology. Annual Review of Clinical Psychology, 9, 91–121. [Google Scholar] [CrossRef]
- Brose, A., Schmiedek, F., Lovden, M., & Lindenberger, U. (2012). Daily variability in working memory is coupled with negative affect: The role of attention and motivation. Emotion, 12(3), 605–617. [Google Scholar] [CrossRef]
- Burnette, J. L., O’Boyle, E. H., VanEpps, E. M., Pollack, J. M., & Finkel, E. J. (2013). Mind-sets matter: A meta-analytic review of implicit theories and self-regulation. Psychological Bulletin, 139(3), 655–701. [Google Scholar] [CrossRef] [PubMed]
- Butler, D. L., & Winne, P. H. (1995). Feedback and self-regulated learning: A theoretical synthesis. Review of Educational Research, 65(3), 245–281. [Google Scholar] [CrossRef]
- Costantini, G., Epskamp, S., Borsboom, D., Perugini, M., Mõttus, R., Waldorp, L. J., & Cramer, A. O. J. (2015). State of the aRt personality research: A tutorial on network analysis of personality data in R. Journal of Research in Personality, 54, 13–29. [Google Scholar] [CrossRef]
- Cramer, A. O. J., & Borsboom, D. (2015). Problems attract problems: A network perspective on mental disorders. In R. A. Scott, & S. M. Kosslyn (Eds.), Emerging trends in the social and behavioral sciences: An interdisciplinary, searchable, and linkable resource (pp. 1–15). John Wiley & Sons, Inc. [Google Scholar] [CrossRef]
- Cramer, A. O. J., Waldorp, L. J., van der Maas, H. L., & Borsboom, D. (2010). Comorbidity: A network perspective. Behavioral and Brain Sciences, 33(2–3), 137–150; discussion 150–193. [Google Scholar] [CrossRef]
- Dalege, J., Borsboom, D., van Harreveld, F., van den Berg, H., Conner, M., & van der Maas, H. L. (2016). Toward a formalized account of attitudes: The Causal Attitude Network (CAN) model. Psychological Review, 123(1), 2–22. [Google Scholar] [CrossRef] [PubMed]
- David, S. J., Marshall, A. J., Evanovich, E. K., & Mumma, G. H. (2018). Intraindividual dynamic network analysis—Implications for clinical assessment. Journal of Psychopathology and Behavioral Assessment, 40(2), 235–248. [Google Scholar] [CrossRef] [PubMed]
- Debatin, T., Hopp, M., Vialle, W., & Ziegler, A. (2015). Why experts can do what they do: The effects of exogenous resources on the Domain Impact Level of Activities (DILA). Psychological Test and Assessment Modeling, 57(1), 94–110. [Google Scholar]
- Dickey, D. A., & Fuller, W. A. (1979). Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association, 74(366a), 427–431. [Google Scholar]
- Dresel, M., Schmitz, B., Schober, B., Spiel, C., Ziegler, A., Engelschalk, T., Jstl, G., Klug, J., Roth, A., Wimmer, B., & Steuer, G. (2015). Competencies for successful self-regulated learning in higher education: Structural model and indications drawn from expert interviews. Studies in Higher Education, 40(3), 454–470. [Google Scholar] [CrossRef]
- Elo, A.-L., Leppnen, A., & Jahkola, A. (2003). Validity of a single-item measure of stress symptoms. Scandinavian Journal of Work, Environment & Health, 29(6), 444–451. [Google Scholar] [CrossRef]
- Epskamp, S. (2017a). graphicalVAR: Graphical VAR for experience sampling data (R package version 0.3.4). Available online: http://CRAN.R-project.org/package=graphicalVAR (accessed on 4 January 2025).
- Epskamp, S. (2017b). Network psychometrics [Ph.D. thesis, University of Amsterdam]. [Google Scholar]
- Epskamp, S., van Borkulo, C. D., van der Veen, D. C., Servaas, M. N., Isvoranu, A. M., Riese, H., & Cramer, A. O. J. (2018a). Personalized network modeling in psychopathology: The importance of contemporaneous and temporal connections. Clinical Psychological Science, 6(3), 416–427. [Google Scholar] [CrossRef]
- Epskamp, S., Waldorp, L. J., Mottus, R., & Borsboom, D. (2018b). The Gaussian graphical model in cross-sectional and time-series data. Multivariate Behavioral Research, 53(4), 453–480. [Google Scholar] [CrossRef]
- Fenn, J., Gouret, F., Gorki, M., Reuter, L., Gros, W., Hüttner, P., & Kiesel, A. (2025). Cognitive-affective maps extended logic: Proposing tools to collect and analyze attitudes and belief systems. Behavior Research Methods, 57(6), 174. [Google Scholar] [CrossRef]
- Fisher, A. J., Medaglia, J. D., & Jeronimus, B. F. (2018). Lack of group-to-individual generalizability is a threat to human subjects research. Proceedings of the National Academy of Sciences, 115(27), E6106–E6115. [Google Scholar] [CrossRef] [PubMed]
- Foygel, R., & Drton, M. (2010, December 6–9). Extended Bayesian information criteria for Gaussian graphical models. 24th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada. [Google Scholar] [CrossRef]
- Freeman, L. C. (1977). A set of measures of centrality based on betweenness. Sociometry, 40(1), 35–41. [Google Scholar] [CrossRef]
- Goetz, T., Frenzel, A. C., Hall, N. C., Nett, U. E., Pekrun, R., & Lipnevich, A. A. (2013). Types of boredom: An experience sampling approach. Motivation and Emotion, 38(3), 401–419. [Google Scholar] [CrossRef]
- Gorban, A. N., Pokidysheva, L. I., Smirnova, E. V., & Tyukina, T. A. (2011). Law of the minimum paradoxes. Bulletin of Mathematical Biology, 73(9), 2013–2044. [Google Scholar] [CrossRef][Green Version]
- Gorban, A. N., Smirnova, E. V., & Tyukina, T. A. (2010). Correlations, risk and crisis: From physiology to finance. Physica A, 389, 3193–3217. [Google Scholar] [CrossRef]
- Granger, C. W. J. (1969). Investigating causal relations by econometric models and cross-spectral methods. Econometrica: Journal of the Econometric Society, 37(3), 424–438. [Google Scholar] [CrossRef]
- Gursakal, N., & Bozkurt, A. (2017). Identifying gatekeepers in online learning networks. World Journal on Educational Technology: Current Issues, 9(2), 75–88. [Google Scholar] [CrossRef]
- Guyon, H., Falissard, B., & Kopf, J.-L. (2017). Modeling psychological attributes in psychology—An epistemological discussion: Network analysis vs. latent variables. Frontiers in Psychology, 8, 798. [Google Scholar] [CrossRef]
- Hadwin, A. F., Sukhawathanakul, P., Rostampour, R., & Bahena-Olivares, L. M. (2022). Do self-regulated learning practices and intervention mitigate the impact of academic challenges and COVID-19 distress on academic performance during online learning? Frontiers in Psychology, 13, 813529. [Google Scholar] [CrossRef]
- Harder, B. (2025). Differential effects of resource availability and usage on learning, achievement, and subjective well-being. Cogent Education, 12(1). [Google Scholar] [CrossRef]
- Harder, B., & May, I. (2024, September 16–19). Ressourcenverfügbarkeit und Ressourceninteraktion bei der Stressbewältigung—Psychometrische Netzwerkmodellierungen [Availability and interaction of resources for stress management—Psychometric network models; Paper presentation]. Kongress der DGPS 2024, Vienna, Austria. [Google Scholar]
- Harder, B., O’Reilly, C., & Debatin, T. (2018). Intelligence, Educational and Learning Capital, and Domain Impact Level of Activities as Predictors of School Achievement. Journal for the Education of the Gifted, 41(4), 327–347. [Google Scholar] [CrossRef]
- Harder, B., Trottler, S., Vialle, W., & Ziegler, A. (2015). Diagnosing resources for effective learning via teacher and parent checklists. Psychological Test and Assessment Modeling, 57(2), 201–221. [Google Scholar]
- Hattie, J., & Timperley, H. (2007). The power of feedback. Review of Educational Research, 77(1), 81–112. [Google Scholar] [CrossRef]
- Hevey, D. (2018). Network analysis: A brief overview and tutorial. Health Psychology and Behavioral Medicine, 6(1), 301–328. [Google Scholar] [CrossRef]
- Koivuniemi, M., Panadero, E., Malmberg, J., & Järvelä, S. (2017). Higher education students’ learning challenges and regulatory skills in different learning situations. Journal for the Study of Education and Development: Infancia y Aprendizaje, 40(1), 19–55. [Google Scholar] [CrossRef]
- Kossakowski, J. J., Epskamp, S., Kieffer, J. M., van Borkulo, C. D., Rhemtulla, M., & Borsboom, D. (2016). The application of a network approach to Health-Related Quality of Life (HRQoL): Introducing a new method for assessing HRQoL in healthy adults and cancer patients. Quality of Life Research, 25(4), 781–792. [Google Scholar] [CrossRef]
- Kroeze, R., van der Veen, D. C., Servaas, M. N., Bastiaansen, J. A., Oude Voshaar, R. C., Borsboom, D., Ruhe, H. G., Schoevers, R. A., & Riese, H. (2017). Personalized feedback on symptom dynamics of psychopathology: A proof-of-principle study. Journal for Person-Oriented Research, 3(1), 1–10. [Google Scholar] [CrossRef]
- Kwiatkowski, D., Phillips, P. C. B., Schmidt, P., & Shin, Y. (1992). Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? Journal of Econometrics, 54(1–3), 159–178. [Google Scholar] [CrossRef]
- Lally, P., Van Jaarsveld, C. H. M., Potts, H. W. W., & Wardle, J. (2010). How are habits formed: Modelling habit formation in the real world. European Journal of Social Psychology, 40(6), 998–1009. [Google Scholar] [CrossRef]
- Liborius, P., Bellhäuser, H., & Schmitz, B. (2019). What makes a good study day? An intraindividual study on university students’ time investment by means of time-series analyses. Learning and Instruction, 60, 310–321. [Google Scholar] [CrossRef]
- Littman, A. J., White, E., Satia, J. A., Bowen, D. J., & Kristal, A. R. (2006). Reliability and validity of 2 single-item measures of psychosocial stress. Epidemiology, 17(4), 398–403. [Google Scholar] [CrossRef] [PubMed]
- Mansueto, A. C., Wiers, R. W., van Weert, J. C. M., Schouten, B. C., & Epskamp, S. (2023). Investigating the feasibility of idiographic network models. Psychological Methods, 28(5), 1052–1068. [Google Scholar] [CrossRef] [PubMed]
- Meier, R. V. (2023). Regulationsverhalten im Lernverhalten von Kindern, Jugendlichen und Studierenden—Eine qualitative Untersuchung auf Grundlage des systemischen Ansatzes [Regulation of learning behavior in children, adolescents and university students—A qualitative investigation based on a system-theoretical approach [Ph.D. thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg]. [Google Scholar]
- Mendl, A., Harder, B., & Vialle, W. (2021). Moderating effects of educational and learning capital on performance feedback. Psychological Test and Assessment Modeling, 63(2), 239–269. [Google Scholar]
- Molenaar, P. C. M. (2004). A manifesto on psychology as idiographic science: Bringing the person back into scientific psychology, this time forever. Measurement: Interdisciplinary Research & Perspective, 2(4), 201–218. [Google Scholar] [CrossRef]
- Montgomery, D. C., Jennings, C. L., & Kulahci, M. (2015). Introduction to time series analysis and forecasting (1st ed.). John Wiley & Sons. [Google Scholar]
- Mõttus, R., & Allerhand, M. (2017). Why do traits come together? The underlying trait and network approaches. In V. Zeigler-Hill, & T. Shackelford (Eds.), SAGE handbook of personality and individual differences: Volume 1. The science of personality and individual differences (pp. 1–22). Sage. [Google Scholar]
- Naujoks-Schober, N., Bakhiet, S., Altuwaijri, A. I., Vialle, W., Essa, Y. A. S., & Ziegler, A. (2025). Talent Development from a Learning Resource Perspective: Testing the Law of the Minimum. Gifted Child Quarterly. under review. [Google Scholar]
- Opsahl, T., Agneessens, F., & Skvoretz, J. (2010). Node centrality in weighted networks: Generalizing degree and shortest paths. Social Networks, 32(3), 245–251. [Google Scholar] [CrossRef]
- Panadero, E. (2017). A review of self-regulated learning: Six models and four directions for research. Frontiers in Psychology, 8, 422. [Google Scholar] [CrossRef]
- Paz-Baruch, N. (2015). Validation study of the Questionnaire of Educational and Learning Capital (QELC) in Israel. Psychological Test and Assessment Modeling, 57(2), 222–235. [Google Scholar]
- Paz-Baruch, N. (2017). Educational and learning capitals of Israeli students with high achievements in mathematics. Journal for the Education of the Gifted, 40(4), 334–349. [Google Scholar] [CrossRef]
- Paz-Baruch, N. (2020). Educational and learning capital as predictors of general intelligence and scholastic achievements. High Ability Studies, 31(1), 75–91. [Google Scholar] [CrossRef]
- Phillipson, S. N., Han, C. D., & Lee, V. C. S. (2023). Artificial neural networks and the actiotope model of giftedness—Clever solutions from complex environments. Journal of Intelligence, 11(7), 128. [Google Scholar] [CrossRef]
- R Core Team. (2024). R: A language and environment for statistical computing. R Foundation for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 4 January 2025).
- Reuter, L., Mansell, J., Rhea, C., & Kiesel, A. (2022). Direct assessment of individual connotation and experience: An introduction to cognitive-affective mapping. Politics and the Life Sciences, 41(1), 131–139. [Google Scholar] [CrossRef] [PubMed]
- Reutlinger, M., Pfeiffer, W., Stoeger, H., Vialle, W., & Ziegler, A. (2020). Domain-specificity of educational and learning capital: A study with musical talents. Frontiers in Psychology, 11(2377), 561974. [Google Scholar] [CrossRef] [PubMed]
- Rovers, S. F. E., Clarebout, G., Savelberg, H. H. C. M., de Bruin, A. B. H., & van Merrinboer, J. J. G. (2019). Granularity matters: Comparing different ways of measuring self-regulated learning. Metacognition and Learning, 14(1), 1–19. [Google Scholar] [CrossRef]
- Saito, M. A., Goepfert, T. J., & Ritt, J. T. (2008). Some thoughts on the concept of colimitation: Three definitions and the importance of bioavailability. Limnology and Oceanography, 53(1), 276–290. [Google Scholar] [CrossRef]
- Salminen, S., Kouvonen, A., Koskinen, A., Joensuu, M., & Vnnen, A. (2014). Is a single item stress measure independently associated with subsequent severe injury: A prospective cohort study of 16,385 forest industry employees. BMC Public Health, 14(1), 543. [Google Scholar] [CrossRef]
- Schwinger, M., Steinmayr, R., & Spinath, B. (2009). How do motivational regulation strategies affect achievement: Mediated by effort management and moderated by intelligence. Learning and Individual Differences, 19(4), 621–627. [Google Scholar] [CrossRef]
- Sedov, K. R., Gorban, A. N., Petushkova, E. V., Manchuk, V. T., & Shalamova, E. N. (1988). Correlation adaptometry as a method of screening of the population. Vestnik Akademii Meditsinskikh Nauk SSSR, 10(1), 69–75. [Google Scholar]
- Stemmer, L. (2020). Frauen in MINT: Ein systemischer erklärungsansatz der Leaky Pipeline [Women in STEM: A resource-oriented explanation approach of the Leaky Pipeline] [Ph.D. thesis, Friedrich-Alexander Universität Erlangen-Nürnberg]. [Google Scholar]
- Thagard, P. (2010). EMPATHICA: A computer support system with visual representations for cognitive-affective mapping. In K. McGregor (Ed.), Proceedings of the workshop on visual reasoning and representation (pp. 79–81). AAAI Press. [Google Scholar]
- Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological), 58, 267–288. Available online: http://www.jstor.org/stable/2346178 (accessed on 20 January 2025). [CrossRef]
- Trentepohl, S., Waldeyer, J., Fleischer, J., Roelle, J., Leutner, D., & Wirth, J. (2023). Self-regulation of resources in higher education. Zeitschrift Fur Padagogische Psychologie. [Google Scholar] [CrossRef]
- Tyukina, T. A. (2022). Models of adaptation and behavioural patterns in complex systems in crisis [Ph.D. thesis, University of Leicester]. [Google Scholar]
- van der Ploeg, R. R., Böhm, W., & Kirkham, M. B. (1999). On the origin of the theory of mineral nutrition of plants and the law of the minimum. Soil Science Society of America Journal, 63(5), 1055–1062. [Google Scholar] [CrossRef]
- Veas, A., Castejón, J., O’Reilly, C., & Ziegler, A. (2018). Mediation analysis of the relationship between educational capital, learning capital, and underachievement among gifted secondary school students. Journal for the Education of the Gifted, 41(4), 369–385. [Google Scholar] [CrossRef]
- Vladut, A., Liu, Q., Leana-Taşcilar, M., Vialle, W., & Ziegler, A. (2013). A cross-cultural validation study of the Questionnaire of Educational and Learning Capital (QELC) in China, Germany, and Turkey. Psychological Test and Assessment Modeling, 55(4), 462–478. [Google Scholar]
- Vladut, A., Vialle, W., & Ziegler, A. (2015). Learning resources within the Actiotope: A validation study of the QELC (Questionnaire of Educational and Learning Capital). Psychological Test and Assessment Modeling, 57(1), 40–56. [Google Scholar]
- Vladut, A., Vialle, W., & Ziegler, A. (2016). Two studies of the empirical basis of two learning resource-oriented motivational strategies for gifted educators. High Ability Studies, 27(1), 39–60. [Google Scholar] [CrossRef]
- Waldeyer, J., Dicke, T., Fleischer, J., Guo, J., Trentepohl, S., Wirth, J., & Leutner, D. (2022). A moderated mediation analysis of conscientiousness, time management strategies, effort regulation strategies, and university students’ performance. Learning and Individual Differences, 100, 102228. [Google Scholar] [CrossRef]
- Winne, P. H. (2001). Self-regulated learning viewed from models of information processing. In J. B. Zimmerman, & D. H. Schunk (Eds.), Self-regulated learning and academic achievement: Theoretical perspectives (2nd ed., pp. 153–189). Lawrence Erlbaum. [Google Scholar]
- Wright, A. G. C., & Woods, W. C. (2020). Personalized models of psychopathology. Annual Review of Clinical Psychology, 16, 49–74. [Google Scholar] [CrossRef]
- Ziegler, A. (2005). The Actiotope model of giftedness. In R. J. Sternberg, & J. E. Davidson (Eds.), Conceptions of giftedness (2nd ed., pp. 411–436). Cambridge University Press. [Google Scholar]
- Ziegler, A., & Baker, J. (2013). Talent development as adaption: The role of educational and learning capital. In N. S. Phillipson, H. Stoeger, & A. Ziegler (Eds.), Exceptionality in East Asia: Explorations in the actiotope model of giftedness (pp. 18–39). Routledge. [Google Scholar]
- Ziegler, A., Chandler, K. L., Vialle, W., & Stoeger, H. (2017). Exogenous and endogenous learning resources in the Actiotope Model of Giftedness and its significance for gifted education. Journal for the Education of the Gifted, 40(4), 310–330. [Google Scholar] [CrossRef]
- Ziegler, A., Debatin, T., & Stoeger, H. (2019). Learning resources and talent development from a systemic point of view. Annals of the New York Academy of Sciences, 1445(1), 39–51. [Google Scholar] [CrossRef]
- Ziegler, A., Hopp, M., Linner, M., Schöferle, T., Thomas, N., Schielein, T., Vladut, A., & Götzfried, W. (2012). Bildungs-und Lernkapitalarmut von Hauptschülern: Ergebnisse einer explorativen Befragungsstudie mit Lehrkräften [Deficits in educational and learning capital among middle school students: Results of an explorative survey among teachers]. Schulpädagogik heute, 3(5), 1–10. [Google Scholar]
- Ziegler, A., & Phillipson, S. N. (2012). Towards a systemic theory of gifted education. High Ability Studies, 23(1), 3–30. [Google Scholar] [CrossRef]
- Ziegler, A., & Stoeger, H. (2017). Systemic gifted education: A theoretical introduction. Gifted Child Quarterly, 61(3), 183–193. [Google Scholar] [CrossRef]
- Ziegler, A., & Stoeger, H. (2019). A nonagonal framework of regulation in talent development (NFRTD). High Ability Studies, 30(1–2), 127–145. [Google Scholar] [CrossRef]
| Name | Definition | Positive Examples |
|---|---|---|
| Educational Capital | ||
| eco | Economic educational capital is every kind of wealth, possession, money, or valuables that can be invested in the initiation and maintenance of educational and learning processes (p. 27). | Salary, financial support by parents or partner, and scholarships |
| inf | Infrastructural educational capital relates to materially implemented possibilities for action that permit learning and education to take place (p. 28). | Learning materials like books and internet sites, and access to native speakers |
| cul | Cultural educational capital includes value systems, thinking patterns, models, and the like, which can facilitate—or hinder—the attainment of learning and educational goals (p. 27). | Family/friends/media valuing learning the language, the country, and the culture |
| did | Didactic educational capital means the assembled know-how involved in the design and improvement of educational and learning processes (p. 29). | Individually tailored instructions and corrective feedback (via learning apps or teachers) |
| soc | Social educational capital includes all persons and social institutions that can directly or indirectly contribute to the success of learning and educational processes (p. 28). | People encouraging and supporting learning and taking over household chores |
| Learning Capital | ||
| org | Organismic learning capital consists of the physiological and constitutional resources of a person (p. 29). | No learning disabilities, a healthy diet, and enough sleep |
| act | Actional learning capital means the action repertoire of a person—the totality of actions they are capable of performing (p. 30). | Knowledge of learning strategies and rules of pronunciation |
| tel | Telic learning capital comprises the totality of a person’s anticipated goal states that offer possibilities for satisfying their needs (p. 30). | Making a plan and prioritizing learning over other hobbies |
| epi | Episodic learning capital concerns the simultaneous goal- and situation-relevant action patterns that are accessible to a person (p. 31). | Successful vocabulary memorizing strategies from prior experiences |
| att | Attentional learning capital denotes the quantitative and qualitative attentional resources that a person can apply to learning (p. 31). | Time window reserved for learning and no interruptions |
| Variables | Original Data | First Difference | ||
|---|---|---|---|---|
| ADF | KPSS | ADF | KPSS | |
| Educational and Learning capitals | ||||
| Organismic | −2.478 | 0.303 | −4.413 ** | 0.088 |
| Attentional | −2.206 | 0.206 | −4.836 ** | 0.101 |
| Actional | −3.286 + | 0.088 | −4.762 ** | 0.047 |
| Episodic | −5.118 ** | 0.523 * | −5.229 ** | 0.045 |
| Telic | −3.206 + | 0.344 | −5.228 ** | 0.071 |
| Economic | −2.784 | 0.814 ** | −6.014 ** | 0.046 |
| Social | −3.105 | 0.088 | −5.507 ** | 0.051 |
| Cultural | −2.760 | 0.138 | −4.704 ** | 0.079 |
| Infrastructural | −1.795 | 0.210 | −5.364 ** | 0.061 |
| Didactic | −3.835 * | 0.532 * | −7.794 ** | 0.047 |
| Stress Level | −2.016 | 0.177 | −4.424 ** | 0.069 |
| Duration of Learning | −2.672 | 0.150 | −4.028 * | 0.120 |
| Performance | ||||
| Correctly Recalled New Words | −2.874 | 0.226 | −4.691 ** | 0.048 |
| Correctly Recalled Repeated Words | −1.805 | 0.240 | −5.052 ** | 0.127 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harder, B.; Naujoks-Schober, N.; Hopp, M.D.S. Capturing the Complex: An Intraindividual Temporal Network Analysis of Learning Resource Regulation. Educ. Sci. 2025, 15, 728. https://doi.org/10.3390/educsci15060728
Harder B, Naujoks-Schober N, Hopp MDS. Capturing the Complex: An Intraindividual Temporal Network Analysis of Learning Resource Regulation. Education Sciences. 2025; 15(6):728. https://doi.org/10.3390/educsci15060728
Chicago/Turabian StyleHarder, Bettina, Nick Naujoks-Schober, and Manuel D. S. Hopp. 2025. "Capturing the Complex: An Intraindividual Temporal Network Analysis of Learning Resource Regulation" Education Sciences 15, no. 6: 728. https://doi.org/10.3390/educsci15060728
APA StyleHarder, B., Naujoks-Schober, N., & Hopp, M. D. S. (2025). Capturing the Complex: An Intraindividual Temporal Network Analysis of Learning Resource Regulation. Education Sciences, 15(6), 728. https://doi.org/10.3390/educsci15060728








