Enhancing Numerical Thinking Through Problem Solving: A Teaching Experience for Third-Grade Mathematics

Abstract

This study introduces a comprehensive educational intervention designed to strengthen numerical thinking in third-grade mathematics education through problem-solving. Anchored in Pólya’s problem-solving framework, this research employs a qualitative, descriptive methodology to design and assess a didactic unit. The intervention comprises six structured activities aimed at evaluating and enhancing students’ competencies in numerical thinking and problem-solving. This study’s findings reveal a marked improvement in students’ mathematical abilities, particularly in applying problem-solving techniques to various mathematical contexts. This progress highlights the intervention’s effectiveness in fostering critical thinking and boosting educational outcomes in mathematics. The proposed model demonstrates versatility, offering a scalable approach for enhancing mathematical competencies in diverse educational environments. By integrating Pólya’s systematic steps into instructional practices, this research contributes significantly to pedagogical strategies in mathematics. The innovative use of problem-solving as a learning and evaluation tool not only bridges theoretical and practical knowledge, but also provides a replicable framework for advancing numerical thinking. The methodological approach, which combines qualitative analysis with tangible classroom applications, underscores the potential for transforming mathematics education and improving students’ engagement and proficiency in the subject.

1. Introduction

Mathematics education research has increasingly emphasized the importance of fostering problem-solving skills in students, as these skills are essential for developing robust numerical thinking (Arfé et al., 2020; Callejo et al., 2016; Govender et al., 2024). Numerical thinking encompasses the ability to understand numbers and operations, reason flexibly with them, and apply them efficiently in problem-solving contexts (Freiman et al., 2017). In this regard, problem-solving is more than just executing algorithmic procedures—it requires students to analyze given situations, identify relevant relationships, formulate strategies, implement them, and critically evaluate the validity of their solutions (Arfé et al., 2020; Callejo et al., 2016).

Research in mathematics education underscores the necessity of integrating both procedural knowledge and problem-solving strategies in teaching (Schoenfeld, 2017). Encouraging students to engage in tasks such as decomposing numbers into different combinations fosters a deeper conceptual understanding and enhances their ability to approach diverse mathematical challenges. Furthermore, connecting mathematics to real-world contexts makes learning more meaningful and engaging, leading to more sustainable knowledge retention (English, 2011). Adapting mathematical tasks to students’ cultural backgrounds can also enhance equity and relevance, ensuring broader accessibility and participation in mathematics learning (Boggs & McGinnis, 2016).

Moreover, incorporating diverse teaching methodologies, real-world applications, and collaborative learning can significantly enhance students’ problem-solving skills. A particularly effective approach involves integrating problem-solving techniques that relate directly to real-life situations. Research indicates that contextualized instruction improves students’ abilities to solve problems by making mathematical concepts more tangible and relevant. For instance, Eshetu and Assefa (2018) demonstrated that context-based teaching strategies enhanced students’ ability to solve physics problems, suggesting that similar approaches in mathematics could make learning more engaging and effective. Additionally, problem-based learning (PBL) has emerged as a powerful pedagogical method for fostering critical thinking and problem-solving skills by placing students in real-world scenarios that require active inquiry and exploration. Almasarweh and Khudairat (2021) found that PBL not only deepens conceptual understanding, but also enhances students’ critical thinking abilities, leading to improved learning outcomes.

Beyond contextualized learning, explicit teaching strategies play a fundamental role in developing problem-solving skills. The self-regulated strategy development (SRSD) model, for example, has been effective in teaching mathematical problem-solving by providing students with a structured framework to plan, monitor, and evaluate their cognitive processes. Popham et al. (2019) highlighted the effectiveness of SRSD in helping students develop self-regulation skills, enabling them to approach problem-solving systematically. Similarly, cognitive strategy instruction, such as the math scene investigator (MSI) approach, has been shown to support elementary students in overcoming difficulties with word problems, thereby improving their overall mathematical comprehension. Pfannenstiel et al. (2014) emphasized the benefits of MSI in enhancing mathematical reasoning among students who struggle with problem-solving tasks.

Collaboration among students is another critical factor in strengthening problem-solving competencies. Studies have shown that cooperative learning environments, where students work in small groups, not only foster engagement, but also deepen their understanding of mathematical concepts. Acquandoh et al. (2022) found that collaborative problem-solving significantly increased student participation and interest in mathematics. Such collaborative settings encourage the exchange of diverse problem-solving strategies and perspectives, often leading to more effective and innovative solutions.

Despite the recognized importance of cultivating mathematical thinking from an early age, international assessments such as the Programme for International Student Assessment (PISA) consistently indicate that a significant proportion of Colombian students fail to achieve the basic proficiency level in mathematics. This persistent challenge underscores the urgent need for targeted educational interventions that prioritize problem-solving and numerical reasoning from the foundational stages of schooling. Colombia has participated in the PISA since 2006, evaluating 15-year-old students in reading, mathematics, and science. In the 2022 edition, the country experienced a decline in average scores compared with 2018: in mathematics, from 391 to 383 points; in reading, from 412 to 409; and in science, from 413 to 411. Although these decreases were relatively smaller than those observed in many OECD countries, Colombia continues to fall significantly below the OECD average across all assessed areas. Notably, only 29% of Colombian students reached at least proficiency level 2 in mathematics, compared with 69% in OECD countries. Similarly, in reading and science, approximately 49% of Colombian students achieved at least level 2, while in the OECD, these percentages stood at 74% and 76%, respectively (OECD—Organization for Economic Cooperation and Development, 2022). These results underscore the urgent need for structural reforms within the Colombian educational system to improve both the quality and equity of student learning outcomes. Therefore, this study emerges from the identification of persistent challenges in students’ mathematical problem-solving skills, as evidenced by national and international assessment results, as well as by the responses of the students to an initial diagnostic task at the start of the teaching unit. The unit was specifically designed to foster the development of numerical thinking, positioning problem-solving as the central focus of the teaching and learning process.

This study presents a didactic proposal designed to enhance numerical thinking in third-grade primary school students in Colombia. Employing a qualitative and descriptive approach, this research focused on designing, implementing, and evaluating a didactic unit based on mathematical problem-solving, guided by Pólya’s methodology. An initial diagnostic assessment was conducted to identify students’ primary difficulties in solving mathematical problems, using national and international test results as benchmarks. Based on these findings, six didactic activities were developed to assess and enhance students’ competencies in numerical reasoning. The primary objective of this study was to evaluate the impact of this didactic unit on the development of numerical thinking, recognizing that problem-solving serves as a fundamental pillar in mathematics education. Strengthening these competencies not only improves students’ mathematical reasoning and analytical abilities, but also equips them with essential skills for solving real-world problems.

2. Theoretical Framework

The interplay between elementary education, problem-solving, and numerical thinking underscores the need for pedagogical approaches that address students’ cognitive development and learning needs. Teacher training is instrumental in this process, as educators must be equipped with the necessary tools and methodologies to guide students effectively (Ramos et al., 2021; Conde-Carmona & Bolívar, 2023). Continuous professional development in innovative teaching strategies is essential for improving the quality of mathematics education and fostering meaningful learning experiences (Heffington et al., 2023).

Problem-solving is not only a goal, but also a method of learning mathematics. In this study, we adopt Pólya’s (1957) framework, which proposes four key stages: (1) understanding the problem, (2) devising a plan, (3) carrying out the plan, and (4) looking back. These stages offer a structured, yet flexible, process through which students engage with mathematical ideas and develop problem-solving competence. Each task in our teaching unit is explicitly designed to correspond with one or more of these stages, and reflective prompts help students to internalize and navigate the problem-solving process. This model is further enriched by the contributions of Boaler (2015), who emphasized the importance of cultivating mathematical thinking that is creative, flexible, and rooted in real problem contexts. Her work advocates for practices that support a growth mindset and encourage students to take intellectual risks, aligning well with the structure and intent of this study.

The first stage, understanding the problem, focuses on clarifying what is known and unknown, identifying relevant information, and representing the problem in a way that makes it more accessible. This involves restating the problem in one’s own words, distinguishing key quantities, and using visual tools such as diagrams or sketches to externalize relationships. In classroom practice, this step is guided by teacher prompts like: “What is the problem asking?”, “What information do you have?”, “Can you explain the problem in your own words?”, and “Could you draw a picture to help you understand it?” These strategies help students to engage deeply with the structure of the problem, rather than rushing toward a solution.

The second stage, devising a plan, encourages students to explore various strategies for solving the problem. This might include approaches such as working backward, identifying patterns, making a systematic list, simplifying the problem, or drawing analogies with previously solved problems. The emphasis here is on fostering strategic thinking and encouraging students to select the method they believe is most effective. Teachers can support this process by asking: “What strategies could you use?”, “Have you encountered a similar problem before?”, “Can you break this into smaller steps?”, and “Would guessing and checking help here?” This stage nurtures flexibility in problem solving and emphasizes that multiple solution paths are possible.

The third stage, carrying out the plan, involves the careful and methodical execution of the chosen strategy. Precision, persistence, and monitoring are key during this phase. Students are encouraged to document their steps, check their reasoning, and remain open to revising their approach if obstacles arise. The teacher’s role is to scaffold metacognitive awareness, posing questions such as: “Can you show how you’re applying your strategy?”, “Explain each step as you go”, “Are you keeping track of your work?”, and “Is this strategy working, or do we need to consider another?”.

Finally, the fourth stage, looking back, emphasizes the evaluation of the solution and reflection on the overall process. Students are guided to verify their results, consider the logic of their reasoning, and assess whether their answers align with the problem’s conditions. Additionally, this stage includes encouraging students to generalize from their solution, identifying principles or methods that could apply to future problems. Teachers may ask: “Does your answer make sense?”, “Can you think of another way to solve it?”, “What did you learn from solving this problem?”, and “How might you use this strategy in other situations?”.

Numerical thinking is understood as the capacity to reason flexibly with numbers and operations, and to apply them efficiently in a variety of problem-solving situations (Gelman & Gallistel, 1978). Research indicates that individual differences in numerical thinking are linked to the ability to detect patterns and understand arithmetic properties (Dowker, 2005), and that early numerical estimation serves as a strong predictor of later mathematical achievement (Siegler & Booth, 2004). Moreover, children begin developing core numerical representations even before formal schooling, with these foundations continuing to evolve through the early grades (Mulligan & Mitchelmore, 2012). Syntheses by Nunes et al. (2009) further underscore the critical role of multiple representations—including symbolization, counting, and estimation—in building a deep and transferable understanding of numbers.

One fundamental aspect of early mathematics education is the development of numerical thinking, which aims to provide students with a solid understanding of numbers and their operations, enabling them to think flexibly and make informed mathematical judgments. This includes the ability to communicate, process, and interpret numerical information effectively (Murcia & Henao, 2015). Additionally, five core mathematical processes should be emphasized in primary education, one of which is problem-solving and problem-posing. According to Stanic and Kilpatrick (1989), problem-solving is not merely a practice tool, but the central mechanism through which students engage in mathematical thinking and construct their knowledge.

Promoting numerical thinking in primary school students requires a multifaceted approach that integrates open-ended learning strategies, problem-based scenarios, symbolic tools, and structured reflection, all supported by rich mathematical communication. These components are essential for cultivating flexibility in reasoning and strengthening the conceptual understanding necessary for problem-solving.

One effective method is the use of open-ended tasks that invite children to explore numbers and symbols creatively. Warmansyah et al. (2023) found that this approach significantly improves young students’ ability to recognize numerical concepts and engage in both critical and creative thinking. This idea is consistent with the learning trajectories framework described by Clements et al. (2023), which emphasizes instructional progressions tailored to children’s interests and developmental levels, thereby deepening their engagement with foundational mathematical ideas. Similarly, symbolic mediation plays a key role in early mathematics development. Hyde et al. (2021) demonstrated that integrating symbolic tools—such as digital abacuses—into numeracy interventions enhances young learners’ numerical skills. For these strategies to be fully effective, however, they must be accompanied by a strong emphasis on mathematical communication. Lee (2015) argues that encouraging dialogue around numerical concepts enables children to articulate, test, and refine their reasoning, ultimately consolidating their understanding and fostering metacognitive awareness.

Complementing these exploratory and communicative approaches, PBL provides a structured pedagogical model that enhances critical thinking and real-world problem-solving. By framing mathematical challenges within authentic contexts, PBL encourages students to construct solutions actively and apply their knowledge across varied situations. However, the success of PBL depends on intentional scaffolding: teachers must guide interactions to ensure inclusive participation and maintain conceptual focus (Narmaditya et al., 2018).

Beyond these instructional strategies, structured reflection is critical to the development of numerical reasoning. Programs like Learning to Think equip students with tools to analyze their own problem-solving processes and metacognitive strategies. Hu et al. (2011, 2013) reported that students who engage in reflective practice not only deepen their conceptual understanding, but also apply mathematical ideas more flexibly in unfamiliar contexts.

Together, these interrelated pedagogical strategies—open-ended exploration, symbolic representation, collaborative dialogue, real-world problem contexts, and structured reflection—form a cohesive framework for fostering robust numerical thinking in primary education. By embedding these elements into a didactic model informed by Pólya’s problem-solving stages, educators can create engaging and inclusive learning environments that empower students to reason mathematically, develop resilience in the face of cognitive challenge, and transfer their knowledge to new domains.

The didactic unit proposed in this study seeks to contribute to the development of mathematical competencies by engaging students in tasks that require them to:

• Decompose: Analyze the structure of a number and its various components;
• Represent: Utilize visual representations to enhance understanding and communication of mathematical concepts;
• Solve problems: Apply mathematical knowledge to new situations and explore multiple solution strategies.

The design and implementation of the unit’s activities are grounded in the problem-solving framework proposed by Pólya (1957), whose seminal work ‘How to Solve It’ introduced a structured, heuristic approach to mathematical problem solving that continues to influence mathematics education today. His model articulates four interconnected stages, understanding the problem, devising a plan, carrying out the plan, and reviewing the solution, which not only support problem resolution, but also cultivate essential aspects of mathematical thinking.

Although Pólya’s framework is often presented as a sequence of structured steps, making the problem-solving process appear more approachable and systematic; it is important to recognize that, in practice, the process is rarely linear. Students frequently move back and forth between stages, revisiting earlier steps as new insights emerge or as obstacles arise. This recursive nature reflects the authentic cognitive demands of mathematical thinking. One of the strengths of Pólya’s model lies in its potential to scaffold students’ reasoning, helping them maintain focus, reduce errors, and engage more thoughtfully with each phase of problem-solving.

By systematically integrating Pólya’s four stages into the instructional sequence, the unit not only scaffolds problem-solving proficiency, but also fosters deeper numerical reasoning, encourages reflection, and promotes the transfer of mathematical knowledge across contexts. This alignment between pedagogical practice and theoretical framework strengthens the coherence and intentionality of the teaching intervention.

These tasks align with international recommendations, such as those from UNESCO and the OECD, which emphasize the importance of fostering mathematical skills through active problem-solving and real-world applications. Encouraging students to explore different ways of representing and decomposing numbers strengthens their mathematical reasoning and promotes an equitable and meaningful learning experience.

This study also resonates with the pedagogical vision advanced by Boaler (2015), who advocated for the development of flexible mathematical thinkers capable of approaching problems from multiple perspectives. By shifting away from a narrow, procedural conception of mathematics, the teaching unit emphasizes conceptual understanding and inquiry-based learning, where problem solving is not merely an application, but a central vehicle for learning mathematics. Integrating elements of Boaler’s approach within the structure provided by Pólya’s model enhances the design of the unit: while Pólya offers a strategic roadmap for navigating problems, Boaler contributes a broader pedagogical framework that fosters a growth mindset, promotes productive struggle, and encourages students to embrace mathematical challenges as opportunities for learning and creativity. This dual alignment provides a strong foundation for cultivating both procedural competence and adaptive reasoning in young learners. Thus, this study hypothesizes that the implementation of a problem-solving-based didactic unit will significantly enhance the development of numerical thinking in third-grade students. This structured problem-solving-based teaching unit was designed to strengthen numerical thinking in elementary students by engaging them in progressively complex mathematical tasks. By integrating real-world problem contexts, collaborative learning strategies, and reflective questioning, the unit aimed to enhance students’ ability to interpret, represent, and manipulate numerical information effectively. The preliminary results of this research indicate that implementing the proposed didactic unit has had a positive impact on students’ performance in mathematical problem-solving. However, further analysis is necessary to assess the full extent of these outcomes and their long-term sustainability.

This study is guided by the central research question: How does the implementation of a problem-solving-based teaching unit support the development of numerical thinking among third-grade students at the institution? To address this question, a qualitative research design was adopted, focusing on a descriptive analysis of students’ learning progress as evidenced through the tasks completed during the teaching unit.

In qualitative research, the interpretive stance and reflexivity of the researchers are fundamental. Their role is not only to observe, but also to make sense of how students interact with mathematical problems, communicate their thinking, and evolve in their understanding. Accordingly, the analysis centers on two complementary aspects:

Activity development. This includes examining student participation and verbal or written interventions during classroom tasks, the diversity and nature of the strategies employed to solve problems, and other behaviors or patterns that emerged throughout the teaching process. This dimension centers the interactional and dynamic context of learning.

Student-produced artifacts. The written records and completed tasks are analyzed with attention to the mathematical language students use to articulate their ideas, the clarity of their reasoning, and the steps taken during problem solving. This provides insight into both their conceptual understanding and their capacity to communicate mathematical thinking effectively.

By integrating these two levels of analysis, this study aims to generate a nuanced account of how structured problem-solving instruction can promote numerical thinking, particularly through students’ evolving strategies, representational fluency, and engagement with mathematical reasoning. Therefore, this study seeks to contribute to the field of mathematics education by providing a contextualized analysis of how problem-solving strategies, specifically those proposed by Pólya (1957), can be implemented through a structured teaching unit to foster numerical thinking in early primary education. Unlike many traditional studies that emphasize quantitative outcomes, this research adopts a qualitative and reflective approach within an action research framework. It seeks to explore how students develop and apply numerical reasoning skills through guided problem-solving activities. This classroom-based inquiry is particularly relevant in the Colombian context, where few empirical studies systematically examine the real-time development of mathematical thinking at the primary level. The insights derived are intended not only to inform teaching practice, but also to offer replicable and adaptable strategies for mathematics educators and curriculum designers in similar socio-educational settings.

3. Materials and Methods

This study follows a descriptive approach within the framework of action research, aiming to understand and enhance the development of numerical thinking in third-grade students from a public primary school in Colombia. This study does not include a pretest-posttest evaluation, as its primary objective is to observe, design, and iteratively refine educational interventions in a reflective and adaptive manner. This study is framed as qualitative action research, chosen for its capacity to both understand and transform classroom practice (Menéndez & Rodríguez, 2012). The approach emphasizes the iterative involvement of the teacher–researcher in identifying a problem, designing an intervention, implementing it in the classroom, and reflecting critically on its outcomes (Zambo, 2011; Shakouri, 2013).

Participants were selected through purposive sampling (Menéndez & Rodríguez, 2012) based on their voluntary agreement to participate in the study. This criterion ensured ethical engagement while allowing for the inclusion of students who were genuinely willing to engage with the instructional activities and contribute meaningfully to the research process.

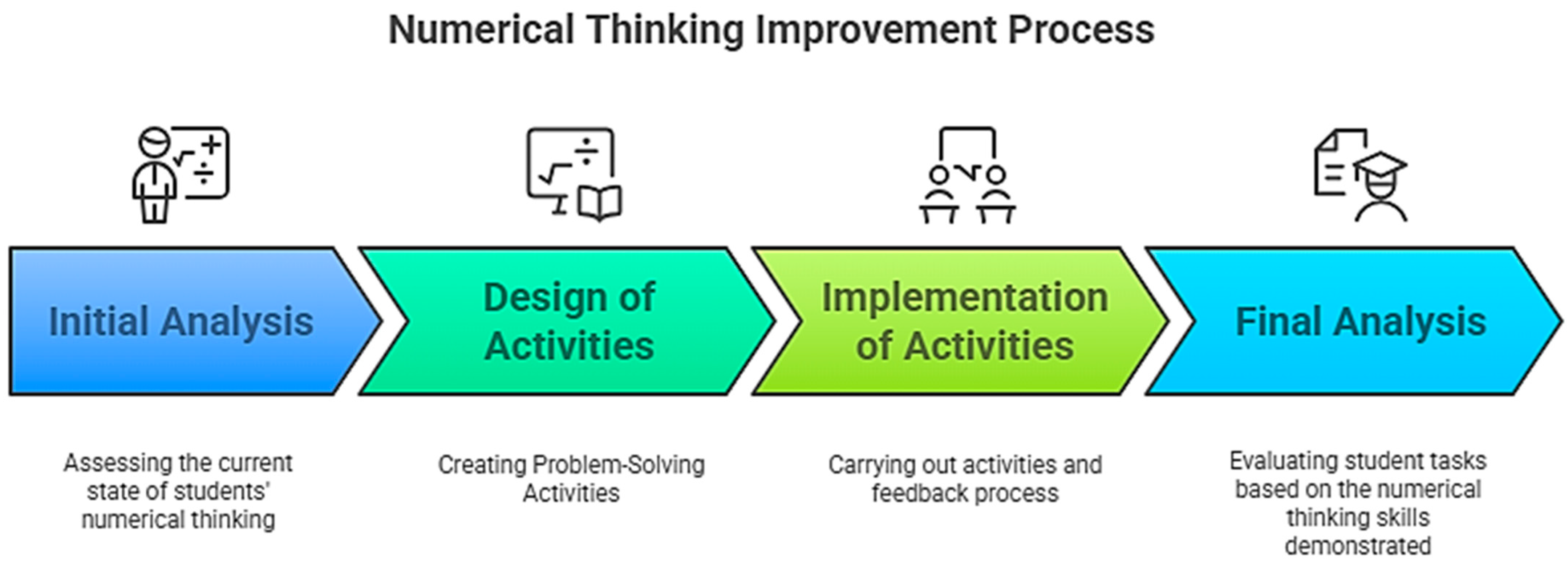
To achieve this goal, this research was structured into four key stages (Figure 1):

• Initial Diagnostic Phase—A diagnostic assessment was conducted to evaluate students’ existing numerical thinking abilities. This diagnosis was based on direct classroom observations, a review of the students’ prior work, and qualitative analysis of their numerical understanding. The objective was to identify both strengths and areas for improvement, which served as the foundation for the subsequent intervention. A set of mathematical tasks was used to identify students’ prior difficulties in solving additive and multiplicative problems, understanding positional value, and using representations. This diagnostic served as the foundation for designing targeted interventions.
• Design of the Teaching Unit—Based on the findings from the diagnostic phase, six didactic tasks were developed using Pólya’s four-stage model (understanding the problem, devising a plan, executing the plan, and reviewing the solution). These tasks were designed to progressively deepen students’ understanding of numerical relationships and promote flexible problem-solving strategies. The design of the instructional activities was guided by the principles of action research (Shakouri, 2013; Zambo, 2011), emphasizing iterative reflection and adaptation based on observed student needs. Drawing from the initial assessment results, tasks were crafted to cultivate essential numerical thinking skills. These include understanding numbers and their various representations, applying operations and their properties, and solving numerical calculation problems. The activities incorporated active learning strategies, promoting problem-solving, reflection, and the construction of numerical concepts, thereby fostering a deeper engagement with mathematical ideas.
• Implementation of the Didactic Unit—The designed tasks were then applied in structured work sessions, fostering a collaborative learning environment and active student participation. The activities aimed to improve students’ engagement with numerical concepts through hands-on problem-solving experiences. The intervention was conducted over multiple sessions and structured into three pedagogical moments:
  • Moment 1 (Introduction): Activation of prior knowledge through basic problem situations;
  • Moment 2 (Development): Group-based problem solving of increasing complexity with teacher facilitation;
  • Moment 3 (Closure): Individual resolution of non-routine tasks followed by formative assessment and adjustments.
  The teacher–researcher observed and documented student interactions, engagement, and reasoning processes during each session.
• Analysis Phase—After completing the intervention, the students’ responses to the tasks were analyzed to identify key numerical thinking skills demonstrated in their written solutions. Data were collected through classroom observations, students’ written responses, and field notes. The written work was analyzed using qualitative content analysis (Miles & Huberman, 1994), identifying emerging patterns and interpreting them based on the theoretical framework. Categories were developed a posteriori and included: understanding place value, flexibility in numerical strategies, use of multiple representations, and application of operations. A qualitative analysis was conducted on students’ responses to the activities. Key indicators of numerical thinking were used to assess their use of representations, selection of strategies, justification of procedures, and interpretation of results. Representative examples of student work are analyzed in the Results section to illustrate the progression in conceptual understanding. This analytical process aligns with qualitative coding practices and is informed by established literature in mathematics education (e.g., Boaler, 2015; Carpenter et al., 1996). The goal was to evaluate the effectiveness of the instructional activities in fostering mathematical reasoning and problem-solving competencies.

The qualitative approach was chosen for its capacity to explore in depth the “how” and “why” behind students’ development of numerical thinking, offering nuanced insights that can inform and refine instructional practices. Unlike quantitative designs that may focus on outcomes alone, this approach enables the identification of specific elements within the teaching unit—as well as students’ interactions and experiences—that contributed to observable growth in numerical understanding. Such insights are critical for adjusting pedagogical strategies to better support student learning.

The assessment process was grounded in direct classroom observations, analysis of students’ prior work, and a qualitative evaluation of their demonstrated levels of numerical understanding. This initial diagnostic phase aimed to identify both individual and group-level strengths as well as areas for growth, which served as a foundation for the second stage: the design of targeted instructional activities. These tasks were informed by principles of active learning and pedagogical strategies that emphasized problem-solving, metacognitive reflection, and the construction of key numerical concepts through meaningful engagement. Designed to challenge students and support conceptual development, the activities were implemented during structured work sessions that promoted collaboration, dialogue, and active participation. In the final stage, students’ written work was systematically analyzed to identify evidence of numerical thinking, such as flexible reasoning, use of representations, and application of numerical strategies. This final analysis provided valuable insights into how students internalized and applied the mathematical ideas explored throughout the unit.

3.1. Initial Analysis

The diagnostic phase involved presenting students with elementary numerical problem-solving tasks to assess their current abilities. The results indicated that most students experienced difficulties in two fundamental areas:

• Understanding and applying operations and properties of natural numbers to establish relationships between numbers in contextualized situations;
• Solving routine additive problems related to composition and transformation, including interpreting the necessary conditions for their resolution.

These findings provided the basis for designing instructional interventions tailored to the specific challenges observed in students’ numerical thinking development.

3.2. Design and Implementation of Activities

The design of instructional activities was informed by the findings from the initial analysis and aimed at developing fundamental numerical thinking skills. These skills include understanding numbers and their representations, applying operations and their properties, and solving numerical calculation problems. To ensure the quality and pedagogical effectiveness of the tasks, they underwent a rigorous review process by experts in mathematics education and educational assessment. These experts evaluated whether the tasks aligned with the intended learning objectives and assessed their potential to enhance numerical thinking skills among students.

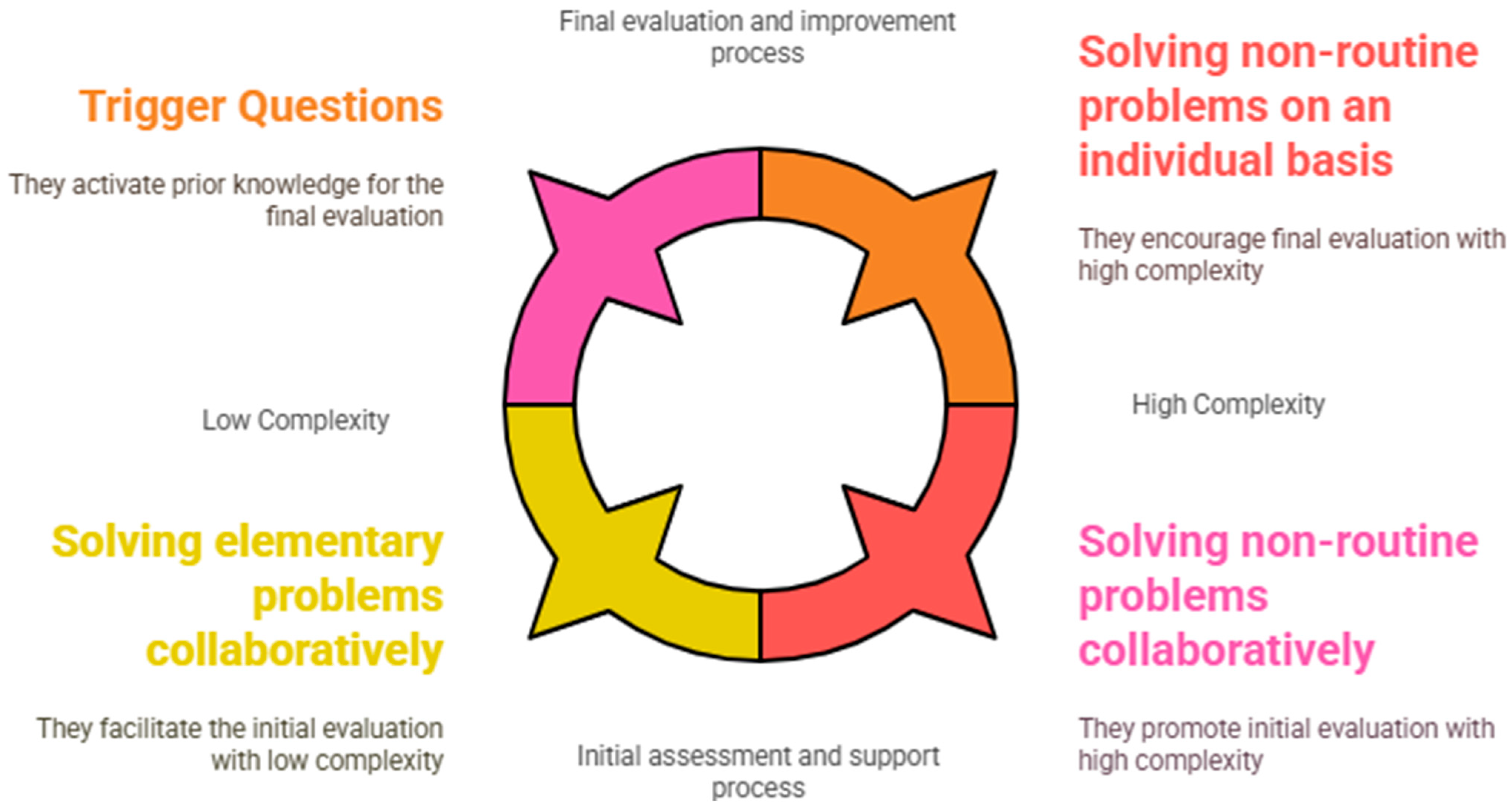
Once the activities were designed and validated, the implementation phase was carried out in three structured moments (Figure 2):

• Moment 1. Introduction and Activation of Prior Knowledge

In this phase, the process begins with trigger questions and the presentation of elementary problems designed to activate students’ prior knowledge. Students work collaboratively to solve these low-complexity problems, sharing their solutions with the class. At this stage, the teacher plays a facilitative role by posing open-ended questions that stimulate discussion and encourage participation from all students.

• Moment 2. Development and Problem-Solving in Groups

During this phase, students work in self-selected groups of three or four, tackling problems of greater complexity. The teacher actively monitors the process by engaging with students through guiding questions, providing feedback, and encouraging multiple solution strategies. Examples of teacher-led guiding questions include:

• How did you approach solving this problem?
• What was your first step? Why?
• Why did you choose this particular operation?
• Did you explore alternative ways to solve the problem?
• Which part of the problem was the most challenging? Why?
• How can you verify if your answer is correct?
• What did you learn from solving this problem?

These scaffolded questions help students to reflect on their thinking process, deepen their numerical understanding, and develop problem-solving autonomy.

• Moment 3. Closure and Individual Problem-Solving

In the final stage, students transition to independent problem-solving, working on non-routine tasks that require higher-order reasoning. This moment serves as a formative assessment, allowing teachers to evaluate students’ progress and identify areas for further reinforcement. The feedback obtained from this phase is used to refine and improve the instructional tasks for subsequent iterations of the didactic unit.

To ensure active and equitable participation among all students throughout the three phases of the instructional sequence, a structured engagement strategy was implemented:

Phase 1: Introduction

Following the presentation of the problem, each student was encouraged to respond simultaneously, either by recording their thoughts individually in notebooks or by raising their hands to contribute orally. Subsequently, different students were invited to share their solutions, both orally and in writing, to prevent repetitive participation by the same individuals. This approach aligns with the “Think–Pair–Share” technique, which promotes equitable participation by allowing students time to process and articulate their ideas before sharing with the larger group.

Phase 2: Development

Students were organized into small groups of up to four members, with rotating roles assigned to each participant. These roles included the facilitator, recorder, presenter, and timekeeper, ensuring that each student assumed specific responsibilities for discussing, documenting, and presenting solutions to the tasks. Rotating roles not only fostered accountability, but also provided students with opportunities to develop diverse skills and prevented dominance by any single group member.

Phase 3: Closure

The teacher maintained a record of student interventions and actively requested oral or written reflections from those who had not yet participated, ensuring that every student’s contributions were recognized and analyzed as part of the formative assessment process. This practice emphasized the importance of inclusive participation and provided insights into each student’s understanding and engagement.

By integrating these strategies, the instructional approach promoted a collaborative learning environment that emphasized active participation, equitable engagement, and the development of critical numerical thinking skills.

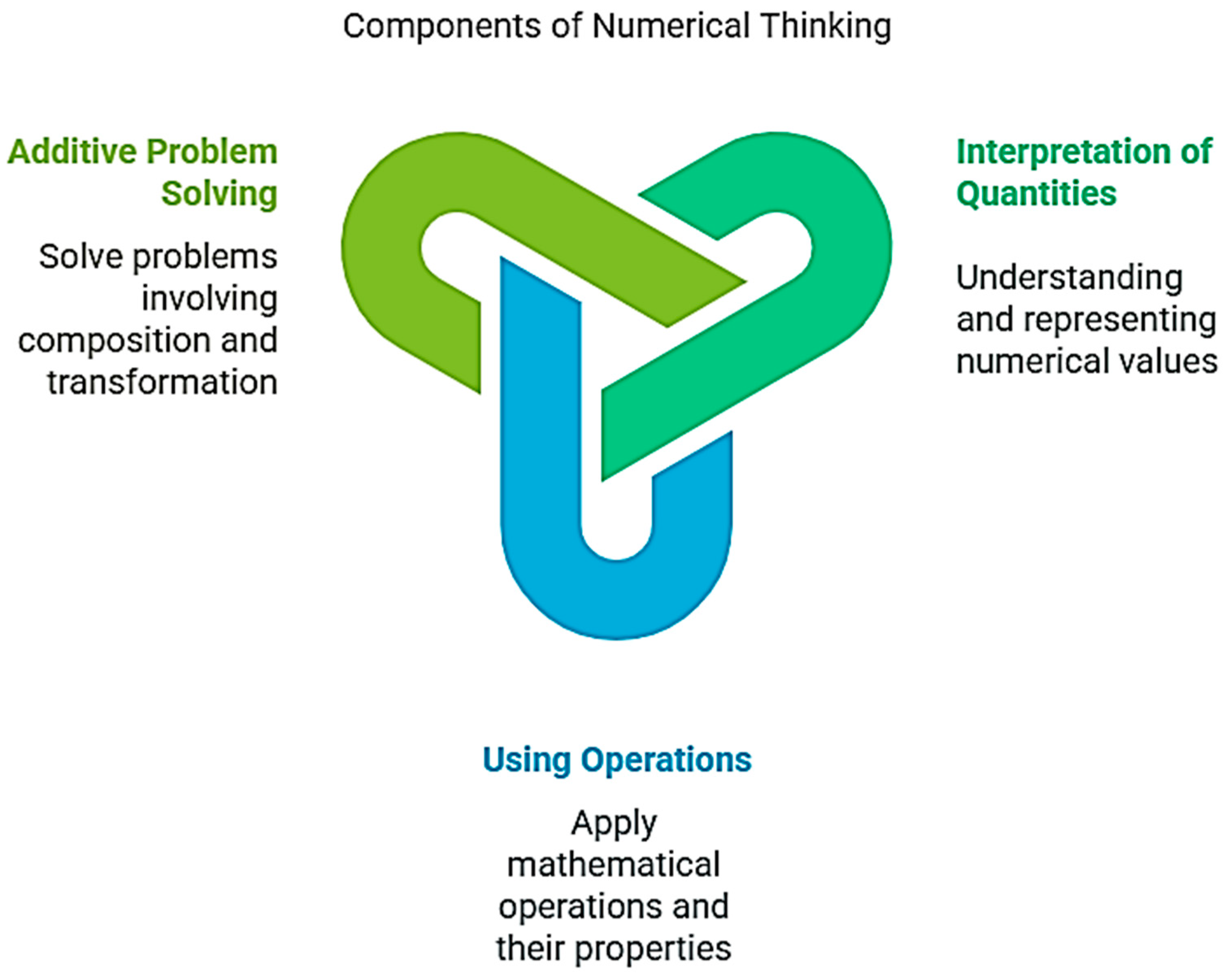
3.3. Assessment of Numerical Thinking Skills

The study focused on evaluating key numerical thinking skills, specifically:

• Interpretation and representation of quantities and mathematical situations across different registers;
• Application of mathematical operations and their properties;
• Solution of additive composition and transformation problems.

Through this analysis, it was possible to assess students’ progress in learning, identify specific areas requiring further support, and reflect on the impact of the instructional activities implemented in the study. The insights gained from this evaluation contributed to refining the pedagogical approach and enhancing future iterations of the didactic unit.

Figure 3 illustrates the core components of numerical thinking that were assessed throughout this study.

3.4. Teaching Unit: Developing Numerical Thinking Through Problem-Solving

To foster the development of numerical thinking in third-grade students, a structured teaching unit was designed based on problem-solving activities. The unit consists of three instructional phases, each presenting elementary, introductory, and complex problem-solving tasks that encourage students to engage actively in numerical reasoning. These activities focus on strengthening key aspects of numerical thinking, including interpreting and solving additive composition, transformation, and comparison problems, as well as multiplicative problems in direct and inverse contexts.

• Expected Learning Outcomes:
  • Interpret and solve additive problems involving composition, transformation, and comparison in various contexts;
  • Solve multiplicative problems in both direct and inverse situations.
• Moment 1. Introduction

Learning Objective: Use concrete, graphic, and pictorial representations to express quantities in different situations.

Activities:

Cut out the educational bills (Figure 4) and use them to represent the given numerical values: 1462, 5647, and 4958.

• Write the corresponding number in words;
• Determine the number of bills of each denomination needed to construct the given amount (Figure 5). Explain the reasoning;
• Analyze a set of educational bills and write the total amount represented;
• Comparison task:
  • Juan has three bills of 1000, seven bills of 100, and four bills of 10;
  • Carlos has two bills of 1000, fifteen bills of 100, three bills of 10, and two bills of 1;
  • Who has more money? Explain.
• Real-world problem:
  • A product costs 2354;
  • Using only bills of 1000, 100, 10, and 1, how many different ways can you create this amount?

• Moment 2. Development

Learning Objective: Represent quantities and relationships between them while solving additive or multiplicative problems.

Activities:

• Visual representation task:
  • Compare the monetary amounts possessed by Ana and Juan (Figure 6);
  • Without performing calculations, determine who has more money and by how much. Explain your reasoning.
• Scenario-based problem-solving:
  • A chocolate bar costs 850;
  • You have 525, and someone gives you 330;
  • Will you have enough money to buy it? Explain your reasoning in detail.
• Multiplicative reasoning task:
  • Juan needs to collect 48 tangerines;
  • He collects the same number each day and has gathered 32 so far;
  • How many days does he need to reach his goal? How many tangerines does he collect per day?

• Moment 3: Closing

Learning Objective: Solve additive and multiplicative problems that involve grouping, ungrouping, and comparing quantities.

Activities:

• Reasoning task:
  • Five students guessed the number of ping-pong balls in a box:

    ■

    Juan: 30;

    ■

    Flor: 28;

    ■

    José: 29;

    ■

    Ana: 25;

    ■

    Luis: 26.

  • Two students were off by one, one student was off by four, another by three, and one was correct;
  • Determine the number of ping-pong balls and explain your solution;
  • Analysis of student learning outcomes
• The evaluation of the activities was conducted through two complementary approaches:
  • Observational analysis:
    During the implementation of activities, students’ participation, problem-solving strategies, and interactions were recorded.
    Special attention was given to the types of interventions students made, the reasoning strategies used, and their engagement in collaborative problem-solving.
  • Analysis of Student Work:
    Upon completion of the activities, students’ written responses were analyzed.
    The focus was on:
  • Clarity of mathematical communication and representation of numerical concepts;
  • Justification of problem-solving procedures;
  • Diversity of strategies employed in approaching numerical tasks.

This dual assessment approach provided insights into students’ numerical thinking development, allowing for refinement of the instructional strategies used in the teaching unit.

4. Results and Discussion

To assess the numerical thinking and problem-solving skills of third-grade students in a public educational institution in Colombia, an analysis was conducted based on students’ written responses. A preliminary review revealed that students exhibited difficulties in using operations and properties of natural numbers to establish relationships between them in specific contexts. Additionally, challenges were observed in solving additive composition and transformation problems, particularly in identifying the necessary conditions for their solution. These findings were derived from the written responses of 31 third-grade students who participated in this study.

One of the tasks designed to assess the ability of the students to decompose numbers, represents place values, and exploring multiple numerical representations involved the following indication: “You buy a product at a stationery store that costs 2354, and you have bills of $1000, $100, $10, and $1. Explain how many different ways you can form this amount using the available bills.”

This problem encouraged students to:

• Break down the number 2354 into its positional values (thousands, hundreds, tens, and units);
• Represent the number pictorially or graphically by using drawings to depict each place value and the quantity of bills of each denomination;
• Explore different combinations, demonstrating multiple ways to construct 2354 using the available denominations;
• Understand place value, recognizing that the numerical value of a digit depends on its position within the number.

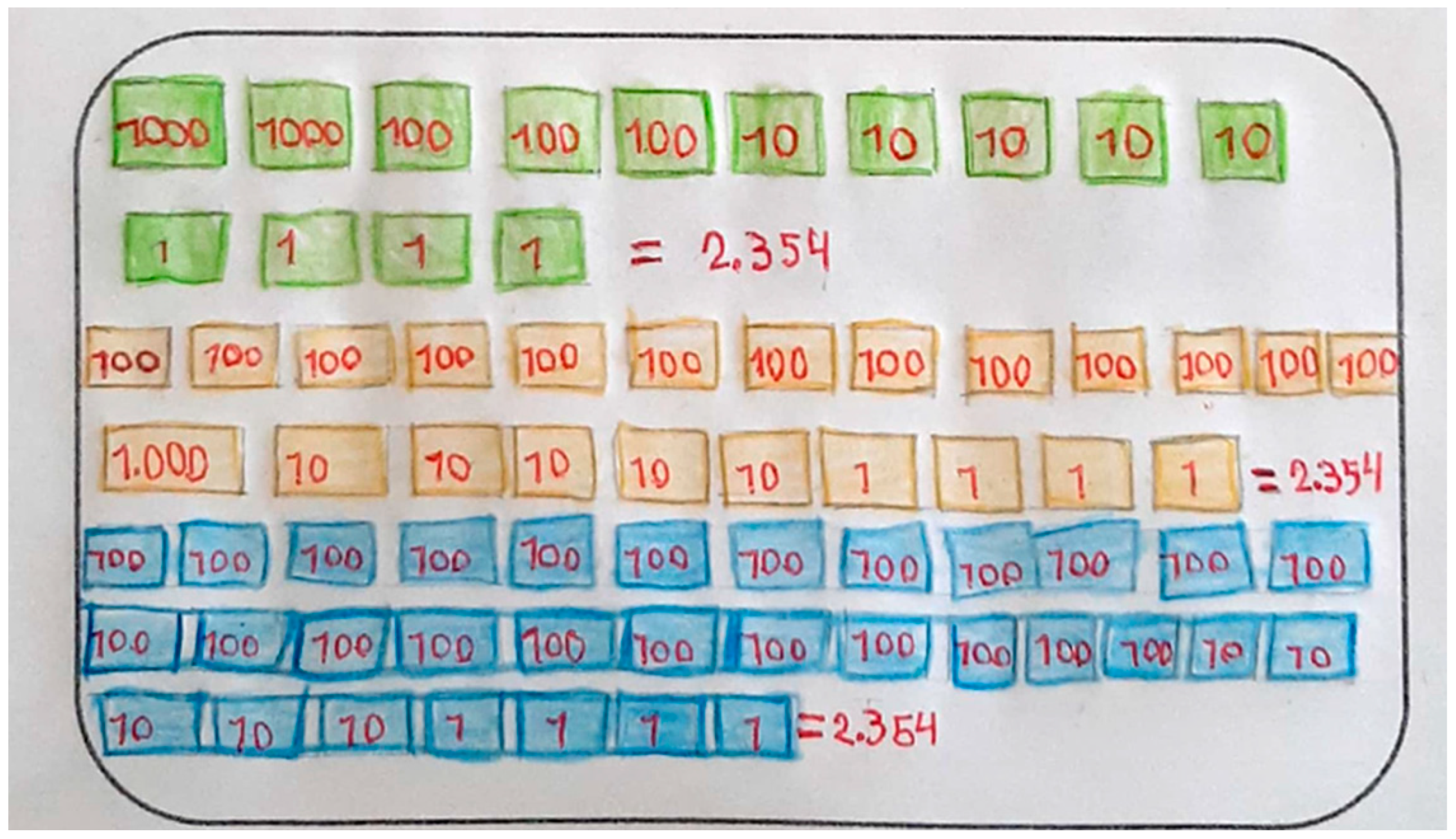
The students generally demonstrated ease in forming quantities by combining different denominations of bills. Their solutions suggest that they did not struggle with recognizing numbers in different formats or decomposing a number into its constituent parts. As an example, Figure 7 presents a student’s solution to this task, visually illustrating the different ways to represent the amount 2354 using the provided denominations.

A key aspect observed in the responses of the students was their ability to represent numerical values pictorially and symbolically, demonstrating an understanding of place value decomposition. One student’s response, illustrated in Figure 7, showcases how they decomposed and represented the number 2354 using different pictorial strategies with currency denominations. The student employed three distinct methods, using different colors to differentiate them. In the first approach, the student used 14 figures to depict the number: 2 figures labeled 1000, 3 labeled 100, 5 labeled 10, and 4 labeled 1, illustrating a direct representation of place value. The second representation contained 23 figures, restructuring the decomposition: 13 figures labeled 100, 1 figure labeled 1000, 5 labeled 10, and 4 labeled 1, demonstrating the ability to break down a unit of 1000 into ten hundreds while maintaining the same numerical value. In the third representation, the student used 32 figures, further decomposing the two thousand units into 20 hundreds, leaving 23 hundreds, 5 tens, and 4 units, which still equals 2354.

These different representations reveal a strong conceptual understanding of place value and show that students are capable of manipulating and decomposing numbers in various ways without altering their total value. Additionally, the ability to express numbers through drawings of bills demonstrates the recognition that a digit’s value depends on its position within the number, for example, understanding that a “1” in the thousands place equals 1000, while in the units place it equals 1. The flexibility observed in the students’ solutions, as well as their ability to find multiple ways to construct the same number, highlights their capacity for mathematical reasoning beyond simple procedural application. Their use of visual representations reinforces the importance of pictorial and manipulative tools in the development of numerical thinking.

The role of visual aid in fostering mathematical understanding is well-documented. Students not only represented numbers through standard symbolic notation, but also explored different ways of structuring the same amount using intuitive models. These findings align with prior research emphasizing the significance of meaningful learning experiences in mathematics, particularly through the use of concrete materials that allow for hands-on exploration of numerical concepts (Carpenter et al., 1996; Vergara et al., 2019).

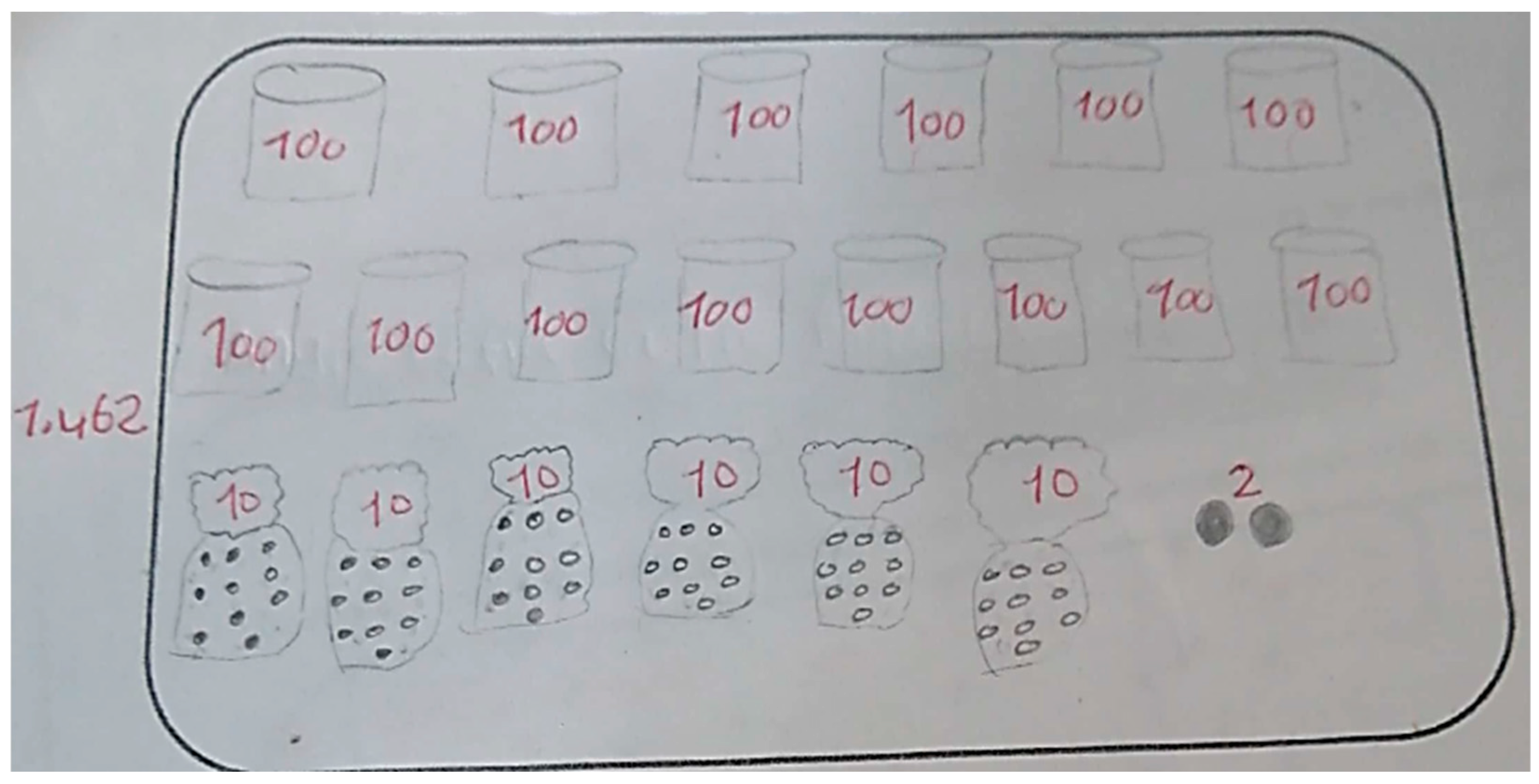
Furthermore, when students were asked to write and represent numerical quantities, their creativity in selecting different representational forms was evident. Some students integrated drawings with numerical symbols to illustrate their solutions, demonstrating an ability to connect multiple registers of representation. Figure 8 presents an example of a student’s visual and symbolic representation of 1462, further confirming that students not only grasp numerical values in written form, but can also translate them into graphical models, reinforcing their numerical reasoning skills.

A notable example of the students’ ability to decompose numbers and utilize multiple representation registers is illustrated in Figure 8. In this case, the student visually represents the number 1462 by drawing 14 cylinders marked with 100, 6 groups of points marked with 10, and 2 individual points marked with 1. This breakdown follows the structure 1400 + 60 + 2, demonstrating an understanding of place value and decomposition through addition. The ability to shift between different modes of representation—numerical, pictorial, and symbolic—provides evidence of progress in numerical thinking development at this stage of schooling. This reinforces the importance of problem-solving-based learning, which allows students to engage with mathematical concepts in an active and meaningful way. These findings align with those of Guzmán (2007), who highlights the role of problem-solving in fostering active learning and the enculturation of mathematical reasoning.

In another problem, students were presented with the following task:

“Juan must collect 48 tangerines, picking the same amount each day. So far, he has collected 32 tangerines. How many days does he have left to complete the order, and how many must he collect per day?”

This exercise required students to apply fundamental arithmetic operations such as multiplication and subtraction. To find a solution, they had to determine the number of tangerines Juan collects daily and the remaining number of days required to complete his order. The correct approach involved first computing 48 − 32 = 16, indicating that 16 more tangerines were needed. Since he collects the same amount each day, the numbers that satisfy the condition must be factors of 16:

• If Juan collects 2 tangerines per day, he needs 8 more days;
• If he collects 4 per day, he needs 4 more days;
• If he collects 8 per day, he needs 2 more days;
• If he collects 16 per day, he only needs 1 more day to complete the order.

This problem encouraged students to recognize different valid solutions, reinforcing their ability to decompose numbers and analyze divisibility. The process of understanding that 16 can be decomposed into its divisors (1, 2, 4, 8, and 16) reflects an essential aspect of flexible numerical reasoning. Students demonstrated that, by understanding the problem scenario, performing basic arithmetic, and identifying relevant patterns, they could arrive at multiple possible answers. As an example, Figure 9 presents a student’s response to this task, illustrating their problem-solving process and use of multiplication, subtraction, and reasoning to arrive at a valid solution.

In solving this problem, the student first selected a six-day period, from Monday to Saturday, and used a multiplication representation to determine the number of tangerines collected daily. Based on this, they concluded that “he has to collect 8 tangerines daily”. The student then created another multiplication diagram to determine how many days were required to complete the order, finding that it would take 4 days. Finally, a subtraction operation was performed to identify the remaining tangerines needed to complete the task. The final response was: “Juan is two days away from completing the order. Juan collects 8 tangerines per day”.

This response highlights several key aspects of the student’s problem-solving approach. First, they correctly understood the problem conditions and identified the necessary mathematical operations. By applying multiplication, they determined the total number of tangerines collected, and through subtraction, they calculated the remaining amount needed. Additionally, the clear and structured presentation of information facilitated the logical flow of reasoning, making the solution easy to follow. The student also provided a verbal explanation of the steps taken, demonstrating a well-developed understanding of the mathematical process involved.

Beyond procedural execution, the student implicitly applied positional value concepts while performing multiplication and subtraction operations. Their approach also illustrates fluency in basic arithmetic operations, effectively applying them within a real-world context. By representing the situation through mathematical operations, the student engaged in mathematical modeling, which is fundamental for problem-solving. This confirms that solving mathematical problems extends beyond algorithmic procedures, requiring an understanding of the problem scenario, recognition of relationships between numerical quantities, and the development and execution of problem-solving strategies (Arfé et al., 2020; Callejo et al., 2016).

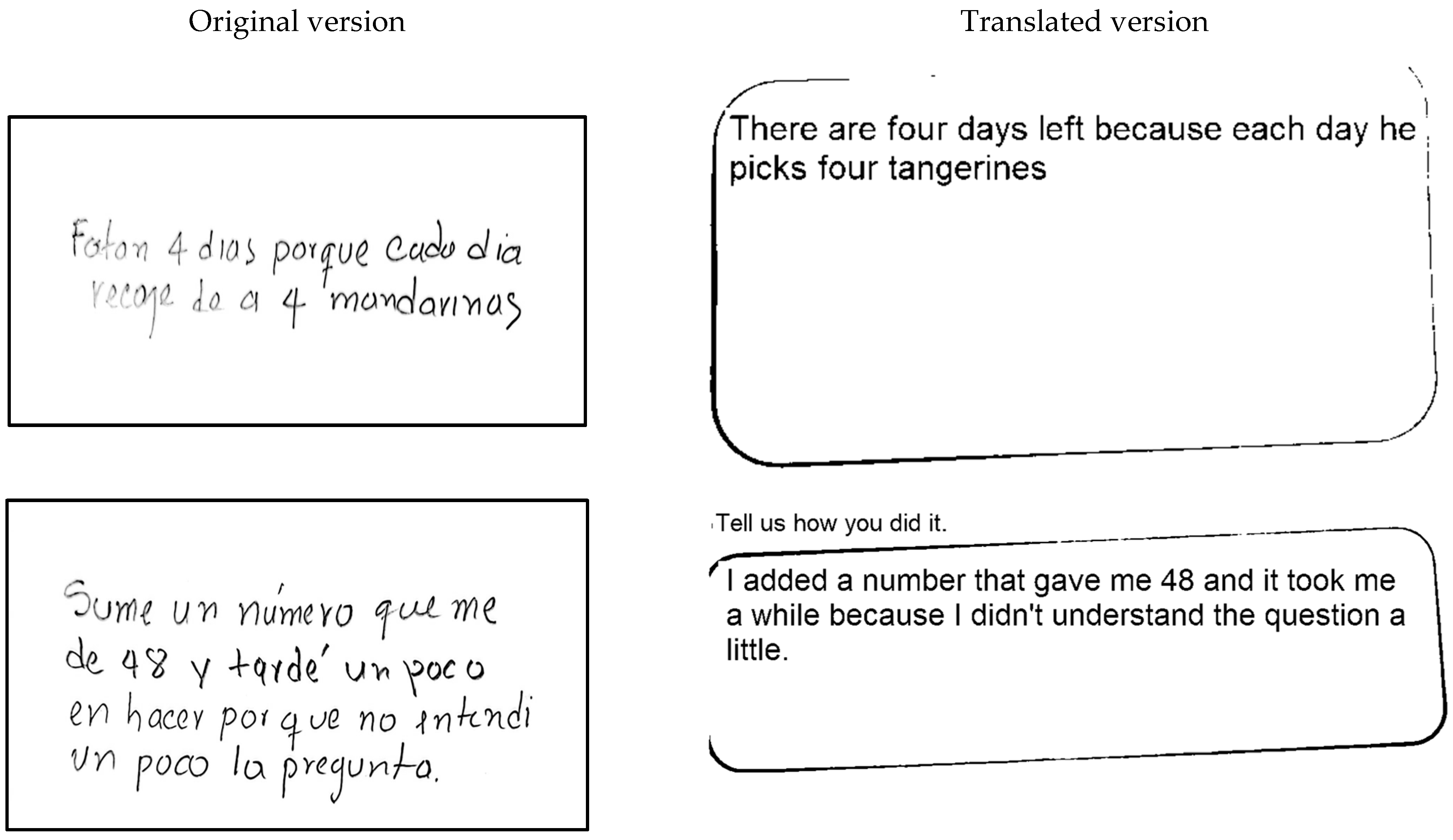
In Figure 10, the student explains their approach by stating: “I added a number that gave me 48 and it took me a while to do it because I didn’t understand the question a little”. Their final response to the task is: “There are 4 days left because every day he collects 4 mandarins”.

The student’s solution indicates the use of repeated addition to determine the correct answer. They attempt to identify a number that, when added multiple times, results in 48, aligning with the information provided in the problem. This suggests that they intuitively applied iterative addition rather than multiplication, demonstrating an alternative approach to problem-solving. However, the written explanation is quite brief and lacks a detailed breakdown of the steps taken to arrive at the answer.

The sentence “I added a number that gave me 48 and it took me a while to do it because I didn’t understand the question a little” suggests that the student may have relied on trial and error or an intuitive strategy rather than a structured mathematical approach. This highlights a common challenge in early mathematical development: students may arrive at correct answers without being able to clearly articulate their reasoning.

These responses emphasize the importance of analyzing both correct elements and potential misunderstandings in students’ answers. By providing constructive feedback and fostering a supportive learning environment, educators can guide students toward stronger mathematical reasoning and encourage them to express their thought processes more effectively. Encouraging students to verbalize their reasoning can help them to bridge the gap between intuitive problem-solving and formal mathematical articulation, ultimately enhancing their confidence and competency in mathematical thinking.

In Figure 11, the student describes their problem-solving process: “I analyzed the data from the exercise and realized that the incorrect calculations when adding and subtracting, based on the values each child provided, led me to 29”. The student then lists each child’s name, draws representations of the ping-pong balls, marks the number of balls each child estimated, and indicates the number of errors in their estimates. Finally, they conclude: “Answer: It can be said that the number of ping-pong balls in the box is 29. The child who got the correct answer was José.”

This response demonstrates a structured approach to problem-solving, as the student first identifies key data and conditions before organizing the information systematically. On a separate sheet, they write each child’s name alongside their estimated number of ping-pong balls and analyze the differences by drawing three lines per name to track calculations. They then perform addition and subtraction to account for the errors in each child’s estimate. By cross-referencing these calculations, the student identifies 29 as the correct number and verifies that José’s estimate was accurate. The student’s response reflects Jo Boaler’s (2015) perspective on the value of struggle and mistake-making in mathematical learning. By attempting to solve the problem using repeated addition, despite initially expressing confusion—“I didn’t understand the question a little”—the student demonstrates engagement with the problem-solving process. Boaler emphasizes that such moments of uncertainty and error are not setbacks, but integral opportunities for cognitive growth. She asserts that, when students grapple with challenging concepts and make mistakes, their brains form new neural connections, thereby enhancing understanding and fostering a growth mindset.

The method used confirms the importance of engaging students in scenarios that require them to actively analyze, compare, and interpret numerical data, as these tasks help in developing critical thinking and problem-solving skills (Almasarweh & Khudairat, 2021). The step-by-step validation of the solution suggests that the student understands numerical relationships, interprets mathematical conditions, and applies logical reasoning to verify their findings.

The general results from the implementation of the teaching unit indicate significant progress in students’ abilities to solve mathematical problems involving addition, subtraction, and multiplication. Throughout the process, students demonstrated their ability to identify relevant operations, analyze given information, and apply appropriate strategies to find solutions. Additionally, improvements were observed in students’ abilities to represent numerical relationships through multiple forms, including drawings, diagrams, and symbolic notation.

Moreover, students exhibited a deeper understanding of the number system and the properties of basic arithmetic operations by associating numerical values with concrete quantities and applying them to real-world problems. This highlights the effectiveness of problem-solving-based learning, which encourages students to actively construct knowledge, explore different solution strategies, and develop mathematical reasoning in a meaningful context.

The results obtained from the implementation of the teaching unit indicate significant progress in students’ numerical thinking development, particularly in their ability to solve mathematical problems and represent numerical relationships effectively. Throughout the activities, students demonstrated an enhanced ability to approach additive and multiplicative problems, applying strategies that involved grouping, ungrouping, and comparing quantities. They also exhibited improved numerical representation skills, using multiple registers—including visual, symbolic, and written forms—to express their reasoning and solutions.

One of the most notable advancements was in the students’ ability to analyze relationships between quantities within a given problem context. By engaging in problem-solving scenarios that required them to interpret, manipulate, and model numerical information, students strengthened their conceptual understanding of numbers and operations. Additionally, their capacity to articulate their thought processes improved, reflecting a deeper cognitive engagement with mathematical reasoning. These findings underscore the effectiveness of problem-solving-based learning approaches, which encourage students to actively construct their understanding rather than relying solely on the memorization of procedures. By working through real-world mathematical situations, students developed not only computational fluency, but also the ability to reason flexibly and adapt their strategies as needed. This aligns with educational research that highlights the role of active learning strategies in fostering mathematical literacy and critical thinking in early education.

In order to explore the connection between students’ initial numerical understanding and their performance in problem-solving tasks, we conducted a comparative analysis based on diagnostic results collected prior to the intervention. Students were grouped according to their scores on the initial assessment: Group A (above the median) and Group B (below the median). This grouping allowed us to examine how different levels of early numeracy influenced the flexibility and sophistication of students’ problem-solving strategies.

We focused this analysis on tasks that explicitly required the proposal of two distinct solution methods, such as the tangerine-collection problem. The responses were coded using a set of strategy categories: (1) repeated addition; (2) visual grouping; (3) factor-based decompositions; and (4) backward reasoning from a known result. Coding was independently validated by two researchers with over 90% inter-rater agreement.

Findings revealed marked differences between the two groups. Students in Group A were significantly more likely to propose two valid and distinct methods (70%) compared with students in Group B (25%). Furthermore, Group A students employed a broader range of advanced strategies, such as decomposition into multiplicative factors and logical inference from final conditions. In contrast, students in Group B tended to rely on more concrete or procedural approaches, such as visual representations (e.g., drawing tangerines in groups) or iterative addition. These findings suggest that stronger initial number sense facilitates not only greater flexibility in problem-solving, but also access to more abstract and generalized solution strategies.

To ensure that all students were actively engaged in the problem-solving process, a series of structured participation strategies were incorporated into each teaching phase. These were designed to promote equitable inclusion and avoid dominance by a few more vocal participants.

• Moment 1—Initiation: Each session began with an individual task where all students responded simultaneously using mini-whiteboards or slates. The teacher would then select a random sample of responses for collective discussion. This practice ensured that all students contributed from the start, regardless of their confidence level;
• Moment 2—Development: Students worked in small, deliberately heterogeneous groups (3–4 members), with rotating roles including the facilitator, recorder, skeptic, and presenter. The rotation ensured that all students had the opportunity to lead discussions, express their reasoning, and explain group solutions to the class. Teachers monitored these interactions closely, providing prompts and support where necessary to maintain balanced participation;
• Moment 3—Closure: During the reflection phase, students were invited to share their problem-solving experiences orally or in writing. Participation logs kept by the teacher ensured that contributions were distributed across students over time. When students had not yet spoken, the teacher would gently invite them to share an idea or pose a question, either during class or through a written note.

Analysis of students’ written work revealed four key dimensions in the development of numerical thinking. First, students demonstrated an understanding of place value by systematically decomposing quantities into thousands, hundreds, tens, and units. Research indicates (Gelman & Gallistel, 1978; Mulligan & Mitchelmore, 2012) that early place-value understanding is a reliable predictor of later arithmetic performance, highlighting its importance in numerical development. Second, students exhibited flexibility in numerical decomposition by generating multiple combinations of bills to solve tasks, reflecting the use of decomposition strategies that facilitate problem-solving. Third, the use of varied representational registers, such as drawings of banknotes and groupings of cylinders, facilitated the communication of mathematical ideas and confirmed progress in the learning process. Finally, while students applied operations and properties in problem-solving, difficulties were observed in additive composition and transformation problems, suggesting the need to strengthen the execution phase of problem-solving strategies. These findings underscore the effectiveness of a problem-solving-based teaching unit that integrates structured frameworks with contextual tasks and diverse representations, fostering the development of robust and flexible numerical thinking.

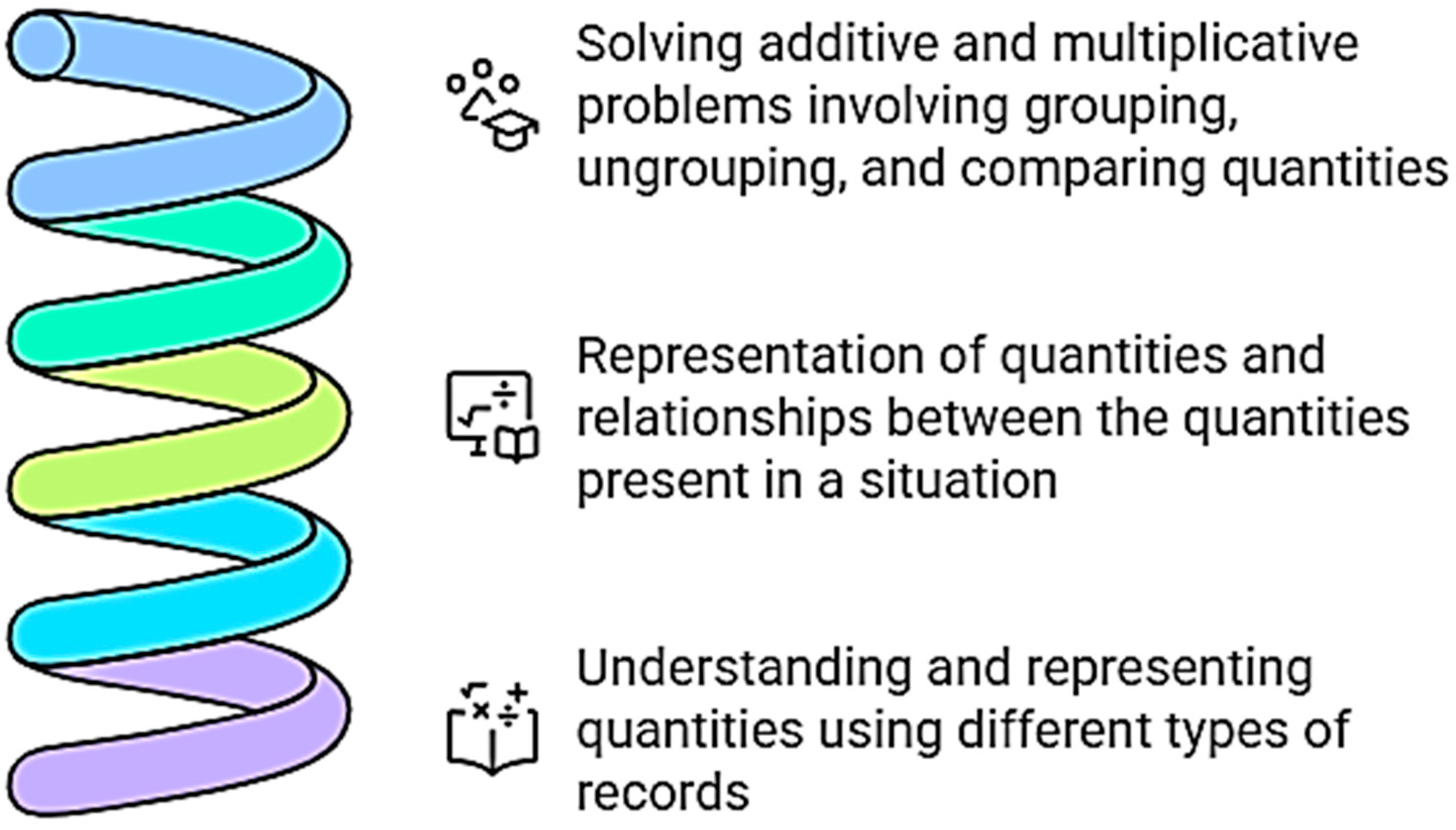
Figure 12 provides an overview of the key learning outcomes derived from the teaching unit. The results highlight three primary areas of improvement: (1) the ability to solve additive and multiplicative problems involving grouping, ungrouping, and comparison; (2) the development of skills in representing numerical quantities and their relationships within mathematical situations; and (3) an improved capacity to understand and express quantities using different types of representations. These findings support the argument that structured problem-solving experiences contribute to a more profound and transferable understanding of mathematical concepts, equipping students with essential skills for future learning.

5. Conclusions and Final Remarks

This study offers valuable insights into the unique context of third-grade students in Colombia, highlighting how their experiences and challenges in mathematical problem-solving differ from those of students in other countries. Specifically, it identifies common difficulties, such as interpreting problem statements, selecting appropriate strategies, and applying suitable algorithms, challenges also observed in similar Latin America settings. By implementing a problem-solving-based instructional unit grounded in Pólya’s four-step methodology—understanding the problem, devising a plan, executing the plan, and reviewing the solution—this study demonstrates how structured guidance can enhance students’ numerical thinking. This approach not only addresses specific learning obstacles, but also fosters a classroom environment conducive to critical thinking and collaborative learning. The findings contribute to a deeper understanding of the effectiveness of Pólya’s framework within the Colombian educational context, offering practical implications for educators aiming to improve mathematical competencies among primary school students.

The use of problem-solving as a strategy in the teaching and learning process proves to be a powerful pedagogical tool, as it encourages students to challenge themselves, explore different solution strategies, and justify the validity and relevance of their approaches. The findings of this study highlight that well-designed mathematical activities, aligned with expected learning outcomes, contribute to the development of essential skills in primary school students. These include the ability to:

• Utilize concrete, graphic, and pictorial representations to explain positional value in numerical quantities;
• Construct diagrams to represent numerical relationships within a given problem context;
• Analyze mathematical calculations and evaluate the plausibility of the results.

Developing numerical thinking is foundational for structuring mathematical knowledge, and one of the most effective ways to strengthen this ability is through problem-solving tasks where solutions are not immediately obvious and require higher-order reasoning. The incorporation of manipulative materials serves as a critical mediator between the teaching process and students’ cognitive development, fostering meaningful learning that supports the acquisition of essential mathematical skills.

Additionally, the use of open-ended questions and guided instructional support plays a key role in enabling students to explore multiple solution paths. Thought-provoking, well-structured questions stimulate intellectual curiosity and encourage students to engage in deeper reasoning, which enhances their problem-solving abilities. The teacher’s role in this process should be to facilitate, rather than dictate, solutions, intervening strategically to guide students only when necessary.

A constructive learning environment must provide students with opportunities to explore, experiment, and make mistakes without fear of failure. This requires educators to closely observe students’ thought processes, identify strengths and weaknesses, and provide specific, process-focused feedback, rather than simply assessing correctness. This approach promotes student autonomy, allowing learners to develop self-regulation skills as they refine their problem-solving techniques and justify their reasoning.

Furthermore, the structured design of a teaching unit—based on an initial assessment of students’ mathematical understanding—enables the development of targeted activities that effectively enhance numerical thinking skills. The transition from understanding numerical representations to solving problems involving grouping, ungrouping, and comparing quantities is a critical step in mathematical development.

This study demonstrates that a problem-solving-based didactic unit, grounded in Pólya’s four-phase framework, significantly enhances numerical thinking among third-grade students—particularly in decomposing numbers, representing quantities across various registers, and applying flexible problem-solving strategies. These findings are consistent with those of Torres-Peña et al. (2024), who emphasized the effectiveness of contextualized and historically grounded problem-solving in fostering conceptual understanding and improving mathematical proficiency among learners. Moreover, the open-ended learning model employed in our intervention aligns with the principles discussed by Warmansyah et al. (2023), who showed that encouraging multiple solution paths cultivates cognitive flexibility and early number sense in young children. Our results also resonate with the learning trajectories framework proposed by Clements et al. (2023), which highlights the importance of sequencing tasks from concrete to abstract to support children’s developmental progression in numerical understanding. The successful use of visual and symbolic aids in our activities further reflects the representational scaffolding described by Hyde et al. (2021), demonstrating that well-aligned symbolic interventions, introduced in tandem with students’ developmental readiness, can enhance numerical comprehension. Notably, this study extends these frameworks by addressing educational equity within socioeconomically diverse settings. The collaborative peer-learning strategies embedded in the teaching unit respond to the gaps identified in Torres-Peña et al. (2025), underscoring the importance of inclusive methodologies that foster engagement and participation among all learners, regardless of background. Future educational interventions could benefit from integrating diverse pedagogical strategies, including historical narratives (Torres-Peña et al., 2024), open-ended inquiry (Clements et al., 2023), and targeted symbolic supports (Warmansyah et al., 2023), to enhance adaptability and scalability across varied instructional contexts and developmental stages. Taken together, these converging lines of research reaffirm the critical role of professional development in equipping educators with the tools needed to balance structured guidance with student-centered creativity. Fostering equitable, reflective, and joyful learning environments in mathematics classrooms requires that teachers draw from evidence-based models while remaining responsive to the diverse needs of their students.

Finally, the progressive introduction of problem-solving tasks—ranging from simple to complex scenarios, accompanied by structured feedback mechanisms—supports students’ conceptual learning and independence. This progressive scaffolding approach reinforces numerical reasoning, promotes problem-solving confidence, and strengthens students’ ability to apply mathematical thinking beyond the classroom.

To enhance students’ numerical thinking and problem-solving skills, it is advisable for approaches to incorporate open-ended, engaging tasks that allow for multiple solutions. Such tasks encourage students to explore various strategies, fostering creativity and deeper understanding. The activities indicated that open-ended problems can enhance mathematical thinking and creativity in elementary mathematics classrooms. Equally important is cultivating a classroom culture that values exploration, discussion, and learning from mistakes. Encouraging students to discuss their thought processes and reasoning can lead to richer mathematical discussions and a deeper understanding of concepts. By creating an environment where students feel safe to take risks and learn from errors, educators can promote a growth mindset and resilience in problem-solving. Implementing these strategies aligns with contemporary educational approaches that emphasize student-centered learning and the development of critical thinking skills. By embracing open-ended tasks and fostering a supportive classroom environment, educators can effectively enhance students’ numerical thinking and problem-solving abilities.