2.1. Methodological Approach
The overarching approach for this development of the curriculum materials follows an iterative, research-informed process, drawing on principles from design-oriented methodologies such as design studies (
Edelson, 2002), design experiments (
The Design-Based Research Collective, 2003), and developmental research (
Richey et al., 2004). These approaches share a focus on refining educational interventions through cycles of design, implementation, analysis, and revision in classroom contexts (
The Design-Based Research Collective, 2003;
Edelson, 2002;
Richey et al., 2004). These approaches aim to produce new theories, artifacts, and practices that impact teaching and learning in real-world settings (
Barab & Squire, 2004). The research reported in this study was conducted within the larger design research project, focusing on field test teachers’ perspectives on the effectiveness of enacting a contextualized, problem-based middle grades mathematics curriculum and its design features.
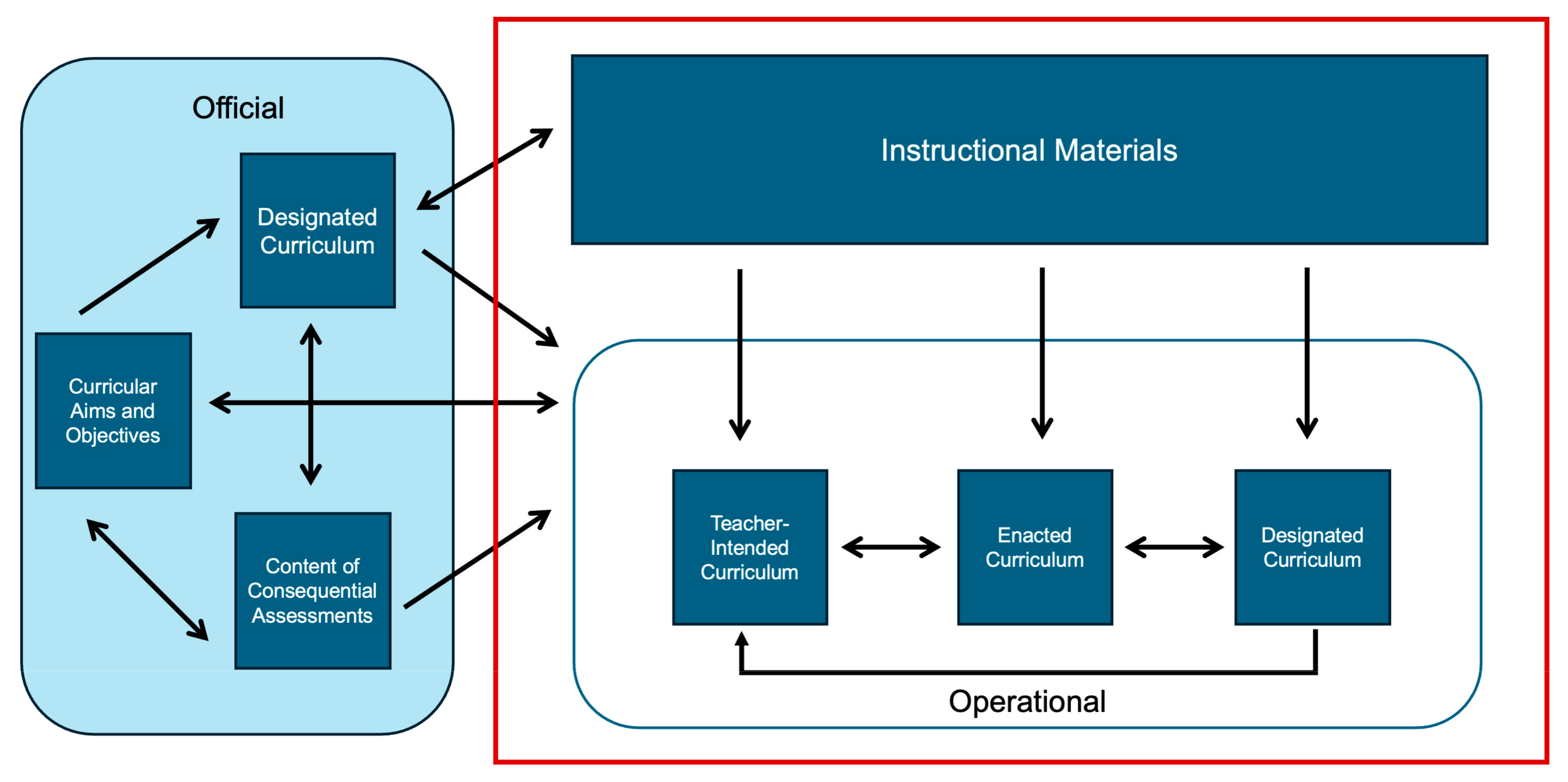
Connected Mathematics®4 (CMP4;
Phillips et al., 2025a,
2025b,
2025c) builds on the foundation set by the Middle Grades Mathematics Project (MGMP). As described in
Edson et al. (
2019), MGMP (
Lappan et al., 1985) helped teachers move from traditional instruction to problem-based learning, with a focus on key mathematical ideas and sequences of problems designed to build understanding. The Launch–Explore–Summarize model developed by MGMP supported this shift and addressed curriculum design tensions, such as identifying core mathematical concepts and sequencing tasks to support deep understanding. It also helped address teacher enactment tensions, such as recognizing varying levels of teacher experience and ensuring effective use of the instructional model.
MGMP teachers reported struggling to apply what they learned from the units across their full curriculum. In response, three of the MGMP authors developed CMP1 (
Lappan et al., 1998), which introduced new features to help teachers implement problem-based instruction in a complete mathematics curriculum for grades 6, 7, and 8. Each grade consisted of eight units, each with 2–6 investigations. Each investigation consisted of 1–6 problems. As described in
Edson et al. (
2019), the addition of Mathematical Reflections at the end of each investigation allowed both students and teachers to pause and assess understanding, addressing curriculum design tensions related to knowing when to close a lesson. CMP1, using the Launch–Explore–Summarize model, also provided extensive teacher support, helping teachers facilitate rich discourse and better navigate the complexities of problem-based teaching, responding to enactment tensions around developing strong pedagogical practices.
CMP2 (
Lappan et al., 2006) was developed based on research and classroom experience with CMP1. This version refined problems and teacher support materials to help students develop a deeper understanding. As described in
Edson et al. (
2019), features like Looking Back, Looking Ahead addressed curriculum design tensions around organizing a coherent sequence of lessons, while the At a Glance feature streamlined lesson planning for teachers, addressing enactment tensions related to managing increasing complexity in materials.
In CMP3 (
Lappan et al., 2014), student problems and teacher support materials were enriched with examples of student thinking, helping teachers anticipate how students might approach problems. As described in
Edson et al. (
2019), this addressed enactment tensions around recognizing and responding to diverse student reasoning. CMP3 also introduced Focus Questions to help teachers maintain focus on key mathematical ideas and guide lesson planning, addressing curriculum design tensions around choosing the right questions to guide student understanding. A one-page resource provided a clearer view of the mathematical progression across units, supporting teachers in managing the flow of concepts and reinforcing the curriculum design tension of developing a connected curriculum.
2.2. The Iterative Development and Field Testing of CMP4
The development and testing of CMP4 field test materials followed a thorough, iterative process involving over 500 teachers over 25 U.S. states and six additional countries (see
Table 1). Throughout this process, field test teachers were primarily recruited from those already using the CMP3 materials, with ongoing professional learning and feedback integrated at each stage. The development process began with an initial phase that involved both the CMP team and the publisher. In this initial phase, the CMP development team began conversations to discuss initial changes to the structure and scope of the curriculum. These discussions focused on key topics such as the table of contents, scope and sequence, and unit organization. A major area of focus was the integration of the CMP STEM Problem format (described later in
Section 2.3), which was being explored as part of a digital collaborative platform with the
Connected Mathematics®4 seventh-grade curriculum. The early work aimed to align the vision for CMP4 with necessary educational goals, ensuring the curriculum would be both innovative and feasible for classroom implementation. These foundational conversations helped to address some of the curriculum design tensions identified in earlier phases of CMP development.
In Year 1 (2018–2019), formal field testing began, focusing on a select group of sixth-grade units. Early field testing helped to evaluate the new features, including the CMP STEM Problem format (described later in
Section 2.3) and the instructional support materials. Feedback from this first round of testing was used to identify areas for improvement and revise the curriculum accordingly. During this year, the CMP team worked closely with a few teachers. A project-developed digital platform funded by the National Science Foundation was also used in parallel with seventh-grade teachers, providing a space for teachers to test the curriculum in a collaborative, digital format. This allowed for real-time adjustments and feedback as teachers engaged with the project-developed digital platform and worked on the same units digitally. The project-developed platform differs from the platform provided by the publisher.
By Year 2 (2019–2020), the field testing expanded significantly, including units from grades 6, 7, and 8. The group of field test teachers included 11 teachers from 10 schools across 7 states. The teachers continued to provide valuable feedback on new features, such as the inclusion of more student reasoning examples and the Focus Questions, which helped guide lesson planning and enactment. Feedback revealed areas for improvement in supporting diverse learners and streamlining the teacher support materials to make lesson planning more manageable. These insights led to revisions and updates, with ongoing collaboration to ensure the materials met the needs of both teachers and students.
In Year 3 (2020–2021), all units for grades 6, 7, and 8 were included in the field testing. This year saw a broadening of feedback, as more teachers participated in testing and provided in-depth insights on how well the curriculum supported problem-based learning and engaged students in rich mathematical problem-solving experiences. The CMP team also continued to make refinements based on feedback related to the teacher’s experience, particularly around managing the increased amount of material and supporting teachers in effective lesson planning and enactment. The project-developed digital platform continued to play a key role in allowing teachers to collaborate and implement the curriculum in a flexible, digital format. The field test in 2020–2021 included 13 teachers from 6 schools across 3 states.
Year 4 (2021–2022) saw the field test units from all grades continuing to evolve. The field test in 2021–2022 included 343 teachers from 155 schools across 18 states, as well as international participants from Colombia and England. Feedback from these participants led to refinements in the curriculum, emphasizing a more cohesive structure, smoother transitions between units, and clearer guidance on orchestrating the problem-solving process. Teachers noted that having a clearer vision of the progression from one unit to the next helped improve both teaching and student learning. The continued involvement of teachers in the field test ensured that the materials remained grounded in classroom realities and continued to evolve in ways that best supported both students and teachers. The project-developed digital platform continued to provide real-time feedback and offered insights into how the curriculum was being implemented across different classrooms.
By Year 5 (2022–2023), the CMP4 units for grades 6–8 were fully field-tested, and significant revisions had been made to the materials. The curriculum was near final draft status, with ongoing minor adjustments. The field test in 2022–2023 included 515 teachers from 409 schools across 22 states, as well as international teachers from Brazil, Colombia, the Netherlands, England, and Vietnam. Surveys and in-depth feedback (through written unit reports and virtual monthly meetings) confirmed that new features—such as the Focus Questions and Mathematical Reflections—were positively impacting both teaching practices and student learning outcomes. The CMP team continued working closely to finalize the materials for wider dissemination, ensuring they met the needs of teachers and aligned with curriculum standards.
In the 2023–2024 academic year, the CMP4 units for all grades were revised and improved based on the feedback received in the previous year. The feedback from the final phase of field testing helped refine the curriculum materials, with a strong emphasis on ensuring that students could build on prior knowledge and deepen their understanding across the full set of units. The units were now ready for broader implementation, having undergone years of feedback, testing, and refinement to become a cohesive, problem-based mathematics curriculum. The field test in 2023–2024 included 318 teachers from 137 schools across 15 U.S. states, as well as international educators from Brazil, England, the Netherlands, and Vietnam. Extensive feedback was provided by teachers in their unit reports and in monthly virtual meetings.
Professional learning for CMP4 field test teachers over the past four years began with a face-to-face meeting that included a small number of CMP3 teachers, teacher leaders, and field test teachers using the project-developed digital platform. From there, professional learning experiences were provided through a combination of webinars, monthly virtual meetings, and informal virtual conversations. These sessions started with introductory meetings and unit overviews, and over time, they progressively focused on specific units and teaching strategies. The professional learning over the years centered on several key aspects, such as an overview of CMP4, which included its philosophy, new student features, and teacher support, along with grade-level overviews that highlighted the development of key mathematical concepts. Teachers were also guided through the instructional model (Launch–Explore–Summarize) and given detailed information on available teacher resources. Unit overviews were provided both synchronously and asynchronously to accommodate varying schedules. Monthly virtual meetings allowed teachers to ask questions, provide feedback, and receive ongoing support. Additionally, extensive written teacher support was made available, offering more in-depth guidance on each instructional phase, including planning, teaching (Launch, Explore, and Summarize), and reflection, with a particular focus on helping teachers deepen their understanding of embedded mathematical concepts. All virtual sessions and webinars were recorded, providing teachers with the flexibility to revisit the material at their own pace. As the years progressed, the professional learning offerings expanded to meet the growing needs of teachers as they implemented CMP4, ensuring they received the necessary support for the successful enactment of the curriculum.
At the end of each field test year, feedback from participating teachers played a critical role in refining the CMP4 materials. Initially, in Year 1, feedback was collected from a small group of teachers who tested the CMP STEM Problem format on the project-developed digital platform. This feedback focused on individual problems and how they were implemented in the digital context. Over the course of the subsequent years, the feedback process evolved to include more extensive forms, which accompanied each unit being tested. The feedback was organized into several key categories, including “big picture” unit feedback, which allowed teachers to reflect on the overall design and flow of the units, as well as problem-by-problem feedback, which delved into specific challenges or successes teachers encountered with tasks. Other categories included feedback on the context of the problems, their applications, connections, and extensions, as well as assessments and teacher support materials. Year-end grade-level feedback helped to gauge the progression and coherence across units for each grade, and a final “big question” invited teachers to reflect on the overarching impact of the materials on student learning. Additionally, the feedback included insights into the effectiveness of the Mathematical Reflections feature, which teachers used to support student understanding throughout the units. This comprehensive feedback loop, collected and analyzed across multiple years, ensured that the materials continuously improved to better support teachers and engage students in rich mathematical problem-solving experiences.
2.3. CMP4 and Its Design Features
The Connected Mathematics Project (CMP) materials are created to support teachers and students in developing deeper mathematical understanding and reasoning.
Connected Mathematics®4 (
Phillips et al., 2025a,
2025b,
2025c) extends the successes of its predecessors, CMP1 (
Lappan et al., 1998), CMP2 (
Lappan et al., 2006), and CMP3 (
Lappan et al., 2014). Each revision of CMP was extensively field-tested in its development phases. After the release of each edition, the CMP development team continues to interact with schools. The development team seeks iterative and in-depth input and reviews from teachers, families, administrators, mathematics educators, mathematicians, educational researchers, and experts in reading, special education, equity, and multilingual learners. Most importantly, the enthusiasm of the teachers and the creative, productive mathematical thinking of their students provide the fuel for the authors to think even more deeply about “Can we do more?” The result is “yes!” This continuous interaction with the field and design research is a critical process in the development of CMP4 and is the foundation of the success of CMP, which has withstood the pressures of various political changes since CMP1 was released in 1996.
Connected Mathematics®4 provides seven student units for sixth grade and eight student units each in seventh and eighth grades. The eighth-grade units offer the possibility of teaching an eighth-grade course or a first-year high school course focused on algebra. Each unit is organized around a big mathematical idea or cluster of related ideas, such as variables and patterns, area and perimeter, ratio and proportion, linear relationships, or nonlinear relationships. The format of the student material promotes student engagement with an exploration of important mathematical concepts and related skills and procedures. Students develop strategies and conceptual understanding by solving problems and discussing their solutions in class.
The CMP4 student material consists of the following components:
Mathematical Goals and Looking Ahead. The mathematical goals guide the development of the big ideas of mathematics for the unit. Each unit opens with three interesting problem situations to draw students into the unit, pique their curiosity and joy in mathematics, and point to the kinds of ideas they will investigate. This is followed by a set of focusing questions that reflect the mathematical goals of the unit. Students can use these questions to help track their progress through the mathematical goals. Students can revisit these questions as part of their reflections on their learning.
Investigations. Mathematics learning is focused on one or two big ideas of mathematics developed through carefully sequenced investigations. Each unit builds toward the mathematical goal of the unit and is comprised of two to four investigations. Each investigation includes the following key elements:
- o
2–4 CMP STEM Problems.
- o
Did You Know? This component connects the context and/or mathematics to real-life anecdotes.
- o
Mathematical Reflections. These contain one overarching question that guides the development of students’ understanding of the big mathematical idea of the unit.
- o
Applications–Connections–Extensions (ACEs). This component allows students to reinforce, connect, or extend their understandings.
Student Notebooks. This notebook provides space for students to record their strategies and understandings as they work through a unit.
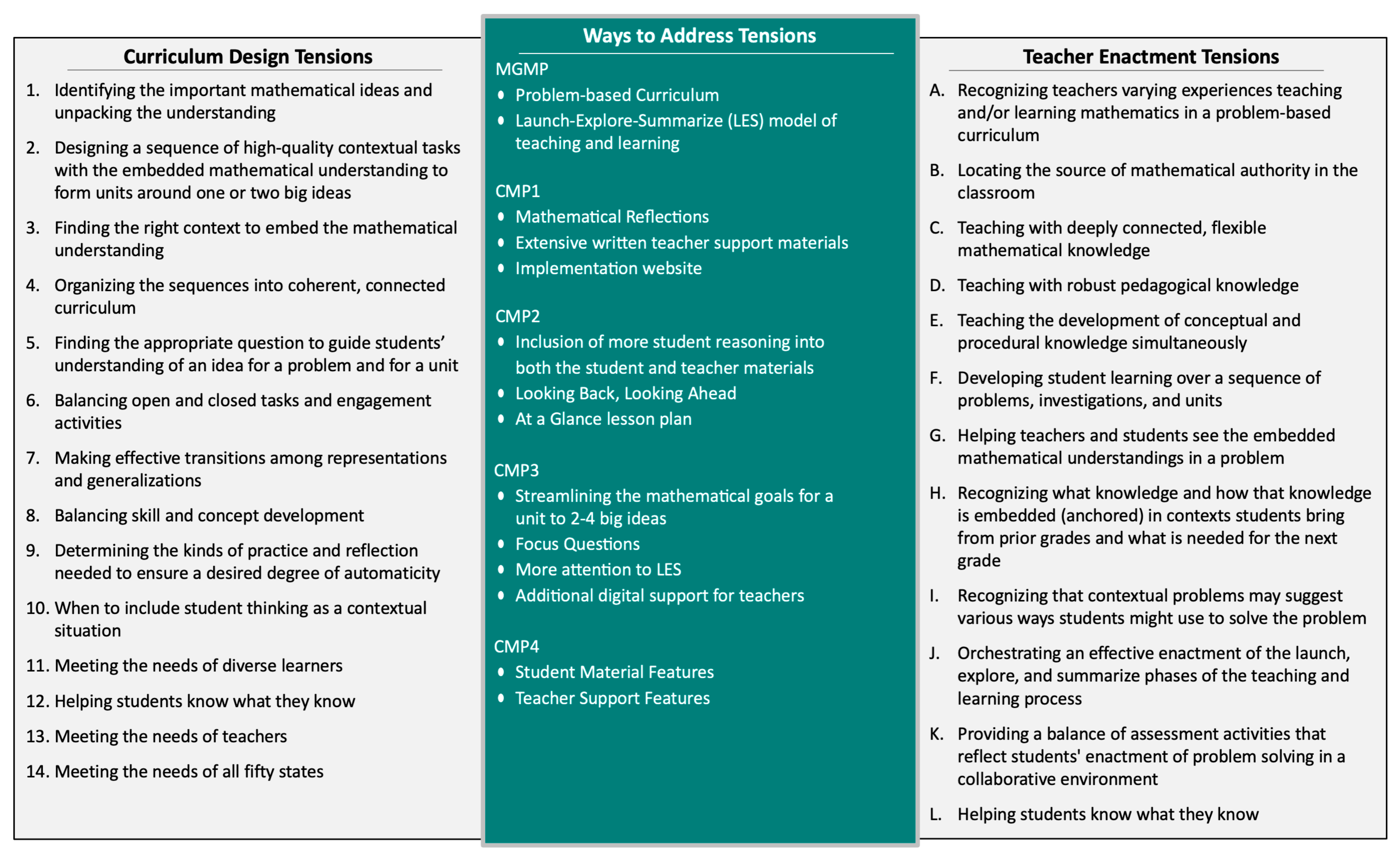
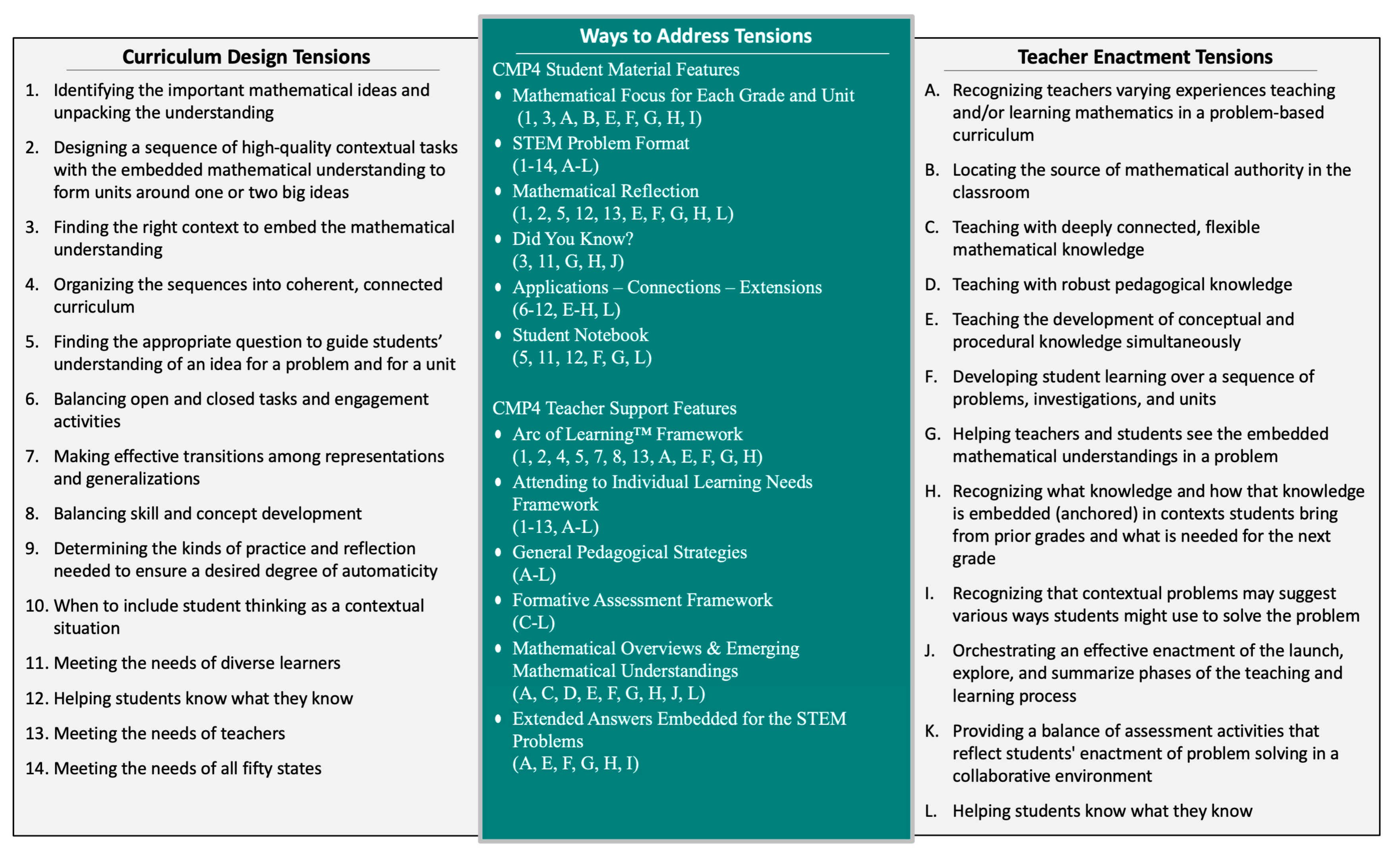
In this section, we address some of the ways CMP4 has attended to the curriculum design issues (see
Figure 3). The design features that address some of the curriculum and enactment tensions are indicated in the middle column labeled CMP4. The numbers next to each design feature refer to a “Curriculum Design Tension” and the letter refers to a “Teacher Enactment Tension”. The bulk of the tensions were addressed by the redesign of the problem format (
Figure 4). It includes a more open challenge, which provides multiple ways of accessing it and provides insights into the embedded mathematical understandings.
CMP4’s new CMP STEM Problem format (see
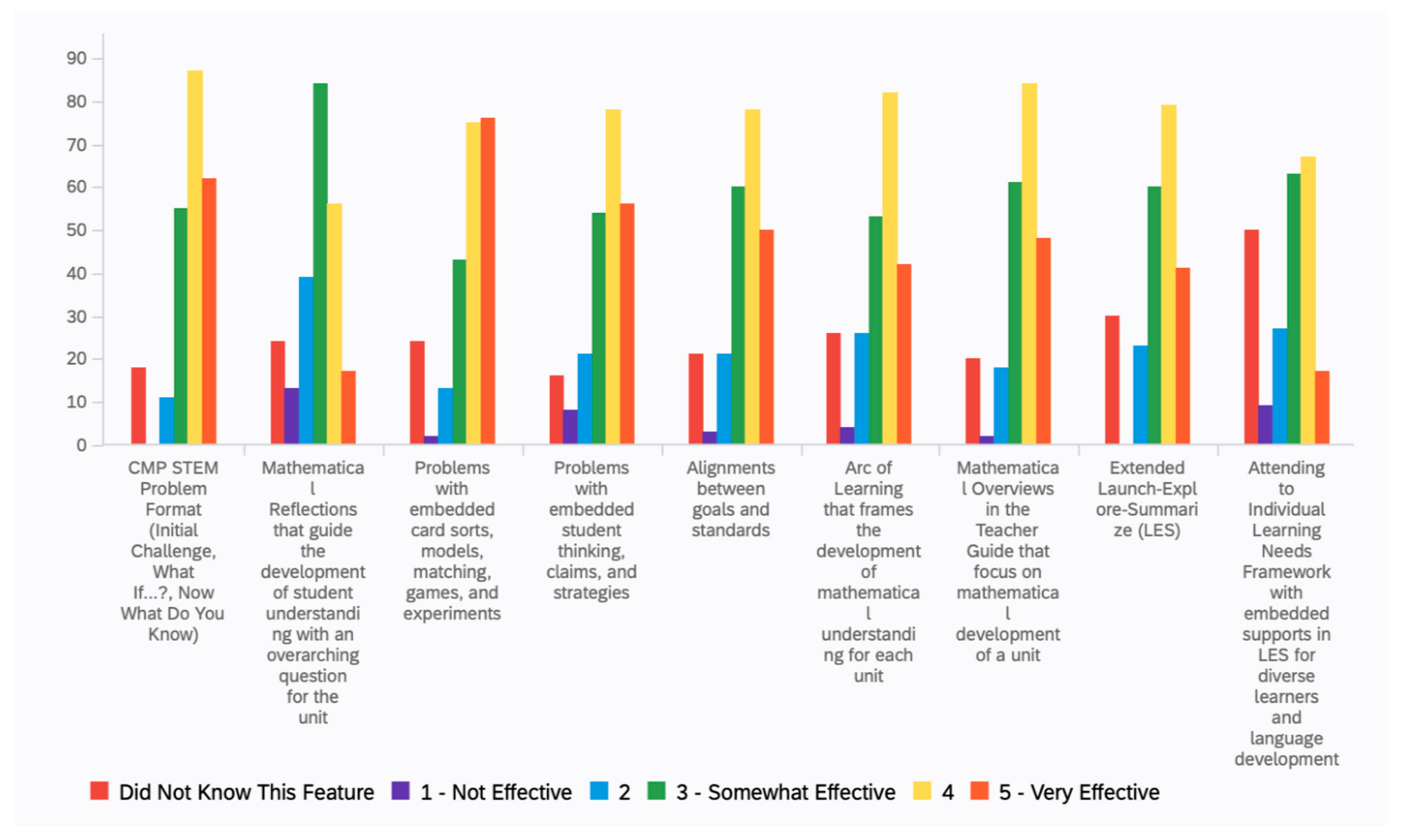
Figure 4) promotes learning and problem-solving that resembles the work of STEM professionals. It attends to some of the curriculum design tensions as the context of the problem in the Initial Challenge is more engaging and open, and thus allows for more students to access the challenge. The What If…? feature provides a balance between open and more closed questions in the Initial Challenge, thus guiding the students’ understanding of the embedded mathematical idea in the Initial Challenge feature. The Now What Do You Know? feature of the problem provides an opportunity for students to know what they know. Collectively, the format promotes students’ problem-solving strategies and hence their ability as doers, creators, and communicators of mathematics. In addition, the CMP STEM Problem format provides teachers with flexibility to carry out equitable practices that help address the individual needs of all students. CMP4, using the CMP STEM Problem format and other features, has streamlined the mathematical focus of each unit, resulting in a 17–20% reduction in the number of problems across the grades.
At the end of each investigation, there is now just one overarching Mathematical Reflection question that guides the students’ mathematical understanding of the big idea in the unit.
Figure 5 illustrates the Mathematical Reflection for the sixth-grade
Variables and Patterns unit. The Now What Do You Know? feature notes can be used to record students’ emerging understanding of the big mathematical idea of the unit that is embedded in the unit’s Mathematical Reflection question.
CMP4 has more examples of student thinking as context for promoting student learning. The student work in Problem 2.1 Situation A (see
Figure 6) provides student work that helps students see there that is sometimes more than one way to solve a problem (Zane, Bruce, and Gwen’s Strategies), and there is not always a direct path to the answer (Yvonne’s Strategy). Situation B enhances students’ understanding of proportional reasoning by altering the ratio of cupcakes in each box and by changing the size of the box (or number of total cupcakes). It also provides a transition among representations and generalizations among pictures, words, and tables. The Now What Do You Know? question helps students reflect on their understanding of ratios as a tool for solving problems. CMP4 strengthens the use of visual representations to develop and recall understanding of important mathematical ideas.
Figure 7 illustrates the Mathematical Reflection for the sixth-grade
Comparing Quantities unit. The Now What Do You Know? feature provides student notes for recording their emerging understanding of the big mathematical idea of the unit, which are then consolidated into the Mathematical Reflection question. For example, the Now What Do You Know? feature in Problem 2.1 in
Figure 5 can provide students with evidence of students’ understanding of ratios at this stage of development in the unit.
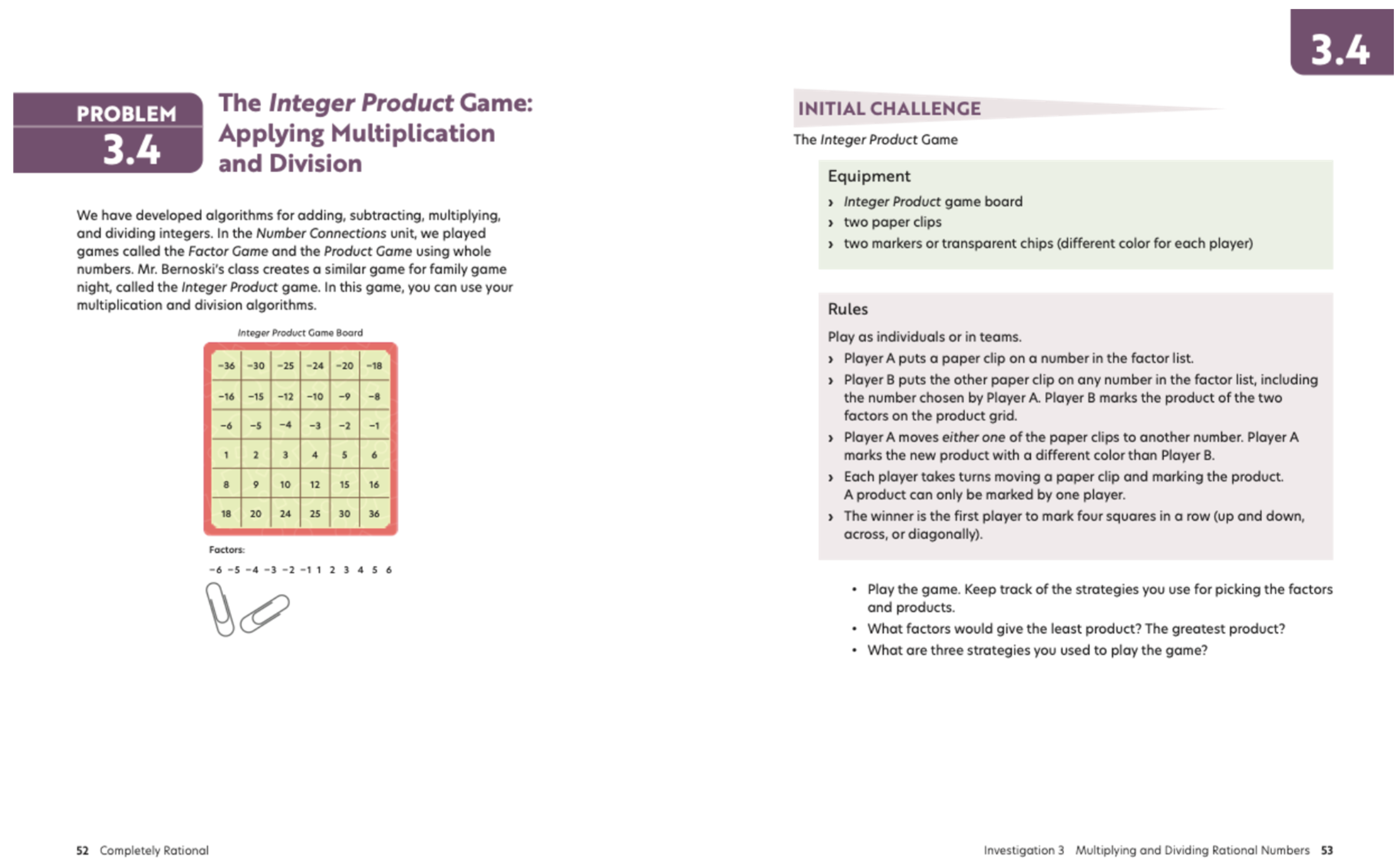
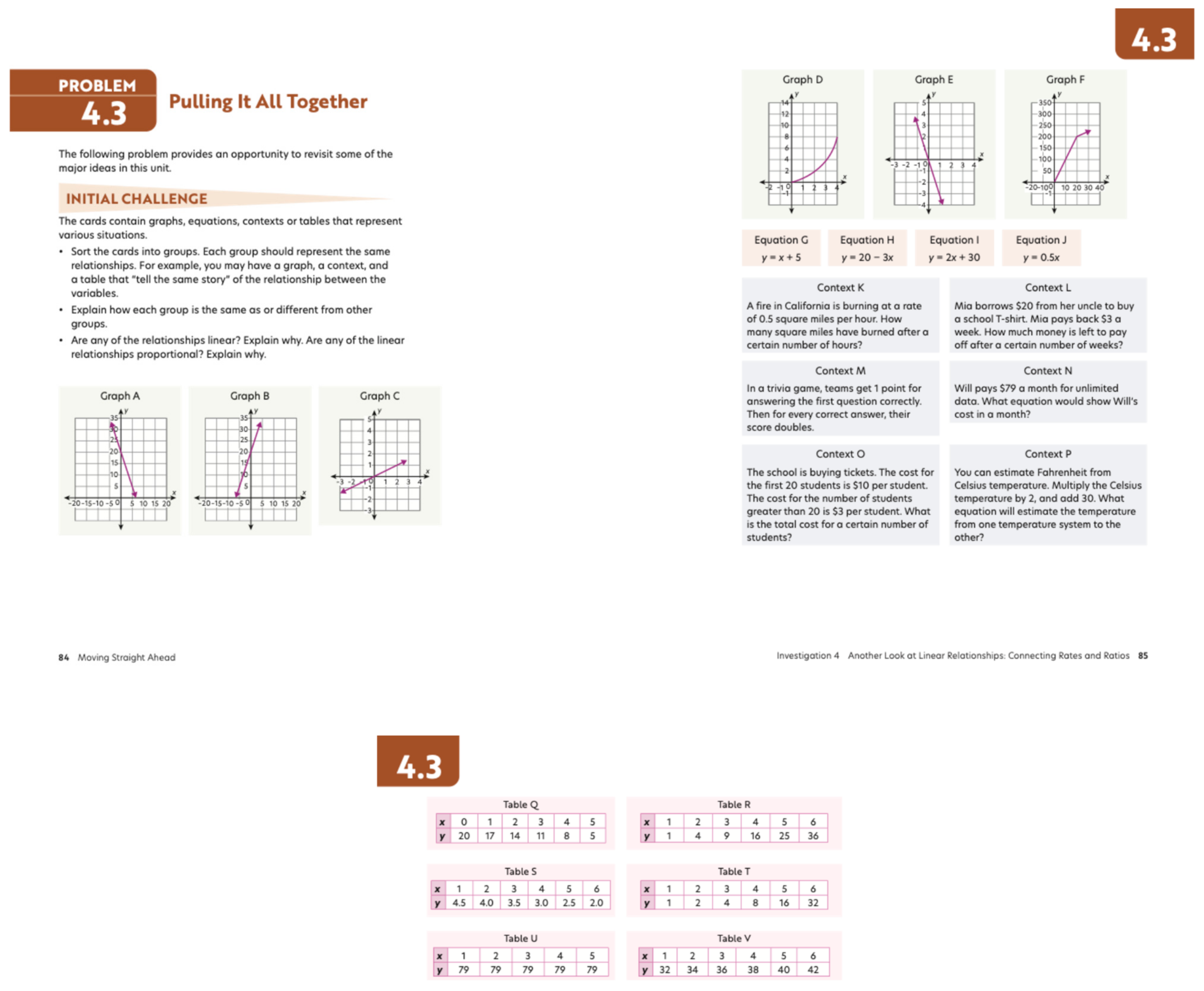
There are more problems with embedded card sorts, models, matching, games, and experiments. These formats promote active engagement by requiring students to manipulate, categorize, visualize, and reason about mathematical concepts, rather than passively absorb information. For example, card sorts and matching tasks prompt learners to identify relationships among representations, quantities, or strategies, encouraging them to justify their thinking and articulate reasoning. The use of visual or physical models facilitates students’ ability to represent and make sense of abstract mathematical ideas, supporting the development of conceptual understanding. Games and experiments introduce playful yet structured contexts in which students can explore mathematical ideas, offering multiple entry points and promoting inclusive participation. These interactive formats often foster collaboration and discourse, providing opportunities for students to engage in mathematical argumentation and refine their ideas through peer interaction. Additionally, such activities serve as rich sources of formative assessment, allowing teachers to observe students’ thinking in action and respond to their needs in real time. For example, in
Figure 8, a game is used to strengthen students’ understanding of integers. In
Figure 9, a card sort (matching) of graphs, equations, and contexts is used to pull together the key understanding of linear functions.
The following activity (see
Figure 10) is an experiment that investigates some of the variables that affect the strength of a bridge. In this experiment, the two variables are the thickness of the bridge and weight. The relationship is linear. In Problem 1.2, they repeat the experiment, looking at the length of the bridge and the weight. This relationship is not linear. It is an inverse relationship.
The prior figures in this section illustrate problems from various units.
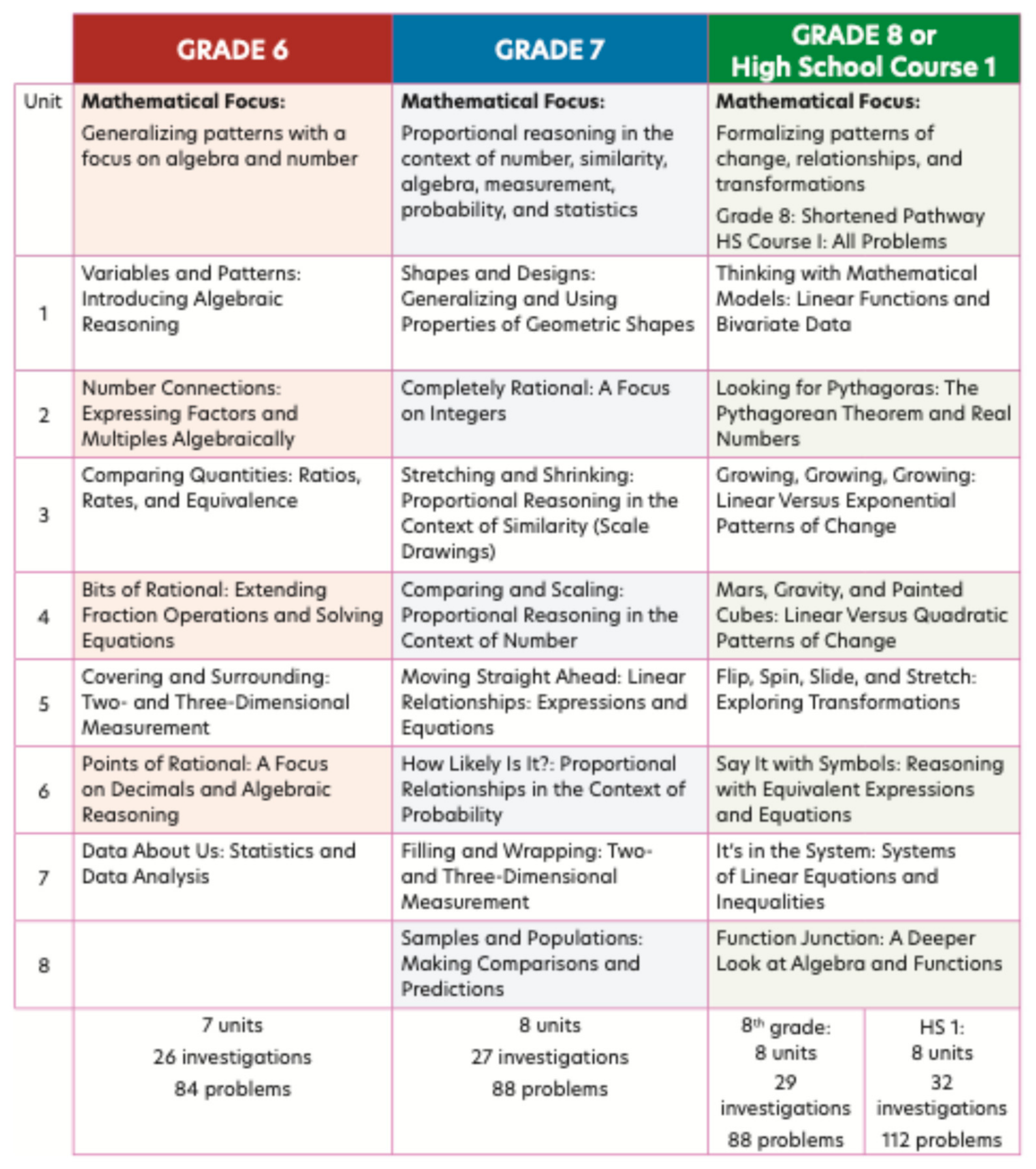
Figure 11 provides an overview of the units for grades six, seven, and eight. In CMP4, there are stronger connections both within and across units and grades. CMP4 strengthens its unique development of algebra and functions, which continues to develop exceptionally strong student algebraic understandings. Starting with
Variables and Patterns as the first unit in grade 6 allows the use of patterns of change and equivalence, representations, and generalization to naturally arise in all the remaining 22 CMP4 units, ending with the Function Junction unit in eighth grade. The unit titles highlight the main contextual thread and the mathematical focus. The mathematical focus for each grade is highlighted in the first row of
Figure 11. The focus of the 8th grade on algebra and functions serves the needs of both grade 8 and High School Course 1.
CMP4 has a stronger, more robust development of proportional reasoning starting with a new grade 6 unit, Comparing Quantities, and continuing with several units in grades 7 and 8. CMP4 incorporates aspects of the statistical problem-solving process throughout all units. The first problem in the first unit of each grade starts with an experiment.
To address some of the teacher enactment tensions, CMP4 (
Phillips et al., 2025a,
2025b,
2025c) provides more support for teachers in its CMP Arc of Learning™ Framework (
Edson et al., 2019) for each unit, CMP Formative Assessment Framework, CMP Attending to Individual Needs Framework, embedded General Pedagogical Strategies, and its new At a Glance teacher support for each problem. These were not robust enough to be fully implemented during field testing. However, the teacher’s comments on the student materials provided insights into the teacher support documents.
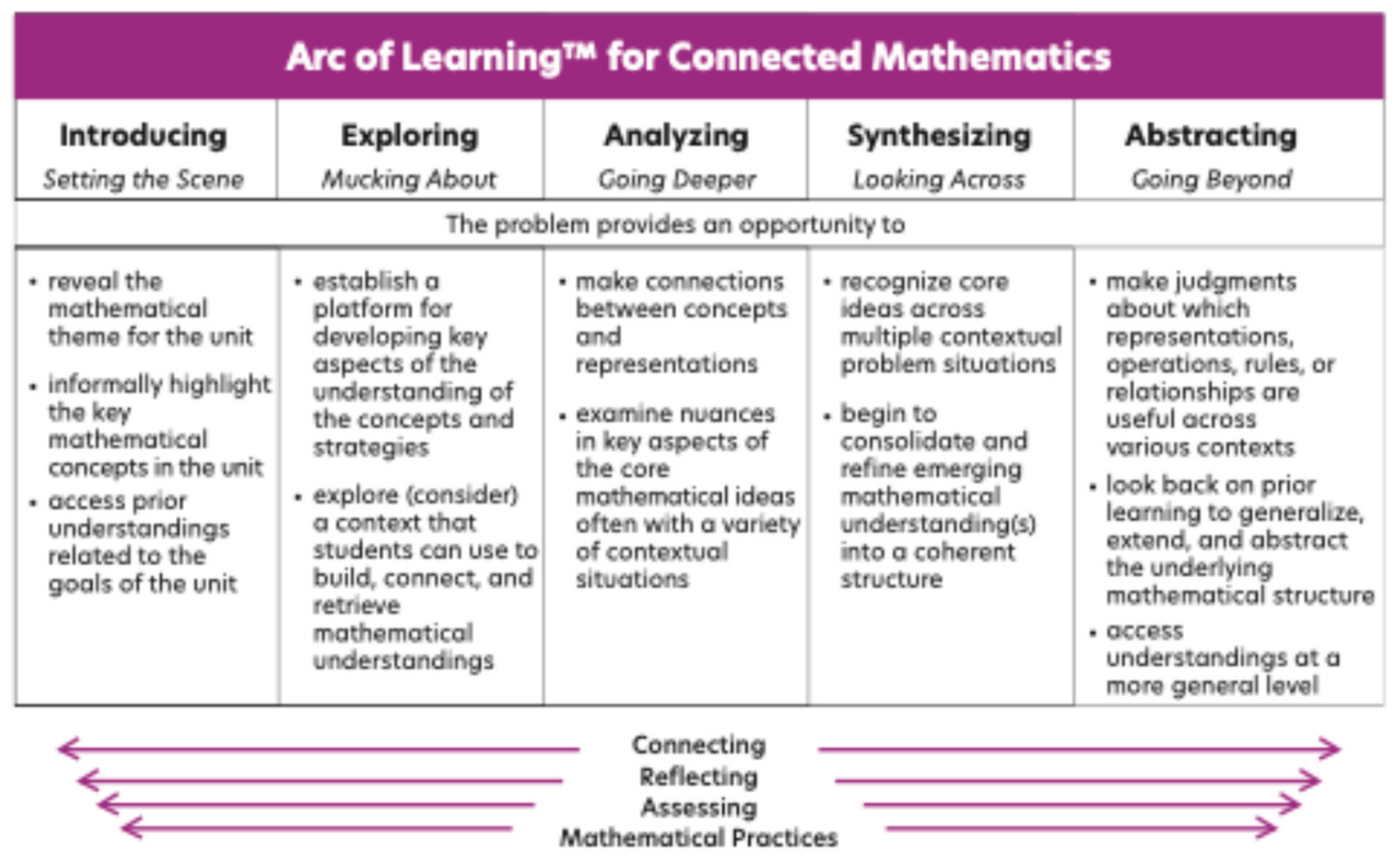
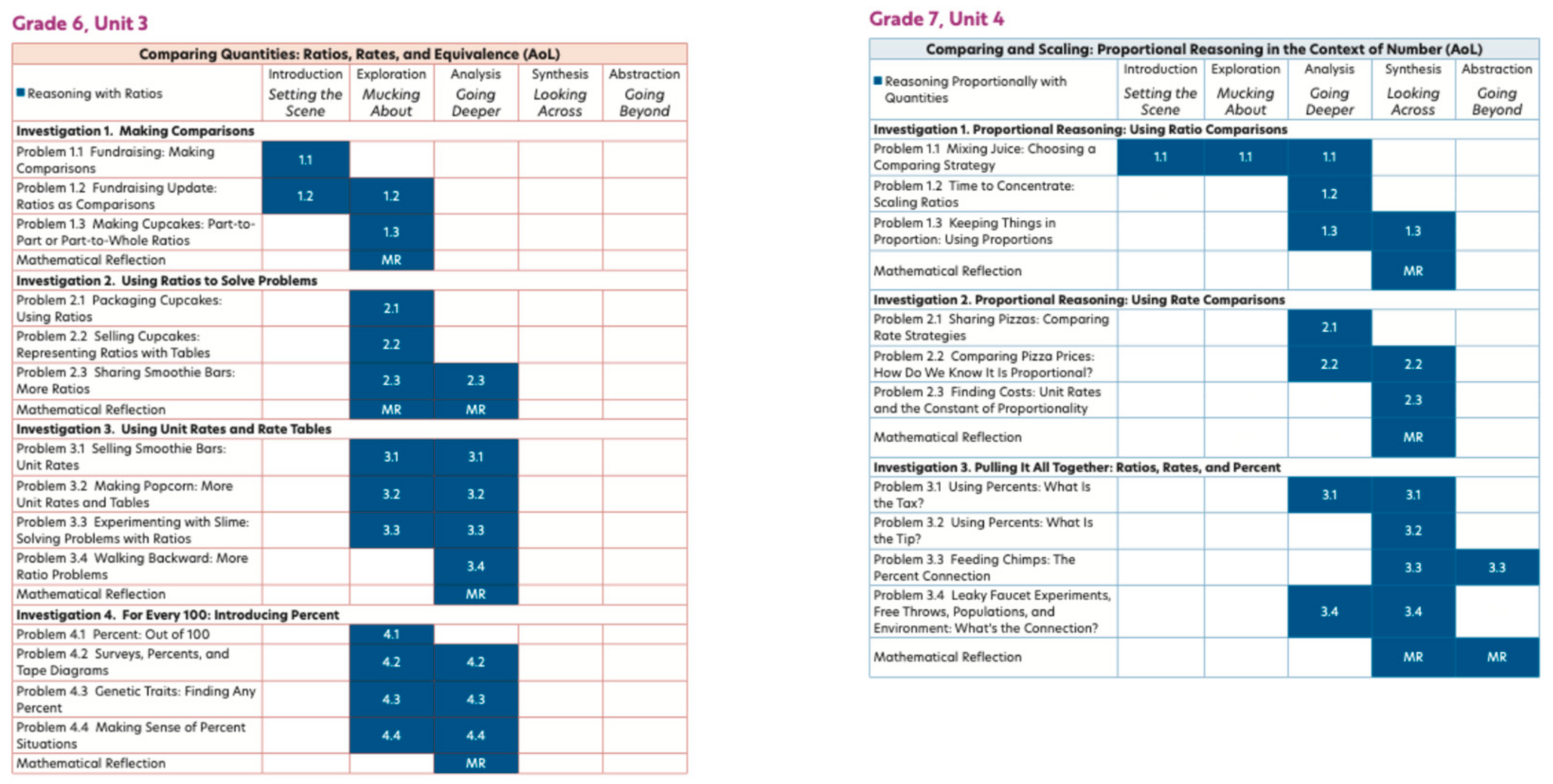
The Arc of Learning™ Framework provides guidance on how the understanding of the big mathematical idea for the unit evolves. In
Figure 12, the Arc of Learning™ Framework is shown for the first unit on proportional reasoning in sixth grade and a third unit of proportional reasoning in seventh grade. The development of proportional reasoning is growing toward abstracting. There are three more seventh-grade units that continue to look at proportional reasoning in the context of linear relationships, probability, and statistics.
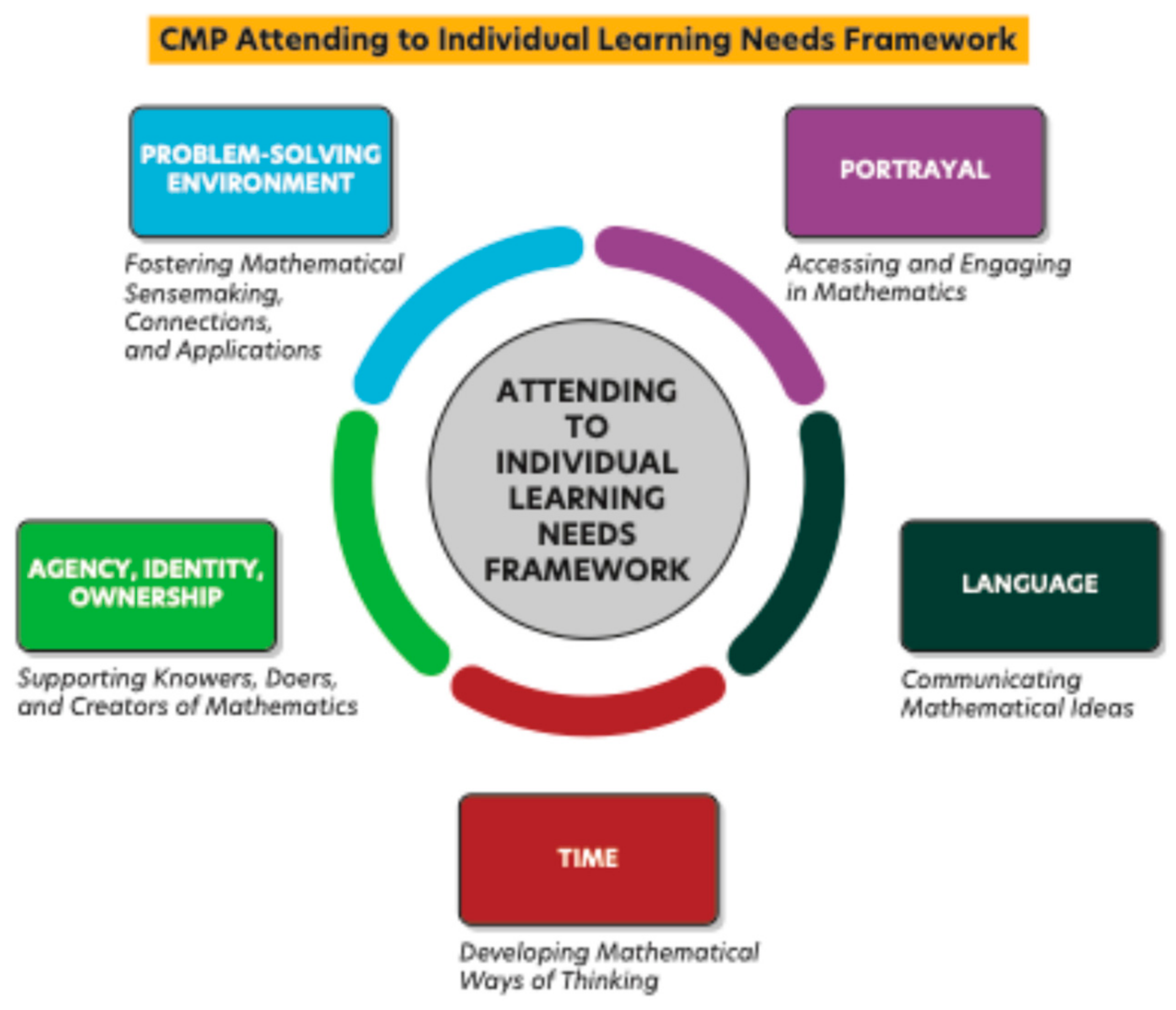
The Attending to Individual Learning Needs (AILNs) framework (see
Figure 13) communicates to teachers the information learned from research and practice over 40 years of field testing in CMP classrooms. It is consistent with the teaching practices set forth by other organizations. The appropriate component of the AILNs framework is indicated in the Launch, Explore, or Summarize phase of instruction in the At a Glance guide for the teacher.
At a Glance is a two-page format that provides the important information needed to implement a CMP4 problem. More details for the Launch–Explore–Summarize instructional phases of a lesson are provided in an extended Launch–Explore–Summarize section.
Figure 14 is an example of an At a Glance for Problem 2.1 in the 6th grade
Comparing Quantities unit. In addition to supplies, pacing, and grouping information, it also provides a sample of questions that can be used during each phase of the lesson. The appropriate Attending to Individual Learning Needs framework is indicated, as well as a suggested pedagogical strategy. Corresponding applications, connections, and extension task suggestions are also included.
2.4. Data Collection
At the close of the 2022–2023 school year, a total of 233 teachers, coaches, and administrators who field tested CMP4 completed a survey about their experience with the curriculum. This was the final year of field testing that provided substantial feedback to inform the published version of CMP4. Recruitment of field test teachers throughout the development process primarily focused on CMP3 teachers, coaches, and administrators, reflecting an intentional effort to gather feedback from educators familiar with prior editions of the curriculum. This provided feedback that was crucial for evaluating how the fourth edition field test materials built upon, refined, or changed previous versions. However, the inclusion of newcomers—such as teachers newly hired into CMP districts and a small number of non-CMP3 schools—was also essential for capturing a broader range of perspectives. Some non-CMP schools participated in field testing, primarily because they requested involvement due to professional learning efforts that made use of the materials with neighboring districts. These educators brought fresh views on the curriculum’s usability and effectiveness for schools that had not previously implemented CMP, offering a unique opportunity to assess how CMP4 field test materials performed in diverse instructional settings.
The survey was conducted electronically at the end of the school year, with responses from stakeholders (teachers, coaches, and administrators) representing approximately 70 cities spanning 20 states in the United States, as well as three additional countries. The participating schools represent a wide range of diversity in terms of gender, race, ethnicity, economic status, and/or disability. The socio-cultural diversity of the countries represented brings a variety of perspectives, each shaped by distinct educational contexts, which may influence how teachers and students engage with the field test materials. This diversity adds complexity to the interpretation of the results, as socio-cultural factors likely affect the implementation and effectiveness of the curriculum in different ways. Given the diversity in the socio-cultural and educational contexts, the design of the survey was intentionally developed to capture a broad range of feedback on the curriculum’s features, effectiveness, and student engagement across varied instructional settings. The survey was built on prior CMP curriculum development and research efforts in middle school mathematics classrooms, and included items specifically focused on the design features of the fourth edition of the materials. The survey included approximately 10–15 quantitative items (e.g., multiple choice, Likert scale, and frequency questions) addressing the courses taught, frequency of collaboration with teachers and/or coaches, students’ levels of math engagement and learning, and the effectiveness of the curriculum and its features. Participants were also asked two open-ended questions: one inviting them to share encouraging stories from teachers, and another asking how they would describe CMP4 to someone unfamiliar with the curriculum. Survey items were developed based on prior CMP research addressing curriculum effectiveness, student engagement, and implementation experiences and reviewed for clarity and alignment with study goals. The results were analyzed using descriptive statistics and inductive coding to identify patterns across diverse instructional settings.