Next Article in Journal
Developing Inclusive Educators: Analyzing the Effectiveness of a Short-Term Technical Assistance Model for Best Practices
Previous Article in Journal
Middle Leadership Roles Questionnaire—School Edition (Catalan) (MLRQ-SE-CAT) as an Instrument to Study the Roles and Practices of Cycle Coordinators as Middle Leaders
Previous Article in Special Issue
The Impact of Online Education as a Supplementary Tool for Special Education Needs (SEN) Students: Teachers’ Perspectives
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Education Sciences
Volume 15
Issue 5
10.3390/educsci15050577
education-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Formative Assessment in Inclusive Mathematics Education in Secondary Schools: A Systematic Review

by
Fynn Töllner
1,*,
Poldi Kuhl
1 and
Michael Besser
2
1
Institute of Psychology in Education, Leuphana University Lüneburg, Universitätsallee 1, 21335 Lüneburg, Germany
2
Institute of Mathematics and Its Didactics, Leuphana University Lüneburg, Universitätsallee 1, 21335 Lüneburg, Germany
*
Author to whom correspondence should be addressed.
Educ. Sci. 2025, 15(5), 577; https://doi.org/10.3390/educsci15050577
Submission received: 24 February 2025 / Revised: 16 April 2025 / Accepted: 28 April 2025 / Published: 7 May 2025
(This article belongs to the Special Issue Assessment and Evaluation in Special and Inclusive Education)
Browse Figures
Versions Notes

Abstract

:
Formative assessment is a way to individualize learning and tailor instruction to learners’ specific needs. These practices are particularly relevant due to the increasing heterogeneity resulting from the transition to an inclusive education system and the associated question of how teachers can deal with this rise in heterogeneity. However, there is no systematic interlinking between these two areas vis-à-vis mathematics secondary education. Therefore, little is known about how the benefits of formative assessment can be achieved in inclusive secondary mathematics education, with its heterogeneous learning groups. Accordingly, we searched the FIS Bildung, PsycInfo, and PSYNDEX-plus Tests databases, resulting in 14 articles addressing either formative assessment in general or diagnostics and feedback as components of formative assessment, particularly in inclusive secondary mathematics education. These publications were coded and analyzed according to their affiliation with one of the key components or formative assessment in general. Results indicate that, first, diagnostics must be highly individualized while considering contextual factors to be accurate; second, teachers should be advised on how to proceed with the diagnosed issues; and, finally, teachers should provide their students with frequent, easily accessible feedback. Furthermore, we identify productive directions for future research, along with implications for inclusive everyday teaching, and discuss limitations.

1. Introduction

Formative assessment is a promising approach for the adaptation of teaching in a way that addresses the individual needs of students (Hattie, 2012)—a fact that was confirmed in a recent umbrella review by Sortwell et al. (2024), who revealed that formative assessment positively impacts student learning in K–12 education. Notably, “atypical students” were excluded from this review, so direct conclusions regarding inclusive education, in particular, can only be drawn to a limited extent. In this context, however, it is often described as a convincing and relevant strategy (Mitchell, 2014; Sach, 2015; Schmidt & Liebers, 2017).
Little is known about how formative assessment should be implemented in the specific context of inclusive secondary mathematics education. Nonetheless, we can draw from a considerable amount of research regarding formative assessment (e.g., Andrade et al., 2019; Bennett, 2011; Heritage, 2007; Kingston & Nash, 2011), as well as regarding inclusive mathematics education (e.g., Häsel-Weide, 2017; Jütte & Lüken, 2021; Kollosche et al., 2019; Prediger & Buró, 2024). However, the linking of these two subject areas, as well as the provision of a systematic overview, is missing—a gap that should be urgently addressed, given the outlined effectiveness of formative assessment and the importance attributed to it for inclusive education. Therefore, the present study aims to systematically review and synthesize what we already know about formative assessment in an inclusive secondary mathematics education framework. To this end, we intend to provide deeper insight into existing concepts related to diagnostics that accompany the learning process and feedback that promotes learning.
This study is part of the research project titled LERN-IF (this abbreviation stands for “Learning process diagnostics and learning supportive performance feedback in inclusive subject teaching”) and is funded by the German Federal Ministry of Education and Research (BMBF) under funding reference 01NV2117.

1.1. Formative Assessment

Formative assessment serves two purposes: The first is to provide teachers with information about the learning process of their students to aid them in their decision making about designing instructions. The second objective is to inform students about their own learning progress. This enables students to bridge gaps between their current achievement level and their desired learning outcome (Andrade, 2010). These procedures support learning. Conversely, summative assessment focuses on providing information at the end of a learning process, with no intention to influence further learning (Dolin et al., 2018). Regarding implementation, formative assessment spans a continuous scale, from informal, unplanned approaches like on-the-fly formative assessments via planned-for-interaction formative assessments to embedded-in-the-curriculum formative assessments (Shavelson et al., 2008).
In their often-cited literature review, Black and Wiliam (1998) showed that formative assessment is an effective way to enhance students’ achievement. However, there are doubts about the effect sizes, which were described in the literature review conducted by Black and Wiliam (1998), as it is questionable whether all included studies were, indeed, methodologically sound (Kingston & Nash, 2011). Therefore, Kingston and Nash (2011) reported smaller effect sizes in their meta-analyses and recommended that future research should “move from looking at the efficacy of formative assessment to determination of the factors influencing the efficacy of formative assessment” (p. 35). Furthermore, more than ten years after this statement, there have been inconsistent findings regarding the effectiveness of formative assessment (Lui & Andrade, 2022). These inconclusive findings stress the importance of analyzing precisely what works when implementing formative assessment in schools. Concretely, the influence of two essential components of formative assessment ought to be discussed both theoretically and empirically: (1) diagnosing students’ learning progress and (2) providing feedback to them (Heritage, 2007; Mitchell, 2014).

1.1.1. Diagnostics

Among other things, diagnostics is defined as the process of analyzing prerequisites, conditions, learning processes, and learning outcomes to optimize individual learning (Ingenkamp & Lissmann, 2008). The successful realization of this goal is a significant challenge for teachers (Hoth et al., 2016). In the course of formative assessment, diagnosing student learning is an essential practice for teachers to identify the topics that students struggle with, allowing them to help students to overcome their learning deficits (Heritage, 2007).
A central aim of diagnostics within formative assessments is to determine what a learner can achieve and to bring them to the next level of achievement (Heritage, 2007). There are several strategies a teacher can use to successfully complete this task. These assessment strategies include—but are not limited to—observing students or engaging in dialogues with them. Furthermore, demonstrations or examinations of written responses are also included in these strategies (Heritage, 2007). However, teachers must ensure that diagnostic procedures are on point, as it must be stressed that finding the right starting point and goal is essential for a successful learning process (Heritage, 2007).

1.1.2. Feedback

The second essential component of formative assessment, which plays an especially critical role in its implementation, is feedback. This insight is based on the current state of research, indicating that the effectiveness of formative assessment depends on whether and to what degree students are supported and if they are cognitively activated by this (potential) support. Both factors draw heavily from teachers’ feedback (Decristan et al., 2015). The purpose of this feedback is to help students to establish their current states of learning, as well as to determine how to continue for further improvement (Heritage, 2007).
Generally, feedback can be provided by different agents, including teachers, peers, or students themselves. In addition to categorization according to the source, feedback can be categorized into different types. Common ways in which different forms of feedback are categorized are according to the purpose, the time the feedback is provided, and the amount of information given (e.g., Shute, 2008). Feedback can also differ in its focus, for example, focusing on either a student’s achievement or their behavior (Rakoczy & Schütze, 2019). According to Hattie and Timperley (2007), effective feedback needs to address three questions; namely, “Where am I going? (What are the goals?), How am I going? (What progress is being made toward the goal?), and Where to next? (What activities need to be undertaken to make better progress?)” (Hattie & Timperley, 2007, p. 86).
How students respond to different kinds of feedback and eventually use it represents the core of the latest explanation for the varying effectiveness of feedback, as well as formative assessment as a whole (Lui & Andrade, 2022). This explanation is an argument that feedback based on an appropriate diagnosis must be tailored as closely as possible to the individual learner to achieve maximum effectiveness. As inclusive classrooms can be characterized by a greater heterogeneity of learners (Borsch, 2018), it seems plausible to assume that diagnosing the right starting point and supporting students with appropriate feedback are relevant challenges in inclusive education.

1.2. Inclusive Education

Inclusive education is defined in different ways in the literature, with no clear, generally recognized definition (Göransson & Nilholm, 2014; Grosche, 2015). These definitions vary from the sole placement of students with disabilities in general education classrooms to the creation of inclusive communities (Göransson & Nilholm, 2014) but often emphasize the heterogeneity of students (Grosche, 2015). In addition, inclusion is not a standardized construct but, rather, encompasses many different dimensions, some of which vary greatly between different authors. This has resulted in many studies that focus on a specific organizational form, such as inclusion classes, special education support centers, or a response-to-intervention approach (Grosche, 2015). In the German context, a focus on common schooling in mainstream schools is recognizable (Federal Ministry of Education and Research, 2019). This discourse on the appropriate school setting for students with special educational needs was intensified by the German ratification of the UN Convention on the Rights of Persons with Disabilities (United Nations, 2006). Due to this convention, Germany must ensure that people with disabilities have the same opportunities to participate in all levels of education as their peers without disabilities. However, this dichotomization between children with and without special educational needs is limiting the meaning of inclusion due to the ambiguity of the term, as described above. This problem is further underlined by the fact that the term special educational needs is not uniformly defined and sometimes has very different meanings (Grosche, 2015).
At the same time, different school tracks at the secondary level have been merged. Both factors have engendered an increase in heterogeneity in German secondary classrooms (Borsch, 2018; Leiss & Tropper, 2014). In such inclusive, heterogeneous classrooms, formative assessment is considered a useful concept for improving individual performance. To this end, formative assessment relies on practices like adapting curricula or teaching (Mitchell, 2014). Adaptive teaching is widely recognized as a part of effective instruction (Parsons et al., 2018). However, considering the individual starting point of every learner is challenging for teachers. Nevertheless, doing so is considered to be highly effective in terms of student achievement (Leiss & Tropper, 2014).

1.3. Mathematics Education

It is important to acknowledge that formative assessment is specific to the domain in question (Andrade et al., 2019). To address this specificity, formative assessment can be developed within a domain (Bennett, 2011). This approach seems to be especially appropriate, as there is a wide range of variation regarding the kind and size of benefits for different subpopulations of students between specific implementations of formative assessment (Bennett, 2011). Taking this into account, it makes sense that there are systematic reviews of formative assessment that focus on different topics, contexts, and subpopulations (e.g., Gikandi et al., 2011; Morris et al., 2021 for higher education; Hartmeyer et al., 2018 for science education; Lee et al., 2020 for US K-12 education). In addition, previous research reveals that teachers’ formative assessment practices differ between primary and secondary education (Grob et al., 2021).
Recent research indicates that formative assessment constitutes a beneficial technique for mathematics education. For example, formative assessment in mathematics lessons has a positive impact on students’ learning process and a significant effect on their performance and attitudes in mathematics (Kültür & Kutlu, 2021). Furthermore, a study conducted in 18 secondary schools revealed that formative assessment is associated with greater perceived feedback usefulness and increased self-efficacy and interest (Rakoczy et al., 2019). Thus, formative assessment seems to be a promising approach in this context. Furthermore, in inclusive mathematics education, teaching should be adapted to the learners’ individual needs and competencies. This supports and involves all learners in the best possible way, regardless of their individual learning requirements, interests, or development potential (Schöttler, 2019). These goals make a good case for linking formative assessment and inclusive mathematics education. However, to the best of our knowledge, there is no literature review on the context of inclusive secondary mathematics education. Furthermore, mathematics teachers perceive teaching this subject in inclusive settings as especially challenging (Jütte & Lüken, 2021). Thus, for successful inclusive teaching, they need advice on how to handle the learners’ different starting points. The rise of heterogeneity in classrooms makes this issue even more urgent. Therefore, it is unclear what a formative assessment should look like in this specific context.

1.4. Research Questions

To address the outlined challenges and determine the factors making formative assessment effective, it is first necessary to summarize the existing literature. By doing so, we not only can better understand the already working concepts but also identify gaps in knowledge to guide future research. Thus, we conducted a systematic review of the superordinate research question of what is already known about formative assessment in inclusive mathematics secondary education. As formative assessment comprises diagnostics and feedback, two additional guiding research questions arise. Our research questions can be summarized as follows: What can be found in the literature on the context of inclusive mathematics secondary education with regard to (1) formative assessment in general, (2) diagnostics, and (3) feedback?

2. Method

The systematic review conducted in this study is based on the PRISMA standard (Page et al., 2021), that is, we conducted a systematic review applying rigorous methods to identify articles relevant to our research questions.
For this purpose, we searched for English and German articles in several well-established educational science literature databases, comprising FIS Bildung, PsycInfo, and PSYNDEX-plus Tests. Notably, FIS Bildung simultaneously searches multiple databases, such as BBF 1945–1993, Casalini Libri, EBSCOhost, ERIC, the Library of Congress, and Online Contents Sondersammelgebietsausschnitte.
Our search string contained three parts and combined keywords related to (1) formative assessment with keywords related to (2) inclusion and (3) mathematics. To conduct a literature review of English and German articles, we searched with both German and English keywords whenever they differed or used an asterisk in a way that covered both languages. The asterisk serves as a placeholder for one or more letters to cover both languages and different endings of the word. The English part of the search strategy is illustrated in Figure 1.

2.1. Inclusion and Exclusion Criteria

To identify articles that match our research interest, the research team agreed on the inclusion and exclusion criteria listed in Table 1.
To be included, the articles had to fulfill multiple inclusion criteria. The first was that the publications had to cover all parts of our search string. In research on inclusive education, different scholars use various definitions of inclusive education. To cover the state of research as broadly as possible, we did not discriminate based on the underlying definition of inclusion. To fulfill the criteria, the sample of students in an article always had to contain an inclusive case, with students either being schooled in an inclusive way (e.g., inclusive classroom or resource room) or at least some cases in the respective article had to be schooled in such a way to fulfill the criteria. In addition, the article either had to address issues affecting secondary education or had to report on secondary education students. To decide if classes were part of primary or secondary education, we defined them depending on their category in their respective countries.
To reflect the current state of research as accurately as possible, the review could include quantitative, qualitative, and theoretical work, but only research pieces published in journal articles, dissertations, or book chapters in English or German were included.
We also specified several exclusion criteria and, thus, did not include publications that focused mainly on elementary/primary education, preschools, behavioral/emotional problems, behavior, AD(H)D, Asperger’s/autism, blind and partially sighted learners, giftedness, test presentations/reviews, mental development/disabilities, English language learners, universities, program evaluations/specific digital tools/technology-based interventions/technology, verbalization, teachers, psychometric studies on test quality/validation, specific tests, test reviews, career changers, peer tutoring, single-case designs, clinical diagnostics, or mode effect studies. We did not make an exclusion criterion with respect to the publication date.

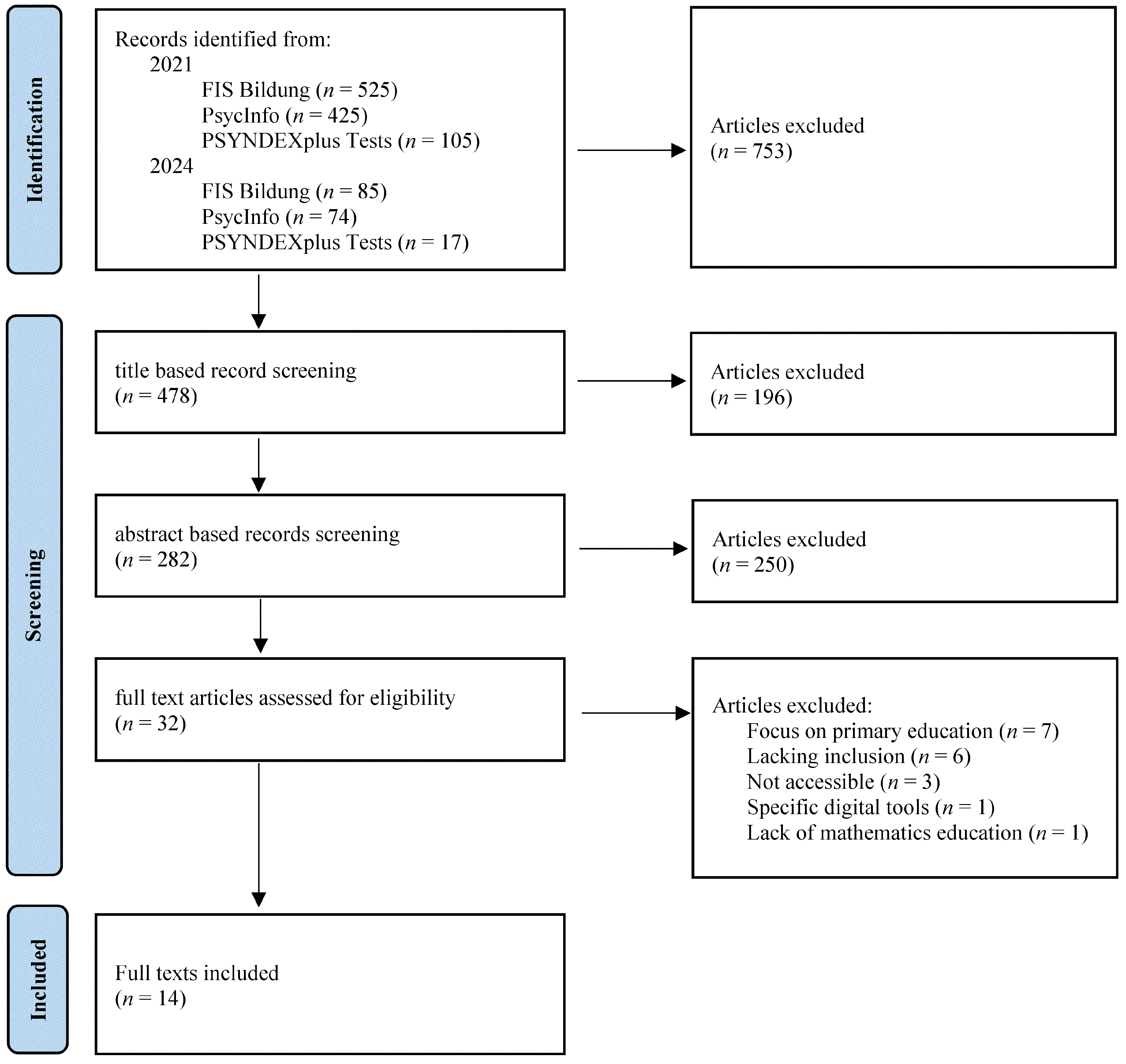
2.2. Selection Process and Search Results

The selection process is depicted as a PRISMA flow diagram in Figure 2. The literature search was performed between December 2021 and January 2022 by two independent researchers and yielded 1055 records. To ensure that this systematic review contains the most up-to-date publications, we conducted a second literature search in May 2024 for 2022–2024 with three researchers. This revealed another 176 publications, resulting in 1231 identified publications. Afterward, we removed duplicates and obvious misfits based on title or publication type, resulting in 389 publications left in the first search. In the second search, 89 publications qualified for further screening after we removed duplicates. In the subsequent process, we made sure that the procedure for the second screening was as similar as possible to the first screening.
In the following title-screening phase, we individually screened the titles based on their fit to our research topic and consensually agreed on which publications to exclude and which to keep. Thereafter, the researchers independently rated the abstracts of the 282 remaining publications based on the inclusion and exclusion criteria. After this phase, we retained the remaining 32 publications that all reviewers agreed contained mathematics, inclusion, and at least one of the three categories (formative assessment in general, diagnostics, or feedback) and subjected them to a full-text analysis. The full-text analysis was performed by the first author, leading to the exclusion of 18 additional articles. Finally, 14 articles formed the basis of the present systematic review and were summarized by indicating their main objectives.

2.3. Data Extracted from the Publications

The relevant publications were coded based on their methodological natures as theoretical, qualitative, or quantitative works. In addition, we categorized the remaining publications with respect to their country of origin, population, the grade level, age of the participants, the mathematical topic, the dependent and independent variables, and their focus on formative assessment in general or diagnostics or feedback in particular. In addition, we extracted the research questions, main findings, and conclusions of the selected publications. Lastly, we extracted their respective definitions of inclusion. This served the purpose of considering that all definitions of inclusion can claim validity for themselves and to follow Grosche’s (2015) recommendation that definitions of inclusion should be disclosed to create transparency with regard to those used. If a publication included primary school students and secondary school students, whenever possible, we only extracted data for the secondary school cases.

2.4. Description of the Synthesis Process

During this phase, the publications were sorted into three categories (formative assessment in general, diagnostics, or feedback). For this process, multiple coding was necessary. A publication could be labeled as relevant for more than one category; thus, a publication could be used to answer more than one research question. After this coding procedure, the findings of the publications were extracted based on their respective categories. Furthermore, these findings were summarized to obtain synthesized evidence about formative assessment in inclusive secondary mathematics education. Moreover, from these findings, we derived implications for designing formative assessments in this specific environment.

3. Results

3.1. Overall Description of the Identified Publications

First, we describe the studies we identified as relevant in terms of their characteristics: 11 of the 14 articles were from the United States, 1 was from Switzerland, 1 was from Austria, and 1 was from Italy. Five of the publications were theoretical, five were quantitative, one was qualitative, and three were reviews or meta-analyses. The publication dates ranged from 1990 to 2023. The results of our search covered a wide range of definitions of inclusion, as well as a variety of mathematical topics. In terms of coding, we labeled five studies as formative assessment, eight as diagnostic, and three as feedback. This resulted in two theoretical articles, one empirical article, and two reviews/meta-analyses constituting the findings regarding formative assessment in general. Regarding diagnostics, we drew our results from four theoretical articles and four empirical articles. The feedback results were derived from three reviews/meta-analyses. Table 2 lists all publications that we identified to answer our research questions. The publications are first sorted by study type, then by their date of publication. The table starts with the theoretical articles at the top, followed by the quantitative studies. Subsequently, the qualitative studies are listed, and the other reviews are at the end of the table. In addition, we carried out a quality assessment for publications that are either single empirical studies or reviews/meta-analyses. Thus, we used the mixed methods appraisal tool (Hong et al., 2018) for the single empirical studies and AMSTAR-2 (Shea et al., 2017) for reviews/meta-analyses. The results of these analyses are available in the electronic supplement, as they are not the subject of this article.

3.2. Results of Included Publications

According to our research question, we classified the identified results of individual studies into three categories: formative assessment in general or diagnostics or feedback in particular. The findings were derived from one or multiple studies. We first describe the insights of the theoretical articles. Then, we report the results of the empirical studies. Finally, we present the results of the reviews and meta-analyses.
Five publications were found with respect to our first research question on what we have already learned about formative assessment in general in inclusive secondary mathematics education. One insight from the theory-oriented articles is that assessment procedures have already been discussed several times as a way to tailor instructional needs to learners’ needs (Calhoon, 2008; Miller & Mercer, 1997). Another theoretical insight is that teachers should break down problems into several steps so that they can diagnose the roots of learners’ problems. This can be achieved using a data collection chart. Such a chart enables teachers to systematically search for patterns in the responses of their students, to obtain clues for further instructional planning, and to provide accurate feedback to the students. Data collection charts are created by breaking down a task into all the steps the students must master and the prior knowledge needed (Accardo & Kuder, 2017). Additionally, on the empirical side, the studies revealed that instructional decisions need to be tied to the individual student’s achievement to reach the full potential of formative assessments. Moreover, test taking without instructional adaptions does not increase student achievement (Stecker & Fuchs, 2000). Furthermore, a meta-analysis reported small effects on students’ mathematics proficiency if teachers were provided with information about the progress of their students. If teachers are given additional advice on how to address students’ learning deficits, the effect remains small but increases from Hedge’s g = 0.21 to Hedge’s g = 0.34. If formative assessment is used as a tool to assess the progress toward a goal, determined together with the students, the effect yields a non-statistically significant Hedge’s g = 0.17 (Gersten et al., 2009).
Regarding our second research question on what we have already learned about diagnostics in inclusive secondary mathematics education, the theoretical work suggests taking a closer look at the errors committed by students. By doing so, they can not only be classified as careless or conceptual but also addressed later accordingly (Katsiyannis & Prillaman, 1990). Another theoretical publication emphasized that diagnostics are the key to understanding individual differences, naming three major categories that should be considered in research on diagnostics: the task, the students, and the learning environment (Sharma, 1998). In addition, Poch et al. (2015) argued for a diagnostic approach that breaks down the subject matter into its components to determine exactly where the problems lie. This approach draws from a competence framework that can be used to investigate what students have already learned. The diagnostic procedure obtains information from two sources—written work and an interview—to obtain deeper insight into the student’s misconceptions. This aligns with the formative assessment approach proposed by Accardo and Kuder (2017). Moreover, Scanlon (2013) emphasized that accurate assessments of skill level should be based on a variety of diagnostic tasks with varying levels of difficulty to obtain a fitting list of learning goals for individualized learning. In addition to the theoretical insights presented by Katsiyannis and Prillaman (1990), Asenova et al. (2023) presented empirical findings emphasizing the relevance of teachers’ semiotic interpretative knowledge. Accordingly, semiotic aspects should be considered when interpreting student responses. This helps to better understand student responses, as students may have already internalized conceptual knowledge but still fail to understand sign conventions, such as whether a full stop or a comma is used. In terms of the heterogeneity to be diagnosed, Gebhardt et al. (2013), with their empirical work, showed that the most relevant predictors for a learning disability diagnosis were calculating and reading performance. In addition, students diagnosed with a learning disability showed poorer calculating, reading, and writing performance than their counterparts, even if they had a comparable intelligence quotient (IQ). Moser Opitz (2005) indicated that students in the eighth grade with competencies below average—those with both average and below-average IQs—lack knowledge about basic mathematical topics that were taught in the first four years of school. This results in using counting strategies and written procedures for calculating more frequently. However, the written procedures are often incorrect, and students with below-average competencies and IQs more often rely on those procedures than their peers with average IQs. Furthermore, students with below-average competencies also tend to struggle with counting and understanding the decimal system, as well as mathematizing with regard to addition, multiplication, and division.
Hwang (2016) added further insights to this. The author categorized students into three groups: typically achieving students, low-achieving students, and students with a mathematical learning disability. She reported that the error patterns of these achievement groups do not differ much, except for when students need to convert a fraction. In this case, the errors of typically achieving students are often due to mathematical errors, whereas those of low-achieving students and students with mathematical disabilities are more often due to misunderstandings and a lack of basic understanding. Furthermore, students from a higher-achieving group are less prone to committing errors, and students with learning disabilities tend to make more errors if the item contains unequal denominators.
However, the results reported by Moser Opitz (2005) and Hwang (2016) are ambiguous. This is particularly reflected in Moser Opitz’s results showing that students with below-average competencies differ from their peers in the errors they make (e.g., counting errors), whereas Hwang (2016) found little evidence for differences in committed errors between different achievement groups. Therefore, it remains unclear to what extent the overall achievement level plays a role in the type of committed errors. However, regarding preferred task approaches, both studies indicate that students with mathematical learning disabilities or below-average competencies differ from their peers. This indicates that heterogeneous approaches must be expected in inclusive teaching.
In relation to our third research question—what we have already learned about feedback in inclusive secondary mathematics classrooms—our findings are solely based on other reviews/meta-analyses, as no single empirical study could be identified in our search. The first is a literature review published by Spooner et al. (2012), who concluded that feedback should be given to students frequently with some type of correction and differential reinforcement. Another literature review concluded that students are more motivated when they receive a graphical visualization of their learning progress (Calhoon, 2008). This finding is principally backed by a meta-analysis by Gersten et al. (2009), who reported a small effect (Hedge’s g = 0.23) on mathematics proficiency for students receiving graphical information about their learning progress.
With respect to the three feedback questions raised by Hattie and Timperley (2007), several implications can be drawn for inclusive mathematics secondary education. Regarding the first question addressing the “Feed Up” aspect, “Where am I going? (What are the goals?)” (Hattie & Timperley, 2007, pp. 86–87), our systematic review adds productive ways to diagnose the student learning level. This is crucial, as diagnostics is both an essential component of formative assessment and necessary for teachers to provide feedback in the first place. Based on our systematic review, we suggest that such diagnostics should be carried out with a specific learning goal in mind and to pinpoint the exact problem to determine the student’s goal. Additionally, in an inclusive learning environment, special emphasis must be placed on contextual factors to support students adequately and to pick the right learning goals. With respect to the “Feed Back” component, which involves the question, “How am I going? (What progress is being made toward the goal?)” (Hattie & Timperley, 2007, pp. 86–87), our results suggest that a beneficial way to convey this information is through graphical visualizations of learning progress. Additionally, our systematic review made clear that students in inclusive environments need feedback more frequently. This indicates that these students need information provided with feedback that is individually tailored and easily accessible. Concerning the last factor, “Feed Forward”, and its assigned question, “Where to next? (What activities need to be undertaken to make better progress?)” (Hattie & Timperley, 2007, pp. 86–87), our results advocate for a formative assessment in inclusive secondary mathematics education that is individually tailored to students and contains guidance for teachers on how to address the issues students are struggling with. Overall, this suggests that students in inclusive education need to receive answers to this question in a highly individualized way. Given this insight, it can also be assumed that equipping teachers with hints is particularly relevant for the third feedback question on what students should do to achieve their goals. This is because these clues can help teachers answer that question by suggesting a strategy or something similar to students.

4. Discussion

Our systematic review was conducted to systematically present the current state of research on formative assessment in inclusive secondary mathematics education. This was meant to draw conclusions from studies factors that instituted effective formative assessment in inclusive mathematics education. To fulfill this goal, we first derive directly implementable recommendations for formative assessment in inclusive mathematics education at the secondary level from our results. Then, we discuss the limitations of our study and outline topics for future research.

4.1. Implications for Designing Formative Assessments in Everyday Inclusive Mathematics Education

According to Shavelson et al. (2008), formative assessments in everyday educational practice can vary between unplanned and planned approaches. However, the current state of research reveals several aspects teachers can consider if they plan to include these practices in their inclusive secondary mathematics classroom. An overall emerging theme of our findings is that appropriately considering heterogeneity in the classroom plays a central role in successfully implementing formative assessment. With respect to what should be considered before developing a formative assessment for inclusive mathematics teaching in secondary schools, we derived five recommendations based on our systematic review of the research.
The first recommendation is to bear in mind that formative assessment should consider and assess different aspects of a learning subject so the individual needs of the students can be addressed. This recommendation is based on the insight that theoretical articles recommend adapting to learners’ characteristics and needs. To do so, formal and informal assessment procedures need to be put in place to plan future instruction by identifying the strengths, weaknesses, and current levels of students’ learning. With these goals, instruction can be tailored to the students’ needs so they can overcome their learning gaps (Miller & Mercer, 1997). One way to identify these could be the data collection chart proposed by Accardo and Kuder (2017), which provides advice on how to systematically search for the error patterns of students. This approach is backed by Poch et al. (2015), who noted that, in addition to analyzing written solutions, teachers should also conduct interviews with their students.
Our second recommendation is that formative assessment should include specific support materials that teachers can give to their students for their specific learning problems. This is backed by the finding that formative assessment has a larger effect size if teachers are equipped with knowledge of how to address the diagnosed problems of the students (Gersten et al., 2009). Therefore, it is especially important to ensure that teachers can adapt to individual students, which is considered effective by Stecker and Fuchs (2000).
For the third recommendation, when teachers diagnose their students, they should take a comprehensive, broad approach, drawing from a wide range of tasks to estimate their exact achievement level. This is because the studies we found reveal that a holistic approach should be taken when diagnosing errors, including the task, the student, and the learning environment (Sharma, 1998). Based on Gebhardt et al. (2013), it can be deduced that to appropriately support students, teachers’ diagnostics should focus on performance, with remediation on calculation and reading. Regarding the tasks used for diagnostics, the literature indicates that these need to be at different difficulty levels to pinpoint students’ performance as accurately as possible (Scanlon, 2013).
The fourth recommendation is that diagnostics should focus on committed errors and verify the acquisition of necessary prior knowledge. This argument is supported by Katsiyannis and Prillaman (1990), who considered diagnosing the nature of committed mistakes to be crucial in designing adequate learning environments. This is further underlined by Asenova et al. (2023), who emphasized the exact knowledge the student is lacking. Matching this, Moser Opitz (2005) stressed that “the basic subject matter” should also be considered within the framework of broad diagnostics to ensure that the cause of an error does not lie within a faulty understanding of the basic material. Hwang (2016) added that there are not many differences between various achievement groups regarding the nature of different errors; therefore, teachers do not need to implement different diagnostics procedures for different achievement groups.
Lastly, the fifth recommendation is that formative assessment requires feedback that focuses on individual learning progress and is easily accessible to students. This recommendation is based on the findings of Spooner et al. (2012), who suggested corrective feedback involving differential reinforcements. Additionally, Calhoon (2008) and Gersten et al. (2009) agreed on visualizing individual learning growth for students in a graphical form.

4.2. Limitations

Like all studies, we must acknowledge some limitations in our work. Similar to all systematic reviews, our results may be subject to publication bias. This describes the phenomenon whereby significant results are more likely to be published (Torgerson, 2006). However, we reduced this risk by including dissertations and the ERIC literature database (via FIS Bildung) in our search. Both are recommended practices for reducing such bias (Torgerson, 2006). Furthermore, we must also consider that our findings are based on different types of literature, with all findings equally included. However, this approach has opened up the opportunity to conduct a comprehensive literature search considering both quantitative and qualitative studies, as well as other reviews and theoretical articles, in order to reflect the current state of research as accurately as possible. Furthermore, we are aware that we might have missed some publications due to our inclusion/exclusion criteria. However, these were set with close consideration of our research questions, leading to a less likely occurrence of this bias. A further result of our work that is in line with earlier publications (e.g., Grosche, 2015) is that we found a wide range of definitions of inclusion in the included publications. This may indicate that a uniform understanding of the term inclusion does not exist with regard to formative assessments in inclusive mathematics education at the secondary school level. In this case, our results demonstrate that only a few publications have focused on inclusive teaching in general education, and most publications have a narrow definition. Put differently, publications have mainly concentrated on students with special educational needs. The publication date of the studies we found might serve as an explanation for the more frequent occurrence of publications with this understanding of the term “inclusive education”. Lastly, we must note that our systematic review focused on information provided by teachers to students. In this regard, it is important to mention that a recent umbrella review (Sortwell et al., 2024) indicated that the possibility of teachers checking the effectiveness of their teaching is a beneficial aspect of formative assessment. Accordingly, our review does not contribute to how teachers can use formative assessment to evaluate their own effectiveness.

4.3. Implications for Future Research

Several implications for future research can be drawn based on our systematic review. Even though feedback was the category for which we found the fewest publications, there are still important take-home messages. It is emphasized that teachers should frequently visualize students’ learning progress and give students feedback, but the realization that there is little research regarding the provision of feedback suggests that further knowledge is especially needed on this topic. This is particularly underlined by a lack of more precise design principles, as it remains unclear how feedback can be designed to be easily accessible for all learners and what amount and kind of information is needed. This seems exceptionally important, as research suggests that the amount of provided information needs to be compatible with prior knowledge (Sweller et al., 2011).
Therefore, it is necessary to examine what characteristics feedback must have so that it is as individually tailored to a student, as it must be in inclusive education. However, students’ use and interpretation of feedback currently represent a black box and may be an explanation for inconsistent findings on the effectiveness of formative assessments (Lui & Andrade, 2022). Thus, future research should strongly emphasize how students perceive feedback. This will help to answer the “How am I going?” (“Feed Back”) question for students brought up by Hattie and Timperley (2007, p. 89), which focuses on the degree of success in task processing. The need for research is further underpinned by our review, which has shown that, overall, there is little research on formative assessment in inclusive mathematics education. This future research should specifically focus on the feedback aspect of formative assessment, as its effectiveness seemingly depends on it (Decristan et al., 2015).
Furthermore, we should keep in mind that the latest technological developments that have been made available to the public (e.g., in the field of artificial intelligence and large language models) can strongly influence the ways in which (digital) feedback can be used (Wardat et al., 2023).
Lastly, the studies we reviewed suggest that using formative assessment to address diverse student needs is promising, as it allows for individualized support. However, as outlined herein, there are still considerable research gaps that need to be addressed in order to establish how this can be effectively and suitably harnessed for everyday use in inclusive secondary mathematics education—a cause that we will continue to pursue as part of the LERN-IF project. As part of this project, the results of this study—together with results from an interview study and an intervention study—will be incorporated into a professional development program for teachers such that the learning-promoting effects of formative assessment can be transferred to everyday school life.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/educsci15050577/s1, Table S1. Quality assessment of the qualitative studies included our systematic review; Table S2. Quality assessment of the quantitative randomized controlled trials included our systematic review; Table S3. Quality assessment of the quantitative descriptive included our systematic review; Table S4. Quality assessment of the Reviews and Meta-analyses included in our systematic reviews.

Author Contributions

Conceptualization, F.T., M.B. and P.K.; investigation, F.T., M.B. and P.K.; data curation, F.T.; writing—original draft preparation, F.T.; writing—review and editing, F.T., M.B. and P.K.; visualization, F.T.; funding acquisition, M.B. and P.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research is part of the LERN-IF project which is funded by the Federal Ministry of Education and Research (BMBF) within the funding line “Förderbezogene Diagnostik in der inklusiven Bildung (InkBi 2)” as part of the framework programme “Empirische Bildungsforschung” under the funding reference 01NV2117. The authors are responsible for the content of this publication.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data sharing is not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
AD(H)DAttention deficit (hyperactivity) disorder
BBFBibliothek für Bildungsgeschichtliche Forschung
BMBFBundesministerium für Bildung und Forschung
DDiagnostics
ERICEducation Resources Information Center
FFeedback
FAFormative Assessment
FISFachinformationssystem Bildung
IQIntelligence Quotient
LERN-IFLearning Process Diagnostics and Learning-Supportive Performance Feedback in Inclusive Subject Teaching
PRISMAPreferred Reporting Items for Systematic reviews and Meta-Analyses
SENSpecial Educational Needs
SENDSpecial Educational Needs and Disabilities
UNUnited Nations
USUnited States

References

  1. Accardo, A. L., & Kuder, S. J. (2017). Monitoring student learning in algebra. Mathematics Teaching in the Middle School, 22(6), 352–359. [Google Scholar] [CrossRef]
  2. Andrade, H. L. (2010). Summing up and moving forward: Key challenges and future directions for research and development in formative assessment. In H. L. Andrade, & G. J. Cizek (Eds.), Handbook of formative assessment (pp. 344–352). Routledge. [Google Scholar]
  3. Andrade, H. L., Bennett, R. E., & Cizek, G. J. (Eds.). (2019). Handbook of formative assessment in the disciplines. Routledge. [Google Scholar] [CrossRef]
  4. Asenova, M., Del Zozzo, A., & Santi, G. (2023). Unfolding teachers’ interpretative knowledge into semiotic interpretative knowledge to understand and improve mathematical learning in an inclusive perspective. Education Sciences, 13(1), 65. [Google Scholar] [CrossRef]
  5. Bennett, R. E. (2011). Formative assessment: A critical review. Assessment in Education: Principles, Policy & Practice, 18(1), 5–25. [Google Scholar] [CrossRef]
  6. Black, P., & Wiliam, D. (1998). Assessment and classroom learning. Assessment in Education: Principles, Policy & Practice, 5(1), 7–74. [Google Scholar] [CrossRef]
  7. Borsch, F. (2018). Alle lernen gemeinsam! Pädagogisch-psychologisches Wissen für den inklusiven Unterricht. V&R eLibrary. Vandenhoeck & Ruprecht. [Google Scholar] [CrossRef]
  8. Calhoon, M. B. (2008). Curriculum-based measurement for mathematics at the high school level: What we do not know … What we need to know. Assessment for Effective Intervention, 33(4), 234–239. [Google Scholar] [CrossRef]
  9. Decristan, J., Klieme, E., Kunter, M., Hochweber, J., Büttner, G., Fauth, B., Hondrich, A. L., Rieser, S., Hertel, S., & Hardy, I. (2015). Embedded formative assessment and classroom process quality: How do they interact in promoting science understanding? American Educational Research Journal, 52(6), 1133–1159. [Google Scholar] [CrossRef]
  10. Dolin, J., Black, P., Harlen, W., & Tiberghien, A. (2018). Exploring relations between formative and summative assessment. In J. Dolin, & R. Evans (Eds.), Contributions from science education research. Transforming assessment (Vol. 4, pp. 53–80). Springer International Publishing. [Google Scholar] [CrossRef]
  11. Federal Ministry of Education and Research. (2019). Bekanntmachung: Richtlinie zur förderung von projekten zum thema “förderbezogene diagnostik in der inklusiven bildung”. Bundesministerium für Bildung und Forschung. Available online: https://www.bmbf.de/bmbf/shareddocs/bekanntmachungen/de/2019/12/2752_bekanntmachung (accessed on 5 May 2025).
  12. Gebhardt, M., Krammer, M., Schwab, S., Rossmann, P., Gasteiger Klicpera, B., & Klatten, S. (2013). What is behind the diagnosis of learning disability in Austrian schools? An empirical evaluation of the results of the diagnostic process. International Journal of Special Education, 28(3), 160–166. [Google Scholar]
  13. Gersten, R., Chard, D. J., Jayanthi, M., Baker, S. K., Morphy, P., & Flojo, J. (2009). Mathematics instruction for students with learning disabilities: A meta-analysis of instructional components. Review of Educational Research, 79(3), 1202–1242. [Google Scholar] [CrossRef]
  14. Gikandi, J. W., Morrow, D., & Davis, N. E. (2011). Online formative assessment in higher education: A review of the literature. Computers & Education, 57(4), 2333–2351. [Google Scholar] [CrossRef]
  15. Göransson, K., & Nilholm, C. (2014). Conceptual diversities and empirical shortcomings—A critical analysis of research on inclusive education. European Journal of Special Needs Education, 29(3), 265–280. [Google Scholar] [CrossRef]
  16. Grob, R., Holmeier, M., & Labudde, P. (2021). Analysing formal formative assessment activities in the context of inquiry at primary and upper secondary school in Switzerland. International Journal of Science Education, 43(3), 407–427. [Google Scholar] [CrossRef]
  17. Grosche, M. (2015). Was ist Inklusion? Ein Diskussions- und Positionsartikel zur Definition von Inklusion aus Sicht der empirischen Bildungsforschung. In P. Kuhl, P. Stanat, B. Lütje-Klose, C. Gresch, H. A. Pant, & M. Prenzel (Eds.), Inklusion von schülerinnen und schülern mit sonderpädagogischem förderbedarf in schulleistungserhebungen (pp. 17–39). Springer VS Wiesbaden. [Google Scholar]
  18. Hartmeyer, R., Stevenson, M. P., & Bentsen, P. (2018). A systematic review of concept mapping-based formative assessment processes in primary and secondary science education. Assessment in Education: Principles, Policy & Practice, 25(6), 598–619. [Google Scholar] [CrossRef]
  19. Hattie, J. (2012). Visible learning for teachers: Maximizing impact on learning. Routledge. [Google Scholar]
  20. Hattie, J., & Timperley, H. (2007). The power of feedback. Review of Educational Research, 77(1), 81–112. [Google Scholar] [CrossRef]
  21. Häsel-Weide, U. (2017). Inklusiven Mathematikunterricht gestalten. In J. Leuders, T. Leuders, S. Prediger, & S. Ruwisch (Eds.), Konzepte und Studien zur Hochschuldidaktik und Lehrerbildung Mathematik. Mit Heterogenität im Mathematikunterricht umgehen lernen (pp. 17–28). Springer Fachmedien Wiesbaden. [Google Scholar] [CrossRef]
  22. Heritage, M. (2007). Formative assessment: What do teachers need to know and do? Phi Delta Kappan, 89(2), 140–145. [Google Scholar] [CrossRef]
  23. Hong, Q. N., Pluye, P., Fabregues, S., Bartlett, G., Boardman, F., Cargo, M., Dagenais, P., Gagnon, M.-P., Griffiths, F., Nicolau, B., O’Cathain, A., Rousseau, M.-C., & Vedel, I. (2018). Mixed methods appraisal tool (MMAT) version 2018. McGill University Department of Family Medicine. Available online: http://mixedmethodsappraisaltoolpublic.pbworks.com/w/file/fetch/127916259/MMAT_2018_criteria-manual_2018-08-01_ENG.pdf (accessed on 5 May 2025).
  24. Hoth, J., Döhrmann, M., Kaiser, G., Busse, A., König, J., & Blömeke, S. (2016). Diagnostic competence of primary school mathematics teachers during classroom situations. ZDM, 48(1–2), 41–53. [Google Scholar] [CrossRef]
  25. Hwang, J. (2016). An examination of error patterns associated with middle school students’ solution pathways when solving fraction computation involving addition [Special Education Dissertation for the degree of Doctor of Philosophy, The Pennsylvania State University]. Available online: https://etda.libraries.psu.edu/files/final_submissions/12513 (accessed on 5 May 2025).
  26. Ingenkamp, K., & Lissmann, U. (2008). Lehrbuch der pädagogischen Diagnostik (6. Auflage). Beltz Pädagogik. Beltz Verlag. [Google Scholar]
  27. Jütte, H., & Lüken, M. M. (2021). Mathematik inklusiv unterrichten—Ein forschungsüberblick zum aktuellen stand der entwicklung einer inklusiven didaktik für den mathematikunterricht in der grundschule. Zeitschrift Für Grundschulforschung, 14(1), 31–48. [Google Scholar] [CrossRef]
  28. Katsiyannis, A., & Prillaman, D. (1990). Teaching math using regular curricula. Teaching Exceptional Children, (23), 26–29. [Google Scholar] [CrossRef]
  29. Kingston, N., & Nash, B. (2011). Formative assessment: A meta-analysis and a call for research. Educational Measurement: Issues and Practice, 30(4), 28–37. [Google Scholar] [CrossRef]
  30. Kollosche, D., Marcone, R., Knigge, M., Penteado, M. G., & Skovsmose, O. (2019). Inclusive mathematics education. Springer International Publishing. [Google Scholar] [CrossRef]
  31. Kültür, Y. Z., & Kutlu, M. O. (2021). The effect of formative assessment on high school students mathematics achievement and attitudes. Journal of Pedagogical Research, 5(4), 155–171. [Google Scholar] [CrossRef]
  32. Lee, H., Chung, H. Q., Zhang, Y., Abedi, J., & Warschauer, M. (2020). The effectiveness and features of formative assessment in US K-12 education: A systematic review. Applied Measurement in Education, 33(2), 124–140. [Google Scholar] [CrossRef]
  33. Leiss, D., & Tropper, N. (2014). Umgang mit heterogenität im mathematikunterricht. Springer. [Google Scholar] [CrossRef]
  34. Lui, A. M., & Andrade, H. L. (2022). The next black box of formative assessment: A model of the internal mechanisms of feedback processing. Frontiers in Education, 7, 751548. [Google Scholar] [CrossRef]
  35. Miller, S. P., & Mercer, C. D. (1997). Educational aspects of mathematics disabilities. Journal of Learning Disabilities, 30(1), 47–56. [Google Scholar] [CrossRef] [PubMed]
  36. Mitchell, D. (2014). What really works in special and inclusive education: Using evidence-based teaching strategies (2nd ed.). Routledge Taylor & Francis Group. [Google Scholar]
  37. Morris, R., Perry, T., & Wardle, L. (2021). Formative assessment and feedback for learning in higher education: A systematic review. Review of Education, 9(3), e3292. [Google Scholar] [CrossRef]
  38. Moser Opitz, E. (2005). Lernschwierigkeiten mathematik in klasse 5 und 8: Eine empirische untersuchung zu fehlenden mathematischen Basiskompetenzen. Vierteljahresschrift Für Heilpädagogik Und Ihre Nachbargebiete, 74(2), 113–128. [Google Scholar]
  39. Page, M. J., McKenzie, J. E., Bossuyt, P. M., Boutron, I., Hoffmann, T. C., Mulrow, C. D., Shamseer, L., Tetzlaff, J. M., Akl, E. A., Brennan, S. E., Chou, R., Glanville, J., Grimshaw, J. M., Hróbjartsson, A., Lalu, M. M., Li, T., Loder, E. W., Mayo-Wilson, E., McDonald, S., … Moher, D. (2021). The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. Systematic Reviews, 10(1), 89. [Google Scholar] [CrossRef]
  40. Parsons, S. A., Vaughn, M., Scales, R. Q., Gallagher, M. A., Parsons, A. W., Davis, S. G., Pierczynski, M., & Allen, M. (2018). Teachers’ instructional adaptations: A research synthesis. Review of Educational Research, 88(2), 205–242. [Google Scholar] [CrossRef]
  41. Poch, A. L., van Garderen, D., & Scheuermann, A. M. (2015). Students’ understanding of diagrams for solving word problems: A framework for assessing diagram proficiency. Teaching Exceptional Children, 47(3), 153–162. [Google Scholar] [CrossRef]
  42. Prediger, S., & Buró, R. (2024). Fifty ways to work with students’ diverse abilities? A video study on inclusive teaching practices in secondary mathematics classrooms. International Journal of Inclusive Education, 28(2), 124–143. [Google Scholar] [CrossRef]
  43. Rakoczy, K., Pinger, P., Hochweber, J., Klieme, E., Schütze, B., & Besser, M. (2019). Formative assessment in mathematics: Mediated by feedback’s perceived usefulness and students’ self-efficacy. Learning and Instruction, 60, 154–165. [Google Scholar] [CrossRef]
  44. Rakoczy, K., & Schütze, B. (2019). Feedback im Unterricht. In E. Kiel, B. Herzig, U. Maier, & U. Sandfuchs (Eds.), Handbuch unterrichten an allgemeinbildenden schulen (pp. 237–249). Verlag Julius Klinkhardt. [Google Scholar]
  45. Sach, E. (2015). An exploration of teachers’ narratives: What are the facilitators and constraints which promote or inhibit ‘good’ formative assessment practices in schools? Education 3–13, 43(3), 322–335. [Google Scholar] [CrossRef]
  46. Scanlon, R. M. (2013). Improving Individualized Educational Program (IEP) mathematics learning goals for conceptual understanding of order and equivalence of fractions [Educational Leadership Dissertation for the Degree of Doctor of Education, University of Delaware]. Available online: https://www.proquest.com/docview/1443870578?pq-origsite=gscholar&fromopenview=true (accessed on 5 May 2025).
  47. Schmidt, C., & Liebers, K. (2017). Formatives assessment im inklusiven Unterricht—Forschungsstand und erste Befunde. In F. Hellmich, & E. Blumberg (Eds.), Inklusiver unterricht in der grundschule (1st ed., pp. 50–65). Verlag W. Kohlhammer. [Google Scholar]
  48. Schöttler, C. (2019). Deutung dezimaler Beziehungen: Epistemologische und partizipatorische Analysen von dyadischen Interaktionen im inklusiven Mathematikunterricht. Springer Fachmedien Wiesbaden. [Google Scholar] [CrossRef]
  49. Sharma, M. C. (1998). Diagnosis: What is the current agenda? Focus on Learning Problems in Mathematics, 20(1), 26–34. [Google Scholar]
  50. Shavelson, R. J., Young, D. B., Ayala, C. C., Brandon, P. R., Furtak, E. M., Ruiz-Primo, M. A., Tomita, M. K., & Yin, Y. (2008). On the impact of curriculum-embedded formative assessment on learning: A collaboration between curriculum and assessment developers. Applied Measurement in Education, 21(4), 295–314. [Google Scholar] [CrossRef]
  51. Shea, B. J., Reeves, B. C., Wells, G., Thuku, M., Hamel, C., Moran, J., Moher, D., Tugwell, P., Welch, V., Kristjansson, E., & Henry, D. A. (2017). AMSTAR 2: A critical appraisal tool for systematic reviews that include randomised or non-randomised studies of healthcare interventions, or both. BMJ, 358, j4008. [Google Scholar] [CrossRef] [PubMed]
  52. Shute, V. J. (2008). Focus on formative feedback. Review of Educational Research, 78(1), 153–189. [Google Scholar] [CrossRef]
  53. Sortwell, A., Trimble, K., Ferraz, R., Geelan, D. R., Hine, G., Ramirez-Campillo, R., Carter-Thuiller, B., Gkintoni, E., & Xuan, Q. (2024). A systematic review of meta-analyses on the impact of formative assessment on K-12 students’ learning: Toward sustainable quality education. Sustainability, 16(17), 7826. [Google Scholar] [CrossRef]
  54. Spooner, F., Knight, V. F., Browder, D. M., & Smith, B. R. (2012). Evidence-based practice for teaching academics to students with severe developmental disabilities. Remedial and Special Education, 33(6), 374–387. [Google Scholar] [CrossRef]
  55. Stecker, P. M., & Fuchs, L. S. (2000). Effecting superior achievement using curriculum-based measurement: The importance of individual progress monitoring. Learning Disabilities Research & Practice, 15(3), 128–134. [Google Scholar]
  56. Sweller, J., Ayres, P., & Kalyuga, S. (2011). The expertise reversal effect. In J. Sweller, P. Ayres, & S. Kalyuga (Eds.), Cognitive load theory (pp. 155–170). Springer. [Google Scholar] [CrossRef]
  57. Torgerson, C. J. (2006). Publication bias: The Achilles’ heel of systematic reviews? British Journal of Educational Studies, 54(1), 89–102. [Google Scholar] [CrossRef]
  58. United Nations. (2006). Convention on the rights of persons with disabilities. Available online: https://www.un.org/development/desa/disabilities/convention-on-the-rights-of-persons-with-disabilities/convention-on-the-rights-of-persons-with-disabilities-2.html (accessed on 5 May 2025).
  59. Wardat, Y., Tashtoush, M. A., Al Ali, R., & Jarrah, A. M. (2023). ChatGPT: A revolutionary tool for teaching and learning mathematics. Eurasia Journal of Mathematics, Science and Technology Education, 19(7), em2286. [Google Scholar] [CrossRef]
Education 15 00577 g001
Figure 1. Search strategy of the systematic review.
Figure 1. Search strategy of the systematic review.
Education 15 00577 g001
Education 15 00577 g002
Figure 2. PRISMA flow diagram of the systematic review for both searches combined.
Figure 2. PRISMA flow diagram of the systematic review for both searches combined.
Education 15 00577 g002
Table 1. Inclusion and exclusion criteria.
Table 1. Inclusion and exclusion criteria.
CriteriumInclusionExclusion
Language1. Published in English or German language.
Type of publication2. Journal article, dissertation, or book chapter.
Topic3. Focus on either formative assessment in general or on diagnostics or feedback in particular.1. Focus on peer tutoring.
2. Validation of specific digital tools or technology-based interventions.
Setting4. Located in an inclusive school environment.
5. Focus on teaching mathematics.
6. Addressing students in secondary education.		3. Focus on one disability, giftedness, or clinical diagnostics.
4. Focus on teachers or career changers.
5. Focus on English language learners.
6. Focus on primary education, preschools, kindergarten, or similar.
7. Focus on tertiary education.
Study
design		7. Either quantitative, qualitative, or theoretical work.8. Psychometric study on test quality/validation or focus on a specific test.
9. Single-case design studies.
Table 2. Summary of the 14 articles included in this review.
Table 2. Summary of the 14 articles included in this review.
ReferenceCountryStudy TypeInclusionPopulationGrade LevelAge of ParticipantsMathematical TopicIndependent VariablesDependent VariablesFormative Assessment (FA)/Diagnostics (D)/Feedback (F)
(Katsiyannis & Prillaman, 1990)USATheoreticalArticle that argues in favor of including students with mild disabilities in the regular education curriculum. D
(Miller & Mercer, 1997)USATheoreticalThe inclusion movement and student diversity are discussed.Students with learning disabilities FA
(Sharma, 1998)USATheoreticalThe article explicitly addresses all learners. D
(Poch et al., 2015)USATheoreticalFocus on students with learning disabilities, but the authors emphasize that the framework may be useful for students without disabilities as well.Students with learning disabilities4, 5, and 7 Diagrams D
(Accardo & Kuder, 2017)USATheoreticalMixed-ability classrooms. 9 Algebra FA
(Stecker & Fuchs, 2000)USAQuantitativeStudents with disabilities in either resource or self-contained settings.Students with mild to moderate disabilities2–86–15 years Instructional adjustments based on curriculum-based measurement dataAchievementFA
(Moser Opitz, 2005)SwitzerlandQuantitativeStudents from regular secondary school classes (“Hauptschule”) and classes for learning-disabled students or integrative classes.Students with arithmetic weakness5 and 812–16.60 yearsSchool subject matter of the first 4 yearsIQ, grade level, and arithmetic weaknessMathematics achievementD
(Gebhardt et al., 2013)AustriaQuantitativeStudents with learning disabilities from mostly integrative classes in regular schools.Students with special educational needs (mostly learning disabilities)511.86, on averageArithmeticGender, age, number of books in household, cognitive abilities (IQ), reading comprehension, decoding speed of words, correctly written graphemes, basic arithmetic skills, and degree of reported social integration in class and emotional integration in schoolSpecial educational needs diagnosisD
(Hwang, 2016)USAQuantitativeStudents from an inclusive and self-contained classroom.Students with individualized educational programs; students with mathematics learning disabilities7 and 8 Addition of fractionsInstruction type, achievement group, grade, and measurement typeConceptual understanding, procedural skills, word problems, contextualized problems, and mixtures thereofD
(Scanlon, 2013)USATheoretical/quantitativeStudents from regular and inclusion classes, students with disabilities, and students who failed the state assessment.Students with severe disabilities, gifted students, regular students, students with disabilities, and students who failed the state assessment5–8 Fractions D
(Asenova et al., 2023)ItalyQualitativeFollowing a broad understanding to consider the starting point of each student.Students with special learning disordersLower and upper secondary school students Mathematical symbols and signs D
(Calhoon, 2008)USAReviewHigh school resource classrooms.Students with mathematics disabilities9–12 FA, F
(Gersten et al., 2009)USAMeta-analysisStudies had to contain more than 50% of students with learning disabilities if results for students with learning disabilities were not reported separately. This means that the authors also included studies that were not solely conducted on students with learning disabilities, thus exhibiting heterogeneity, which makes this publication feasible for inclusion in our review.Students with learning disabilities “School-aged children” Approaches to instruction and/or curriculum design, providing ongoing formative assessment data and feedback to teachers on students’ mathematics performance, providing data and feedback to students with learning disabilities on their mathematics performance, and peer-assisted mathematics instructionOperations, word problems, fractions, algebra, and general math proficiencyFA, F
(Spooner et al., 2012)USAReviewAmong others, general education classrooms, special education settings, and community settings.Students with severe developmental disabilities Task analytic instruction, discrete responses, and time delayAcquisition of a targeted skill in mathematics, literacy, or science educationF
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Töllner, F.; Kuhl, P.; Besser, M. Formative Assessment in Inclusive Mathematics Education in Secondary Schools: A Systematic Review. Educ. Sci. 2025, 15, 577. https://doi.org/10.3390/educsci15050577

AMA Style

Töllner F, Kuhl P, Besser M. Formative Assessment in Inclusive Mathematics Education in Secondary Schools: A Systematic Review. Education Sciences. 2025; 15(5):577. https://doi.org/10.3390/educsci15050577

Chicago/Turabian Style

Töllner, Fynn, Poldi Kuhl, and Michael Besser. 2025. "Formative Assessment in Inclusive Mathematics Education in Secondary Schools: A Systematic Review" Education Sciences 15, no. 5: 577. https://doi.org/10.3390/educsci15050577

APA Style

Töllner, F., Kuhl, P., & Besser, M. (2025). Formative Assessment in Inclusive Mathematics Education in Secondary Schools: A Systematic Review. Education Sciences, 15(5), 577. https://doi.org/10.3390/educsci15050577

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop