Optimizing University Admission Processes for Improved Educational Administration Through Feature Selection Algorithms: A Case Study in Engineering Education
Abstract
1. Introduction
1.1. Contributions and Limitations of the Study
- Validation of ML for the analysis of the university admission system.
- Incorporation of concept drift management and outlier handling in the data preprocessing stage.
- Establishment of precision as a performance measure for the models.
- Development of a procedure to determine the weights of selection criteria.
1.2. Literature Related to Machine Learning for Optimizing University Selection
1.2.1. Reducing Bias in Data Selection
1.2.2. Measuring Performance in Predictive Models
1.2.3. Distortion Due to Outliers
1.2.4. Feature Selection in Knowledge Mining
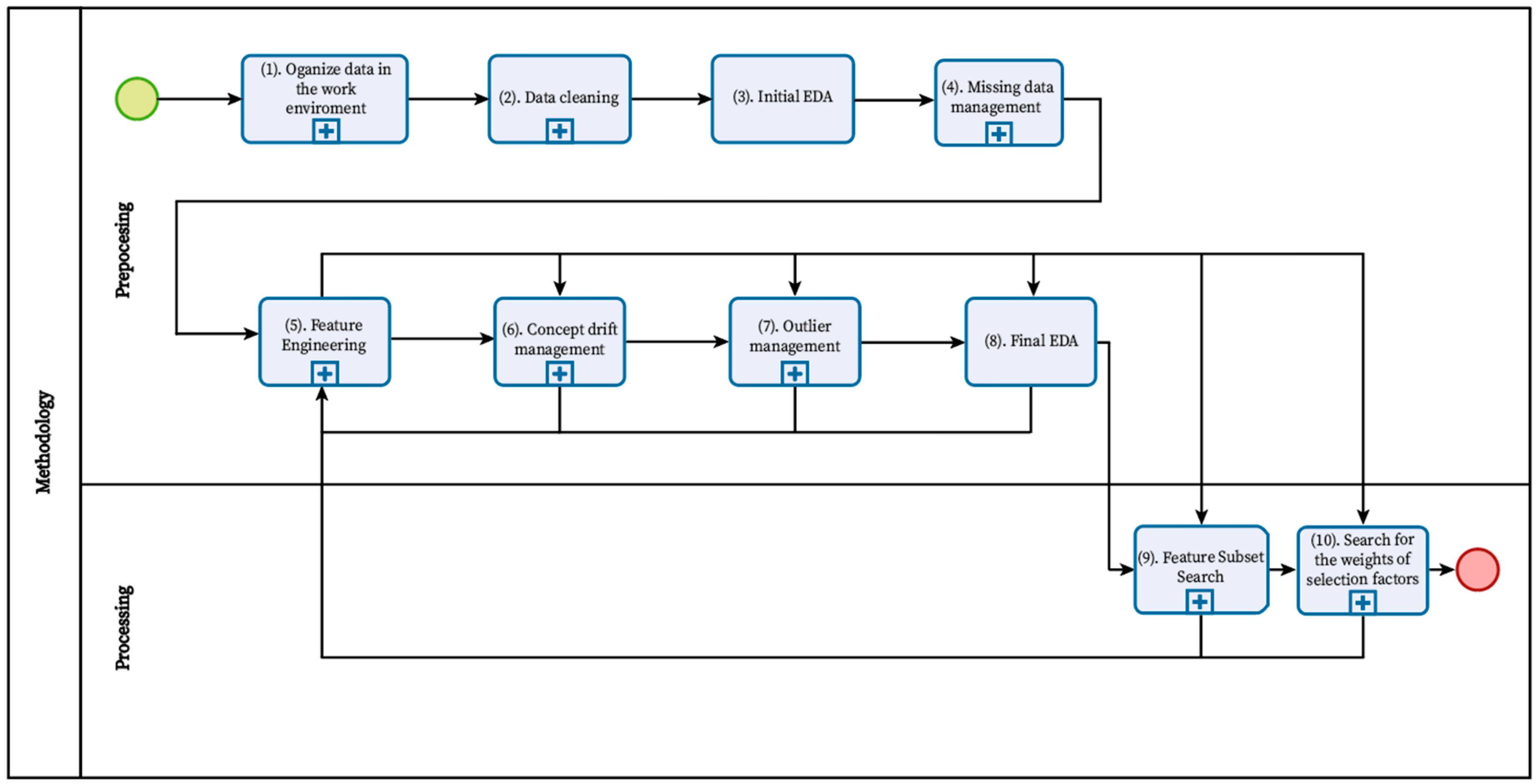
2. Methodology
2.1. Preprocessing Stage
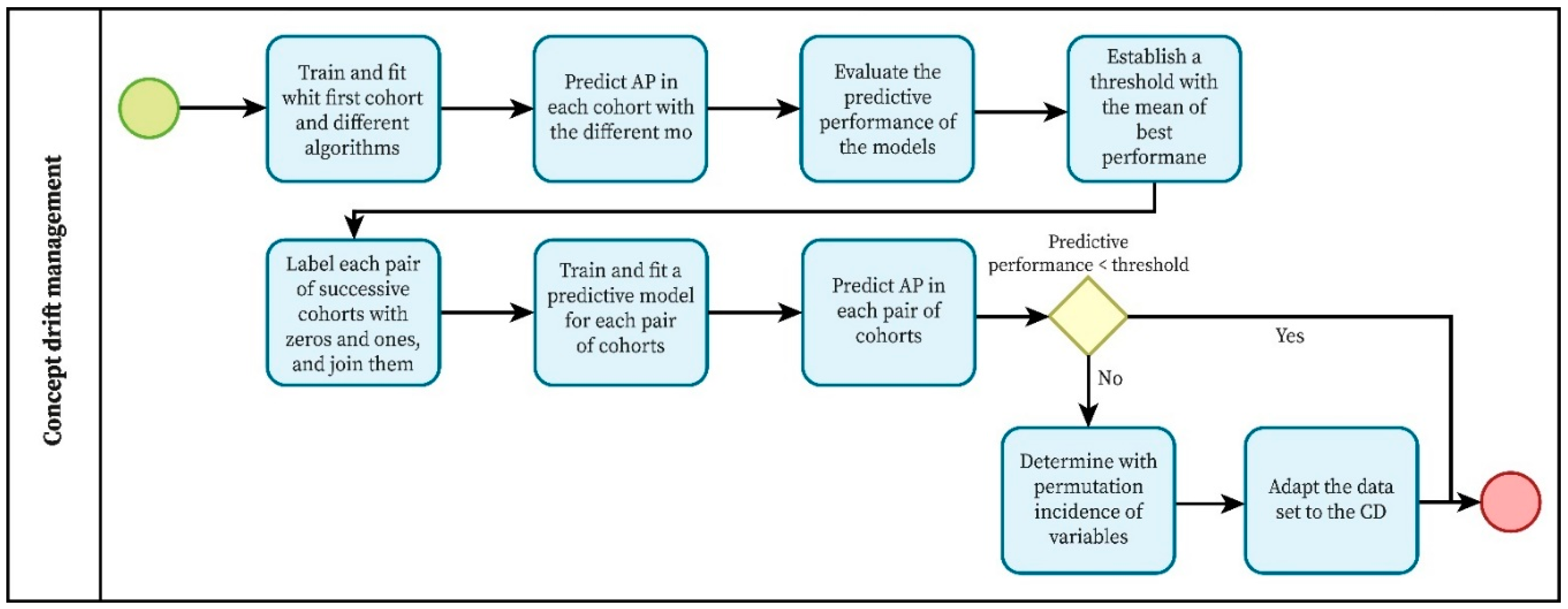
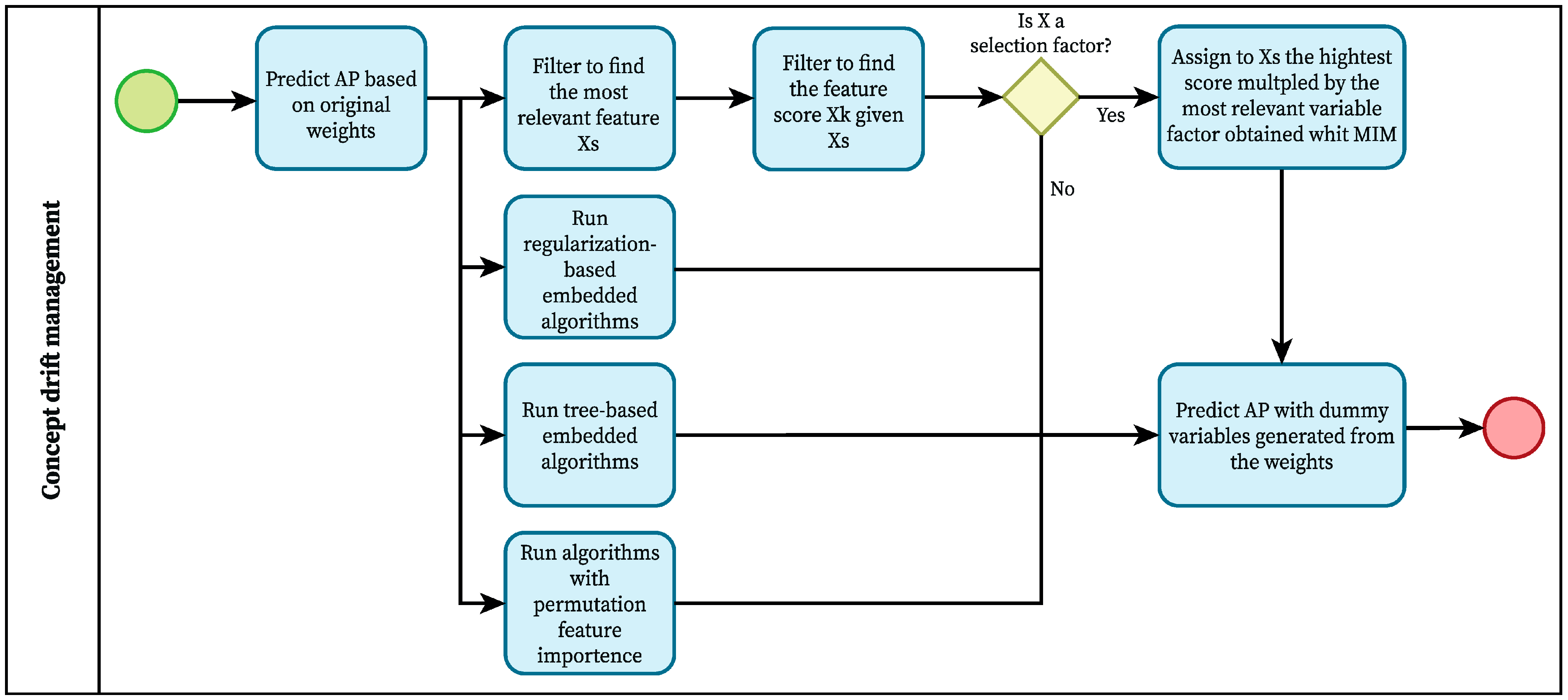
2.1.1. Concept Drift Management
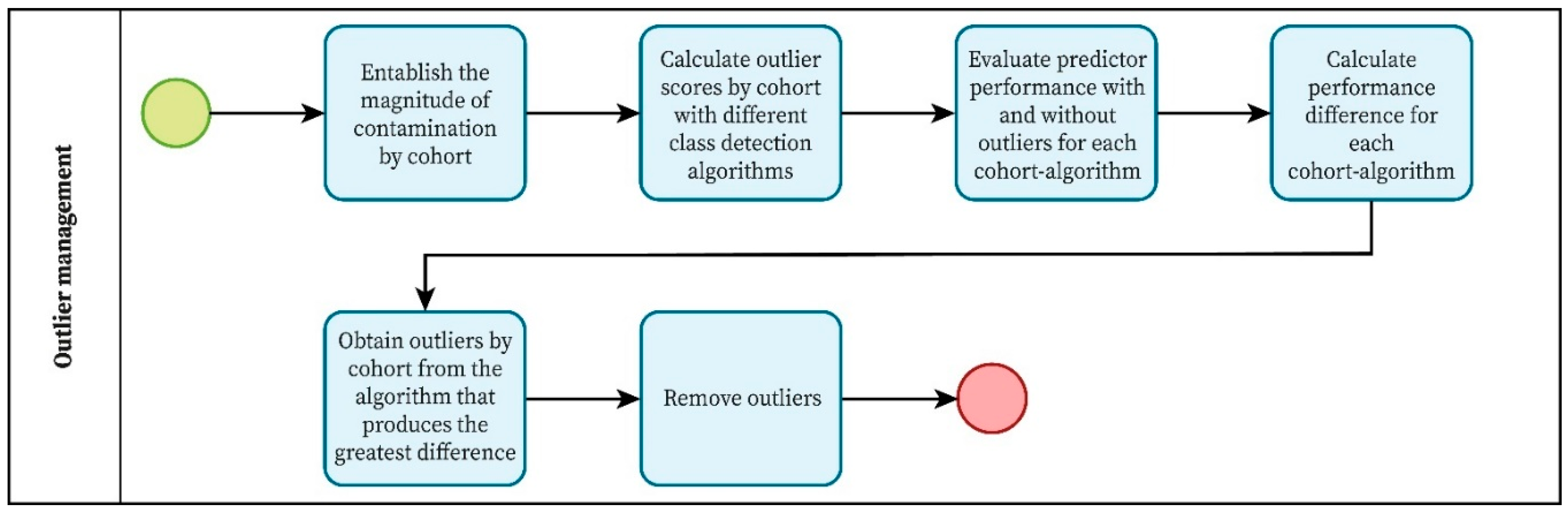
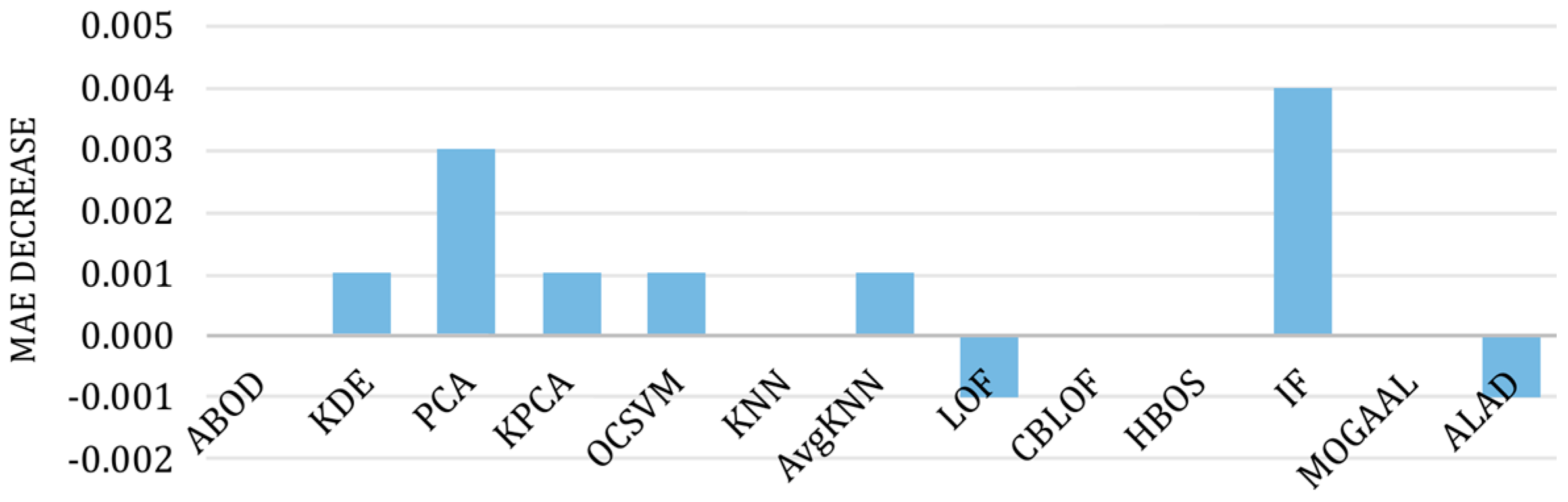
2.1.2. Outlier Management
2.2. Processing Stage
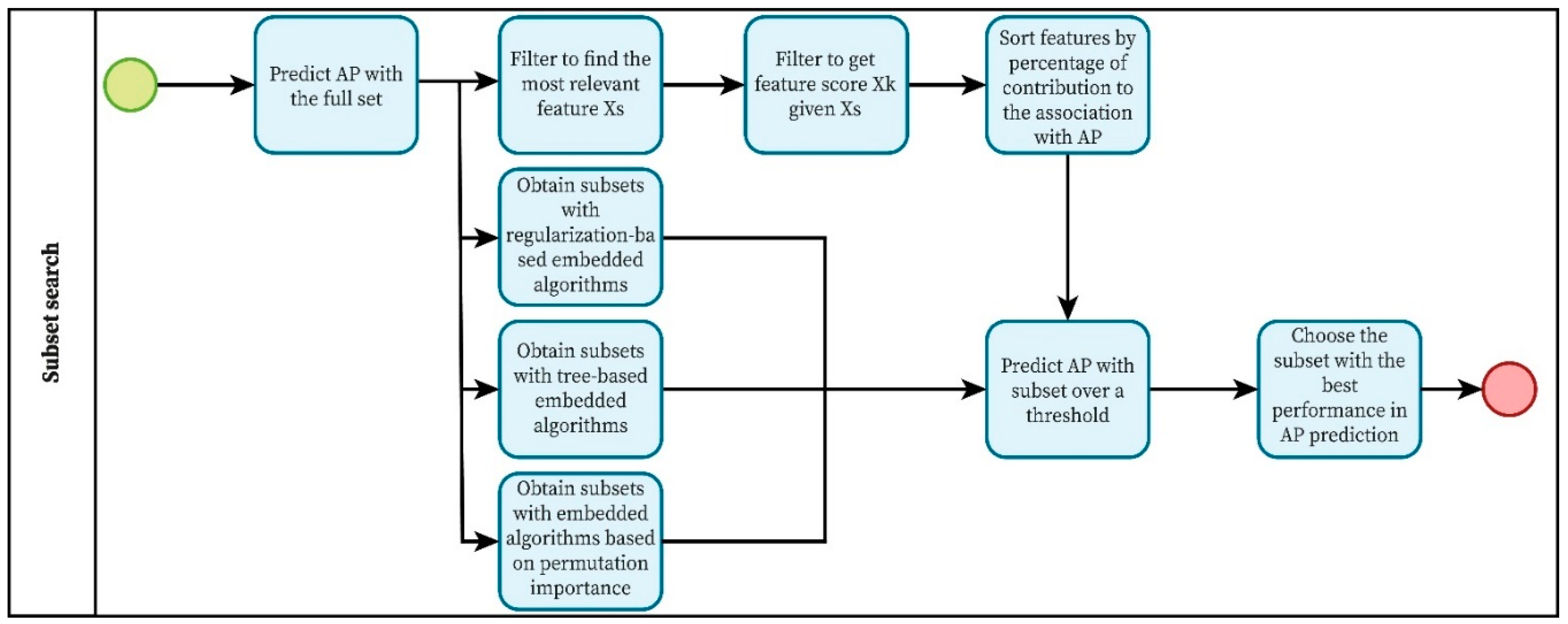
2.2.1. Feature Subset Search
2.2.2. Search for the Selection Criteria Weight
3. Results
3.1. Preprocessing
3.2. Processing
3.2.1. Prediction Without Feature Selection
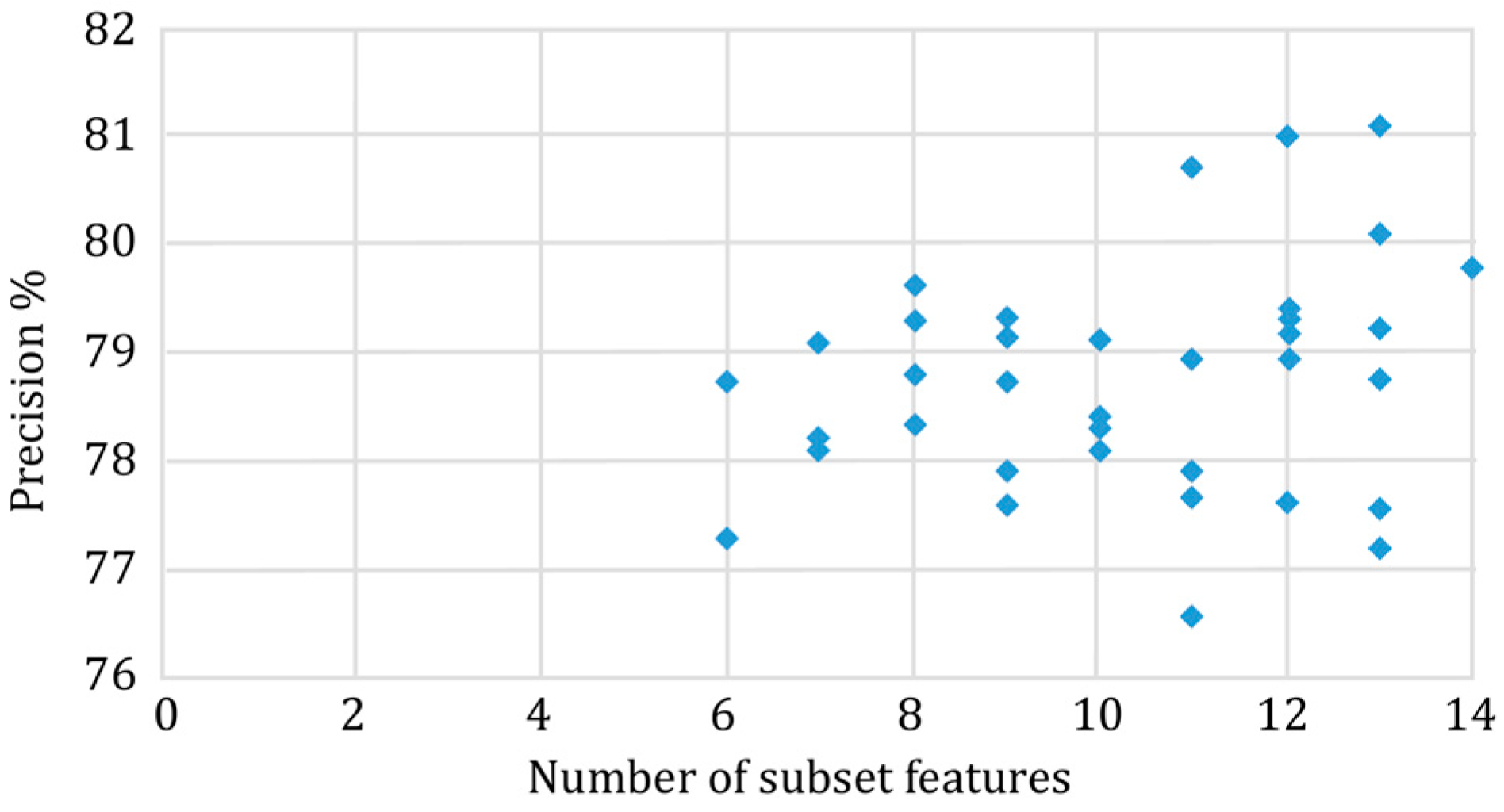
3.2.2. Optimal Feature Subset
3.2.3. Ranking of Selection Criteria
4. Discussions
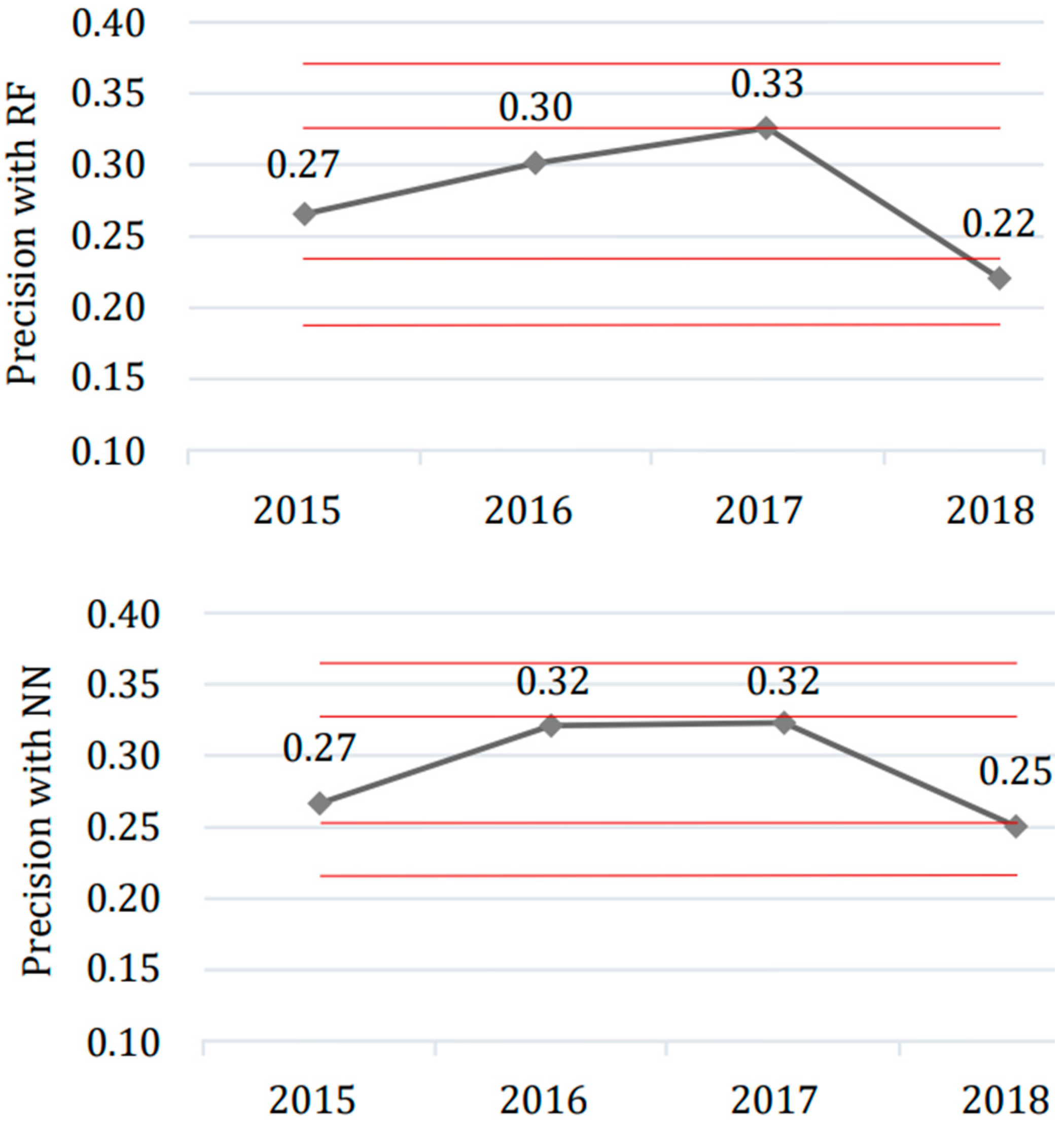
4.1. Improvement in Precision Through Concept Drift and Outlier Management
4.2. Validity of the Optimal Subset of Features
4.3. Predictive Ability with Obtained Weights
4.4. Methodological Justification and Data Validity in the Optimization of the Admission Process
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notations
| FS | Feature selection |
| CV | Cross-validation |
| CD | Concept drift |
| SC | Selection criteria |
| AP | Academic performance |
| Pearson coefficient | |
| ML | Machine learning |
| NN | Neural networks |
| DE | Demographic |
| AC | Academic |
| SE | Socioeconomic |
| kNN | k-nearest neighbors |
| MIM | Mutual information maximization |
| JMI | Joint mutual information |
| CFR | Composition of feature relevancy |
| MRI | Maximal relevance and maximal independence |
| EDA | Exploratory data analysis |
| CMIM | Conditional mutual information maximization criterion |
| HBGB | Histogram-based gradient boosting tree |
| DCSF | Dynamic change in the selected feature |
| MIFS | Mutual information-based feature selection |
| CIFE | Conditional infomax feature extraction |
| IWFS | Interaction weight-based feature selection |
| mRMR | Minimal redundancy maximal relevance |
References
- Abdel-Basset, M., Ding, W., & El-Shahat, D. (2021). A hybrid Harris Hawks optimization algorithm with simulated annealing for feature selection. Artificial Intelligence Review, 54(1), 593–637. [Google Scholar] [CrossRef]
- Adeyemo, A. B., & Kuyoro, S. O. (2013). Investigating the effect of students socio-economic/family background on students academic performance in tertiary institutions using decision tree algorithm. Journal of Life & Physical Sciences, 4(2), 61–78. Available online: https://www.researchgate.net/publication/370205648_Investigating_the_Effect_of_Students_Socio-EconomicFamily_Background_on_Students_Academic_Performance_in_Tertiary_Institutions_using_Decision_Tree_Algorithm (accessed on 10 October 2024).
- Affendey, L., Paris, I., Mustapha, N., Sulaiman, M., & Muda, Z. (2010). Ranking of influencing factors in predicting students’ academic performance. Information Technology Journal, 9(4), 832–837. [Google Scholar] [CrossRef][Green Version]
- Aguayo-Hernández, C. H., Sánchez Guerrero, A., & Vázquez-Villegas, P. (2024). The learning assessment process in higher education: A grounded theory approach. Education Sciences, 14(9), 984. [Google Scholar] [CrossRef]
- Alalawi, K., Athauda, R., & Chiong, R. (2024). An extended learning analytics framework integrating machine learning and pedagogical approaches for student performance prediction and intervention. International Journal of Artificial Intelligence in Education, 1–49. [Google Scholar] [CrossRef]
- Albreiki, B., Zaki, N., & Alashwal, H. (2021). A systematic literature review of student’ performance prediction using machine learning techniques. Education Sciences, 11(9), 552. [Google Scholar] [CrossRef]
- Al-Okaily, M., Magatef, S., Al-Okaily, A., & Shehab Shiyyab, F. (2024). Exploring the factors that influence academic performance in Jordanian higher education institutions. Heliyon, 10(13), e33783. [Google Scholar] [CrossRef]
- Amini, F., & Hu, G. (2021). A two-layer feature selection method using genetic algorithm and elastic net. Expert Systems with Applications, 166, 114072. [Google Scholar] [CrossRef]
- Anaconda. (2024). The operating system for AI. Available online: https://www.anaconda.com/ (accessed on 10 October 2024).
- Battiti, R. (1994). Using mutual information for selecting features in supervised neural net learning. IEEE Transactions on Neural Networks, 5(4), 537–550. [Google Scholar] [CrossRef]
- Chorev, S., Tannor, P., Israel, D. B., Bressler, N., Gabbay, I., Hutnik, N., Liberman, J., Perlmutter, M., Romanyshyn, Y., & Rokach, L. (2022). Deepchecks: A library for testing and validating machine learning models and data. Journal of Machine Learning Research, 23(285), 1–6. Available online: http://jmlr.org/papers/v23/22-0281.html (accessed on 10 October 2024).
- Contreras, L. E., Fuentes, H. J., & Rodríguez, J. I. (2020). Academic performance prediction by machine learning as a success/failure indicator for engineering students. Formación Universitaria, 13(5), 233–246. [Google Scholar] [CrossRef]
- Cunningham, P., & Delany, S. J. (2021). K-nearest neighbour classifiers—A tutorial. ACM Computing Surveys, 54(6). [Google Scholar] [CrossRef]
- d’Astous, P., & Shore, S. H. (2024). Human capital risk and portfolio choices: Evidence from university admission discontinuities. Journal of Financial Economics, 154, 103793. [Google Scholar] [CrossRef]
- Deepchecks. (2023). Deepchecks documentation. Available online: https://docs.deepchecks.com/en/stable/getting-started/welcome.html (accessed on 10 October 2024).
- Deepika, K., & Sathyanarayana, N. (2022). Relief-F and budget tree random forest based feature selection for student academic performance prediction. International Journal of Intelligent Engineering and Systems, 12(1), 30–39. [Google Scholar] [CrossRef]
- DEMRE. (2022). Instrumentos de acceso, especificaciones y procedimientos. Available online: https://demre.cl/publicaciones/2023/2023-22-06-07-instrumentos-acceso-p2023 (accessed on 10 October 2024).
- Echegaray-Calderon, O. A., & Barrios-Aranibar, D. (2016, October 13–16). Optimal selection of factors using Genetic Algorithms and Neural Networks for the prediction of students’ academic performance. Latin-America Congress on Computational Intelligence (pp. 1–6), Curitiba, Brazil. [Google Scholar] [CrossRef]
- Eshet, Y. (2024). Academic integrity crisis: Exploring undergraduates’ learning motivation and personality traits over five years. Education Sciences, 14(9), 986. [Google Scholar] [CrossRef]
- Espinoza, O., González, L., Sandoval, L., Corradi, B., McGinn, N., & Vera, T. (2024a). The impact of non-cognitive factors on admission to selective universities: The case of Chile. Educational Review, 76(4), 979–995. [Google Scholar] [CrossRef]
- Espinoza, O., Sandoval, L., González, L. E., Corradi, B., McGinn, N., & Vera, T. (2024b). Did free tuition change the choices of students applying for university admission? Higher Education, 87(5), 1317–1337. [Google Scholar] [CrossRef]
- Fleuret, F. (2004). Fast binary feature selection with conditional mutual information. Journal of Machine Learning Research, 5, 1531–1555. [Google Scholar]
- Frías-Blanco, I., Del Campo-Ávila, J., Ramos-Jiménez, G., Morales-Bueno, R., Ortiz-Díaz, A., & Caballero-Mota, Y. (2015). Online and non-parametric drift detection methods based on Hoeffding’s bounds. IEEE Transactions on Knowledge and Data Engineering, 27(3), 810–823. [Google Scholar] [CrossRef]
- Fuertes, G., Vargas Guzman, M., Soto Gomez, I., Witker Riveros, K., Peralta Muller, M. A., & Sabattin Ortega, J. (2015). Project-based learning versus cooperative learning courses in engineering students. IEEE Latin America Transactions, 13(9), 3113–3119. [Google Scholar] [CrossRef]
- Gama, J., Medas, P., Castillo, G., & Rodrigues, P. (2004). Learning with drift detection. Symposium on Artificial Intelligence, 3171, 286–295. [Google Scholar] [CrossRef]
- Gao, W., Hu, L., & Zhang, P. (2018a). Class-specific mutual information variation for feature selection. Pattern Recognition, 79, 328–339. [Google Scholar] [CrossRef]
- Gao, W., Hu, L., Zhang, P., & He, J. (2018b). Feature selection considering the composition of feature relevancy. Pattern Recognition Letters, 112, 70–74. [Google Scholar] [CrossRef]
- Github. (2024). University feature selection library ITMO. Available online: https://github.com/ctlab/ITMO_FS (accessed on 10 October 2024).
- Granger, B. E., & Perez, F. (2021). Jupyter: Thinking and storytelling with code and data. Computing in Science and Engineering, 23(2), 7–14. [Google Scholar] [CrossRef]
- Guo, H., Zhang, S., & Wang, W. (2021). Selective ensemble-based online adaptive deep neural networks for streaming data with concept drift. Neural Networks, 142, 437–456. [Google Scholar] [CrossRef] [PubMed]
- Harsono, S., Utami, E., & Yaqin, A. (2024, February 21). The association rule methods and k-means clustering for optimization mapping of new students admission. International Conference on Artificial Intelligence and Mechatronics System, Bandung, Indonesia. [Google Scholar] [CrossRef]
- Hashmani, M. A., Jameel, S. M., Rehman, M., & Inoue, A. (2020). Concept drift evolution in machine learning approaches: A systematic literature review. International Journal on Smart Sensing and Intelligent Systems, 13(1), 1–16. [Google Scholar] [CrossRef]
- Hilbert, S., Coors, S., Kraus, E., Bischl, B., Lindl, A., Frei, M., Wild, J., Krauss, S., Goretzko, D., & Stachl, C. (2021). Machine learning for the educational sciences. Review of Education, 9(3), e3310. [Google Scholar] [CrossRef]
- Hinojosa, M. F. (2021). Adaptation of the balanced scorecard to Latin American higher education institutions in the context of strategic management: A systematic review with meta-analysis. In International conference of production research-Americas, 1408 CCIS (pp. 125–140). Springer. [Google Scholar] [CrossRef]
- Huang, S. H. (2015). Supervised feature selection: A tutorial. Artificial Intelligence Research, 4(2), 22–37. [Google Scholar] [CrossRef]
- Jeong, Y. S., Shin, K. S., & Jeong, M. K. (2015). An evolutionary algorithm with the partial sequential forward floating search mutation for large-scale feature selection problems. Journal of the Operational Research Society, 66(4), 529–538. [Google Scholar] [CrossRef]
- Li, Y., Li, T., & Liu, H. (2017). Recent advances in feature selection and its applications. Knowledge and Information Systems, 53(3), 551–577. [Google Scholar] [CrossRef]
- Lin, D., & Tang, X. (2006, May 7–13). Conditional infomax learning: An integrated framework for feature extraction and fusion. European Conference on Computer Vision, 3951 LNCS (pp. 68–82), Graz, Austria. [Google Scholar] [CrossRef]
- Lu, J., Liu, A., Dong, F., Gu, F., Gama, J., & Zhang, G. (2019). Learning under concept drift: A review. IEEE Transactions on Knowledge and Data Engineering, 31(12), 2346–2363. [Google Scholar] [CrossRef]
- Marbouti, F., Ulas, J., & Wang, C. H. (2021). Academic and demographic cluster analysis of engineering student success. IEEE Transactions on Education, 64(3), 261–266. [Google Scholar] [CrossRef]
- Matsushita, R. (2024). Toward an ecological view of learning: Cultivating learners in a data-driven society. Educational Philosophy and Theory, 56(2), 116–125. [Google Scholar] [CrossRef]
- Mineduc. (2008). Estudio sobre causas de la deserción universitaria. Available online: https://bibliotecadigital.mineduc.cl/handle/20.500.12365/17988 (accessed on 10 October 2024).
- Palacios, C. A., Reyes-Suárez, J. A., Bearzotti, L. A., Leiva, V., & Marchant, C. (2021). Knowledge discovery for higher education student retention based on data mining: Machine learning algorithms and case study in Chile. Entropy, 23(4), 485. [Google Scholar] [CrossRef]
- Pan, J., Zou, Z., Sun, S., Su, Y., & Zhu, H. (2022). Research on output distribution modeling of photovoltaic modules based on kernel density estimation method and its application in anomaly identification. Solar Energy, 235, 1–11. [Google Scholar] [CrossRef]
- Peng, H., Long, F., & Ding, C. (2005). Feature selection based on mutual information: Criteria of max-dependency, max-relevance, and min-redundancy. IEEE Transactions on Pattern Analysis and Machine Intelligence, 27(8), 1226–1238. [Google Scholar] [CrossRef]
- Pilnenskiy, N., & Smetannikov, I. (2020). Feature selection algorithms as one of the python data analytical tools. Future Internet, 12(3), 54. [Google Scholar] [CrossRef]
- Putpuek, N., Rojanaprasert, N., Atchariyachanvanich, K., & Thamrongthanyawong, T. (2018, June 6–8). Comparative study of prediction models for final gpa score: A case study of rajabhat rajanagarindra university. International Conference on Computer and Information Science (pp. 92–97), Singapore. [Google Scholar] [CrossRef]
- Rachburee, N., & Punlumjeak, W. (2015, October 29–30). A comparison of feature selection approach between greedy, IG-ratio, Chi-square, and mRMR in educational mining. International Conference on Information Technology and Electrical Engineering: Envisioning the Trend of Computer, Information and Engineering (pp. 420–424), Chiang Mai, Thailand. [Google Scholar] [CrossRef]
- Rawal, A., & Lal, B. (2023). Predictive model for admission uncertainty in high education using Naïve Bayes classifier. Journal of Indian Business Research, 15(2), 262–277. [Google Scholar] [CrossRef]
- Shmueli, G., & Koppius, O. R. (2011). Predictive analytics in information systems research. MIS Quarterly, 35(3), 553–572. [Google Scholar] [CrossRef]
- United Nations. (n.d.). Transforming our world: The 2030 agenda for sustainable development. Available online: https://sdgs.un.org/2030agenda (accessed on 8 October 2024).
- Uvidia Fassler, M. I., Cisneros Barahona, A. S., Dumancela Nina, G. J., Samaniego Erazo, G. N., & Villacrés Cevallos, E. P. (2020). Application of knowledge discovery in data bases analysis to predict the academic performance of university students based on their admissions test. In M. Botto-Tobar, J. León-Acurio, A. Díaz Cadena, & P. Montiel Díaz (Eds.), The international conference on advances in emerging trends and technologies, ICAETT 2019 (Vol. 1066, pp. 485–497). Springer. [Google Scholar] [CrossRef]
- Van Rossum, G., & Drake, F. L. (2003). An introduction to python. Network Theory Ltd. [Google Scholar]
- Vargas, M., Alfaro, M., Fuertes, G., Gatica, G., Gutiérrez, S., Vargas, S., Banguera, L., & Durán, C. (2019). CDIO project approach to design polynesian canoes by first-year engineering students. International Journal of Engineering Education, 35(5), 1336–1342. [Google Scholar]
- Vargas, M., Nuñez, T., Alfaro, M., Fuertes, G., Gutierrez, S., Ternero, R., Sabattin, J., Banguera, L., Durán, C., & Peralta, M. A. (2020). A project based learning approach for teaching artificial intelligence to undergraduate students. International Journal of Engineering Education, 36(6), 1773–1782. [Google Scholar]
- Velmurugan, T., & Anuradha, C. (2016). Performance evaluation of feature selection algorithms in educational data mining. Performance Evaluation, 5(2), 131–139. [Google Scholar]
- Venkatesh, B., & Anuradha, J. (2019). A review of feature selection and its methods. Cybernetics and Information Technologies, 19(1), 3–26. [Google Scholar] [CrossRef]
- Vergara-Díaz, G., & Peredo-López, H. (2017). Relación del desempeño académico de estudiantes de primer año de universidad en Chile y los instrumentos de selección para su ingreso. Revista Educación, 41(2), 95–104. [Google Scholar] [CrossRef]
- Wainer, J., & Cawley, G. (2021). Nested cross-validation when selecting classifiers is overzealous for most practical applications. Expert Systems with Applications, 182, 115222. [Google Scholar] [CrossRef]
- Wan, J., Chen, H., Li, T., Huang, W., Li, M., & Luo, C. (2022). R2CI: Information theoretic-guided feature selection with multiple correlations. Pattern Recognition, 127, 108603. [Google Scholar] [CrossRef]
- Wang, J., Wei, J. M., Yang, Z., & Wang, S. Q. (2017). Feature selection by maximizing independent classification information. IEEE Transactions on Knowledge and Data Engineering, 29(4), 828–841. [Google Scholar] [CrossRef]
- Wang, L., Jiang, S., & Jiang, S. (2021). A feature selection method via analysis of relevance, redundancy, and interaction. Expert Systems with Applications, 183, 115365. [Google Scholar] [CrossRef]
- Webb, G. I., Hyde, R., Cao, H., Nguyen, H. L., & Petitjean, F. (2016). Characterizing concept drift. Data Mining and Knowledge Discovery, 30(4), 964–994. [Google Scholar] [CrossRef]
- Williams, D. (2021). Imaginative constraints and generative models. Australasian Journal of Philosophy, 99(1), 68–82. [Google Scholar] [CrossRef]
- Wu, X., & Wu, J. (2020). Criteria evaluation and selection in non-native language MBA students admission based on machine learning methods. Journal of Ambient Intelligence and Humanized Computing, 11(9), 3521–3533. [Google Scholar] [CrossRef]
- Xu, S., & Wang, J. (2017). Dynamic extreme learning machine for data stream classification. Neurocomputing, 238, 433–449. [Google Scholar] [CrossRef]
- Yang, H. H., & Moody, J. (1999). Data visualization and feature selection: New algorithms for nongaussian data. Advances in Neural Information Processing Systems, 12, 687–693. [Google Scholar]
- Yang, Z., Al-Dahidi, S., Baraldi, P., Zio, E., & Montelatici, L. (2020). A novel concept drift detection method for incremental learning in nonstationary environments. IEEE Transactions on Neural Networks and Learning Systems, 31(1), 309–320. [Google Scholar] [CrossRef]
- Yarkoni, T., & Westfall, J. (2017). Choosing prediction over explanation in psychology: Lessons from machine learning. Perspectives on Psychological Science, 12(6), 1100–1122. [Google Scholar] [CrossRef]
- Zeng, Z., Zhang, H., Zhang, R., & Yin, C. (2015). A novel feature selection method considering feature interaction. Pattern Recognition, 48(8), 2656–2666. [Google Scholar] [CrossRef]
- Zhao, Y., Nasrullah, Z., & Li, Z. (2019). PyOD: A python toolbox for scalable outlier detection. Journal of Machine Learning Research, 20(96), 1–7. Available online: http://jmlr.org/papers/v20/19-011.html (accessed on 10 October 2024).
- Zhou, X., Lo Faro, W., Zhang, X., & Arvapally, R. S. (2019). A framework to monitor machine learning systems using concept drift detection. International Conference Business Information Systems, 353, 218–231. [Google Scholar] [CrossRef]
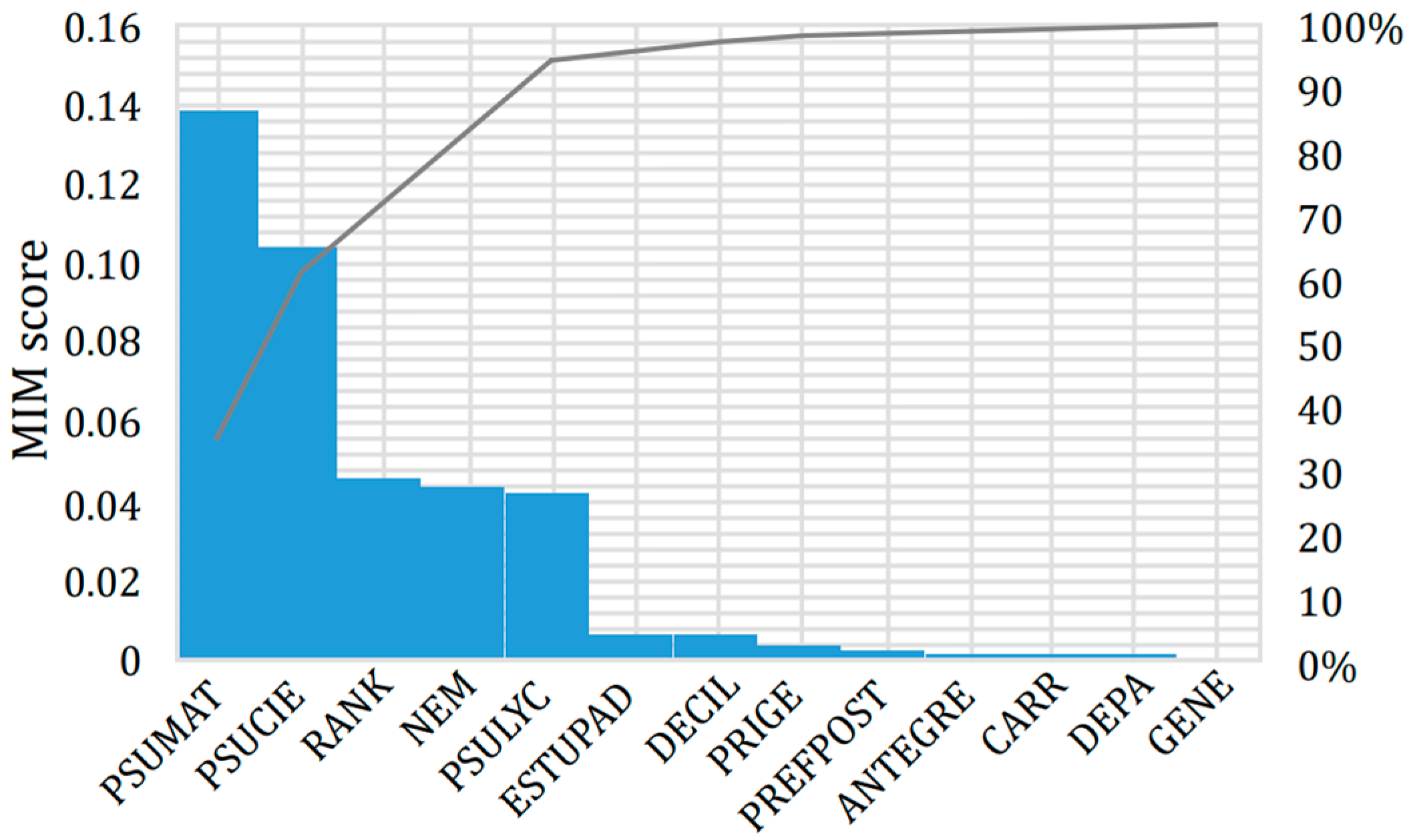
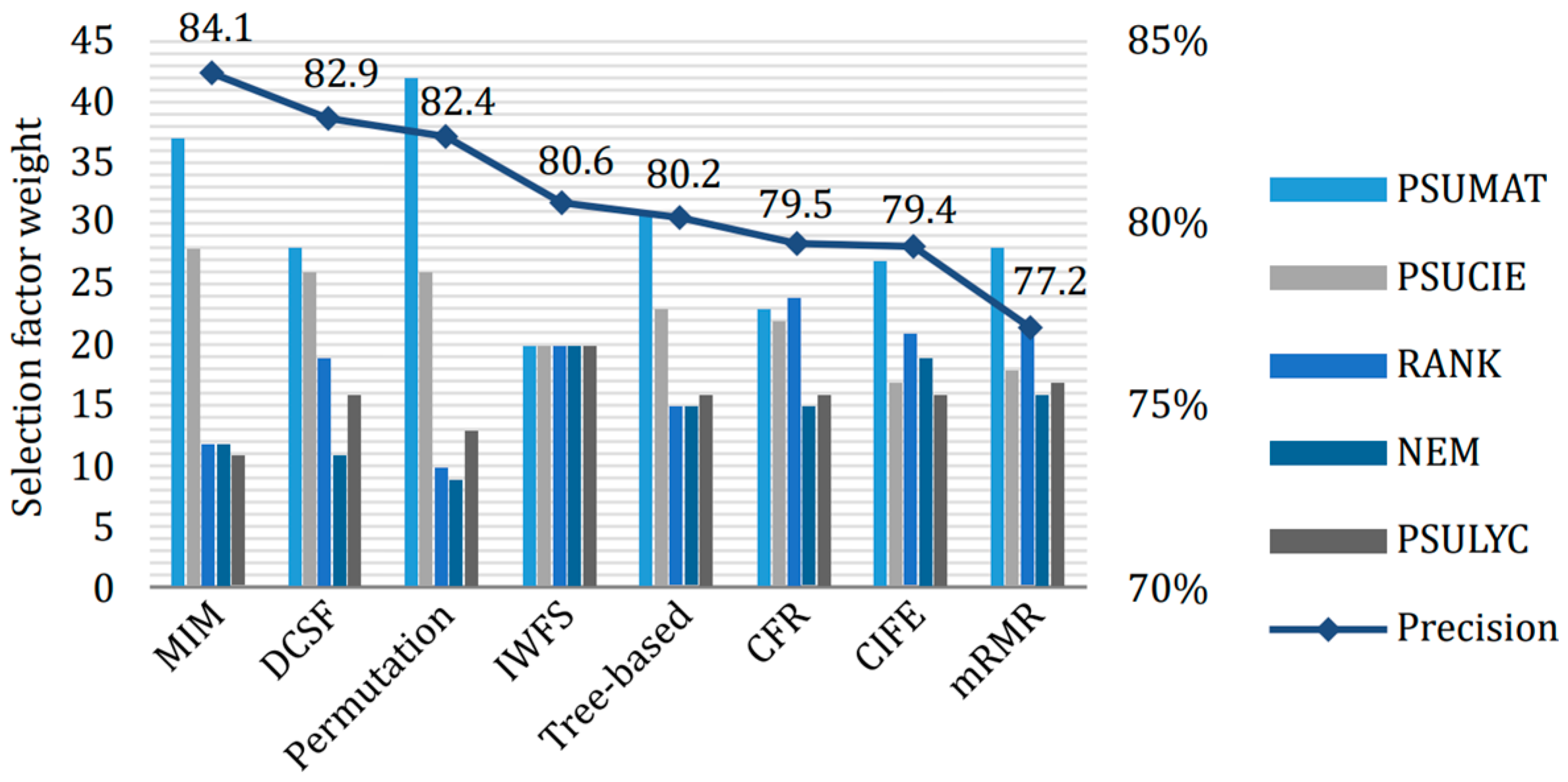
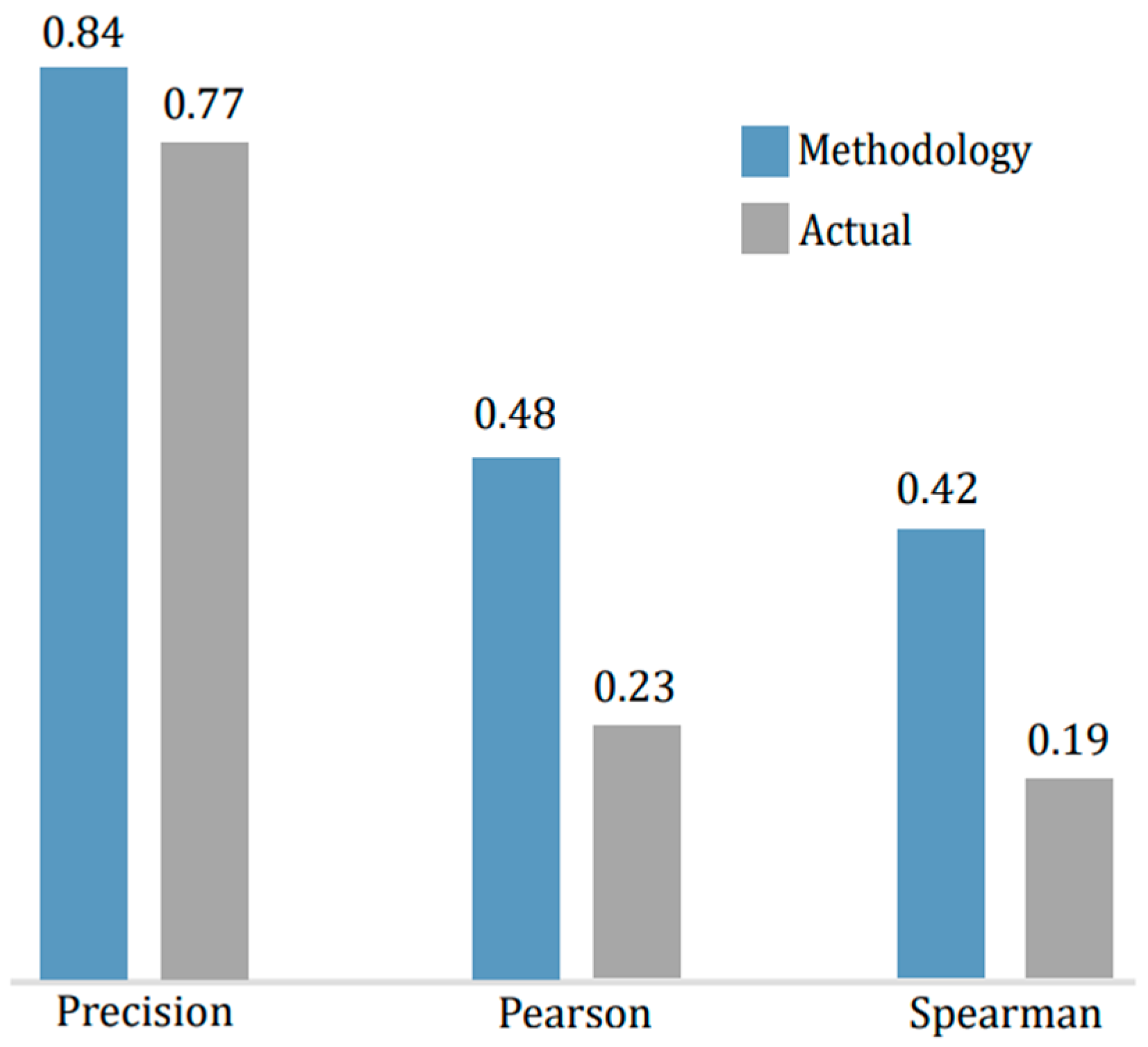
| Ref. | Domain | Academic Program | Variables | Tasks and Algorithms | Performance |
|---|---|---|---|---|---|
| (Wu & Wu, 2020) | Determine the influence of factors on admission and final AP. | Administration | Input: 20 academic, demographic, and personal variables. Output: Continuous grade point average. | REG: RLR, SVM, RF, GBDT, LR FS: Relevance with R and ReliefF, and redundancy with R. | Without FS: MAE-SVM = 3.38, RMSE-SVM = 4.48. With FS: MAE-SVM = 3.41, RMSE-SVM = 4.48 |
| (Contreras et al., 2020) | Determine the variables that most influence AP | Engineering | Input: Admission tests, socioeconomic, demographic, cultural, institutional, and personal data. Output: Categorized AP. | CL: DT, kNN, NN, SVM. FS: Chi2; ANOVA; Pearson; RFE with LgR, LR, and SVM; RF and BS with DT. | pSVM with FS = 0.61. SVM and NN are the best |
| (Putpuek et al., 2018) | Compare two prediction models for AP | Education | Input: Demographic, socioeconomic, academic. Output: Final grade point average. | CL: DT, NB, kNN FS: SFS, BS, EFS | pID3 = 28.9% NB higher Acc = 43% |
| (Adeyemo & Kuyoro, 2013) | Evaluate the effect of socioeconomic background on AP | All | Input: Socioeconomic, demographic, and academic. Output: Cumulative grade point average of the 1st year in 7 classes. | CL: DT FS: CFS and COE, importance with CFS and COE wrappers. | pC4.5 (DT) = 73.3% |
| (Echegaray-Calderon & Barrios-Aranibar, 2016) | Identify the factors that affect AP | All | Input: Demographic, socioeconomic, academic admission, and current data. Output: AP of 5 classes. | CL: NN FS: GA, the importance of GA | Without FS: Acc = 89% With FS: Acc = 80% |
| (Rachburee & Punlumjeak, 2015) | Compare FS methods to improve the prediction of AP | Engineering | Input: Demographic and academic admission data; 15 in total. Output: Grade point average in 3 classes. | CL: NB, DT, kNN, NN FS: Chi2, IG, mRMR, SFS | AccSFS (NN) = 91% |
| (Velmurugan & Anuradha, 2016) | Compare the performance of various FS techniques in predicting exam scores | High school | Input: Demographic, socioeconomic, academic (admission), and current data. Output: Final exam score in 4 classes. | CL: DT, NB, kNN FS: CFS, BFS, Chi2, IG, Relief Usan Weka | With FS: pCFS(NB) = 99.8%. Best classifier IBK (kNN)p = 99.7% |
| (Affendey et al., 2010) | Rank the factors contributing to the prediction of AP | Informatics | Input: AP in subjects. Output: Dichotomous AP. | NB, DT, NN. | AccNB = 93% |
| (Deepika & Sathyanarayana, 2022) | Select active features to reduce high dimensionality and manage data uncertainty using the hybrid method RFBT-RF | All | No information | DT, NB, SVM, and KNN. | Acc RFBT-RF between 81.5% and 97.9%, |
| Variable Name | Description |
|---|---|
| DE_COHORTE | Year the student enrolled at the university. |
| DE_ANTEGRE | Number of years from the student’s high school graduation year to the year of application. |
| DE_NAC | Nationality of the student. |
| DE_REGION | Determines whether the student is from the Metropolitan Region or another region, according to their place of origin. |
| DE_GENE | Gender of the student. |
| DE_TAMFAM | Number of family members of the student. |
| AC_DEPA | Name of the department to which the student’s major belongs. |
| AC_CARR | Name of the student’s major. |
| SE_DECIL | Socioeconomic level of the student as per capita household income. |
| SE_ESTUMAD | Mother’s level of education. |
| SE_ESTUPAD | Father’s level of education. |
| SE_PRIGE | Determines if the student is the first in their family to attend university. |
| SE_ESTADEP | Administrative dependency of the high school from which the student graduated. |
| SE_ESTADIF | Differentiated high school education at the student’s graduating institution. |
| AC_PREFPOST | The preferred major choice at the time of the student’s application. |
| AC_PSUMAT | Score on the mathematics admission test PSUMAT. |
| AC_PSULYC | Score on the language and communication admission test PSULYC. |
| AC_PSUPROM | Average score of PSUMAT and PSULYC. |
| AC_PSUCIE | Score on the science admission test PSUCIE. |
| AC_NEM | Score equivalent to the average grade in high school NEM. |
| AC_RANK | Score equivalent to the high school ranking. |
| AC_ PJEPOST | Weighted or application score for engineering programs. |
| AP | The number of courses passed is divided by the number of courses enrolled in the first year. |
| Numerical Scale | Conceptual Scale | Percentage Scale | Number of Cases |
|---|---|---|---|
| 7.0 | A = excellent | 100 | 1117 |
| [6.0; 7] | B = very good | [86; 100] | 715 |
| [5.0; 6.0] | C = good | [73; 86] | 1310 |
| [4.0; 5.0] | D = sufficient | [60; 73] | 1001 |
| [2.5; 4.0] | E = insufficient | [30; 60] | 1488 |
| [1.0; 2.5] | F = bad | [0; 30] | 569 |
| Indicator | 2014–2015 | 2015–2016 | 2016–2017 | 2017–2018 |
|---|---|---|---|---|
| Meets DV < 0.26 | Yes | No | Yes | No |
| DV | 0.17 | 0.26 | 0.25 | 0.73 |
| Variables that contribute the most to the drift | PJEPOST (58%) CARR (24%) | PREFPOST (82%) CARR (15%) | DECIL (91%) | ESTUPAD (100%) |
| Item\Cohort (Number of Cases) | 2014 (1244 Cases) | 2015 (1196 Cases) | 2016 (875 Case) | 2017 (792 Cases) |
|---|---|---|---|---|
| Dropout rate (%) | 12 | 19 | 25 | 21 |
| Minimum Dropout by Vocation | 30% × 12% = 3.6% | 30% × 19% = 5.7% | 30% × 25% = 7.5% | 30% × 21% = 6.3% |
| Maximum Dropout by Vocation | 66% × 12% = 7.92% | 66% × 19% = 12.54% | 66% × 25% = 16.5% | 66% × 21% = 13.86% |
| Minimum Dropout by Skills | 14% × 12% = 1.68% | 14% × 19% = 2.7% | 14% × 25% = 3.5% | 14% × 21% = 2.94% |
| Maximum Dropout by Skills | 33% × 12% = 3.96% | 33% × 19% = 6.3% | 33% × 25% = 8.25% | 33% × 21% = 6.93% |
| Minimum Total Dropout | 5.28% (3.6% + 1.68%) | 8.4% (5.7% + 1.68%) | 11% (7.5% + 3.5%) | 9.2% (6.3% + 2.94%) |
| Maximum Total Dropout | 11.88% (7.92% + 3.96%) | 18.84% (12.54% + 6.3%) | 24.75% (16.50% + 8.25%) | 20.79% (13.86% + 6.93%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hinojosa, M.; Alfaro, M.; Fuertes, G.; Ternero, R.; Santander, P.; Vargas, M. Optimizing University Admission Processes for Improved Educational Administration Through Feature Selection Algorithms: A Case Study in Engineering Education. Educ. Sci. 2025, 15, 326. https://doi.org/10.3390/educsci15030326
Hinojosa M, Alfaro M, Fuertes G, Ternero R, Santander P, Vargas M. Optimizing University Admission Processes for Improved Educational Administration Through Feature Selection Algorithms: A Case Study in Engineering Education. Education Sciences. 2025; 15(3):326. https://doi.org/10.3390/educsci15030326
Chicago/Turabian StyleHinojosa, Mauricio, Miguel Alfaro, Guillermo Fuertes, Rodrigo Ternero, Pavlo Santander, and Manuel Vargas. 2025. "Optimizing University Admission Processes for Improved Educational Administration Through Feature Selection Algorithms: A Case Study in Engineering Education" Education Sciences 15, no. 3: 326. https://doi.org/10.3390/educsci15030326
APA StyleHinojosa, M., Alfaro, M., Fuertes, G., Ternero, R., Santander, P., & Vargas, M. (2025). Optimizing University Admission Processes for Improved Educational Administration Through Feature Selection Algorithms: A Case Study in Engineering Education. Education Sciences, 15(3), 326. https://doi.org/10.3390/educsci15030326










