Embedding Math Problems in Cultural City Tours to Increase Student Engagement and Inclusion

Abstract

This paper aims to investigate whether embedding mathematical problems in cultural tours around cities can effectively increase student engagement, enhance knowledge retention, and promote inclusivity among students with varying abilities. First, we present the content development process and then the evaluation process with the participation of 78 high school students and six teachers. Quantitative data were collected through pre- and post-tour questionnaires, while qualitative data were gathered through teacher interviews to evaluate engagement, knowledge acquisition, and inclusivity. The results indicate that the pedagogical tours significantly enhance student engagement and foster collaboration among students of different abilities. This study contributes to the development of innovative pedagogical approaches by integrating storytelling, gamification elements, and real-world contexts to make mathematics learning more engaging.

1. Introduction

Mathematics education has long faced challenges related to student disengagement, often due to its abstract nature and perceived detachment from real-world applications. Traditional instructional methods, which emphasize rote memorization and procedural problem-solving, frequently fail to spark curiosity or provide meaningful learning experiences (Boaler, 2016). In response, researchers and educators have explored various alternative pedagogical approaches that enhance engagement, relevance, and interdisciplinary connections in mathematics education (Hunter et al., 2020; Kalelioğlu, 2015). For example, Inquiry-Based Learning (IBL) and Project-Based Learning (PBL) offer innovative, student-centered alternatives to traditional mathematics instruction. IBL engages learners in questioning, exploration, and problem-solving, helping them build deep conceptual understanding and critical reasoning (Sen et al., 2021; Khasawneh et al., 2023). PBL complements this approach by connecting mathematical learning to real-world contexts through collaborative projects that involve designing solutions, analyzing data, and modeling phenomena (Sujatha & Vinayakan, 2023). Research shows that both methods enhance engagement, motivation, and retention, particularly for students who struggle with conventional teaching (Almulla, 2020; Lee et al., 2019).

Storytelling has emerged as an effective pedagogical strategy (Lazarinis et al., 2020) for engaging students in mathematics by connecting abstract concepts to narratives that evoke curiosity and emotional involvement (Irmayanti & Chou, 2025). Research suggests that students retain information more effectively when it is presented within a compelling story rather than as isolated facts (Lazarinis & Konstantinidou, 2025; Zazkis & Liljedahl, 2019). Storytelling provides a narrative structure that helps students see the logic and progression of mathematical ideas, making it easier to understand and remember concepts. One approach to mathematical storytelling involves embedding mathematical challenges within narratives that require problem-solving to advance the story (Walters et al., 2018). For example, teachers can use detective-style problems where students must solve algebraic equations to decode a mystery or historical narratives where students explore mathematical breakthroughs through the lens of famous mathematicians (Jahnke, 2014). Additionally, ethnomathematics—an approach that explores the mathematics embedded in different cultures—has been used to create stories that make mathematics more accessible and meaningful to diverse learners (Kabuye Batiibwe, 2024).

Mathematics is inherently connected to various disciplines, and interdisciplinary teaching leverages these connections to enhance learning. The integration of mathematics with science, technology, engineering, and the arts (STEAM) has gained significant attention in recent years (Belbase et al., 2022). For example, mathematical modeling is widely used in physics, economics, and computer science, allowing students to see the practical applications of abstract mathematical theories (English, 2016). Computational thinking, a core component of modern mathematics and computer science education, encourages students to use programming and algorithmic problem-solving to tackle complex problems (Wing, 2006).

Gamification applies game-based elements, such as challenges, points, and rewards, to enhance student motivation in mathematics learning (Alt, 2023). Gamified learning environments increase student participation and improve problem-solving skills (Hellín et al., 2023; Barreto et al., 2017). Games like Prodigy Math integrate storytelling elements to teach algebraic and arithmetic concepts in an engaging way, leading to higher retention and enthusiasm for learning mathematics (Laato et al., 2020).

The above alternative pedagogical approaches provide meaningful strategies to address common challenges in mathematics education, making the subject more engaging and applicable to real-world contexts. In this paper we propose a different approach for engaging in problem solving. Our proposal involves the integration of mathematical problems in a real-world context. More specifically, our work includes the use of mathematics problems in city routes, which unfold an inclusive story enriched with historical facts and cultural monuments. By integrating mathematics with cultural exploration, educators can create immersive and engaging learning experiences that extend beyond the classroom. This paper highlights the potential of these mathematical and cultural routes in a city, evaluating their impact on student motivation, conceptual understanding, and interdisciplinary learning. Through case studies and empirical research, we will demonstrate how these approaches enhance engagement, improve problem-solving abilities, and foster a deeper appreciation of mathematics as a dynamic and culturally rich discipline.

2. Pedagogical Tours Around Cities

From the previous works on alternative methods for teaching mathematics, it is clear that devising engaging methods for mathematics is important. In our approach, we employ pedagogical tours around cities, which offer a blend of mathematical problems and cultural exploration, transforming urban landscapes into dynamic learning environments. By integrating mathematical concepts with historical and architectural landmarks, these tours provide an interactive and immersive educational experience. Participants explore key locations in Cities, uncovering the hidden mathematical structures behind famous monuments, urban planning, and artistic designs. Through hands-on activities, storytelling, and problem-solving challenges, learners engage with mathematics in a real-world context, fostering deeper engagement.

The development of the project follows a structured and iterative process to ensure high-quality content and an engaging learning experience. Each step involves collaboration among partners, experts, and educators, integrating feedback and refinements at every stage. The key steps are as follows:

1.

Selection of the city, monuments, and route and historical research:

• A city is chosen as the focus of a pedagogical tour, along with key monuments and landmarks that will be included in the route.
• Historical research is conducted to identify significant events, cultural influences, and noteworthy historical facts related to the selected locations.
• This research serves as the foundation for the content, ensuring accuracy and depth in the storytelling approach.

2.

Definition of the storyline, inclusive elements, and gaming characteristics:

• A storyline is developed to guide users through the historical and mathematical exploration of the city.
• Inclusive elements are incorporated to ensure accessibility for diverse audiences, considering cultural representation, language inclusivity, and varying learning needs.
• Gamification features are designed to enhance engagement, including interactive challenges, problem-solving activities, and digital rewards.

3.

Content development using specified templates in Canva:

• The researched content is structured using predefined templates in Canva, ensuring consistency in design and presentation.
• Visual and textual elements, including images, infographics, and interactive materials, are integrated to make the experience more immersive.
• The templates also facilitate easy adaptation for different formats and languages.

4.

Development of solutions to the problems:

• Based on the content, analytical solutions are created to enhance the user experience.

5.

Finalization and publication of outputs in different forms

• The final versions of the materials are published in different formats and print-friendly versions.
• Dissemination strategies are implemented to ensure broad accessibility, allowing educators, students, and the public to benefit from the project.

Throughout all steps, the outputs are continuously assessed and refined by partners and experts, ensuring that the content meets educational standards, remains historically accurate, and effectively engages diverse audiences. Feedback from test users and stakeholders plays a crucial role in iterating and enhancing the final versions of the project materials.

An Example of a Pedagogical Tour: The Case of Athens

The Athens pedagogical tour (https://visitmath.eu/resources-2/pedagogical-tours-around-european-cities-and-towns/ accessed on 5 December 2025) is an interactive educational journey that combines mathematics, history, and cultural exploration through key historical landmarks of Athens (Figure 1). Designed in Cannva.com as a gamified learning experience, the tour is led by an ancient Greek philosopher who is supposed to wake up in modern Athens and invites participants to explore historical sites while solving mathematical challenges.

The Athens tour consists of seven place-based activities situated at major monuments (Temple of Olympian Zeus, Hadrian’s Gate, Tower of the Winds, Temple of Hephaestus, the “Sacred Triangle,” Thiseio, and the Parthenon). Students work in small groups to model real structures and distances: recovering original dimensions from scaled miniatures; estimating the perimeter of an arch idealized as a semicircle; computing area/volume for a regular octagon (Tower of the Winds); deriving unknown temple dimensions from architectural ratios; and solving an isosceles “sacred triangle” using trigonometry and map data. The interlude at Thiseio introduces classical cryptography (Polybius, Caesar shift), culminating in a decryption task (“Democracy”), while the Parthenon activity invites discussion of the golden ratio and the role of approximation in historical reconstructions. These tasks require assumption-making, estimation, and validation against provided solutions and museum information, aligning the tour with guided inquiry, storytelling and modeling rather than traditional drill.

The following list explains the key Features of the Tour:

1.

Historical and cultural insights:

• Participants visit significant Athenian landmarks such as the Temple of Olympian Zeus, Hadrian’s Gate, the Tower of the Winds, the Temple of Hephaestus, and the Acropolis-Parthenon.
• Each stop provides historical context, highlighting the city’s evolution from ancient Greece to the Roman era and its impact on philosophy, democracy, and science.

2.

Mathematical challenges and problem-solving

• The tour integrates mathematical problems linked to each site, encouraging participants to calculate proportions, areas, volumes, and geometric relationships.
• Examples include scaling a miniature temple, computing the perimeter of a semicircle, estimating an octagonal tower’s volume, and solving an isosceles triangle’s dimensions based on historical locations.

3.

Gamification and interactivity

• The experience is interactive, requiring participants to assist the philosopher in solving mathematical puzzles.
• Gamification elements include encryption challenges (e.g., Caesar’s Cipher), secret messages, and real-world applications of steganography.

4.

Reflection and final challenge

• The journey ends at the Acropolis and the Parthenon, where participants reflect on the mathematical and cultural contributions of ancient Greece.
• A final encrypted message invites them to decode the most significant Greek contribution to humanity using a shift cipher.

The tour transforms the city into a living classroom, making mathematics engaging and relevant by linking it to historical and cultural narratives. Through problem-solving, storytelling, and interactive learning, students gain a deeper appreciation of ancient Greek achievements while enhancing their mathematical reasoning and critical thinking skills in a joyful and practical approach. The tour is accompanied by solutions explaining the necessary calculations (https://visitmath.eu/?sdm_process_download=1&download_id=1817 accessed on 5 December 2025). The whole set of pedagogical tours in various languages can be found in https://visitmath.eu/resources-2/pedagogical-tours-around-european-cities-and-towns/ (accessed on 5 December 2025).

Overall, the developed mathematical tours incorporate a variety of context-driven problems that blend mathematical concepts with real-world exploration. For instance, students might calculate the height of an ancient monument using trigonometry, determine the surface area of a dome by analyzing its geometric properties, or estimate the volume of a historical well based on its cylindrical structure. Other activities could involve deciphering coded messages using classical encryption methods like substitution ciphers, uncovering hidden patterns in architectural designs, or exploring mathematical symmetry in historical mosaics. Problems related to economics, e.g., cost of restoration, or sports, e.g., how many calories could be burnt to cover a specific distance within a park, etc., can also be embedded. These hands-on challenges not only reinforce mathematical principles but also make learning interactive and immersive, connecting abstract concepts to tangible, real-world applications.

3. Methodology

This section outlines the research approach adopted to assess the effectiveness of our approach in fostering student engagement and promoting the inclusion of students with different abilities. The study follows a structured research design, ensuring a comprehensive evaluation of the intervention’s impact. By employing both qualitative and quantitative methods, the study aims to capture a holistic view of student participation and experiences, emphasizing a joyful and inclusive learning environment.

3.1. Research Aims and Design

The primary aim of this study is to evaluate the effectiveness of the mathematical tours in increasing student engagement and inclusion of students with different abilities in a joyful approach. The specific research questions are:

RQ1. 

Does the specific approach to learning mathematics increase students’ engagement?

RQ2. 

Do the math activities in the tours help students to improve their math knowledge and skills?

RQ3. 

Are the pedagogical tours suitable for students with different abilities?

RQ4. 

Do students retain mathematical concepts better when they are taught through an experiential learning activity such as the pedagogical tours with embedded math activities?

To answer these questions, a mixed-methods research design was employed, incorporating both quantitative and qualitative approaches. Through pre- and post-intervention student questionnaires, observational data, and teacher feedback, we measure the effectiveness of the intervention.

3.2. Participants

The study involved a total of 78 high school students, aged 15 to 18 years old, representing a diverse range of socio-economic backgrounds. These students were selected through purposive sampling, ensuring a balanced representation across key demographic factors, including gender, socio-economic status, and prior mathematical knowledge. This sampling approach was chosen to capture a broad spectrum of student experiences, making the findings more comprehensive and applicable to various educational settings.

In addition to student participants, 6 teachers played an integral role in the study. Through their involvement, they provided observational data and professional insights regarding student engagement and learning behaviors. The teachers’ perspectives contributed qualitative depth to the study, complementing the quantitative data collected from students. Their feedback helped to assess the effectiveness of the intervention in creating an inclusive and engaging learning environment.

By incorporating both student self-reports and teacher observations, the study aimed to offer a well-rounded understanding of how the intervention impacted student participation, learning outcomes, and overall engagement in mathematics.

3.3. Data Collection and Analysis

To evaluate the impact of mathematical tours on student engagement and learning, a structured data collection and analysis approach was implemented. The students were randomly divided into three groups. Each group first participated in a mathematical tour within their own city (https://visitmath.eu/?sdm_process_download=1&download_id=1809 accessed on 5 December 2025), allowing them to explore mathematical concepts in familiar surroundings. Subsequently, all students engaged in an Athens-based mathematical tour conducted in a laboratory setting, providing them with a historical and cultural learning experience through digital technologies. The field tour lasted 3 h (180 min) and the lab intervention lasted 2 teaching hours (90 min).

Alongside student participation, one STEM teacher and one history teacher accompanied each group. These teachers rotated across groups to ensure a diverse range of educator perspectives, ultimately involving multiple teachers throughout the study. The role of the six teachers was to facilitate, observe, and support students as they engaged with the mathematical challenges presented in the tours.

To systematically gather data, students were required to complete pre- and post-tour questionnaires. The pre-tour questionnaire (Appendix A) aimed to assess their initial attitudes toward mathematics, their level of engagement, and their beliefs about alternative forms of teaching mathematics. The post-tour questionnaire (Appendix B) was designed to measure changes in these topics by asking students to ask the same questions again, in addition to student engagement, their perceived learning outcomes, and their overall experience with the mathematical activities. Appendix C shows the classification of the questions in relation to the research questions.

Data collection for the teachers entailed a semi-structured interview conducted post-intervention. The four research questions directed the interviews, during which teachers were asked to express their agreement or disagreement with the questions, justify their perspectives, discuss potential changes and enhancements, highlight preferred aspects of the specific learning approach, and describe student behaviors observed during or after the intervention, etc. We expect the interviews to yield comprehensive qualitative insights regarding the efficacy of the tours, the extent of student engagement, and the inclusivity of the methodology.

Ethical procedures involved obtaining informed consent from parents or guardians and assent from child participants. To ensure confidentiality and anonymity, all questionnaires were completed anonymously. Participation was entirely voluntary, with participants having the option to withdraw at any time without consequence.

4. Results

The following sections present the results of the evaluation. First, we discuss the pre- and post-tour common questions to realize the changes in student attitudes, and then we present the post-tour questions that survey the experiences of the students. Finally, we present the findings of the teacher questionnaires.

4.1. Pre- and Post-Tour Common Questions

The analysis of the pre- and post-tour questionnaire results indicates notable improvements in students’ perceptions of mathematics, particularly regarding engagement, the connection between mathematics and history and culture, and the possibility of learning mathematics outside the classroom. The graphs in Figure 2 present the results of the questions in a comparative manner.

Regarding students’ enjoyment of learning mathematics (Q1), there was a modest positive shift. Before the tour, 67.95% of students disagreed or strongly disagreed that they enjoyed learning mathematics. After the tour, this percentage decreased to 58.97%, while those who agreed or strongly agreed increased from 20.51% to 29.49%. The perception of mathematics as an important subject in daily life (Q2) saw a more substantial change. Initially, 58.97% of students did not see its relevance, but after the tour, this number dropped to 34.61%. At the same time, those who agreed or strongly agreed that mathematics is important in daily life increased from 30.77% to 58.97%. This indicates that the tour helped students better understand how mathematical concepts apply beyond the classroom.

A significant improvement was seen in students’ perception of mathematics as interesting and engaging (Q3). Before the tour, 73.08% of students disagreed or strongly disagreed with this statement, showing a generally negative view of the subject. However, after the tour, this number dropped to 47.44%, while agreement increased from 17.95% to 43.59%. The increase suggests that the tour introduced engaging elements or new perspectives that made mathematics more appealing to students.

Feelings of anxiety before a math test (Q4) remained largely unchanged. The lack of improvement suggests that while the tour may have influenced attitudes toward mathematics in general, it did not alleviate test-related stress, which might require more targeted and prolonged interventions. Interest in exploring alternative methods for learning mathematics (Q5) was already high before the tour, with 87.18% of students agreeing or strongly agreeing. This number further increased to 96.15% after the tour, suggesting that the experience reinforced students’ desire to engage with mathematics through different approaches, possibly through interactive or applied learning methods.

The connection between school mathematics and real-world problems (Q6) remained a challenge. A large percentage (83.33%) of students initially disagreed or strongly disagreed that what they learn in school relates to real-world problems, and this number increased slightly to 92.31% post-tour. This outcome indicates that, once students observed the potential for more realistic and contextualized problems, they became increasingly convinced that school mathematics lacks relevance to the real world.

A major shift occurred on how students viewed the connection between mathematics and history or culture (Q7). Before the tour, 67.95% of students disagreed or strongly disagreed that incorporating historical and cultural contexts could make mathematics more interesting. After the tour, this percentage dropped significantly to 29.49%, while those who agreed or strongly agreed increased from 20.51% to 58.97%. This suggests that the tour demonstrated effectively how mathematics has evolved across different cultures and time periods, making the subject feel more dynamic and relevant.

One of the most prominent changes was in students’ perception of whether mathematics can be taught outside the classroom (Q8). Initially, 82.05% of students disagreed or strongly disagreed with this idea, indicating that they viewed mathematics as a subject confined to traditional classroom instruction. After the tour, however, this number dropped significantly to 17.95%, while agreement increased to 78.2%. This suggests that the tour showcased alternative learning environments for mathematics, helping students see that mathematical concepts can be explored in different and more engaging ways.

Among all the areas analyzed, the most significant improvements were seen in engagement with mathematics (Q3), the recognition of its historical and cultural connections (Q7), and the idea that it can be taught outside traditional classroom settings (Q8). These findings suggest that integrating mathematics with history, culture, and alternative learning environments can enhance students’ interest and engagement in the subject. However, challenges remain in areas such as test anxiety and real-world applications, indicating potential areas for further educational interventions.

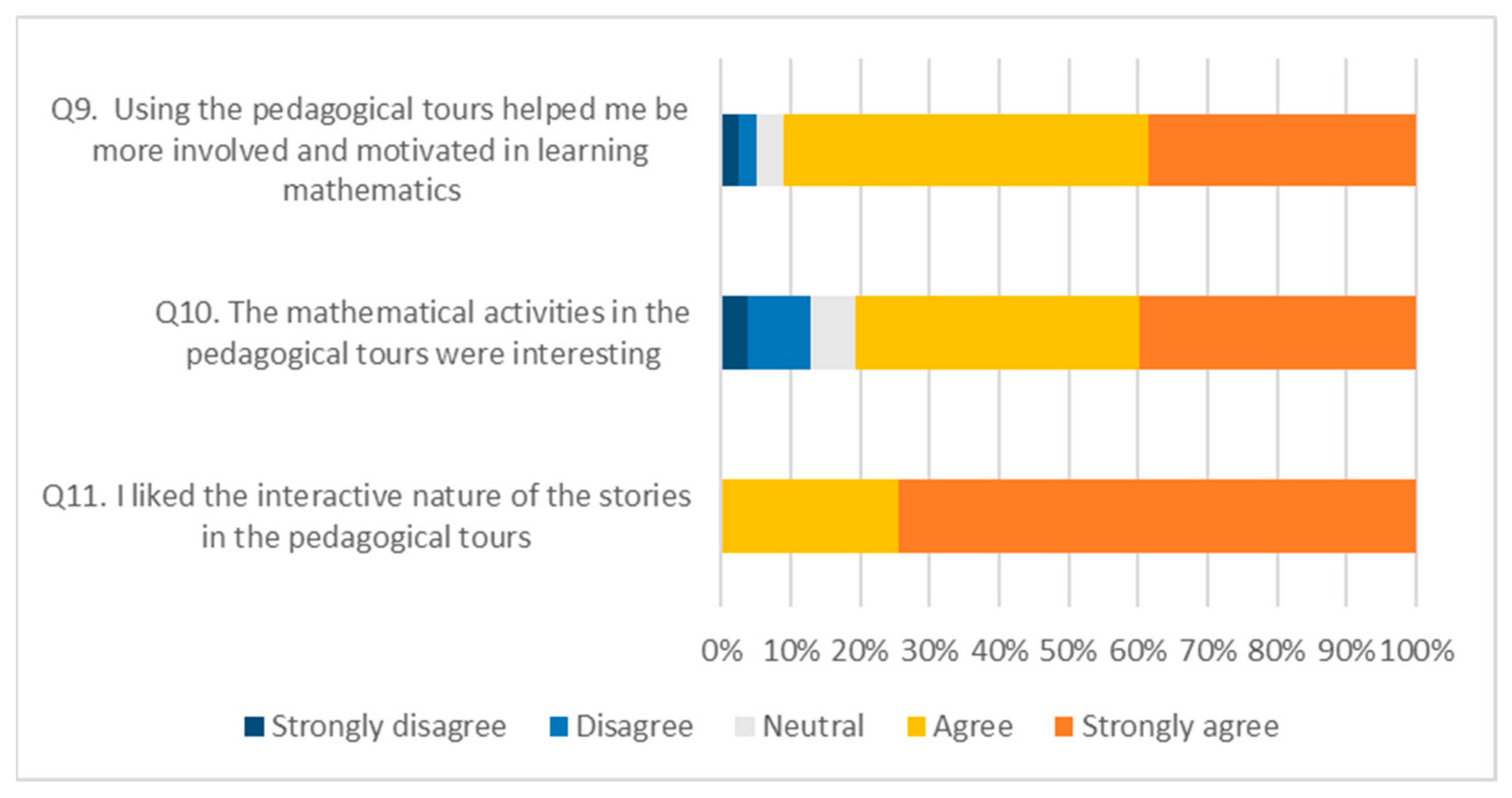
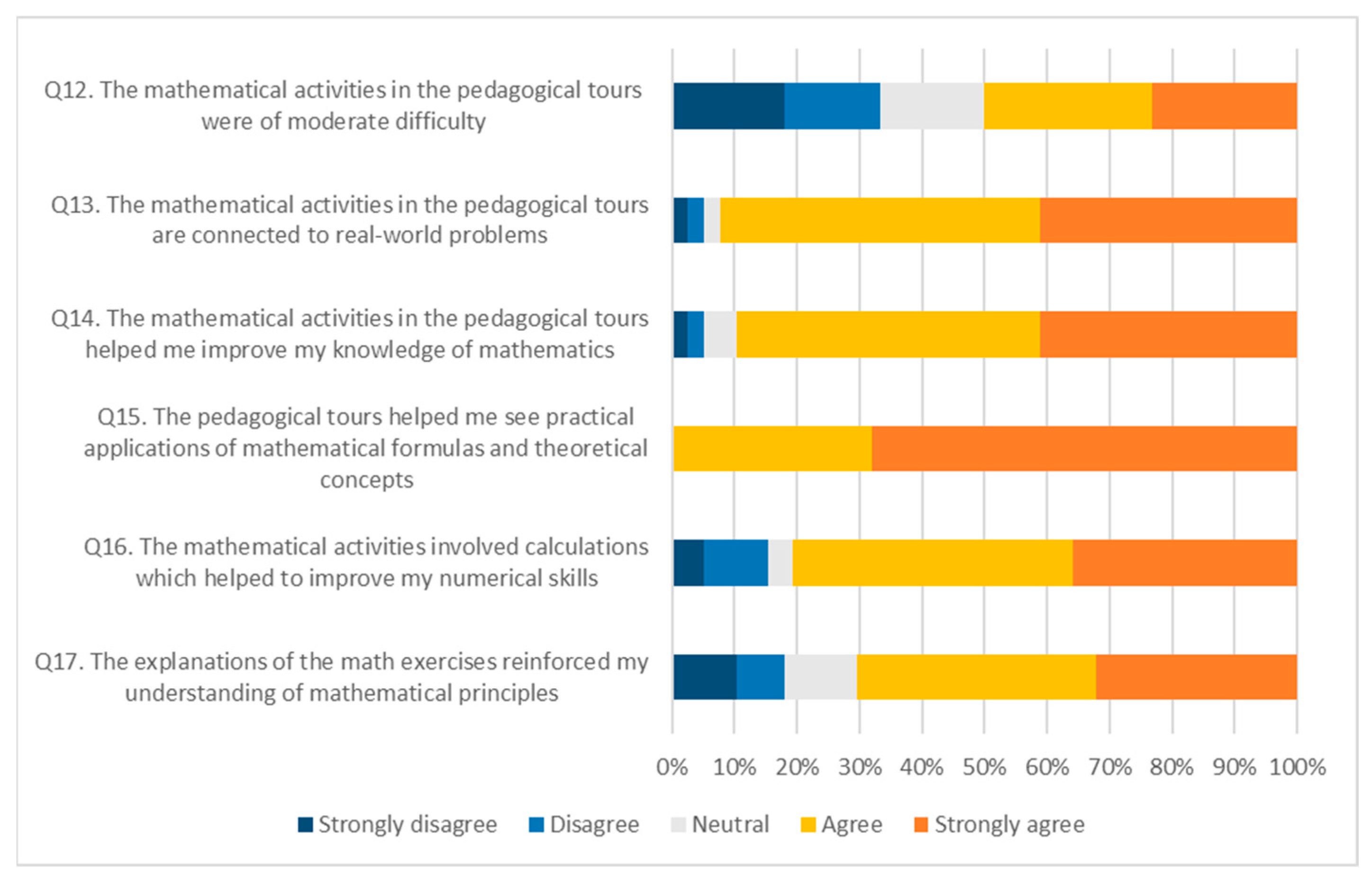
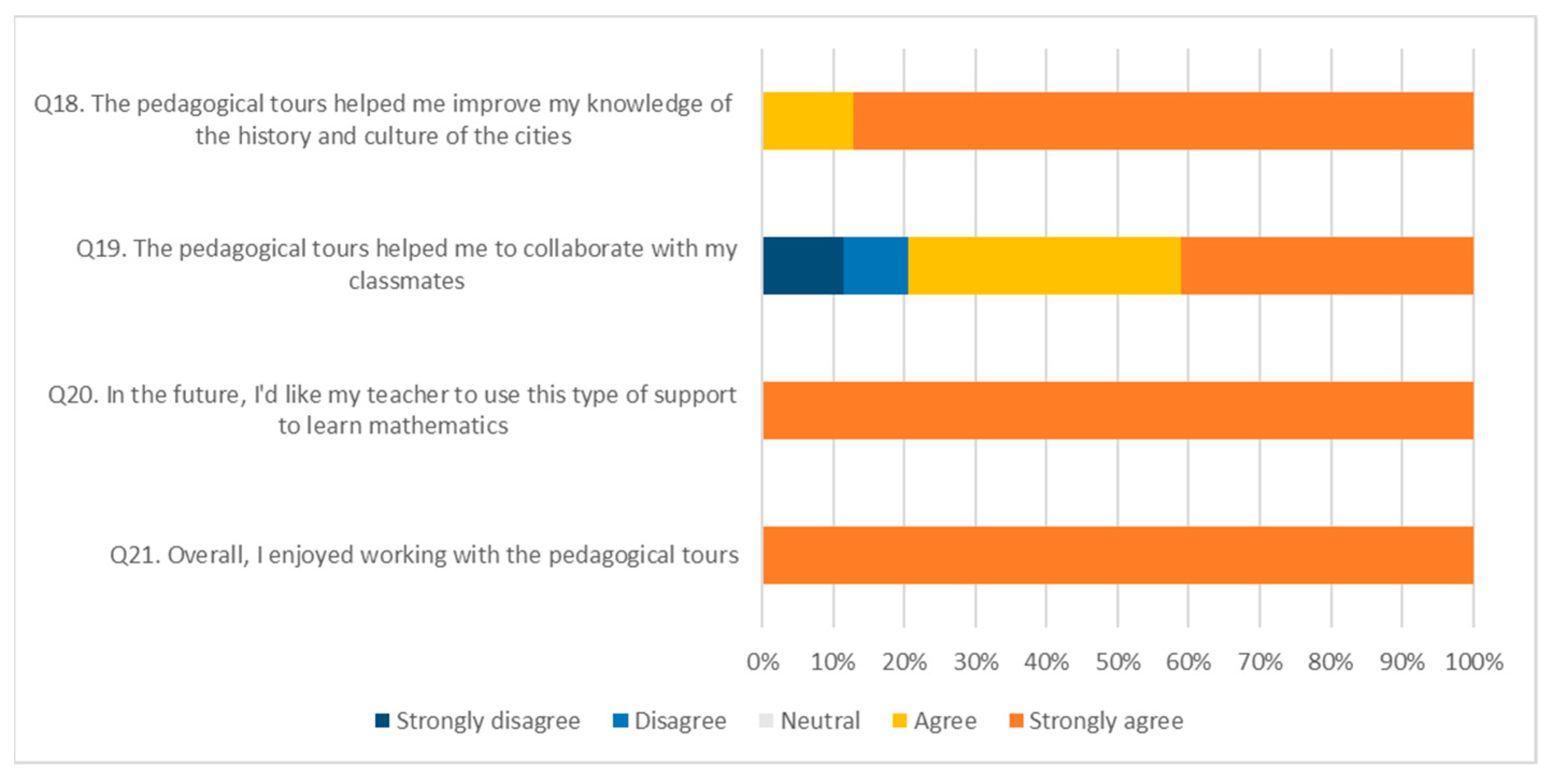
4.2. Post-Tour Questions

In this section we analyze the post-tour questions which surveyed the experiences of the students after the utilization of the two pedagogical tours. The first questions (Figure 3) concern the engagement of the students. The analysis of student responses to the pedagogical tours reveals strong positive feedback across key aspects of the experience. For Q9, which assessed whether the tours increased involvement and motivation in learning mathematics, the overwhelming majority (91.02%) agreed or strongly agreed, with only a small fraction (5.12%) expressing disagreement, highlighting the tours’ effectiveness in fostering engagement. The next question, Q10, evaluated the interest level of the math exercises, a significant majority (80.77%) found the exercises interesting, and only a small portion (12.82%) expressed disagreement. Finally, question Q11 focused on whether the students like the interactive nature of the stories. The results were unanimously positive, with 100% of respondents agreeing or strongly agreeing, underscoring the effectiveness of interactive storytelling as a central and highly engaging feature of the tours.

The next set of questions (Figure 4) reveals a generally positive reception of the pedagogical tours in mathematics education, with participants acknowledging their effectiveness in enhancing understanding and demonstrating real-world applications. A significant majority of respondents (92.31%) agreed or strongly agreed that the mathematics in the tours was connected to real-world problems (Q13), and all participants (100%) felt that the tours helped them see practical applications of mathematical formulas and theoretical concepts (Q15). This strong consensus underscores the success of the tours in bridging the gap between abstract mathematical principles and their real-world relevance, which is crucial for engaging learners and fostering deeper understanding. Additionally, a large proportion of respondents (89.75%) reported that the math exercises helped them to improve their knowledge of mathematics (Q14), and 80.77% agreed that the exercises enhanced their numerical skills (Q16). These findings suggest that the tours were effective in both reinforcing theoretical knowledge and developing practical skills.

The responses to Q12 reveal a split in participants’ perceptions of the difficulty of the math exercises, with 50% agreeing they were moderately difficult and 33.33% disagreeing. This divergence likely stems from varying mathematical skills and attitudes and from the fact that many students previously indicated they do not enjoy learning mathematics. More than 70% showed a strong level of agreement in Q17, attesting that the explanations of the math exercises reinforced their understanding of mathematical principles. A notable 17.95% disagreed or strongly disagreed, suggesting that while the explanations were beneficial for most, they may not have been equally clear or accessible for all participants, which is something that needs more research and probably some future improvements.

The survey results for Q18 to Q21 (Figure 5) demonstrate strong positive feedback regarding the pedagogical tours, highlighting their effectiveness in enhancing knowledge, collaboration, and overall enjoyment. For Q18, more than 87% of participants strongly agreed that the tours improved their knowledge of the history and culture of the cities, with the remaining 12.82% agreeing. For Q19, 79.49% agreed or strongly agreed that the tours helped them collaborate with classmates. The responses to Q20 and Q21 were unequivocally positive, with 100% of participants strongly agreeing that they would like teachers to use this type of support in the future (Q20) and that they enjoyed working with the pedagogical tours overall (Q21). This universal approval highlights the tours’ success in creating an engaging and effective learning environment that resonates strongly with participants.

4.3. Teachers’ Interviews

This section presents the results from interviews conducted with six teachers. Three educators instruct STEM-related subjects, while the remaining three specialize in history, which may affect the responses in some instances. The educators oversaw and assisted the instructional process using the pedagogical tours. The tasks may be conducted either individually or in small teams as preferred by the pupils. However, each team should consist of fewer than five pupils to ensure manageability and to enhance involvement chances for the students.

Question 1: Does the specific approach to learning mathematics increase students’ engagement?

All six teachers unanimously agreed that the specific approach to learning mathematics effectively increases students’ engagement. Teachers highlighted that the joyful, interactive and contextualized activities play a crucial role in maintaining students’ interest and enthusiasm throughout the activities. Such consistency in responses demonstrates strong support for the pedagogical method, indicating that it may be particularly effective in enhancing student engagement in mathematical learning.

All the teachers attested that all the students participated in the mathematical activities and they had fun with the stories they followed. A repeating observation is that the pedagogical tour was handled like a kind of game where teams had an informal competition. 4 teachers observed that some of the teams also collaborated further to verify the results or to help each other. One important aspect raised by the teachers is the interdisciplinary nature of the specific approach, as students learn cultural, historical and math topics. This approach accommodates different learning styles and abilities.

The history instructors emphasized that the pedagogical tour was captivating from both cultural and historical viewpoints, since the inclusion of brief historical facts, images, and visits to specific sites significantly increased student attention compared to traditional classroom settings.

One history instructor indicated that they could independently conduct the educational activity without assistance from a STEM teacher, as there are solutions available for the mathematical activities, enabling students to receive support if necessary.

Finally, the sub-questions that arose and were considered during the interviews pertained to the actions necessary to assist the students or to establish order among them. All participants indicated that the assistance needed mirrored that required in the classroom; however, the interventions necessary to maintain order were in comparison reduced, since all students experienced enjoyment and thereby, they were more actively engaged in the activities.

Question 2: Do the math activities in the tours help students to improve their math knowledge and skills?

According to the responses, all STEM teachers agreed that the activities enhance students’ mathematical skills, attributing this improvement to the analytical nature of the tasks, which promote critical thinking and problem-solving. History teachers also strongly agreed with the statement; however, they acknowledged that their assessment is based on observation rather than formal expertise in mathematics. Their perspective is grounded in the observation that all students appeared actively engaged in the mathematical activities, suggesting a high level of participation and interest.

Furthermore, it was mentioned that the mathematical activities helped students work with practical applications of mathematical formulas and theoretical concepts, thereby bridging the gap between abstract knowledge and the real world. Finally, it was mentioned that students had to collaboratively do a number of calculations and correct mistakes of their peers, which helped all the participants.

Question 3: Are the pedagogical tours suitable for students with different abilities?

As noted by all six teachers, the pedagogical tours are effective in engaging students of diverse learning abilities and styles. The inclusion of storytelling elements was particularly praised for promoting empathy among students, which is a valuable aspect of fostering inclusivity. Additionally, the storytelling approach was found to effectively engage students with varying learning styles and abilities, making it a versatile educational tool. They mentioned that students not only learnt about mathematics, but also learnt about history and culture, which in some cases is very difficult to teach in the class.

STEM teachers specifically highlighted that providing contextualized mathematical activities within the tours significantly improved student understanding and participation, suggesting that this approach effectively motivates different students.

Some areas for improvement were identified to enhance accessibility and inclusivity. One teacher suggested improving graphical elements to accommodate students with visual impairments. Additionally, it was recommended to research the accessibility of the places included in the tours to ensure physical accessibility for all students. Furthermore, a mathematics teacher proposed introducing easier activities at the beginning of the tours to help students immerse themselves more naturally and gradually build their understanding and confidence.

Question 4: Do students retain mathematical concepts better when they are taught through an experiential learning activity such as the pedagogical tours with embedded math activities?

All the participants agreed that indeed students are expected to retain mathematical concepts more effectively when taught through experiential learning activities like the pedagogical tours with embedded math activities. They supported their belief that through real-world examples, they significantly enhanced students’ ability to understand and retain concepts.

Further, it was mentioned that the engaging and enjoyable nature of the tours was noted as a motivating factor, making learning feel more like a game or a friendly competition. They noticed that this interactive approach not only increased student motivation but also fostered collaboration among students of varying abilities, as they worked together within teams, staying focused and involved throughout the activities. Teachers reported that similar non-gamified or in-class school activities used in ordinary lessons did not produce the same sustained focus.

Question 5: Additional comments

At the end teachers were asked if they have additional comments, suggestions or any other issue that they would like to discuss. The feedback gathered from the teachers highlights again the positive reception of the pedagogical tours as an educational tool. All the teachers reiterated their approval of the game-based learning approach, emphasizing its value as a complementary teaching method. Additionally, some remarks made are:

5. Discussion

The previous section discussed our approach and presented the results of the evaluation experiments. In the current section, we review the findings of the evaluation with respect to our research questions.

The evaluation results provide strong evidence supporting the first research question regarding increased engagement through the pedagogical tours. Enjoyment of learning mathematics (Q1) showed a positive shift, with the proportion of students who agreed or strongly agreed rising from 20.51% before the tour to 29.49% afterward. A more pronounced improvement appeared in students’ perception of mathematics as interesting and engaging (Q3), where agreement increased from 17.95% to 43.59%, indicating that the tours made mathematics more appealing and accessible. Students also expressed a growing openness to alternative methods of learning (Q5), with agreement levels rising from 87.18% to 96.15%, suggesting that the experience validated the value of hands-on and experiential approaches. Post-tour responses confirmed high levels of situational engagement: 91.02% of students reported that the tours increased their motivation and involvement in mathematics (Q9), 80.77% found the mathematical activities interesting (Q10), and all participants (100%) appreciated the interactive storytelling (Q11). Similarly, every student expressed a desire for their teachers to continue using such approaches in the future (Q20) and reported overall enjoyment of the tours (Q21). From the perspective of teachers, unanimous agreement was reached regarding the positive impact of the tours on student engagement. They consistently noted that the playful, interactive, and contextualized activities were essential in maintaining student interest and enthusiasm (Fernández-Oliveras et al., 2021). Teachers also observed full student participation, with many students treating the activity as a friendly competition and even collaborating to verify results or assist each other. Additionally, the interdisciplinary nature of the tours was praised for its ability to blend cultural, historical, and mathematical learning, appealing to different learning styles and abilities.

Regarding the second research question, i.e., whether the tours enhance students’ mathematical knowledge and skills, the findings from both students and teachers provide mutually reinforcing evidence that the approach is promising. A large majority of students (92.31%) agreed or strongly agreed that the activities were connected to real-world problems (Q13), indicating that the tours effectively linked mathematical theory with authentic contexts. This practical orientation was further reinforced by the finding that all respondents (100%) agreed that the tours helped them see concrete applications of mathematical formulas and theoretical concepts (Q15), suggesting enhanced understanding of how mathematics operates beyond the classroom. Similarly, 89.75% of students reported that the activities improved their overall mathematical knowledge (Q14), confirming that the tasks supported conceptual reinforcement and skill development. In addition, 80.77% of students agreed that the exercises required active calculation and improved their numerical skills (Q16), demonstrating engagement with computational practice in a meaningful context. Finally, 70% of students felt that the explanations accompanying the mathematical activities strengthened their understanding of mathematical principles (Q17). These perceptions are closely aligned with teachers’ observations: all STEM teachers agreed that the activities strengthened students’ mathematical and analytical skills, promoting critical thinking and problem-solving. Notably, even history teachers, whose expertise lies outside mathematics, recognized that students were meaningfully engaged, collaborating to solve problems, compare strategies, and correct one another’s errors.

Although the increase in mathematical knowledge and skills is not formally examined, and thus it can be recognized as a limitation of the present study, the overall feeling from the participants is that the engaging and collaborative nature of the tours promotes both individual learning and teamwork. Even if the students had the required mathematical skills prior to their engagement with the tours, the application of their knowledge and skills in real problems strengthened their competencies.

The analysis of questions Q12 and Q19 suggests that the pedagogical tours were generally suitable for students with different abilities, promoting inclusivity and collaboration. Responses to Q12 were mixed: half of the participants (50%) agreed that the exercises were appropriately challenging, while 33.33% disagreed. This variation likely reflects the diversity of students’ mathematical backgrounds and comfort levels with problem-solving tasks. Further, collaboration emerged as a particularly strong feature of the tours. In Q19, 79.49% of students agreed or strongly agreed that the tours helped them collaborate with their classmates, demonstrating that the group-based, inquiry-oriented format supported peer learning and mutual assistance. From the teachers’ perspective, the inclusion of storytelling elements was particularly praised for promoting empathy, which contributes to a positive and inclusive atmosphere. Teachers noted that the storytelling approach made learning accessible to students with diverse learning styles and abilities (Zazkis & Liljedahl, 2019). STEM teachers specifically highlighted that contextualizing mathematical activities within the tours significantly improved student understanding and participation. Moreover, they observed that students were not only learning mathematics but also gaining insights into history and culture—subjects that are often challenging to teach in a traditional classroom setting. This interdisciplinary approach further supports students with different strengths and learning preferences. By fostering collaboration, empathy, and diverse educational experiences, the tours effectively accommodate a wide range of student needs and preferences.

The fourth research question examines whether students retain mathematical concepts better through experiential learning activities like pedagogical tours with embedded math tasks. The results support those of other research studies (Indriayu, 2019; Weinberg et al., 2011). Students’ recognition of mathematics as important in daily life (Q2) increased from 30.77% to 58.97%, while agreement that mathematics can be taught outside the classroom (Q8) rose dramatically from 17.95% to 78.2%, demonstrating the impact of learning in real contexts. Interest in linking mathematics with history and culture (Q7) also grew from 20.51% to 58.97%, highlighting the value of interdisciplinary connections. Although students continued to perceive school mathematics as somewhat disconnected from real-world problems (Q6), the tours clearly helped them appreciate mathematics as relevant, engaging, and applicable beyond the classroom. Moreover, 87% agreed that the tours improved their understanding of the cities’ history and culture (Q18), suggesting that contextualized, place-based experiences promote deeper and more lasting mathematical learning. From the teachers’ perspective, real-world examples and visits to specific sites significantly improved students’ ability to understand and retain mathematical concepts. They noted that students were more attentive and active during the pedagogical tours than in traditional classroom settings, and the need for interventions to maintain order was notably reduced.

6. Conclusions

This study demonstrates that embedding mathematical problems within cultural tours in a city or in some other place (e.g., urban, suburban, areas of archeological interest, etc.) is an effective approach for increasing student engagement, promoting inclusivity, and enhancing mathematical understanding. By integrating storytelling, gamification, and real-world contexts, the approach transforms abstract mathematical concepts into engaging, relevant experiences. A structured development approach was followed involving city selection, historical research, content development, creation of analytical solutions, and finalization of materials for publication. Collaboration among partners and experts, along with continuous feedback and refinement, ensured high-quality content and effective dissemination of the approach.

Although the process seems time-consuming, with the utilization of AI tools, graphical tools with integrated AI modules and experienced teachers, the creation and continuing enrichment of mathematical tours is a manageable process. The sharing of the designs into repositories could also facilitate reuse and adaptation by other educators, gradually reducing the workload and improving the quality of the tours over time. The involvement of students in the creation in the context of class projects could also help the development of more tours integrating the views of students as well.

The tour context was a distinctive and meaningful element of the program, turning mathematics learning into an active, place-based experience. By exploring mathematical ideas within real urban settings, participants were able to connect abstract concepts with physical structures, spatial relationships, and cultural artifacts. This approach encouraged inquiry, collaboration, and reflection, helping learners see mathematics as part of everyday life and human creativity rather than a set of formal rules. Moving through the city and engaging with authentic contexts made learning more engaging and relevant, showing that mathematics can be observed, discussed, and experienced beyond the classroom.

The specific tour has been tested with 78 students and 6 teachers. The findings indicate that the pedagogical tour significantly enhanced student engagement, collaboration, and enjoyment in learning mathematics. Students reported improved motivation, teamwork, and appreciation of real-world applications of mathematical concepts. Teachers noted the interdisciplinary nature of the tour, which combines cultural, historical, and mathematical learning, making it accessible to students of diverse abilities. Teachers also supported that this approach is engaging and that students can acquire mathematical skills more effectively.

While the tour was generally effective, we need to underline the time-consuming nature of content creation and the limitations in formally measuring mathematical knowledge improvements. Formal assessments of mathematical knowledge retention should be implemented to strengthen the evidence base. By comparing our approach with traditional methods and focusing on groups who have lower abilities in mathematics, we could further research the effectiveness of our approach. Developing more interactive versions that could improve the immersion of students is another research direction. Overall, our work contributes to the literature on alternative, more joyful and engaging learning approaches to mathematics.