Unveiling Mathematical Creativity: The Interplay of Intelligence, Intellect, and Education

Abstract

Mathematical creativity remains a complex and often contested construct, with its definition and measurement still subject to debate. While the four classic indicators—elaboration, flexibility, fluency, and originality have provided a foundation for research, they alone cannot resolve the field’s conceptual “fuzziness.” This paper examines mathematical creativity through three intersecting lenses: intelligence, intellect, and education. Intelligence is viewed as cognitive capacity, providing the mental resources for abstraction, problem transformation, and reasoning. Education offers the conceptual tools, heuristics, and domain knowledge necessary for productive problem solving. Intellect—closely associated with the personality trait of openness—supports curiosity, tolerance for ambiguity, and exploration. We argue that the interaction among these three factors influences the likelihood of producing mathematically creative processes and products. Drawing on contemporary research, we propose a model that integrates cognitive ability, educational attainment, and personality characteristics to better predict creative potential. This model highlights how educational environments can either foster or inhibit creativity and suggests that creativity is not a fixed trait but a dynamic outcome shaped by opportunity, knowledge, and affect. We conclude by discussing implications for assessment, curriculum design, and future research, encouraging a more nuanced approach to cultivating mathematical creativity across diverse educational and cultural contexts.

1. Introduction

Mathematics is both a creative endeavor and a versatile tool—an applied discipline and an art-like pursuit. Nevertheless, many encounter it primarily through formal schooling, where it is often presented as a rigid, abstract system of rules leading to correct answers. While mathematical knowledge is essential in many professions (Zager, 2017), developing the imagination needed to address complex, real-world problems requires moving beyond this narrow framing. Students benefit from experiencing mathematics as a way of thinking, pattern-finding, and imaginative exploration.

Mathematical creativity has been conceptualized in multiple ways. Poincaré (1913) analyzes his own creative process to theorize how mathematicians arrive at new discoveries. He argued that mathematical discovery is not solely a product of conscious logic but also heavily relies on the subconscious, operating through periods of incubation and culminating in moments of sudden insight. Wallas (1926) built on Poincaré’s work describing creativity through the Gestalt stages of preparation, incubation, illumination, and verification. The influence of Poincaré’s thoughts is prominent in Jacques Hadamard’s writings on the psychology of invention in mathematics (Hadamard, 1945). Krutetskii (1976) characterized mathematical creativity as a multidimensional construct involving problem formation, invention, independence, and originality. Drawing on Torrance (1979), other researchers have emphasized fluency, flexibility, originality, and elaboration, sometimes adding sensitivity—critical evaluation of standard methods. Across these perspectives, mathematical creativity develops over time and is nurtured by rich, reflective experiences.

Rhodes (1962) synthesized forty definitions of creativity into four dimensions—person, product, process, press—expanded by Mann (2020) to include a fifth: problem.

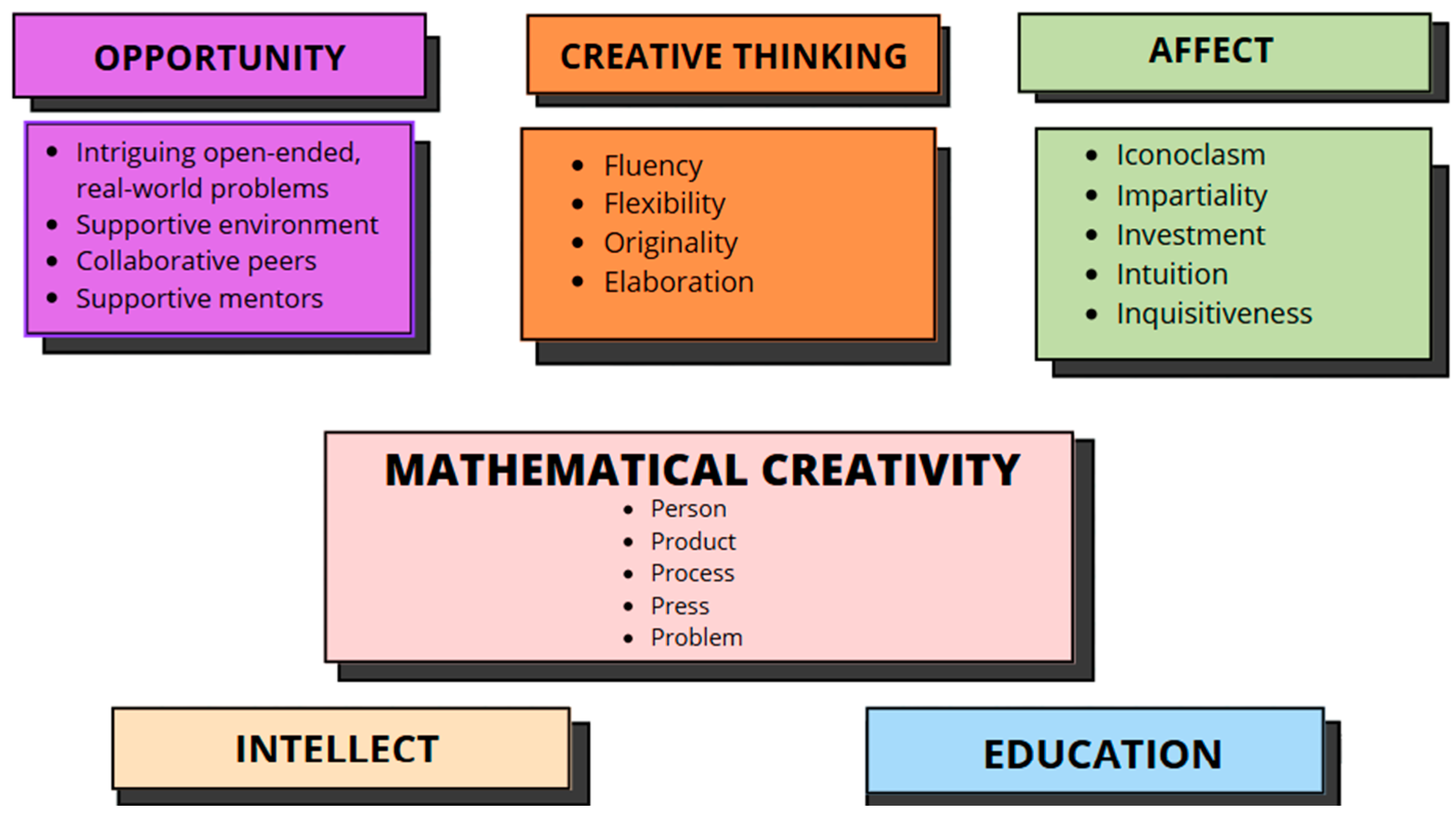
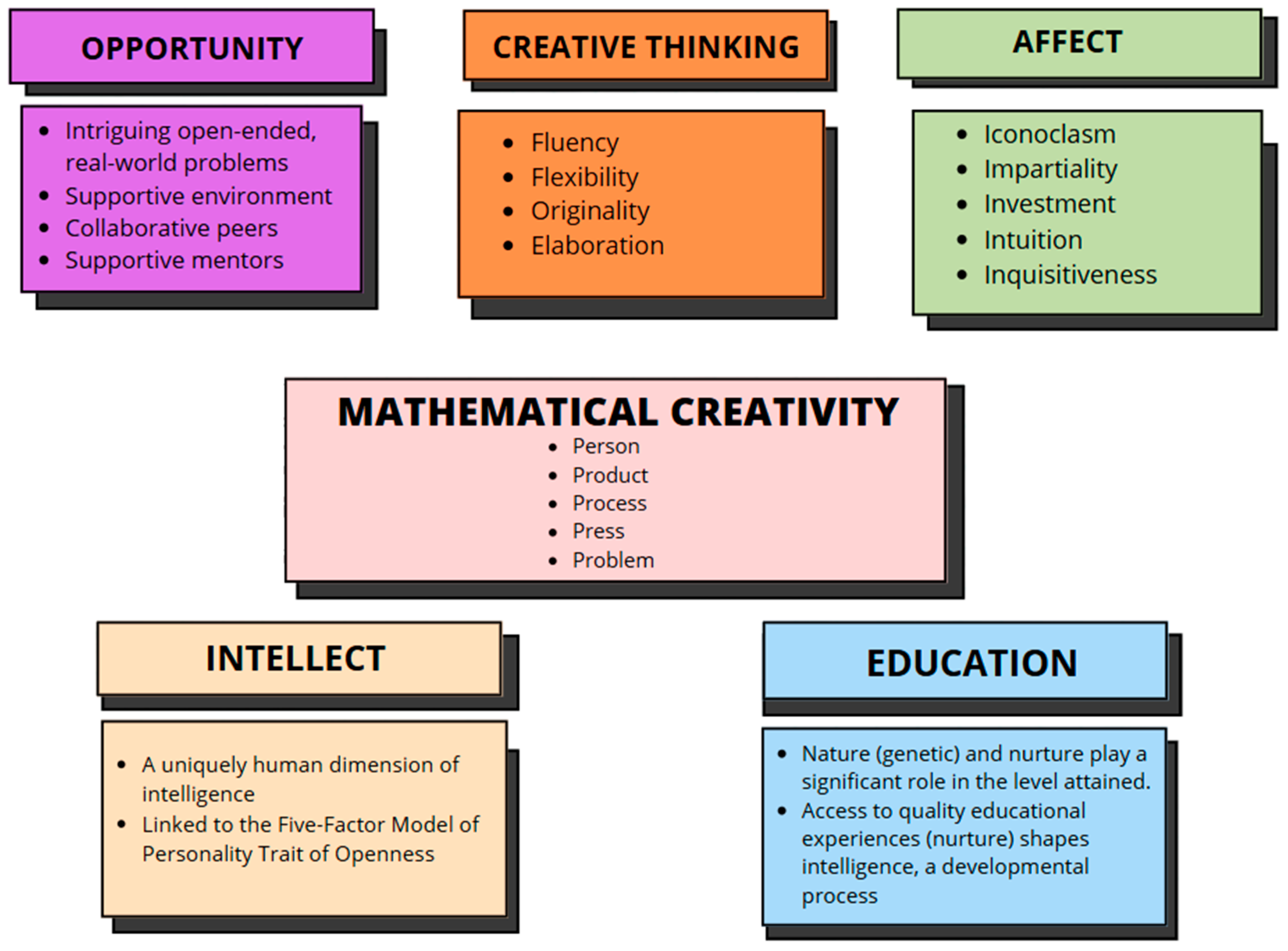
• Person—Traits such as curiosity, openness, risk-taking, and persistence influence creative potential.
• Product—Creative outcomes are novel and valuable relative to the creator’s expertise.
• Process—Iterative and nonlinear, creativity extends beyond standard rules (Wallas, 1926; Pólya, 1962).
• Press—Supportive, collaborative environments foster creativity.
• Problem—Creativity often begins with meaningful, challenging problems, frequently involving generalization or reframing.

The terminology surrounding mathematical creativity varies. Mann (2006, 2020) links it to beauty, echoing portrayals of mathematics as an aesthetic discipline (Breitenbach & Rizza, 2018). Ford and Harris (1992) define it as “a modifiable, deliberate process that exists to some degree in each of us… verified through the uniqueness and utility of the product created” (p. 187). “Uniqueness” corresponds to originality—one of the four widely cited pillars of mathematical creativity, along with flexibility, fluency, and elaboration (Imai, 2000; Leikin, 2013; Suherman & Vidákovich, 2022), further detailed by Sriraman (2009) and Sadak et al. (2022). Despite decades of research, mathematical creativity remains a “fuzzy psychological construct” (Kozlowski et al., 2019), making its identification elusive. Chamberlin and Mann (2021) emphasize that it need not be rare; affective factors influence its emergence and can be deliberately cultivated.

Beghetto and Kaufman’s (2007) Four C model further distinguishes types of creativity:

• Big-C—Transformative contributions that redefine a field.
• Pro-c—Professional-level creativity developed through extensive training.
• Little-c—Everyday creativity in practical contexts.
• Mini-c—Personally meaningful, novel interpretations often seen in learning.

In educational settings, mini-c creativity is most common, emerging as students forge new connections and explore multiple problem-solving approaches. This view aligns with the Vygotskian perspective that creative potential develops through the internalization and transformation of cultural tools via social interaction, reorganizing knowledge in light of personal characteristics and prior understanding (J. C. Kaufman & Beghetto, 2009).

A complementary approach is to examine how individual characteristics, such as intellectand educational experiences, intersect to influence mathematically creative output (Figure 1) This discussion considers intellect to clarify its role in fostering mathematical creativity.

Mathematics is far more than a collection of procedures—it is, as Halmos (1985) observed, a way of thinking that grows through curiosity and exploration. This article builds on that vision by examining how students can engage with mathematics as a creative endeavor. In the spirit of Pólya’s (1962) classic problem-solving framework (Pólya, 1945), we focus on teaching strategies that invite learners to understand problems deeply, devise strategies, and reflect on their reasoning rather than rushing to answers. More recently, Su (2021) has argued that mathematics is a deeply human pursuit that cultivates virtues such as persistence, creativity, and a sense of belonging. Our work is situated at the intersection of these perspectives: it seeks to show how mathematics classrooms can foster not just problem-solving skills, but also the habits of mind and human flourishing that Halmos, Pólya, and Su each champion.

2. Intellect, Education, and Creativity

Before discussing the relationships between intellect, education, and creativity, we consider the question: Is there a difference between intellect and intelligence? The American Psychological Association (APA)’s Concise Dictionary of Psychology (APA, 2009) defines:

Intellect n. an individual’s capacity for abstract, objective reasoning, especially as contrasted with his or her capacity for feeling, imagining, or acting.

Intelligence n. the ability to derive information, learn from experience, adapt to the environment, understand, and correctly utilize thought and reason. There are many different definitions of intelligence, and there is currently much debate, as there has been in the past, over the exact nature of intelligence.

(p. 252)

Often, these terms are used interchangeably, broadly, and inconsistently. “In today’s world, we make extensive use of the word ‘intelligence’. We talk about ‘artificial intelligence’, ‘smart cars’, and ‘multiple intelligences’. Superficially, we all understand each other. However, when we perform a deeper analysis, nobody knows exactly what intelligence is.” (Palanca-Castan et al., 2021, p. 3). In their work, Palanca-Castan et al. drew inspiration from Aristotle in conceptualizing the difference between intelligence in human and non-human systems as differences in purposeful behavior, “a term that can encompass any system that shows behavior that is directed towards some sort of goal” (p. 5) that has three dimensions: access to information, the ability to process information, and the ability to act on that information in a behavioral space.

Within the context of our work, we chose to draw from Palanca-Castan et al. (2021) and view intellect as a uniquely human dimension of intelligence that privileges deliberate reasoning and abstract conceptualization over goal-oriented behavior alone. Where intelligence may involve purposeful action across various systems (human and non-human), intellect implies a more profound, often self-reflective engagement with meaning and ideas.

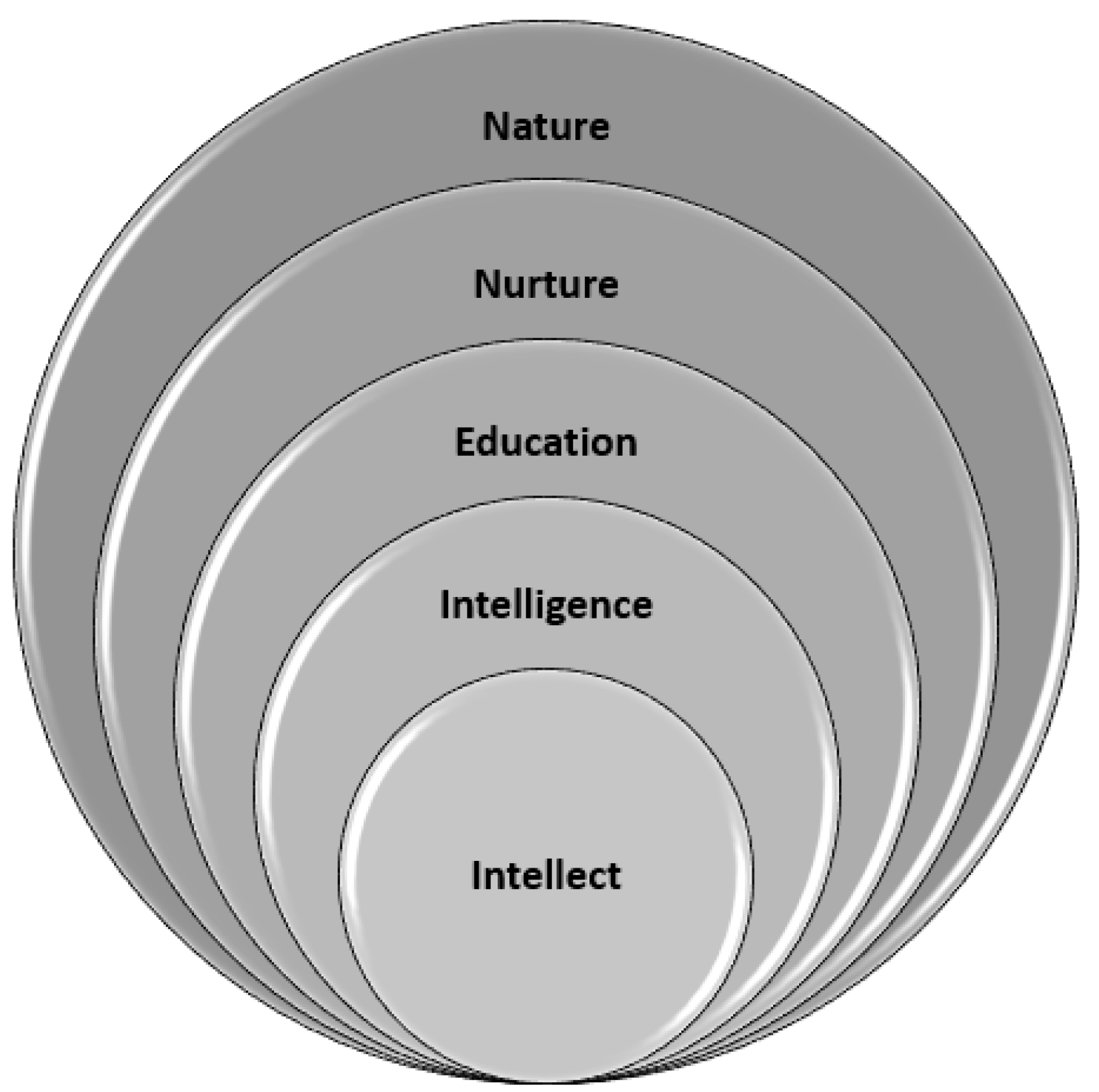
2.1. Relationships Between Intellect and Education

A search of the literature on the relationship between intellect and education will affirm that intelligence and intellect are used interchangeably, broadly, and inconsistently. Education provides access to information and seeks to develop an individual’s ability to process that information in helpful and constructive ways, which closely aligns with APA’s (2009) definition of intelligence. Intelligence is quantified through assessments to determine an Intelligence Quotient (IQ). Intellect assessments are less common and often linked to the personality trait of openness.

Openness, as a high-level construct within the Five-Factor Model of personality traits, includes various facets such as imagination, perceptiveness, and intellect. These facets configure a spectrum of cognitive and behavioral patterns and habits associated with various attributes such as broad-mindedness, creativity, intellectual sophistication, curiosity, cognitive flexibility, receptivity to diverse perspectives and cultural practices, desire for novelty, as well as appreciation for varied experiences, values, and beliefs.

(Abu Raya et al., 2023, p. 1)

In a study of Norwegians with a master’s degree equivalent, Thørrisen and Sadeghi (2023) examined the role of personality in academic performance in secondary and higher education, as well as in the choice of the field of study. The strongest predictors of academic performance were conscientiousness (C) and openness (O) personality.

Unlike the C dimension, which overall showed a positive association across both educational levels (upper secondary school and higher education), the O dimension exhibited divergent relationships in upper secondary and higher education. While O was negatively correlated with student success in upper secondary education, the relationship was positive in particular higher education settings. Given that O is associated with traits such as open-mindedness and intellectual curiosity (Gatzka & Hell, 2018), as well as productive learning strategies like deep and strategic learning (Swanberg & Martinsen, 2010), the negative association in upper secondary education seemed counterintuitive (Thørrisen & Sadeghi, 2023, p. 10). Differences in learning expectations and environment may be a factor here.

Nickerson’s (2011) discussion of the development of intelligence through instruction summarizes differing views and finds that “researchers on intelligence agree that both nature and nurture play major roles in determining intelligence and cognitive performance, despite differences of opinion regarding the relative contributions of the two types of factors” (p. 121) and “that enhancing intelligence through instruction is an ambitious, but attainable, goal (p. 107).

The nature (or genetic) aspects of intelligence are often viewed as a significant influence on the level of education one completes. If IQ tests can measure intelligence, then how those tests are influenced by educational attainment is relevant. In his literature review of the influence of schooling on intelligence, Ceci (1991) offers an alternative view, “namely that schooling exerts a substantial influence on IQ formation and maintenance” (p. 703). Hegelund et al. (2020) conducted a longitudinal study of the Metropolitan 1953 Danish Male Birth Cohort to investigate the influence of educational attainment on intelligence. Their results indicated a positive link between educational attainment and intelligence test scores in both young adulthood and midlife, even after controlling for earlier levels of intelligence. These findings align with the incremental intelligence theorists (Thomas & Sarnecka, 2015). Dweck and Yeager (2019) summarize their research on an incremental intelligence theory they label “growth mindset,” which is the belief that human capacities can be developed —a fundamental goal of education.

Are intellect and intelligence the same construct? They are closely linked, and both have implications for educational practice. Factoring in personality is relevant as intellect is a component of openness that also includes imagination and perceptiveness. Vygotsky (1967/2004) viewed “imagination as the basis of all creative activity” (p. 9) and Abu Raya et al. (2023) write that “creativity … [is] highly related to the personality trait of openness, describes the mental agility needed to perceive and embrace novel esthetic and intellectual information in order to synthesize it with the goal of generating original ideas, concepts and works of art” (p. 2). Intellect and intelligence share common ground; their distinctions highlight the nuanced ways individuals approach learning, creativity, and the pursuit of knowledge. In seeking to understand the nature of mathematical creativity, intellect plays a prominent role. Figure 2 presents a nested view of our understanding of intellect organized around these constructs.

2.2. Relationships Between Intelligence and Creativity

J.P. Guilford’s Presidential address to the American Psychological Association in 1950 sparked a renewed interest in research seeking ways to discover creative potential and promote its development. He defined creativity and a creative personality as follows:

Creativity refers to the abilities that are most characteristic of creative people. Whether or not the individual who has the requisite abilities will produce results of a creative nature will depend upon his motivation and temperamental traits. The creative personality is then a matter of those patterns of traits that are characteristic of creative persons…which include such activities as inventing, designing, contriving, composing, and planning

(Guilford, 1950, p. 444)

The relationship between intelligence and creativity has been explored in various ways, yielding differing perspectives. Guilford’s (1956) Structure of the Intellect (SOI) model viewed the intellect as a three-dimensional construct of operation (five attributes), product (six attributes), and content (five attributes), creating 150 components of intelligence. As one of the first to attempt a comprehensive definition of intelligence, Guilford provided a theoretical framework for exploring the factors that contribute to creativity and sparked modern efforts to gain a deeper understanding of the relationships between intellect and creativity. Within his model, creativity is closely associated with 16 factors representing divergent production grouped into four categories:

• Fluency (which includes word fluency, ideational fluency, associationistic fluency, and expressional fluency) is the ability to produce a large number of ideas.
• Flexibility is the ability to produce a wide variety of ideas.
• Originality is the ability to produce unusual ideas.
• Elaboration is the ability to develop or embellish ideas and to produce many details to “flesh out” an idea. (Baer, 1993; as cited in Baer, 2015, p. 71)

These four categories formed the foundation for the development of numerous creativity assessments; the best-known may be the Torrance Test of Creative Thinking (Torrance, 1974).

The work of Raymond Cattell, John Horn, and John Carroll led to the Cattell–Horn–Carroll (CHC) theory (Schneider & McGrew, 2018), which viewed Spearman’s (1927) general intelligence (g) as a combination of fluid intelligence (gf) and crystallized intelligence (gc). Cattell’s descriptions of both factors read:

Fluid ability has the character of a purely general ability to discriminate and perceive relations between any fundamentals, new or old. It increases until adolescence and then slowly declines. It is associated with the action of the whole cortex. It is responsible for the intercorrelations, or general factors, found among children’s tests and among the speeded or adaptation-requiring tests of adults.

Crystallized ability consists of discriminatory habits long established in a particular field, initially through the operation of fluid ability, but no longer requiring insightful perception for their successful operation.

(Cattell, as cited in Schneider & McGrew, 2018, pp. 102, 104).

Vestena et al. (2020) investigated the relationship between intelligence and creativity and found three models that predominated the literature.

• There exists a strong correlation between creativity and intelligence.
• Intelligence and creativity are independent concepts.
• The relationship between creativity and intelligence is not linear.

Jauk et al. (2013) found similar views:

• Intelligence and creativity are subsets of each other.
• Intelligence and creativity are coincident sets.
• Intelligence and creativity are independent but overlapping sets.
• Intelligence and creativity are entirely disjoint sets (pp. 212–213).

A prominent theory of the relationship between intelligence and creativity is the threshold hypothesis, which suggests that above-average intelligence is a prerequisite for high creativity. Where the threshold falls is a matter of debate and varies depending on the criteria used. Jauk et al. (2013) found evidence that above the threshold, personality factors are more predictive. While literature on creativity and intelligence is abundant, finding work specific to the relationship between intellect and creativity is more challenging. Oleynick et al. (2017) reviewed the history of the openness/intellect construct found that “openness/intellect is the core of the creative personality” (p. 11).

2.3. Intelligence, Education, and Creativity

Mathematical creativity is a complex psychological construct, partly due to the intricate relationships between intelligence and its development through education. Creativity in mathematics is essential for solving novel problems where previously learned methods are ineffective in finding a viable solution and advancing the discipline. Often cited is Ervynck’s (1991) discussion of the role of mathematical creativity as “the first stages of the development of mathematical theory when possible conjectures are framed as a result of the individual’s experience of mathematics as a context” (p. 42). He offered a tentative definition of mathematical creativity:

Mathematical creativity is the ability to solve problems and/or develop thinking in structures taking account of the peculiar logico-deductive nature of the discipline, and of the fitness of the generated concepts to integrate into the core of what is important in mathematics.

(p. 47)

Sriraman et al. (2011) reviewed existing research on mathematical creativity and mathematics education, folding in Ervynck’s (1991) work along with others. In their discussion, Sriraman et al. define two levels of mathematical creativity. At the professional level, mathematical creativity results in original work that significantly extends the body of knowledge and opens new areas of inquiry. This level fits well with Beghetto and Kaufman’s (2007) Pro-C level of creativity. In an educational environment, mathematical creativity involves offering an unusual, insightful solution to a problem, raising new questions to explore, or providing a new perspective on an old problem (Liljedahl & Sriraman, 2006; as cited in Sriraman et al., 2011, p. 120). Work at this level may be at the Little-C or mini-C levels in Beghetto and Kaufman’s model.

Relationships between general intelligence (g), fluid intelligence (gf), crystallized intelligence (gc), openness, and intellect are all in play, but they are still not well understood. Thørrisen and Sadeghi’s (2025) work suggests that the educational environment can foster or hinder creativity. In their article, they cited a study by Brandt et al. (2020) that “discovered that associations between personality and performance varied across school subjects (C strongly predicted performance in maths, but not in language, while O displayed an opposite pattern)” (p. 2). Noted in Brandt’s work is a view of mathematics education as a rigid and structured, “In math, dealing with numbers and equations involves mainly the exact application of fixed mathematical rules” (p. 251), which may leave little room for creative thought.

An environment that encourages creativity is discussed in the National Council of Teachers of Mathematics (NCTM)’s Catalyzing Change series1 which encourages teachers and students to view mathematics as a lens through which to see the world. “When students approach what they encounter with a notice and wondering lens, they have opportunities to broaden their understanding of what mathematics is through understanding and critiquing their world and engaging in the wonder, joy, and beauty of mathematics.” (Wilkerson, 2021, para. 2). Likely, the differences Thørrisen and Sadeghi (2025) found in openness between upper secondary and higher education are due to the way mathematics was encountered in the classroom.

2.4. Levels of Creativity—Revisiting the Four-C Model

Helfand et al. (2017) explore creativity from the perspective of originality, task appropriateness, and context. Originality should be considered, taking into consideration the individual’s level of experience and maturity. The task should be accessible while also offering the opportunity to explore mathematical relationships. Context also matters. For example, the creative work of Vincent Van Gogh, Emily Dickinson, and Nikola Tesla was not fully appreciated or adopted until after their lifetimes. What might be seen as a creative approach to solving a mathematical problem from an elementary student would be a routine, even mundane, task for a graduate student. The Four-C model of creativity (Beghetto & Kaufman, 2007; J. C. Kaufman & Beghetto, 2009, 2013) provides a framework for levels of creativity.

• Big-C Creativity: Eminent creativity that leads to groundbreaking achievements with historical or cultural impact.
• Pro-C Creativity: Professional-level creativity within a specific domain.
• Little-c Creativity: Everyday creativity, solving problems in everyday life.
• Mini-c Creativity: Creativity that is novel and meaningful to the individual.

3. The Relationship Between Mathematical Creativity and Education, Intelligence, and Intellect—A Model to Identify Potential

In their exploratory study of a measure of mathematical creativity for adults, Meier et al. (2021) reported that, “Mathematical creativity showed a positive relationship with intelligence, mathematical competence, and general creativity, but only general creativity as well as numerical intelligence explained the unique variance of mathematical creativity…” (p. 9). Their study adds to the body of research on the relationship between intelligence, mathematical knowledge (competence), and mathematical creativity. In a subsequent study, Meier et al. (2024) investigated relationships between mathematical creativity and Big Five personality traits (openness to experiences/open-mindedness, conscientiousness, extraversion, agreeableness, neuroticism/negative emotionality). Their study found “… that personality traits can explain 9% variance of mathematical creativity scores. Neuroticism, agreeableness, and psychopathy were significant predictors that could explain unique variance in mathematical creativity scores…” (p. 7). However, they found no significant correlations for openness (O) or conscientiousness (C).

In a study on personality across domains, J. C. Kaufman et al. (2010) found openness to have the highest correlation with creativity in mathematics and science (p. 201). S. B. Kaufman et al. (2016) applied a four-factor model of Openness/Intellect, investigating its relationships with creative achievement in the arts and sciences, reporting that the

Two factors relating to Openness (affective engagement and aesthetic engagement) were significantly associated with creative achievement in the arts, whereas two factors relating to Intellect (explicit cognitive ability and intellectual engagement) were significantly associated with creative achievement in the sciences.

(p. 249)

Discriminating between levels of intellect proves to be more challenging, which may be why researchers have fallen back on using an IQ test score as a substitute. Oleynick et al. (2017) believe that

… openness/intellect is the core of the creative personality. This means that the best route to understanding why some people are more creative than others is likely to be through research on openness/intellect. If we can understand why openness/intellect is one of the major dimensions of personality, we may better understand the significance of creativity in human functioning. And if we can understand the various components of openness/intellect and their sources in psychological and biological processes, we will be well on our way to understanding what it is about creative people that enables them to create.

(p. 11)

In our efforts to identify and encourage individuals with creative potential in mathematics, a better understanding of the relationship between education, intelligence (cognitive ability as measured by IQ), and intellect (as measured by the personality trait of openness) is needed. To create a model, we prompted ChatGPT (GPT-5) to create a model for the relationship of high and low education, intelligence, and openness to mathematical creativity, which generated

Table 1. Expected level of mathematical creativity as an outcome of levels of education, intelligence, and openness (OpenAI, 2025; see Appendix A for the full transcript).

Intelligence (IQ)	Education	Openness (Intellect)	Expected Mathematical Creativity	Why
Low	Low	Low	Very Low	Few tools, limited exploration.
Low	Low	High	Low–Moderate	Openness sparks attempts but hits knowledge/skill limits.
Low	High	Low	Low–Moderate	Knowledge present, but little flexible use.
Low	High	High	Moderate	Openness leverages schooling despite lower g.
High	Low	Low	Low–Moderate	Raw ability without tools/habits limits output.
High	Low	High	Moderate–High	Openness turns ability into novel strategies even with sparse schooling.
High	High	Low	High	Strong ability + tools; creativity constrained by low exploration.
High	High	High	Very High	Synergy: rich knowledge, strong ability, exploratory style.

. This model has applications in different educational settings with age-appropriate IQ, personality, and mathematical creativity assessments.

4. The Relationship Between Mathematical Creativity and Education, Intelligence, and Intellect—A Model to Understand Mathematically Creative/Productive Adults

The model in Table 1 can also serve as a better way to understand the emergence of mathematical creativity in adults. The United Nations Educational, Scientific, and Cultural Organization’s (UNESCO) educational classification system offers a structure for establishing educational levels:

Level 0—Early childhood education

Level 1—Primary education

Level 2—Lower secondary education

Level 3—Upper secondary education

Level 4—Post-secondary non-tertiary education

Level 5—Short-cycle tertiary education

Level 6—Bachelor’s or equivalent level

Level 7—Master’s or equivalent level

Level 8—Doctoral or equivalent level

(UNESCO, 2011)

However, it is important to note that access to education remains limited in many economically disadvantaged contexts due to structural, financial, and systemic barriers. Financial constraints often block entry into higher education, while inadequate primary and secondary schooling—caused by under-resourced schools, poor infrastructure, or economic pressures forcing early work—reduces students’ readiness for advanced study. In some cultures, limited recognition of education’s practical value further weakens demand. These challenges are compounded by underdeveloped higher education systems with restricted capacity, reach, and support. Limited educational access reflects inequities in opportunity, not intellectual potential.

For our discussion, we define High and Low Intelligence and Openness as one standard deviation above and below the population mean, respectively.

4.1. High Intelligence/High Education (HI/HE)

This model suggests that individuals with high intelligence and high education (HI/HE) are the most likely to generate mathematically creative products, with openness being a constraining factor. The only real exception to the idea that HI/HE individuals might lead in creative mathematical output is the Einstellung Effect (Bilalić et al., 2008; Ellis & Reingold, 2014), which theorizes that advanced understanding of conventions in a field may negatively influence one’s ability to think creatively in solving problems. In other words, having an in-depth understanding of a domain might be a constraint in idea generation because experts may resort to using established conventions. An individual in this category might have a Ph.D. in an advanced field, working to solve a mathematical modeling problem that alters the path of a satellite in orbit for improved reception. Having potentially worked in the industry for several decades, with a highly advanced degree, such knowledge could serve as a constraint in formulating a response that does not adhere to standard approaches. Highly intelligent/highly educated individuals may not have appropriate affective states (e.g., courage) to be iconoclastic in that they feel that the experts who have shaped the field have exhausted all innovative paths.

This is not to suggest that all such individuals in the HI/HE category are somehow negatively influenced by the Einstellung Effect. Nevertheless, the prospect of an exceedingly advanced level of knowledge in a domain negatively influencing creative output exists. This occurrence may be due, in part, to a level of automaticity in performing mathematical tasks. HI/HE individuals develop with experience. While automaticity is often associated with expertise, it may lead to impaired performance. Experts might overlook creative opportunities when their habitual, automatic responses take over, bypassing deliberate thought. This decrease in conscious awareness and control can lead to rigidity and reduce attentiveness. As expert-level performance often depends on adaptability and creative thinking, too much reliance on automatic processes can undermine these strengths and negatively impact effectiveness (Dror, 2011). Without novel ideas, vocations that require knowledge in mathematical sciences stagnate (Bahar et al., 2024).

4.2. High Intelligence/Low Education (HI/LE)

Individuals with high intelligence and low education may have vocational pursuits and accomplishments that range from incredibly successful to moderately successful to minimally successful, considering their impact on society and the revenue generated. The final two categories require little explanation, but some readers may be surprised at the first category. Individuals with high intellect and low education have made a considerable impact in society, such as Bill Gates (Microsoft), Michael Dell (Dell Technologies, Larry Ellison (Oracle), and Steve Jobs (Apple). All were accepted into prominent higher education institutions, only to drop out to pursue other interests. Evidence in this category does not suggest that individuals with entrepreneurial ambitions should shun university life, but such anomalies may have become increasingly common in recent decades. In short, a college education may not be the missing ingredient to high societal impact or financial stability that it was once believed to be. Srinivasa Ramanujan, who, without formal training in pure mathematics, made substantial contributions that continue to advance the field,2 is likely the best example of an individual without financial resources to pursue advanced education, yet with a profound understanding of mathematics that far surpasses that of his contemporaries in academia (Cepelewicz, 2024).

4.3. Low Intelligence/High Education (LI/HE)

Individuals with low intelligence who have achieved a high level of education are often goal-oriented individuals with a high degree of persistence, which has allowed them to be successful. Such can make significant contributions to society with the personality trait of openness, once again a determinant in the level of mathematical creativity applied to problems in everyday life (little-c creativity).

4.4. Low Intelligence/Low Education (LI/LE)

While cognitive impairments may contribute to lower levels of intelligence or educational attainment, the relationship is not straightforward. If intelligence, as measured by IQ tests, is shaped by access to education, then limited educational opportunities may artificially suppress measured intelligence. Restricted schooling also reduces exposure to formal mathematical concepts, yet it does not erase intuitive or informal mathematical reasoning. For example, research with Brazilian street vendors (Nunes et al., 1985) found that children with little formal education solved arithmetic problems effectively in real-life selling contexts. However, they struggled with the same problems if presented in a traditional classroom textbook format. Their creativity emerged in the form of context-specific strategies.

Educational inequities and inadequate infrastructure disproportionately affect large segments of the population, leading to deficits in human capital and reinforcing cycles of poverty and marginalization. Identifying and fostering mathematical creativity should therefore extend across all sectors of society, not only among the highly educated.

5. A Revised Model of Contributing Factors in Mathematical Creativity

Research on the relationship between intelligence and creativity continues to yield mixed or modest correlations, particularly within mathematical domains. This paper introduces a revised model that differentiates intelligence from intellect and situates both within the broader influence of educational experiences. In this model, mathematical creativity emerges from the interaction of three factors: cognitive ability, educational access and depth of learning, and openness/intellect as a dispositional trait.

The model conceptualizes intelligence as domain-general cognitive capacity, education as access to and engagement with mathematical tools and conceptual structures, and intellect as openness to experience, curiosity, and willingness to explore uncertainty. These three dimensions interact rather than operate independently. High levels of education can amplify or suppress cognitive ability; intellect can influence whether knowledge is applied flexibly; and intelligence can shape how deeply individuals benefit from instruction. The resulting framework provides a more coherent account of why mathematically creative output varies widely across learners and contexts.

This perspective aligns with Pólya’s (1945) emphasis on understanding, planning, and reflection, Halmos’s (1985) call to “think deeply of simple things,” and Su’s (2021) framing of mathematics as a pursuit grounded in human flourishing. When learners are encouraged to justify their thinking, notice patterns, and explore multiple approaches, the interplay among knowledge, intellect, and ability becomes visible and productive.

The revised model also foregrounds the role of the inequitable. In the spirit of Pólya’s (1945) reminder that teaching mathematics is less about delivering solutions and more about guiding students to think—to understand the problem, plan, try, and reflect—this work underscores the importance of cultivating habits of mind that encourage persistence and reflection. Halmos’s (1985) call to “think deeply of simple things” resonates here: by inviting students to justify their reasoning, connect ideas, and explore multiple strategies, we help them transform simple observations into meaningful mathematical insights. Su (2021) deepens this vision by framing mathematics as a pursuit of human flourishing. When students experience mathematics not merely as the search for right answers but as a way to belong, persist, and delight in discovery, creativity becomes a pathway to dignity and joy rather than just an intellectual exercise. When access to mathematical learning varies widely, measured ability and observed creativity may reflect structural constraints rather than actual potential. By highlighting these interacting factors, the model offers a more nuanced basis for interpreting mathematical creativity across diverse settings. Adding aspects of intellect and education to the individual characteristics that influence the emergence of mathematical creativity (Figure 3) provides a more comprehensive and equitable framework for understanding how mathematical creativity develops—and why it may remain unrealized for many learners despite underlying potential.

6. Conclusions

This paper contributes to the literature by emphasizing that mathematical creativity is not a fixed trait, but a dynamic outcome shaped by cognitive, educational, and dispositional factors. The revised model underscores the need to consider how intelligence, educational opportunity, and intellect jointly influence the development and expression of creative mathematical thinking.

Three specific contributions advance this work. First, the distinction between intelligence and intellect helps clarify the role of openness—expressed through curiosity, flexibility, and tolerance for ambiguity—in mathematical creativity. Second, the integrated interaction-based framework offers a unified theoretical approach to understanding creative output. Third, the introduction of a testable 2 × 2 × 2 model provides a practical tool for researchers and educators seeking to interpret learner profiles and examine creative potential in systematic ways.

Future research should investigate how different instructional environments support creativity across a broad range of learners, how dispositional traits such as openness interact with increasing mathematical knowledge, and how creativity can be assessed in ways that reflect diverse cultural and educational contexts. Continued refinement of this framework may support more equitable and comprehensive understandings of mathematical creativity and help guide instructional practices that foster it.