Fostering Reflection and Attention to Enhance Struggling Students’ Mathematical Problem Solving—A Case Study
Abstract
1. Introduction
2. Theoretical Background
2.1. Learning Mathematics and Individual Differences
2.2. Why Struggling Students Have Difficulty in Problem Solving
2.3. Rethinking P-S Teaching Strategies: Toward a Unified Pedagogical Approach
2.4. Attention and Mathematical Problem-Solving
2.5. Theory for Data Analysis
3. Materials and Methods
3.1. The CCRSRC Intervention Process
3.2. Research Goals
3.3. Research Question
3.4. Participant Profiles
3.5. Research Population
3.6. Rationale for Selecting an Illustrative Example
- Tri-stage development: Progressing through all three levels—building SCs at the formulation level, transitioning to the algorithmic level, and finally developing heuristic-level connections
- Bi-stage development (formulation to algorithmic): Building SCs at the formulation level followed by transition to the algorithmic level; heuristic strategies were rarely or never developed
- Bi-stage development (algorithmic to heuristic): Formulation-level connections were rarely or never employed; focus shifted from algorithmic to heuristic levels
- Bi-stage development (formulation to heuristic): The algorithmic level was typically bypassed, with students moving directly from formulation to heuristic connections
3.7. One-on-One Intervention—General Procedure
3.8. Qualitative Research Design: Rationale and Methodological Approach
3.9. Reflexivity and Trustworthiness in Qualitative Research
3.10. Data Analysis
4. Results
4.1. Micro View: Ronny’s Intervention Sessions
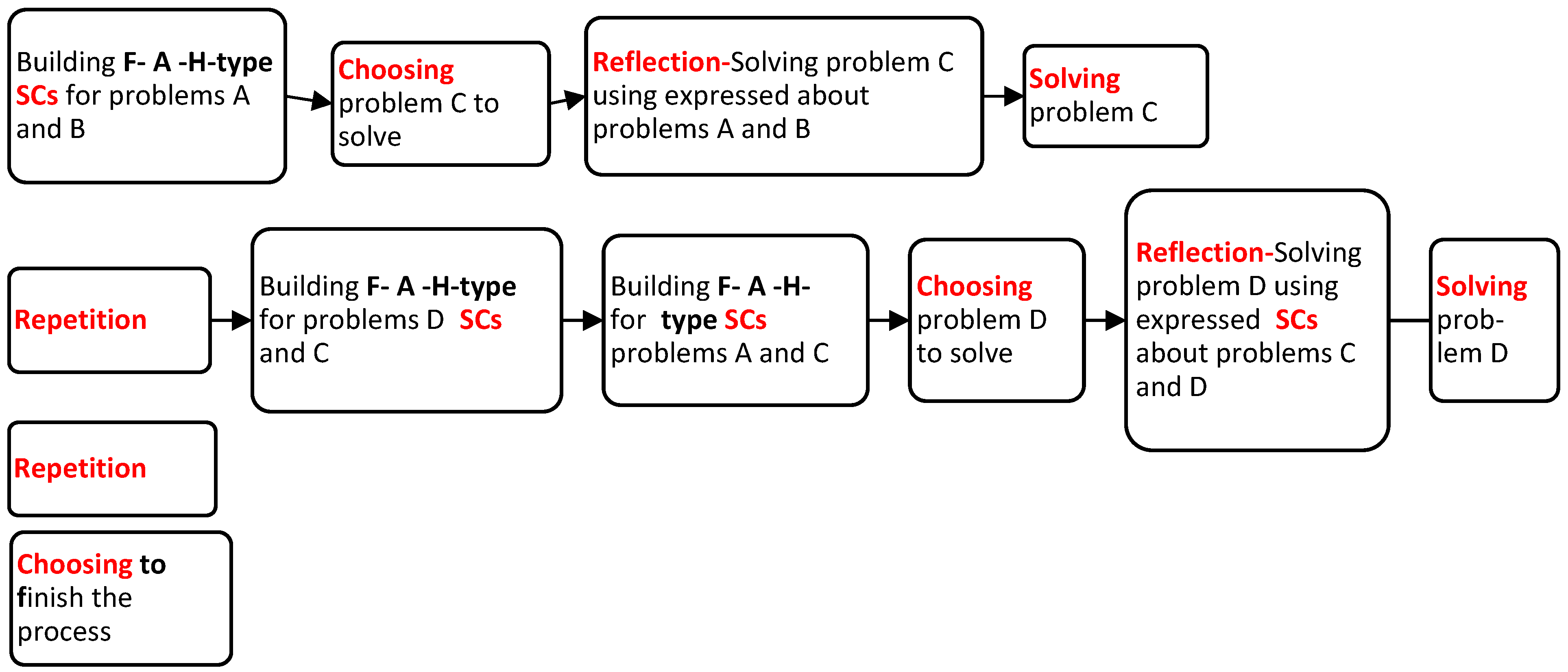
4.2. First Intervention Session: Solving Five Problems by CCRSRC Actions
Description of the CCRSRC Flowchart
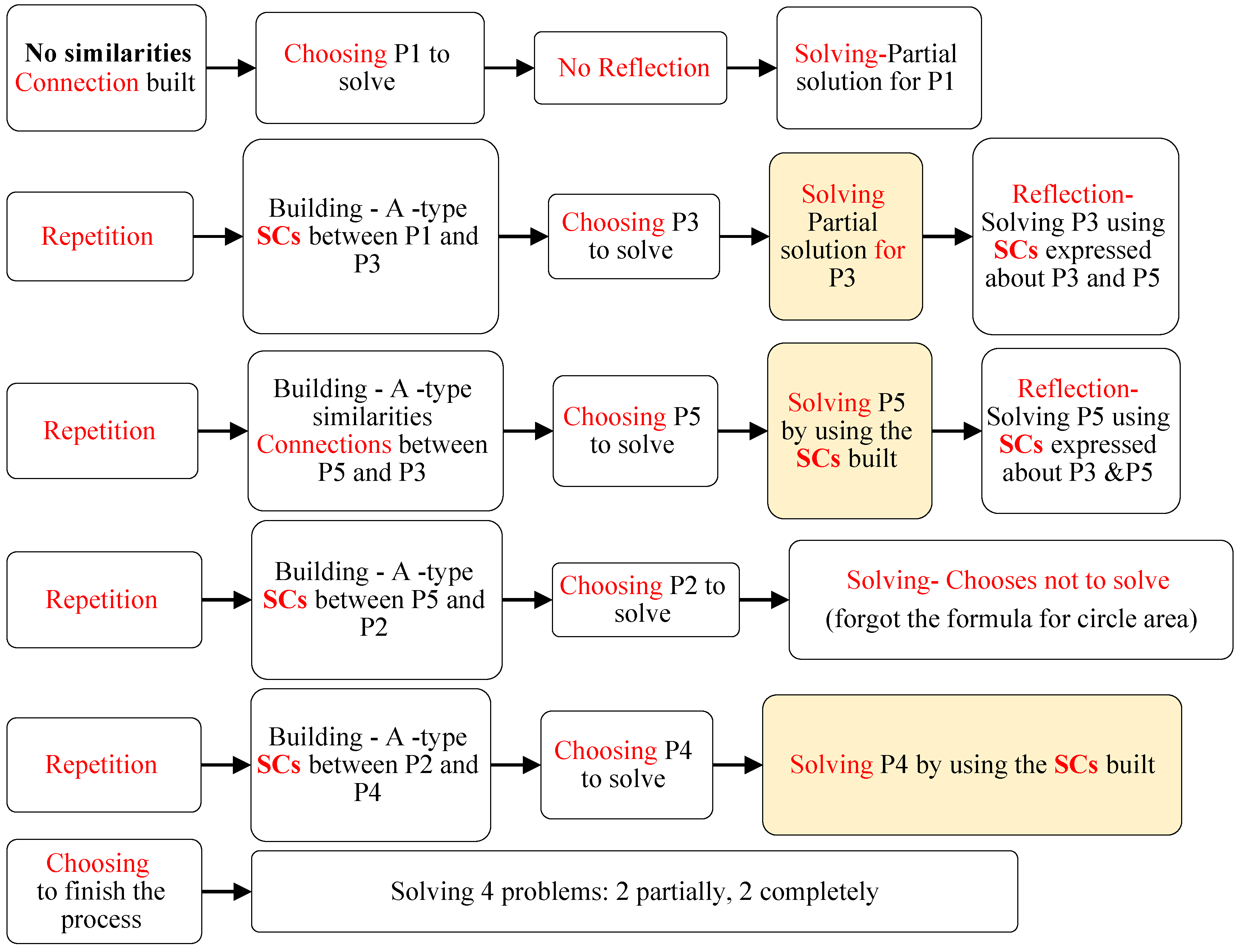
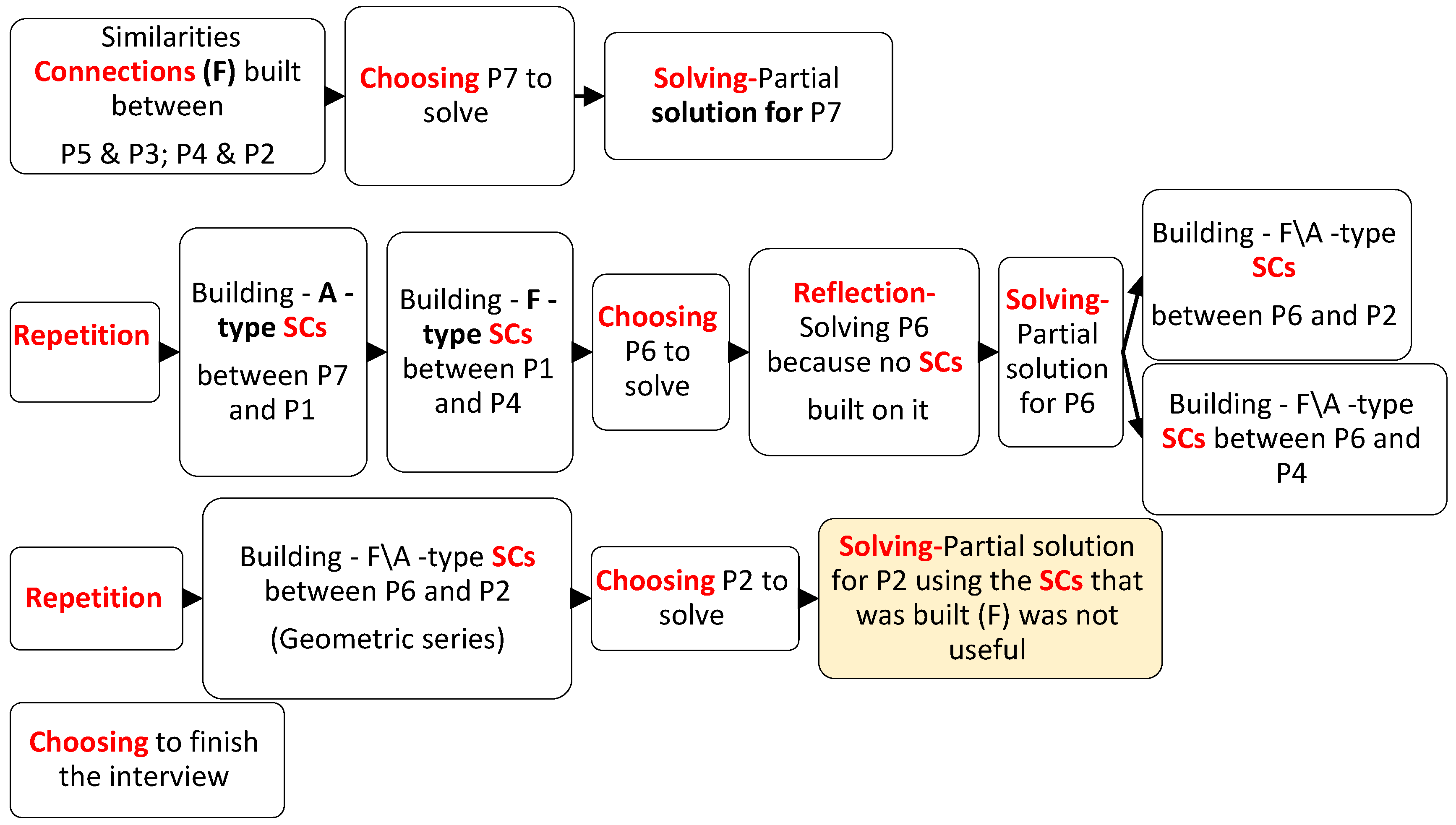
4.3. Second Intervention Session: Solving Seven Problems by CCRSRC Actions
Description of the CCRSRC Flowchart
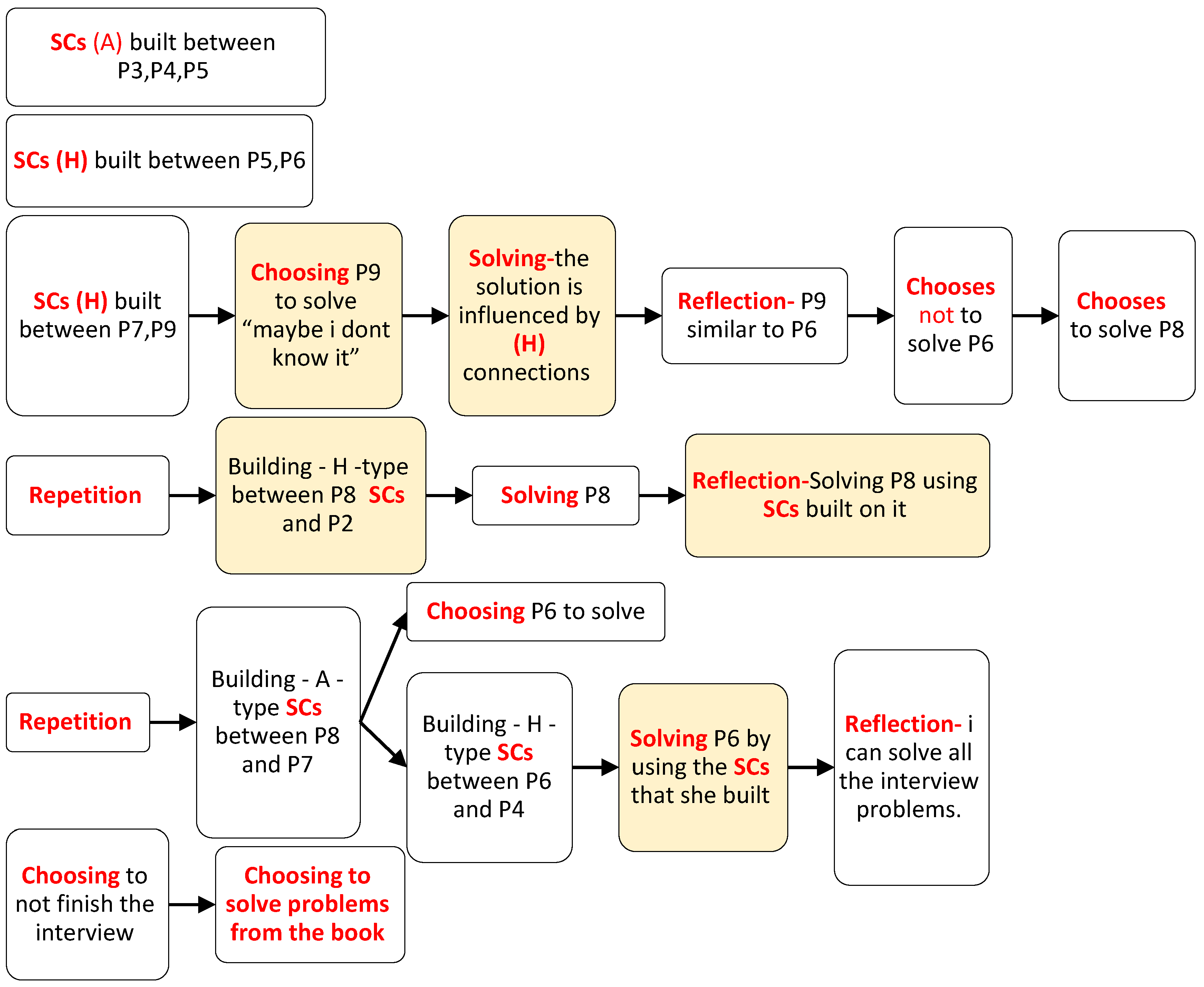
4.4. Third Intervention Session: Solving Nine Problems by CCRSRC Actions
Description of the CCRSRC Flowchart
4.5. Ronny’s Intervention Summary
4.6. Macro View: Participants’ Attention Levels in a One-on-One Intervention
5. Discussion
Conclusions That Can Be Drawn
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CCRSRC | Connections; Choice; Reflection; Solving; Repetition; Choice |
| SCs | Similarity Connections |
Appendix A. (Ovadiya, 2025)
| Session No. | Problems |
|---|---|
| 1 |
|
| 2 | Problems 1 to 5 plus …
|
| 3 | Problems 1 to 7 plus …
|
Appendix B
| Problem/Action | Ronny’s Observed Behavior | CCRSRC Action | Mason’s Level of Attention | Notes/Interpretation |
|---|---|---|---|---|
| P3 and P5 | Noted connection: both geometric progression | Connections (SC) | Holding wholes → Discerning details | Initially sees general pattern, then identifies a specific connection |
| P2 and P4 | Recognized additional connection after comparing data | Connections (SC) + Reflection | Recognizing relationships | Moves beyond superficial similarity to recognize relational structure |
| P7 | No SC identified → chose to solve | Choice + Solving | Recognizing relationships | Chooses unfamiliar problem to generate new connections |
| P7 and P1 | Reflected: “both require solving quadratic equation” | Reflection | Discerning details → Perceiving properties | Recognizes algorithmic property; unclear if deep or superficial |
| P6 | Could not create SC → solved problem → discovered SCs with P2 and P4 | Solving + Reflection + Connections | Recognizing relationships | Problem-solving leads to new connections, illustrating bidirectional attention shift |
| P2 | Sketched circles but could not proceed | Solving | Holding wholes → Discerning details | Task definition without solution; attention limited by knowledge gaps |
| Termination | Chose to stop | — | — | Session ended; attention did not progress to reasoning based on perceived properties |
References
- Barrouillet, P., Bernardin, S., Portrat, S., Vergauwe, E., & Camos, V. (2007). Time and cognitive load in working memory. Journal of Experimental Psychology: Learning, Memory, and Cognition, 33(3), 570–585. [Google Scholar] [CrossRef]
- Busetto, L., Wick, W., & Gumbinger, C. (2020). How to use and assess qualitative research methods. Neurological Research and Practice, 2(1), 14. [Google Scholar] [CrossRef]
- Cai, D., Ge, Y., Wang, L., & Leung, A. W. (2024). Improvement in math ability and cognitive processing in children with low attention: An intervention based on PASS theory. Journal of Intelligence, 12(9), 83. [Google Scholar] [CrossRef] [PubMed]
- Carcoba Falomir, G. A. (2019). Diagramming and algebraic word problem solving for secondary students with learning disabilities. Intervention in School and Clinic, 54(4), 212–218. [Google Scholar] [CrossRef]
- Castro-Sánchez, M., Zurita-Ortega, F., García-Marmol, E., & Chacón-Cuberos, R. (2019). Motivational climate in sport is associated with life stress levels, academic performance and physical activity engagement of adolescents. International Journal of Environmental Research and Public Health, 16(7), 1198. [Google Scholar] [CrossRef]
- Chen, O., Paas, F., & Sweller, J. (2023). A cognitive load theory approach to defining and measuring task complexity through element interactivity. Educational Psychology Review, 35(2), 63. [Google Scholar] [CrossRef]
- Colletti, L., Krik, S., Lugli, P., & Corni, F. (2023). Teaching and investigating on modelling through analogy in primary school. Education Sciences, 13(9), 872. [Google Scholar] [CrossRef]
- Common Core State Standards Initiative (CCSSI). (2012). Introduction: Standards for mathematical practice. Available online: https://learning.ccsso.org/wp-content/uploads/2022/11/ADA-Compliant-ELA-Standards.pdf (accessed on 14 October 2025).
- Das, J. P., Naglieri, J. A., & Kirby, J. R. (1994). Assessment of cognitive processes: The PASS theory of intelligence. Allyn & Bacon. [Google Scholar]
- Doz, E., Cuder, A., Pellizzoni, S., Granello, F., & Passolunghi, M. C. (2024). The interplay between ego-resiliency, math anxiety and working memory in math achievement. Psychological Research, 88, 2401–2415. [Google Scholar] [CrossRef] [PubMed]
- Erath, K., Ingram, J., Moschkovich, J., & Prediger, S. (2021). Designing and enacting instruction that enhances language for mathematics learning: A review of the state of development and research. ZDM–Mathematics Education, 53, 245–262. [Google Scholar] [CrossRef]
- Fiorella, L., & Mayer, R. E. (2016). Eight ways to promote generative learning. Educational Psychology Review, 28, 717–741. [Google Scholar] [CrossRef]
- Fuchs, L. S., Bucka, N., Clarke, B., Dougherty, B., Jordan, N. C., Karp, K. S., & Morgan, S. (2021). Assisting students struggling with mathematics: Intervention in the elementary grades. Educator’s practice guide. WWC 2021006. What Works Clearinghouse. [Google Scholar]
- Gattegno, C. (1970). What we owe children: The subordination of teaching to learning. Routledge and Kegan Paul. [Google Scholar]
- Gersten, R., Chard, D. J., Jayanthi, M., Baker, S. K., Morphy, P., & Flojo, J. (2009). Mathematics instruction for students with learning disabilities: A meta-analysis of instructional components. Review of Educational Research, 79, 1202–1242. [Google Scholar] [CrossRef]
- Hagen, P. (2023). Discourse analysis. In D. Ayton, T. Tsindos, & D. Berkovic (Eds.), Qualitative research: A practical guide for health and social care researchers and practitioners. CAUL OER Collective. Available online: https://oercollective.caul.edu.au/qualitative-research (accessed on 21 March 2023).
- Hennink, M., & Kaiser, B. N. (2022). Sample sizes for saturation in qualitative research: A systematic review of empirical tests. Social Science & Medicine, 292, 114523. [Google Scholar] [CrossRef] [PubMed]
- Hermanowicz, J. C. (2013). The longitudinal qualitative interview. Qualitative Sociology, 36(2), 189–208. [Google Scholar] [CrossRef]
- Hiebert, J., & Carpenter, T. P. (1992). Learning and teaching with understanding. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 65–97). Macmillan. [Google Scholar]
- Hiebert, J., & Grouws, D. A. (2007). The effects of classroom mathematics teaching on students’ learning. In Second handbook of research on mathematics teaching and learning (Vol. 1, pp. 371–404). Information Age. [Google Scholar]
- Holyoak, K. J., Ichien, N., & Lu, H. (2022). From semantic vectors to analogical mapping. Current Directions in Psychological Science, 31(4), 355–361. [Google Scholar] [CrossRef]
- Holyoak, K. J., Ichien, N., & Lu, H. (2023). Analogy and the generation of ideas. Creativity Research Journal, 36(3), 532–543. [Google Scholar] [CrossRef]
- Hord, C., Ladrigan, E., & Saldanha, R. L. (2020). A student with a learning disability and multistep equations with fractions. Learning Disabilities: A Contemporary Journal, 18(1), 113–123. [Google Scholar]
- Hord, C., Marita, S., Ayaz, S., Tomaro, T.-M., Gordon, K., Tunningley, J., & Haskins, S. (2018). Diverse needs of students with learning disabilities: A case study of tutoring two students in algebra. Journal of Research in Special Educational Needs, 18(1), 25–35. [Google Scholar] [CrossRef]
- Jitendra, A. K., Lein, A. E., Im, S. H., Alghamdi, A. A., Hefte, S. B., & Mouanoutoua, J. (2018). Mathematical interventions for secondary students with learning disabilities and mathematics difficulties: A meta-analysis. Exceptional Children, 84(2), 177–196. [Google Scholar] [CrossRef]
- Johnson, H. L., McClintock, E., & Gardner, A. (2021). Opening possibilities: An approach for investigating students’ transfer of mathematical reasoning. In C. Hohensee, & J. Lobato (Eds.), Transfer of learning. research in mathematics education. Springer. [Google Scholar] [CrossRef]
- Justicia-Galiano, M. J., Martín-Puga, M. E., Linares, R., & Pelegrina, S. (2017). Math anxiety and math performance in children: The mediating roles of working memory and math self-concept. British Journal of Educational Psychology, 87(4), 573–589. [Google Scholar] [CrossRef]
- Kaitera, S., & Harmoinen, S. (2022). Developing mathematical problem-solving skills in primary school by using visual representations on heuristics. LUMAT: International Journal on Math, Science and Technology Education, 10(2), 111–146. [Google Scholar] [CrossRef]
- Korstjens, I., & Moser, A. (2018). Series: Practical guidance to qualitative research. Part 4: Trustworthiness and publishing. European Journal of General Practice, 24(1), 120–124. [Google Scholar] [CrossRef]
- Krawec, J. L. (2014). Problem representation and mathematical problem solving of students of varying math ability. Journal of Learning Disabilities, 47, 103–115. [Google Scholar] [CrossRef]
- Lake, W., Wallin, M., Woolcott, G., Boyd, W., Foster, A., Markopoulos, C., & Boyd, W. (2017). Applying an alternative mathematics pedagogy for students with weak mathematics: Meta-analysis of alternative pedagogies. International Journal of Mathematical Education in Science and Technology, 48(2), 215–228. [Google Scholar] [CrossRef]
- Lester, F. K., Jr. (2013). Thoughts about research on mathematical P-S instruction. The Mathematics Enthusiast, 10(1), 245–278. [Google Scholar] [CrossRef]
- Lester, F. K., Jr., & Cai, J. (2016). Can mathematical problem solving be taught? Preliminary answers from 30 years of research. In P. Felmer, E. Pehkonen, & J. Kilpatrick (Eds.), Posing and solving mathematical problems. Advances and new perspectives (Research in mathematics education series) (pp. 117–136). Springer. [Google Scholar] [CrossRef]
- Mason, A., & Singh, C. (2010). Helping students learn effective problem solving strategies by reflecting with peers. American Journal of Physics, 78(7), 748–754. [Google Scholar] [CrossRef]
- Mason, J. (1989). Mathematical abstraction as the result of a delicate shift of attention. For the Learning of Mathematics, 9(2), 2–8. [Google Scholar]
- Mason, J. (2008). Being mathematical with and in front of learners: Attention, awareness, and attitude as sources of differences between teacher educators, teachers and learners. In B. Jaworski, & T. Wood (Eds.), The handbook of mathematics teacher education, Volume 4: The mathematics teacher educator as a developing professional (pp. 31–56). Sense. [Google Scholar]
- Mason, J. (2010). Attention and intention in learning about teaching through teaching. In R. Leikin, & R. Zazkis (Eds.), Learning through teaching mathematics: Development of teachers’ knowledge and expertise in practice (pp. 23–47). Springer. [Google Scholar]
- Mason, J. (2016). Part 1 reaction: Problem posing and solving today. In P. Felmer, E. Pehkonen, & J. Kilpatrick (Eds.), Posing and solving mathematical problems. Research in mathematics education. Springer. [Google Scholar] [CrossRef]
- Masson, N., Dormal, V., Stephany, M., & Schiltz, C. (2024). Eye movements reveal that young school children shift attention when solving additions and subtractions. Developmental Science, 27(1), e13452. [Google Scholar] [CrossRef]
- Masson, N., & Pesenti, M. (2016). Interference of lateralized distractors on arithmetic problem solving: A functional role for attention shifts in mental calculation. Psychological Research, 80(4), 640–651. [Google Scholar] [CrossRef]
- Matthews, J. S. (2018). When am I ever going to use this in the real world? Cognitive flexibility and urban adolescents’ negotiation of the value of mathematics. Journal of Educational Psychology, 110(5), 726–746. [Google Scholar] [CrossRef]
- Miller, G. A. (1956). The magical number seven plus minus two: Some limits on our capacity for processing information. Psychological Review, 29, 106–112. [Google Scholar] [CrossRef]
- Myers, J. A., Witzel, B. S., Powell, S. R., Li, H., Pigott, T., Xin, Y. P., & Hughes, E. M. (2022). A meta-analysis of mathematics word-problem solving interventions for elementary students who evidence mathematics difficulties. Review of Educational Research, 92(5), 695–742. [Google Scholar] [CrossRef]
- Nguyen, T., & Spall, S. (2008). Peer debriefing. In L. M. Given (Ed.), The SAGE encyclopedia of qualitative research methods (pp. 603–604). SAGE Publications. [Google Scholar]
- Norqvist, M., Jonsson, B., & Lithner, J. (2025). Shifts in student attention on algorithmic and creative practice tasks. Educational Studies in Mathematics, 118, 409–428. [Google Scholar] [CrossRef]
- Olmos-Vega, F. M., Stalmeijer, R. E., Varpio, L., & Kahlke, R. (2022). A practical guide to reflexivity in qualitative research: AMEE Guide No. 149. Medical Teacher, 45(3), 241–251. [Google Scholar] [CrossRef]
- Orakcı, Ş. (2021). Exploring the relationships between cognitive flexibility, learner autonomy, and reflective thinking. Thinking Skills and Creativity, 41, 100838. [Google Scholar] [CrossRef]
- Ormerod, T. C., & MacGregor, J. N. (2017). Enabling spontaneous analogy through heuristic change. Cognitive Psychology, 99, 1–16. [Google Scholar] [CrossRef]
- Ovadiya, T. (2021). Implementing theoretical intervention principles in teaching mathematics to struggling students to promote problem-solving skills. International Journal of Mathematical Education in Science and Technology, 54(1), 4–28. [Google Scholar] [CrossRef]
- Ovadiya, T. (2024). Selective memory may be at play during written reflection: Analysis of the noticing of mathematics teacher-researchers. Reflective Practice, 25(6), 711–732. [Google Scholar] [CrossRef]
- Ovadiya, T. (2025). Training problem-solving skills by building connections: The case of struggling high school students. International Journal of Mathematical Education in Science and Technology, 1–25. [Google Scholar] [CrossRef]
- Russo, J., Bobis, J., Downton, A., Hughes, S., Livy, S., McCormick, M., & Sullivan, P. (2020a). Elementary teachers’ beliefs on the role of struggle in the mathematics classroom. The Journal of Mathematical Behavior, 58, 100774. [Google Scholar] [CrossRef]
- Russo, J., Bobis, J., Sullivan, P., Downton, A., Livy, S., McCormick, M., & Hughes, S. (2020b). Exploring the relationship between teacher enjoyment of mathematics, their attitudes towards student struggle and instructional time amongst early years primary teachers. Teaching and Teacher Education, 88, 102983. [Google Scholar] [CrossRef]
- Schoenfeld, A. H. (1985). Mathematical problem solving. Academic Press. [Google Scholar]
- Schoenfeld, A. H. (2022). Why are learning and teaching mathematics so difficult? In Handbook of cognitive mathematics (pp. 1–35). Springer International Publishing. [Google Scholar]
- Shi, Y., Yang, H., Dou, Y., & Zeng, Y. (2023). Effects of mind mapping-based instruction on student cognitive learning outcomes: A meta-analysis. Asia Pacific Education Review, 24(3), 303–317. [Google Scholar] [CrossRef]
- Silver, E. A. (1987). Foundations of cognitive theory and research for mathematics problem-solving. In A. H. Schoenfeld (Ed.), Cognitive science and mathematics education. Routledge. [Google Scholar]
- Simon, M., Saldanha, L., McClintock, E., Akar, G. K., Watanabe, T., & Zembat, I. O. (2010). A developing approach to studying students’ learning through their mathematical activity. Cognition and Instruction, 28(1), 70–112. [Google Scholar] [CrossRef]
- Strohmaier, A. R., MacKay, K. J., Obersteiner, A., & Reiss, K. M. (2020). Eye-tracking methodology in mathematics education research: A systematic literature review. Educational Studies in Mathematics, 104(2), 147–200. [Google Scholar] [CrossRef]
- Swanson, H. L., & Beebe-Frankenberger, M. (2004). The relationship between working memory and mathematical problem solving in children at risk and not at risk for serious math difficulties. Journal of Educational Psychology, 96(3), 471–491. [Google Scholar] [CrossRef]
- Sweller, J. (2024). Cognitive load theory and individual differences. Learning and Individual Differences, 110, 102423. [Google Scholar] [CrossRef]
- Trinchero, R., & Sala, G. (2016). Chess training and mathematical problem solving: The role of teaching heuristics in transfer of learning. Eurasia Journal of Mathematics, Science and Technology Education, 12(3), 655–668. [Google Scholar] [CrossRef]
- U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics. (2022). The nation’s report card: 2022 NAEP mathematics assessment highlighted results at grades 4 and 8 for the nation, states, and districts (NCES 2022-124). Available online: https://nces.ed.gov/pubsearch/pubsinfo.asp?pubid=2022124 (accessed on 2 September 2025).
- Vasileiou, K., Barnett, J., Thorpe, S., & Young, T. (2018). Characterising and justifying sample size sufficiency in interview-based studies. BMC Medical Research Methodology, 18(1), 148. [Google Scholar] [CrossRef] [PubMed]
- Wakhata, R., Mutarutinya, V., & Balimuttajjo, S. (2023). Relationship between active learning heuristic problem-solving approach and students’ attitude towards mathematics. EURASIA Journal of Mathematics, Science and Technology Education, 19(2), em2231. [Google Scholar] [CrossRef]
- Warshauer, H. K. (2015). Productive struggle in middle school mathematics classrooms. Journal of Mathematics Teacher Education, 18(4), 375–400. [Google Scholar] [CrossRef]
- Wiley, J., & Jarosz, A. F. (2012). Working memory capacity, attentional focus, and problem solving. Current Directions in Psychological Science, 21(4), 258–262. [Google Scholar] [CrossRef]
- Witzel, B. S., Myers, J. A., & Xin, Y. P. (2022). Conceptually intensifying word problem solving for students with math difficulties. Intervention in School and Clinic, 58(1), 9–14. [Google Scholar] [CrossRef]
- Xin, Y. P., Kim, S. J., Lei, Q., Liu, B. Y., Wei, S., Kastberg, S. E., & Chen, Y. V. (2023). The effect of model-based problem solving on the performance of students who are struggling in mathematics. The Journal of Special Education, 57(3), 181–192. [Google Scholar] [CrossRef]
- Xin, Y. P., Tzur, R., & Thouless, H. (Eds.). (2022). Enabling mathematics learning of struggling students: International perspectives. Springer. [Google Scholar] [CrossRef]
| Attention Level | Mason’s Definition | Examples from Mason’s Ideas | Example Statement from the Interview, Explanation Keywords/Actions Expressed |
|---|---|---|---|
| Holding wholes | The individual stares at the whole without focusing on particular details. Precedes the phase of making distinctions. | Looking at the whole expression without noticing details | ‘There is a graph here.’ The student’s statement is uttered before reading the question as a result of the visual identification of a graph. Keywords: There is/are, I see, It looks like…, This seems…, I see the whole…, silence before speaking |
| Discerning details | Attention focuses on one particular detail that stands out from the rest of the elements. | Noticing that there is a minus sign. | ‘I am not sure I remember the connection between radius and area of a circle or the geometric series in this question.’ The student is referring to Problem 2. Attention is on context between geometric series, area of a circle, and radius. In his opinion, geometric series are connected to a circle. This diverts his attention from understanding the problem. Concept from the question, shape from a graph, number. Keywords: Here is…, This part…, I notice…, There is a minus/sign/line/number… |
| Recognizing relationships | Discerning specific connections between specific elements. Often occurs spontaneously. | “This is related to what we did earlier.” | ‘I think the vertex of a parabola determines the positive values’ In problem 7, the student has identified a specific relationship between a vertex and positive values in the function. Connection between data and strategy. Keywords: This goes with…, This is like…, It connects to…, If this, then that…, Same as before |
| Perceiving properties | Attention is focused on structured relationships as instantiations of properties. | This triangle is isosceles. The function is continuous here. | ‘. 4, 2, and 68 are all numbers that can be represented with 22n’. The student noticed that the bases of the number are related to the number 2 and expressed a significant connection. If… then… Keywords: It is [even/odd/symmetric/continuous]…, This shape is…, This must be equal/exact/opposite… |
| Reasoning based on perceived properties | Selected properties are attended to as the only basis for further reasoning. | Since the function is continuous, the Intermediate Value Theorem applies. | ‘What percentage of cows yield more than 25 liters per day’. Ahh! I can draw a curve, enter the data ‘25 liters’, and calculate. It is simple!’ The student considers drawing a curve a very important step after reading the problem. She understood the procedure since she created it by plotting data on the graph. Drawing a curve. Keywords: Because… therefore…, Since it is [property], then…, So we can conclude…, That means… |
| Problem | P1 | P2 | P3 | P4 | P5 | Attention Levels | P6 | P7 | Attention Levels | P8 | P9 | Attention Levels | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Student–Session | |||||||||||||
| R1 | A | A | A | A | HW, DD, RR, PP, PRR | ||||||||
| R2 | A | A | A | HW, RR | |||||||||
| R3 | H | H | H | RR, PP, PRR | |||||||||
| OS1 | F(p) | F(p) | HW | ||||||||||
| OS2 | A(p) | A(p) | HW | ||||||||||
| OS3 | H(p) | H(p) | RR, PP, PRR | ||||||||||
| G1 | F(p) | F(p) | HW | ||||||||||
| G2 | A | A | HW, DD, RR, PP | ||||||||||
| G3 | H | H | HW, DD, RR, PP, PRR | ||||||||||
| M1 | A | A | H | HW, DD, RR, PP, PRR | |||||||||
| M2 | F | A(p) | HW, DD, PP | ||||||||||
| M3 | A | A | H | HW, DD, RR, PP, PRR | |||||||||
| L1 | A | A | HW, DD, RR, PP, PRR | ||||||||||
| L2 | A(p) | HW | |||||||||||
| L3 | A | H | H | HW, DD, RR, PP, PRR | |||||||||
| J1 | F(p) | HW | |||||||||||
| J2 | A(p) | A | A | HW, DD | |||||||||
| J3 | H | H | A | DD, RR, PP, PRR | |||||||||
| B1 | F(p) | HW, DD | |||||||||||
| B2 | A | A | A | HW, DD, RR | |||||||||
| B3 | A(p) | DD, RR, PP, PRR | |||||||||||
| Y1 | A | HW, DD | |||||||||||
| Y2 | H | H | DD, RR, PP, PRR | ||||||||||
| Y3 | H | H | DD, RR, PP, PRR | ||||||||||
| C1 | F(p) | HW | |||||||||||
| C2 | A | A | DD, PP, RR, PRR | ||||||||||
| C3 | A | DD, RR, PP, PRR | |||||||||||
| RC1 | A | HW | |||||||||||
| RC2 | A | A | H | DD, PP, RRP | |||||||||
| RC3 | H | H | H | DD, RR, PP, PRR | |||||||||
| O | A | A | HW, DD | ||||||||||
| O | A | H | A | DD, RR, PP, PRR | |||||||||
| O | H | A | H | DD, RR, PP, PRR | |||||||||
| A1 | A(p) | A | HW, DD | ||||||||||
| A2 | A | A | A | DD, RR, PP | |||||||||
| A3 | A | A | H | HW, DD, RR, PP, PRR | |||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ovadiya, T. Fostering Reflection and Attention to Enhance Struggling Students’ Mathematical Problem Solving—A Case Study. Educ. Sci. 2025, 15, 1538. https://doi.org/10.3390/educsci15111538
Ovadiya T. Fostering Reflection and Attention to Enhance Struggling Students’ Mathematical Problem Solving—A Case Study. Education Sciences. 2025; 15(11):1538. https://doi.org/10.3390/educsci15111538
Chicago/Turabian StyleOvadiya, Tikva. 2025. "Fostering Reflection and Attention to Enhance Struggling Students’ Mathematical Problem Solving—A Case Study" Education Sciences 15, no. 11: 1538. https://doi.org/10.3390/educsci15111538
APA StyleOvadiya, T. (2025). Fostering Reflection and Attention to Enhance Struggling Students’ Mathematical Problem Solving—A Case Study. Education Sciences, 15(11), 1538. https://doi.org/10.3390/educsci15111538






