Abstract
In this study, a PRISMA-guided scoping review of research papers on teachers’ epistemic meta didactic–mathematical knowledge with regard to functions is carried out. The objective is to identify the factors that characterize the epistemic meta didactic–mathematical knowledge of teachers who lead epistemically suitable instructional processes for functions. The Web of Science and Scopus databases were used to select 15 papers published between 2019 and 2024 that examine mathematics teachers’ epistemic meta didactic–mathematical knowledge when teaching functions. Two qualitative analyses of the chosen texts were performed. With the support of the R interface for multidimensional analysis of texts and questionnaires, five categories were obtained from the first analysis. Those categories guided the second analysis, which consists of a manual study of the documents. The result is the following characterization of the meta didactic–mathematical knowledge a teacher should have when teaching functions: (1) complexity of functions in the history of mathematics and in the curriculum, (2) personal practice of multiple processes using functions in different contexts, and (3) analysis of the tasks designed in instructional processes and reflection on teaching practice. The main conclusion of this research is that the presence of these contents in teacher preparation programs can contribute to improving the teaching of functions.
1. Introduction
In the specialized literature, various authors have proposed theoretical models that explain the knowledge teachers should have in order to perform their teaching duties effectively (Shulman, 1987; Mishra & Koehler, 2006). Along these lines, Amaya de Armas et al. (2016) stress the importance of identifying the knowledge necessary for teaching mathematics. It is therefore necessary to use a theoretical model that allows inferring and structuring said knowledge.
One of the theoretical approaches that addresses both the analysis of mathematical activity—conceived as historical–social and historical–cultural practice—and the identification of the knowledge necessary for its teaching is the Onto-semiotic Approach (OSA) (Godino et al., 2007, 2019). This approach provides theoretical and methodological tools that facilitate the description and explanation of the teaching and learning processes of mathematics, as well as their assessment in terms of suitability.
The Didactic–Mathematical Knowledge (DMK) model, a refinement of the model proposed by Ball et al. (2008), is found within this framework. This model characterizes teachers’ knowledge based on three dimensions: the mathematical dimension, the didactic dimension, and the meta didactic–mathematical dimension (Pino-Fan & Godino, 2015).
The first two dimensions enable describing and explaining the teaching and learning processes of mathematics, while the meta didactic–mathematical dimension is aimed at assessing these processes by means of a tool called Didactic Suitability Criteria (CIDs), which includes six aspects: epistemic, cognitive, interactional, affective, mediational, and ecological suitability (Godino, 2013; Godino et al., 2006).
In the DMK model of the OSA, according to Pino-Fan and Godino (2015), the mathematical dimension includes two subcategories of knowledge: common content knowledge (sufficient knowledge of a specific mathematical object to solve problems or tasks proposed in the mathematics curriculum of a given educational level) and extended content knowledge (knowledge of mathematical concepts that are either ahead in the current curriculum or in a subsequent educational level).
The didactic dimension of DMK includes the following subcategories of knowledge: specialized knowledge of the mathematical dimension (epistemic facet); knowledge of students’ cognitive development and learning (cognitive facet); knowledge of students’ emotions and attitudes (affective facet); knowledge of classroom interactions (interactional facet); knowledge of resources and tools that can enhance student learning (mediational facet); and knowledge of curricular, contextual, social, political, economic, and other aspects that influence student learning (ecological facet).
The meta didactic–mathematical dimension characterizes the knowledge teachers need to reflect on their own practice, to identify and analyze the set of norms and meta-norms that regulate the teaching and learning processes of mathematics, and evaluate didactic suitability to enhance the design and implementation of these processes (Godino et al., 2009; Pino-Fan et al., 2016).
For each of the components of DMK, the OSA has “theoretical-methodological” tools that have been described and used in various research papers (Godino, 2009, 2012; Godino et al., 2019). For instance, for the development of instruments that enable systematic assessment and analysis of teachers’ knowledge regarding the meta didactic–mathematical dimension, the didactic suitability criteria (DSCs) tool is used as a consensual principle that emerged from trends and research results in didactics of mathematics (Giacomone et al., 2018). According to Font et al. (2010), DSCs are a set of six criteria: epistemic suitability (mathematical quality of the content taught), cognitive suitability (appropriate level of difficulty for students’ prior knowledge), interactional suitability (ability to resolve doubts and difficulties), mediational suitability (resource adequacy), affective suitability (student motivation and involvement), and ecological suitability (alignment with the curriculum and socio-cultural context).
In order for the DSCs to be operational in the analysis and assessment of instructional processes, they are broken down into components and indicators. Table 1 describes the components and indicators of epistemic suitability in detail. The complete table of the six DSCs can be found in Breda et al. (2017).

Table 1.
Components and characteristics of epistemic suitability.
A fundamental principle of the OSA was considered in the case of epistemic suitability. Including nuances specific to each approach, it is (or can be) assumed by other theoretical approaches in the field. The principle is formulated as follows: mathematical objects emerge from practices, which accounts for their complexity (Font et al., 2013; Rondero & Font, 2015). This principle gives rise to a component (representativeness of the complexity of the mathematical object). The objective is to incorporate this complexity into the design and redesign of teaching sequences (Pino-Fan et al., 2013). The component of the representativeness of the complexity of the mathematical object (understood as a plurality of partial meanings) refers to the degree of representativeness and interconnectedness of the institutional meanings implemented (or intended) with respect to a reference meaning (Font et al., 2020; Giacomone et al., 2018). Each of these meanings allows solving different types of problems. Therefore, if the aim is for students to become competent in solving a variety of problems in which the mathematical object in question plays a decisive role, they need a network of partial meanings of that object that are well connected to each other (Burgos et al., 2021; Seckel & Font, 2020).
A function, for example, is a highly complex mathematical object, as shown by its historical evolution. According to Godino et al. (2006), throughout the history of different civilizations, different partial meanings of this notion were generated, some of which served to generalize other pre-existing ones. The authors organized this evolution into four partial senses: tabular, graphical, analytical, and conjunctive sense. These four partial senses somehow summarize the development of the notion of function that was transposed into textbooks through two types of epistemic configurations: formal (or intra-mathematical) epistemic configurations and empirical (extra-mathematical) configurations. The former refer to the conjunctive sense, while the latter refer to a combination of the other three (tabular, graphical, and analytical sense) (Font et al., 2012).
Another example is to consider the teacher’s knowledge in relation to the design and resolution of tasks rich in relevant mathematical processes (richness of processes component), such as argumentation and representational change (Malaspina, 2017; Malaspina & Font, 2010; Malaspina et al., 2019; Torres, 2020). Finally, mathematical knowledge should consider the errors and ambiguities of teachers from a mathematical point of view (error and ambiguity components) (Beltrán-Pellicer & Giacomone, 2018; Font et al., 2024; Sánchez et al., 2022).
Given the above, this research focuses on the meta didactic–mathematical dimension of teacher knowledge, which refers to the following:
The knowledge needed by teachers to: reflect on their own practice, identify and analyze the set of norms and meta-norms that regulate the teaching and learning processes of mathematics, and assess the didactic suitability in order to find potential improvements in both the design and implementation stages of such processes of study.(Pino-Fan et al., 2016, p. 68)
This study mainly focuses on the epistemic facet of meta didactic–mathematical knowledge, and more specifically on the epistemic meta didactic–mathematical knowledge (henceforth EMDMK) mathematics teachers should have to teach functions. As Font (2011) maintains, the notion of function is very important in mathematics education because of its unifying and modeling nature, as well as its epistemic richness and complexity. To improve both initial teacher preparation programs and continuing professional development, it is necessary to explain which elements are present in the EMDMK of those teachers that design and implement suitable teaching and learning processes for functions. For this reason, a scoping review (ScR) was carried out in this field.
A literature review is conducted to answer the following question: “What are the factors that characterize the EMDMK of teachers who lead epistemically suitable instructional processes for functions?” With the aim of improving initial teacher preparation programs and continuing professional development, this study seeks to identify the factors that characterize the EMDMK of teachers in charge of epistemically suitable instructional processes for functions.
2. Methodology
The methodology of this research is framed within the ScR of literature through text data mining, using PRISMA-ScR (Tricco et al., 2018) as part of the protocol development. Document S1: PRISMA-ScR Checklist can be consulted in the Supplementary Materials. The research was organized into three phases. The first phase focused on selecting documents. In the second phase, a lexicometric analysis of the texts was carried out using the R interface for multidimensional analysis of texts and questionnaires (IRaMuTeQ) software version 0.8 alpha 7 to infer initial categories on which to structure the analysis in the third phase. In that last phase, the papers were analyzed without using software in order to identify elements that could enhance the development of secondary school teachers’ EMDMK when teaching functions.
2.1. First Phase: Document Selection Process
As this study aims to characterize the EMDMK mathematics teachers should have when teaching functions, one of the inclusion criteria is for the papers to focus on the mathematical teaching and learning of functions, considering the epistemic dimension.
Another inclusion criterion is the relevance and quality of the documents that serve as the basis for the evidence of this ScR. Because of their broad coverage and rigorous indexing standards, the information sources selected were Scopus and Web of Science (WoS), two major bibliographic databases. Scopus covers approximately 24,500 serial titles from over 5000 publishers in 140 countries, including peer-reviewed journals in the fields of science, technology, medicine, and social sciences, including arts and humanities. WoS contains some 36 million records from over 230 disciplines in science, social sciences, arts, and humanities. The search was narrowed down to papers published between 1 January 2019 and 30 April 2024, as the aim was to review recent work on the topic. This period coincides with the five years prior to the start of this research and the first four months of 2024.
The languages of the documents were limited to English, the language in which most papers are published, and to Spanish and Portuguese, the languages the authors of this study know in depth. The initial idea was to only use journal papers, but given the small number of papers, the following documents were included: journal papers, a master’s thesis, a doctoral dissertation, and conference proceedings.
Given the fact that titles, abstracts, and keywords in papers written in any language are translated into English, the following descriptors in English were used in the search for documents: function, mathematics education, secondary teacher education, and epistemology. Based on these descriptors, the search was initiated in Scopus, restricting it to the title, abstract, and keywords. As shown in Table 2, different search structures were tested, varying the degree of restriction depending on the number of results obtained until a number between 10 and 30 was attained. The same procedure was then repeated when searching the WoS database. However, as this database has a “subject” field, the search structure was entered in that field without having to limit it to the title, abstract, and keywords.

Table 2.
Search structures and number of results.
To examine the documents obtained, first, three were identified that were present in both lists and one that appeared twice in the WoS list. Four papers were thus excluded from the initial total of 34 (see Figure 1). Second, the first author read the title, abstract, and keywords of each paper to decide whether to include or exclude it. A total of 13 documents were accepted. This number was considered acceptable, but expanding the selection would strengthen the research conclusions. Therefore, a master’s thesis and a doctoral dissertation that had been rejected for not being journal or conference papers were also included. Finally, 15 full-text documents were selected and assessed to determine their eligibility. Of those documents, after checking they all met the inclusion criteria, none were excluded (see Figure 1). It is worth mentioning that the first author read all of the papers.
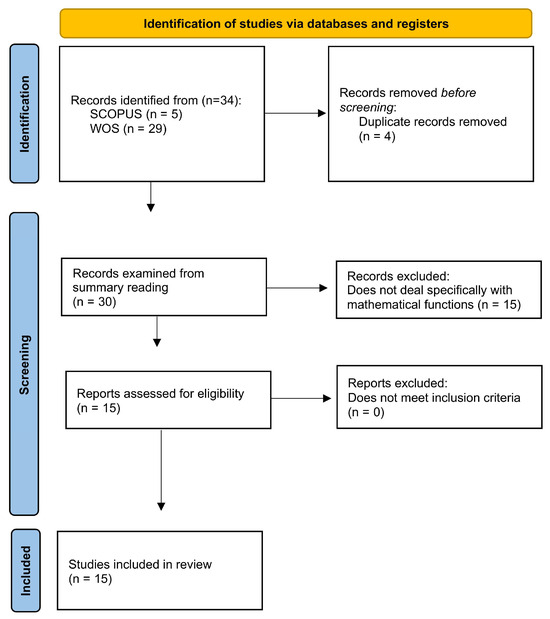
Figure 1.
Flowchart for inclusion and exclusion of papers. Source: Flowchart based on PRISMA 2020 (Page et al., 2021).
Table 3 shows the papers analyzed in this paper. Each one is coded as n_i, where i is the number of the order in which it was included in the paper. The authors, publication year, and database in which it was found are also indicated.

Table 3.
Documents selected for the study.
2.2. Second Phase: Lexicometric Analysis Using IRaMuTeQ
To obtain emerging categories from the texts in the most objective and rigorous way possible, IRaMuTeQ software version 0.8 alpha 7, created by Pierre Ratinaut (University of Toulouse, France) in Ratinaut (2009), was used: “It is a GNU GPL (v2) licensed software that provides users with statistical analysis on text corpus and tables composed by individuals/words. It is based on R software (version 4.5.2) and on python language (version 3.14.0)” (Camargo & Justo, 2013b, p. 1).
In this second phase, the methodology employed has a dual approach. On the one hand, a quantitative approach was used, as the program performs exploratory data analysis using statistical and comparative calculations. On the other hand, using a qualitative approach was key, as it was the authors’ task to interpret and contextualize the data to give them meaning. According to Amaral-Rosa et al. (2024), Lima et al. (2021) and Ramos et al. (2019), creating categories that emerge from software does not invalidate the manual procedure. Both are complementary and can provide different inferences about the same corpus. IRaMuTeQ focuses on information and provides the structure of lexical fields in the corpus and in each of the texts in an accurate and targeted manner (Martins et al., 2022). It shows lexical coexistences or recurring and overrepresented words. It identifies descriptive statistics, obtaining, for example, characteristic shapes, as well as the themes present in the corpus. It also considers the structure, interactions, and distance between the shapes in the corpus, which facilitates interpreting data and inferring categories (Moreno & Ratinaud, 2022). In this study, two of the software analyses were used. First, the Descending Hierarchical Classification (DHC) method was employed. Based on matrix analyses that cross-reference text segments (TSs) (text fragments of approximately three lines in length into which IRaMuTeQ divides the corpus) and words, it obtains classes of TSs that, at the same time, have similar vocabulary to each other, and different vocabulary from the TSs of other classes. The program performs calculations and provides results that allow each of the classes to be described, mainly by their characteristic vocabulary (Camargo & Justo, 2013a). Second, the program provides another manner of presenting results by means of the Correspondence Factor Analysis (CFA) performed on the DHC, which enables verifying the associations of dependencies and independencies of each class. The representation on a Cartesian plane, in which each class is identified by a color, shows these dependency relationships.
To process the documents using IRaMuTeQ, the first step was to create the corpus. This was done using the abstract and conclusion of each of the selected documents. Only these two sections were used in order to focus the programme’s analysis on the parts of the documents that contain the most relevant contributions from the research included in the study corpus. Limiting the size of the text facilitates the process of preparing it for processing in IRaMuTeQ. This limitation does not imply a loss of information, since, as detailed in the third phase of the analysis, the fifteen complete documents was examined manually.
As the chosen language was English, the conclusions of the papers that were not published in that language (n_01, n_04, n_08, n_13, and n_14) were translated. In order for the computer program to work with the corpus, it was necessary to code it following the instructions of Camargo and Justo (2013b): (1) review the entire text, correcting punctuation and/or typographical errors where necessary; (2) standardize, or present only the acronyms or the complete expression of the expressions that can be represented by acronyms; (3) join compound words using underscores instead of hyphens; (4) do not justify texts and do not use bold and/or italics; (5) keep numbers in their numerical form; (6) do not use the following characters: quotation marks, apostrophes, hyphens, dollar signs, percentages, ellipses, and asterisks. Furthermore, the origin of each submitted text was identified for the researcher to be able to identify it throughout the analysis. Therefore, after preparing the corpus, all texts were added to the same file, separated by their respective identifications. These identifications, to be used by IRaMuTeQ, were standardized using command lines represented by four asterisks followed by a space, a new asterisk, and the coding chosen for each text. In this study, the documents were coded by assigning the number corresponding to the order in which they were saved (n); the year of publication (t); the content of the functions worked on (C), whether it focuses on the teacher, the student, or the curriculum; the educational institution (F); and the theoretical framework (M). Thus, for example, for the first document selected, the following identification appears: **** *n_01 *t_2024 *C_Derivative *F_Teacher *M_Ontosemiotic_Approach_to_Mathematical_Cognition_and_Instruction, etc. The file had to be in UTF-8 format in order to be processed by the IRaMuTeQ software. As this study does not aim to work with the citations present in the selected papers, they were removed from the corpus to facilitate computer processing. In accordance with Camargo and Justo (2013b), most of the default settings were maintained. The language chosen was English, and “utf_8_sig—all languages” was selected in the “encoding” option. A total of 392 TSs were identified in the corpus processing. The percentage of hapaxes, words that appear only once, was 4.67%, which was considered adequate. Next, the DHC, using the IRaMuTeQ’s default parameters, and the CFA were performed. The data shown in Figure 2 were obtained from the DHC: the software takes into account 300 of the 392 defined TSs in this classification, or 76.53%. Camargo and Justo (2013b) claim that for an analysis to be taken into account, the percentage should be equal to or greater than 75%.
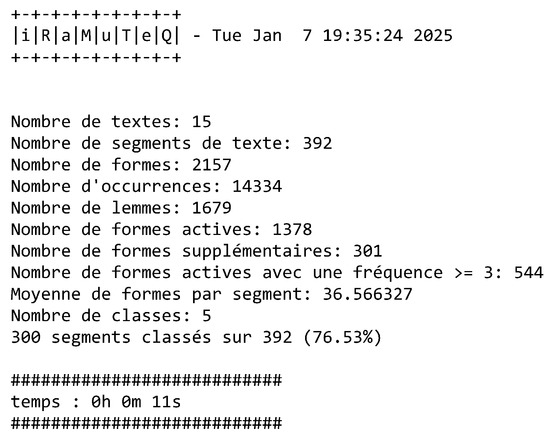
Figure 2.
DHC data. Source: IRaMuTeQ version 0.8 alpha 7 (2025).
Based on the DHC, the program proposes the five classes shown in the dendrogram in Figure 3. From this dendrogram, relationships of proximity and distance between classes can be established (Martins et al., 2022). The size of the rectangles and their percentage show the number of occurrences of each class in relation to the entire corpus. It is observed that class 5 (purple) has the most occurrences, 26%. It is followed by class 3 (green), with 22.7%, then class 4 (blue), 21%, and class 1 (red), 17.3%. Class 1 (gray) only has 13% of occurrences. Although the percentage of the most represented group is double that of the smallest, it should be noted that their sizes are sufficiently homogeneous.
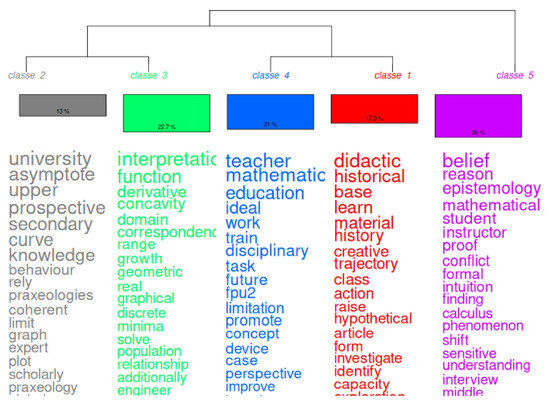
Figure 3.
DHC dendrogram. Source: IRaMuTeQ version 0.8 alpha 7 (2025).
The dendrogram is structured into branching levels: First, a bifurcation occurs, generating two branches. On the right, there is only class 5. The left branch divides into two new branches, which, in turn, separate into two new branches. Each of these contains one of the remaining classes, so that class 2 and class 3 belong to the same branch, as do class 4 and class 1. The most relevant terms in each class are those that appear below each rectangle. The higher the word appears, the more important it is. Based on the CFA, the program generated the graph in Figure 4. The relationship of dependence and independence between the classes is stressed, and can be observed according to their position in relation to the x-axis, the y-axis, and the location in the quadrants (Martins et al., 2022). The interrelationship between the gray and green classes, on the one hand, and between the blue and red classes, on the other, as well as the fact that the purple class is less connected to the other four classes, is more explicitly observed in this graph than in the dendrogram.
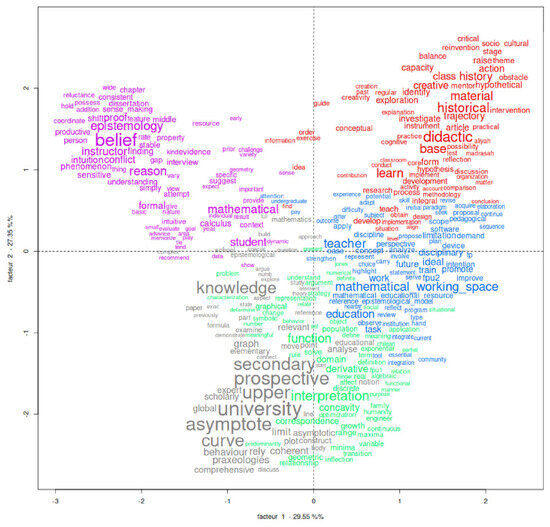
Figure 4.
CFA data Source: IRaMuTeQ version 0.8 alpha 7 (2025).
The program’s feature that shows each occurrence in the different TSs in which it appears is then used to infer an initial category from each class. The 20 most relevant terms in each class are considered (Table 4). “Prospective” in class 2 refers to future teachers. Praxeology in class 2 refers to the theoretical framework of the Anthropological Theory of the Didactic.

Table 4.
Most relevant words in each class.
The initial categories related to the epistemic knowledge of mathematics teachers when teaching functions, as inferred from the dendrogram provided by the IRaMuTeQ software, are as follows:
- Initial category 1: Historical research
- Initial category 2: Graphical representation to facilitate functions
- Initial category 3: Different meanings of function
- Initial category 4: Reflection on practice
- Initial category 5: Lack of interest in resolving conflicts between intuition and knowledge
The inference process for initial category 5 is outlined below as an example. First, with the help of the program, all the TSs in which the 20 occurrences with the highest frequency in class 5 appear were identified (Table 4). These text fragments were then read in order to extract the most notable underlying ideas. Some of the TSs that reflect these ideas are listed below. The document they belong to is indicated and the occurrences that appear in Table 4 are written in italics.
For instance, in Katalenić et al. (2020, p. 1203) (n_05): the occurrences mathematical and students appear, as can be seen in the following fragment: “(…) we could question what kind of approach in basic and advanced mathematical courses with elementary functions would have made a difference in students’ available graphing strategies.”
Mendes (2021, p. 19) (n_10) mentions the occurrences intuitive and intuition: “(…) for such exercises to be successfully carried out, it is necessary, however, to determine a creative thinking that productively explores intuitive (imagination, invention, intuition), operative (logic, chain of ideas), and symbolic (perception, attribution of meanings) activities.”
In Pino-Fan et al. (2019, p. 217) (n_13) the occurrences student and mathematical also appear: “(…) attempting an approach to build it on concepts that play the dual role of being familiar to the student and also provide a foundation for later mathematical development.”
Merighi (2020) (n_15) mentions a few more:
(…) the results also suggest that this belief coexists with relatively strong beliefs that formal notation is a more important part of mathematics. In addition to the contextual nature of these beliefs, we see that calculus students and middle school teachers alike tend to consider intuitive knowledge as less valid than formal mathematical notation (p. 159).
Another example can be found in Merighi (2020) (n_15):
(…) also, students’ stated epistemologies seem to differ from their epistemologies in practice. I found that no student attempted to reconcile the conflict between the answers they got from using formal mathematical knowledge and their intuitive approaches, and none seemed particularly surprised nor concerned about the reasons why they were getting different answers (p. 154).
The following occurrences are observed in Merighi (2020, p. iii) (n_15) “(…) middle school mathematics teachers tend to pay more attention to aesthetic features of proof than to features more strongly tied to mathematical meaning and sense making.”
Finally, it was agreed these ideas stress that the lack of interest in resolving conflicts between intuition and knowledge, both in students and in mathematics teachers when teaching functions, hinders the teaching and learning processes. Therefore, initial category 5 was given the name “Lack of interest in resolving conflicts between intuition and knowledge.”
2.3. Third Phase: Manual Analysis
In the third phase, the different papers were reread, and 290 citations were selected that were classified under 28 codes inferred by the authors of this paper. The approach used was open coding, and the five initial categories defined in the previous phase were the only preconceived notions. Each code derives from a citation, and is linked to an initial category. Subsequently, to explain the results of the analysis, the 28 codes were categorized into eight groups according to the thematic field they belong to (see Table 5).

Table 5.
Coding.
As can be seen in Table 6, the code groups are related to the documents selected in this ScR:

Table 6.
Citations selected by document and code group.
The data in Table 6 show the number of citations selected in each document and the code group it belongs to. The sum of all the values in this table, 328, is higher than the number of citations mentioned above, 290, because some citations were associated with more than one code group. Cells with a value greater than or equal to five were highlighted, thus showing the most frequent code groups. It is also observed that 25.61% of the groups refer to strengthening the presence of the complexity of functions in instructional processes, 18.29% refer to the importance of working on numerous mathematical processes in the classroom, 11.89% insist it is advisable for teachers to carry out research taking into account the history of functions in the design of their lesson plans, and 11.28% warn of the need for teachers to encourage students to seek coherence between their intuition and what they are learning about functions. To this end, it is essential for teachers themselves to pursue this coherence.
After analysing the code groups and the selected citations linked to each of them in greater depth, the authors associated them in such a way that they describe elements of the mathematics teachers’ EMDMK with regard to functions. Finally, three final categories were defined. According to highly qualified literature, they should be part of teachers’ EMDMK when teaching functions.
3. Results
The data obtained in the three previous methodological phases enable achieving the objective of this study, which is to identify the factors that characterize the EMDMK of teachers who lead epistemically suitable instructional processes for functions. The final categories in which the elements of teachers’ EMDMK were organized when teaching functions are the following:
3.1. Complexity of Functions in the History of Mathematics and in the Curriculum
This first final category emerges from the code groups Complexity, Curriculum, and Paper. Virtually all of the selected papers (n_01, n_02, n_03, n_04, n_05, n_08, n_09, n_10, n_12, n_13, n_14, and n_15) stress that for teaching functions, in-depth knowledge of the different meanings of the mathematical object of a function should be present in EMDMK.
For example, Inglada et al. (2024) (n_03) explain that, for a teaching process on functions to be epistemically rich, different meanings of function should be worked on, which is why it is essential for teachers to know them:
Epistemic suitability studies the representativeness of the different meanings of mathematical objects that appear in the instruction process. For example, in the case of teaching functions in 4th year of ESO (compulsory secondary education), the aim is to reduce teaching to the operational aspect and its algebraic representation (low suitability), or to work on different meanings of function, such as correspondence, relationship between variables, relationship between magnitudes, and their different verbal, algebraic, tabular, graphical, and iconic (high suitability) representations (p. 48).
Jannah et al. (2019) (n_12) also coincide on the need for this knowledge. Teachers could hence provide their students with learning situations in which multiple representations emerge to analyze the different meanings of functions in greater depth:
The concept of function can be defined formally and symbolically, almost without the use of words. The concept of function admits a variety of representations, while several representations of the concept offer information about particular aspects of the concept without being able to describe it completely (p. 1411).
Likewise, Pino-Fan et al. (2019, p. 204) (n_13) refer to this knowledge so that teachers can implement it properly in the curriculum: “(…) the importance of the meanings intended by the curriculum being representative of the true meaning of the notion of function (holistic meaning of reference).”
Some papers maintain this is obtained from the history of mathematics (n_03, n_08, n_10, n_11, n_13, n_14). It enables the teacher to connect it with the curriculum and be critical of it by making new proposals (n_04, n_06, n_08, n_10, n_13). Fallas-Soto and Lezama (2022, p. 138) (n_08) state: “To historicise is to recognise the historical value (past, present, or future) of the object of study described in the problem, based on connecting with a situated epistemology and a social history of the object.” In other words, knowing the historical evolution of functions allows discovering their different meanings, uses and representations. Along the same lines, Mendes (2021) (n_10) sets forth:
(…) as these outlooks are present in the histories of mathematics produced in times and space, giving rise to points of epistemological support, as we can see in the history of human culture, in general, always with possibilities of looking at and borrowing various outlooks, so that we can have a greater amplitude regarding the object we want to look at (p. 4)
Rodrigues et al. (2021) (n_11) also stress that the history of functions reveals their different meanings and applications:
As for historical elements, it is observed that the concept of function underwent modifications over time, and its understanding broadened as mathematicians’ contributions were incorporated into the definition of function. As a result, its application also expanded to new fields of study (p. 619).
Several documents explicitly state teachers should draw on research in mathematics education on functions (n_01, n_05, n_06, n_09, n,10, and n_12). For instance, Mendes (2021) (n_10) argues that teaching and learning processes should be based on the teacher’s investigative attitude:
I define this investigative spirit as the spirit of the researcher, which I always refer to when talking about research as a teaching and learning principle. I understand this spirit was what ignited my personal and professional development throughout my training as a teacher and as a researcher (p. 2).
Jannah et al. (2019, p. 1410) (n_12) when they maintain that “Students will be prospective teachers in the future, they must master mathematical concepts well, especially the concept of functions that is related to many other topics”, underline the importance for teachers to be aware of the results of research on functions in mathematics education.
Another element of EMDMK for teaching functions is the use of multiple representations and conversion between them. Almost all of the selected papers link this to students’ deep understanding of functions (n_01, n_02, n_03, n_04, n_05, n_08, n_09, n_10, n_11, n_12, n_13, n_14).
Numerous papers (n_01, n_04, n_05, n_08, n9, n_11, n_14, and n_15) highlight the importance of graphical representation, and n_01, n_04, n_05, n_09, n_11, and n_14 add that the use of technology to graph them is very helpful. Galindo and Breda (2024, p. 20) (n_01) refer to the use of technological resources to graphically represent functions as an innovative element that contributes to the improvement of teaching “(...) the innovative aspects of this research. The first aspect was the cross-curricular use of ICT resources (applets, GeoGebra, QR codes) throughout the teaching unit.” Katalenić et al. (2020) (n_05), for their part, highlight the importance of working on multiple representations of functions and conversions between them in the process of teaching functions:
They studied how mathematical experts link formulas to graphs, what formulas they can instantly visualize, and what processes they activate to identify the graph that corresponds to each formula. Mathematical expertise is related to the highest levels of graph recognition of the basic function families, and therefore provides valuable suggestions for teaching (p. 1187).
This idea is confirmed by Jannah et al. (2019) (n_12):
One characteristic of the concept of function is that it can be represented in various ways (e.g., tables, graphs, symbolic equations, and verbal representations). An important aspect of understanding the concept of function is the ability to use various representations and transfer them from one form to another (p. 1409).
Katalenić et al. (2023, p. 151) (n_9) support the same idea: “We interpreted that students were focused on different representations: graphical, numerical or algebraic ones.”
3.2. Personal Practice of Multiple Processes Using Functions in Different Contexts
This final category originates from the Coherence, Processes, and Context code groups. Most documents (n_01, n_02, n_03, n_04, n_07, n_08, n_09, n_10, n_11, n_12, n_13, and n_15) consider functions that should be worked on in different contexts, both mathematical and non-mathematical, in various academic disciplines and in real contexts. Galindo and Breda (2024, p. 20) (n_01) contextualize working with functions in economics and business management: “This research is focused on function graphs and function optimisation linked to the context of economics and business.”
Another example is related to one of the indicators in the guidelines for analyzing teaching and learning processes for functions in Inglada et al. (2024, p. 50) (n_03): “(…) proposed problems in purely mathematical contexts to reinforce learning about functions, where intra-mathematical connections are worked on and contextualized from everyday life or other sciences.”
Pino-Fan et al. (2019, p. 202) (n_13) insist on the importance of contextualizing working on functions: “Some studies on proposals for teaching functions establish the need to approach them from contextualized situations.” Merighi (2020, p. 161) (n_15) specify that working in different contexts makes it easier for students to put different resources and skills to use:It may be that a shift in context prompts students to engage with different knowledge resources and ways of reasoning. There is not necessarily a need to replace students’ ideas with different ones, but rather a need to catalyze shifts in the mathematical resources they draw upon.
They also insist that students should be encouraged to work on as many mathematical processes as possible: argumentation, algorithmization, conjecturing, estimation, generalization, validation, and modeling (n_01, n_03, n_04, n_05, n_06, n_07, n_08, n_09, n_10, n_11, n_12, n_14, and n_15). Inglada et al. (2024) (n_03) mention the processes that should be worked on when studying functions:
Problem statements are read and interpreted correctly. Conjectures and propositions are stated. Argumentation: conjectures and procedures are justified. Definitions and procedures are institutionalized. Variables and quantities are identified. It is determined whether a relationship is functional, and, if so, the type is determined. Algorithms, routines, or calculations are applied. Generalization and abstraction processes are carried out (p. 49).
Henríquez-Rivas and Verdugo-Hernández (2023) (n_04) explain the processes that enrich the teaching of functions:
They achieve a certain degree of autonomy to work with semiotic activities, and/or on converting semiotic activities. This means using more than two registers of representation in solutions, based on the interpretation of a single source of information by reasoning and inferring. They are also able to explain their interpretations and justify their results (p. 197).
Finally, Katalenić et al. (2023, p. 133) (n_9) specifically discuss the process of exploring: “(…) used different tools to explore functions with a finite or infinite number of intersections with their asymptotes.”
More than two-thirds of the selected documents (n_01, n_02, n_05, n_06, n_07, n_08, n_09, n_10, n_12, n_14, and n_15) argue that for student learning to be robust, it is necessary for students to seek coherence between their intuition and new knowledge.
For instance, Hanke (2024, p. 2) (n_06) suggests promoting students’ understanding through debate for the students to compare different lines of reasoning: “The challenges that arise, however, supply stimulating points for discussion in classrooms and may foster students’ holistic understanding of integrals throughout the curricula.” Along the same lines, Rodrigues et al. (2021, p. 616) (n_11) note that students do not usually check the soundness of their learning: “Students respond to activities by reproducing the results of previous activities, believing that they have understood the concept studied.” Vivas Pachas (2021, p. 14) (n_14) explains what type of learning teachers should promote in their students:
Complete mathematical work: Mathematical work is complete when there is a genuine relationship between the epistemological and cognitive planes. According to the authors, this means that students are able to select the tools that are useful for tackling a problem, and then use them appropriately as instruments for solving the given task. There is a connection between the different origins and vertical planes of the mathematical working space (p. 14).
Teachers need to experience it themselves to be able to encourage this search in their students. Therefore, another element of EMDMK is the competence to put into practice the search for coherence between intuition and new knowledge through multiple mathematical processes using functions in different contexts. Students can hence be accompanied in the teaching and learning processes of functions.
3.3. Analysis of the Tasks Designed in the Instructional Processes and Reflection on Teaching Practice
The third final category derives from the code groups Task Development and Reflection on Practice. The selected papers suggest the competence of designing tasks about functions, and analyzing them to ensure their epistemic richness (n_01, n_02, n_03, n_04, n_05, n_07, n_08, n_09, n_10, n_11, n_12, and n_14) are part of EMDMK. Henríquez-Rivas and Verdugo-Hernández (2023, p. 181) (n_04) emphasize that teachers should design tasks, or choose pre-designed tasks that activate mathematical activity in their students, as can be seen in the following statement: “(…) refer to a task as materials or environments designed to promote a complex mathematical activity.” Rodrigues et al. (2021, p. 621) (n_11) confirm this idea: “Every didactic problem begins with a problem constructed by the teacher, in this case, a teaching problem.” Vivas Pachas (2021, p. 83) (n_14) also coincides with this idea: “(…) the way the teacher approaches the teaching process with the aim of encouraging students to do mathematical work would allow us to understand how solving a task on exponential functions can be organized to enable students to engage with it.”
Reflection on the epistemic suitability of teaching practice with regard to functions (n_02, n_03, n_04, n_05, n_07, n_08, n_09, n_10, n_11, and n_14) is part of it too. This contributes to the improvement of teaching and learning processes for functions and increases teachers’ EMDMK. Muin and Fatma (2021) (n_02) explain how reflection on teaching practice improved teaching processes for functions in junior and senior high school in South Tangerang, Indonesia:
The target of community service activities in the form of Participatory Action Research (PAR) assistance is a community of high school level mathematics teachers within the Ministry of Religion. PAR is a collective, self-reflective inquiry conducted by researchers and participants, so that they can understand and improve the practices in which they participate and the situations in which they find themselves (p. 2).
In a similar manner, Henríquez-Rivas and Verdugo-Hernández (2023) (n_04) point out that reflection on teaching practice can improve the teaching of functions:
[The teacher] hardly reflects on the use of representations of continuous functions in relation to the meaning of the real values the domain of this function can take on, and in the context of the situation presented, which would be relevant to consider from a teaching perspective (p. 200).
Mendes (2021, p. 3) (n_10) also supports this approach when stating that: “Some metacognitive strategies, such as monitoring and evaluation, are needed. They can be used at different stages of the process.”
Rodrigues et al. (2021, p. 618) (n_11) confirm this view when they explain that: “Reference epistemological models are working hypotheses that can constantly be questioned and revised, allowing for the analysis of mathematical knowledge before it is taught.”
Documents n_02, n_03, n_05, n_07, n_09, n_11, and n_14 maintain that the guidelines that guide teachers’ reflection contribute to making it more profound. Inglada et al. (2024, p. 54) (n_03) ensure that “(…) if teachers were given tools such as the RIEF, the reflection on their own practice could be improved, since they would have a specific guideline to carry out a more rigorous, clear, and efficient analysis.” Hinojos-Ramos et al. (2023, p. 52) (n_07) also defend this idea: “The methodology for didactic intervention (pre-intervention, intervention, and post-intervention) led a structured and guided process for the teacher-researcher to perform the implementation of the instrument.”
In n_03, a specific guideline for functions is proposed. The indicators of this guideline are classified in the following seven categories (Inglada et al., 2024) (n_03):
3.1. RIEF indicators. We obtained the following adaptation of epistemic suitability to facilitate the analysis of teaching processes related to functions in compulsory secondary education. 3.1.1 Errors. 3.1.2 Ambiguities. 3.1.3 Appropriate didactic option. 3.1.4. Richness of processes. 3.1.5. Meanings. 3.1.6. Representations and conversions. 3.1.7 Problem situations (p. 49).
4. Discussion and Conclusions
The results of this ScR contribute to characterizing teachers’ EMDMK of the mathematical object of function, structured into three final categories: (1) complexity of functions in the history of mathematics and in the curriculum, (2) personal practice of multiple processes using functions in different contexts, and (3) analysis of tasks designed in instructional processes and reflection on teaching practice. From the first category, it is concluded that an in-depth study of the complexity of functions is an essential requirement in initial teacher preparation programs and continuing professional development: their different meanings, multiple representations, and conversion between them. It is also concluded that this should be conveyed through the history of mathematics. In the literature, papers are found that justify the importance of considering the evolution of functions throughout the history of mathematics when preparing teaching and learning processes to be implemented in the classroom. Within the theoretical framework of the OSA, Pino-Fan and Parra-Urrea (2021) claim the following:
Suitable instructional processes for functions require teachers to be familiar with the historical evolution of functions. In other words, they need to understand the holistic meaning of the object (its richness of meanings and how to address and promote them) to have a broader and deeper understanding of the notion of function (pp. 47–48).
According to Pino-Fan et al. (2011), partial meanings of mathematical objects are associated with the epistemic configurations that were used to solve certain problem situations in specific historical periods, and that gave rise to the emergence, evolution, formalization, and generalization of a particular mathematical object. Fallas-Soto and Lezama (2022) (n_08) claim that, from the framework of socio-epistemology, it is advisable to address school mathematical knowledge by recognizing its historical value. Mendes (2021) (n_10) also affirms that paying attention to the history of mathematics is a starting point for enriching teachers’ EMDMK. Rodrigues et al. (2021) (n_11) emphasize that the changes and expansions the concept of function has undergone over time, as well as its different applications to various fields and contexts, should be considered in the design of learning materials for secondary mathematics education. Godino et al. (2006) consider that this evolution can be organized into four partial senses: tabular, graphical, analytical, and conjunctural sense. For this reason, and in agreement with Fuertes-Prieto et al. (2022), it is considered necessary to review initial teacher preparation programs to ensure that future teachers are competent in researching the history of mathematics and its application to the design of tasks for teaching mathematics in secondary education. The documents analyzed in this ScR also show the importance of the graphical representation of functions in students’ understanding. Merighi (2020, p. 163) (n_15) points out the following nuance: “I would also recommend that calculus courses ask students to reason with graphs of functions as primary mathematical entities, rather than only as supporting representations for functions with nice, neat symbolic representations.” He also recommends the use of technology for the graphical representation of functions. Vivas Pachas (2021) (n_14) defends the importance of digital technology in the learning and teaching of functions. This aspect is consistent with the component of representativeness of the complexity of the mathematical object (see Table 1), and more particularly with the importance of considering the history of mathematics in order to work on the different partial meanings of functions at school. It allows students to acquire greater competence in solving a variety of problems involving functions (Araya et al., 2021).
It can also be deduced from the first category that teachers should draw on research in mathematics education on functions. Mendes (2021) (n_10) talks about research as a principle of teaching and learning. Some authors go a step further, arguing that it is the teacher who, from this perspective, should explore the curriculum to implement it with their students, and even, if they consider it appropriate, develop new curricular proposals. For example, Henríquez-Rivas and Verdugo-Hernández (2023) (n_04) consider the Chilean curriculum guidelines and guiding standards do not provide sufficient information on the various representations of functions. Hinojos-Ramos et al. (2023) (n_07) report that some curriculum proposals are the result of research conducted by teachers. The authors of this ScR agree with the lines of action outlined in the literature analyzed, but note that teachers need to be provided with the necessary resources to be able to carry out this training activity. Initial teacher training is not sufficient. Continuing professional development should consider the elements included in this first final category. One of the educational implications of this category is therefore the design of continuing training for teachers with regard to the complexity of functions and their historical evolution to design and implement tasks within the framework of the current curriculum.
From the second category, it can be inferred that teachers should practice different mathematical processes in different contexts in order to construct their own knowledge and be able to guide that of their students. It enables them to encourage their students to seek coherence between their intuition and new knowledge. This is necessary because, as Merighi (2020) (n_15) points out:
More specifically, tensions exist within each student’s complex set of epistemologies of mathematics that may result in them suppressing their own abilities to reason intuitively about mathematical phenomena because they do not believe that these intellectual resources are valuable when solving mathematical problems (p. 154).
This second category is in line with the richness of processes component of epistemic suitability (see Table 1), since, in order for students to learn functions, teachers should design and implement tasks that involve relevant mathematical processes, such as changing representations, the process of argumentation, and the process of extra-mathematical and intra-mathematical connections, among others. However, it is true that, due to the working conditions of secondary school teachers, they may not always have the necessary time and training to carry out these tasks. One of the educational implications is to encourage students to seek consistency between their intuition and the mathematical practices they perform.
Finally, according to Godino et al. (2017), it can be inferred from the third category that one of the competences teachers should have is the ability to reflect on the teaching and learning processes of mathematics implemented in practice. Mendes (2021) (n_10) also specifies that teachers should apply three skills that can be developed together: synthesis, analysis, and conversion of abstract ideas into practical achievements. Henríquez-Rivas and Verdugo-Hernández (2023) (n_04), using the Theory of Mathematical Working Spaces, find evidence that reflection on the tasks designed to teach functions contributes to their improvement. Various authors (Muin and Fatma (2021) (n_02); Inglada et al. (2024) (n_03); Katalenić et al. (2020) (n_05); Hinojos-Ramos et al. (2023) (n_07) and Vivas Pachas (2021) (n_14)) claim that guidelines for teacher reflection contribute to making it more profound. Inglada et al. (2024) (n_03) propose a specific guideline for functions and state that, if teachers were provided with this type of tool, their reflection on the resources they have or design, as well as on their own practice, could improve. As a result, their EMDMK and their teaching practice could also improve.
This third category coincides with the DMK model of the OSA in its meta didactic–mathematical dimension (Breda et al., 2017; Pino-Fan & Godino, 2015), which considers that one of the teachers’ competences is reflection on practice and the assessment of mathematical teaching and learning processes. Given the complexity of teaching and learning processes, the authors of this paper consider that the ability to reflect on one’s own teaching practice is essential for these processes to be appropriate in the contexts in which they take place. Furthermore, this ability encourages students to reflect on their own learning and to self-regulate (Hidalgo Moncada, 2025; Hidalgo-Moncada et al., 2023). It is therefore considered that one of the educational implications of this category is to ensure that teachers’ work schedules reserve time for the collaborative design and analysis of teaching processes, followed by individual and collective reflection on the implementation of future redesigns.
Finally, although some of the selected documents refer to errors teachers make (Hanke, 2024, (n_06); Henríquez-Rivas & Verdugo-Hernández, 2023, (n_04); Jannah et al., 2019, (n_12); Pino-Fan et al., 2019, (n_13)), they only do so occasionally or with regard to a particular context. Therefore, none of the categories that emerged are related to the components of errors or ambiguities of the epistemic criterion (see Table 1), which is considered a limitation of this study. Future reviews of the literature should analyze teachers’ errors and ambiguities. The small number of documents selected is also considered to be a limitation as it stresses the lack of papers that focus on the EMDMK of functions.
The main conclusion of this research is that the presence of the different elements of EMDMK identified in this ScR could contribute to the improvement of the teaching of functions in teacher preparation programs. Future research on teacher training proposals related to functions is necessary. It should be based on the different elements of EMDMK described in the final categories of this study, including the components of errors and ambiguities in the epistemic suitability of the OSA.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/educsci15111526/s1. Document S1: Checklist PRISMA-Scoping Review.
Author Contributions
Conceptualization, N.I., A.B. and G.S.-S.; methodology, N.I., A.B. and G.S.-S.; software, N.I.; validation, N.I., A.B., G.S.-S. and Y.V.; formal analysis, N.I.; investigation, N.I., A.B. and G.S.-S.; resources, A.B. and G.S.-S.; data curation, N.I.; writing—original draft preparation, N.I.; writing—review and editing, N.I., A.B., G.S.-S. and Y.V.; visualization, N.I.; supervision, A.B., G.S.-S. and Y.V.; project administration, A.B. and G.S.-S.; funding acquisition, A.B. and G.S.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was conducted within the following projects: (a) Pensament Computacional i robòtica amb perspectiva de gènere a l’educació Infantil i Primària. EDU145/23/000006 funded by the Department of Education of the government of Catalonia (Spain); (b) PID2021-127104NB-I00, funded by MCIN/ AEI/10.13039/501100011033/ and by the ERDF (European Regional Development Fund) a way of making Europe. The APC was funded by this same entity.
Institutional Review Board Statement
This research has followed the Code of Ethics on Integrity and Best Practices by the Universitat de Barcelona (available at http://hdl.handle.net/2445/137937, accessed on 18 February 2025), and it was approved by the permanent committee of the Council of the Department of Language, Science, and Mathematics Education from the Faculty of Education of the Universitat de Barcelona, on 17 August 2025.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We wish to express our gratitude to Ann Swinnen for her invaluable assistance with the article’s translation and for her insightful comments, which significantly enhanced its clarity and readability for the reader.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analysis, or interpretation of the data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| ScR | Scoping Review |
| EMDMK | Epistemic meta didactic–mathematical knowledge |
| WoS | Web of Science |
| IRaMuTeQ | R INTERFACE for Multidimensional analysis of Texts and Questionnaires |
| OSA | Onto-semiotic Approach |
| DMK | Didactic–mathematical knowledge |
| DSC | Didactic Suitability Criteria |
| DHC | Descending Hierarchical Classification |
| TS | Text segment |
| CFA | Correspondence Factor Analysis |
References
- Amaral-Rosa, M., do Rosário Lima, V. M., Breda, A., & de Lima, D. F. (2024). Comparative category analysis: Craft AC & ATD supported by IRaMuTeQ software. In J. Ribeiro, C. Brandão, M. Ntsobi, J. Kasperiuniene, & A. P. Costa (Eds.), Computer supported qualitative research, WCQR 2024, lecture notes in networks and systems (vol. 1061, pp. 271–284). Springer. [Google Scholar] [CrossRef]
- Amaya de Armas, T. R., Pino-Fan, L. R., & Medina Rivilla, A. (2016). Evaluación del conocimiento de futuros profesores de matemáticas sobre las transformaciones de las representaciones de una función. Educación Matemática, 28(3), 111–144. [Google Scholar] [CrossRef]
- Araya, D., Pino-Fan, L., Medrano, I., & Castro, W. F. (2021). Epistemic criteria for the design of tasks about limits on a real variable function. Bolema, 35(69), 179–205. [Google Scholar] [CrossRef]
- Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching what makes it special? Journal of Teacher Education, 59(5), 389–407. [Google Scholar] [CrossRef]
- Beltrán-Pellicer, P., & Giacomone, B. (2018). Desarrollando la competència de análisis y valoración de la idoneidad didáctica en un curso de postgrado mediante la discusión de una experiencia de enseñanza. REDIMAT, Journal of Research in Mathematics Education, 7(2), 111–133. [Google Scholar] [CrossRef]
- Breda, A., Pino-Fan, L. R., & Font, V. (2017). Meta didactic-mathematical knowledge of teachers: Criteria for the reflection and assessment on teaching practice. Eurasia Journal of Mathematics, Science and Technology Education, 13(6), 1893–1918. [Google Scholar] [CrossRef]
- Burgos, M., Bueno, S., Godino, J. D., & Pérez, O. (2021). Onto-semiotic complexity of the Definite Integral. Implications for teaching and learning Calculus. REDIMAT. Journal of Research in Mathematics Education, 10(1), 4–40. [Google Scholar] [CrossRef]
- Camargo, B. V., & Justo, A. M. (2013a). IRaMuTeQ: Um software gratuito para análise de dados textuais. IRaMuTeQ: Interface de R pour les analyses multidimensionnelles de textes et de questionnaires. Temas em Psicologia, 21(2), 513–518. [Google Scholar] [CrossRef]
- Camargo, B. V., & Justo, A. M. (2013b). Tutorial para uso do software de análise textual IRaMuTeQ. Available online: http://www.iramuteq.org/documentation/fichiers/tutoriel-en-portugais (accessed on 27 September 2024).
- Fallas-Soto, R. D., & Lezama, J. (2022). Argumentos variacionales en la comprensión de la concavidad en gráficas de funciones. Perfiles Educativos, 44(178), 130–148. [Google Scholar] [CrossRef]
- Font, V. (2011). Funciones. Evolución histórica de la noción de función. Algunas ideas clave que nos ofrece la evolución de la noción de función. In J. M. Goñi (Ed.), Matemáticas. Complementos de formación disciplinar (pp. 145–186). Ed Graó. [Google Scholar]
- Font, V., Breda, A., Sala-Sebastià, G., & Pino-Fan, L. (2024). Future teachers’ reflections on mathematical errors made in their teaching practice. ZDM-Mathematics Education, 13(6), 1893–1918. [Google Scholar] [CrossRef]
- Font, V., Giménez, J., Larios, V., & Zorrilla, J. F. (2012). Competencias del profesor de matemáticas de secundaria y bachillerato (eBook). Edicions Universitat Barcelona. [Google Scholar]
- Font, V., Godino, J. D., & Gallardo, J. (2013). The emergence of objects from mathematical practices. Educational Studies in Mathematics, 82(1), 97–124. [Google Scholar] [CrossRef]
- Font, V., Pino-Fan, L. R., & Breda, A. (2020). Una evolución de la mirada sobre la complejidad de los objetos matemáticos. Paradigma XLI, 107–129. [Google Scholar] [CrossRef]
- Font, V., Planas, N., & Godino, J. D. (2010). Modelo para el análisis didáctico en educación matemática. Infancia y Aprendizaje, 33(1), 89–105. [Google Scholar] [CrossRef]
- Fuertes-Prieto, M. A., Santágueda-Villanueva, M., & Lorenzo-Valentín, G. (2022). Creencias e ideas de los futuros maestros sobre el uso de la história de las matemáticas como recurso didáctico. In T. F. Blanco, C. Núñez-García, M. C. Cañadas, & J. A. González-Calero (Eds.), Investigación en educación matemática XXV (pp. 277–284). SEIEM. [Google Scholar]
- Galindo, M. K., & Breda, A. (2024). Instructional process of the derivative applied in business engineering students in Chile. Uniciencia, 38(1), 303–325. [Google Scholar] [CrossRef]
- Giacomone, B., Godino, J. D., & Beltrán-Pellicer, P. (2018). Developing the prospective mathematics teachers’ didactical suitability analysis competence. Educação e Pesquisa, 44, e172011. [Google Scholar] [CrossRef][Green Version]
- Godino, J. D. (2009). Categories for analysing the knowledge of mathematics teachers. Unión, RevistaIberoamericana de Educación Matemática, 20, 13–31. Available online: https://www.ugr.es/~jgodino/eos/JDGodino%20Union_020%202009.pdf (accessed on 27 September 2024).[Green Version]
- Godino, J. D. (2012). Origen y aportaciones de la perspectiva ontosemiótica de investigación en Didáctica de la Matemática. In A. Estepa, A. Contreras, J. Deulofeu, M. C. Penalva, F. J. García, & L. Ordóñez (Eds.), Investigación en educación matemática XVI (pp. 49–68). Universidad de Granada. [Google Scholar][Green Version]
- Godino, J. D. (2013). Indicadores de la idoneidad didáctica de procesos de enseñanza y aprendizaje de las matemáticas. Cuadernos de Investigación y Formación en Educación Matemática, 8(11), 111–132. Available online: https://revistas.ucr.ac.cr/index.php/cifem/article/view/14720 (accessed on 27 September 2024).[Green Version]
- Godino, J. D., Batanero, C., & Font, V. (2007). The onto-semiotic approach to research in mathematics education. ZDM—International Journal on Mathematics Education, 39(1–2), 127–135. [Google Scholar] [CrossRef]
- Godino, J. D., Batanero, C., & Font, V. (2019). The onto-semiotic approach: Implications for the prescriptive character of didactics. For the Learning of Mathematics, 39(1), 37–42. Available online: https://www.jstor.org/stable/26742011 (accessed on 27 September 2024).
- Godino, J. D., Bencomo, D., Font, V., & Wilhelmi, M. R. (2006). Análisis y valoración de la idoneidad didáctica de procesos de estudio de las matemáticas. Paradigma, 27(2), 221–252. Available online: https://ugr.es/~jgodino/funciones-semioticas/idoneidad-didactica.pdf (accessed on 27 September 2024).
- Godino, J. D., Font, V., Wilhelmi, M. R., & Castro, C. (2009). Aproximación a la dimensión normativa en didáctica de la matemática desde un enfoque ontosemiótico. Enseñanza de las Ciencias, 27(1), 59–76. Available online: https://repositorio.uam.es/bitstream/handle/10486/668515/aproximacion_godino_RELME_2007.pdf?sequence=3 (accessed on 27 September 2024). [CrossRef]
- Godino, J. D., Giacomone, B., Batanero, C., & Font, V. (2017). Enfoque ontosemiótico de los conocimientos y competencias del profesor de matemáticas. Bolema, 31(57), 90–113. [Google Scholar] [CrossRef]
- Hanke, E. (2024). On using a core idea to foster the transition to advanced mathematics—Transferring the idea of average to complex path integrals. International Journal of Mathematical Education in Science and Technology, 1–21. [Google Scholar] [CrossRef]
- Henríquez-Rivas, C., & Verdugo-Hernández, P. (2023). Diseño de tareas en la formación inicial docente de matemáticas que involucran las representaciones de una función. Educación Matemática, 35(3), 178–208. [Google Scholar] [CrossRef]
- Hidalgo Moncada, D. (2025). Análisis de la promoción del aprendizaje autorregulado en la enseñanza y aprendizaje de las matemáticas por futuros profesores de secundaria. Universitat de Barcelona. Available online: https://www.tdx.cat/handle/10803/695408 (accessed on 17 October 2025).
- Hidalgo-Moncada, D., Díez-Palomar, J., & Vanegas, Y. (2023). Prácticas de autorregulación en la propuesta didáctica de un futuro profesor de matemáticas: Un instrumento para la reflexión. Paradigma, 44(4), 112–146. [Google Scholar] [CrossRef]
- Hinojos-Ramos, J. E., Torres-Corrales, D., & Camacho-Ríos, A. (2023). The construction of the integral for the arc length of a curve based on van Heuraet and Fermat’s works. British Journal for the History of Mathematics, 38(1), 41–54. [Google Scholar] [CrossRef]
- Inglada, N., Breda, A., & Sala-Sebastià, G. (2024). Guideline to reflect on the education functions and improve their teaching. Alteridad, 19(1), 45–56. [Google Scholar] [CrossRef]
- Jannah, U. R., Nusantara, T., Sudirman, S., Yulianto, F. E., & Amiruddin, M. (2019). Student’s learning obstacles on mathematical understanding of a function: A case study in Indonesia higher education. TEM Journal, 8(4), 1409–1417. [Google Scholar] [CrossRef]
- Katalenić, A., Čižmešija, A., & Milin Šipuš, Ž. (2023). Prospective mathematics teachers’ knowledge of asymptotes and asymptotic behaviour in calculus. International Journal of Science and Mathematics Education, 21, 131–158. [Google Scholar] [CrossRef]
- Katalenić, A., Milin Šipuš, Ž., & Čižmešija, A. (2020). Asymptotes and asymptotic behaviour in graphing functions and curves: An analysis of the croatian upper secondary education within the Anthropological Theory of the didactic. International Journal of Science and Mathematics Education, 18, 1185–1205. [Google Scholar] [CrossRef]
- Lima, V. M. R., Amaral-Rosa, M., & Ramos, M. G. (2021). Software-supported discursive textual analysis: IRaMuTeQ and subcorpus analysis. New Trends in Qualitative Research, 7, 1–9. [Google Scholar] [CrossRef]
- Malaspina, U. (2017). The creation of problems as a means to enhance the articulation of skills and knowledge of the mathematics teacher. In J. M. Contreras, G. R. C. P. Arteaga, M. M. Gea, B. Giacomone, & M. M. López-Martín (Eds.), Actas del segundo congreso internacional virtual sobre el enfoque ontosemiótico del conocimiento y la instrucción matemáticos. Available online: https://enfoqueontosemiotico.ugr.es/civeos/malaspina.pdf (accessed on 27 September 2024).
- Malaspina, U., & Font, V. (2010). The role of intuition in the solving of optimization problems. Educational Studies in Mathematics, 75(1), 107–130. [Google Scholar] [CrossRef]
- Malaspina, U., Torres, C., & Rubio, N. (2019). How to stimulate in-service teachers’ didactic analysis competence by means of problem posing. In P. Liljedahl, & M. Santos-Trigo (Eds.), Mathematical problem solving (pp. 133–151). Springer. [Google Scholar] [CrossRef]
- Martins, K. N., Sarro-Gomes, L. P., & Corrêa de Paula, M. (2022). Software IRaMuTeQ: Uma ferramenta auxiliar na análisi textual discursiva. Paradigma, 43(2), 205–227. [Google Scholar] [CrossRef]
- Mendes, I. A. (2021). Historical creativities for the teaching of functions and infinitesimal calculus. International Electronic Journal of Mathematics Education, 16(2), em0629. [Google Scholar] [CrossRef]
- Merighi, C. J. (2020). Contextuality of mathematical beliefs and reasoning [Ph.D. thesis, Tufts University]. Available online: https://www.proquest.com/dissertations-theses/contextuality-mathematical-beliefs-reasoning/docview/2414416560/se-2 (accessed on 27 September 2024).
- Mishra, P., & Koehler, M. J. (2006). Technological pedagogical content knowledge: A new framework for teacher knowledge. Teachers College Record, 108(6), 1017–1054. [Google Scholar] [CrossRef]
- Moreno, M., & Ratinaud, P. (2022). Manual para el usuario. IRaMuTeQ. Available online: http://www.iramuteq.org/documentation/fichiers/manual-usuario (accessed on 27 September 2024).
- Muin, A., & Fatma, M. (2021). Hypothetical learning trajectory design in development of mathematics learning didactic design in madrasah. Journal of Physics: Conference Series, 1836, 012070. [Google Scholar] [CrossRef]
- Page, M. J., McKenzie, J. E., Bossuyt, P. M., Boutron, I., Hoffmann, T. C., Mulrow, C. D., Shamseer, L., Tetzlaff, J. M., Akl, E. A., Brennan, S. E., Chou, R., Glanville, J., Grimshaw, J. M., Hróbjartsson, A., Lalu, M. M., Li, T., Loder, E. W., Mayo-Wilson, E., McDonald, S., … Moher, D. (2021). The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ, 372, n71. [Google Scholar] [CrossRef] [PubMed]
- Pino-Fan, L. R., Castro, W. F., Godino, J. D., & Font, V. (2013). Idoneidad epistémica del significado de la derivada en el currículo de bachillerato. Paradigma, 34(2), 129–150. [Google Scholar]
- Pino-Fan, L. R., & Godino, J. D. (2015). Perspectiva ampliada del conocimiento didáctico-matemático del profesor. Paradigma, 36(1), 87–109. [Google Scholar]
- Pino-Fan, L. R., Godino, J. D., & Font, V. (2011). Faceta epistémica del conocimiento didáctico-matemático sobre la derivada. Educação Matemática Pesquisa, 13(1), 141–178. Available online: https://www.ugr.es/~jgodino/eos/Pino-Fan_Mat_Pesquisa%202011.pdf (accessed on 27 September 2024).
- Pino-Fan, L. R., Godino, J. D., & Font, V. (2016). Assessing key epistemic features of didactic-mathematical knowledge of prospective teachers: The case of the derivative. Journal of Mathematics Teacher Education, 21(1), 63–94. [Google Scholar] [CrossRef]
- Pino-Fan, L. R., & Parra-Urrea, Y. E. (2021). Criterios para orientar el diseño y la reflexión de clases sobre funciones. ¿Qué nos dice la literatura científica? Uno. Revista de Didáctica de las Matemáticas, 91, 45–54. [Google Scholar]
- Pino-Fan, L. R., Parra-Urrea, Y. E., & Castro-Gordillo, W. F. (2019). Significados de la función pretendidos por el currículo de matemáticas chileno. Magis. Revista Internacional de Investigación en Educación, 11(23), 201–220. [Google Scholar] [CrossRef]
- Ramos, M. G., Lima, V. M. R., & Amaral-Rosa, M. P. (2019). IRAMUTEQ software and discursive textual analysis: Interpretive possibilities. In A. Costa, L. Reis, & A. Moreira (Eds.), Computer supported qualitative research, WCQR 2018, advances in intelligent systems and computing (vol. 861, pp. 58–72). Springer. [Google Scholar] [CrossRef]
- Ratinaut, P. (2009). IRaMuTeQ (0.8 alpha 7) [R INTERFACE for multidimensional analysis of texts and questionnaires]. Université de Toulouse. Available online: http://iramuteq.org/ (accessed on 27 September 2024).
- Rodrigues, R. F., Lucas, C. O., Castro, S. L., Menezes, M. B., & Câmara dos Santos, M. (2021). Elaboração, análise e aplicação de um modelo epistemológico de referência para o ensino do conceito de função na licenciatura em matemática. Bolema: Boletim de Educação Matemática, 35(70), 614–636. [Google Scholar] [CrossRef]
- Rondero, C., & Font, V. (2015). Articulation of the mathematical complexity of the arithmetic mean. Enseñanza de las Ciencias, 33(2), 29–49. [Google Scholar] [CrossRef][Green Version]
- Sánchez, A., Breda, A., Ledezma, C., Sala-Sebastià, G., Sol, T., & Font, V. (2022). ¿Qué conflictos semióticos detectan los futuros profesores en las clases de matemáticas que imparten? In Investigación en Educación Matemática XXV (pp. 530–537). Sociedad Española de Investigación en Educación Matemática, SEIEM. [Google Scholar][Green Version]
- Seckel, M., & Font, V. (2020). Competencia reflexiva en formadores del profesorado en matemáticas. Magis, Revista Internacional de Investigación en Educación, 12(25), 127–144. [Google Scholar] [CrossRef]
- Shulman, L. S. (1987). Knowlendge and Teaching Fundations of the new reform. Harvard Educational Review, 57(1), 1–22. Available online: https://bit.ly/3PPkNGL (accessed on 27 September 2024). [CrossRef]
- Torres, C. (2020). Developing teachers’ didactic analysis competence by means of a problem-posing strategy and the quality of posed mathematical problems. In K. O. Villalba-Condori, F. J. G.-P. A. Adúriz-Bravo, J. Lavonen, L.-H. Wong, & T.-H. Wang (Eds.), Education and technology in sciences: First international congress (pp. 88–100). Springer. [Google Scholar]
- Tricco, A., Lillie, E., Zarin, W., O’Brien, K., Colquhoun, H., Levac, D., Moher, D., Peters, M., Horsley, T., Weeks, L., Hempel, S., Akl, E., Chang, C., McGowan, J., Stewart, L., Hartling, L., Aldcroft, A., Wilson, M., Garritty, C., … Straus, S. (2018). PRISMA extension for scoping reviews (PRISMA-ScR): Checklist and explanation. Annals of Internal Medicine, 169(7), 467–473. [Google Scholar] [CrossRef]
- Vivas Pachas, J. L. (2021). Trabajo matemático de estudiantes de humanidades en tareas sobre función exponencial [Master’s thesis, Pontificia Universidad Católica del Perú]. Available online: http://hdl.handle.net/20.500.12404/18104 (accessed on 27 September 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).