Mathematics with|in Conocimientos: A Mathematical Embodiment and Conscious-Raising Experience

Abstract

Mathematics interwoven with Youth Participatory Action Research (YPAR) EntreMunods is an ontological playground for youth liberation, where mathematical learning helped to create an experience where youth empower themselves by engaging in critical social science research. In this study, seven stages of conocimientos are expanded to help understand how consciousness shifts while engaged in mathematics. Thematic analysis of student reflections on the YPAR mathematics activities revealed how students developed a mathematical critical consciousness. This manuscript is a theatrical conceptualizing of the Math YPAR experience, leading to development of the Mathematics with|in Conocimientos framework; seven mathematical embodiments or stages that once experienced, represent a change in mathematical consciousness. In situating mathematics as a guiding epistemology, method, and pedagogy to the YPAR methodological design, this study highlights the transformative power of mathematics rooted in challenging systemic injustices.

1. Introduction

Rich mathematical learning experiences allow us to have a relationship with mathematics; it is then our connection with math that proves that we are living and that mathematics is alive. Mathematics is epistemologically defined through indigenous cosmologies as a living entity (Martinez et al., 2021; Gutiérrez, 2017), thus math learning needs to be an experience, so we can focus on the relationships we gain with others, with nature, and with mathematics. Uniting Mathematics with Youth participatory action research (YPAR) EntreMundos epistemology creates a rich educational playground allowing mathematics to be an experience, where youth can empower themselves by challenging multiple forms of injustice. As such, mathematics is transformed into a collective process that solidifies the formation of relationships between self, others, and mathematics.

In this conceptualization of Anzaldúa’s (2003) theory of conocimientos, consciousness was analyzed while youth engaged in a mathematics YPAR EntreMundos summer program. The stages of conocimientos acted as an analytic framework to understand data and as a foreground for theorizing. YPAR created a rich education space for young people to explore societal issues, and mathematics was introduced to enhance the YPAR experience. This allows for the expansion and development of individual–collective1 consciousness. The question guiding this study is as follows:

Based on how the stages of conocimientos that emerged during a mathematics-based youth participatory action research study, how can the seven stages of conocimientos be conceptualized within a mathematics context?

In order to center consciousness, the seven stages of conocimientos (Anzaldúa, 2003, 2015) will be used to represent one way of understanding how consciousness develops and shifts towards action upon the world (Keating, 2016). In understanding how learners engage with mathematics with YPAR, this study will explore the epistemological, ontological, and axiological nature of mathematics towards creating spaces where mathematics can be part of self, society, and mathematical transformation in the development of critical consciousness. In investigating how students’ consciousness shifts in the process of mathematical learning, conocimientos (Anzaldúa, 2003), a form of conscious-raising knowledge (Reza-López et al., 2014), becomes an embodiment of mathematical being.

2. Critical Literacy and Critical Consciousness with Mathematics

Mathematics as a form of Critical Literacy can best be summarized by Gutstein’s adaptation of Freire and Macedo’s (2005) Literacy: Reading the word and the world framework that Gutstein (2006) calls reading and writing the world with mathematics (RWWM). Freire and Macedo’s framework is a way to understand the world by understanding the previous world through Critical Literacy (Freire, 1996). Critical Literacy is not just the ability to read and write. It is the ability (and power) of communication and reflection inherent in being able to read and write (Freire, 2000). In a Critical Literacy approach (Freire & Macedo, 2005), the ability to reflect (read) and commit to action (write) is inherently a process of socio-historical–political–cultural development. The praxis behind reading and writing the word is a revolutionary praxis (Freire, 1973) that requires critical consciousness. Critical consciousness is defined as a socio-historical–political–cultural understanding of society with the self-awareness of being able to bring about change in society (Freire, 1973). Critical consciousness is an elastic concept, given society is constantly in flux (Freire, 1973, 2000). Prior to the development of critical consciousness is what Freire (1973) calls a transitional consciousness. Given that a critical consciousness is not permanent, those with a sense of critical consciousness are always between transitional and critical consciousness. Individuals not seeking critical consciousness are said to have a naïve consciousness (Freire, 1973) because they have been rendered objects due to dehumanization (Freire, 2000).

Gutstein (2006) developed RWWM and incorporated the role of mathematics as a way to read the current and previous world. A “[c]ritical mathematics literacy enables the oppressed to use mathematics to accomplish their own ends and purpose” (Leonard, 2009, p. 326). RWWM provides an example where reading the world is the process that engages mathematics as a Critical Literacy through knowing how to use mathematics to read the word (understanding history) to read the world with mathematics. More so, reading and writing is a cyclic process, because understanding the word (reading) leads to action (writing) upon the world. Being able to read and write the world within a Critical Literacy paradigm leads to empowerment and understanding of one’s own agency (Freire, 1973, 1998, 2000).

Youth Participatory Action Research and Mathematics

YPAR is, first and foremost, an epistemology—a life choice and commitment to revolutionary action upon the systemic inequities of society (Cammarota & Fine, 2008; Fals-Borda & Rahman, 1991). The action component of YPAR comes after youth generate and research their own question(s) that directly affect their lives (Aleman & Martinez, 2024). The process of conducting and presenting research is an empowering experience for young people as they engage in transformational resistance and develop a critical consciousness (Cammarota & Fine, 2008). Transformational resistance is a form of resistance that requires a commitment to social justice and a critique of social oppression (Solorzano & Bernal, 2001). A goal for YPAR is to create opportunities for youth to empower themselves, where “YPAR teaches young people that conditions of injustice are produced, not natural; are designed to privilege and oppress; but are ultimately challengeable and thus changeable” (Cammarota & Fine, 2008, p. 2). YPAR seeks to create spaces where youth empower themselves by viewing the research process as more than a method and a methodology but as a critical epistemological commitment (Cammarota, 2017) or, in general, by being a philosophy of life connected to real-world outcomes (Fals-Borda & Rahman, 1991). As for YPAR and mathematics, it is still an emerging area that was first discussed by Yang (2009), who bridged statistics within YPAR, wherein “mathematics was more than just a tool to critique social inequalities. It was also a sociocultural activity through which to examine complex codes of power, identity, and culture in human society” (p. 144). To date, only a few cases systematically connecting YPAR and mathematics have appeared in the literature (see, Battey & Coleman, 2021; Levy et al., 2024; Martinez, 2020; Martinez et al., 2021; Martinez et al., 2023; Edirmanasinghe, 2020; Severns, 2023).

3. Conocimientos

Related to a transitional consciousness, Anzaldúa (2003) offers conocimientos, seven stages of how consciousness changes (see

Table 1. Stages of Conocimientos.

Stage	Description
el arrebato, C1	The beginning of fragmentation and transformation. Known as the stage that kicks you out of your comfort zone, it represents moments where an individual is forced to react.
nepantla, C2	The acknowledgment that in between two ideas, people, or physical places, there is a third entity composed partially of those two ideas. There is always a midpoint, always an in-between space.
Coatlicue, C3	This is known as desconocimiento and reflects the pain of knowing. There is a need to change and reflect on one’s own history and trauma from knowing the truth.
Compromison (el compromise), C4	This is the multiplicity of history, self, others, and the future. The world is constantly changing and is not static and hopeless.
putting Coyolxauhqui together, C5	The reinvention of self and a complete understanding of the old self and the current self help in dismantling the difference between the two and creating a new self.
the blow up, C6	This is the realization that you are no longer the person you were based on interactions with others. Here, learning from defeat and continuing to grow is sustained by connections/bridges made with others.
shifting realities, C7	A spiritual transformation, being conscious of yourself and others, and the action taken in committing to collective change.

Note: The information in this table comes from Anzaldúa’s (2015).

) that provide a more refined way of mapping transitional-to-critical consciousness development. An example of conocimientos in education can be seen in Nepantlera pedagogy (Reza-López et al., 2014), which pairs the seven stages of conocimientos with Freire’s ideas of critical consciousness. Conocimientos represents a spiritual interconnected form of knowledge that allows for mathematics to become a conscious-raising experience that represents both spiritual and scientific knowledge (Martinez et al., 2021). The seven stages are non-linear, non-sequential, nested, and cyclic, where each stage provides insight to each other. For this reason, the stages are interdependent.

The seven stages of conocimientos represent the culmination of Anzaldúa theorizing and the coming-together of multiple bodies of work developed over her lifetime (Anzaldúa, 2015) For example, nepantla has multiple epistemological lineages that were developed in parallel to the seven stages of conocimientos. In mathematics education, nepantla has been utilized to explore secondary preserve teachers’ experiences as they develop new forms of mathematical knowledge, highlighting the need to understand and navigate nepantla as a space where learning and growth happen (Gutiérrez, 2012). Furthermore, “nepantla also helps us as teachers and teacher educators to develop a better familiarity with uncertainty and risk, a feature that is key to all teaching (Gutiérrez, 2015, p. 271).” Without risk the seven stages of conocimientos cannot be fully engaged, and learning becomes stagnant and mechanical. Nepantla is a stage that acts as the epistemic glue of the stages of conocimientos, because all the other stages are both independent of and dependent on nepantla.

4. A Theoretical Framework of (Y)PAR EntreMundos

The epistemology of YPAR is central to creating spaces where youth can liberate themselves by being owners of their own knowledge construction. By “positioning youth as experts in their own right, encouraging them to identify issues that might not be visible to adults, question the root causes of these issues, and dream of new solutions to known and unforeseen challenges (Martinez & Aleman, 2025, p. 3),” it can create an epistemological alignment between theory, practice, and research methodology. Building on mathematics as a form of Critical Literacy and the inherent praxis of YPAR being a space to develop critical consciousness, this study intentionally designed every aspect of the methods to align with a theoretical grounding of YPAR EntreMundos. As YPAR is an expansion of PAR, PAR EntreMundos is an expansion of PAR by bringing Latinx theorizing to the forefront of what and how PAR and YPAR are and have been used/lived and theorized (Berta-Ávila et al., 2020). PAR EntreMundos gathers the many selves we carry and weaves them into an integrated whole—amidst, or perhaps through, the frictions and choques that shape us (Ayala et al., 2018). To practice PAR EntreMundos is to enter a process of healing (Torre & Ayala, 2009).

PAR EntreMundos begins with the southern tradition, which refers to the centering of Latinx scholars who have historically contributed to the development of PAR. The southern tradition fully encompasses the epistemological reach of the theoretical lineages of PAR EntreMundos. The theoretical foundation of PAR EntreMundos consists of the southern traditions, critical race praxes, feminist theorizing, Indigenous ways of being, and critical consciousness of the collective (Ayala et al., 2018). Precisely, PAR-EntreMundos consists of eight guiding principles, see

Table 2. PAR-EntreMundos Guiding Principles.

Guiding Principle	Description
Participation.	Practitioners and stakeholders should be involved in all steps of research (design, data collection, analysis, and dissemination).
Critical inquiry.	The work needs to be grounded in critical race and decolonizing theories that examine the socio-historical, socio-political, and material contexts and conditions of our lives.
Knowledge co-construction.	Knowledge that informs action is produced in collaboration with communities, where researchers and research become a collective of knowledge producers/actors.
Power with(in)	The collective critically reflects on its own process, fosters trusting relationships of mutuality between members, examines power within the group, and engages in deep self-inquiry.
Indigenous cosmologies	In the spirit of an approach to PAR that is EntreMundos and that grows from the southern tradition, we see it as a way to reclaim and reimagine indigenous ways of knowing and engaging in this work as a healing process for the individual and community.
Creative praxes.	The methods for collecting and presenting data are embedded in the cultural and creative productions of the local community, which may include poetry, music, dance, theater, and other forms of cultural and artistic expressions.
Transformational action.	There is a commitment to conscious action and social change using creative praxes and engaged policy.
Concientizacion para la colectiva.	This work is part of a movement, not simply separate sets of isolated actions, whose goals include critical consciousness, social justice, and mutual liberation/emancipation from oppression.

Note: Information for this table is directly from Ayala et al. (2018).

, that guided this study. PAR EntreMundos is both the epistemology and methodological structure of data collection, as it provides mathematical learning with both the physical and metaphysical spaces to better understand how relationships can be formed with mathematics.

5. Methods

It is common in YPAR studies for the researcher to be an active participant. I (first author) was the sole creator and curator of the REALM (Reflection Equals Action in Liberatory Mathematics) curriculum described later. The history and context of REALM are essential to understanding my role as a participant-observer (Creswell & Poth, 2016) fully engaged as the sole facilitator of REALM activities. PAR is as much a life choice as it is a methodological approach to qualitative inquiry (Fals-Borda, 1987; Fine, 2008), and as a form of investigation, YPAR brings together and forms collectives between researchers, students, community activists, and/or various other community members. For the three years prior to this study, I (first author) had been involved with El Sol (pseudonym), a Latinx community-based organization that provides programming for youth on Latinx history and culture to prepare students to become leaders within their community. El Sol provides educational services in eight Midwestern cities and runs over 32 programs for middle to high-school-aged youth. With El Sol, I facilitated programming with youth for two hours a week in a city 45 miles away from the research site. The Director of El Sol then informed me of an El Sol youth who was trying to create a three to four-day writing and science summer camp for El Sol and La Luna (pseudonym) scholars. La Luna is an Agriculture STEM college pathways program that provides underrepresented students with additional learning opportunities in STEM starting in the eighth grade. La Luna students must meet yearly academic and service requirements to earn a 4-year tuition scholarship at the local state university. I met with the student who wanted to create a summer opportunity for her peers and then, after a discussion with the Director of La Luna and El Sol, we decided to do a ten-day summer program where I would have four hours each day to engage students in mathematics-driven YPAR.

5.1. Context

The study took place in a predominantly white mid-large Midwestern city in the United States. All youth were either of Latinx or African descent and represented an ethnically minoritized group in society and STEM fields. All youth were from the same school district, which has 63 schools, including 38 elementary schools, 11 middle schools, 5 comprehensive high schools, and 10 schools that provide a range of specialized and alternative educational programs. Those participating in REALM represented five different high schools. The daily meeting place for REALM was a middle school within the school district. El Sol selected the site through their partnership with the school district. We had two classrooms for REALM activities. The classes had individual desks, a whiteboard, and a projector. Additionally, the middle school was used by the local Boys and Girls Club. El Sol and the Boy and Girls Club were the only two youth groups in the building, but we had no daily interactions.

5.2. Recruitment

To participate in REALM, students had to either be part of El Sol or part of La Luna. El Sol recruited internally via a word-of-mouth approach, in which the director of the program individually informed students about the program. La Luna had an internal recruitment process where students had to apply to take part in the program. A flyer giving an overview of the program to prospective La Luna scholars was used to help recruit. All youth who applied were allowed to participate in REALM. If a student was not part of El Sol or La Luna, they could still participate by joining El Sol on the day they arrived at REALM—requiring students to join El Sol if they were not part of La Luna or El Sol was strictly performed for liability reasons. In total, 28 youth signed up for REALM, but only 17 participated, with 13 being part of this study. Three young people were part of El Sol, and the rest were part of La Luna, with one individual being active in both programs.

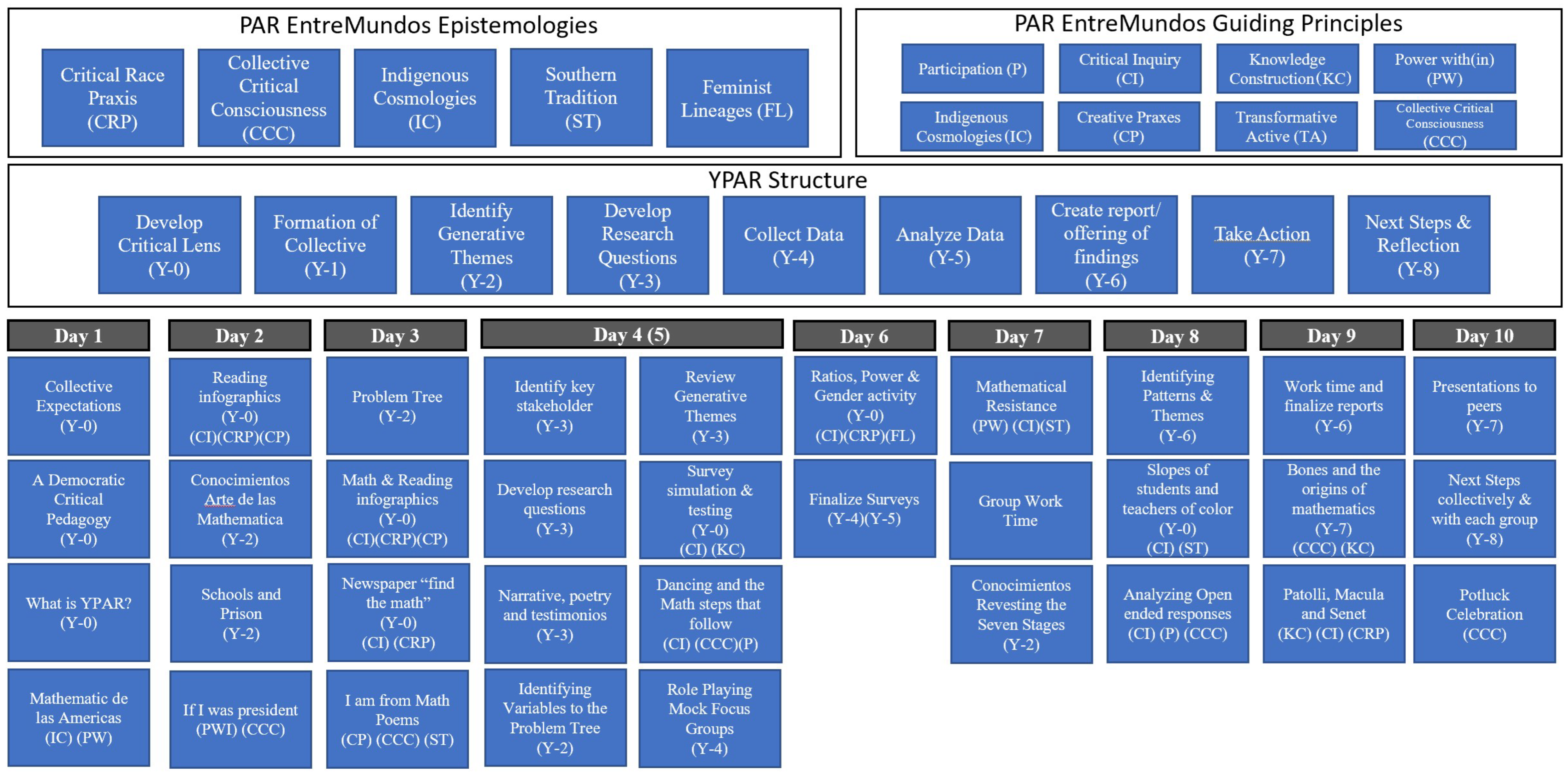
5.3. REALM Methodological Structure

An overview of the methodological alignment of REALM to the theoretical framework is displayed in Figure 1, followed by detailed bullet points.

I.

Day 1: Establishing group expectations, defining YPAR, and beginning the formation of a collection.

a.

Mathematicas de las Americas is a presentation that focuses on the mathematics and science history of the Aztec, Maya, and Inca peoples. The presentation was created to connect both the guiding principles of Indigenous cosmologies and allow youth the opportunity to reflect on the power with(in).

b.

Patolli, the oldest known board game from the Americas, was played to allow youth to get to know each other (formation of a collective) by playing a game that allowed them to explore probability, specifically the expected values of outcomes. Additionally, this connects mathematics to Indigenous cosmologies.

II.

Day 2: Developing a critical lens and identifying generative themes.

a.

Infographic-centered mathematical literacy (knowledge) is a way to develop a critical understanding of the world while learning about societal injustices.

b.

Music, as a creative praxes, was used to help youth reflect on societal injustices and issues in their math class. Youth were asked what they would do if they were the president of the country and then if they had complete control of their math class.

III.

Day 3: Developing a critical lens and reflecting on generative themes.

a.

“Mathematics in the news” is an activity modified after Skovsmose’s (2011) activity of having learners identify or find the mathematics in the newspaper.

b.

Poems were created using an I am Math poem template (reference Appendix A) as a creative praxes to identify generative themes.

IV.

Day 4 and 5: Developing a research question and research training.

a.

Youth were trained to be researchers.

i.

How to take field notes.

ii.

How to write observation memos.

iii.

How to conduct interviews and focus groups.

iv.

Survey design.

1.

Open-ended (qualitative).

2.

Yes/No: check all that apply, ranking and Likert (quantitative).

v.

Survey pilot testing.

V.

Day 6: Developing a critical lens, collecting data, and beginning to analyze data.

a.

A ratio of power activity connected the gender wage gap to the disproportionate number of men to women in positions of power. The activity shows how ratios can help develop a critical lens and the importance of knowing how to read and communicate with mathematics.

VI.

Day 7: Developing a critical lens and analyzing data.

a.

Mathematics problems contextually grounded around the Delano grape strike and the Black Panther Party’s free breakfast program connect history to math.

VII.

Day 8: Developing a critical lens, analyzing data, and creating reports.

a.

Comparing slopes of Students and Teachers of Color over the last seventeen years allowed youth to see at what rate their school is changing. The activity allows for developing a critical lens on how to use data to compare variables over time. In this case, the rate of change in Students of Color versus Teachers of Color in their school district.

VIII.

Day 9: Analyzing data and creating reports.

a.

Origins of mathematics, a description of the oldest known mathematical artifact, the Lebombo Bone, circa 35,000 BC, along with the game Gebet’a (also known as mancala), circa 700 BC, showed the African origins of mathematics.

IX.

Day 10: Present reports and reflect on the next steps.

a.

Youth presented the graphs, charts, art, and infographics they created.

6. Data

The data in

Table 3. Data used for each research question.

Data	Description
Youth Journals	At the end of each activity or day (except the first journal), youth were asked to reflect on what they learned and how the learning made them feel. Before any activity, youth were asked to journal based on the prompts “What is math?” and “What do you expect over the next two weeks?” The journal is where youth wrote and worked on all but three activities.
Group Audio	Each group was audio recorded during the entire duration of REALM.
Whole Audio	An audio recorder was placed between the youth and me, capturing the audio of the entire room.
Teaching Memos	After each day, I wrote a memo reflecting on the lesson.
Additional Artifacts	Additional artifacts consisted of activities performed outside of the youth journals and consisted of problem trees, I am Math poems, newspaper from the math in the news activity, and worksheets used for the gender ratio activity.
Teaching Slides	The PowerPoints used to teach each day of the program were saved.
Final Presentations	The final products or presentations that each group of youth created.

, excluding teaching memos and teaching slides, were collected as youth worked in groups during REALM activities.

Youth assigned themselves to groups based on their own interests. All groups were in close enough proximity to hear and speak with other groups. Each group had an audio recorder placed in or around their working space, and an audio recorder was set up in front of the classroom to capture whole-group discussions. Each youth was given a notebook that acted as their journal. Youth were told to write as much as they felt comfortable sharing and that they did not have to address each question.

Data Analysis

Thematic coding, a rigorous approach to analyzing themes (Fereday & Muir-Cochrane, 2006), was used to analyze youth journal entries. Each sentence was coded to honor every word written by each participant. Youth were given prompts to help them reflect at the end of each activity or day, reference Appendix A. Braun and Clarke (2006) provide six phases for thematic analysis: (1) Familiarization with the data, (2) Coding, (3) Searching for themes, (4) Reviewing themes, (5) Defining and naming themes, and (6) Writing up. This analysis method is flexible enough to use pre-established codes, i.e., the seven stages of conocimientos, which is the analytic framework of this study.

Appendix B can be viewed as a methodological companion that gives additional details on the thematic analysis. In short, (1) familiarization with the data was achieved by reviewing each journal, all teaching presentations, audio of whole-group sessions, teaching memos, and all additional artifacts. (2) deductive coding using the seven stages of conocimientos was completed (reference Appendix B,

Table A1. Codebook with example.

Stage	Simplified Description	Excerpt Example
el arrebato, C1	Things that cause discomfort	Although I love a-ha moments, one word [to describe math in school]! Confused.
nepantla, C2	Comparisons and definitions of worlds	Math can be used in many ways to show records from sports of all sorts and to also the diversity of places like schools.
Coatlicue, C3	The pain of knowing|tied to (negative) history	Why don’t our teachers tell us the “truth” about our Ancestors and where math actually comes from?
compromison, C4	The process of change or knowing change can happen	Math can be used to describe the world we live in and change it for the better.
putting Coyolxauhqui together, C5	Comparing the past to the present self—the connection between worlds/ideas.	I wasn’t only learning slope but I was learning the rate of admin and teachers of color decreasing from schools.
the blow up, C6	Being aware of others and learning from them. Growing from pushback.	It surprised me how it really connected to who I am and who we are.
shifting realities, C7	Enacting Spiritual Activism—collective action	Because of this program I can tell my math teacher to teach us of our deep math history to encourage us to use this skill to better our community and better the lives of those around us.

) to further explore how consciousness shifts. The stages of conocimientos are interdependent, which meant that student reflections could be double, triple, or in rare instances, quadruple coded. Moreover, content analyses (Neuendorf, 2016) were performed to provide a summative view of the observed codes (reference Appendix B,

Table A2. Frequency of codes across journals.

Code	J0	J1	J2	J3	J4	J5	J6	J7	J8	J9	J10	Total
C1, el arrebato	10	7	7	11	13	0	0	2	3	3	4	60
C2, nepantla	17	14	12	23	10	8	9	8	7	7	29	144
C3, Coatlicue	3	5	4	1	4	1	2	4	3	5	15	47
C4, compromison	4	8	5	7	1	5	8	10	4	2	13	67
C5, putting Coyolxauhqui together	3	1	11	8	14	4	3	6	5	12	16	83
C6, the blow up	1	2	2	7	6	1	9	7	4	18	17	74
C7, shifting realities	1	1	3	6	1	1	5	4	0	7	12	41
Total	39	38	44	63	49	20	36	41	26	54	106	516

) in both (3) searching for themes and (4) reviewing themes while searching for any patterns across codes. While all data assisted in the writing of the findings, content analysis was performed only on the youth journals because they contained reflections on learning, which is the best data for exploring the formation of consciousness. Journals were coded line by line to honor the time youth spent writing. A narrative of the YPAR experience was constructed to situate the codes in the context of the study, along with the multiple graphs and tables from the content analysis, which assisted in (5) defining and naming themes. (6) the result of the coding represents the implications and discussion of the data in this study. The process of thematic analysis utilized data to revisit the analytical framework to develop a conceptualizationof the mathematical interpretations of the seven stages of conocimienots.

7. Findings

Consciousness ranges from the rational modes of thinking related to the natural world to imaginative modes of consciousness related to fantasy and the intangibles of the natural world, and consciousness has several dimensions with multiple modes of consciousness shifting and overlapping between rational and imaginative modes (Anzaldúa, 2009). In order to understand consciousness, the seven stages of conocimientos (Anzaldúa, 2003 will be discussed to represent one way of understanding how consciousness develops and shifts towards action upon the world (Keating, 2016). In the following section, we will describe each of the seven stages of conocimientos through the youth reflection data. It is important to recall conocimientos are a collective and communal experience that is not a linear progression. The underpinnings of conocimientos offer a metaphysical and temporal unboundedness, where one student’s experience has the possibility to be something experienced by all students, and where what a student experiences at one point in time is inherently connected to experiences that take place at other points in time. Coatlicue is intentionally discussed as the last stage to emphasize the non-linear and cyclical characteristics of the seven stages of conocimientos.

7.1. El arrebato: A Catalyst for Mathematics

The start of learning is at the heart of el arrebato, where dislocation leads to questions, and the process of finding answers comes from relationships made with others and the world. El arrebato can be found at the end of learning, as it can lead to new questions being asked as people reflect upon what they have just learned, or when they can be shaken up by what they still do not know in the middle of mathematical learning. El arrebato is as much a starting point as it is a continuation of education. More so, at any aspect of the learning process, an el arrebato can manifest due to the context of the learning and/or how it impacts the learner’s world. For example, on Day 2, when one of the youth looked for mathematics in the newspaper, they stated, “looking at the newspaper, it surprised me how easily things can be overlooked.” The act of being surprised is an el arrebato, and it occurs when the information within the content of the activity is overlooked. When foreign and abstract context is used, learners feel distant and disengaged, causing an additional shake-up. The results of this research revealed that el arrebatos are signifiers of opportunities to learn mathematics connected to either positive or negative feelings. A positive example of an el arrebato is a statement from one youth: “It surprised me how much math you can find in a newspaper about everyday things.” Both positive and negative reactions to learning led individual youth to ask more questions and engage with the other stages of conocimientos.

El arrebato is important because it represents the shake-up needed to have learners realize that mathematics is useful, fun, cool, confusing, and more than emotionless logic. The multiple ways people see mathematics is inherent because of the multiple layers of how mathematics manifests in each individual, and el arrebato, along with the rest of the stages of conocimientos are one way to understand mathematics, self, and the world better. Take the example of a youth stating, “So [I] don’t see myself as a mathematician just because I’ve never been good at it, I’ve always struggled or end up frustrated in the end.” We can see how struggling and being frustrated leads to a shake-up in how they see themself as a mathematician, and if this el arrebato is left alone, then it will only continue to affect this young person in a not-positive way. The same young person wrote the following journal entry on the last day of the program.

The difference between the math we’ve learned in the past 2 weeks and what we learn at school is that the math we learned here was connected to some part of history or poetry, and I’ve learned something new while doing math, but at school they don’t tie math to outside stories, it’s just all about math. … One thing I would tell my math teacher to change [in] the way they teach would be that connecting math to the real world have so many kids to get involved, it would have their attention more, and maybe more students would pass.

The el arrebato of not being a mathematician because of its difficulty can be challenged by the shifting realities stage in connecting mathematics to the real world (nepantla) so it can be more engaging. Connecting mathematics to history and current “outside” stories can lead to the compromison to change the classroom (and world) because both are not fixed conditions. Without el arrebato people cannot act to change the world (compromison, the blow up and shifting realities) or to change themselves (Coatlicue, putting Coyolxauhqui together, the blow up), and nepantla, an infinite zone of possibilities, cannot be experienced.

7.2. Nepantla: Embracing Infinity Nested in Infinity

Nepantla is multilayered in that it represents all forms of epistemic friction between any two people and/or different ideas. Every time you read something, you are engaged in nepantla, in that your ideas (worlds) meet the ideas (worlds) of the writer. The differences between the reader and writer can be absolute, minimum, or near zero, where the distance between the two is nepantla. Learning mathematics within nepantla acknowledges the differences between teachers and learners, along with the differences between learners. Furthermore, nepantla welcomes the differences between individuals and ideas as it relates to the multiplicity of mathematics and the multilayered facets of identity. An example of how nepantla is nested and represents the comparison of multiple worlds can be seen in one youth writing, “math is everything, from the structure of our bodies to the layout of a building, math can be applied to everything” where the idea of mathematics being everything is comparing the world of mathematics with the structure of the body and the structure of buildings.

Nepantla is an exploration of worlds (physical and metaphysical) through connections between worlds, and thus, nepantla can be used to explain all facets of life. During REALM, a youth wrote, “what we have been learning is more important than normal math,” wherein they are comparing and adding value to two different ways of experiencing mathematics. The idea of normal math (classroom mathematics) is problematic as it creates a divide between the mathematics learned at school and the mathematics experienced/lived outside of the classroom. Nepantla is a focus on the paths that connect these multiple worlds.

7.3. Compromison: Mathematics Can Change the World

Mathematics and compromison focus on changing society, as stated by one of the REALM youth, wherein youth are “trying to discover better ways to improve problems in the world” with the acceptance that changing the future is possible. Two different young people wrote, “[m]ath can be used to describe the world we live in and change it for the better” and “math can change the world because we use it every day to do challenging problems,” which best reveals the significance of compromison. Mathematics should not be limited to finding a better or more efficient approach to a problem, and a better approach needs to lead to changes. Compromison has inherently been part of mathematics since its origin, in that new types of mathematics have always been possible.

Mathematical learning must connect to the real world for learners to connect and know they can change the world. Youth wanted to learn new ways of connecting to mathematics, because they were already aware that new skills could be useful for their future. Mathematical learning allows for multiple futures to relate to the multiplicity of each individual and their experiences. When asked, what is one thing you would tell your teacher, on the last day of REALM, one young person wrote, “[o]ne thing I would tell my math teacher about changing the way they teach is to understand how their students learn and to fit that into their experiences.” Compromison thrives in embracing the multiplicity of a person’s identity and lived experience because multiple histories represent multiple potential futures. Mathematics can welcome the histories of students and incorporate them into the classroom, or we can choose to do nothing and create additional barriers for students to learn about the real world when learning mathematics.

Mathematics that lives with compromison can best be summarized by these two youth voices:

Youth Voice 1: Seeing where math comes from makes me feel like a mathematician, because math is everywhere.

Youth Voice 2: I think that inequality should be taught in math class because people need to be informed about the truth in society.

Being informed about the mathematical truth requires an examination of multiple mathematical histories, along with uncovering inequalities and dismantling barriers that keep us from the potential for equitable futures.

7.4. Putting Coyolxauhqui Together: Reading Mathematics to Know Self and World

Coyolxauhqui represents transformation in deconstructing and reconstructing one’s own identity. Where el arrebato and mathematics represent how feelings are drawn out in the process of learning, putting Coyolxauhqui together focuses on how reflecting upon emotions, feelings, and desires constructs identity. During REALM, after the ratio of power activity, which looked at the gender wage gap, a young person reflected by writing, “This activity taught me and replenished my math skill that I have learned the statistics for the Latinx community.” The idea of learning and replenishing a person is a reconstruction of their ability. Additionally, for young people to learn more about their community, it is vital for them to understand problems in their community at deeper levels. The compromison stage in mathematical learning is for understanding the past and the future, whereas putting Coyolxauhqui together allows mathematics to aid learners in understanding how the present self fits between the past and future. During REALM, a young person wrote, “as people learn math nowadays, they don’t learn how useful it can be to predict or determine statistics to paint a picture of someone’s struggle,” when reflecting on finding the rate of change in Students, Teachers, and Principals of Color over time in their school district. It captures the importance of mathematical critical self-literacy in understanding issues within society. Putting Coyolxauhqui together is mathematical self-critical literacy and the transformation of self, others, and mathematics.

Critical Literacy in mathematics directly connects mathematics to the real world, as stated by a REALM youth; “the math we did led me to think more about how math can be used in the world around us.” Furthermore, when young people learn about the world in the classroom, they begin to see that mathematics exists outside of the classroom, diminishing the divide between mathematics in the classroom and outside of the classroom as two different entities. Critical Literacy is central to developing a critical consciousness, and REALM youth had multiple opportunities to develop this as they learned history while learning about the mathematics of the Aztec people; they learned the history behind social programs created by the Black Panther Party; they learned about the Delano Grape strike; they learned about the wages of men and women in the United States; they explored mathematics found in local and national newspapers; and they learned about the demographics of the students, teachers, and administrators in their schools. Critical Literacy was an essential aspect of REALM, and putting Coyolxauhqui together shifted mathematical Critical Literacy from an understanding of the world to an understanding of how an individual transforms and constructs their consciousness due to a better understanding of the world—a critical self-literacy.

7.5. The Blow up: Meeting Others to Write Mathematics

Identity and consciousness do not form in a vacuum; where putting Coyolxauhqui together represents the process of individual–collective transformation, the blow up is the internal change at the end of the process of transformation because of others. The blow up is when the individual acknowledges collective learning and how learning has implications for everyone’s future. This occurs in mathematical learning when an individual sees beyond themselves. The understanding of mathematics being a collective learning process is exemplified in a young person reflecting on what math is on the last day of REALM, “we understand the world with math because we try solutions to make the world livable for society with advanced technology and more” which led another youth to say “It made me feel so empowered to have such a revolutionary skill.” The first quote highlights that an understanding of the world (Critical Literacy) leads to solutions for all of us, as we understand the world with math, and the second quote returns to the individual where they are now empowered. Putting Coyolxauhqui together and the blow up are deeply intertwined, yet differ, because the blow up focuses on others, and it is a collective understanding that signifies the results of internal transformation.

The impact of the blow up in mathematics is a challenge against individualism in mathematics education through advocating for group work that leads to quality mathematical discussion and collective understanding. On Day 2 of REALM, youth were asked what they would do if they were in charge of their mathematics class; one youth wrote, “I’d make sure everyone understands the lessons, even some of the kids who sit in the back,” showing a desire for collective understanding and seeing the world outside of themselves. Another youth wrote, “group projects are no longer prioritized, but asking for helping each other is encouraged,” which highlights that the blow up does not just mean that group work is the best approach. Without a classroom space that welcomes collective understanding, group work will function as a continuation of individual learning in the classroom. For that reason, it is essential that the context of learning is engaging and connected to the real world.

The blow up with respect to mathematics requires teachers to question their role in how students learn. Teachers are the gatekeepers to the content, context, and connections made due to pedagogical approaches to teaching (Martin et al., 2010). During REALM, one youth responded to the question of why they think teachers do not utilize lessons with historical content and real-world connections by writing, “I think my math teacher doesn’t use these b/c that’s not how they taught them to teach.” This shows an interesting take on the blow up by connecting the teacher’s teaching knowledge to how they were taught, in that it shows the teacher’s need to understand mathematics as a collective endeavor of self and societal becoming, which provides an example of why compromison is so important in breaking the cycle of teaching the way we were taught, because the future is dynamic and always changing. A teacher should first ask themselves, “How can math be used to understand the world?” so they may arrive at what the REALM youth learned and see that “Well math wasn’t just found in one place. So, to understand math, we must open our minds to being more understanding and loving towards cultures.” The blow up youth experienced due to REALM can be seen in the following two excerpts. “I learned more about myself… understanding more about understanding people’s perspective,” wherein we see that learning about others leads to individual change, and REALM activities “surprised me how it really connected to who I am and who we are” where the surprise (el arrebato) is not just I (individualism), it is we (collective understanding).

7.6. Shifting Realities: Counting Our Acts of Resistance

Shifting realities and mathematics represent the external action taken upon the world to disseminate mathematical knowledge that keeps us from ourselves and others. On Day 2 of REALM, when two different young people asked if they could have a copy of the Patolli game board to share with their families, they committed to an action that shares mathematics with others. Putting Coyolxauhqui together and the blow up provide context (Critical Literacy) to ensure that mathematics allows for the formation of conocimientos. The stages of conocimientos are not linear, and the action of shifting realities does not have to be a direct action but can result from reflection on a previous action. For example, one youth wrote in a journal entry as follows.

I really hope middle school students can have the opportunity of learning how they can use math in the real world. I remember asking my sister how can fractions be used and she said for splitting foods like apples. But in truth fractions can be used for so much more.

By learning the importance of connecting mathematics to the real world, this young person was able to reflect on a time when they spoke to their sibling about the use of fractions, where they were engaging with their sibling in shifting realities. Another example from a different young person, “Now I do see myself as a mathematician I use it in my daily life when baking when shopping and the types of math we learned at school,” shows how reflecting upon seeing oneself as a mathematician leads to the recollection of previously using mathematics in the real world. Shifting realities links reflection to action and actions to reflection. Shifting realities does not only look back at previous actions but looks forward to future action. For example, one young person at the end of REALM wrote, “Because of this program I can tell my math teacher to teach us of our deep math’s history to encourage us to use this skill to better our community and better the lives of those around us.” In this excerpt, we can see two actions, the action of telling the teacher what to teach and the action of bettering the lives of others, which represents shifting realities. This excerpt also represents putting Coyolxauhqui together in that the young person mentions how the program is the reason for the action that they (an individual) can take; it represents the blow up in acknowledging making the community better for all of us (collective acknowledgement); it represents compromison in showcasing that the betterment of the community is possible, along with mentioning math’s history; and we see the multiple worlds (nepantla) referenced.

Furthermore, this shows the multiplicity of the seven stages of conocimientos, and the impact REALM had on the youth. As one person said about their experience, “Through our stories, we realize why we are who we are and [it] made me open my eyes to the connections in life” where the significance of shifting realities and mathematics is the ability to make connections in life through actions. Hence, Critical Literacy in mathematics education should learn from YPAR epistemologies and commit to understanding mathematical actions for social transformation.

7.7. Coatlicue: The Power and Fear of Knowing Mathematics

Multiple perspectives come together in this stage, in that the pain of knowing is a pain rooted in dissonance due to differences and unknown similarities. Harmony begins by healing mathematical trauma through experiences, and the fostering of motivation comes from Coatlicue because “math is fun and at the same time sad.” Mathematical trauma begins at school when “the teacher shows you and then you have to regurgitate it back to them,” a form of banking education, a dehumanizing of mathematical learners (Freire, 1996). The pain of mathematics is not only found in school but is interwoven in society, where school mathematics is a form of status. Knowledge construction is key in understanding Coatlicue and mathematics because when young people do not believe they can contribute to their own education, then they do not see education for themselves. Mathematics interwoven with YPAR allows young people to know the injustices that limit them and gives them an opportunity to recognize their own agency. As one REALM youth stated, “After [REALM] I feel like math in school is missing something.” The unsettling feeling of school mathematics missing something is powerful, because post-REALM, youth will be aware that their high school math class makes them feel like they do not belong, yet they will know that it is not their fault but that of the school system as a whole. Both being at fault and being a victim are painful, but if a person believes they are at fault when they are not, it begins to strip away their agency. Whereas, if a person knows the system is the problem and not them, then they can engage other stages of conocimientos and commit to action in transforming the system. El arrebato is the shock that pushes a person to change and Coatlicue is the fuel needed to dive deeper into nepantla.

Coatlicue has a profound impact on mathematical learning, in that it can cause barriers to student reflections, or it can motivate them to continue learning. When asked what is one thing that you would want to tell your teacher, one young person said “why don’t our teachers tell us the ‘truth’ about our Ancestors and where math actually comes from?” and a different young person wrote to teachers saying, “Students wouldn’t hate you if you weren’t so condescending. Students wouldn’t fall asleep if you gave them something to care about.” This evidence shows students are acutely aware of how teachers see them, and it negatively affects how they learn. In REALM, Coatlicue is indicative of the lack of diversity in mathematics. The lack of acknowledging the mathematical histories of all people creates a hierarchy, making those already part of the curriculum feel welcomed and everyone else othered. One of the REALM youth said “when I’m at school I don’t feel like I’m as smart as other kids,” which is a consequence of teachers not seeing/knowing that mathematics is already alive in each student; it may just look different.

7.8. Discussion: Reconceptualization of Mathematics with Conocimientos

The findings of this study bring us to mathematics with|in conocimientos (M|C) and conocimientos with|in2 mathematics (C|M), a conceptualization of a mathematical embodiment of the stages of conocimientos. M|C honors the multiple types of mathematics that have existed in human history and the various future possibilities of mathematics.

Table 4. Mathematics with|in conocimientos framework.

Stage	Mathematical Embodiment
el arrebato, Mathematical Ruptures.	Mathematics is connected to emotions, from the surprise and joy of learning to the anxiety and fear created by mathematics. A challenging or interesting math problem or learning something that seems to break the rules. This is related to discovery.
nepantla, Multiplicity of Mathematics.	The wonder and the possibility of connections made while learning mathematics. Connections can be between learners, mathematical ideas, or between a wide range of physical and metaphysical forms of mathematics. This is the inherent tension of asset-based approaches and the struggle of incorporating culture into the mathematics classroom.
Coatlicue, Mathematical Feelings.	The pain of learning mathematics and other strong feelings associated with reflecting upon the mathematical world. Deeply connected to history and the lived experience. This is related to the impact of discovery.
compromison, Speculative Mathematics.	A mathematical imaginary between mathematical history and future mathematics that is not fixed. How people understand the history of mathematics can change just as much as the future of mathematics will change.
putting Coyolxauhqui together, Mathematical critical self-literacy.	Mathematical critical self-literacy. The ability to use mathematics to better understand how one undergoes internal transformation. Mathematics is used to reflect on and about self.
the blow up, Collective mathematical reflection.	Dialogue of mathematical learning in identifying that mathematics is already a part of each individual person. Mathematics works to interconnect people so that reflection is no longer about me and I. It is about us and we, in search of a collective mathematical identity.
shifting realities, Mathematical critical action.	Living with mathematics means using mathematics when no one is looking and when everyone is watching. This is the action associated with sharing mathematical knowledge for collective well-being. A community identity committed to action.

gives a mathematical embodiment for the seven stages of conocimientos.

The stages of conocimientos can be listed in any order and are communicated in line with how Anzaldúa first communicated the stages. The order does not matter because any one stage can lead to any other stage. There will be patterns in how all seven manifest, but those patterns are not guaranteed. Each stage of M|C represents its own sub-area of research; future research does not need to focus on all seven stages—it is just important to know that all seven stages must be engaged to show that consciousness is being developed.

The implication of the seven stages of conocimientos within mathematical learning is an opportunity for the unification of a mathematics education that changes an individual’s consciousness on a collective level. Concimientos provides the key steps to understanding mathematics to be able to understand the development of critical consciousness. To experience all seven stages of conocimientos about one topic is to have critical consciousness. Thus, understanding how the seven stages manifest in and with mathematical learning is important. Table 4 connects mathematical learning based on the data of this study to conceptualize a mathematical embodiment of each of the seven stages of conocimientos. M|C allows mathematical learning to come alive as it makes a companion out of all of us. Mathematics that is alive forges a relationship between learners, as a shared experience reveals our interconnected selves.

7.9. Implications: For Our Spirit

The framework provides multiple areas of future research to better understand how students, teachers, and mathematics teacher educators develop forms of collective, communal, and collaborative Critical Literacy that leads to critical consciousness development. For example, M|C is currently being used to analyze a single lesson (manuscript under review) to determine if the lesson leads to changes in consciousness related to the multiplicity of identity. This lesson is one of five lessons, part of an NSF-funded grant where M|C is the guiding framework for the project. Multiple interconnected moments of mathematical learning are where M|C can best be used. Utilizing M|C for a single lesson will rarely encompass all seven stages, but by analyzing multiple lessons, we can start to see how the overall curriculum does or does not provide opportunities for learners to experience all seven stages. The M|C framework can also be used for educators to review and reflect on their own practice. Does your teaching lead to changes in consciousness? If so, how? Using M|C as either an analytic framework or as a reflective tool is one way to better understand the impact of your teaching.

Additionally, each individual stage of M|C can be its own research focus. For Anzaldúa, Conocimientos was the culmination of decades of theorizing, wherein others were theorizing with her to focus on individual stages of conocimientos. In this article, we offer M|C as an invitation to build knowledge with us to continue to have collective changes in consciousness. It is sufficient to only focus on one or two stages of M|C as part of a research project. Similarly, to being between transitional and critical consciousness, everyone engages the stages of conocimientos differently. In this study, we used deductive codes, and future levels of analysis could use inductive codes to add a second layer to better understand individual aspects of the seven stages of M|C. Yet, in this study, focusing only on the deductive codes allowed for the theorization of the stages of conocimientos within a mathematics learning space. Consciousness is shifting and developing within mathematics; this is evident in Appendix B and by sharing how youth reflected on REALM. The interdependent nature of the data and guiding epistemology allow for studies to be examined as a collective experience.

The mathematical embodiment of M|C represents a framework of Critical Literacy that can be used to map how consciousness is shifting toward critical consciousness. It begins with the multiplicity of mathematics (nepantla) and moves away from single-minded binary thinking. Youth need Mathematical Ruptures (el arrebato) that engage learners in critical inquiry with mathematics. Speculative Mathematics (compromison) represents the hope and reality that systemic injustices in mathematics teaching and learning can be rectified. Mathematical critical self-literacy (putting Coyolxauhqui together) and collective mathematical reflection (the blow up) are vital to reflecting on how mathematics is connected with understanding ourselves and the world. We cannot forget that Mathematical Feelings (coatlicue) are reminders that we are alive. Without the actualization of those sensitivities, then, we have no guide for mathematical critical action (shifting realities).