The Role of Spatial Reasoning in Growing and Spatial-Repeating Patterns in First and Second Graders’ Structural Development of Mathematics

Abstract

A cross-sectional qualitative study examined how different pattern types accounted for wide variation in children’s Awareness of Mathematical Pattern and Structure (AMPS), illustrating how spatial and patterning skills are interrelated. An interpretive descriptive analysis of responses was conducted for two interview-based Growing Square Array (GA) and Spatial-Repeating Pattern (SP) tasks with 405 children from Grade 1 (n = 189) and Grade 2 (n = 216). Analysis of developmental levels of AMPS indicated that advanced multiplicative spatial structures were employed in GA patterns for 20% of Grade 1 and 35% of Grade 2 children, respectively. Responses to SP tasks extended beyond the ‘unit of repeat’ to the use of dynamic visualization, and orientation and transformation skills for 60% of children. Responses showing advanced structural features moderately increased at Grade 2 for both tasks. Micro-level analyses of illustrations of interview responses and from a Pattern Construction task, drawn from five case studies, revealed how multiplicative and transformation skills were utilized in forming repetitions and growing patterns in complex and novel ways. While the ‘unit of repeat’ is fundamental, the integration of more complex multi-dimensional patterning with spatial concepts can re-focus learning and pedagogy on establishing interrelationships between patterning and spatial concepts, and broader mathematical knowledge.

1. Introduction

Research is early childhood1 mathematics education has been extensive and increasing over many decades, with a broad aim of gaining a deep understanding of mathematical development in order to inform effective research-based practice (Björklund et al., 2020; D. H. Clements et al., 2023; Russo et al., 2024). A wide range of studies have focused on single concepts such as counting, shape, or pattern, and mathematical reasoning (e.g., English & Mulligan, 2013; Kinnear et al., 2018; Wijns et al., 2019a). More broadly, studies in early schooling have focused on pedagogical and developmental approaches to learning and instruction, such as learning trajectories (e.g., Baroody et al., 2021; D. H. Clements & Sarama, 2009). The investigation of early mathematical patterning can be traced to studies from cognitive, developmental and educational psychology, and mathematics education domains (e.g., Baumanns et al., 2024; Fyfe et al., 2017; Lee et al., 2011; Lüken & Sauzet, 2021; Miller et al., 2016; Mix, 2019; Mulligan et al., 2020a; Papic et al., 2011; Pitta-Pantazi et al., 2024; Rittle-Johnson et al., 2013, 2015; Wijns et al., 2019b; Zippert et al., 2020). Indeed, in recent decades, research in early childhood mathematics education has witnessed unprecedented attention given to the role of patterning in the acquisition of broader mathematical knowledge (Larkin et al., 2024; Wijns et al., 2019a). Early patterning competencies have been found influential to mathematics achievement and learning (e.g., Björklund & Pramling, 2014; Junker et al., 2024; Lüken & Sauzet, 2021; Wijns et al., 2021) and to the development of mathematical structure—abstraction and generalization, and algebraic reasoning (e.g., Alsina et al., 2024; Du Plessis, 2018; Mulligan et al., 2020a). Recent studies have investigated children’s spontaneous and guided patterning experiences (Lüken, 2025), the effect of different types, such as repetitions and growing patterns (Larkin et al., 2024; Wijns et al., 2019b), and their complexities and representational modes (e.g., Alsina et al., 2024; Diago et al., 2022). Research on repeating-pattern skills has also been extended to preschoolers’ engagement in pattern-oriented picture books (Wijns et al., 2023).

These studies have established the consensus that repeating patterns are fundamental, but advanced structural awareness is only developed with recognition and application of a ‘unit of repeat’—a significant advance from unitary counting and additive strategies. Evidence of young children’s ability to recognize and extend growing patterns has been less prominent but critical to advancing the field (Mulligan et al., 2020a; Wijns et al., 2019b). Evidence of the acquisition of multiplicative concepts, i.e., equal grouping and colinear array structure, has emerged through studies of both growing and spatial patterns with preschoolers and children in early schooling. Spatial structuring and the application of transformation skills, such as translating a ‘unit of repeat’ or using symmetry, were found interrelated in children’s repeating and growing patterns, and in their creations and representations of two- and three-dimensional patterns (Lüken, 2025; Mulligan & Mitchelmore, 2018; Mulligan et al., 2020a; Papic et al., 2011).

Taking another perspective, the research literature on the role of spatial ability and spatial reasoning has also questioned how patterning and mathematics learning, and patterning and spatial skills are interrelated (Mulligan et al., 2020b; Resnick & Lowrie, 2023; Rittle-Johnson et al., 2019). While a causal relationship has been established between spatial reasoning and mathematics achievement, it is not clear how patterning and spatial skills are interrelated and translated in the early development of mathematical knowledge. The complexities of investigating such interrelationships with young children have not been sufficiently distinguished, and there remains a need to adopt broader theoretical perspectives and appropriate methodologies to tease out the mechanisms by which these interrelationships are developed (Bruce et al., 2017).

2. Literature

An extensive range of studies has found that young children from prior-to-school through to early schooling can recognize, complete, extend, represent, and create different types of mathematical patterns: repeating, growing, and spatial patterns (e.g., Collins & Laski, 2015; Junker et al., 2024; Larkin et al., 2024; Lüken & Sauzet, 2021; Mulligan et al., 2020a; Papic et al., 2011; Pasnak et al., 2019; Wijns et al., 2021). Patterning skills are found to be interrelated with numerical competencies such as counting, multiplicative reasoning, and number line estimation (e.g., Junker et al., 2024; Lee et al., 2011; Lüken & Sauzet, 2021; Wijns et al., 2020). Pattern-oriented intervention studies have aimed to promote the development of early patterning in different preschool and schooling contexts, utilizing a range of approaches (Acosta et al., 2024; Junker et al., 2024). Common findings indicate that early intervention can both support and advantage young children’s mathematical competencies (Gripton, 2023; Mulligan et al., 2020a; Papic et al., 2011; Tsamir et al., 2017; Zippert et al., 2021). However, findings are inconclusive about the influence of a range of competing factors on the effectiveness of interventions across the early childhood years.

Several recent studies are pertinent to interpreting current research with young children on the structural development of patterns. In a longitudinal mixed-method study on repeating patterns with three-to-five-year-olds, Acosta et al. (2024) investigated the relationship between algebraic and computational thinking by teaching repetitions with technological tools using robotic toys. They found developmental differences in the type of justifications children used, showing that the ‘elaboration’ of patterns was prominent for this age group, with progress to ‘validation’ of their representations at the age of five. The study exemplifies that early algebraic thinking can be fostered through a pedagogical model and appropriate tools that support the development of justification, inference, and prediction. The findings support other research indicating that children as young as five years can be encouraged to develop and justify mathematical structure and develop emergent generalizations (Mulligan et al., 2020a; Warren & Miller, 2010).

Lüken (2025) extended her early studies on repeating patterns to the investigation of 84 children’s pattern making in free-play situations in their early childhood classrooms. The number and type of children’s self-initiated patterns varied widely between individuals. The majority of patterns comprised transformations such as reflections, translations, and rotations, and these were constructed as repeating and growing patterns. Significant age-related differences indicated a development from the creation of basic repetitions as alternate items, to those with a more advanced composite structure of the ‘unit of repeat’, and to the extension of growing patterns. These findings were consistent with the work of Papic et al. (2011).

A number of studies have advanced the research on repeating patterns to investigate preschoolers’ ability to construct and interpret growing patterns. Wijns et al. (2019b, 2021) found that growing patterns are appropriate for children as young as four years, and some able children could even abstract patterns. They suggested that, in line with other researchers, early childhood research and practice should not be restricted to (simple) repeating patterns (Fyfe et al., 2017; Kidd et al., 2013; Papic et al., 2011; Pasnak et al., 2019). These studies are consistent with findings from studies with five- to six-year-old children (Mulligan & Mitchelmore, 2009; Mulligan et al., 2020a) who engaged in a range of spatial and growing patterns involving transformations and multiple dimensions. Although there were developmental and age-related differences, the studies found that growing and spatial patterns are interrelated and central to the development of other mathematical concepts, such as multiplication.

Recent studies of children’s patterning skills have also extended to the investigation of picture books designed to highlight repeating patterns (Wijns et al., 2023). While the study found there was a positive influence on the preschoolers’ ability to continue simple repetitions, some children were unable to recognize the structural features of the patterns. A further study focused on aligning the patterning content embedded in the books with materials to support children’s representation of patterns, found that the approach was supportive but not significant in promoting more complex patterning skills.

Overall, the extensive research effort has provided a more coherent and complementary body of evidence that supports an increased emphasis on patterning experiences in prior-to-school and early schooling contexts at the international level (Gripton, 2022). Although the majority of studies have found that early patterning experiences play a part in mathematical development, there is growing consensus that patterning capabilities extend well beyond simple linear repetitions. Thus, recent research has focused on how the acquisition of patterning concepts differs by pattern type and mode, and with different resources and pedagogical approaches. Studies include longitudinal and mixed-methods studies for preschoolers through to the early years of schooling (Alsina et al., 2024; Larkin et al., 2024; Mulligan et al., 2020a; Tsamir et al., 2020; Wijns et al., 2020, 2021). While the majority of these studies provide analyses of repeating-pattern strategies, few have analyzed children’s representations and justifications at interview, and/or compared these responses with their strategies used in open-ended investigations. Other recent studies have focused on the relationships between growing and repeating patterns and numerical competence, but the role of spatial ability has not yet been sufficiently established (Resnick & Lowrie, 2023; Rittle-Johnson et al., 2019; Wijns et al., 2021). Thus, further research aims to provide new evidence of the relative difficulty of different types and modes of patterning, as well as to describe variation in mathematical structural development. A broader goal is to inform pedagogy, assessment, and curricula. The purpose of the present study is to support this aim by conducting a micro-level analysis of patterning concepts and processes with a large cross-sectional sample of children in early schooling. Further, the study provides a comparative analysis of case studies of children’s strategies and explanations from two contrasting situations, i.e., structured interviews and their engagement in a small-group Pattern Construction task.

3. Theoretical Approach

It is widely accepted that the recognition, creation, application, and translation of patterning skills are critical to the development of multiplicative and geometric concepts, and early algebra, including equivalence and functional thinking. Essentially, patterning requires the identification of any predictable regularity in number, spatial, measurement, and statistical concepts and representations (Liljedahl, 2004; Mulligan & Mitchelmore, 2009). More critical is that structural awareness is interrelated across mathematics, which can emerge from, or underlie concepts, procedures, and relationships, and which supports abstraction and generalization in later years (Warren & Cooper, 2008; Warren & Miller, 2010). Such structural development is more than simply recognizing patterns or individual elements or properties of a relationship; it must also include the development of a deeper awareness of how elements or properties are used, explicated, or connected (Mason et al., 2009). In this sense, structural relationships can be seen as integral to conceptual connections in mathematics. For example, in the relationship between a pattern of square numbers, its spatial representation, and multiplicative structure. More broadly, the development of interrelationships within and between mathematical concepts can occur for the child from an early age within an emerging complex conceptual system (Mulligan & Woolcott, 2015). Further, individuals may develop and operate within conceptual networks in very different ways.

Awareness of Mathematical Pattern and Structure (AMPS) has been observed, described, and measured as a general construct that underpins structural thinking and its ties to emergent generalization in early years’ mathematics (Mulligan & Mitchelmore, 2009). AMPS can be considered as two interdependent components: one cognitive, a knowledge of structure, and one meta-cognitive, a tendency to seek and analyze patterns. Structural knowledge refers essentially to the abstraction and eventual generalization of concepts and elements of that structure, e.g., base ten structure. Meta-cognitive components comprise the ability to spontaneously notice and seek patterns across mathematical concepts, reason logically, and use executive function in problem solving.

Spatial structuring has been found integral to the development of AMPS involving both cognitive and meta-cognitive features (Mulligan, 2022; Mulligan & Mitchelmore, 2009, 2018). Battista (1999) initially defined spatial structuring as ‘the mental operation of constructing an organization or form for an object or set of objects. It determines the object’s nature, shape, or composition by identifying its spatial components, relating and combining these components and establishing interrelationships between components and the new object’ (p. 418). In line with this definition, spatial structuring, for example, is utilized in the delineation and representation of ‘unit of repeat’ as equal groups’ structure, the colinearity required for arrays and grids in two and three dimensions, and transformation and orientation skills used in extending patterns systematically. Spatial structuring also enables other interrelationships to develop, for example, in plotting data graphically, constructing measurement units, and partitioning space.

3.1. Background to the Study

In a series of related studies with four- to eight-year-olds, an extensive research program, the Pattern and Structure Project (including clinical task-based interviews, assessment measures, longitudinal interventions, and developmental design studies) was conducted over two decades. Mulligan and colleagues found that children demonstrating highly-advanced AMPS spontaneously searched for mathematical patterns, noticed and represented common structural features, and formed emergent generalizations (Mulligan et al., 2020a; Mulligan & Mitchelmore, 2009, 2013, 2018; Papic et al., 2011). In contrast, children showing pre-structural AMPS used idiosyncratic ideas and did not recognize structural features. While wide developmental differences were found, the majority of children were able to spontaneously construct simple repeating patterns, while some advanced to using a ‘unit of repeat’ and recognizing and extending growing patterns. The use of visualization and spatial structuring was observed as integral to children’s AMPS and related mathematical knowledge. Thus, in view of these findings and the extant literature, the need for in-depth investigation of interrelationships between patterning and spatial skills became apparent, and informed further studies, including secondary analyses of data sets and new studies on the role of spatial reasoning in learning (Mulligan et al., 2020b).

The Pattern and Structure Project studies enabled reliable descriptors of levels of structural development to be developed and re-evaluated several times, along with the construction of Rasch-modeled scales of AMPS (Mulligan & Mitchelmore, 2013; Mulligan et al., 2015), and the evaluation of intervention and design studies. In particular, in a longitudinal quasi-experimental evaluation study of 316 kindergartners, highly significant differences in responses to a Pattern and Structure Assessment (PASA) interview (p < 0.002) (Mulligan et al., 2015) were found between students engaged in a pattern-oriented intervention program and the ‘regular’ group after two years (Mulligan & Mitchelmore, 2013; Mulligan et al., 2020a).

Explicit interpretation of structural levels of responses, supported by video data, informed the development of pedagogical ‘pathways’, resulting in the Pattern and Structure Mathematics Awareness Program (PASMAP) (Mulligan & Mitchelmore, 2018, 2016/2025). The PASMAP comprises an interrelated network of mathematical concepts and relationships (‘pathways’) based on a pedagogical model: modeling, representing, visualizing, generalizing, and sustaining. The ‘pathways’ formed a series of lesson guidelines for Kindergarten to Grade 3 with illustrations of student engagement and descriptions of the pedagogy. Findings gleaned from the PASA interview and PASMAP implementation across educational contexts confirmed that, while repetitions (‘unit of repeat’) are fundamental, they are limited in advancing structural development. The pedagogical strategies that integrated both simple and complex repetitions, and growing and spatial patterns were promoted as critical to the children’s interrelated mathematical knowledge (e.g., Ferrington, 2018).

3.2. Aims

The main aim of the qualitative analyses reported in this paper is to develop a more coherent understanding of the interrelationships between different forms of patterns (spatial repetitions and growing) and between patterning, spatial skills, and mathematical knowledge. Our broader aim is to inform pedagogy that promotes connected, structured mathematical pathways. We raise two key research questions (RQs).

RQ 1: How do different pattern types, such as Growing Square Array (GA) and Spatial-Repeating Pattern (SP), account for qualitative differences in children’s levels?

RQ2: How are spatial and patterning skills interrelated in solving Growing Square Array (GA) and Spatial-Repeating Pattern (SP) tasks?

4. Methods

A cross-sectional qualitative study employed descriptive interpretive methods to analyze variation in Grade 1 and Grade 2 children’s AMPS, identified through their video-recorded interview responses to the GA and SP tasks. Micro-level deductive analysis of pertinent illustrations and justifications of responses from five cases was supported by constant comparative analysis of transcripts (Strauss & Corbin, 2008). Analysis of dialogic engagement in a teacher-supported Pattern Construction task completed by the five cases complemented the micro-level analyses.

4.1. Context and Participants

The total number of participants in the larger research project comprised 618 children from Kindergarten (n = 213), Grade 1 (n = 189), and early Grade 2 (n = 216), aged from 5y 9mo to 7y 3mo at the time of interview. The entire cross-sectional sample was drawn from eight Kindergarten, nine Grade 1, and nine Grade 2 classes across two large public primary (elementary) schools in metropolitan Sydney, Australia. In the analysis reported here, a sub-sample comprising 405 children from Grade 1 (n = 189) and Grade 2 (n = 216) (balanced for gender) was drawn from the larger sample for the purpose of micro-level analysis of two of the 16 PASA interview tasks (Growing Square Array [GA] and Spatial-Repeating Pattern [SP]). The schools served middle socio-economic communities from a wide range of multicultural backgrounds. Of the 405 children, 45% had a language background other than English (LBOTE), with all being fluent in English. Participants were of mixed academic ability and represented a wide range of mathematical competencies with standardized measures on a Progressive Achievement Test of Mathematics (PATMaths4) (Stephanou & Lindsey, 2013), indicating over 60% of scores above the 50th percentile ranking. All participants had engaged in preschool ‘free play’ activities where they constructed, copied, and represented simple repetitions with a range of materials in different modes. Prior instruction in the Kindergarten and Grade 1 (the first two years of formal schooling) was limited to simple linear repetitions, comprising less than 5% of the mandated curriculum. No prior formal instruction in either growing or spatial patterns was reported by the participating teachers or identified in pedagogical program records.

Institutional ethical approval and consent were obtained from school principals, teachers, children, and caregivers for the collection of PASA interview and classroom data, including work samples and digital recordings.

4.2. Data Sources and Analyses

Qualitative analyses were conducted in three phases. In Phase 1, descriptive statistics provide an overview of task responses categorized by AMPS’ levels and by grade for the entire sample (n = 405). Phase 2 comprised the main micro-level deductive analysis of pertinent illustrations and justifications of five cases (C1–C5), supported by constant comparative analysis of transcripts (Strauss & Corbin, 2008). Phase 3 involved qualitative analysis of the Pattern Construction task and dialogic interaction between the group (C1–C5) and the teacher. Video and digital photographic data, and observation records were consulted. These data supported the Phase 1 and 2 findings, utilizing comparative and case study techniques (Strauss & Corbin, 2008; Yin, 1994). Analysis of the Phase 3 data set is beyond the scope of this paper.

4.3. Data Collection Process

Interview data were collected daily over four consecutive weeks of school Term 4 for Grade 1 (October to December) and for four weeks of Term 1 (February) of the following school year for Grade 2. The total interview duration was between 12 and 25 minutes, depending on the pace and complexity of a child’s task response. The SP and GA tasks were presented as Tasks 7 and 13, respectively, of the entire PASA interview.

Interviews were conducted by six trained interviewers, including two experienced members of the research team (one being the author). Interviewers were engaged in a pilot program to establish the reliability of interview techniques and the moderation of response coding (see Table 1). Interview responses were categorized and recorded in a booklet allocated to individuals, specifying AMPS’ codes. Interviewers noted children’s explanations and gestures for each task response. Digital records of 20% of a total of 405 interviews were later transcribed by the corresponding interviewer. Inter-coder reliability was established with initial measures (0.76) and following resolution of any disagreements, inter-coder reliability reached 0.86.

A group-initiated Pattern Construction task followed the interview phase as an introductory activity to the PASMAP implementation, subsequently conducted by 12 Grade 2 teachers (following a three-month interval) with their class. As an example, in one class, the teacher engaged five children (C1–C5) (subjects of the micro-level analysis in Section 5.2 in the Pattern Construction task, during a one-hour timeslot devoted to regular mathematics class activities. The episode was digitally recorded and observed by a member of the research team, and later transcribed and reviewed by the teacher and the research team.

Coding Scheme

Coding descriptors for the interview responses were defined (and subject to inter-coder reliability), in order to distinguish qualitative differences in the variation in responses to GA and SP tasks according to five increasing levels of structural development (see Mulligan & Mitchelmore, 2009; Mulligan et al., 2020a). Table 1 defines descriptors, based on the entire data set of strategies, explanations, and representations gleaned from the total sample (n = 405).

Table 1. Coding Descriptors by AMPS’ level: Growing Square Array (GA) and Spatial-Repeating Pattern (SP).

AMPS Level	Growing Square Array	Spatial-Repeating Pattern
Advanced	Explains multiplicative structure of squared numbers. Generalizes pattern sequence and uses spatial structure of array. Predicts pattern sequence to at least 10 × 10, integrating spatial structure of areas. Visualizesspatial structure of the pattern as increasing and decreasing (‘shrinking’) and as a reflection.	Replicates, extends, and generalizes spatial structure of ‘unit of repeat’. Transforms and extends pattern as full rotation of arrows. Uses spatial structure of angle and transformation skills to form square turns. Uses spatial visualization and gesture to create and transform the rotation and shape dynamically.
Structural	Recognizes square array multiplicative structure to systematically extend pattern of squares using coherent spatial structure. Uses equal groups’ strategies and spatial structure to delineate and calculate number of squares in next item.	Replicates ‘unit of repeat’ twice, indicating unit and spatial structure. Replicates ‘unit of repeat’ with arrows in reverse order or direction (symmetry).
Partial	Extends pattern in one dimension vertically, forming rectangle. Maintains array structure without systematic spatial structuring. Uses additive and counting strategies.	Constructs partial repetition of unit with two symbols. Alternates vertical and horizontal arrows without initial ‘unit of repeat’ or coherent spatial structuring.
Emergent	Replicates partial array as growing without square spatial formation or organizational structure. Uses unitary counting.	Replicates given arrows randomly without pattern formation or systematic spatial organization. Explains that arrows have directional pattern.
Pre-structural	Gives idiosyncratic response, or replicates dots randomly or without ‘unit of repeat’. Absence of spatial organization.	Gives idiosyncratic response or replicates one arrow in same or random directions. Absence of spatial organization.

Table 1. Coding Descriptors by AMPS’ level: Growing Square Array (GA) and Spatial-Repeating Pattern (SP).

AMPS Level	Growing Square Array	Spatial-Repeating Pattern
Advanced	Explains multiplicative structure of squared numbers. Generalizes pattern sequence and uses spatial structure of array. Predicts pattern sequence to at least 10 × 10, integrating spatial structure of areas. Visualizesspatial structure of the pattern as increasing and decreasing (‘shrinking’) and as a reflection.	Replicates, extends, and generalizes spatial structure of ‘unit of repeat’. Transforms and extends pattern as full rotation of arrows. Uses spatial structure of angle and transformation skills to form square turns. Uses spatial visualization and gesture to create and transform the rotation and shape dynamically.
Structural	Recognizes square array multiplicative structure to systematically extend pattern of squares using coherent spatial structure. Uses equal groups’ strategies and spatial structure to delineate and calculate number of squares in next item.	Replicates ‘unit of repeat’ twice, indicating unit and spatial structure. Replicates ‘unit of repeat’ with arrows in reverse order or direction (symmetry).
Partial	Extends pattern in one dimension vertically, forming rectangle. Maintains array structure without systematic spatial structuring. Uses additive and counting strategies.	Constructs partial repetition of unit with two symbols. Alternates vertical and horizontal arrows without initial ‘unit of repeat’ or coherent spatial structuring.
Emergent	Replicates partial array as growing without square spatial formation or organizational structure. Uses unitary counting.	Replicates given arrows randomly without pattern formation or systematic spatial organization. Explains that arrows have directional pattern.
Pre-structural	Gives idiosyncratic response, or replicates dots randomly or without ‘unit of repeat’. Absence of spatial organization.	Gives idiosyncratic response or replicates one arrow in same or random directions. Absence of spatial organization.

5. Results

Initially, an overview of findings comparing tasks by AMPS’ levels and by grade is reported (Section 5.1). Following, pertinent illustrations of the micro-level qualitative analysis of a group of five children’s responses (C1–C5) are highlighted and described (Section 5.2). An example of the digital data, including interview excerpts of the transcript of the Pattern Construction task illustrating dialogic interaction between the five cases (C1–C5) and the teacher, follows.

5.1. Phase 1–Macro-Level Analysis

Table 2. Percentage of responses for Growing Array (GA) and Spatial-Repeating Pattern (SP) tasks by AMPS’ level and by Grade.

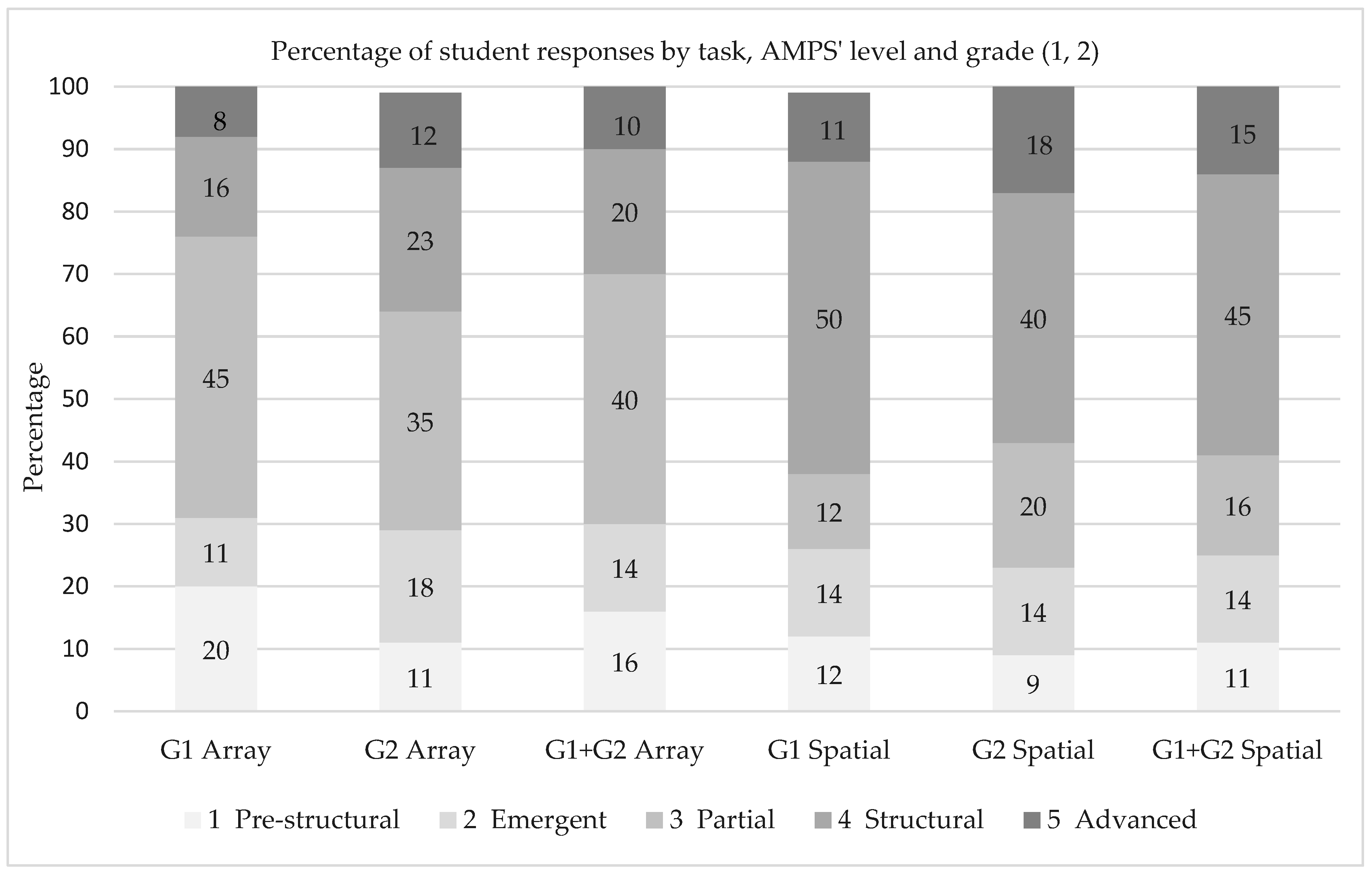
AMPS Level	Growing Square Array (GA)					Spatial-Repeating Pattern (SP)
	G1	%	G2	%	Total %	G1	%	G2	%	Total %
Advanced	15	8	25	12	10	22	11	37	18	15
Structural	31	16	49	23	20	98	50	83	40	45
Partial	89	45	74	35	40	24	12	41	20	16
Emergent	21	11	37	18	14	28	14	29	14	14
Pre-structural	40	20	24	11	16	24	12	19	9	11
Total	196	100 *	209	100 *	100 *	196	100 *	209	100	100

* Total% rounded.

presents descriptive statistics for the GA and SP tasks, and summarizes combined data related to the percentage of responses by AMPS’ level and by task. Although there are some distinctions between AMPS’ levels, findings overall indicated responses for GA were predominantly partial, and for SP, structural. For combined data, pre-structural and emergent responses comprised approximately 30% of responses.

Figure 1 illustrates these data, showing marked differences at the partial and structural levels between tasks: 40% at the partial level for GA compared with 16% for SP tasks. However, there were marked differences at the structural level for SP (45%) compared with GA (20%). This increase occurred in synchrony as responses decreased at the partial level. This response pattern was also evident in the proportion of advanced-level responses. Responses at pre-structural and emergent levels across tasks remained relatively consistent. When comparing these data by grade level within tasks, moderate differences were revealed. The proportion of responses at each AMPS level moderately increased at Grade 2 for both tasks. In particular, there was a marked increase for SP at Grade 1 from partial to structural levels (12% to 50%), and a moderate increase at the advanced level from Grade 1 to Grade 2 (11% to 18%), respectively. Combined data for SP revealed advanced visualization skills with 15% of children able to replicate, extend, and generalize the ‘unit of repeat’, and identify and extend the pattern as a complete rotation.

5.2. Micro-Level Analyses: Illustrations of Interview Responses

The following interpretive analysis draws upon some pertinent illustrations and accompanying interview excerpts from the selected sample of five cases that demonstrated a range of AMPS levels in their responses.

5.2.1. Responses to the Growing Square Array Pattern (GA)

The descriptive analysis indicated that the majority of children (40% at partial structural level) recognized the pattern as growing vertically by one dimension by forming a ‘taller’ rectangular shape (Table 2). Figure 2 illustrates a partial structural response where the child (C1) extends the pattern as a partial repetition of the ‘unit of repeat’ (two dots, then three dots), as ‘growing’. The interviewer (I2) acknowledges the child’s response meaningfully and encourages them to explain their thinking. The explanation is limited to ‘it’s just twos and threes going up’, characterized by C1’s additive thinking. The child then transformed the pattern into a rectangular array structure, as they could not recognize a geometric pattern of squares or a square number pattern. Colinearity of the array was retained.

In comparison, the response from C2 reveals a more complex extension of the pattern that retains the square array structure by using the 3 × 3 structure as a baseline (Figure 3). In this case, C2 ‘grows’ the pattern below the baseline. In the interview extract following (

Table 3. Extract 1 Growing Pattern—Child 2 (C2), LL37–58.

Line	Interviewer/ Child	Dialog
37	I2	These dot pictures make a pattern.
38		The number of dots in the pattern is getting larger each time.
39		What would come next in this pattern?
40		Draw the next two dot pictures here (points to space and waits).
41		Tell me about your pattern.
42	C2	I can count it as one, two, three, four, five along the top first.
43	I2	(Nods). Tell me something else about your pattern.
44	C2	My pattern is growing fatter and sinking (emphasis).
45	I2	So, tell me more about how it is growing and sinking.
46	C2	It grows because I counted one more each time.
47		One, two, three, four, five. But it’s sinking down there.
48		I put an extra one in there (six) to make it square.
49	I2	Oh, I see it. So, could you draw your pattern any other way?
50	C2	I could draw it going up…
57	I2	What would your pattern look like if you made it grow up?
58	C2	It would still get fatter and I would put one more each time.

), C2 describes the pattern as ’sinking’ (Line 47).

Figure 4 illustrates a growing pattern of squares depicting multiplicative structure. The row-by-column structure is highlighted as a ‘corner’ shape representing the spatial form and the pattern of consecutive odd numbers, i.e., 1, 3, 5, 7, and 9.

In the following interview extract (

Table 4. Extract 2 Growing Pattern—Child 3 (C3), LL56–69.

Line	Interviewer/ Child	Dialog
56	I2	These dot pictures make a pattern. The number of dots in the pattern is getting larger each time. What would come next in this pattern? Draw the next two dot pictures here (points to space and waits). Tell me about your pattern.
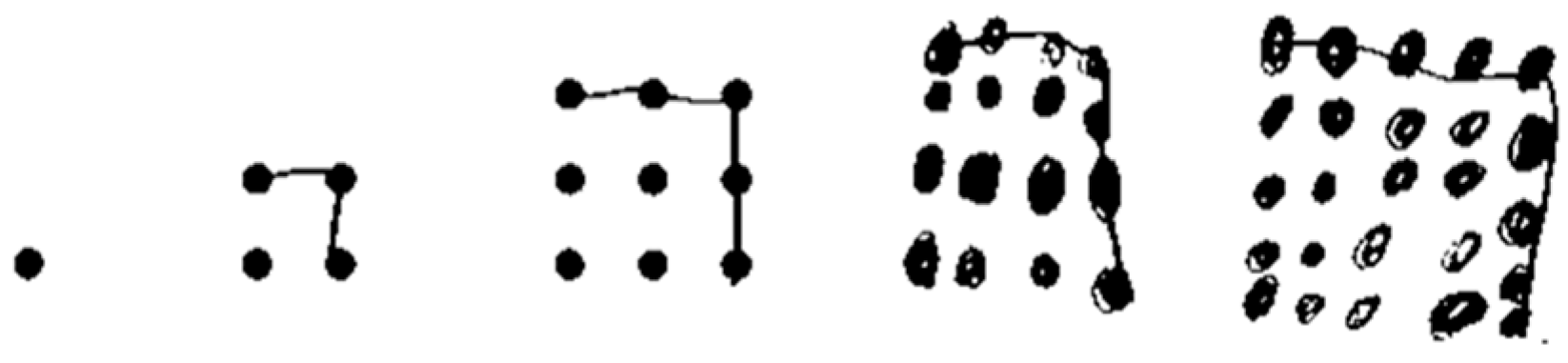
61	C3	I could see it was making squares by growing across and down the side each time … like a corner shape.
62		So, it was one, then three more, then five.
63	I2	How did you make your pattern grow?
64	C3	So, it had to be squares, across and down one more each time like four across and down, then five across and down.
65	I2	Did you notice anything else about your pattern? Tell me about it.
66	C3	Well, they had rows of the same number of dots like 4 and 4 and 4 and 4 which makes 16, and it was the same going down.
67	C3	Then it was 5 and 5 and 5 and 5 and 5 which is 10, 10, 5, that’s 25.
68	I2	If you kept going with the pattern what would it look like?
69	C3	It gets bigger and bigger squares, one more row and down each time.

), the interviewer (I2) seeks to elicit the child’s mathematical reasoning and how they connect numerical and spatial knowledge.

Extract 2 illustrates how C3 initially recognizes the array structure, which they use to generate numerical and spatial patterns. The growth of the pattern is visualized as increasing by two dimensions using colinearity, where C3 uses an ‘equal groups’ structure and counting strategies to calculate the number pattern: 1, 4, 9, 16, and 25. It appears that C3 used repeated addition to calculate the number sequence while also demonstrating an understanding of the multiplicative and spatial structure of the pattern.

In a comparable interview with C4 (

Table 5. Extract 3 Growing Pattern—Child 4 (C4) LL71–82.

Line	Interviewer/ Child	Dialog
71	I2	If you kept going with the pattern, what would it look like?
76	C4	It would get bigger and bigger squares, one more row and ‘down’ each time like 6 rows and 6 ‘downs’.
77	I2	Is there anything else you would like to tell me about that idea?
78 79 80	C4	Well, it could go on forever and the squares would be really big … but always one row across and ‘down’ bigger, no matter how big the square grows, and it must always have four corners. (I2 nods)
81	C4	And I can see the pattern could go the other way. (C4 gestures)
82	C4	It could grow up and down like a staircase, ‘growing’ and ‘shrinking’ and you can draw it on the other side.

), the interviewer (I2) enquires about C4’s visualization and explanation of their predicted extension of the pattern sequence.

C4 attempts to explain their emerging generalized view of the pattern ‘growing’ consistently by two dimensions while retaining the square form, regardless of the number of items extending the sequence. The child also visualizes their representation of the pattern as decreasing systematically in the same direction, explaining this as ‘shrinking’. C4 uses their concept of symmetry to imagine the pattern as a reflection ‘on the other side’.

5.2.2. Responses to the Spatial-Repeating Pattern (SP)

The analysis of SP task responses distinguished whether children perceived the pattern as a simple repetition of three alternating arrows, a ‘unit of repeat’, and/or a pattern of directions forming a partial or full rotation. The use of transformation skills was identified as integral to children’s solutions. Initial analysis of AMPS’ levels indicated that 16% of children reconceptualized the pattern as ‘going up and down’, including some that drew a reflection of the first two arrows using line symmetry (Table 1 indicates this code as partial structural). A majority of students (45%) represented the pattern as a ‘unit of repeat’ of three given arrows (Table 1 indicates this code as structural). At the most advanced level, 15% of children also visualized the pattern dynamically as a partial or full rotation that was subsequently repeated.

Figure 5 illustrates three different responses from C5. Initially, C5 extends the pattern as a ‘unit of repeat’ of arrows (‘down’, ‘across’, ‘up’), with this representation characterizing 45% of total SP responses. The second sequence depicts a partial rotation (‘down’ and ‘across’), followed by the pattern of arrows representing a full rotation (‘down’ and ‘turn’, ‘across’ and ‘turn’, ‘up’ and ‘turn’, and ‘across’).

In the following interview extract (

Table 6. Extract 4 Spatial-Repeating Pattern (SP) extension—Child 5 (C5), LL24–41.

Line	Interviewer/ Child	Dialog
24	I2	This pattern is made from arrows.
25		Draw the next five arrows here.
26		Explain your drawing.
27		Why did you draw the arrows this way?
28	C5	It goes down, across, up and repeat it.
29	I2	Good (Interviewer nods). I can tell that you want to draw another pattern (C5 gestures to draw).
30 31	C5	You could just go down, across, down, across, and repeat that all the way along. But there’s a better pattern.
32	I2	So, what would this look like? Can you draw it and explain it to me?
33 34 35 36	C5	It’s like going around in circles but it would make a square. It goes down, across right, up, then across to the left. I can draw it again as a square. You get back to the same spot. You could draw it over and over to make a pattern…
39	I2	So, if you were following the arrows what would you be doing?
40	C5	I would be turning each time. Can turns be patterns?
41	I2	Yes, turns can be patterns when you go around and around.

), the interviewer (I2) encourages C5 to elicit alternative patterns and to explain their reasoning. C5 demonstrates a spontaneous dynamic visualization of the rotation, explaining the pattern as ‘it would make a square’ (Line 33) and ‘I would be turning’ (Line 40).

The illustrations of children’s responses to these two interview tasks exemplify the interrelationships between children’s patterning and spatial, as well as other mathematical concepts. The micro-analysis of responses was critical to revealing the complexity of children’s patterning concepts. However, this analysis comprised one component of the larger study of the PASMAP that informed further learning and instructional strategies. The following section illustrates a classroom episode of a Pattern Construction task involving the same five cases whose interview responses were provided in the micro-level analysis.

5.3. Pattern and Structure Classroom Program: Group-Initiated Pattern Construction Task

In the PASMAP implementation in Grade 2 classrooms that followed the interviews, teachers encouraged children to visualize, construct, and draw patterns of their choice using a range of materials, working both independently and in small groups. Figure 6 presents an example of a digital image of a complex pattern negotiated between and created by the group members (G1).

The following interview extracts (

Table 7. Extract 5 Group-initiated pattern construction (G1, C1–C5), LL126–139.

Line	Teacher/ Child	Dialog
126	T1	You can make any types of patterns and use any types of materials.
127		You don’t have to use all the blocks or all of the colors.
128	C1	Let’s use the counters that look like flowers.
129	T1	Talk about what you would like to make; each student must have a turn to say what they want.
130		Imagine what the pattern will look like and how much space you will need to make it on the floor.
131	C2	First, we need to sort the counters into colors.
132	C3	There’s lots of colors. I don’t know how many or which colors.
133	T1	It depends on what kind of pattern and how big it will grow.
134	C4	So, we need to decide on what type of pattern.
135	C3	We can do a line or we can do a growing one.
136	C5	Let’s do a line with each color and repeat it over and over. Like blue, green, yellow, orange, red.
137	C4	But you can make it grow up like a staircase …one, two, three, four…
138	T1	Maybe you can make different patterns together.
139	C3	So, it’s one more each time but the colors are the same like a line. It should be blue, green, yellow, orange, red over and over both ways.

and

Table 8. Extract 6 Group-initiated pattern construction (G1, C1–C5), LL143–159.

Line	Teacher/ Child	Dialog
143	C1	You can make a staircase with any colors that you like.
144	T1	Would the staircase have the five colors that you chose?
145	C2	Yes. If you make it both ways.
146		The line first and then grow it up.
147	T1	That’s a great idea making it both ways. Explain it to me.
148 149	C3	It goes up by one more each time like 1, 2, 3, 4, 5. All the way up to 20. It’s 20 both ways … along the line and going up.
150	T1	Can you see any other patterns?
151	C4	The first one on the top line is blue so five more will get you a blue then five more will get you another blue.
152 153 154	C3	So, you could work out all the colors like that… the second one is green so it will be five more to get green again. It’s five colors each time…you could count 5, 10, 15, 20. Like a pattern.
155	C5	I can see a triangle. Our pattern makes a triangle.
156	T1	Interesting C5. Can you make your pattern grow in any other ways?
157	C3	We could make it a bigger triangle by making it on the other side.
158	C5	We could spin it around if we made it on a board.
159	C5	If we made four of them it would make a big diamond.

) illustrate the dialogic interaction between the teacher (T1) and the group (G1) of five children (C1–C5) (previously interviewed), which highlights the integrated, complex, two-dimensional repetitive and growing pattern construction and the children’s spatial skills.

At this initial stage in the group negotiation of the pattern type and construction, the children focus attention on a repetition of alternating colors, typical of the regular classroom experience of pattern formation. In a critical interjection, T1 raises the possibility (i.e., gives ‘permission’) for the children to explore other options. C3 adopts from C4 the idea of a growing pattern and justifies the need for a coordinated ‘unit of repeat’ in both forms of the pattern sequence.

Table 8 highlights the continuation of the group’s negotiated pattern construction. C1 visualizes a ‘staircase’ consistent with their emergent structural thinking of ‘growing one more each time’. C2 and C3 simultaneously integrate repetition and growing pattern sequences in two dimensions. The teacher (T1) encourages further options. The spatial structure of the pattern promotes C3’s idea of the ‘unit of repeat’ as a multiplicative sequence where they predict the order of items systematically (LL152–154). The integrated pattern results in a triangular shape, limited only by the available floor space. C3 and C5 extend their reasoning by using dynamic visualization to imagine a reflection.

6. Discussion

In addressing the first research question, the macro-level analysis indicated that there was wide variation in AMPS’ levels of response for each task, with an expected distribution of responses for the GA task. However, for the SP task, there was more variation, with 45% of responses at the structural level. Consistent patterns of response were found for children operating at an advanced structural level. In addressing the second research question, the illustrative examples and the Pattern Construction task revealed some important insights into how spatial and patterning skills are interrelated in growing and repetitive patterns, but in different ways.

For the SP task, it was not expected that 15% of responses would reflect an advanced structural level. It was observed that children visualized and embodied the pattern dynamically as a rotation, where they mentally ‘picked up the arrows’ and placed them as right turns to form a square shape. It was not possible to distinguish whether children initially identified the ‘unit of repeat’ as ‘objects’ or as a set of directions, or whether spatial reorientation of the arrows was transformed from a holistic view using rotation or navigation (see Way & Ginns, 2024). Further, there was a large proportion of students who used structural thinking (45%) to interpret the sequence of arrows as a ‘unit of repeat’ and who also recognized the rotational aspects of the arrows as symbols. This finding raises the question of how transformation and navigation (directionality) skills influence the child’s perception of both repetitions and growing patterns, and how the use of ar spatial visualization skills may determine whether the structure of a pattern can be noticed and generalized.

The Pattern Construction task highlighted how the children combined their experience of repetitions and growing patterns with spatial skills, as well as other mathematical skills such as abstracting and ordering number sequences. The visualization of a pattern as a simple linear repetition was extended to and simultaneously transformed and represented as a growing pattern. Unitary and group counting, and additive and multiplicative concepts were utilized to integrate structural features of the growing pattern. Multiplicative structure was observed as distinctive from additive strategies for some children. Spatial-reasoning was utilized in the dynamic visualization process that enabled the children to rotate the pattern. Here, the fundamental idea of symmetry was employed.

The group’s creative construction encouraged negotiation and justification that repeating and growing patterns can be two-dimensional, symmetrical, and rotated. These insights into the children’s reasoning and advanced mathematical capabilities could not have been shown through the interview-based structured tasks alone. This illustrative account supports other studies showing that self-initiated patterning, along with the teachers’ critical questioning and support, complement more creative approaches to mathematics learning (Assmus & Fritzlar, 2022; Lüken, 2025; Papic et al., 2011).

Three key outcomes were achieved from these analyses. First, children’s representations and reasoning revealed the integral role of spatial skills—dynamic visualization, orientation, and transformation in their early mathematical knowledge. There was a wide variation observed in the types of spatial skills and in how these skills were used. Second, these findings could not be attributed to the influence of prior formal instruction, limited to simple repetitions and basic shape recognition and construction. We can only infer that these findings reflect the children’s intuitive and informal acquisition of patterning and spatial concepts, and it appeared that transformation skills had already developed for the majority. This development may have been influenced by play-based experiences in the home, preschool, or kindergarten environments. It was not possible to speculate or evaluate, how the influence of digital technologies had influenced this development. Finally, the underlying cognitive development of AMPS must have influenced the increasingly abstract developmental levels in structural thinking to a large extent. This pattern of development was found consistent with our earlier studies and others in the field (e.g., Björklund & Pramling, 2014; Junker et al., 2024; Mulligan et al., 2020a; Pitta-Pantazi et al., 2024).

6.1. Limitations

Since the analysis is essentially descriptive, it is not possible to generalize the findings or determine causal relationships. This was not the main aim of the study. These data were limited to 2 of 16 tasks focused on assessing mathematical patterns and structures from a much larger study. However, the scope and depth of analysis of the two purposively-selected tasks afforded new and important insights into the complexity of the structural development of patterning. Interview-based tasks are commonly used as a preferred method in qualitative studies of this kind, and in this study, both interview and classroom data for five contrasting cases were analyzed. Initial conceptualization of five distinct AMPS’ levels of structural development, fundamental to the reliable coding of responses, was perhaps limited, given the much wider variation in responses gleaned from micro-level analysis of aligned interview and classroom video data. Further analysis of video data could also determine whether individual patterns of response were consistent across AMPS’ levels and across different tasks. These forms of analysis are complex, and resource dependent, but needed in order to gain a coherent and accurate picture of the child’s mathematical development. In hindsight, the influence of children’s spatial ability could have been more closely investigated, considering the interrelationships observed with both SP and GA tasks.

Given the role of spatial skills, these findings raise questions about the design and representational format of patterning tasks used in pedagogy and curricula. The design of both interview tasks set up an expectation for the child to extend the patterns in a horizontal–unidirectional (L-R) form aligned with a baseline and limited by the drawing space. Although these data showed that some children translated and re-designed the pattern in two dimensions and with rotation, the task design may have restricted other children’s responses. The traditional representation of repeating patterns drawn in a set space and in horizontal linear form should be re-evaluated and redesigned to support a full range of possible responses and children’s capabilities.

The data gleaned from the Pattern Construction task provided but one illustrative dialogic account. Although the children employed in the task were considered representative of a range of abilities, our findings cannot be generalized to the wider sample (n = 405). Our video data of the classroom interaction and the micro-analysis of individuals’ mathematical thinking does not extend to this depth.

6.2. Implications for Research and Practice

In considering further research and practice, a more complex view of the early structural development of mathematics might be adopted: developing synergies within and between patterning concepts, and as networked interrelationships between all mathematical concepts. These interrelationships may not yet be explicitly defined and measured, or even considered central to learning and instruction. In particular, the role of spatial structuring in these networks may be significant. In designing further studies, the development and evaluation of new conceptual frameworks in practice could provide more coherent evidence of how patterning and spatial skills are inextricably linked. Further studies may facilitate the disentanglement of different patterning and spatial forms, and difficulty levels, as well as the design mode, context, and resources, since these may depend on prior knowledge and pedagogical opportunities. Controlled and developmental design studies, as well as microgenetic analyses of patterning and spatial task type on the growth of AMPS (and vice versa), could contribute to better coherence and collaboration in the field.

Theoretical approaches, such as those based on spatial reasoning (Mulligan et al., 2020b; Resnick & Lowrie, 2023; Way & Ginns, 2024), could potentially inform the design of interdisciplinary studies that may ‘cross’ existing boundaries between experimental and qualitative methods. A more holistic approach could also contribute to acquiring more compelling evidence of the potential and critical development of very early abstraction and generalization. If this approach is adopted, then it may be feasible to differentiate pedagogy and to accommodate individuals’ grasp of structure. Studies of children with neurodiverse profiles and learning difficulties are scant. In tandem, new studies can inform further development and evaluation of pedagogical approaches and learning trajectories that can advance effective curricula reform (e.g., Alsina et al., 2024; Baroody et al., 2021; D. H. Clements et al., 2023; Gripton, 2023).

The role of pre-service and practitioner knowledge and confidence in understanding and supporting the development of mathematical pattern and spatial reasoning cannot be underestimated (McGarvey, 2012; Tirosh et al., 2019). An important implication from this study is the restructuring of professional programs so that patterning and spatial skills are integrated with all mathematical content domains rather than ‘siloed’ as curriculum-directed content strands. Professionals’ mathematical and pedagogical content knowledge, affective factors, and the increasing demands of curricula may also influence whether patterning and spatial concepts can be substantially integrated with early numeracy programs (e.g., Alsina et al., 2024; Gripton, 2023; Reuter, 2023).

7. Conclusions

Taken together, the descriptive and micro-level analyses, and the aligned interpretive account of the Pattern Construction task illustrated that children as young as six years employed additive, multiplicative structures and spatial skills in solving GA and SP tasks, respectively. These analyses indicated that advanced patterning and spatial-reasoning skills, particularly transformations, had developed informally and intuitively and in complex and unique ways, consistent with increasingly abstract levels of AMPS. Given the growing and compelling extant research evidence of the central role of patterning and spatial skills in mathematical development, early mathematics learning and instruction, including assessment and curricula, need to be re-conceptualized and reformed. Instructional design could aim to promote abstraction and generalization, albeit emergent, based on pedagogical approaches that emphasize pattern-seeking and interrelationships between patterning and spatial concepts.