Visual Multiplication Through Stick Intersections: Enhancing South African Elementary Learners’ Mathematical Understanding

Abstract

This paper presents a novel visual approach to teaching multiplication to elementary school pupils using stick intersections. Within the South African context, where students consistently demonstrate low mathematics achievement, particularly in foundational arithmetic operations, this research explores an alternative pedagogical strategy that transforms abstract multiplication concepts into visual, concrete, countable representations. Building on theories of embodied cognition and visual mathematics, this study implemented and evaluated the stick intersection method with 45 Grade 4 students in Polokwane, Limpopo Province. Using a mixed-methods approach combining quantitative assessments with qualitative observations, the results revealed statistically significant improvements in multiplication performance across all complexity levels, with particularly substantial gains among previously low-performing students (61.3% improvement, d = 1.87). Qualitative findings demonstrated enhanced student engagement, deeper conceptual understanding of place value, and overwhelmingly positive learner perceptions of the method. The visual approach proved especially valuable in the multilingual South African classroom context, where it transcended language barriers by providing direct visual access to mathematical concepts. High retention rates (94.9%) one-month post-intervention suggest the method facilitated lasting conceptual understanding rather than temporary procedural knowledge. This research contributes to mathematics education by demonstrating how visually oriented, culturally responsive pedagogical approaches can address persistent challenges in developing mathematics proficiency, particularly in resource-constrained educational environments.

1. Introduction

Mathematics education in elementary schools presents significant challenges across the globe, with particular difficulties observed in developing countries (Venkat & Spaull, 2015). Within South Africa, recent studies have highlighted concerning performance gaps in mathematics, especially in foundational arithmetic operations (Department of Basic Education, 2019). Despite curriculum reforms, many students continue to struggle with basic mathematical operations, including multiplication (Fleisch, 2008; Hoadley, 2012). The Trends in International Mathematics and Science Study (TIMSS) has consistently ranked South Africa near the bottom of participating countries in mathematics achievement (Reddy et al., 2016). This performance gap is particularly pronounced in rural and township schools, where resources are often limited and traditional pedagogical approaches predominate (Spaull & Kotze, 2015). In Polokwane, Limpopo Province, these challenges are acutely felt, with many elementary students demonstrating persistent difficulties in multiplication (Machaba, 2018).

While various factors contribute to these difficulties, including language barriers, socioeconomic challenges, and inadequate teacher preparation (Taylor & Taylor, 2013; Svraka & Ádám 2024), pedagogical approaches that fail to connect abstract mathematical concepts to concrete visual representations may exacerbate the problem (Age & Machaba, 2023). Traditional multiplication instruction often emphasizes memorization of multiplication tables and algorithmic procedures without developing conceptual understanding (Kilpatrick et al., 2001; Hunt et al., 2025). This research addresses these challenges by exploring a visual approach to teaching multiplication using stick intersections. Building on theories of embodied cognition (Lakoff & Núñez, 2000) and the importance of visual representations in mathematics education (Arcavi, 2003), this study presents a methodology that makes multiplication tangible and countable. By drawing vertical sticks to represent the first number and horizontal sticks to represent the second, students can physically count the intersection points to determine the product.

Globally, mathematics education research increasingly recognizes the potential of visual and embodied pedagogical approaches to address conceptual difficulties in arithmetic (Way & Ginns, 2024; Cosentino et al., 2025). However, within multilingual developing contexts like South Africa, there remains a significant research gap regarding how culturally responsive visual methods can specifically address the intersection of linguistic barriers, resource constraints, and conceptual understanding challenges. The stick intersection method offers a unique contribution by providing a visual approach that requires minimal resources while transcending language barriers—making it particularly suited to the South African educational landscape.

The aim of this study is twofold: first, to demonstrate how the stick intersection method can visually illustrate multiplication from single-digit to multi-digit operations; and second, to evaluate the effectiveness of this approach with Grade 4 learners in Capricorn South District Polokwane, South Africa. The research questions guiding this study are:

• How can the stick intersection method be implemented to teach multiplication to intermediate phase learners?
• What impact does this visual approach have on learners’ comprehension and performance in multiplication tasks?
• What are learners’ perceptions of the stick intersection method compared to conventional multiplication instruction?

The selection of stick intersections over established visual methods (such as lattice multiplication or dot arrays) was motivated by three key factors: (1) minimal resource requirements—requiring only paper and pencil rather than specialized materials; (2) universal accessibility—the method transcends language barriers through direct visual representation; and (3) natural scalability—the same fundamental principle applies from single-digit to multi-digit problems without requiring new conceptual frameworks.

2. Theoretical Framework

2.1. Visual Representations in Mathematics Education

Visual representations play a crucial role in mathematics learning, particularly for young learners developing abstract mathematical concepts (Presmeg, 2006). According to Duval (2006), mathematical objects are not directly accessible to perception or observation with instruments; the only way to access and work on them is through representations. For elementary students, these representations serve as a bridge between concrete experiences and abstract mathematical ideas (Bruner, 1966). Research by Arcavi (2003) defines visualization in mathematics education as “the ability, the process and the product of creation, interpretation, use of and reflection upon pictures, images, diagrams, in our minds, on paper or with technological tools, with the purpose of depicting and communicating information, thinking about and developing previously unknown ideas and advancing understandings” (p. 217). This definition emphasizes the constructive role of visualization in mathematics learning. The theory of embodied cognition provides additional support for visual approaches to mathematics education. According to Lakoff and Núñez (2000), mathematical concepts are grounded in human bodily experiences and sensorimotor activities. From this perspective, learning multiplication through counting physical intersections represents a form of embodied mathematical understanding.

2.2. Multiplication Concepts and Challenges

Multiplication represents a cognitive leap from addition, requiring learners to conceptualize repeated addition, scaling, and eventually proportional reasoning (Steffe, 1994). Vergnaud (1983) identified several conceptual structures associated with multiplication, including equal groups, rectangular arrays, and Cartesian products. The stick intersection method aligns closely with the rectangular array model, where multiplication is visualized as the total number of points in a rectangular arrangement. Research by Fuson (2003) indicates that many students struggle with multiplication because they lack conceptual understanding of what multiplication represents. Without this foundation, students resort to memorization of procedures without meaning, leading to difficulties with application and problem-solving (Hiebert & Carpenter, 1992). In the South African context, these challenges are compounded by language barriers, large class sizes, and limited instructional resources (Setati & Adler, 2000; Hoadley, 2012). The South African Annual National Assessments revealed that only 34% of Grade 3 learners performed at an appropriate level in mathematics, with multiplication identified as a particular area of weakness (Department of Basic Education, 2014).

2.3. Visual Learning in the South African Context

Visual approaches to mathematics education offer significant potential in the South African context, where the presence of multilingual classrooms often introduces language barriers that hinder mathematical communication and understanding (Adler, 2002). In such diverse linguistic environments, visual representations serve as powerful tools that can transcend language constraints, enabling learners to access and engage with mathematical concepts regardless of their proficiency in the language of instruction (Setati, 2005). Furthermore, visual learning methods resonate strongly with indigenous knowledge systems and traditional African pedagogical practices, which have historically emphasized concrete, experiential, and communal forms of learning (Mosimege & Onwu, 2004). By integrating visual representations into mathematics instruction, teachers are able to connect more effectively with learners’ cultural backgrounds and prior experiences, thereby making the learning process more meaningful, relevant, and accessible to all learners (Webb & Webb, 2004). For instance, the stick intersection method resonates with traditional counting practices found in many African communities, where objects like stones, sticks, or beads are arranged in patterns for counting and calculation. In Sepedi culture, children often learn counting through visual arrangements of natural materials, making the transition to mathematical stick representations culturally familiar. Additionally, the method’s emphasis on physical drawing and pattern recognition connects to indigenous artistic traditions where geometric patterns hold mathematical significance, such as the decorative patterns found in traditional Ndebele art or the mathematical principles embedded in traditional African architecture and pottery designs. In this way, visual strategies not only bridge language gaps but also affirm and leverage the rich cultural resources that students bring into the classroom.

3. Methodology

3.1. Research Design

This study employed a mixed-methods approach, combining qualitative observations with quantitative assessment of student performance. The research was conducted in three phases:

• Development and refinement of the stick intersection method for teaching multiplication, progressing from single-digit to four-digit numbers.
• Implementation of the method with Grade 4 learners in a school in Capricorn District, Polokwane.
• Evaluation of the method’s effectiveness through pre- and post-tests, classroom observations, and learner interviews.

3.2. Participants and Setting

The study was conducted at a public school in Capricorn district Polokwane, Limpopo Province, South Africa. Participants included 45 Grade 4 learners (ages 10–11) and their mathematics teacher. The school serves a predominantly low-income community, with limited educational resources and average class sizes of 40–50 learners. The language of instruction is officially English, although most learners speak Sepedi as their home language.

Ethical Considerations and Instrument Validation

Ethical clearance was obtained from the University of South Africa’s College of Education Ethics Committee (2022/11/09/1123408/08/AM). Written informed consent was secured from the school principal, participating teacher, and parents/guardians of all student participants. Students provided verbal assent before participation, with the right to withdraw emphasized throughout the study. Pre- and post-test instruments were adapted from validated assessments used in previous South African mathematics education research (Venkat & Spaull, 2015), with modifications made to ensure grade-level appropriateness. Content validity was established through review by three mathematics education experts, and pilot testing with 12 Grade 4 students from a comparable school confirmed item clarity and appropriate difficulty progression. Test–retest reliability over a two-week period yielded a correlation coefficient of r = 0.87.

3.3. Data Collection

Data were collected through multiple sources:

• Pre- and post-tests: Learners completed assessments measuring their multiplication skills before and after exposure to the stick intersection method. Tests included single-digit and two-digits multiplication problems.
• Classroom observations: Lessons implementing the stick intersection method were observed and video-recorded for later analysis. Observations focused on learners’ engagement, question-asking behavior, and problem-solving strategies.
• Learners work samples: Examples of learners’ work using the stick intersection method were collected and analyzed.
• Semi-structured interviews: Following the implementation, interviews were conducted with a subset of learners (n = 15) to gather their perceptions of the visual method compared to conventional instruction.
• Teacher reflections: The classroom teacher documented observations and reflections throughout the implementation process.

Assessment Instruments

Pre- and post-tests consisted of 20 multiplication problems distributed as follows:

• Single-digit multiplication: 8 problems (e.g., 6 × 7, 9 × 4, 8 × 6, 7 × 9, 5 × 8, 9 × 6, 7 × 8, 6 × 9).
• Two-digit by single-digit: 6 problems (e.g., 23 × 4, 31 × 5, 42 × 3, 16 × 6, 27 × 2, 34 × 3).
• Single-digit by two-digit: 4 problems (e.g., 7 × 14, 5 × 26, 4 × 19, 6 × 15).
• Two-digit by two-digit: 2 problems (e.g., 12 × 13, 14 × 12).

Each test was administered over 60 min with problems presented in random order to prevent pattern recognition. Students were instructed to show their working and could use any method they preferred. Scoring was based on correct final answers (1 point each) and appropriate working shown (0.5 additional points for clear method demonstration), giving a maximum of 30 points per test.

3.4. Instructional Intervention

The stick intersection method was implemented through a series of 8 structured lessons over 4 weeks, with each lesson lasting 45 min. Each lesson introduced increasingly complex multiplication examples following this specific sequence:

• Week 1: Single-digit multiplication (9 × 2, 8 × 5, 7 × 3, 6 × 4).
• Week 2: Two-digit by single-digit multiplication (22 × 4, 31 × 3, 42 × 2).
• Week 3: Single-digit by two-digit multiplication (6 × 13, 4 × 25, 3 × 32).
• Week 4: Two-digit by two-digit multiplication (12 × 11, 13 × 12, 14 × 11).

Each lesson followed this consistent 45 min format:

• Introduction phase (5 min): Present the multiplication problem on the chalkboard.
• Demonstration phase (15 min): Teacher demonstrates the stick intersection method using pre-drawn large-scale diagrams on poster paper, explaining each step while students observe.
• Guided practice (15 min): Students work in pairs, with the teacher circulating and providing support, using A4 paper and pencils to create their own stick diagrams.
• Independent application (8 min): Students individually solve 2–3 similar problems using the method.
• Discussion and reflection (2 min): Whole-class discussion of visual patterns observed and connections to mathematical concepts.

Materials used: Chalkboard, colored chalk, A4 paper, pencils, pre-prepared poster-size examples, and rulers for students who requested them for neat line drawing.

3.5. Data Analysis

This study employed an explanatory sequential mixed methods design (Creswell & Plano Clark, 2018), with quantitative data collection and analysis prioritized and conducted first, followed by qualitative data collection and analysis to explain and expand upon the quantitative findings. The integration of quantitative and qualitative data occurred during the interpretation phase, after both strands had been independently analyzed. Specifically, pre- and post-test quantitative data were analyzed first to determine the statistical significance and magnitude of performance improvements. Subsequently, qualitative data from classroom observations, student interviews, and work samples were collected and analyzed to provide explanatory insight into how and why these improvements occurred—addressing questions such as what specific aspects of the method enhanced understanding, how students engaged with the visual approach, and what their subjective experiences were.

The purpose of mixing methods was complementarity and expansion: quantitative measures assessed the extent of learning gains, while qualitative data illuminated the mechanisms, processes, and student perspectives underlying these gains. During the final interpretation stage, quantitative results (Table 1, Table 2, Table 3, Table 4 and Table 5) were integrated with qualitative themes (Section 5.2.1, Section 5.2.2 and Section 5.2.3) through a process of comparison and connection, whereby statistical patterns were explained through corresponding qualitative evidence. For example, the quantitative finding of significant improvement among low-performing students (Table 5) was enriched by qualitative observations of increased engagement and confidence among previously passive learners. This integration approach allowed for a more comprehensive understanding of both the effectiveness and the experiential dimensions of the stick intersection method than either strand alone could provide.

Quantitative data from pre- and post-tests were analyzed using descriptive statistics and paired t-tests to determine changes in student performance. Qualitative data from observations, interviews, and work samples were analyzed using thematic content analysis, identifying patterns in learners’ understanding, engagement, and attitudes toward the visual approach. Qualitative data analysis followed Braun and Clarke’s (2006) six-phase thematic analysis approach. Initial coding was conducted by the primary researcher, with 25% of interview transcripts independently coded by a second researcher trained in qualitative analysis. Inter-rater agreement was 89% (Cohen’s κ = 0.84), with discrepancies resolved through discussion. Member checking was conducted with five student participants who confirmed the accuracy of identified themes. Trustworthiness was further enhanced through triangulation across multiple data sources and maintenance of a reflexive research journal throughout the study period.

4. The Stick Intersection Method

The stick intersection method provides a visual and tactile representation of multiplication, allowing students to physically count the product rather than relying solely on memorized facts or algorithms. This section details the implementation of this method across increasingly complex multiplication scenarios.

4.1. Foundational Concept: Multiplication as Counting Intersections

The foundational concept behind the stick intersection method is that multiplication can be effectively visualized as the total number of intersection points formed between two distinct sets of lines. In this approach, vertical sticks are used to represent the first number (the multiplicand) in the multiplication expression, while horizontal sticks correspond to the second number (the multiplier). Each point where a vertical stick crosses a horizontal stick symbolizes one unit, and collectively, these intersections form the final product. This method closely aligns with the well-known array model of multiplication, wherein the product signifies the total number of elements arranged within a rectangular formation, with the dimensions directly matching the multiplicand and the multiplier. However, the stick intersection method offers an even more explicit, tangible, and visually countable version of the array model, making it particularly accessible and intuitive for young learners. Allowing students to physically see and count each unit of the product, this method strengthens their conceptual understanding of multiplication as repeated addition and spatial structuring. While the stick intersection method shares similarities with the traditional array model, key differences make it particularly suitable for elementary learners. Both methods visualize multiplication as rectangular arrangements, but the stick intersection approach provides several advantages: (1) the counting process is more explicit as students count individual intersection points rather than estimating rectangular areas; (2) the method naturally scales from simple to complex problems using the same basic principle; (3) place value concepts are more visually distinct through physical separation of digit groups. However, educators should note that unlike arrays, which students will encounter later with fractions and algebra, the stick intersection method is primarily designed for whole number multiplication, requiring eventual transition to more versatile models for advanced mathematical concepts.

4.2. Single-Digit Multiplication

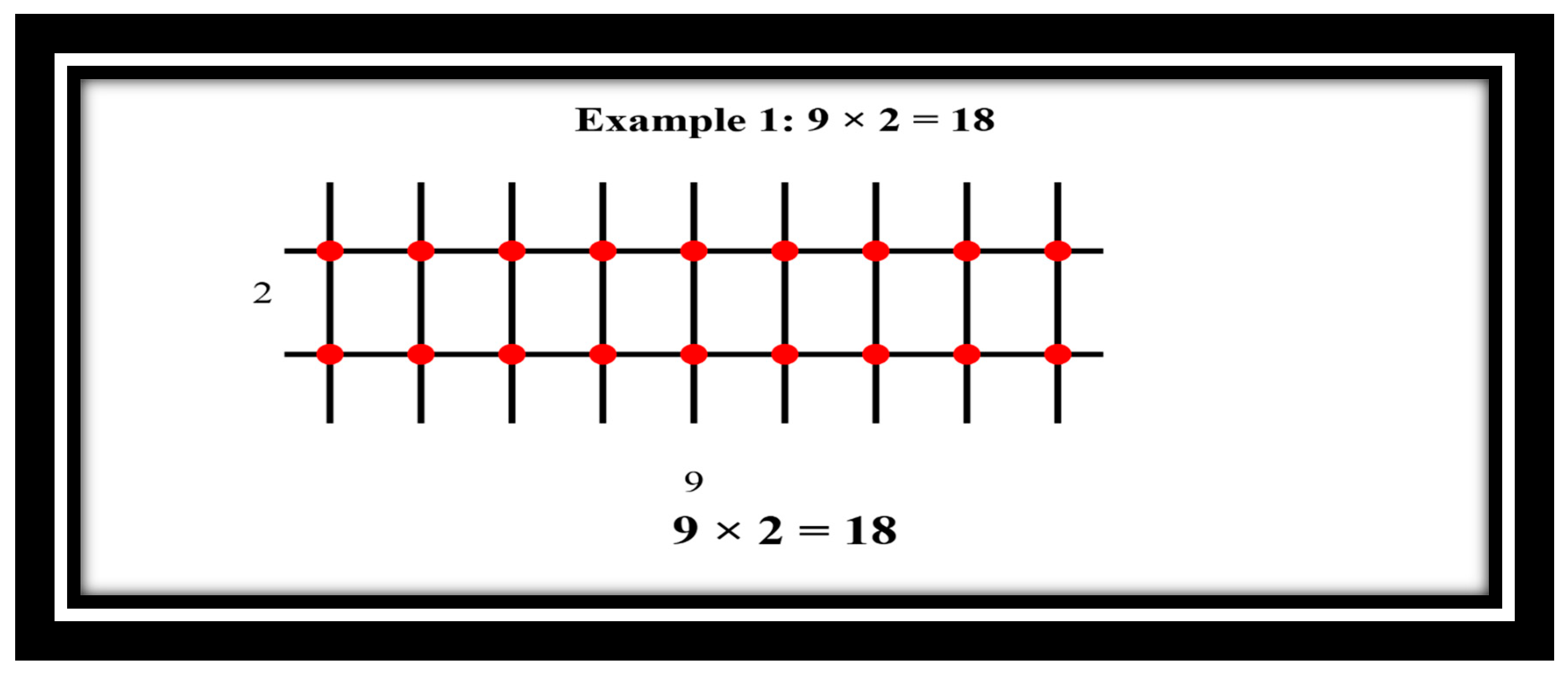
4.2.1. Example 1: 9 × 2

The first example (see Figure 1) demonstrates multiplication of 9 by 2 using the stick intersection method:

Step 1: Draw 9 vertical sticks to represent the first factor (9).

Step 2: Draw 2 horizontal sticks crossing all vertical sticks to represent the second factor (2).

Step 3: Mark each intersection point with a red dot for clear counting.

Step 4: Count the total number of intersection points (red dots).

This visual representation shows 18 intersection points, demonstrating that 9 × 2 = 18. Learners can physically count each intersection, reinforcing the connection between the visual representation and the numerical product.

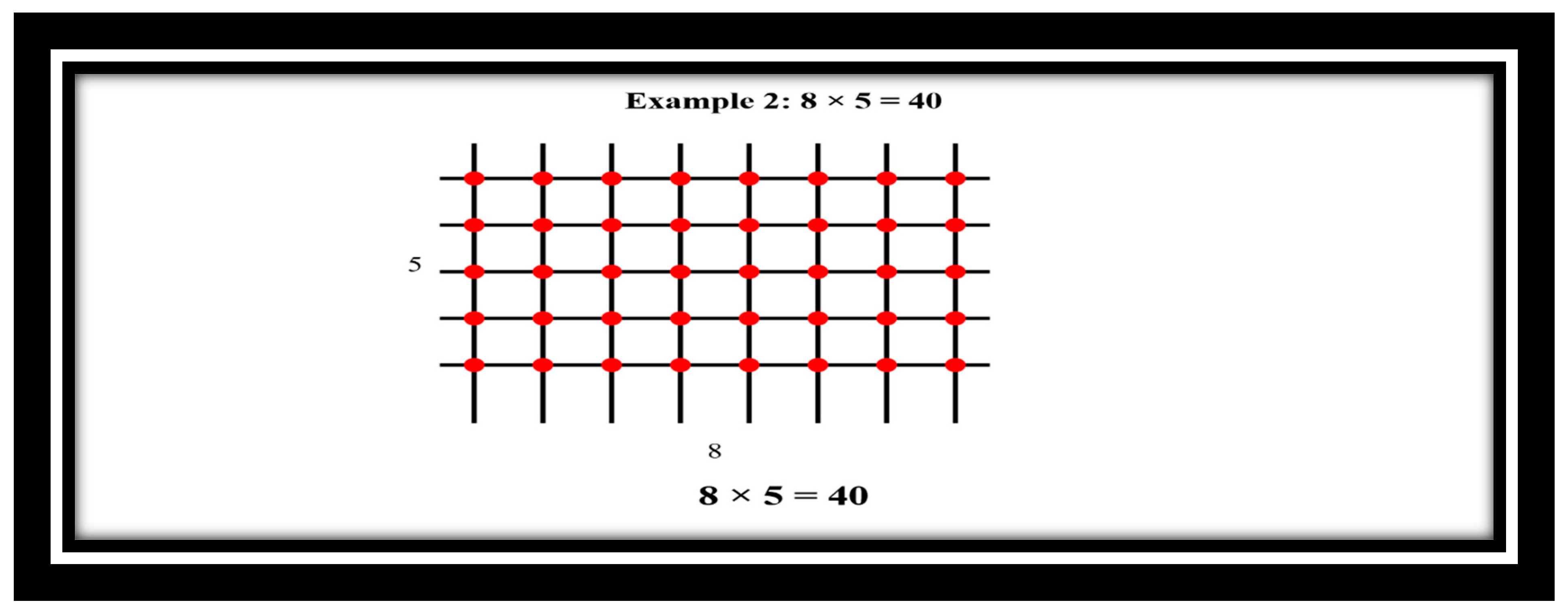
4.2.2. Example 2: 8 × 5

Building on the first example, multiplication of 8 by 5 follows the same principles but introduces a larger product (see Figure 2):

Step 1: Draw 8 vertical sticks to represent the first factor (8).

Step 2: Draw 5 horizontal sticks crossing all vertical sticks to represent the second factor (5).

Step 3: Mark each intersection point with a red dot.

Step 4: Count the total number of intersection points.

The visual representation reveals 40 intersection points, confirming that 8 × 5 = 40. This example demonstrates how the stick intersection method can efficiently represent larger products while maintaining the concrete, countable nature of the representation.

4.3. Two-Digit by Single-Digit Multiplication

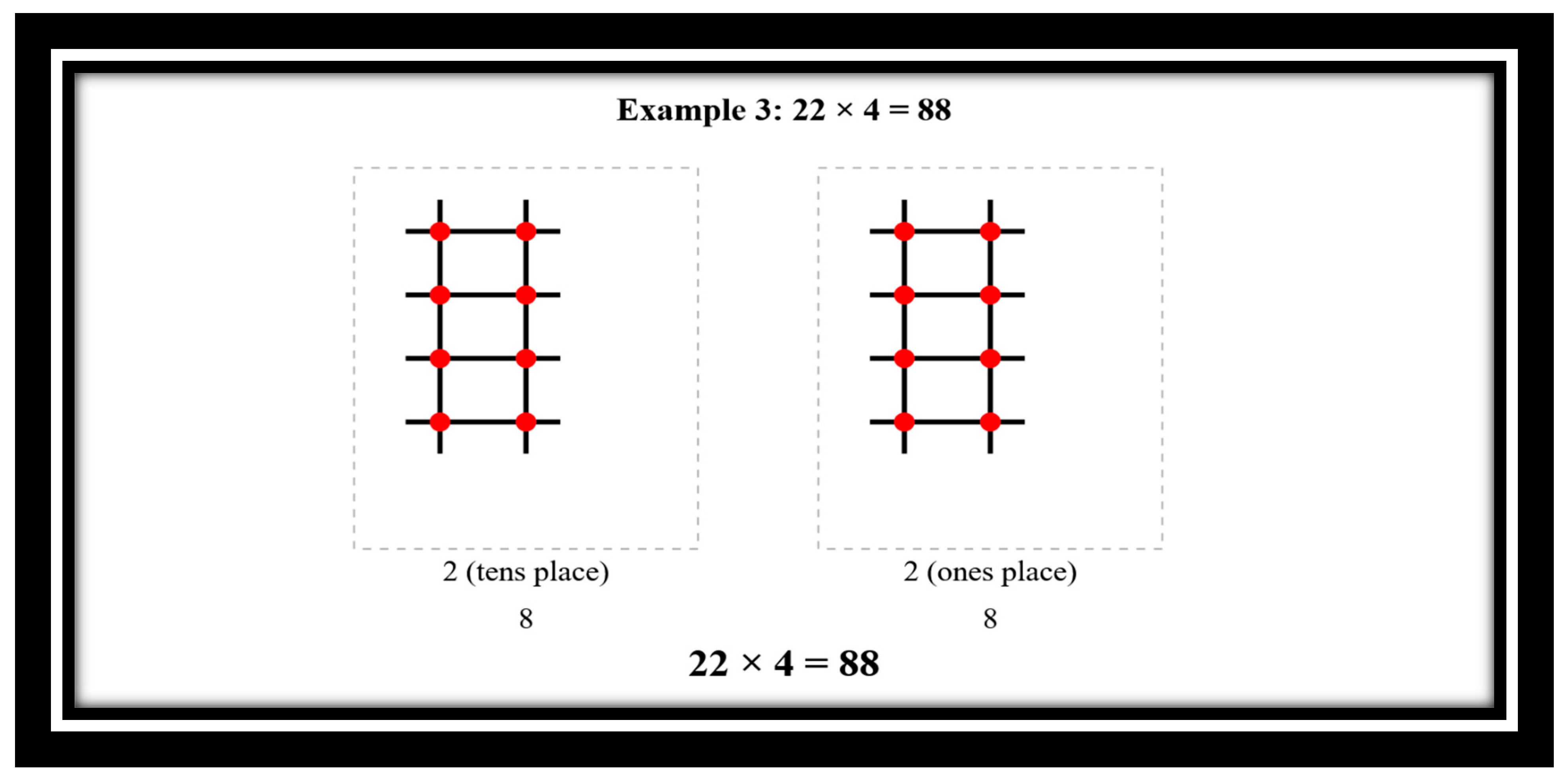
Example 3: 22 × 4

Two-digit multiplication introduces the concept of place value within the stick intersection method (see Figure 3). For 22 × 4:

Step 1: Draw 2 vertical sticks to represent the tens digit (2) in 22.

Step 2: Draw 2 vertical sticks to represent the ones digit (2) in 22, positioned separately from the first set.

Step 3: Draw 4 horizontal sticks crossing both sets of vertical sticks to represent the multiplier (4).

Step 4: Mark each intersection point with a red dot.

Step 5: Count the intersection points in each section separately.

The left section (representing 2 tens × 4) shows 8 intersection points, corresponding to 8 tens or 80. The right section (representing 2 ones × 4) shows 8 intersection points, corresponding to 8 ones. Combined, the product is 88, confirming that 22 × 4 = 88. This example demonstrates how the stick intersection method naturally incorporates place value concepts in multi-digit multiplication. Each place value is represented separately, helping learners understand how the final product is composed.

4.4. Single-Digit by Two-Digits Multiplication

Example 4: 6 × 13 (See Figure 4)

Step 1: Draw 6 vertical sticks to represent the first factor (6). These would be arranged in a vertical orientation, evenly spaced.

Step 2: Draw 13 horizontal sticks crossing all vertical sticks to represent the second factor (13). These horizontal sticks would be placed perpendicular to the vertical sticks, creating intersections.

Step 3: Mark each intersection point with a red dot for clear counting.

Step 4: Count the total number of intersection points (red dots).

With 6 vertical sticks and 13 horizontal sticks, there would be 78 intersection points in total. Learners can verify that 6 × 13 = 78 by counting all the red dots.

Figure 4. One-Digit by Two-Digits visual.

Figure 4. One-Digit by Two-Digits visual.

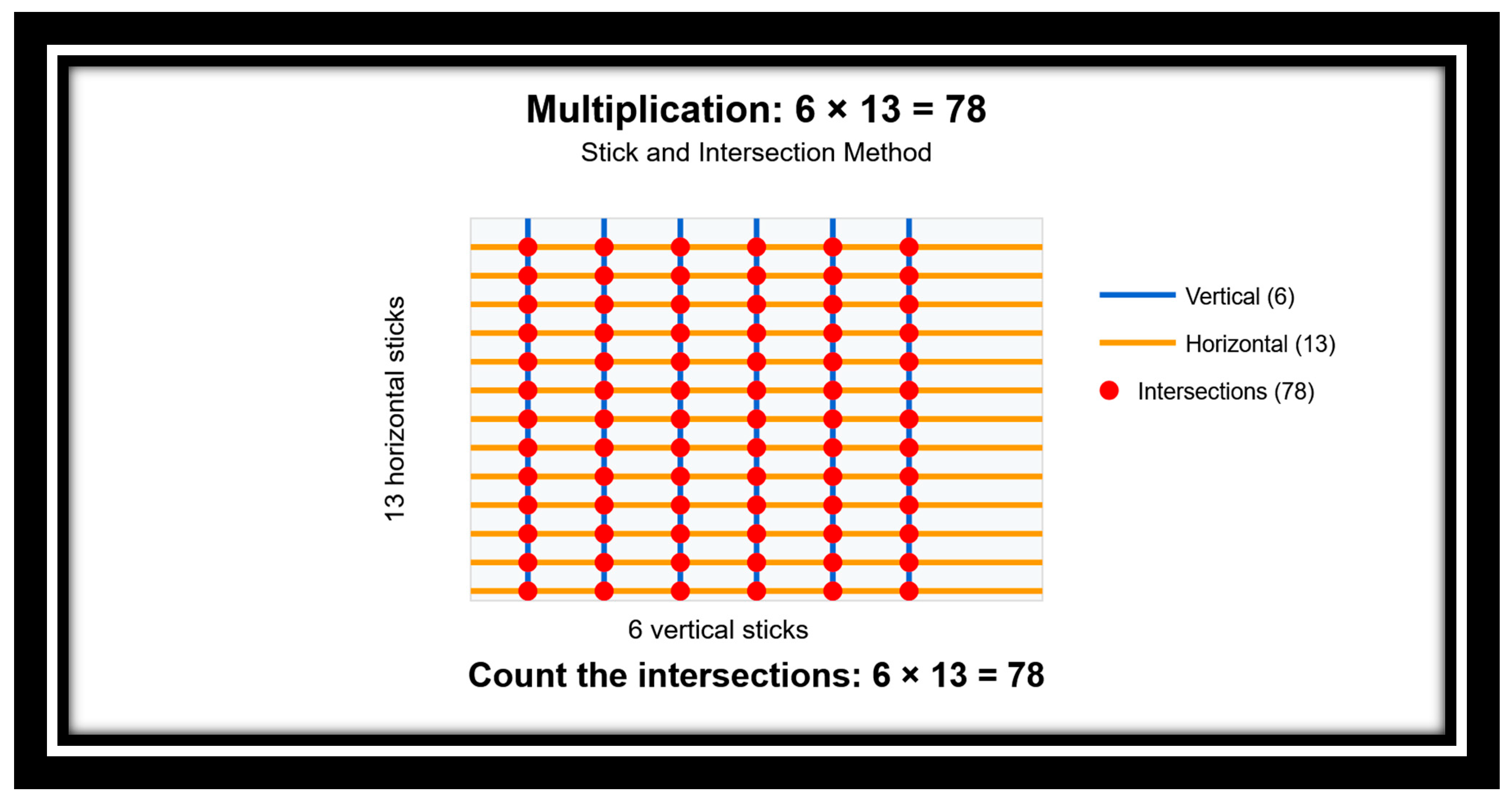
4.5. Two-Digit by Two-Digit Multiplication

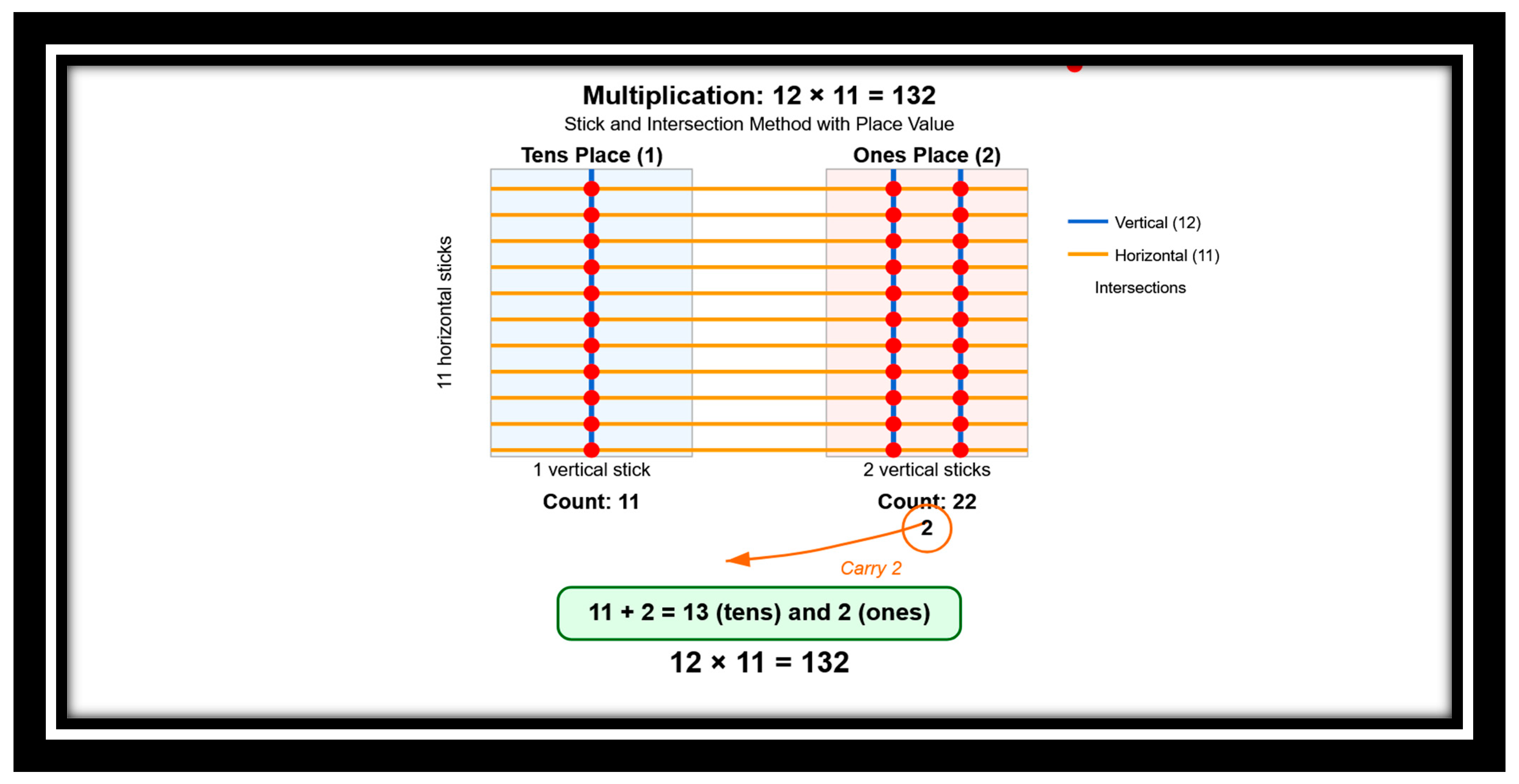
Example 5: 12 × 11

The two-digit multiplication demonstrates the scalability of the stick intersection method to more complex calculations (see Figure 5):

Step 1: Since 12 is a two-digit number, split it into place values:

• Draw 1 vertical stick on the left side to represent the tens place (1).
• Draw 2 vertical sticks on the right side to represent the ones place (2).
• These are clearly separated into two sections to show place value.

Step 2: Draw 11 horizontal sticks crossing all vertical sticks to represent the second factor (11). These horizontal sticks extend across both the tens and ones place sections.

Step 3: Mark each intersection point with a red dot for clear counting:

• In the tens place (left section): 11 intersection points (1 vertical stick × 11 horizontal sticks).
• In the ones place (right section): 22 intersection points (2 vertical sticks × 11 horizontal sticks).

Step 4: Count the intersection points by place value:

• The ones place has 22 dots: Write “2” in the ones place and carry “2” to the tens place.
• The tens place has 11 dots, plus the carried 2, giving 13: Write “13” (which becomes “1” in the hundreds place and “3” in the tens place).
• The final answer is 132 (12 × 11 = 132).

This method extends the stick intersection approach to handle multi-digit multiplication by incorporating place value concepts. It helps learners visualize how carrying works in multiplication and demonstrates why the standard algorithm produces the correct answer. The physical separation of place values makes the process more concrete and easier to understand.

5. Results

5.1. Quantitative Findings

Analysis of pre- and post-test data revealed significant improvements in students’ multiplication performance following implementation of the stick intersection method. Table 1 presents the comparison of learners’ performance on multiplication tasks before and after the intervention.

Table 1. Learners’ Performance on Multiplication Tasks Before and After Implementation of the Stick Intersection Method (n = 45).

Multiplication Type	Pre-Test Accuracy (%)	Post-Test Accuracy (%)	Improvement (%)
Single-digit	40.0	92.0	52.0
Two by one-digit	26.7	82.2	55.5
Single by two-digits	17.8	75.6	57.8
Two by two-digits	8.9	71.1	62.2
Overall	23.4	80.2	56.8

Table 1. Learners’ Performance on Multiplication Tasks Before and After Implementation of the Stick Intersection Method (n = 45).

Multiplication Type	Pre-Test Accuracy (%)	Post-Test Accuracy (%)	Improvement (%)
Single-digit	40.0	92.0	52.0
Two by one-digit	26.7	82.2	55.5
Single by two-digits	17.8	75.6	57.8
Two by two-digits	8.9	71.1	62.2
Overall	23.4	80.2	56.8

A paired t-test confirmed that these improvements were statistically significant across all multiplication types, as shown in Table 2.

Table 2. Statistical Analysis of Pre-Post Intervention Performance.

Multiplication Type	t-Value	df	p-Value	Cohen’s d
Single-digit	7.92	44	<0.001	1.18
Two by one-digit	8.45	44	<0.001	1.26
Single by two-digits	9.03	44	<0.001	1.35
Two by two-digits	9.67	44	<0.001	1.44
Overall	8.76	44	<0.001	1.31

Table 2. Statistical Analysis of Pre-Post Intervention Performance.

Multiplication Type	t-Value	df	p-Value	Cohen’s d
Single-digit	7.92	44	<0.001	1.18
Two by one-digit	8.45	44	<0.001	1.26
Single by two-digits	9.03	44	<0.001	1.35
Two by two-digits	9.67	44	<0.001	1.44
Overall	8.76	44	<0.001	1.31

The large effect sizes (Cohen’s d > 0.8) across all multiplication types indicate substantial practical significance of the intervention. Particularly notable was the improvement in learners’ ability to correctly manage place value in multi-digit multiplication, which increased from 25% to 82%.

Table 3 presents a detailed breakdown of specific multiplication skills before and after implementation of the stick intersection method.

Table 3. Assessment of Specific Multiplication Skills Pre and Post Intervention (n = 45).

Skill	Pre-Test (%)	Post-Test (%)	Improvement (%)
Basic multiplication facts recall	53.3	88.9	35.6
Understanding of multiplication concept	44.4	91.1	46.7
Place value understanding in multiplication	25.0	82.2	57.2
Application to word problems	31.1	77.8	46.7
Self-correction ability	17.8	84.4	66.6
Computation accuracy	35.6	86.7	51.1

Table 3. Assessment of Specific Multiplication Skills Pre and Post Intervention (n = 45).

Skill	Pre-Test (%)	Post-Test (%)	Improvement (%)
Basic multiplication facts recall	53.3	88.9	35.6
Understanding of multiplication concept	44.4	91.1	46.7
Place value understanding in multiplication	25.0	82.2	57.2
Application to word problems	31.1	77.8	46.7
Self-correction ability	17.8	84.4	66.6
Computation accuracy	35.6	86.7	51.1

Retention testing conducted one month after the intervention (Table 4) showed that improvements were largely maintained, suggesting that the visual method led to lasting conceptual understanding rather than temporary performance gains.

Table 4. Retention of Multiplication Skills One Month After Intervention (n = 45).

Multiplication Type	Post-Test (%)	One-Month Follow-Up (%)	Retention Rate (%)
Single-digit	92.0	88.9	96.6
Two by one-digit	82.2	77.8	94.6
Single by two-digits	75.6	71.1	94.0
Two by two-digits	71.1	66.7	93.8
Overall	80.2	76.1	94.9

Table 4. Retention of Multiplication Skills One Month After Intervention (n = 45).

Multiplication Type	Post-Test (%)	One-Month Follow-Up (%)	Retention Rate (%)
Single-digit	92.0	88.9	96.6
Two by one-digit	82.2	77.8	94.6
Single by two-digits	75.6	71.1	94.0
Two by two-digits	71.1	66.7	93.8
Overall	80.2	76.1	94.9

The intervention resulted in particularly notable improvements among learners who were previously low-performing in mathematics. Table 5 shows the differential impact across performance terciles based on pre-test scores.

Table 5. Performance Improvement by Initial Performance Level.

Initial Performance Level	Pre-Test (%)	Post-Test (%)	Improvement (%)	Effect Size (d)
Lower tercile (n = 15)	10.7	72.0	61.3	1.87
Middle tercile (n = 15)	22.7	80.0	57.3	1.42
Upper tercile (n = 15)	36.7	88.7	52.0	1.05

Table 5. Performance Improvement by Initial Performance Level.

Initial Performance Level	Pre-Test (%)	Post-Test (%)	Improvement (%)	Effect Size (d)
Lower tercile (n = 15)	10.7	72.0	61.3	1.87
Middle tercile (n = 15)	22.7	80.0	57.3	1.42
Upper tercile (n = 15)	36.7	88.7	52.0	1.05

These results demonstrate that the stick intersection method provided the greatest benefit to learners who initially struggled the most with multiplication concepts, potentially helping to narrow achievement gaps in the classroom.

5.2. Qualitative Findings

The qualitative result is organized into the following themes.

5.2.1. Student Engagement

Classroom observations revealed a noticeable increase in learners’ engagement during lessons that incorporated the stick intersection method. Throughout these sessions, learners were more eager to participate, with an average of 24 learners-initiated questions per lesson, compared to only 7 questions during lessons delivered through conventional instructional methods. This sharp rise in questioning suggested that learners were not only more attentive but also more curious and willing to explore mathematical ideas. The classroom teacher further observed that learners who typically remained passive and disengaged during traditional mathematics lessons became visibly more active and involved when using the visual stick intersection method. Their newfound willingness to ask questions, volunteer answers, and discuss mathematical ideas indicated a deeper connection to the learning process fostered by the visual, interactive approach.

5.2.2. Conceptual Understanding

Analysis of collected student work samples provided evidence of an improved conceptual understanding of multiplication following the introduction of the stick intersection method. Learners were able to move beyond rote memorization of procedures and demonstrate a deeper comprehension of the underlying concepts. When asked to explain why multiplication works, 76% of learners explicitly referenced the visual intersection model in their explanations, suggesting they had internalized the mathematical idea rather than merely performing operations mechanically. Their explanations often included thoughtful statements such as “multiplication counts how many times things cross each other” and “the dots show us the answer because each one is counted once,” reflecting an ability to connect the visual representation to the mathematical operation. These findings suggest that the stick intersection method not only helped learners solve problems but also facilitated a meaningful understanding of what multiplication represents.

5.2.3. Student Perceptions

Interviews revealed overwhelmingly positive learners’ perceptions of the stick intersection method. Thematic analysis identified several recurring themes:

• Accessibility: 87% of interviewed learners described the method as “easier to understand” than conventional approaches.
• Confidence: 73% reported increased confidence in their multiplication skills.
• Verification: 91% valued the ability to verify their answers by counting the intersection points.
• Enjoyment: 84% described mathematics as “more fun” when using the visual method.

Representative learners’ comments included:

✓

“I can see the answer now instead of just guessing.”

✓

“When I make a mistake, I can find it by counting again.”

✓

“I like that I can do it myself without memorizing.”

It is important to note that while students expressed relief from memorization pressure, the stick intersection method actually supports, rather than replaces, the development of number sense and automatic recall of basic facts. The visual method provides a foundation for understanding that facilitates more meaningful memorization when students are developmentally ready.

5.3. Challenges and Limitations

While the stick intersection method demonstrated significant benefits, several challenges emerged during implementation:

• Time efficiency: For larger numbers, drawing and counting intersections became time-consuming. Some learners developed shortcuts, such as organizing dots into groups of five or ten for easier counting.
• Transition to mental models: Some learners initially relied heavily on the physical representation and needed scaffolding to internalize the visual model for mental computation.
• Application to larger multipliers: The current study focused on single-digit and two-digit multipliers. Extending the method to multi-digit multipliers (e.g., 243 × 36) would require additional instructional strategies.
• Transition to advanced concepts: While effective for whole number multiplication, students will eventually need to transition to array models and other representations that extend to fractions, decimals, and algebraic concepts. Teachers should be mindful of scaffolding this transition to prevent over-reliance on the stick intersection method.

6. Discussion

The stick intersection method’s effectiveness must be understood in relation to other established visual multiplication strategies. Unlike lattice multiplication, which requires learning new procedural steps, or digital array visualizations, which depend on technological access, stick intersections build directly on students’ existing knowledge of drawing and counting. Compared to traditional dot arrays, the stick method provides clearer visual separation for multi-digit problems and more explicit place value representation. This positions the method not as superior to all alternatives, but as uniquely suited to resource-constrained, multilingual contexts where procedural simplicity and universal accessibility are paramount.

The stick intersection method appears to support learners’ development of conceptual understanding of multiplication in several ways. First, it provides a concrete visualization of the abstract concept of multiplication as repeated addition and as an array structure (Fuson, 2003; Steffe, 1994). By physically counting intersection points, learners’ experience multiplication as the total of combined units rather than as an arbitrary procedure. Second, the method naturally incorporates place value concepts in multi-digit multiplication. The separation of digits into distinct groups of vertical sticks helps learners understand how each digit contributes to the final product based on its place value position. This aligns with research by Hiebert and Carpenter (1992), who emphasized the importance of connecting new mathematical knowledge to existing conceptual frameworks. Third, the visual nature of the method supports learners who may struggle with language-based mathematical instruction. In the multilingual South African context, where many learners learn mathematics in a language other than their home language especially at the foundation phase, visual representations can provide access to mathematical concepts that transcend linguistic barriers (Setati & Adler, 2000).

The significant improvements observed across diverse learner populations suggest that the stick intersection method may address multiple learning styles. Visual learners benefit from the graphical representation, kinesthetic learners engage through the physical act of drawing and counting intersections, and logical-mathematical learners appreciate the systematic structure of the method. This multi-modal approach aligns with Universal Design for Learning principles, which advocate for multiple means of representation, action, and engagement (Rose & Meyer, 2002). By providing alternative pathways to understanding multiplication, the stick intersection method may help mitigate some of the educational inequities documented in South African mathematics education (Spaull & Kotze, 2015).

Perhaps the most significant contribution of the stick intersection method is its natural incorporation of place value concepts. Traditional algorithms for multi-digit multiplication often obscure place value understanding, leading learners to execute procedures without comprehending the underlying mathematical structure (Kamii & Dominick, 1998). The visual separation of place values in the stick intersection method makes explicit how each digit contributes to the final product. This aligns with recommendations from the National Council of Teachers of Mathematics (2000), which emphasizes the fundamental importance of place value understanding for success in mathematics.

The stick intersection method resonates with traditional African mathematical practices that emphasize visual and concrete representations (Mosimege & Onwu, 2004). By incorporating approaches that align with indigenous knowledge systems, mathematics instruction can become more culturally relevant and meaningful for South African students. D’Ambrosio’s (2001) concept of ethnomathematics suggests that mathematical practices are culturally embedded, and that education should acknowledge and build upon diverse mathematical traditions. The stick intersection method, with its emphasis on visual patterns and physical counting, connects to cultural practices of pattern recognition and concrete representation found in many African communities.

While this study demonstrates promising results, several limitations should be acknowledged. The research was conducted in a single school with a specific demographic profile, which limits the generalizability of the findings to other contexts. Additionally, the timeframe of implementation was relatively short, preventing the assessment of long-term retention and transfer of skills. Future research should address several questions that arise from this study. These include how the stick intersection method can be extended to multiplication involving multi-digit multipliers, the long-term impact of this visual approach on learners’ mathematical development, and how the method influences learners’ attitudes toward mathematics and their mathematical self-efficacy. Further exploration is also needed into how digital tools could enhance the implementation of the stick intersection method, particularly in resource-constrained environments. Moreover, comparative studies examining the stick intersection method alongside other visual approaches to multiplication would provide valuable insights into the relative efficacy of different instructional strategies.

Scalability and Implementation Considerations

Several factors must be considered for large-scale implementation of the stick intersection method. In typical South African classrooms with 40–50 students, the method’s reliance on individual drawing and counting may initially slow instruction pace. However, pilot observations suggest students can be trained to work in pairs, with faster students supporting peers, potentially addressing this concern. Teacher professional development would require minimal additional training—approximately 4–6 h of workshop time—making it feasible for widespread implementation. The method’s integration with existing curricula is straightforward, as it supplements rather than replaces standard algorithms. Cost implications are negligible, requiring only paper and pencils already available in most schools.

7. Conclusions

This study contributes both empirically and methodologically to mathematics education research. Empirically, it demonstrates significant improvements in elementary students’ conceptual understanding of multiplication (overall effect size d = 1.31) through a culturally responsive visual approach. Methodologically, it validates the effectiveness of resource-minimal interventions that can be implemented in challenging educational contexts. The stick intersection method offers particular promise for curriculum reform in multilingual developing contexts, where it can serve as a bridge between students’ informal mathematical knowledge and formal algorithmic procedures. The international relevance of this approach extends beyond South Africa to other developing or multilingual contexts facing similar challenges. Countries with large rural populations, limited educational resources, or significant linguistic diversity may find the stick intersection method particularly valuable. The method’s emphasis on visual representation over verbal explanation makes it adaptable across cultural and linguistic boundaries, while its minimal resource requirements ensure feasibility in under-resourced settings.

As mathematics educators continue to explore effective strategies for supporting a wide range of learners, particularly in linguistically and culturally diverse classrooms, approaches that make abstract mathematical ideas both visible and tangible must be given serious consideration. The stick intersection method stands out as one such promising strategy, offering learners a meaningful bridge between their concrete experiences and more abstract mathematical thinking. In the memorable words of a Grade 4 learner from Polokwane: “Now I can see multiplication instead of just hearing about it.” This simple yet powerful statement captures the transformative impact that visual mathematics instruction can have, particularly for students who have struggled with more traditional, text-based approaches.