Revisiting Popular Frameworks of Geometric Thinking: The Case of Mariah’s Thinking About Hierarchical Relationships and Diagrams
Abstract
1. Introduction
2. Conceptual Framework
2.1. Frameworks of Geometric Thinking
2.2. Set–Subset Diagrams vs. Compare-and-Contrast Diagrams
Kimmins and Winters define the meaning of “Venn diagram” in mathematics as follows:In language arts, the circles in a Venn diagram typically represent things that can be compared and contrasted. For example, the items could be characters in a story, philosophies of teaching, or classes of animals. In this usage, the characteristics are placed in the circles, with characteristics that both share placed in the overlapping portion of the circles and characteristics unique to one placed in the nonoverlapping portion of the appropriate circle. This serves to highlight similarities and dissimilarities of the items being compared. (pp. 486–487)
Given these two different meanings, Kimmins and Winters found the term “Venn diagram” to be a source of miscommunication between a teacher educator and a group of teachers. Likewise, we have found this term to be a source of miscommunication in our work with preservice teachers (Whitacre et al., 2025a, 2025b). To avoid miscommunication with readers of this manuscript, we use unique names to distinguish these two types of diagrams.In contrast, in the subject area of mathematics, the circles typically represent not things but their attributes or characteristics. The things are typically mathematical objects, such as numbers or geometric figures. The objects themselves, or representations of the objects, are placed in the circles instead of characteristics of the objects being placed in the circles. In this case, the Venn diagram is used to sort the objects into sets, or in other words, to classify the objects according to whether they possess the characteristics represented by the circles. (p. 487)
3. Literature Regarding Thinking and Learning About Hierarchical Geometric Relationships
3.1. Theoretical Framing in the Literature
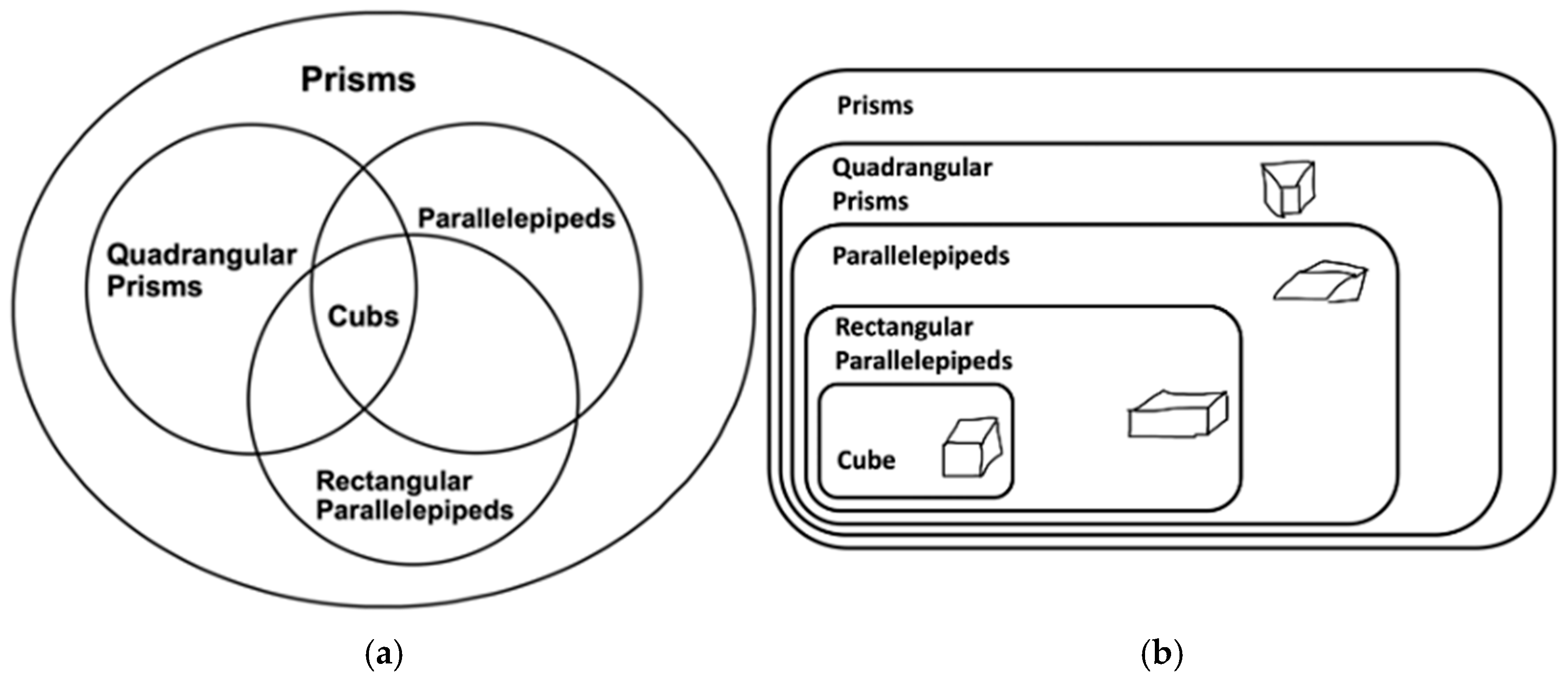
An evident theme in this literature is the conceptualization of a kind of competition between figural and conceptual aspects and the need for the conceptual to prevail or take precedence. Related to this framing is the implicit association of figural with exclusive and conceptual with inclusive.Although a predominance of the figural component, not even in this case, can we speak of pure figural thinking. In fact, the characterisation of a parallelepiped in terms of its rectangular faces requires the intervention of the conceptual component; this conceptualisation is adequate to describe the parallelepiped, as it appears, and to distinguish it from other solids, but it is inadequate to include the parallelepiped within the more general class of prisms. Because of the need of settling the disagreement, the conceptual component is mobilised and suddenly, Chiara (69) shifts to a new point of view. She attempts to characterize the parallelepiped by means of the geometrical property of parallelism of faces. (p. 230)
3.2. Findings Reported in the Literature
3.2.1. Studies of Learners’ Thinking About Quadrilaterals
3.2.2. Studies Focused on the Learning of Hierarchical Geometric Relationships
Teacher: Why is a square a special sort of rectangle?
Clearly, Russell’s response treats “rectangle” as meaning oblong rectangle, in which case a square is not a special sort of rectangle. Jones acknowledges “issues to do with… the language used for class inclusions” and the fact that Russell’s response implied an exclusive definition of rectangle (p. 79). This example highlights the need for explicit discussion of types of definitions, inclusive vs. exclusive, which was not reported in Jones’ description of the instructional sequence used in that study.Russell: Because they’ve both got right angles [at the vertices] but with a rectangle [indicating one that is not a square] one of the sides is bigger than the other. (p. 77)
3.2.3. Instructional Recommendations from the Literature
3.2.4. Questioning Assumptions Evident in the Literature
This quote clearly illustrates the assumption that learners’ claims regarding classification follow from their PFCs. It also frames the goal of instruction in terms of convincing learners to “accept” the canonical claims about hierarchical relationships.When we classify quadrilaterals, we exercise our own personal figural concepts, and the result depends on what personal figural concepts of quadrilaterals we have… For example, if one’s personal figural concept of parallelograms excludes rhombuses from the images of parallelograms, one may not accept a rhombus is a special type of parallelogram. (p. 6).
4. Materials and Methods
4.1. Setting and Participant
4.2. Instructional Sequence
4.3. Research Questions, Data Collection, and Analysis
4.3.1. Initial Analysis Focusing on Mariah’s PFCs of Quadrilaterals and Related Claims About Hierarchical Relationships
4.3.2. Analysis to Answer Emergent Questions
5. Results
- It is possible for a learner to entertain definitions and their consequences without necessarily changing their PFCs for the shapes. It is possible for a learner to reason logically about the consequences of definitions, whether or not they prefer or agree with the definitions involved.
- Communication with diagrams is nontrivial and, in fact, can be intertwined with learners’ conceptualizations of relationships. Learners’ conceptualizations of hierarchical relationships, especially those that are not simple set–subset relationships, do not necessarily follow trivially from their PFCs for the shapes involved.
5.1. Argument 1: Changes in PFCs vs. Becoming Aware of and Applying Definitions

M3.068—I: And, again, you might not have thought about trapezoids in a while, but does one of these better fit how you think about trapezoids?
M3.069—M: … I think the bottom one because usually, I wouldn’t think of like, rectangles, or parallelograms, or squares or anything as trapezoids. So, the bottom one kind of, it—it kind of only fits trapezoid, and that’s what I think when I think of a trapezoid.
5.2. Argument 2: The Role of Diagrams in Reasoning About Three-Way Relationships
5.2.1. Relevant Details from Session 1
M1.222—M: I feel like they’re also kind of the genre and the sub-genre which is very useful with the Container Diagrams [Mariah’s invented name for set–subset diagrams]. So, similar to ice cream and chocolate chip ice cream. I feel like a parallelogram is the broader and then you can get more specific using other characteristics such as equal sides for the rhombi.
5.2.2. Prelude to the Focal Episode
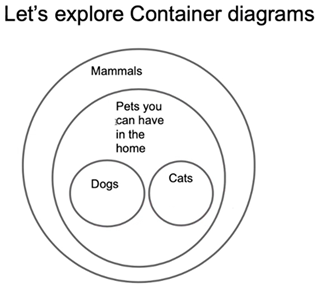
She said that if someone wanted to show another characteristic that cats and dogs have in common besides just being mammals, they could create a larger circle around Cats and Dogs and within the Mammals circle for that characteristic. Note: it is possible that at this point Mariah thought overlap could not happen within a Container diagram. However, Mariah and the instructor subsequently discussed examples of Container diagrams that did include overlap.M2.122—M: Umm, if there is overlap, I would just feel like it’s like kind of combining the Compare and Contrast diagram with the Container Diagram. So, that’s probably why I just did the other circle just to make it like all Container.
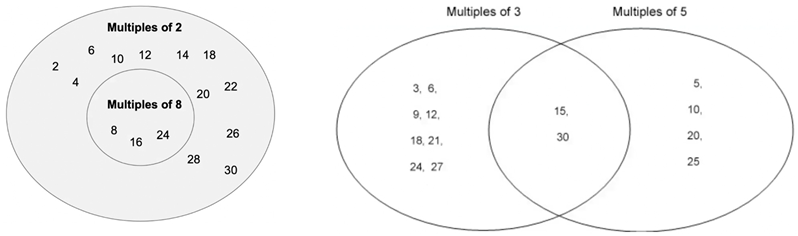
M2.128—M: So, 8, 16 and 24 are, they’re multiples of two, but they’re also multiples of eight. So rather than listing them in multiples of two and multiples of eight, they just listed them and multiples of eight since included within multiples of two.
M2.129—I: Okay, because it’s a Container?
M2.130—M: Yeah, that kind of suggests that all multiples of eight are multiples of two.
M2.133—M: Yeah, so in here, I kind of feel like it’s the same thing, just like a different layout with like a different comparison, I guess. Because multiples of 3 are like 15 and 30, which are both multiples of three, but they’re also multiples of five. So, rather than list them in both, they put them in the overlap, which means they’re both multiples of three and multiples of five.
M2.145—M: Because in the other one, not all multiples of three are multiples of five and not all multiples of five are multiples of three. So, they couldn’t really be included within each other. So, they kind of have to put them where there’s overlap.
M2.167—M: Like list out some things? So, red like, an apple’s a red. I mean apple is red. Like a red crayon is red, or yeah, and then like vehicles, and if you want to be like, specific, but like, we can put like, say me put like a school bus and overlap could be like a fire truck because it’s a red and it is a vehicle.
M2.2.18—M: Mint chocolate chip. It won’t fit, but it’s supposed to go in this middle section.
M2.219–I: Yeah, okay, I get it. Alright, can you talk about the decision that you made here?
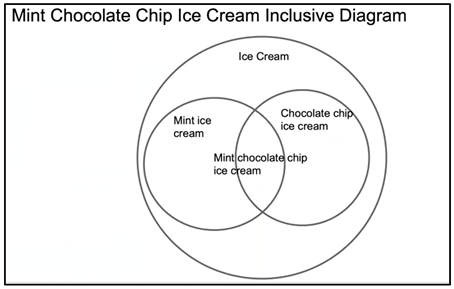
M2.220—M: Yes. So, I started off with a big circle ice cream, because all of them are considered ice cream, and then I kind of did the Overlapping Container Diagram rather than the entire Container Diagram for both because the mint chocolate chip ice cream is an overlap of mint ice cream and chocolate chip ice cream. But, like chocolate chip ice cream couldn’t really fit into the mint ice cream bubble but I don’t think really mint could fit into the chocolate chip, that’s why I didn’t really like circle, circle, circle. And then I put mint ice cream on the outside because it has its own property like mint flavored ice cream, and chocolate chip ice cream with chocolate types, and they overlap where mint chocolate chip ice cream is because it’s mint flavored ice cream with chocolate chips.
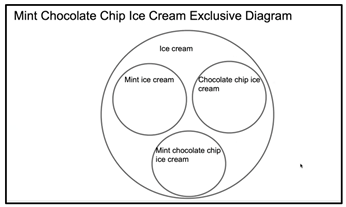
M2.236—M: Yeah, so since they’re all exclusive definitions, I didn’t really feel like you could contain any within each other, and they couldn’t really overlap. Because, like we said, like mint ice cream has to be strictly mint; it can’t have like chocolate chips. So, like there will be no overlap. And chocolate chip ice cream has to be just chocolate chip, like with vanilla; it can’t be like mint ice cream. So, they’re still all ice cream, so they’re contained within the ice cream circle, but they’re all separate subsets.
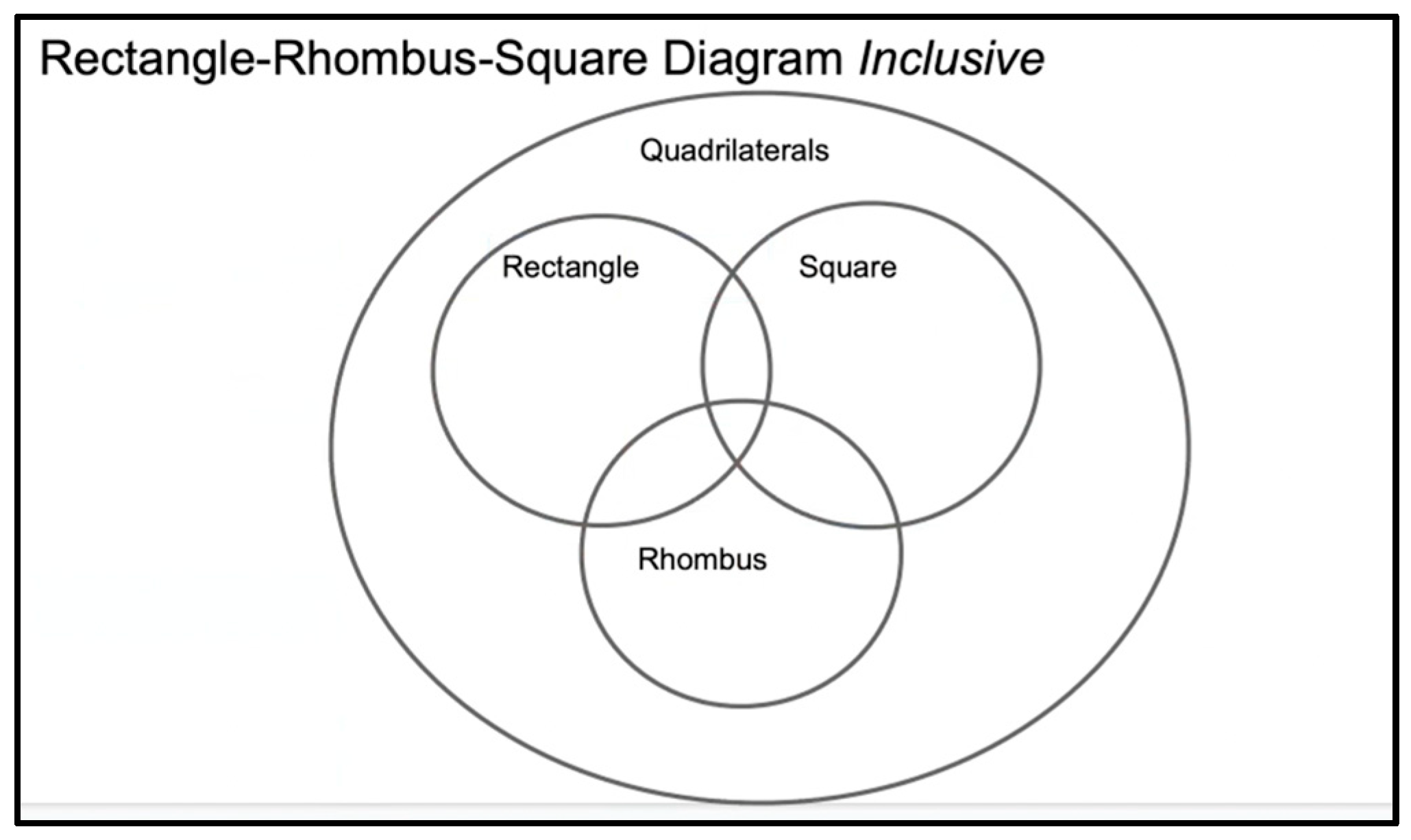
5.2.3. Focal Episode: Resolving the Rectangle–Rhombus–Square Relationship
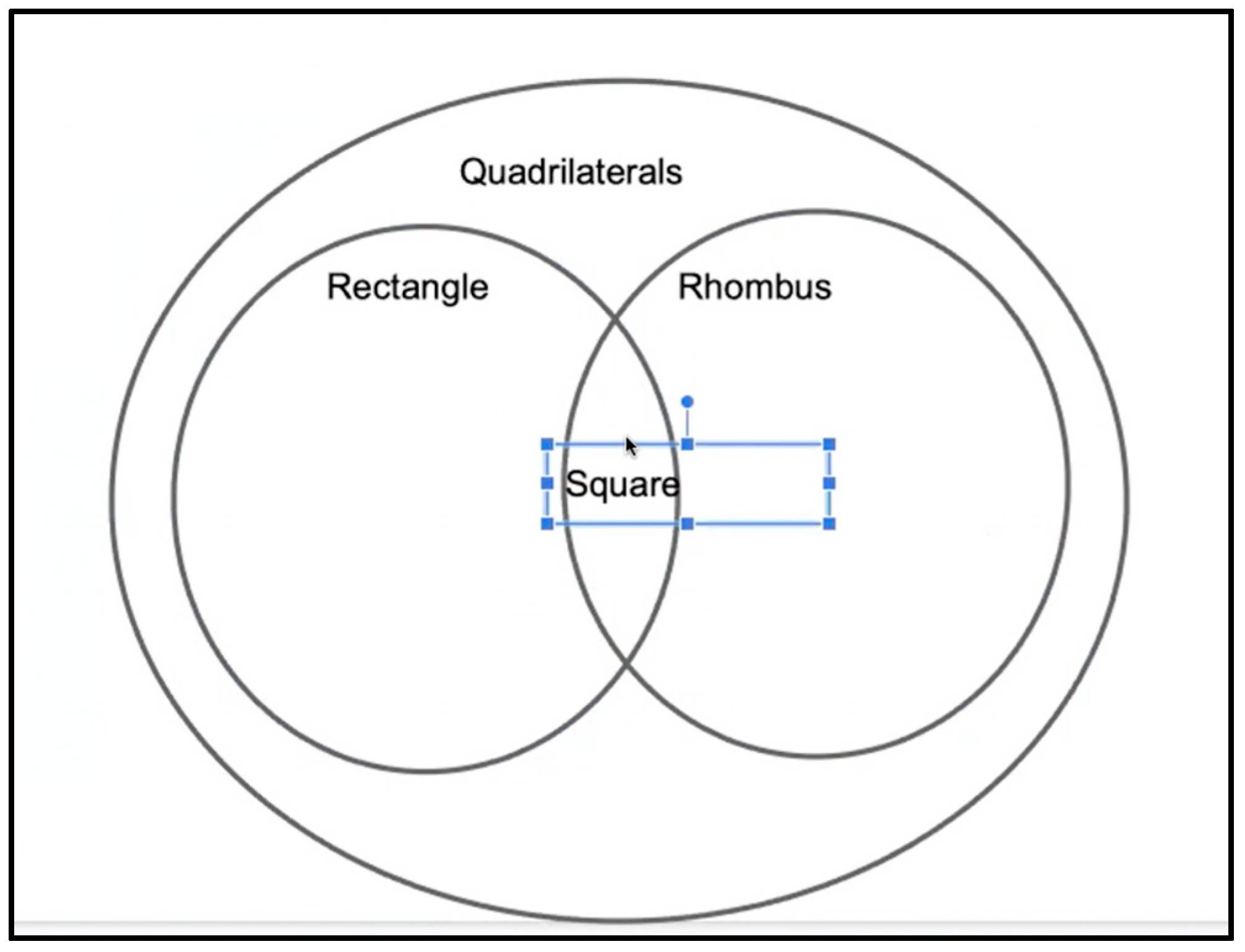
She continued,M2.265—M: So, I did quadrilaterals, the four sided shape to the top, because all of them are considered quadrilaterals and then I have a circle for rectangle and then within that circle, rectangle, I have squares, because squares are like a subset of rectangles, they have the four right angles, and they have the four sides, but they’re just have all four sides equal.
M2.266—M: And then I did rhombus at the bottom because I don’t feel like it fits within square and rectangle, but I did it kind of overlapping the section where square and rectangle both are. Because I feel like all four of them have those parallel sides. The only re—the only like area that I’m kind of like shaded in is that, umm, the square and the rhombus, but also have specific, like the four equal sides, which I guess you can kind of make the circle bigger maybe [Pause, Mariah moves some words and shapes in the diagram], and then squared out a little, a little rhombus too, where it’s like specifically overlapping and square and rectangle here. Both have well, I guess. Yeah. And then they all have two pairs of parallel sides and then square and the rhombus also share the four equal sides and so that will be in that area, which ideally there wouldn’t be the two little slivers right here. of rectangle circle.
M2.276—M: Yeah. So, here, the reason I changed it is because of this kind of area [She points to the overlapped area between Rectangle and Rhombus in the diagram], where I don’t see anything that the rectangle and rhombus just them to have in common. But they all have something in common with the square, and the rhombus and square have something in common. So that’s kind of—and I kind of want square inside the rectangle, because I feel like the square is a subset of a rectangle. So, this just makes more sense in my brain.
M2.287—I: What about in the football shaped region? Because that one’s not labeled, what would be in there?
M2.288—M: I think that would just be the four equal sides. So, it’d be kind of still in the square’s circle, but it would be also sharing with this little football overlap.
M2.289—I: But I mean, what was the name of that shape? What do those shapes look like in there?
M2.290—M: Squares and rhombuses—rhombi—and, but I feel like rectangles couldn’t be in there because it’s all the four equal sides. So, that’d just be an overlap of square and rhombi—what they have in common.
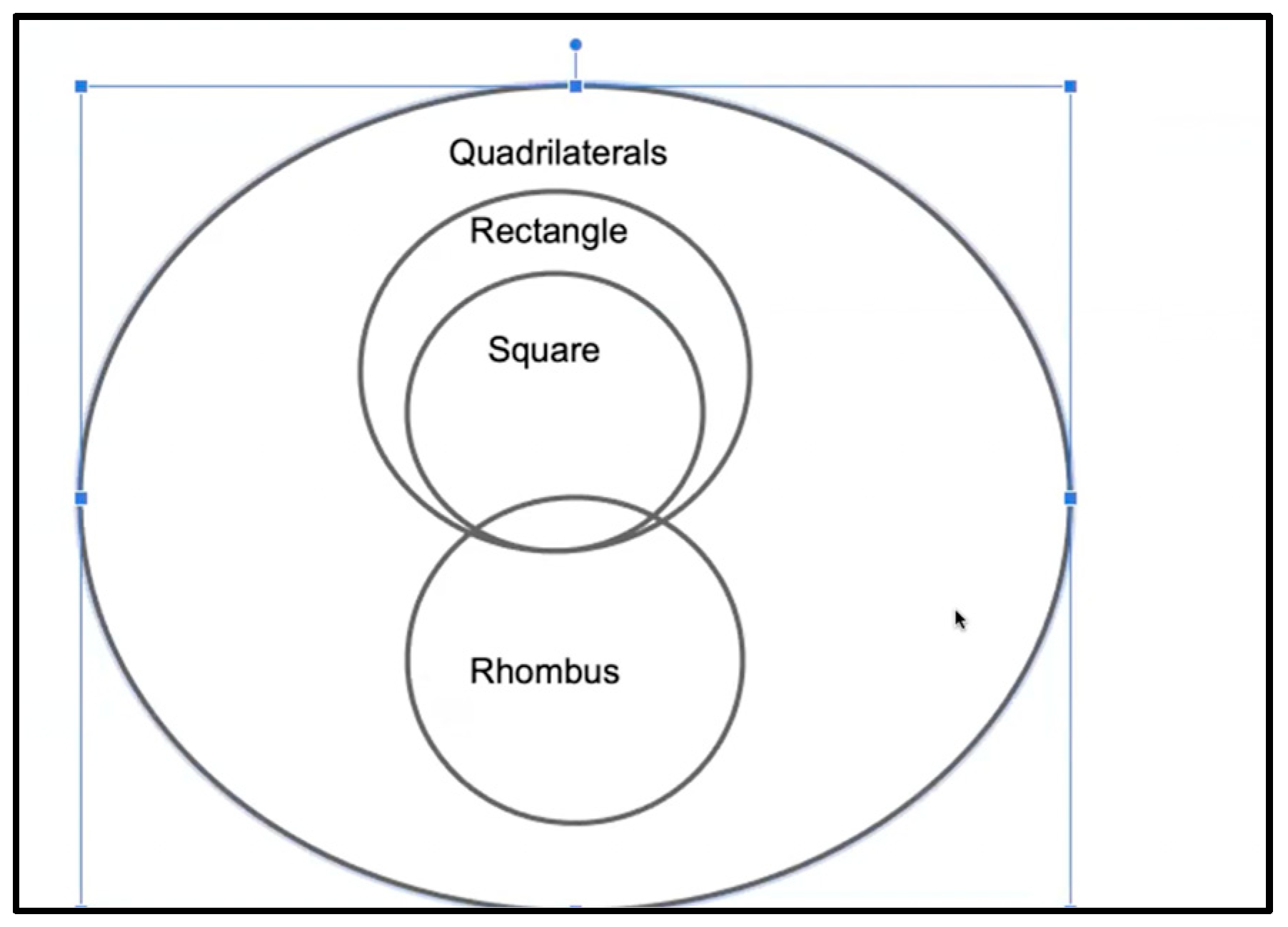
The instructor realized that they had not explicitly considered the inclusive definition of a rhombus. Official, inclusive definitions of parallelogram and rectangle had been discussed, and the instructor had said to use inclusive definitions for the task, but an inclusive definition of rhombus had not previously been written down. The instructor clarified the relevant definitions, listing them together on the slide with the task instructions:M2.294—M: Okay. Hold on. So, here I think these, like the common the commonality between them two, is that, like all sides are equal on the square and then also like equal in rhombus and of course, you could change the rhombus into square, here. But then I feel like it wouldn’t really be a rhombus anymore. It’d just be a square still.
Rectangle: Quadrilateral with four right angles
Square: Quadrilateral with four right angles and four congruent sides
Mariah subsequently applied the given definition of rhombus in her thinking about the task.Rhombus: Quadrilateral with four congruent sides
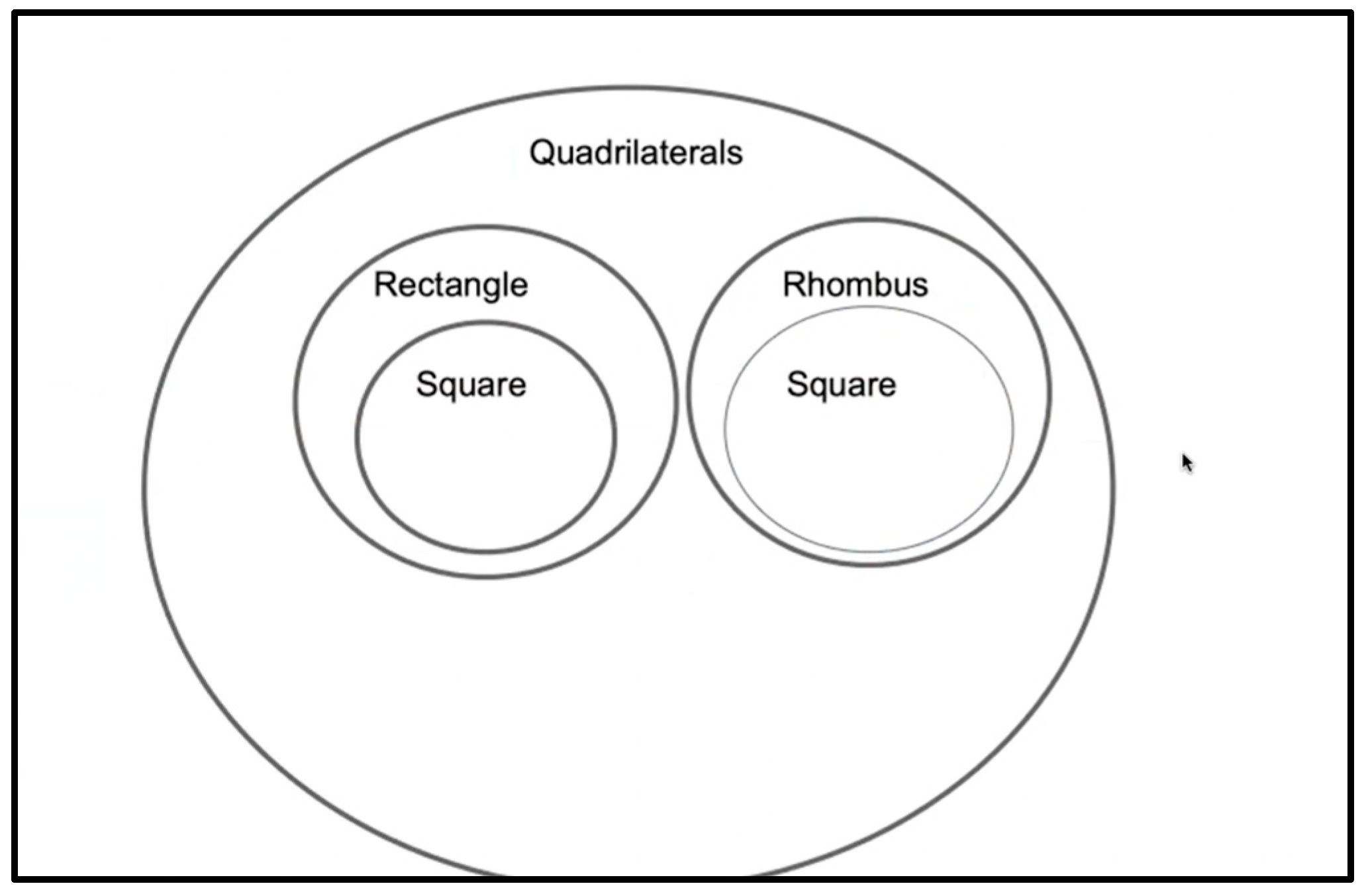
M2.311—M: I kinda feel like it can be quadrilaterals and then a rectangle, which has four sides and four right angles. And the square also has four right angles, four sides, and then it’s also congruent, so the sides are congruent. So, it would be a specific subset of rectangles.
M2.312—M: And then a rhombus is just four congruent sides. So, it’d be in the quadrilateral circle, but it’d be separate from rectangles because it doesn’t have four right angles. But the square has four congruent sides. It just has another specific thing, which is four right angles, so it can be included within a rhombus too.
M2.313—I: Okay, I see how you’re thinking about that. So, square is a special type of rectangle, and square is also a special type of rhombus.
M2.314—M: Yes.
M2.315—I: Is it okay that the squares are in two different places?
M2.316—M: I don’t really know, I guess, because I don’t really see a way to overlap it. And have it showing like this relationship where it can be like a square can be considered a rhombus. Because like if you put like the other one where it’s like this [referring back to her second version], I feel like this [her second version] doesn’t really show that the square can be considered a rhombus.
She also explained the relationship in clear if-then statements: “If the shape is a rectangle, then it has four right angles. If the first shape is a rhombus, then it has four congruent sides. And if it has four right angles and four congruent sides, then it’s a square.” Mariah called Version 4 her “final answer.”M2.325—M: So, the quadrilateral is four-sided shapes: rectangle and rhombi are both four-sided shapes. The rectangle has its own properties, which is four right angles. The rhombus has its own property, which is the four congruent sides. And the square is kind of where they overlap, with a square has both four right angles and four congruent sides.
5.2.4. Unpacking the Focal Episode
- Why did Mariah use overlap in her first two rectangle–rhombus–square diagrams to represent commonalities as in a compare-and-contrast diagram when she was asked to produce a Container Diagram instead? In particular, being that Mariah quickly abandoned Version 1 in favor of Version 2, why did she create a hybrid diagram in Version 2?
- Why had Mariah been able to interpret overlap in examples of Container Diagrams in previous tasks?
- Why had Mariah been able to create an Overlapping Container Diagram for ice cream flavors without any apparent difficulty?
- What specific challenges did Mariah overcome to produce her final version of the rectangle–rhombus–square diagram?
5.2.5. Summary of Argument 2
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | These are also sometimes called “Euler diagrams” (e.g., Hub & Dawkins, 2018). In fact, our usage of “set–subset diagram” is more consistent with the diagrams of Euler than those of Venn (1880). However, that point is neither here nor there. Our concern lies not in the history of diagrams but in facilitating clear communication with both preservice teachers and readers of our work in the world today. |
| 2 | In fact, doing so is what the informal deduction level is all about—not accepting certain definitions and the relationships that follow from them, but reasoning logically based on definitions (Crowley, 1987; Van Hiele, 2004). The case in point is being able to entertain both definitions of trapezoid and reason logically about the consequences of the choice of definition, not to accept the inclusive definition and reject the exclusive definition. |
References
- Abdullah, A. H., & Shin, B. (2019). A comparative study of quadrilaterals topic content in mathematics textbooks between Malaysia and South Korea. Journal on Mathematics Education, 10(3), 315–340. [Google Scholar] [CrossRef]
- Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5), 389–407. [Google Scholar] [CrossRef]
- Brunheira, L., & da Ponte, J. P. (2019). From the classification of quadrilaterals to the classification of prisms: An experiment with prospective teachers. Journal of Mathematical Behavior, 53, 65–80. [Google Scholar] [CrossRef]
- Bulut, N., & Bulut, M. (2012). Development of pre-service elementary mathematics teachers’ geometric thinking levels through an undergraduate geometry course. Procedia—Social and Behavioral Sciences, 46, 760–763. [Google Scholar] [CrossRef]
- Clements, D. H., & Sarama, J. (2014). Learning and teaching early math: The learning trajectories approach (2nd ed.). Routledge. [Google Scholar]
- Common Core Standards Writing Team. (2013). Progressions for the common core state standards in mathematics (draft). Grades K–5, geometry. Institute for Mathematics and Education, University of Arizona. Available online: https://achievethecore.org/content/upload/ccss_progression_gk6_2014_12_27.pdf (accessed on 24 May 2025).
- Crowley, M. L. (1987). The Van Hiele model of the development of geometric thought. In M. M. Lindquist (Ed.), Learning and teaching geometry, K–12, 1987 Yearbook of the national council of teachers of mathematics. NCTM. [Google Scholar]
- Decano, R. S. (2017). Cognitive development of college students and their achievement in geometry: An evaluation using Piaget’s theory and Van Hiele’s levels of thinking. American Journal of Applied Sciences, 14(9), 899–911. [Google Scholar] [CrossRef][Green Version]
- Department of Basic Education. (2011). Curriculum and assessment policy statement, grades 7–9: Mathematics. Available online: https://www.education.gov.za/Portals/0/CD/National%20Curriculum%20Statements%20and%20Vocational/CAPS%20SP%20%20MATHEMATICS%20GR%207-9.pdf?ver=2015-01-27-160141-373 (accessed on 24 May 2025).[Green Version]
- de Villiers, M. (1994). The role and function of a hierarchical classification of quadrilaterals. For the Learning of Mathematics, 14(1), 11–18. [Google Scholar][Green Version]
- Fischbein, E. (1993). The theory of figural concepts. Educational Studies in Mathematics, 24, 139–162. [Google Scholar] [CrossRef]
- Florida Department of Education. (2023). Florida’s B.E.S.T. standards for mathematics. Available online: https://cpalmsmediaprod.blob.core.windows.net/uploads/docs/standards/best/ma/mathbeststandardsfinal.pdf (accessed on 24 May 2025).
- Fogarty, R. (2007). Literacy matters: Strategies every teacher can use (2nd ed.). Corwin Press. [Google Scholar]
- Fujita, T. (2008). Learners’ understanding of the hierarchical classification of quadrilaterals. Proceedings of the British Society for Research into Learning Mathematics, 28(2), 31–36. [Google Scholar]
- Fujita, T. (2012). Learners’ level of understanding of the inclusion relations of quadrilaterals and prototype phenomenon. Journal of Mathematical Behavior, 31, 60–72. [Google Scholar] [CrossRef]
- Fujita, T., & Jones, K. (2007). Learners’ understanding of the definitions and hierarchical classification of quadrilaterals: Towards a theoretical framing. Research in Mathematics Education, 9(1–2), 3–20. [Google Scholar] [CrossRef]
- Hershkowitz, R. (1989). Visualization in geometry—Two sides of the coin. Focus on Learning Problems in Mathematics, 11(1), 61–76. [Google Scholar]
- Houghton Mifflin Harcourt. (2010). Go math! Grade 3 common core edition: Standards practice book for home or school. Houghton Mifflin Harcourt. [Google Scholar]
- Hub, A., & Dawkins, P. C. (2018). On the construction of set-based meanings for the truth of mathematical conditionals. The Journal of Mathematical Behavior, 50, 90–102. [Google Scholar] [CrossRef]
- Jones, K. (2000). Providing a foundation for deductive reasoning: Students’ interpretations when using dynamic geometry software and their evolving mathematical explanations. Educational Studies in Mathematics, 44, 55–85. [Google Scholar] [CrossRef]
- Kimmins, D. L., & Winters, J. J. (2015). Caution: Venn diagrams ahead! Teaching Children Mathematics, 21(8), 484–493. [Google Scholar] [CrossRef]
- Mariotti, M. A., & Fischbein, E. (1997). Defining in classroom activities. Educational Studies in Mathematics, 34(3), 219–248. [Google Scholar] [CrossRef]
- Mensah, N. B., Odro, E. M., & Williams, D. A. (2023). Examination of 9th graders’ levels of geometric thinking. International Journal of Research in Education and Science, 9(3), 688–703. [Google Scholar] [CrossRef]
- Ministry of Education. (2024). New Zealand curriculum: Mathematics and statistics. Available online: https://newzealandcurriculum.tahurangi.education.govt.nz/getting-in-shape---level-3-4-geometry/5637200362.p (accessed on 24 May 2025).
- National Governors Association Center for Best Practices & Council of Chief State School Officers. (2010). Common core state standards for mathematics. Available online: https://learning.ccsso.org/wp-content/uploads/2022/11/ADA-Compliant-Math-Standards.pdf (accessed on 24 May 2025).
- Naufal, M. A., Abdullah, A. H., Osman, S., Abu, M. S., & Ihsan, H. (2021). Reviewing the Van Hiele Model and the application of metacognition on geometric thinking. International Journal of Evaluation and Research in Education, 10(2), 597–605. [Google Scholar] [CrossRef]
- NCTM. (2000). Principles and standards for school mathematics. NCTM. [Google Scholar]
- Nelson, D. (2008). The Penguin dictionary of mathematics. Penguin Books. [Google Scholar]
- Ontario Ministry of Education. (2020). The Ontario curriculum, grades 1–8: Mathematics. Available online: https://www.dcp.edu.gov.on.ca/en/curriculum/elementary-mathematics/grades/g6-math/strand-e/e1 (accessed on 24 May 2025).
- Pickreign, J. (2007). Rectangles and rhombi: How well do preservice teachers know them? Issues in the Undergraduate Mathematics Preparation of School Teachers, 1, 1–7. [Google Scholar]
- Steffe, L. P., & Thompson, P. W. (2000). Teaching experiment methodology: Underlying principles and essential elements. In A. E. Kelly, & R. A. Lesh (Eds.), Handbook of research design in mathematics and science education (pp. 267–306). Routledge. [Google Scholar]
- Tall, D., & Vinner, S. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational Studies in Mathematics, 12, 151–169. [Google Scholar] [CrossRef]
- van de Walle, J. A., Karp, K. S., & Bay-Williams, J. M. (2019). Elementary and middle school mathematics: Teaching developmentally (10th ed.). Pearson Education, Inc. [Google Scholar]
- Van Hiele, P. M. (2004). The child’s thought and geometry. In T. P. Carpenter, J. A. Dossey, & J. L. Koehler (Eds.), Classics in mathematics education research (pp. 60–68). National Council of Teachers of Mathematics. [Google Scholar]
- Venn, J. (1880). On the diagrammatic and mechanical representation of propositions and reasonings. Philosophical Magazine, 10(59), 1–18. [Google Scholar] [CrossRef]
- Whitacre, I., Kamaldar, A., & Caro-Rora, D. (2025a). Investigating preservice elementary teachers’ reasoning about set–subset, compare-and-contrast, and hybrid diagrams [Manuscript submitted for publication]. School of Teacher Education, Florida State University. [Google Scholar]
- Whitacre, I., Kamaldar, A., & Caro-Rora, D. (2025b). Supporting and documenting advances in preservice elementary teachers’ hierarchical geometric discourse [Manuscript submitted for publication]. School of Teacher Education, Florida State University. [Google Scholar]
- Wolfram. (2025). Wolfram MathWorld. Available online: https://mathworld.wolfram.com/ (accessed on 24 May 2025).
- Zembat, I. O., & Gürhan, S. (2023). Fostering a student’s abstraction of the relationship between parallelogram and trapezoid within quadrilateral hierarchy. Investigations in Mathematics Learning, 15(4), 241–265. [Google Scholar] [CrossRef]
- Zhou, L., Liu, J., & Lo, J.-J. (2022). A comparison of U.S. and Chinese geometry standards through the lens of van Hiele levels. International Journal of Education in Mathematics, Science, and Technology, 10(1), 38–56. [Google Scholar] [CrossRef]

| Quadrilateral | Mariah’s Personal Figural Concept | Evidence from Session 1 Transcripts |
|---|---|---|
| Square | A square has four equal sides and four right angles. It is not allowed to be oblong. | M1.076—M: Ok, the rectangle has four sides, four right angles, but that, the square is more specific to where the four sides are equal. |
| Rectangle | A rectangle has four sides and four right angles. It is allowed to be equilateral. | M1.080—M: Oh, parallel. Yeah. And there are two sides are parallel. And four right angles. M1.180—M: Yes. So, like what the rectangle, we can change it, and we can change the sides into a figure that’s square. So, like the definition of the rectangle, it’s just more broad, which allows for more room to be, but the square is specific to where it cannot be changed into a rectangle. |
| Parallelogram | A parallelogram has four sides, two pairs of parallel sides, two acute angles, and two obtuse angles. It is allowed to have sides of equal length. It is not allowed to have right angles. | M1.207—M: …The parallelogram can have two different length sides. But it’s still like the two sides are parallel and they’re kind of at an angle also. like those shapes you can kinda– M1.218—M: For both of them [referring to parallelogram and rhombus], I saw that they have like two acute angles, two obtuse angles, they both have four sides, and they both have two pairs of parallel sides like the top and the bottom in parallel, the two sides are parallel. M1.219—M: …like for the parallelogram, like the two, the top and the bottom are equal, and the sides are equal, but they’re not necessarily the same length. |
| Rhombus | A rhombus has four equal sides, two pairs of parallel sides, two acute angles, and two obtuse angles. It is not allowed to have right angles. | M1.207—M: Yeah, so I feel like the rhombus is kind of like the square where it has four equal sides. M1.218—M: For both of them [referring to parallelogram and rhombus], I saw that they have like two acute angles, two obtuse angles, they both have four sides, and they both have two pairs of parallel sides like the top and the bottom in parallel, the two sides are parallel. M1.219—M: But for the rhombus, all the sides are equal… |
| Quadrilateral Relationship | Mariah’s Explanations from Session 3 |
|---|---|
| Trapezoid–parallelogram relationship | 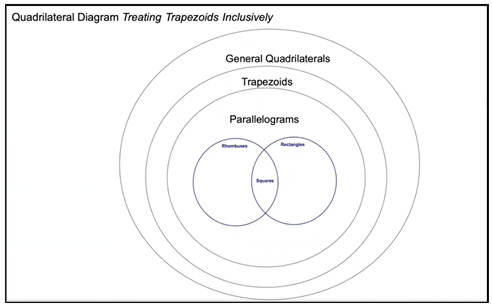 |
| M3.221—I: Okay, and how did you decide to put trapezoids there? M3.222—M: So, for our inclusive definition of trapezoids, we just said one pair of parallel sides, and we already said the circle of parallelograms all shapes included within that circle had two pairs parallel sides. So, if it’s at least one, then it would just be a broader circle. So, there’s some like trapezoids to just to one– there’s just some shapes with just one pair of parallel sides and that would be on the outside like this area [She points to the ring labeled “Trapezoids”] and then once you move onto two, you go into here [She points to the region labeled “Parallelograms”] and then it gets more specific as you go. | |
| Types of Parallelograms |  |
| M3.243—M: …the parallelogram branches off even more, and it [referring to one of the branches] has four right angles. And this one has four equal sides. So, the four right angles is the rectangle, four equal sides is a rhombus. But then there’s one category that’s included under the two and so, I kind of connected them both to the square down here, because the square has four—um, four right angles and four equal sides. |
| Diagram Type | Mariah’s Personal Figural Concept | Evidence from Session 1 Transcripts |
|---|---|---|
| “Venn diagram” | A “Venn diagram” consists of two overlapping circles and is used for comparing and contrasting. Similarities are listed in the overlapping region. Differences are listed in the non-overlapping regions. | M1.021—I: What is a Venn diagram to you? M1.022—M: Umm, usually, I feel like it’s like two overlapping circles and like, it discusses the differences on the non-overlapping parts and the similarities of two different things… |
| “Compare and Contrast Diagram” | Same as above. In response to the instructor’s request, Mariah renamed “Venn Diagram” as “Compare and Contrast Diagram.” | M1.090—I: …And because “Venn diagram” could actually mean different things to different people, can we make up a name for this kind of diagram too? M1.091—M: Umm, I feel well [Pause], I feel like we just call this compare and contrast diagram. |
| “Container Diagram” (Mariah’s invented name for set–subset diagram) | A “Container Diagram” consists of a big circle with a small circle inside it. The big circle is for the “genre”, and the small circle is for the “subgenre.” The subgenre has the characteristics of the genre, plus something more specific. | M1.072—M: So usually, like, the smaller circle is, it’s like, has the same characteristics as the bigger circle, but it’s more specific than the bigger circle. M1.088—I: Could you make up a name for it? M1.089—M: [Pause] Maybe like container diagram. M1.122—M: Yeah, so in the bigger circle, I put ice cream and I said it’s a sweet frozen desert. And then in the little circle, I put chocolate chip ice cream and I said has chocolate chips. But by putting the chocolate chip ice cream in a little circle, I mean that it’s still a part of the ice cream genre. It’s just a specific type of ice cream. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Whitacre, I.; Kamaldar, A.; Caro-Rora, D. Revisiting Popular Frameworks of Geometric Thinking: The Case of Mariah’s Thinking About Hierarchical Relationships and Diagrams. Educ. Sci. 2025, 15, 1283. https://doi.org/10.3390/educsci15101283
Whitacre I, Kamaldar A, Caro-Rora D. Revisiting Popular Frameworks of Geometric Thinking: The Case of Mariah’s Thinking About Hierarchical Relationships and Diagrams. Education Sciences. 2025; 15(10):1283. https://doi.org/10.3390/educsci15101283
Chicago/Turabian StyleWhitacre, Ian, Azar Kamaldar, and Domonique Caro-Rora. 2025. "Revisiting Popular Frameworks of Geometric Thinking: The Case of Mariah’s Thinking About Hierarchical Relationships and Diagrams" Education Sciences 15, no. 10: 1283. https://doi.org/10.3390/educsci15101283
APA StyleWhitacre, I., Kamaldar, A., & Caro-Rora, D. (2025). Revisiting Popular Frameworks of Geometric Thinking: The Case of Mariah’s Thinking About Hierarchical Relationships and Diagrams. Education Sciences, 15(10), 1283. https://doi.org/10.3390/educsci15101283






